人教版(理)高考数学《大一轮复习讲义》题库 1.2 命题与量词、基本逻辑联结词

合集下载

高考数学一轮复习第一章集合与常用逻辑用语 1.2 命题与量词、基本逻辑联结词练习题(含解析)(1

高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题（含解析）(1)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题（含解析）(1)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高考数学一轮复习第一章集合与常用逻辑用语1.2 命题与量词、基本逻辑联结词练习题（含解析）(1)的全部内容。

命题与量词、基本逻辑联结词一、选择题1．下列命题中的假命题是( )．A．∃x0∈R，lg x0＝0 B．∃x0∈R，tan x0＝1C．∀x∈R，x3＞0 D．∀x∈R,2x＞0解析对于A,当x0＝1时，lg x0＝0正确；对于B，当x0＝错误!时,tan x0＝1，正确；对于C，当x＜0时，x3＜0错误；对于D，∀x∈R,2x＞0，正确．答案C2。

已知命题p:函数f(x)＝错误!x－log错误!x在区间错误!内存在零点,命题q：存在负数x使得错误!x〉错误!x.给出下列四个命题:①p或q；②p且q；③p的否定；④q的否定．其中真命题的个数是（）A．1 B．2 C．3 D．4解析命题p为假命题,命题q也为假命题．利用真值表判断．答案B3．命题“∀x＞0，x2＋x＞0”的否定是( )．A．∃x0＞0，x20＋x0＞0 B．∃x0＞0,x20＋x0≤0C．∀x＞0，x2＋x≤0 D．∀x≤0，x2＋x＞0解析根据全称命题的否定是特称命题,可知该命题的否定是：∃x0＞0，x20＋x0≤0.答案B4．已知p：|x－a｜＜4；q：（x－2)（3－x)＞0，若非p是非q的充分不必要条件,则a的取值范围为（）．A．a＜－1或a＞6 B．a≤－1或a≥6C．－1≤a≤6 D．－1＜a＜6解析解不等式可得p：－4＋a＜x＜4＋a,q：2＜x＜3，因此非p：x≤－4＋a或x≥4＋a,非q：x≤2或x≥3，于是由非p是非q的充分不必要条件，可知2≥－4＋a且4＋a≥3，解得－1≤a≤6.答案C5．若函数f（x)＝－x e x，则下列命题正确的是（)A．∀a∈错误!,∃x∈R，f(x）〉aB．∀a∈错误!，∃x∈R，f（x)〉aC．∀x∈R，∃a∈错误!，f（x)〉aD．∀x∈R,∃a∈错误!,f(x）〉a解析f′(x）＝－e x（x＋1），由于函数f（x）在(－∞，－1)上递增,在(－1，＋∞）上递减，故f（x)max＝f(－1)＝错误!，故∀a∈错误!，∃x∈R，f（x）〉a.答案A6．若函数f(x）＝x2＋错误!(a∈R)，则下列结论正确的是( ）．A．∀a∈R,f(x)在(0，＋∞)上是增函数B．∀a∈R，f（x）在（0，＋∞）上是减函数C．∃a∈R，f（x)是偶函数D．∃a∈R，f（x)是奇函数解析对于A只有在a≤0时f(x)在（0，＋∞）上是增函数，否则不成立;对于B，如果a≤0就不成立；对于D若a＝0，则f(x）为偶函数了,因此只有C是正确的，即对于a＝0时有f（x)＝x2是一个偶函数，因此存在这样的a，使f（x）是偶函数．答案C7．已知p：∃x0∈R，mx错误!＋2≤0.q：∀x∈R,x2－2mx＋1＞0，若p∨q为假命题，则实数m 的取值范围是( ）．A．[1,＋∞）B．（－∞，－1］C．（－∞，－2］D．[－1,1]解析(直接法)∵p∨q为假命题，∴p和q都是假命题．由p：∃x0∈R，mx20＋2≤0为假，得∀x∈R,mx2＋2＞0，∴m≥0.①由q：∀x∈R,x2－2mx＋1＞0为假,得∃x0∈R，x2，0－2mx0＋1≤0，∴Δ＝(－2m)2－4≥0⇒m2≥1⇒m≤－1或m≥1。

人教a版高考数学(理)一轮课件：1.2命题与量词、基本逻辑联结词

否命题与命题的否定不是同一概念,否命题是对原命题“若 p 则 q” 既否定其条件,又否定其结论;而命题 p 的否定即非 p,只是否定命题的结论. 命题的否定与原命题的真假总是相对立的,即一真一假;而否命题与原命题的真假无必然联系.在书写命题的否定及否命题时需掌握正面叙述词和它的否定词语.如下表:
1 x 1 y
)
【答案】A 【解析】若 x2=1,则 x=± 1,排除 B; 若 x=y, x与 y不一定存在,排除 C; 若 x<y,且 x=-3,y=-2,则 x2>y2,排除 D.
2.p:2n-1(n∈Z)是奇数,q:2n+1(n∈Z)是偶数,则下列说法中正确的是( A.p 或 q 为真 C.非 p 为真【答案】A B.p 且 q 为真 D.非 q 为假
)
【解析】由题设知:p 真 q 假,故 p 或 q 为真命题.
3 3.(2012·湖北卷,2)命题“∃ x0∈∁ RQ,x0 ∈Q”的否定是( 3 A.∃ x0∉ ∁ RQ,x0 ∈Q 3 B.∃ x0∈∁ RQ,x0 ∉ Q
)
C.∀ x∉ ∁ RQ,x3∈Q
D.∀ x∈∁ RQ,x3∉ Q
第2讲
命题与量词、基本逻辑联结词
考纲展示
1.理解命题的概念. 2. 了解逻辑联结词 “或”、“且”、“非”的含义. 3. 理解全称量词和存在量词的意义. 4. 能正确地对含一个量词的命题进行否定.
考纲解读
1. 命题与量词部分在高考命题时常以选择题和填空题的形式出现, 以本讲知识作为载体综合考查函数及导数、三角、数列、向量、不等式、立体几何、解析几何等几乎所有的高中内容;以逻辑推理知识为命题背景的解答题也可能会出现. 在考查的方向上主要以命题的真假判断和基本逻辑联结词的考查为主. 2.全称量词与存在量词的考查明确提出 “ 能正确地对含有一个量词的命题进行否定 ”, 因此应该对全称命题和特称命题的否定加以足够的重视.

高考人教B版数学理大一轮复习课件1.2命题与量词、基本逻辑联结词

难点正本疑点清源
2．逻辑联结词“或”的含义
逻辑联结词中的“或”的含义，与并集概念中的“或 ”的含义相同．如 “x∈A 或 x∈B”，是指：x∈A 且 x∉B； x∉A 且 x∈B；x∈A 且 x∈B 三种情况．再如“p 真或 q 真” 是指： p 真且 q 假； p 假且 q 真； p 真且 q 真三种情况．
定而得到的命题，它既否定其条件，又否定其结论；“命题的否定”即“非 p”，只是否定命题
(2)全称命题：含有全称量词的命题． p 的结论． (3)全称命题的符号表示：命题的否定与原命题的真假总形如“对 M 中的所有 x，p(x)”的命题，用符号简记为“ ∀x∈M， p(x) ”．
是对立的，即两者中有且只有一个为真，而原命题与否命题的真假无必然联系．
题型分类·深度剖析
题型一含有逻辑联结词的命题的真假
x
－x
【例 1】已知命题 p1：函数 y＝2 －2
思维启迪
解析
答案
探究提高
在 R 上为增函数，p2：函数 y＝2x＋ 2
－x
命题 p1 是真命题，p2 是假命题，
在 R 上为减函数，则在命题 q1：故 q1 为真，q2 为假，q3 为假，q4
p1∨p2 ， q2 ： p1∧p2 ， q3 ： ( 綈 p1)∨p2 为真．和 q4：p1∧(綈 p2)中，真命题是( A．q1，q3 C．q1，q4 B．q2，q3 D．q2，q4 )
题型分类·深度剖析
题型一含有逻辑联结词的命题的真假
x
－x
【例 1】已知命题 p1：函数 y＝2 －2
思维启迪
基础知识·自主学习
要点梳理
3．存在量词与存在性命题 (1)存在量词：短语“ 有一个 ” 或“ 有些 ”或“至少有一个” 在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在

专题02 命题与量词、基本逻辑联结词(理)(解析版)

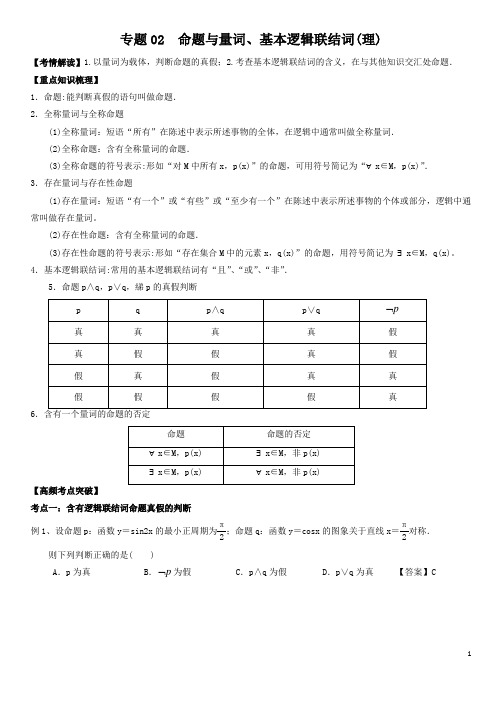
专题02 命题与量词、基本逻辑联结词(理)【考情解读】1.以量词为载体，判断命题的真假；2.考查基本逻辑联结词的含义，在与其他知识交汇处命题．【重点知识梳理】1．命题:能判断真假的语句叫做命题． 2．全称量词与全称命题(1)全称量词：短语“所有”在陈述中表示所述事物的全体，在逻辑中通常叫做全称量词． (2)全称命题：含有全称量词的命题．(3)全称命题的符号表示:形如“对M 中所有x ，p(x)”的命题，可用符号简记为“∀x ∈M ，p(x)”． 3．存在量词与存在性命题(1)存在量词：短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词。

(2)存在性命题：含有全称量词的命题．(3)存在性命题的符号表示:形如“存在集合M 中的元素x ，q(x)”的命题，用符号简记为 ∃x ∈M ，q(x)。

4．基本逻辑联结词:常用的基本逻辑联结词有“且”、“或”、“非”．5．命题p ∧q ，p ∨q ，綈p 的真假判断6【高频考点突破】考点一：含有逻辑联结词命题真假的判断例1、设命题p ：函数y ＝sin2x 的最小正周期为π2；命题q ：函数y ＝cosx 的图象关于直线x ＝π2对称．则下列判断正确的是( )A ．p 为真B ．p ⌝为假C ．p ∧q 为假D ．p ∨q 为真【答案】C【规律小结】“p ∧q ”、“p ∨q ”、“p ⌝”形式命题的真假判断步骤：(1)准确判断简单命题p 、q 的真假．(2)判断命题“p ∧q ”、“p ∨q ”、“非p ”的真假．其判断规律是： ①p ∨q ：p 、q 中有一个为真，则p ∨q 为真，即一真全真；②p ∧q ：p 、q 中有一个为假，则p ∧q 为假，即一假即假；③非p ：与p 的真假相反．【变式探究】已知命题p 1：函数y ＝2x－2－x在R 上为增函数；p 2：函数y ＝2x＋2－x在R 上为减函数，则在命题q 1：p 1∨p 2，q 2：p 1∧p 2，q 3：(非p 1)∨p 2和q 4：p 1∧(非p 2)中，真命题是( )A ．q 1，q 3B ．q 2，q 3C ．q 1，q 4D ．q 2，q 4【解析】选C.p 1为真命题，p 2为假命题，∴非p 1为假命题，非p 2为真命题．故选C.【答案】C 考点二：全称(存在性)命题及真假判断例2.判断下列命题的真假．(1)∀x ∈R ，x 2－x ＋1>12； (2)∃α，β，cos(α－β)＝cos α－cos β；(3)∀x ，y ∈N ，x －y ∈N ； (4)∃x 0，y 0∈Z ，2x 0＋y 0＝3. 【解析】(1)真命题，x 2－x ＋1＝(x －12)2＋34≥34>12. (2)真命题，如α＝π4，β＝π2符合题意．(3)假命题，如x ＝1，y ＝5，但x －y ＝－4∉N. (4)真命题，如x 0＝0，y 0＝3符合题意．【规律小结】(1)要判断全称命题是真命题，必须确定对集合中的每一个元素都成立，若是假命题，举一反例即可．(2)要判断存在性命题是真命题，只要在限定集合中，找到一个元素使得命题成立即可．【变式探究】写出下列命题的否定形式，并判断其真假．(1)p ：∀x ∈R ，x 2－x ＋14≥0； (2)s ：至少存在一个实数x ，使x 3＋1＝0.【解析】(1)綈p ：∃x ∈R ，x 2－x ＋14＜0，是假命题，因为∀x ∈R ，x 2－x ＋14＝⎝ ⎛⎭⎪⎫x －122≥0恒成立．(2)s ：∀x ∈R ，x 3＋1≠0，是假命题，因为当x ＝－1时，x 3＋1＝0. 考点三:求参数的取值范围例3、已知p ：方程x 2＋mx ＋1＝0有两个不等的负实根；q ：方程4x 2＋4(m －2)x ＋1＝0无实根，若p 或q 为真， p 且q 为假，求实数m 的取值范围．综上，m 的取值范围是m ≥3或1<m ≤2.【误区警示】在求m 的取值范围时，一是不注意端点值，二是由p ，q 的真假列关于m 的不等式不正确．【方法技巧】1.有的“p 或q ”与“p 且q ”形式的复合命题语句中，字面上未出现“或”与“且”字，此时应从语句的陈述中搞清含义，从而分清是“p 或q ”还是“p 且q ”形式．一般地，若两个命题属于同时都要满足的为“且”，属于并列的为“或”．2.逻辑联结词中，较难理解含义的是“或”，应从以下两个方面来理解概念：(1)逻辑联结词中的“或”与集合中的“或”含义的一致性．(2)结合实例，剖析生活中的“或”与逻辑联结词中的“或”之间的区别．生活中的“或”一般指“或此或彼只必具其一，但不可兼而有之”，而逻辑联结词中的“或”具有“或此或彼或兼有”三种情形．3.“非”的含义就是对“命题的否定”．课标只要求能正确地对“含有一个量词的命题”进行否定．【变式探究】设集合A ＝{ (x ，y)|(x －4)2＋y 2＝1}，B ＝{(x ，y)|(x －t)2＋(y －at ＋2)2＝1}，如果命题“∃t ∈R ，A ∩B ≠∅”是真命题，则实数a 的取值范围是________．答案：⎣⎢⎡⎦⎥⎤0，43【真题感悟】1.【2015新课标1】设命题p ：2,2nn N n ∃∈>，则p ⌝为( )A.2,2n n N n ∀∈>B.2,2n n N n ∃∈≤C.2,2n n N n ∀∈≤D.2,=2nn N n ∃∈ 【答案】C 【解析】p ⌝:2,2nn N n ∀∈≤，故选C.2.【2015浙江】命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是（）A.**,()n N f n N ∀∈∈且()f n n >B.**,()n N f n N ∀∈∈或()f n n >C.**00,()n N f n N ∃∈∈且00()f n n >D.**00,()n N f n N ∃∈∈或00()f n n > 【答案】D. 【解析】根据全称命题的否定是特称命题，可知选D.3.【2014陕西】原命题为“若z 1，z 2互为共轭复数，则|z 1|＝|z 2|”，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是( )A.真，假，真B.假，假，真C.真，真，假D.假，假，假【答案】B4.【2014重庆】已知命题p ：对任意x ∈R ，总有2x>0，q ：“x>1”是“x>2”的充分不必要条件，则下列命题为真命题的是( )A ．p ∧qB ．非p ∧非qC ．非p ∧qD ．p ∧非q 【答案】D5.【2013湖北】在一次跳伞中，甲、乙两位学员各跳一次，设命题p 是“甲降落在指定范围”， q 是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为( )A ．(⌝p)∨(⌝q)B ．p ∨(⌝q)C ．(⌝p)∧(⌝q)D ．p ∨q 【答案】A 【解析】“至少一位学员没降落在指定区域”即“甲没降落在指定区域或乙没降落在指定区域”，可知选A. 【押题专练】1．下列命题中的假命题是( )．A ．∃x 0∈R ，lgx 0＝0B ．∃x 0∈R ，tan x 0＝1C ．∀x ∈R ，x 3＞0 D ．∀x ∈R,2x＞0 【答案】C2. 已知命题p ：函数f(x)＝⎝ ⎛⎭⎪⎫12x －log 13x 在区间⎝ ⎛⎭⎪⎫0，13内存在零点，命题q ：存在负数x 使得⎝ ⎛⎭⎪⎫12x >⎝ ⎛⎭⎪⎫13x .给出下列四个命题：①p 或q ；②p 且q ；③p 的否定；④q 的否定．其中真命题的个数是( )A ．1B ．2C ．3D ．4 【解析】命题p 为假命题，命题q 也为假命题．利用真值表判断．【答案】B 3．命题“∀x ＞0，x 2＋x ＞0”的否定是( )．A.∃x 0＞0，x20＋x 0＞0B.∃x 0＞0，x20＋x 0≤0C.∀x ＞0，x 2＋x ≤0D.∀x ≤0，x 2＋x ＞0【解析】根据全称命题的否定是特称命题，可知该命题的否定是：∃x 0＞0，x20＋x 0≤0.【答案】B 4．已知p ：|x －a|＜4；q ：(x －2)(3－x)＞0，若非p 是非q 的充分不必要条件，则a 的取值范围为( )．A.a ＜－1或a ＞6B.a ≤－1或a ≥6C.－1≤a ≤6D.－1＜a ＜6【解析】解不等式可得p ：－4＋a ＜x ＜4＋a ，q ：2＜x ＜3，因此非p ：x ≤－4＋a 或x ≥4＋a ，非q ：x ≤2或x ≥3，于是由非p 是非q 的充分不必要条件，可知2≥－4＋a 且4＋a ≥3，解得－1≤a ≤6.【答案】C 5．若函数f(x)＝－xe x，则下列命题正确的是( )A.∀a ∈⎝ ⎛⎭⎪⎫－∞，1e ，∃x ∈R ，f(x)>aB.∀a ∈⎝ ⎛⎭⎪⎫1e ，＋∞，∃x ∈R ，f(x)>aC.∀x ∈R ，∃a ∈⎝ ⎛⎭⎪⎫－∞，1e ，f(x)>aD.∀x ∈R ，∃a ∈⎝ ⎛⎭⎪⎫1e ，＋∞，f(x)>a 【解析】f ′(x)＝－e x(x ＋1)，由于函数f(x)在(－∞，－1)上递增，在(－1，＋∞)上递减，故f(x)max ＝f(－1)＝1e ，故∀a ∈⎝ ⎛⎭⎪⎫－∞，1e ，∃x ∈R ，f(x)>a.【答案】A6．若函数f(x)＝x 2＋a x(a ∈R )，则下列结论正确的是( )．A.∀a ∈R ，f(x)在(0，＋∞)上是增函数B.∀a ∈R ，f(x)在(0，＋∞)上是减函数C.∃a ∈R ，f(x)是偶函数D.∃a ∈R ，f(x)是奇函数【答案】C7．已知p ：∃x 0∈R ，mx 20＋2≤0.q ：∀x ∈R ，x 2－2mx ＋1＞0，若p ∨q 为假命题，则实数m 的取值范围是( ) A ．[1，＋∞) B ．(－∞，－1] C ．(－∞，－2] D ．[－1,1] 【答案】A8．若命题“∃x 0∈R,2x20－3ax 0＋9＜0”为假命题，则实数a 的取值范围是________．【解析】因为“∃x 0∈R,2x20－3ax 0＋9＜0”为假命题，则“∀x ∈R,2x 2－3ax ＋9≥0”为真命题．因此Δ＝9a 2－4×2×9≤0，故－22≤a ≤2 2.【答案】－22≤a ≤2 29.已知命题p ：x 2＋2x －3＞0；命题q ：13－x ＞1，若非q 且p 为真，则x 的取值范围是________．【答案】(－∞，－3)∪(1,2]∪[3，＋∞)10.已知命题p ：f(x)＝1－2m x 在区间(0，＋∞)上是减函数；命题q ：不等式(x －1)2>m 的解集为R .若命题“p ∨q ”为真，命题“p ∧q ”为假，则实数m 的取值范围是________．【答案】0≤m<1211. 已知定义在R 上的函数f(x),写出命题”若对任意实数x 都有f(-x)=f(x),则f(x)为偶函数”的否定: .【解析】所给命题是全称命题,其否定为存在性命题. 【答案】若存在实数0x ,使得00()()f x f x -≠,则f(x)不是偶函数12．已知命题“∀x ∈R ，x 2－5x ＋152a ＞0”的否定为假命题，则实数a 的取值范围是________．【答案】⎝ ⎛⎭⎪⎫56，＋∞13.已知命题p ：∀x ∈[1,2]，x 2－a ≥0，命题q ：∃x 0∈R ，x20＋2ax 0＋2－a ＝0，若“p 且q ”为真命题，求实数a 的取值范围．14．写出下列命题的否定，并判断真假．(1)q ：∀x ∈R ，x 不是5x －12＝0的根；(2)r ：有些质数是奇数；(3)s ：∃x 0∈R ，|x 0|＞0.【解析】(1)非q ：∃x 0∈R ，x 0是5x －12＝0的根，真命题．(2)非r ：每一个质数都不是奇数，假命题． (3)非s ：∀x ∈R ，|x|≤0，假命题．15．设命题p ：函数f(x)＝x 3－ax －1在区间[－1,1]上单调递减；命题q ：函数y ＝ln(x 2＋ax ＋1)的值域是R . 如果命题p 或q 为真命题，p 且q 为假命题，求a 的取值范围．16.已知m ∈R ,命题p:对任意[08]x ∈,,不等式log 13(1)x +≥23m m-;命题q:对任意x ∈R ,不等式|1+sin2x-cos2x|2m ≤|cos()4x π-|恒成立. (1)若p 为真命题,求m 的取值范围; (2)若p 且q 为假,p 或q 为真,求m 的取值范围.故m 的取值范围是[1(2)⋃,+∞.。

2019届高三数学一轮复习人教B版(理科)全国通用课件 1.2命题与量词、基本逻辑联结词

(2)(2018· 深圳联考) 已知命题p：不等式ax2 ＋ax＋1>0 的解集为 R ，则实数a∈(0，4)，命题q：“x2－2x－8>0”是“x>5”的必要不充分条件，则下列命题正确的是( A.p∧q B.p∧(綈q) C.(綈p)∧(綈q) D.(綈p)∧q
解析 (1)取a＝c＝(1，0)，b＝(0，1)，显然a· b＝0，b· c＝0，但a· c＝1≠0，∴p是假命题. 又a，b，c是非零向量，
∃x∈M，q(x) ．形如“存在集合M中的元素x，q(x)”的命题，用符号简记为______________
3.基本逻辑联结词 (1)命题中的且、或、非
叫做逻辑联结词.
(2)命题 p∧q，p∨q，綈 p 的真假判断
P 真真
假假
q 真假
真假
p∧q
真假假假
p∨q 真
真真假
綈p
假
假
真
真
4.命题的否定
存在性命题；存在性命题的否定是_______ 全称命题． (1)全称命题的否定是________ 非p或非q ． (2)p或q的否定为：非p且非q；p且q的否定为：____________
[常用结论与微点提醒]
1.含有逻辑联结词的命题真假判断口诀： p∨q→见真即真，p∧q→见假即假，p与綈p→真假相反. 2.含有一个量词的命题的否定规律是“改量词，否结论”.
全称量词的命题． (2)全称命题：含有____________
(3)全称命题的符号表示： ∀x∈M，p(x) 形如“对M中的所有x，p(x)”的命题，用符号简记为“________________”．
2.存在量词与存在性命题
有些有一个至少有一个 (1)存在量词：短语“________”或“______”或“_____________”在陈述中表示所 ∃ 存在量词，并用符号“___”表示．个体或_______ 部分，逻辑中通常叫做___________ 述事物的______ 存在量词的命题． (2)存在性命题：含有______________ (3)存在性命题的符号表示：

2019届高三数学(人教A版全国通用)一轮复习讲义：§1.2命题与量词、基本逻辑联结词

§1.2命题与量词、基本逻辑联结词1．命题的概念能够判断真假的语句叫做命题．其中判断为真的语句叫真命题，判断为假的语句叫假命题．2．全称量词与全称命题(1)全称量词：短语“所有”在陈述中表示所述事物的全体，逻辑中通常叫做全称量词，并用符号“∀”表示．(2)全称命题：含有全称量词的命题．(3)全称命题的符号表示：形如“对M中的所有x，p(x)”的命题，用符号简记为“∀x∈M，p(x)”．3．存在量词与存在性命题(1)存在量词：短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词，并用符号“∃”表示．(2)存在性命题：含有存在量词的命题．(3)存在性命题的符号表示：形如“存在集合M中的元素x，q(x)”的命题，用符号简记为∃x∈M，q(x)．(4)全称命题与存在性命题的否定4.基本逻辑联结词(1)命题中的“且”、“或”、“非”叫做逻辑联结词．(2)命题真值表知识拓展1．含有逻辑联结词的命题真假的判断规律(1)p∨q：p，q中有一个为真，则p∨q为真，即有真为真．(2)p∧q：p，q中有一个为假，则p∧q为假，即有假即假．(3)綈p：与p的真假相反，即一真一假，真假相反．2．含有一个量词的命题的否定的规律是“改量词，否结论”．3．命题的否定和否命题的区别：命题“若p，则q”的否定是“若p，则綈q”，否命题是“若綈p，则綈q”．题组一思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)命题“3≥2”是真命题．(√)(2)命题p和綈p不可能都是真命题．(√)(3)若命题p，q中至少有一个是真命题，则p∨q是真命题．(√)(4)“全等三角形的面积相等”是特称命题．(×)(5)命题綈(p∧q)是假命题，则命题p，q中至少有一个是真命题．(×)题组二教材改编2．已知p：2是偶数，q：2是质数，则命题綈p，綈q，p∨q，p∧q中真命题的个数为() A．1 B．2C．3 D．4答案 B解析p和q显然都是真命题，所以綈p，綈q都是假命题，p∨q，p∧q都是真命题．3．命题“正方形都是矩形”的否定是__________________________________．答案存在一个正方形，这个正方形不是矩形题组三易错自纠4．命题“全等三角形的面积一定都相等”的否定是()A．全等三角形的面积不一定都相等B．不全等三角形的面积不一定都相等C．存在两个不全等三角形的面积相等D．存在两个全等三角形的面积不相等答案 D解析命题是省略量词的全称命题，易知选D.5．(2017·贵阳调研)下列命题中的假命题是()A．∃x∈R，lg x＝1 B．∃x∈R，sin x＝0C．∀x∈R，x3＞0 D．∀x∈R,2x＞0答案 C解析当x＝10时，lg 10＝1，则A为真命题；当x＝0时，sin 0＝0，则B为真命题；当x＜0时，x3＜0，则C为假命题；由指数函数的性质知，∀x∈R,2x＞0，则D为真命题．故选C.6．已知命题p：∀x∈R，x2－a≥0；命题p：∃x∈R，x2＋2ax＋2－a＝0.若命题“p∧q”是真命题，则实数a的取值范围为__________．答案(－∞，－2]解析由已知条件可知p和q均为真命题，由命题p为真得a≤0，由命题q为真得Δ＝4a2－4(2－a)≥0，即a≤－2或a≥1，所以a≤－2.题型一含有逻辑联结词的命题的真假判断1．(2018·济南调研)设a，b，c是非零向量．已知命题p：若a·b＝0，b·c＝0，则a·c＝0；命题q：若a∥b，b∥c，则a∥c.则下列命题中的真命题是()A．p∨q B．p∧qC．(綈p)∧(綈q) D．p∨(綈q)答案 A解析如图所示，若a ＝A 1A →，b ＝AB →，c ＝B 1B →，则a ·c ≠0，命题p 为假命题；显然命题q 为真命题，所以p ∨q 为真命题．故选A.2．(2017·山东)已知命题p ：∀x ＞0，ln(x ＋1)＞0；命题q ：若a ＞b ，则a 2＞b 2.下列命题为真命题的是( ) A ．p ∧q B ．p ∧(綈q ) C ．(綈p )∧q D ．(綈p )∧(綈q )答案 B解析 ∵x ＞0，∴x ＋1＞1，∴ln(x ＋1)＞ln 1＝0. ∴命题p 为真命题，∴綈p 为假命题．∵a ＞b ，取a ＝1，b ＝－2，而12＝1，(－2)2＝4，此时a 2＜b 2，∴命题q 为假命题，∴綈q 为真命题．∴p ∧q 为假命题，p ∧(綈q )为真命题，(綈p )∧q 为假命题，(綈p )∧(綈q )为假命题．故选B. 3．已知命题p ：若平面α⊥平面β，平面γ⊥平面β，则有平面α∥平面γ.命题q ：在空间中，对于三条不同的直线a ，b ，c ，若a ⊥b ，b ⊥c ，则a ∥c .对以上两个命题，有以下命题： ①p ∧q 为真；②p ∨q 为假；③p ∨q 为真；④(綈p )∨(綈q )为假．其中正确的是________．(填序号) 答案 ②解析命题p 是假命题，这是因为α与γ也可能相交；命题q 也是假命题，这两条直线也可能异面，相交．思维升华“p ∨q ”“p ∧q ”“綈p ”等形式命题真假的判断步骤 (1)确定命题的构成形式； (2)判断其中命题p 、q 的真假；(3)确定“p ∧q ”“p ∨q ”“綈p ”等形式命题的真假．题型二含有一个量词的命题命题点1 全称命题、存在性命题的真假典例下列四个命题：p 1：∃x ∈(0，＋∞)，⎝⎛⎭⎫12x ＜⎝⎛⎭⎫13x； p 2：∃x ∈(0,1)，12log x ＞13log x ；p 3：∀x ∈(0，＋∞)，⎝⎛⎭⎫12x ＞12log x ；p 4：∀x ∈⎝⎛⎭⎫0，13，⎝⎛⎭⎫12x ＜13log x . 其中真命题是( ) A ．p 1，p 3 B ．p 1，p 4 C ．p 2，p 3 D ．p 2，p 4答案 D解析对于p 1，当x ∈(0，＋∞)时，总有⎝⎛⎭⎫12x ＞⎝⎛⎭⎫13x成立，故p 1是假命题；对于p 2，当x ＝12时，有1＝12log 12＝13log 13＞13log 12成立，故p 2是真命题；对于p 3，结合指数函数y ＝⎝⎛⎭⎫12x与对数函数y ＝12log x 在(0，＋∞)上的图象，可以判断p 3是假命题；对于p 4，结合指数函数y ＝⎝⎛⎭⎫12x与对数函数y ＝13log x 在⎝⎛⎭⎫0，13上的图象，可以判断p 4是真命题．命题点2 含一个量词的命题的否定典例(1)命题“∀x ∈R ，⎝⎛⎭⎫13x＞0”的否定是( ) A ．∃x ∈R ，⎝⎛⎭⎫13x ＜0 B ．∀x ∈R ，⎝⎛⎭⎫13x≤0 C ．∀x ∈R ，⎝⎛⎭⎫13x ＜0 D ．∃x ∈R ，⎝⎛⎭⎫13x ≤0答案 D解析全称命题的否定是存在性命题，“>”的否定是“≤”．(2)(2017·河北五个一名校联考)命题“∃x ∈R,1＜f (x )≤2”的否定形式是( ) A ．∀x ∈R,1＜f (x )≤2 B ．∃x ∈R,1＜f (x )≤2 C ．∃x ∈R ，f (x )≤1或f (x )＞2 D ．∀x ∈R ，f (x )≤1或f (x )＞2答案 D解析存在性命题的否定是全称命题，原命题的否定形式为“∀x ∈R ，f (x )≤1或f (x )＞2”．思维升华 (1)判定全称命题“∀x ∈M ，p (x )”是真命题，需要对集合M 中的每一个元素x ，证明p (x )成立；要判断存在性命题是真命题，只要在限定集合内找到一个x ＝x 0，使p (x 0)成立． (2)对全称(存在性)命题进行否定的方法①找到命题所含的量词，没有量词的要结合命题的含义先加上量词，再改变量词； ②对原命题的结论进行否定．跟踪训练 (1)下列命题是假命题的是( ) A ．∃α，β∈R ，使cos(α＋β)＝cos α＋cos β B ．∀φ∈R ，函数f (x )＝sin(2x ＋φ)都不是偶函数C ．∃x ∈R ，使x 3＋ax 2＋bx ＋c ＝0(a ，b ，c ∈R 且为常数)D ．∀a >0，函数f (x )＝ln 2x ＋ln x －a 有零点答案 B解析取α＝π2，β＝－π4，cos(α＋β)＝cos α＋cos β，A 正确；取φ＝π2，函数f (x )＝sin ⎝⎛⎭⎫2x ＋π2＝cos2x 是偶函数，B 错误；对于三次函数y ＝f (x )＝x 3＋ax 2＋bx ＋c ，当x →－∞时，y →－∞，当x →＋∞时，y →＋∞，又f (x )在R 上为连续函数，故∃x ∈R ，使x 3＋ax 2＋bx ＋c ＝0，C 正确；当f (x )＝0时，ln 2x ＋ln x －a ＝0，则有a ＝ln 2x ＋ln x ＝⎝⎛⎭⎫ln x ＋122－14≥－14，所以∀a >0，函数f (x )＝ln 2x ＋ln x －a 有零点，D 正确，综上可知，选B.(2)(2017·福州质检)已知命题p ：“∃x ∈R ，e x －x －1≤0”，则綈p 为( ) A ．∃x ∈R ，e x －x －1≥0 B ．∃x ∈R ，e x －x －1>0 C ．∀x ∈R ，e x －x －1>0 D ．∀x ∈R ，e x －x －1≥0 答案 C解析根据全称命题与存在性命题的否定关系，可得綈p 为“∀x ∈R ，e x －x －1>0”，故选C. 题型三含参命题中参数的取值范围典例(1)已知命题p ：关于x 的方程x 2－ax ＋4＝0有实根；命题q ：关于x 的函数y ＝2x 2＋ax ＋4在[3，＋∞)上是增函数，若p ∧q 是真命题，则实数a 的取值范围是________________．答案 [－12，－4]∪[4，＋∞)解析若命题p 是真命题，则Δ＝a 2－16≥0，即a ≤－4或a ≥4；若命题q 是真命题，则－a4≤3，即a ≥－12.∵p ∧q 是真命题，∴p ，q 均为真， ∴a 的取值范围是[－12，－4]∪[4，＋∞)．(2)已知f (x )＝ln(x 2＋1)，g (x )＝⎝⎛⎭⎫12x－m ，若对∀x 1∈[0,3]，∃x 2∈[1,2]，使得f (x 1)≥g (x 2)，则实数m 的取值范围是________________．答案 ⎣⎡⎭⎫14，＋∞ 解析当x ∈[0,3]时，f (x )min ＝f (0)＝0，当x ∈[1,2]时， g (x )min ＝g (2)＝14－m ，由f (x )min ≥g (x )min ，得0≥14－m ，所以m ≥14.引申探究本例(2)中，若将“∃x 2∈[1,2]”改为“∀x 2∈[1,2]”，其他条件不变，则实数m 的取值范围是________________．答案 ⎣⎡⎭⎫12，＋∞ 解析当x ∈[1,2]时，g (x )max ＝g (1)＝12－m ，由f (x )min ≥g (x )max ，得0≥12－m ，∴m ≥12.思维升华 (1)已知含逻辑联结词的命题的真假，可根据每个命题的真假，利用集合的运算求解参数的取值范围．(2)对于含量词的命题中求参数的取值范围的问题，可根据命题的含义，利用函数值域(或最值)解决．跟踪训练 (1)已知命题“∃x ∈R ，使2x 2＋(a －1)x ＋12≤0”是假命题，则实数a 的取值范围是( )A ．(－∞，－1)B ．(－1,3)C ．(－3，＋∞)D ．(－3,1)答案 B解析原命题的否定为∀x ∈R,2x 2＋(a －1)x ＋12＞0，由题意知，其为真命题，即Δ＝(a －1)2－4×2×12＜0，则－2＜a －1＜2，即－1＜a ＜3.(2)(2017·洛阳模拟)已知p ：∀x ∈⎣⎡⎦⎤14，12，2x <m (x 2＋1)，q ：函数f (x )＝4x ＋2x ＋1＋m －1存在零点，若“p 且q ”为真命题，则实数m 的取值范围是__________．答案 ⎝⎛⎭⎫45，1解析由2x <m (x 2＋1)，可得m >2x x 2＋1，又x ∈⎣⎡⎦⎤14，12时，⎝⎛⎭⎫2x x 2＋1max ＝45，故当p 为真时，m >45；函数f (x )＝4x ＋2x ＋1＋m －1＝(2x ＋1)2＋m －2，令f (x )＝0，得2x ＝2－m －1，若f (x )存在零点，则2－m －1>0，解得m <1，故当q 为真时，m <1.若“p 且q ”为真命题，则实数m 的取值范围是⎝⎛⎭⎫45，1.常用逻辑用语考点分析有关命题及其真假判断或求参数的取值范围、量词等问题几乎在每年高考中都会出现，多与函数、数列、立体几何、解析几何等知识相结合，难度中等偏下．解决这类问题应熟练把握各类知识的内在联系．一、命题的真假判断典例1 (1)(2017·江西红色七校联考)已知函数f (x )＝⎩⎪⎨⎪⎧3x，x ＜0，m －x 2，x ≥0，给出下列两个命题：命题p ：∃m ∈(－∞，0)，方程f (x )＝0有解，命题q ：若m ＝19，则f (f (－1))＝0，则下列命题为真命题的是( ) A ．p ∧q B ．(綈p )∧q C ．p ∧(綈q )D ．(綈p )∧(綈q )(2)(2018届全国名校大联考)已知命题p ：∀x ∈R,3x <5x ；命题q ：∃x ∈R ，x 3＝1－x 2，则下列命题中为真命题的是( ) A ．p ∧q B ．(綈p )∧q C ．p ∧(綈q )D ．(綈p )∧(綈q )解析 (1)因为3x ＞0，当m ＜0时，m －x 2＜0，所以命题p 为假命题；当m ＝19时，因为f (－1)＝3－1＝13，所以f (f (－1))＝f ⎝⎛⎭⎫13＝19－⎝⎛⎭⎫132＝0，所以命题q 为真命题，逐项检验可知，只有(綈p )∧q 为真命题，故选B. (2)若x ＝0，则30＝50＝1，∴p 是假命题， ∵方程x 3＝1－x 2有解，∴q 是真命题， ∴(綈p )∧q 是真命题．答案 (1)B (2)B 二、求参数的取值范围典例2 (1)已知命题p ：∀x ∈[0,1]，a ≥e x ，命题q ：∃x ∈R ，x 2＋4x ＋a ＝0，若命题“p ∧q ”是真命题，则实数a 的取值范围是__________．(2)已知函数f (x )＝x ＋4x ，g (x )＝2x ＋a ，若∀x 1∈⎣⎡⎦⎤12，3，∃x 2∈[2,3]使得f (x 1)≥g (x 2)，则实数a 的取值范围是________．解析 (1)命题“p ∧q ”是真命题，p 和q 均是真命题．当p 是真命题时，a ≥(e x )max ＝e ；当q 为真命题时，Δ＝16－4a ≥0，a ≤4，所以a ∈[e,4]． (2)∵x ∈⎣⎡⎦⎤12，3，∴f (x )≥2x ·4x＝4，当且仅当x ＝2时，f (x )min ＝4，当x ∈[2,3]时，g (x )min ＝22＋a ＝4＋a ，依题意知f (x )min ≥g (x )min ，即4≥a ＋4，∴a ≤0. 答案 (1)[e,4] (2)(－∞，0]1．已知命题p ：对任意x ∈R ，总有2x ＞0；q ：“x ＞1”是“x ＞2”的充分不必要条件．则下列命题为真命题的是( ) A ．p ∧q B ．(綈p )∧(綈q ) C ．(綈p )∧q D ．p ∧(綈q )答案 D解析因为指数函数的值域为(0，＋∞)，所以对任意x ∈R ，y ＝2x ＞0恒成立，故p 为真命题；因为当x ＞1时，x ＞2不一定成立，反之，当x ＞2时，一定有x ＞1成立，故“x ＞1”是“x ＞2”的必要不充分条件，故q 为假命题．则p ∧q ，綈p 为假命题，綈q 为真命题，(綈p )∧(綈q )，(綈p )∧q 为假命题，p ∧(綈q )为真命题，故选D.2．设命题p ：函数y ＝sin2x 的最小正周期为π2；命题q ：函数y ＝cos x 的图象关于直线x ＝π2对称，则下列判断正确的是( ) A ．p 为真 B ．綈q 为假 C ．p ∧q 为假 D ．p ∨q 为真答案 C解析函数y ＝sin2x 的最小正周期为2π2＝π，故命题p 为假命题；x ＝π2不是y ＝cos x 的对称轴，故命题q 为假命题，故p ∧q 为假．故选C. 3．下列命题中为假命题的是( ) A ．∀x ∈⎝⎛⎭⎫0，π2，x ＞sin x B ．∃x ∈R ，sin x ＋cos x ＝2 C ．∀x ∈R,3x ＞0 D ．∃x ∈R ，lg x ＝0 答案 B解析对于A ，令f (x )＝x －sin x ，则f ′(x )＝1－cos x ，当x ∈⎝⎛⎭⎫0，π2时，f ′(x )＞0.从而f (x )在⎝⎛⎭⎫0，π2上是增函数，则f (x )＞f (0)＝0，即x ＞sin x ，故A 正确；对于B ，由sin x ＋cos x ＝2sin ⎝⎛⎭⎫x ＋π4≤2＜2知，不存在x ∈R ，使得sin x ＋cos x ＝2，故B 错误；对于C ，易知3x ＞0，故C 正确；对于D ，由lg 1＝0知，D 正确．故选B.4．(2017·豫西五校联考)若定义域为R 的函数f (x )不是偶函数，则下列命题中一定为真命题的是( )A ．∀x ∈R ，f (－x )≠f (x )B ．∀x ∈R ，f (－x )＝－f (x )C ．∃x ∈R ，f (－x )≠f (x )D ．∃x ∈R ，f (－x )＝－f (x ) 答案 C解析由题意知∀x ∈R ，f (－x )＝f (x )是假命题，则其否定为真命题，∃x ∈R ，f (－x )≠f (x )是真命题，故选C.5．(2017·安庆二模)设命题p ：∃x ∈(0，＋∞)，x ＋1x ＞3；命题q ：∀x ∈(2，＋∞)，x 2＞2x ，则下列命题为真的是( )A ．p ∧(綈q )B ．(綈p )∧qC ．p ∧qD ．(綈p )∨q答案 A 解析对于命题p ，当x ＝4时，x ＋1x ＝174＞3，故命题p 为真命题；对于命题q ，当x ＝4时，24＝42＝16，即∃x ∈(2，＋∞)，使得2x ＝x 2成立，故命题q 为假命题，所以p ∧(綈q )为真命题，故选A.6．(2018届东莞外国语学校月考)已知命题p ：∃x ∈R ，cos x ＝54；命题q ：∀x ∈R ，x 2－x ＋1>0.则下列结论正确的是( )A ．命题p ∧q 是真命题B ．命题p ∧(綈q )是真命题C ．命题(綈p )∧q 是真命题D ．命题(綈p )∨(綈q )是假命题答案 C解析因为对任意x ∈R ，都有cos x ≤1成立，而54>1，所以命题p ：∃x ∈R ，cos x ＝54是假命题；因为对任意的x ∈R ，x 2－x ＋1＝⎝⎛⎭⎫x －122＋34>0，所以命题q ：∀x ∈R ，x 2－x ＋1>0是真命题．由此对照各个选项，可知命题(綈p )∧q 是真命题．7．下列命题中，真命题是( )A ．∃x ∈R ，e x ≤0B ．∀x ∈R,2x ＞x 2C ．a ＋b ＝0的充要条件是a b＝－1 D ．“a ＞1，b ＞1”是“ab ＞1”的充分条件答案 D解析因为y ＝e x ＞0，x ∈R 恒成立，所以A 不正确；因为当x ＝－5时，2－5＜(－5)2，所以B 不正确； “a b＝－1”是“a ＋b ＝0”的充分不必要条件，C 不正确；当a ＞1，b ＞1时，显然ab ＞1，D 正确．8．命题p ：∀x ∈R ，ax 2＋ax ＋1≥0，若綈p 是真命题，则实数a 的取值范围是( )A ．(0,4]B ．[0,4]C ．(－∞，0]∪[4，＋∞)D ．(－∞，0)∪(4，＋∞)答案 D 解析因为命题p ：∀x ∈R ，ax 2＋ax ＋1≥0，所以綈p ：∃x ∈R ，ax 2＋ax ＋1＜0，则a ＜0或⎩⎪⎨⎪⎧a ＞0，Δ＝a 2－4a ＞0，解得a ＜0或a ＞4. 9．命题p 的否定是“对所有正数x ，x >x ＋1”，则命题p 可写为____________________．答案 ∃x ∈(0，＋∞)，x ≤x ＋1解析因为p 是綈p 的否定，所以只需将全称命题变为存在性命题，再对结论否定即可．10．已知函数f (x )的定义域为(a ，b )，若“∃x ∈(a ，b )，f (x )＋f (－x )≠0”是假命题，则f (a ＋b )＝________.答案 0解析若“∃x ∈(a ，b )，f (x )＋f (－x )≠0”是假命题，则“∀x ∈(a ，b )，f (x )＋f (－x )＝0”是真命题，即f (－x )＝－f (x )，则函数f (x )是奇函数，则a ＋b ＝0，即f (a ＋b )＝f (0)＝0.11．以下四个命题：①∀x ∈R ，x 2－3x ＋2>0恒成立；②∃x ∈Q ，x 2＝2；③∃x ∈R ，x 2＋1＝0；④∀x ∈R,4x 2>2x －1＋3x 2.其中真命题的个数为________．答案 0解析 ∵x 2－3x ＋2＝0的判别式Δ＝(－3)2－4×2>0，∴当x >2或x <1时，x 2－3x ＋2>0才成立，∴①为假命题；当且仅当x ＝±2时，x 2＝2，∴不存在x ∈Q ，使得x 2＝2，∴②为假命题；对∀x ∈R ，x 2＋1≠0，∴③为假命题；4x 2－(2x －1＋3x 2)＝x 2－2x ＋1＝(x －1)2≥0，即当x ＝1时，4x 2＝2x －1＋3x 2成立，∴④为假命题．∴①②③④均为假命题．故真命题的个数为0.12．(2017·江西五校联考)已知命题p ：∃x ∈R ，(m ＋1)·(x 2＋1)≤0，命题q ：∀x ∈R ，x 2＋mx ＋1>0恒成立．若p ∧q 为假命题，则实数m 的取值范围为____________．答案 (－∞，－2]∪(－1，＋∞)解析由命题p ：∃x ∈R ，(m ＋1)(x 2＋1)≤0，可得m ≤－1，由命题q ：∀x ∈R ，x 2＋mx ＋1>0恒成立，可得－2<m <2，因为p ∧q 为假命题，所以m ≤－2或m >－1.13．已知命题p ：x 2＋2x －3>0；命题q ：13－x>1，若“(綈q )∧p ”为真，则x 的取值范围是________________．答案 (－∞，－3)∪(1,2]∪[3，＋∞)解析因为“(綈q )∧p ”为真，即q 假p 真，而当q 为真命题时，13－x －1＝－x －2x －3>0，即2<x <3，所以当q 为假命题时，有x ≥3或x ≤2；当p 为真命题时，由x 2＋2x －3>0，解得x >1或x <－3，由⎩⎪⎨⎪⎧x >1或x <－3，x ≥3或x ≤2，得x ≥3或1＜x ≤2或x <－3，所以x 的取值范围是{x |x ≥3或1＜x ≤2或x ＜－3}．14．下列结论：①若命题p ：∃x ∈R ，tan x ＝1；命题q ：∀x ∈R ，x 2－x ＋1>0，则命题“p ∧(綈q )”是假命题；②已知直线l 1：ax ＋3y －1＝0，l 2：x ＋by ＋1＝0，则l 1⊥l 2的充要条件是a b＝－3； ③命题“若x 2－3x ＋2＝0，则x ＝1”的逆否命题是“若x ≠1，则x 2－3x ＋2≠0”．其中正确结论的序号为________．答案 ①③解析 ①中命题p 为真命题，命题q 为真命题，所以p ∧(綈q )为假命题，故①正确；②当b ＝a ＝0时，有l 1⊥l 2，故②不正确；③正确，所以正确结论的序号为①③.15．已知命题p ：∃x ∈R ，e x －mx ＝0，命题q ：∀x ∈R ，x 2＋mx ＋1≥0，若p ∨(綈q )为假命题，则实数m 的取值范围是________．答案 [0,2]解析若p ∨(綈q )为假命题，则p 假q 真．由e x－mx ＝0，可得m ＝e x x ，x ≠0，设f (x )＝e x x，x ≠0，则 f ′(x )＝x e x －e x x 2＝(x －1)e xx 2，当x >1时，f ′(x )>0，函数f (x )＝e x x在(1，＋∞)上是单调递增函数；当0<x <1或x <0时，f ′(x )<0，函数f (x )＝e x x在(0,1)和(－∞，0)上是单调递减函数，所以当x ＝1时，函数取得极小值f (1)＝e ，所以函数f (x )＝e x x的值域是(－∞，0)∪[e ，＋∞)，由p 是假命题，可得0≤m <e. 当命题q 为真命题时，有Δ＝m 2－4≤0，即－2≤m ≤2.所以当p ∨(綈q )为假命题时，m 的取值范围是0≤m ≤2.16．已知函数f (x )＝x 2－x ＋1x －1(x ≥2)，g (x )＝a x (a >1，x ≥2)． (1)若∃x ∈[2，＋∞)，使f (x )＝m 成立，则实数m 的取值范围为________________；(2)若∀x 1∈[2，＋∞)，∃x 2∈[2, ＋∞)，使得f (x 1)＝g (x 2)，则实数a 的取值范围为________________．答案 (1)[3，＋∞) (2)(1，3]解析 (1)因为f (x )＝x 2－x ＋1x －1＝x ＋1x －1＝x －1＋1x －1＋1≥2＋1＝3，当且仅当x ＝2时等号成立，所以若∃x ∈[2，＋∞)，使f (x )＝m 成立，则实数m 的取值范围为[3，＋∞)．(2)因为当x ≥2时，f (x )≥3，g (x )≥a 2，若∀x 1∈[2，＋∞)，∃x 2∈[2，＋∞)，使得f (x 1)＝g (x 2)，则⎩⎪⎨⎪⎧a 2≤3，a ＞1，解得a ∈(1，3]．。

高考数学总复习 1.2命题与量词、基本逻辑联结词课件

＝sinx＋π6cosπ2－x＋π6
题型分类·深度剖析
题型一
含有逻辑联结词命题的真假判断
【例 1】命题 p：将函数 y＝sin 2x 的图象向右平移π3个单位得到函数 y＝sin2x－π3的图象；命题 q：函数 y＝sinx＋π6cosπ3－x的最小正
题型一
含有逻辑联结词命题的真假判断
【例 1】命题 p：将函数 y＝sin 2x 的图象向右平移π3个单位得到函数 y＝sin2x－π3的图象；命题 q：函数 y＝sinx＋π6cosπ3－x的最小正
周期为 π，则命题
思维启迪解析答案思维升华
“p∨q”“p∧q”“綈 p”形式命题真假的判断步骤： (1)确定命题的构成形式； (2)判断其中命题 p、q 的真假；
数学 R B（理）
§1.2 命题与量词、基本逻辑联结词
第一章集合与常用逻辑用语
基础知识·自主学习
要点梳理
知识回顾理清教材
1．命题的概念能够判断真假的语句叫做命题．其中判断为真的语句叫真命题，判断为假的语句叫假命题．
2．全称量词与全称命题 (1) 全称量词：短语 “ 所有 ” 在陈述中表示所述事物的全体，逻辑中通常叫做全称量词，并用符号“∀ ”表示． (2)全称命题：含有全称量词的命题． (3)全称命题的符号表示：形如“对 M 中的所有 x，p(x)”的命题，用符号简记为 “ ∀x∈M，p(x) ”．
＝sin2x＋π6＝12－12cos2x＋π3， ∴其最小正周期为 T＝22π＝π， ∴命题 q 是真命题．
“p∨q”“p∧q”“綈 p”为真命由此，可判断命题“p∨q”为真，
题的个数是 A．1 B．2

高考数学一轮复习第讲命题与量词、基本逻辑联结词课件文新人教版

考点突破考点二全(特)称命题的否定及其真假判定
【训练2】命题“存在实数x，使x＞1”的否定是( ) A．对任意实数x，都有x＞1 B．不存在实数x，使x≤1 C．对任意实数x，都有x≤1 D．存在实数x，使x≤1
解析 “存在实数x，使x＞1”的否定是 “对任意实数x，都有x≤1”．故选C．答案 C
解析 (1)全称命题的否定是特称命题，即命题“∀x∈R，|x|＋x2≥0”的否定为“∃x0∈R，|x0|＋x20＜0”．故选C． (2)∀x∈R，x2≥0，故A错； ∀x∈R，－1≤sin x≤1，故B错； ∀x∈R，2x＞0，故C错，故选D．答案 (1)C (2)D
考点突破考点二全(特)称命题的否定及其真假判定
故a与c方向相同或相反，
∴a∥c，即q是真命题，则¬q是假命题，故p∨q是真命题， p∧q，(¬p)∧(¬q)，p∨(¬q)都是假命题．
考点突破考点一含有逻辑联结词的命题及其真假判断
【例1】(2)在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为( ) A．(¬p)∨(¬q) B．p∨(¬q) C．(¬p)∧(¬q) D．p∨q 一位或多位
解析 (1)由于a，b，c都是非零向量， ∵a·b＝0， ∴a⊥b. ∵b·c＝0， ∴b⊥c. 如图，则可能a∥c，∴a·c≠0， ∴命题p是假命题， ∴¬p是真命题．
命题q中，a∥b，则a与b方向相同或相反； b∥c，则b与c方向相同或相反．
考点突破考点一含有逻辑联结词的命题及其真假判断
【例1】 (1)(2014·辽宁卷)设a，b，c是非零向量．已知命题p：若a·b＝0，b·c＝0，则a·c＝0；命题q：若a∥b，b∥c，则a∥c. 则下列命题中真命题是( ) A．p∨q B．p∧q C．(¬p)∧(¬q) D．p∨(¬q) (2)在一次跳伞训练中，甲、乙两位学员各跳一次．设命题p是 “甲降落在指定范围”，q是“乙降落在指定范围”，则命题 “至少有一位学员没有降落在指定范围”可表示为( ) A．(¬p)∨(¬q) B．p∨(¬q) C．(¬p)∧(¬q) D．p∨q 一位或多位

2025年新人教版高考数学一轮复习讲义第一章 §1.2 常用逻辑用语

2025年新人教版高考数学一轮复习讲义第一章§1.2　常用逻辑用语1.理解充分条件、必要条件、充要条件的意义；理解判定定理与充分条件、性质定理与必要条件、数学定义与充要条件的关系.2.理解全称量词和存在量词的意义，能正确对两种命题进行否定.第一部分落实主干知识第二部分探究核心题型课时精练第一部分落实主干知识1.充分条件、必要条件与充要条件的概念若p ⇒q ，则p 是q 的条件，q 是p 的条件p 是q 的条件p ⇒q 且q ⇏p p 是q 的条件p ⇏q 且q ⇒p p 是q 的条件p ⇔q p 是q 的条件p ⇏q 且q ⇏p充分必要充分不必要必要不充分充要既不充分也不必要2.全称量词与存在量词(1)全称量词：短语“所有的”“任意一个”在逻辑中通常叫做全称量词，并用符号“ ”表示.(2)存在量词：短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词，并用符号“ ”表示.∀∃3.全称量词命题和存在量词命题名称全称量词命题存在量词命题结构对M 中任意一个x ，p (x )成立存在M 中的元素x ，p (x )成立简记__________________________否定∃x ∈M ，綈p (x )_______________∀x ∈M ，p (x )∃x ∈M ，p (x )∀x ∈M ，綈p (x )常用结论1.充分、必要条件与对应集合之间的关系设A＝{x|p(x)}，B＝{x|q(x)}.(1)若p是q的充分条件，则A⊆B；(2)若p是q的充分不必要条件，则A B；(3)若p是q的必要不充分条件，则B A；(4)若p是q的充要条件，则A＝B.2.含有一个量词命题的否定规律是“改变量词，否定结论”.3.命题p与p的否定的真假性相反.1.判断下列结论是否正确.(请在括号中打“√”或“×”)(1)当p 是q 的充分条件时，q 是p 的必要条件.( )(2)“三角形的内角和为180°”是全称量词命题.( )(3)“x >1”是“x >0”的充分不必要条件.( )(4)命题“∃x ∈R ， ”是真命题.( )×√√√2.(必修第一册P30例4(1)改编)(多选)已知命题p：∀x∈R，x＋2≤0，则下列说法正确的是A.p是真命题B.綈p：∀x∈R，x＋2>0√√C.綈p是真命题D.綈p：∃x∈R，x＋2>0当x＝0时，x＋2≤0不成立，故p是假命题，故A错误；由含量词命题的否定可知，p：∀x∈R，x＋2≤0的否定为綈p：∃x∈R，x＋2>0，故D正确，B错误；綈p是真命题，故C正确.3.(必修第一册P22T2(5)改编)设x>0，y>0，则“x2>y2”是“x>y”的A.充分不必要条件B.必要不充分条件√C.充要条件D.既不充分也不必要条件4.已知A＝(－∞，a]，B＝(－∞，3)，且x∈A是x∈B的充分不必要条件，(－∞，3)则a的取值范围为__________.由题意知，x∈A⇒x∈B，x∈B⇏x∈A，即A B，所以a<3.返回第二部分探究核心题型例1　(1)(2023·葫芦岛模拟)已知向量n 为平面α的一个法向量，向量m 为直线l 的一个方向向量，则m ∥n 是l ⊥α的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件题型一　充分、必要条件的判定√当m ∥n 时，l ⊥α，当l ⊥α时，m ∥n ，综上所述，m ∥n 是l ⊥α的充要条件.(2)在等比数列{a n}中，“a1>0，且公比q>1”是“{a n}为递增数列”的√A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件当a1>0，且q>1时，有a n＋1－a n＝a1q n－a1q n－1＝a1q n－1(q－1)>0，所以a n＋1>a n(n∈N*)，即{a n}为递增数列；当{a n}为递增数列时，即对一切n∈N*，有a n＋1>a n恒成立，所以a n＋1－a n＝a1q n－1(q－1)>0，但a1<0且0<q<1时，上式也成立，显然无法得出a1>0，且q>1.则“a1>0，且公比q>1”是“{a n}为递增数列”的充分不必要条件.思维升华充分、必要条件的三种判定方法(1)定义法：根据p⇒q，q⇒p是否成立进行判断.(2)集合法：根据p，q成立对应的集合之间的包含关系进行判断.(3)等价转化法：对所给题目的条件进行一系列的等价转化，直到转化成容易判断充分、必要条件是否成立为止.跟踪训练1　(1)(2024·贵阳模拟)已知函数f(x)＝cos(2x＋φ)，则“φ＝”是“f(x)是奇函数”的√A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件f(x)是奇函数等价于cos(－2x＋φ)＝－cos(2x＋φ)，即cos(－2x＋φ)＝cos(π－2x－φ)，故－2x＋φ＝π－2x－φ＋2kπ，k∈Z，(2)当命题“若p，则q”为真命题，则“由p可以推出q”，即一旦p成立，q就成立，p是q成立的充分条件.也可以这样说，若q不成立，那么p一定不成立，q对p成立也是很必要的.王安石在《游褒禅山记》中也说过一段话：“世之奇伟、瑰怪，非常之观，常在于险远，而人之所罕至焉，故非有志者不能至也”.从数学逻辑角度分析，“有志”是“能至”的√A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件因为“非有志者不能至也”即“有志”不成立时“能至”一定不成立，所以“能至”是“有志”的充分条件，“有志”是“能至”的必要条件.题型二　充分、必要条件的应用例2　在①“x∈A”是“x∈B”的充分条件；②“x∈∁R A”是“x∈∁R B”的必要条件这两个条件中任选一个，补充到本题第(2)问的横线处，并求解下列问题.问题：已知集合A＝{x|a≤x≤a＋2}，B＝{x|(x＋1)(x－3)<0}.(1)当a＝2时，求A∩B；由(x＋1)(x－3)<0，解得－1<x<3，所以B＝{x|－1<x<3}，当a＝2时，A＝{x|2≤x≤4}，所以A∩B＝{x|2≤x<3}.(2)若________，求实数a的取值范围.注：如果选择多个条件分别解答，按第一个解答计分.选①“x∈A”是“x∈B”的充分条件，则A⊆B，选②“x∈∁R A”是“x∈∁R B”的必要条件，则A⊆B，微拓展充分不必要条件的等价形式p是q的充分不必要条件，等价于綈q是綈p的充分不必要条件.典例　已知命题p：|x|≤1，q：x＜a，若綈q是綈p的充分不必要条件，则(1，＋∞)实数a的取值范围为____________.由|x|≤1，即－1≤x≤1，由题意知p是q的充分不必要条件，所以a＞1.思维升华求参数问题的解题策略(1)把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.(2)要注意区间端点值的检验.跟踪训练2　从①“充分不必要条件”，②“必要不充分条件”这两个条件中任选一个，补充到本题第(2)问的横线处，并解答下列问题：已知集合A＝，B＝{x|x2－4x＋4－m2≤0，m∈R}.(1)若m＝3，求A∪B；依题意，得2－2≤2x≤25，解得－2≤x≤5，即A＝{x|－2≤x≤5}，当m＝3时，解不等式x2－4x－5≤0，得－1≤x≤5，即B＝{x|－1≤x≤5}，所以A∪B＝{x|－2≤x≤5}.(2)若存在正实数m，使得“x∈A”是“x∈B”成立的________，求正实数m的取值范围.注：如果选择多个条件分别解答，按第一个解答计分.选①，由(1)知，A＝{x|－2≤x≤5}，m>0，解不等式x2－4x＋4－m2≤0，得2－m≤x≤2＋m，即B＝{x|2－m≤x≤2＋m}，因为“x∈A”是“x∈B”成立的充分不必要条件，则有A B，所以正实数m的取值范围是m≥4.选②，由(1)知，A＝{x|－2≤x≤5}，m>0，解不等式x2－4x＋4－m2≤0，得2－m≤x≤2＋m，即B＝{x|2－m≤x≤2＋m}，因为“x∈A”是“x∈B”成立的必要不充分条件，则有B A，于是得－2<2－m<2＋m≤5或－2≤2－m<2＋m<5，解得0<m≤3或0<m<3，即有0<m≤3，所以正实数m的取值范围是0<m≤3.命题点1　含量词的命题的否定例3　(1)(多选)下列说法正确的是A.“正方形是菱形”是全称量词命题B.∃x ∈R ，e x <e x ＋1C.命题“∃x ∈R ，x 2－2x ＋3＝0”的否定为“∀x ∈R ，x 2－2x ＋3≠0”D.命题“∀x >1，都有2x ＋1>5”的否定为“∃x ≤1，使得2x ＋1≤5”√题型三　全称量词与存在量词√√对于A，“正方形是菱形”等价于“所有的正方形都是菱形”，是全称量词命题，故A正确；对于B，当x＝1时，e<e＋1成立，故B正确；对于C，命题“∃x∈R，x2－2x＋3＝0”的否定为“∀x∈R，x2－2x ＋3≠0”，故C正确；对于D，命题“∀x>1，都有2x＋1>5”的否定为“∃x>1，使得2x＋1≤5”，故D不正确.(2)写出“所有实数都不是无理数”的否定形式：______________________.至少有一个实数是无理数命题点2　含量词的命题的真假判断例4　(多选)下列命题中的真命题是A.∀x ∈R ,2x －1>0B.∀x ∈N *，(x －1)2>0C.∃x ∈R ，lg x <1D.∃x ∈R ，tan x ＝2√√√指数函数的值域为(0，＋∞)，所以∀x∈R,2x－1>0，故A正确；当x＝1时，(x－1)2＝0，所以∀x∈N*，(x－1)2>0是假命题，故B错误；当x＝1时，lg x＝0<1，所以∃x∈R，lg x<1，故C正确；函数y＝tan x的值域为R，所以∃x∈R，tan x＝2，故D正确.命题点3　含量词的命题的应用例5　(1)若命题“∀x∈[－1,2]，x2＋1≥m”是真命题，则实数m的取值范围是√A.(－∞，0]B.(－∞，1]C.(－∞，2]D.(－∞，5]由“∀x∈[－1,2]，x2＋1≥m”是真命题可知，不等式m≤x2＋1，对∀x∈[－1,2]恒成立，因此只需m≤(x2＋1)min，x∈[－1,2]，易知函数y＝x2＋1在x∈[－1,2]上的最小值为1，所以m≤1.即实数m的取值范围是(－∞，1].(2)(多选)命题p：∃x∈R，x2＋2x＋2－m<0为假命题，则实数m的取值可以√√√是A.－1B.0C.1D.2若命题p：∃x∈R，x2＋2x＋2－m<0为真命题，则Δ＝22－4(2－m)＝4m－4>0，解得m>1，所以当命题p：∃x∈R，x2＋2x＋2－m<0为假命题时，m≤1，符合条件的为A，B，C选项.思维升华含量词命题的解题策略(1)判定全称量词命题是真命题，需证明都成立；要判定存在量词命题是真命题，只要找到一个成立即可.当一个命题的真假不易判定时，可以先判断其否定的真假.(2)由命题真假求参数的范围，一是直接由命题的真假求参数的范围；二是可利用等价命题求参数的范围.跟踪训练3　(1)下列命题为真命题的是A.任意两个等腰三角形都相似B.所有的梯形都是等腰梯形√C.∀x∈R，x＋|x|≥0D.∃x∈R，x2－x＋1＝0对于A，任意两个等腰三角形不一定相似，故A错误；对于B，所有的梯形都是等腰梯形是假命题，故B错误；对于C，因为∀x∈R，|x|≥－x，即x＋|x|≥0，故C正确；(2)(多选)已知命题p ：∀x ∈[0,1]，不等式2x －2≥m 2－3m 恒成立，命题q ：∃x ∈[1,3]，不等式x 2－ax ＋4≤0，则下列说法正确的是A.命题p 的否定是“∃x ∈[0,1]，不等式2x －2<m 2－3m ”B.命题q 的否定是“∀x ∈[1,3]，不等式x 2－ax ＋4≥0”C.当命题p 为真命题时，1≤m ≤2D.当命题q 为假命题时，a <4√√√命题p的否定是“∃x∈[0,1]，不等式2x－2<m2－3m”，故A正确；命题q的否定是“∀x∈[1,3]，不等式x2－ax＋4>0”，故B错误；若命题p为真命题，则当x∈[0,1]时，(2x－2)min≥m2－3m，即m2－3m ＋2≤0，解得1≤m≤2，故C正确；知识过关一、单项选择题1.命题“∃x>0，sin x－x≤0”的否定为A.∀x≤0，sin x－x>0B.∃x>0，sin x－x≤0√C.∀x>0，sin x－x>0D.∃x≤0，sin x－x>0由题意知命题“∃x>0，sin x－x≤0”为存在量词命题，其否定为全称量词命题，即∀x>0，sin x－x>0.2.下列命题中，p是q的充分条件的是A.p：ab≠0，q：a≠0B.p：a2＋b2≥0，q：a≥0且b≥0C.p：x2>1，q：x>1√对于C，x2>1⇔x>1或x<－1⇏x>1，故p不是q的充分条件；3.设λ∈R，则“λ＝1”是“直线3x＋(λ－1)y＝1与直线λx＋(1－λ)y＝2平行”的√A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件若直线3x＋(λ－1)y＝1与直线λx＋(1－λ)y＝2平行，则3(1－λ)－λ(λ－1)＝0，解得λ＝1或λ＝－3，经检验，当λ＝1或λ＝－3时，两直线平行.即“λ＝1”是“直线3x＋(λ－1)y＝1与直线λx＋(1－λ)y＝2平行”的充分不必要条件.。

高考数学第一轮基础复习课件1-2命题、量词、逻辑联结词新人教B版

5．准确理解逻辑联结词“或”的含义：“p 或 q” 为真命题时，包括三种情形：p 真 q 假，p 假 q 真，p 真 q 真．如“x∈A 或 x∈B”包括“x∈A 且 x∉B”，“x∈ A 且 x∈B”，“x∉A 且 x∈B”．
1．判断含有逻辑联结词的命题的真假，一定要先确定命题的形式，再判断简单命题的真假，最后按真值表进行．
3．注意对全称命题的否定与存在性命题的否定的区别．全称命题的否定是存在性命题，存在性命题的否定是全称命题．
4．讨论原命题的逆命题、否命题、逆否命题是在命题为“若 p，则 q”形式或可改写为这种形式的前提下进行的．不具备这种形式的命题讨论其逆、其否是没有意义的．故复习本章内容一定要紧扣概念．
第二节命题、量词、逻辑联结词
重点难点重点：①四种命题的关系及命题的否定 ②全称量词与存在量词使用上的区别难点：①逻辑联结词“或”、“且”的含义及命题的否定形式与否命题的区别 ②全称量词与存在量词的区别运用．
知识归纳 1．命题 (1)用语言、符号或式子表达的，可以判断真假的语句叫做命题．判断为真的为真命题，判断为假的为假命题． (2)把一个命题表达为“若 p，则 q”的形式，则 p 叫做命题的条件，q 叫做命题的结论．
(2011·安徽省百校论坛高三联考)已知命题 p：对任意 x∈R，有 cosx≤1，则( )
A．綈 p：存在 x0∈R，使 cosx0≥1 B．綈 p：对任意 x∈R，有 cosx≥1 C．綈 p：存在 x0∈R，使 cosx0>1 D．綈 p：对任意 x∈R，有 cosx>1
解析：对于命题 p：对任意 x∈R，有 cosx≤1 的否定，应该把全称命题换为存在性命题，然后否定结论，
(4)存在性命题：含有存在量词的命题叫存在性命题． (5)含有一个量词的命题的否定： ①全称命题 p：∀x∈M，p(x)；它的否定綈 p：“∃ x∈M，綈 p(x)”是存在性命题． ②存在性命题 p：“∃x∈M，p(x)”；它的否定綈 p： “∀x∈M，綈 p(x)”是全称命题．

高考数学一轮复习 1.2 命题与量词、基本逻辑联结词理

第2讲命题与量词、基本逻辑联结词基础巩固1.由“p:8+7=16,q:π>3”构成的复合命题,下列判断正确的是( )A.p∨q为真,p∧q为假, p为真B.p∨q为假,p∧q为假, p为真C.p∨q为真,p∧q为假, p为假D.p∨q为假,p∧q为真, p为真【答案】A【解析】因为p假q真,所以p∨q为真,p∧q为假, p为真.2.若p,q是两个简单命题,且“p∨q”的否定是真命题,则必有( )A.p真q真B.p假q假C.p真q假D.p假q真【答案】B【解析】∵“p∨q”的否定是真命题,∴“p∨q”是假命题.故p,q都为假命题.3.命题“存在x0∈Z,使2+x0+1≤0”的否定是( )A.存在x0∈Z,使2+x0+1<0B.不存在x0∈Z,使2+x0+1>0C.对任意x∈Z,都有2x2+x+1≤0D.对任意x∈Z,都有2x2+x+1>0【答案】D【解析】特称命题的否定是全称命题.4.(2012·河南洛阳高三统考)若命题p:∀x∈,tan x>sin x,则命题 p为( )A.∃x0∈,tan x0≥sin x0B.∃x0∈,tan x0>sin x0C.∃x0∈,tan x0≤sin x0D.∃x0∈,tan x0>sin x0【答案】C【解析】命题 p为∃x0∈,tan x0≤sin x0.5.(2012·河南郑州质检)下列四个命题中的真命题为( )A.∃x0∈Z,1<4x0<3B.∃x0∈Z,5x0+1=0C.∀x∈R,x2-1=0D.∀x∈R,x2+x+2>0【答案】D【解析】由1<4x0<3,得<x0<,这样的整数x0不存在,故选项A为假命题;由5x0+1=0,x0=-∉Z,故选项B 为假命题;x2-1=0,x=±1,故选项C为假命题;对任意实数x,都有x2+x+2=>0,故选D.6.已知命题p:∃a,b∈(0,+∞),当a+b=1时,=3;命题q:∀x∈R,x2-x+1≥0恒成立,则下列命题是假命题的是( )A.( p)∨( q)B.( p)∧( q)C.( p)∨qD.( p)∧q【答案】B【解析】由基本不等式可得:×(a+b)=2+≥4,故命题p为假命题, p为真命题;∀x∈R,x2-x+1=>0,故命题q为真命题, q为假命题.因此( p)∧( q)为假命题,故选B.7.(2012·山东潍坊月考)已知定义在R上的函数f(x),写出命题“若对任意实数x都有f(-x)=f(x),则f(x)为偶函数”的否定:.【答案】若存在实数x0,使得f(-x0)=f(x0),则f(x)不是偶函数【解析】所给命题是全称命题,其否定为特称命题.8.已知命题p:∃x0∈R,+2ax0+a≤0.若命题p是假命题,则实数a的取值范围是.【答案】(0,1)【解析】∵p是假命题,∴对∀x∈R,x2+2ax+a>0.∴Δ=4a2-4a<0,即4a(a-1)<0,得0<a<1.9.已知命题p:不等式|x|+|x-1|>m的解集为R,命题q:函数f(x)=-(5-2m)x是减函数.若p或q为真命题,p且q为假命题,则实数m的取值范围是.【答案】 1≤m<2【解析】 p:∵|x|+|x-1|的最小值为1,∴m<1.q:5-2m>1,∴m<2.∵p∨q为真,p∧q为假,∴p真q假或p假q真.∴∴1≤m<2.10.写出由下列各组命题构成的p∨q,p∧q, p形式的新命题,并判断其真假.(1)p:2是4的约数,q:2是6的约数;(2)p:矩形的对角线相等,q:矩形的对角线互相平分;(3)p:方程x2+x-1=0的两实根的符号相同,q:方程x2+x-1=0的两实根的绝对值相等.【解】(1)p∨q:2是4的约数或2是6的约数,真命题;p∧q:2是4的约数且2也是6的约数,真命题;p:2不是4的约数,假命题.(2)p∨q:矩形的对角线相等或互相平分,真命题;p∧q:矩形的对角线相等且相互平分,真命题;p:矩形的对角线不一定相等,假命题.(3)p∨q:方程x2+x-1=0的两个实数根符号相同或绝对值相等,假命题;p∧q:方程x2+x-1=0的两个实数根符号相同且绝对值相等,假命题;p:方程x2+x-1=0的两实数根符号不同,真命题.11.(2012·山西四校联考)设命题p:函数f(x)=x2-2ax-1在区间(-∞,3]上单调递减;命题q:函数y=ln(x2+ax+1)的定义域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.【解】由p为真命题,可得-≥3,即a≥3.由q为真命题可知,x2+ax+1>0在x∈R上恒成立,可得Δ=a2-4<0恒成立,即-2<a<2.由题意可知p和q有且只有一个是真命题.即当p真q假⇔⇔a≥3.当p假q真⇔⇔-2<a<2.综上所述,a的取值范围是(-2,2)∪[3,+∞).12.设命题p:函数f(x)=log a|x|在(0,+∞)上单调递增;q:关于x的方程x2+2x+log a=0的解集只有一个子集.若p∨q为真,( p)∨( q)也为真,求实数a的取值范围.【解】当命题p是真命题时,应有a>1.当命题q是真命题时,关于x的方程x2+2x+log a=0无解,所以Δ=4-4log a<0,解得1<a<.由于p∨q为真,所以p和q中至少有一个为真.又( p)∨( q)也为真,所以 p和 q中至少有一个为真,即p和q中至少有一个为假,故p和q中一真一假.p假q真时,a无解.p真q假时,a≥.综上所述,实数a的取值范围是a≥.拓展延伸13.已知m∈R,命题p:对任意x∈[0,8],不等式lo(x+1)≥m2-3m恒成立;命题q:对任意x∈R,不等式|1+sin 2x-cos 2x|≤2m恒成立.(1)若p为真命题,求m的取值范围;(2)若p且q为假,p或q为真,求m的取值范围.【解】(1)令f(x)=lo(x+1),则f(x)在(-1,+∞)上为减函数.因为x∈[0,8],所以当x=8时,f(x)min=f(8)=-2.不等式lo(x+1)≥m2-3m恒成立,等价于-2≥m2-3m,解得1≤m≤2.(2)不等式|1+sin 2x-cos 2x|≤2m,即|2sin x(sin x+cos x)|≤m|sin x+cos x|,所以m≥|sin x|.即命题q:m≥.若p且q为假,p或q为真,则p与q有且只有一个为真.若p为真,q为假,那么则1≤m<.若p为假,q为真,那么则m>2.综上所述,1≤m<或m>2.故m的取值范围是[1,)∪(2,+∞).。

2018高中数学理人教A版一轮参考课件：1-2 命题与量词、基本逻辑联结词

1 �� 1 ��
)
若 x=y, �� 与 �� 不一定存在,排除 C; 若 x<y,且 x=-3,y=-2,则 x2>y2,排除 D. 答案:A
主干梳理
要点梳理
考点自测
1
2
3
4
5
2.在一次跳伞训练中,甲、乙两位学员各跳一次.设命题 p 是 “甲降落在指定范围”,q 是 “乙降落在指定范围 ”,则命题 “至少有一位学员没有降落在指定范围”可表示为( A.(�� p)∨(�� q) ) B.p∨(�� q) C.(�� p)∧(�� q) D.p∨q
考向1
考向2
考向3
类题通法提炼
思维透析先判断命题 p,q 的真假,然后利用真值表判断 p∧q,p ∧
(�� q),(�� p)∨q,(�� p)∨(�� q)的真假. 解析:因为对任意实数 x,|sin x|≤1,而 sin x= >1,所以 p 为假;因为 x +x+1=0 的判别式 Δ<0,所以 q 为真.故结论②③正确. 答案: B
的取值范围为
.
2 解析:∃ x0∈R,2 ��0 -3ax0+9<0 为假命题,则∀ x∈R,2x2-3ax+9≥0 恒成立,有
Δ=9a -72≤0,解得-2 2≤a≤2 2. 答案:[-2 2,2 2]
2
考向1
考向2
考向3
类题通法提炼
考向 1
含有逻辑联结词命题的真假判断
5 2
【例 1】已知命题 p :∃ x∈R,使 sin x= ;命题 q :∀ x∈R,都有 x2+x+1>0.给出下列结论 :①命题 “p ∧q”是真命题;②命题“p ∧�� q”是假命题;③命题“�� p ∨q”是真命题;④命题 “�� p∨�� q”是假命题,其中正确的是( A.②④ C.③④ B.②③ D.①②③ )

人教版高三数学一轮复习精品课件1：1.2命题、量词、逻辑联结词

2．(2014·苏北三市质检)由命题“∃x∈R，x2＋2x＋m≤0” 是假命题，求得实数m的取值范围是(a，＋∞)，则实数a ＝________. 解析：由题意得命题“∀x∈R，x2＋2x＋m>0”是真命题，所以 Δ＝4－4m<0，即 m>1，故实数 m 的取值范围是(1，＋∞)，从而实数 a 的值为 1. 答案：1
[针对训练]
写出下列命题的否定并判断其真假： (1)p：不论m取何实数值，方程x2＋mx－1＝0必有实数根；
(2)p：有的三角形的三条边相等； (3)p：菱形的对角线互相垂直； (4)p：∃x0∈N，x20－2x0＋1≤0.
解：(1)綈 p：存在一个实数 m0，使方程 x2＋m0x－1＝0 没有实数根．因为该方程的判别式 Δ＝m20＋4>0 恒成立，故綈 p 为假命题． (2)綈 p：所有的三角形的三条边不全相等．显然綈 p 为假命题． (3)綈 p：有的菱形的对角线不垂直．显然綈 p 为假命题． (4)綈 p：∀x∈N，x2－2x＋1>0. 显然当 x＝1 时，x2－2x＋1>0 不成立，故綈 p 是假命题．
[练一练] 1．(2013·南通二模)命题“∃x∈ 0，π2 ，tan x>sin x”的否
定是________．
解析：根据存在性命题与全称命题之间的关系可知原命题的否定是：∀x∈0，π2，tan x≤sin x. 答案：∀x∈0，π2，tan x≤sin x
2．已知命题p：∃x0∈R，x
2 0
∈M，q(x)”，则綈 p 为“∃x∈M，綈 q(x)”． [答案] ∃x1，x2∈R，[f(x2)－f(x1)](x2－x1)<0
[类题通法] 全称命题与存在性命题的否定与命题的否定有一定的区别，否定全称命题和存在性命题时，一是要改写量词，全称量词改写为存在量词，存在量词改写为全称量词；二是要否定结论，而一般命题的否定只需直接否定结论即可．

高考数学(理)一轮复习精品资料专题02 命题与量词、基本逻辑联结词(教学案) Word版含解析

专题02命题与量词、基本逻辑联结词（教学案）高考数学（理）一轮复习精品资料1.以量词为载体，判断命题的真假；2.考查基本逻辑联结词的含义，在与其他知识交汇处命题．1．命题能判断真假的语句叫做命题．2．全称量词与全称命题(1)全称量词：短语“所有”在陈述中表示所述事物的全体，在逻辑中通常叫做全称量词．(2)全称命题：含有全称量词的命题．(3)全称命题的符号表示形如“对M中所有x，p(x)”的命题，可用符号简记为“∀x∈M，p(x)”．3．存在量词与存在性命题(1)存在量词：短语“有一个”或“有些”或“至少有一个”在陈述中表示所述事物的个体或部分，逻辑中通常叫做存在量词。

(2)存在性命题：含有全称量词的命题．(3)存在性命题的符号表示形如“存在集合M中的元素x，q(x)”的命题，用符号简记为∃x∈M，q(x)。

4．基本逻辑联结词常用的基本逻辑联结词有“且”、“或”、“非”．5．命题p∧q，p∨q，綈p的真假判断6．含有一个量词的命题的否定高频考点一命题及其关系例1、(1)命题“若x ，y 都是偶数，则x ＋y 也是偶数“的逆否命题是() A ．若x ＋y 是偶数，则x 与y 不都是偶数 B ．若x ＋y 是偶数，则x 与y 都不是偶数 C ．若x ＋y 不是偶数，则x 与y 不都是偶数 D ．若x ＋y 不是偶数，则x 与y 都不是偶数(2)原命题为“若z1，z2互为共轭复数，则|z1|＝|z2|”，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是()A ．真，假，真B ．假，假，真C ．真，真，假D ．假，假，假答案(1)C(2)B【感悟提升】(1)写一个命题的其他三种命题时，需注意： ①对于不是“若p ，则q“形式的命题，需先改写； ②若命题有大前提，写其他三种命题时需保留大前提．(2)判断一个命题为真命题，要给出推理证明；判断一个命题是假命题，只需举出反例． (3)根据“原命题与逆否命题同真同假，逆命题与否命题同真同假”这一性质，当一个命题直接判断不易进行时，可转化为判断其等价命题的真假．【变式探究】(1)命题“若α＝π3，则cos α＝12”的逆命题是()A ．若α＝π3，则cos α≠12B ．若α≠π3，则cos α≠12C ．若cos α＝12，则α＝π3D ．若cos α≠12，则α≠π3(2)已知命题α：如果x<3，那么x<5；命题β：如果x≥3，那么x≥5；命题γ：如果x≥5，那么x≥3.关于这三个命题之间的关系，下列三种说法正确的是()①命题α是命题β的否命题，且命题γ是命题β的逆命题； ②命题α是命题β的逆命题，且命题γ是命题β的否命题； ③命题β是命题α的否命题，且命题γ是命题α的逆否命题． A ．①③ B ．② C ．②③ D ．①②③ 答案(1)C(2)A高频考点二充分必要条件的判定例2、(1)(2019·四川)设a ，b 都是不等于1的正数，则“3a＞3b ＞3”是“loga3＜logb3”的()A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件(2)一次函数y ＝－m n x ＋1n 的图象同时经过第一、三、四象限的必要不充分条件是()A ．m>1，且n<1B ．mn<0C ．m>0，且n<0D ．m<0，且n<0 答案(1)B(2)B解析(1)根据指数函数的单调性得出a ，b 的大小关系，然后进行判断．∵3a>3b>3，∴a>b>1，此时loga3<logb3正确；反之，若loga3<logb3，则不一定得到3a>3b>3，例如当a ＝12，b ＝13时，loga3<logb3成立，但推不出a>b>1.故“3a>3b>3”是“loga3<logb3”的充分不必要条件．(2)∵y＝－m n x ＋1n 经过第一、三、四象限，故－m n >0，1n <0，即m>0，n<0，但此为充要条件，因此，其必要不充分条件为mn<0.【感悟提升】充要条件的三种判断方法 (1)定义法：根据p ⇒q ，q ⇒p 进行判断；(2)集合法：根据p ，q 成立的对象的集合之间的包含关系进行判断；(3)等价转化法：根据一个命题与其逆否命题的等价性，把判断的命题转化为其逆否命题进行判断．这个方法特别适合以否定形式给出的问题，如“xy≠1”是“x≠1或y≠1”的某种条件，即可转化为判断“x＝1且y ＝1”是“xy＝1”的某种条件．【变式探究】(1)(2019·陕西)“sin α＝cos α”是“cos2α＝0”的() A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件(2)若命题p ：φ＝π2＋k π，k∈Z，命题q ：f(x)＝sin(ωx ＋φ)(ω≠0)是偶函数，则p是q 的()A ．充要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件答案(1)A(2)A高频考点三充分必要条件的应用例3、已知P ＝{x|x2－8x －20≤0}，非空集合S ＝{x|1－m≤x≤1＋m}．若x∈P 是x∈S 的必要条件，求m 的取值范围．解由x2－8x －20≤0，得－2≤x≤10， ∴P＝{x|－2≤x≤10}，由x∈P 是x∈S 的必要条件，知S ⊆P. 则⎩⎪⎨⎪⎧1－m≤1＋m ，1－m≥－2， ∴0≤m≤3.1＋m≤10，∴当0≤m≤3时，x∈P 是x∈S 的必要条件，即所求m 的取值范围是．【感悟提升】充分条件、必要条件的应用，一般表现在参数问题的求解上．解题时需注意：(1)把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解．(2)要注意区间端点值的检验．【变式探究】(1)ax2＋2x ＋1＝0至少有一个负实根的充要条件是() A ．0<a≤1 B ．a<1 C ．a≤1 D ．0<a≤1或a<0(2)已知条件p ：2x2－3x ＋1≤0，条件q ：x2－(2a ＋1)x ＋a(a ＋1)≤0.若綈p 是綈q 的必要不充分条件，则实数a 的取值范围是________．答案(1)C(2)⎣⎢⎡⎦⎥⎤0，12方法二(排除法)当a ＝0时，原方程有一个负实根，可以排除A ，D ；当a ＝1时，原方程有两个相等的负实根，可以排除B.(2)命题p 为⎩⎨⎧⎭⎬⎫x|12≤x≤1，命题q 为{x|a≤x≤a＋1}．綈p 对应的集合A ＝{x|x>1或x<12}，綈q 对应的集合B ＝{x|x>a ＋1或x<a}． ∵綈p 是綈q 的必要不充分条件， ∴⎩⎪⎨⎪⎧a ＋1>1，a≤12或⎩⎪⎨⎪⎧a ＋1≥1，a<12，∴0≤a≤12.【2019高考浙江理数】命题“*x n ∀∈∃∈，R N ，使得2n x >”的否定形式是（） A ．*x n ∀∈∃∈，R N ，使得2n x <B ．*x n ∀∈∀∈，R N ，使得2n x < C ．*x n ∃∈∃∈，R N ，使得2n x <D ．*x n ∃∈∀∈，R N ，使得2n x < 【答案】D【解析】∀的否定是∃，∃的否定是∀，2n x ≥的否定是2n x <．故选D ．【2019高考新课标1，理3】设命题p ：2,2n n N n ∃∈>，则p ⌝为() （A ）2,2n n N n ∀∈>（B ）2,2nn N n ∃∈≤ （C ）2,2n n N n ∀∈≤（D ）2,=2n n N n ∃∈ 【答案】C【解析】p ⌝:2,2nn N n ∀∈≤，故选C.【2019高考浙江，理4】命题“**,()n N f n N ∀∈∈且()f n n ≤的否定形式是（） A.**,()n N f n N ∀∈∈且()f n n > B.**,()n N f n N ∀∈∈或()f n n >C.**00,()n N f n N ∃∈∈且00()f n n >D.**00,()n N f n N ∃∈∈或00()f n n >【答案】D.【解析】根据全称命题的否定是特称命题，可知选D.【2019·陕西卷】原命题为“若z1，z2互为共轭复数，则|z1|＝|z2|”，关于其逆命题，否命题，逆否命题真假性的判断依次如下，正确的是()A．真，假，真B．假，假，真C．真，真，假D．假，假，假【答案】B【2019·重庆卷】已知命题p：对任意x∈R，总有2x>0，q：“x>1”是“x>2”的充分不必要条件，则下列命题为真命题的是()A．p∧q B．綈p∧綈qC．綈p∧q D．p∧綈q【答案】D【解析】根据指数函数的图像可知p为真命题．由于“x>1”是“x>2”的必要不充分条件，所以q为假命题，所以綈q为真命题，所以p∧綈q为真命题．【2019·湖北卷】在一次跳伞中，甲、乙两位学员各跳一次，设命题p是“甲降落在指定范围”，q是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为()A．(⌝p)∨(⌝q)B．p∨(⌝q)C．(⌝p)∧(⌝q)D．p∨q【答案】A【解析】“至少一位学员没降落在指定区域”即“甲没降落在指定区域或乙没降落在指定区域”，可知选A.1．命题“若一个数是负数，则它的平方是正数”的逆命题是()A．“若一个数是负数，则它的平方不是正数”B．“若一个数的平方是正数，则它是负数”C．“若一个数不是负数，则它的平方不是正数”D．“若一个数的平方不是正数，则它不是负数”答案B解析依题意，得原命题的逆命题：若一个数的平方是正数，则它是负数．2．给出命题：若函数y ＝f (x )是幂函数，则函数y ＝f (x )的图象不过第四象限，在它的逆命题、否命题、逆否命题3个命题中，真命题的个数是()A ．3B ．2C ．1D ．0 答案C解析原命题是真命题，故它的逆否命题是真命题；它的逆命题为“若函数y ＝f (x )的图象不过第四象限，则函数y ＝f (x )是幂函数”，显然逆命题为假命题，故原命题的否命题也为假命题．因此在它的逆命题、否命题、逆否命题3个命题中真命题只有1个． 3．下列结论错误的是()A ．命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0” B ．“x ＝4”是“x 2－3x －4＝0”的充分条件C ．命题“若m >0，则方程x 2＋x －m ＝0有实根”的逆命题为真命题D ．命题“若m 2＋n 2＝0，则m ＝0且n ＝0”的否命题是“若m 2＋n 2≠0，则m ≠0或n ≠0” 答案C解析C 项命题的逆命题为“若方程x 2＋x －m ＝0有实根，则m >0”．若方程有实根，则Δ＝1＋4m ≥0，即m ≥－14，不能推出m >0.所以不是真命题，故选C.4．设四边形ABCD 的两条对角线为AC ，BD ，则“四边形ABCD 为菱形”是“AC ⊥BD ”的() A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件答案A5．设U 为全集．A ，B 是集合，则“存在集合C 使得A ⊆C ，B ⊆∁U C ”是“A ∩B ＝∅”的() A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要的条件答案C解析由Venn 图易知充分性成立．反之，A ∩B ＝∅时，由Venn 图(如图)可知，存在A ＝C ，同时满足A ⊆C ，B ⊆∁U C .故“存在集合C 使得A ⊆C ，B ⊆∁U C ”是“A ∩B ＝∅”的充要条件．6．函数f (x )＝⎩⎪⎨⎪⎧log2x ，x >0，－2x＋a ，x ≤0有且只有一个零点的充分不必要条件是()A ．a <0B ．0<a <12C.12<a <1 D ．a ≤0或a >1答案A7．“若a ≤b ，则ac 2≤bc 2”，则命题的原命题、逆命题、否命题和逆否命题中真命题的个数是________．答案2解析其中原命题和逆否命题为真命题，逆命题和否命题为假命题．8．若x <m －1或x >m ＋1是x 2－2x －3>0的必要不充分条件，则实数m 的取值范围是________．答案解析由已知易得{x |x 2－2x －x |x <m －1或x >m ＋1}，又{x |x 2－2x －3>0}＝{x |x <－1或x >3}，∴⎩⎪⎨⎪⎧－1≤m －1，m ＋1<3，或⎩⎪⎨⎪⎧－1<m －1，m ＋1≤3，∴0≤m ≤2.9．给定两个命题p 、q ，若綈p 是q 的必要而不充分条件，则p 是綈q 的________条件．答案充分不必要解析若綈p 是q 的必要不充分条件，则q ⇒綈p 但綈p q ，其逆否命题为p ⇒綈q 但綈q ⇒/p ，所以p 是綈q 的充分不必要条件．10．下列命题： ①若ac 2>bc 2，则a >b ；②若sin α＝sin β，则α＝β；③“实数a ＝0”是“直线x －2ay ＝1和直线2x －2ay ＝1平行”的充要条件； ④若f (x )＝log 2x ，则f (|x |)是偶函数．其中正确命题的序号是________．答案①③④解析对于①，ac 2>bc 2，c 2>0，∴a >b 正确；对于②，sin30°＝sin150°30°＝150°，所以②错误；对于③，l 1∥l 2⇔A 1B 2＝A 2B 1，即－2a ＝－4a ⇒a ＝0且A 1C 2≠A 2C 1，所以③正确； ④显然正确．11．设a ，b ∈R ，则“a >b ”是“a |a |>b |b |”的() A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分又不必要条件答案C12．已知集合A ＝⎩⎨⎧⎭⎬⎫x |12<2x <8，x ∈R ，B ＝{x |－1<x <m ＋1，x ∈R }，若x ∈B 成立的一个充分不必要条件是x ∈A ，则实数m 的取值范围是________．答案(2，＋∞)解析A ＝⎩⎨⎧⎭⎬⎫x |12<2x <8，x ∈R ＝{x |－1<x <3}，∵x ∈B 成立的一个充分不必要条件是x ∈A ， ∴AB ，∴m ＋1>3，即m >2.13．设a ，b 为正数，则“a －b >1”是“a 2－b 2>1”的________条件．答案充分不必要解析∵a －b >1，即a >b ＋1.又∵a，b为正数，∴a2>(b＋1)2＝b2＋1＋2b>b2＋1，即a2－b2>1成立，反之，当a＝3，b＝1时，满足a2－b2>1，但a－b>1不成立．所以“a－b>1”是“a2－b2>1”的充分不必要条件．14．下列四个结论中：①“λ＝0”是“λa＝0”的充分不必要条件；②在△ABC中，“AB2＋AC2＝BC2”是“△ABC 为直角三角形”的充要条件；③若a，b∈R，则“a2＋b2≠0”是“a，b全不为零”的充要条件；④若a，b∈R，则“a2＋b2≠0”是“a，b不全为零”的充要条件．正确的是________．答案①④。

【把握高考】高三数学第一轮总复习 1-2命题、量词、逻辑联结词新人教A版(含解析)

1-2命题、量词、逻辑联结词基础巩固强化1.(2013·江西吉安一中上学期期中考试)下列命题中，不是真命题的为( )A．“若b2－4ac>0，则二次方程ax2＋bx＋c＝0有实数根”的逆否命题B．“四边相等的四边形是正方形”的逆命题C．“x2＝9则x＝3”的否命题D．“对顶角相等”的逆命题[答案] D[解析] A中原命题为真命题，故逆否命题为真；B中逆命题为“正方形的四条边相等”，它是真命题；C中否命题为“若x2≠9，则x≠3”显然为真命题；D中逆命题为“若两个角相等，则这两个角互为对顶角”显然为假，故选D.2．(文)(2011·聊城模拟)下列命题中为假命题的是( )A．∀x∈R,2x－1>0 B．∀x∈N*，(x－1)2>0C．∃x∈R，lg x<1 D．∃x∈R，tan x＝2[答案] B[解析] 由指数函数值域知2x－1>0恒成立；当x＝1时，lg x＝0<1；∵直线y＝2与y＝tan x 的图象有交点，∴方程tan x＝2有解；∴A、C、D都是真命题，当x＝1∈N*时，(x－1)2>0不成立，∴B为假命题．(理)(2011·山东实验中学模拟)下列命题中是真命题的为( )A．∀x∈R，x2<x＋1B．∀x∈R，x2≥x＋1C．∃x∈R，∀y∈R，xy2＝y2D．∀x∈R，∃y∈R，x>y2[答案] C[解析] 令f(x)＝x2－x－1，∵Δ>0，∴f(x)的图象与x轴有交点，∴f(x)的值有正有负，故A、B假；令x＝－1，则对任意y∈R都有x<y2，故D假．当x＝1时，∀y∈R，xy2＝y2，故C真．3．(2011·西安二检)命题“对任意的x∈R，x3－x2＋1≤0”的否定是( )A．不存在x∈R，x3－x2＋1≤0B．存在x∈R，x3－x2＋1≤0C．存在x∈R，x3－x2＋1>0D．对任意的x∈R，x3－x2＋1>0[答案] C[解析] 依题意得，命题“对任意的x∈R，x3－x2＋1≤0”的否定是“存在x∈R，x3－x2＋1>0”，选C.4．(2011·辽宁铁岭六校联合考试)与命题“若p ，则q ”的否命题真假相同的命题是( )A ．若q ，则pB ．若綈p ，则qC ．若綈q ，则pD ．若綈p ，则綈q[答案] A[解析] 原命题的否命题与原命题的逆命题是等价命题，真假相同，故选A.5．(文)(2012·安阳模拟)已知命题p ：∃m ∈R ，m ＋1≤0，命题q ：∀x ∈R ，x 2＋mx ＋1>0恒成立．若p ∨q 为假命题，则实数m 的取值范围是( )A ．m ≥2B ．m ≤－2C ．m ≤－2或m ≥2D ．－2≤m ≤2[答案] A[解析] 由p ∨q 为假命题可知p 和q 都是假命题，即非p 是真命题，所以m >－1；再由q ：∀x ∈R ，x 2＋mx ＋1>0恒成立为假命题知m ≥2或m ≤－2，∴m ≥2，故选A.(理)(2011·广东省东莞市一模)已知命题p ：∃x ∈(－∞，0)，2x<3x；命题q ：∀x ∈(0，π2)，cos x <1，则下列命题为真命题的是( ) A ．p ∧q B ．p ∨(綈q ) C ．(綈p )∧q D ．p ∧(綈q )[答案] C[解析] 在x ∈(－∞，0)上，y ＝2x的图象恒在y ＝3x的上方，所以不存在这样的x 使得2x<3x成立，命题p 为假命题，命题q 为真命题，所以(綈p )∧q 为真命题，故选C.6．(文)(2011·山东潍坊一模)下列命题中是真命题的是( ) A ．若向量a ，b 满足a ·b ＝0，则a ＝0或b ＝0 B ．若a <b ，则1a >1bC ．若b 2＝ac ，则a ，b ，c 成等比数列 D ．∃x ∈R ，使得sin x ＋cos x ＝43成立[答案] D[解析] 对于A ，当a ⊥b 时，a ·b ＝0也成立，此时不一定是a ＝0或b ＝0；对于B ，当a ＝0，b ＝1时，该命题就不成立；对于C ，b 2＝ac 是a ，b ，c 成等比数列的必要不充分条件；对于D ，因为sin x ＋cos x ＝2sin(x ＋π4)∈[－2，2]，且43∈[－2，2]，所以该命题正确．(理)(2012·合肥第一次质检)下列命题： ①∀x ∈R ，不等式x 2＋2x >4x －3均成立； ②若log 2x ＋log x 2≥2，则x >1；③“若a >b >0且c <0，则c a >cb”的逆否命题是真命题；④若命题p ：∀x ∈R ，x 2＋1≥1，命题q ：∃x ∈R ，x 2－x －1≤0，则命题p ∧(綈q )是真命题．其中真命题为( )A ．①②③B ．①②④C ．①③④D ．②③④[答案] A[解析] 由x 2＋2x >4x －3推得x 2－2x ＋3＝(x －1)2＋2>0恒成立，故①正确；根据基本不等式可知要使不等式log 2x ＋log x 2≥2成立需要log 2x >0，∴x >1，故②正确；由a >b >0得0<1a <1b，又c <0，可得c a >c b，则可知其逆否命题为真命题，故③正确；命题p 是真命题，命题q 是真命题，所以p ∧(綈q )为假命题，故④错误．所以选A.7．(文)(2011·济南模拟)命题p ：∃x ∈R ，lg x ＝0，q ：∀x ∈R,2x>0，命题(綈p )∧q 的真假为________(填“真”或“假”)．[答案] 假[解析] ∵x ＝1时，lg x ＝0，∴p 真；由指数函数值域知2x>0恒成立，∴q 真； ∴(綈p )∧q 为假．(理)(2011·南京一调)设p ：函数f (x )＝2|x －a |在区间(4，＋∞)上单调递增；q ：log a 2<1.如果“非p ”是真命题，“p 或q ”也是真命题，那么实数a 的取值范围是________．[答案] (4，＋∞)[解析] ∵“非p ”为真命题，∴p 为假命题，又p 或q 为真命题，∴q 为真命题．若a >1，由log a 2<1知a >2，又f (x )＝2|x －a |在(a ，＋∞)上单调递增，且p 为假命题，∴a >4，因此得，a >4；若0<a <1，则p 、q 都是真命题，不合题意．综上，a 的取值范围是(4，＋∞)．8．命题“存在x ∈R ，使得x 2＋2x ＋5＝0”的否定是____________． [答案] 对∀x ∈R ，都有x 2＋2x ＋5≠0.9．(2012·洛阳部分重点中学教学检测)给出下列命题： ①y ＝1是幂函数；②函数f (x )＝2x－log 2x 的零点有1个； ③x －1(x －2)≥0的解集为[2，＋∞)； ④“x <1”是“x <2”的充分不必要条件； ⑤函数y ＝x 3是在O (0,0)处的切线是x 轴．其中真命题的序号是________(写出所有正确命题的序号)． [答案] ④⑤[解析] y ＝1不是幂函数，①是假命题；作出函数y ＝2x与y ＝log 2x 的图象，由两图象没有交点知函数f (x )＝2x－log 2x 没有零点，②错误；x ＝1是不等式x －1(x －2)≥0的解，③错误；x <1⇒x <2，而x <2⇒/ x <1，④正确；y ′＝(x 3)′＝3x 2，∴切线的斜率k ＝0，过原点的切线方程为y ＝0，⑤正确．10．给出下列三个结论：①命题“若a >b ，则a 2>b 2”的逆命题为假命题；②已知直线l 1：ax ＋2y －1＝0，l 2：x ＋by ＋2＝0，则l 1⊥l 2的充要条件是ab＝－2； ③对于任意实数x ，有f (－x )＝－f (x )，g (－x )＝g (x )且x >0时，f ′(x )>0，g ′(x )>0，则x <0时，f ′(x )>g ′(x )．其中正确结论的序号是________．(填上所有正确结论的序号)． [答案] ①③[解析] ①显然正确．②中l 1⊥l 2⇔a ＋2b ＝0，但a ＋2b ＝0与a b＝－2不等价，∵当a ＝b ＝0时，a b＝－2不成立，故②错；③由条件知，f (x )为奇函数，在x >0时单调增，故x <0时单调增，从而x <0时，f ′(x )>0；g (x )为偶函数，x >0时单调增，从而x <0时单调减，∴x <0时，g ′(x )<0，∴x <0时，f ′(x )>g ′(x )，故③正确.能力拓展提升11.(2011·北京模拟)下列命题中，真命题是( ) A ．∃x ∈R ，sin 2x 2＋cos 2x 2＝12B ．∀x ∈(0，π)，sin x >cos xC ．∃x ∈R ，x 2＋x ＝－1 D ．∀x ∈(0，＋∞)，e x>1＋x [答案] D[解析] ∵对任意x ∈R ，sin 2x 2＋cos 2x 2＝1，∴A 假；当x ＝π4时，sin x ＝cos x ，∴B 假；对于函数y ＝x 2＋x ＋1，∵Δ＝－3<0，∴y >0恒成立，∴C 假；对于函数y ＝e x－x －1，∵y ′＝e x －1，当x >0时，y ′>0，∴y ＝e x －x －1在(0，＋∞)上为增函数，∴y >e 0－0－1＝0，即e x >1＋x 恒成立，∴D 真．12．(文)(2011·大连质检)下列命题中真命题的个数是( ) ①∀x ∈R ，x 4>x 2；②若p ∧q 是假命题，则p ，q 都是假命题；③命题“∀x ∈R ，x 3－x 2＋1≤0”的否定是“∃x ∈R ，x 3－x 2＋1>0”． A ．0 B ．1 C ．2 D ．3 [答案] B[解析] 当x ＝0时，x 4>x 2不成立，∴①假；p ∧q 是假命题，则p 、q 至少有一个为假，∴②假；③显然为真，故选B.(理)(2011·汕头模拟)下列说法中，正确的是( ) A ．命题“若am 2<bm 2，则a <b ”的逆命题是真命题B ．命题“∃x ∈R ，x 2－x >0”的否定是“∀x ∈R ，x 2－x ≤0” C ．命题“p ∨q ”为真命题，则命题“p ”和命题“q ”均为真命题 D ．已知x ∈R ，则“x >1”是“x >2”的充分不必要条件 [答案] B[解析] 命题“若am 2<bm 2，则a <b ”的逆命题为“若a <b ，则am 2<bm 2”为假命题，∵m ＝0时，命题不成立；p ∨q 为真命题时，p 、q 至少一真，故C 假；x >1⇒/ x >2，但x >2⇒x >1，∴x >1是x >2的必要不充分条件，故D 假，B 显然为真．13．(2011·宿州模拟)已知命题p ：∃x ∈[0，π2]，cos2x ＋cos x －m ＝0为真命题，则实数m 的取值范围是( )A ．[－98，－1]B ．[－98，2]C ．[－1,2]D ．[－98，＋∞)[答案] C[解析] 依题意：cos2x ＋cos x －m ＝0在x ∈[0，π2]上有解，即cos2x ＋cos x ＝m 在x ∈[0，π2]上有解．令f (x )＝cos2x ＋cos x ＝2cos 2x ＋cos x －1＝2(cos x ＋14)2－98，由于x ∈[0，π2]，所以cos x∈[0,1]，于是f (x )∈[－1,2]，因此实数m 的取值范围是[－1,2]．14．(文)(2011·长沙调研)下列结论：①若命题p ：∃x ∈R ，tan x ＝1；命题q ：∀x ∈R ，x 2－x ＋1>0.则命题“p ∧(綈q )”是假命题；②已知直线l 1：ax ＋3y －1＝0，l 2：x ＋by ＋1＝0，则l 1⊥l 2的充要条件是ab＝－3； ③命题“若x 2－3x ＋2＝0，则x ＝1”的逆否命题为：“若x ≠1，则x 2－3x ＋2≠0”．其中正确结论的序号为________．(把你认为正确结论的序号都填上)[答案] ①③[解析] ①中命题p 为真命题，命题q 为真命题，所以p ∧(綈q )为假命题，故①正确； ②当b ＝a ＝0时，有l 1⊥l 2，故②不正确； ③正确．所以正确结论的序号为①③.(理)(2011·常德模拟)已知命题“如果|a |≤1，那么关于x 的不等式(a 2－4)x 2＋(a ＋2)x －1≥0的解集为∅”，它的逆命题、否命题、逆否命题及原命题中是假命题的共有________个．[答案] 2[解析] 由|a |≤1，得－1≤a ≤1，且Δ＝(a ＋2)2＋4(a 2－4) ＝5(a ＋25)2－45－12≤5(1＋25)2－645<0，∴原命题为真，逆否命题亦为真．反之，如a ＝－2时，所给不等式的解集即为空集，但a ∉[－1,1]，所以逆命题为假，故否命题亦为假．15．在平面直角坐标系xOy 中，直线l 与抛物线y 2＝2x 相交于A 、B 两点． (1)求证：“如果直线l 过点T (3,0)，那么OA →·OB →＝3”是真命题； (2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由． [解析] (1)设过点T (3,0)的直线l 交抛物线y 2＝2x 于点A (x 1，y 1)，B (x 2，y 2)．当直线l 的斜率不存在时，直线l 的方程为x ＝3，此时，直线l 与抛物线相交于点A (3，6)、B (3，－6)． ∴OA →·OB →＝3.当直线l 的斜率存在时，设直线l 的方程为y ＝k (x －3)，其中k ≠0.由⎩⎪⎨⎪⎧y 2＝2x ，y ＝k x －，得，ky 2－2y －6k ＝0，则y 1y 2＝－6.又∵x 1＝12y 21，x 2＝12y 22，∴OA →·OB →＝x 1x 2＋y 1y 2 ＝14(y 1y 2)2＋y 1y 2＝3. 综上所述，命题“如果直线l 过点T (3,0)，那么OA →·OB →＝3”是真命题．(2)逆命题是：设直线l 交抛物线y 2＝2x 于A 、B 两点，如果OA →·OB →＝3，那么直线过点T (3,0)．该命题是假命题．例如：取抛物线上的点A (2,2)，B ⎝ ⎛⎭⎪⎫12，1，此时OA →·OB →＝3，直线AB 的方程为y ＝23(x ＋1)，而T (3,0)不在直线AB 上．16．(文)已知命题p ：在x ∈[1,2]时，不等式x 2＋ax －2>0恒成立；命题q ：函数f (x )＝log 13(x 2－2ax ＋3a )是区间[1，＋∞)上的减函数．若命题“p ∨q ”是真命题，求实数a 的取值范围．[解析] ∵x ∈[1,2]时，不等式x 2＋ax －2>0恒成立， ∴a >2－x 2x ＝2x－x 在x ∈[1,2]上恒成立，令g (x )＝2x－x ，则g (x )在[1,2]上是减函数，∴g (x )max ＝g (1)＝1， ∴a >1.即若命题p 真，则a >1.又∵函数f (x )＝log 13(x 2－2ax ＋3a )是区间[1，＋∞)上的减函数，∴u (x )＝x 2－2ax ＋3a 是[1，＋∞)上的增函数，且u (x )＝x 2－2ax ＋3a >0在[1，＋∞)上恒成立，∴a ≤1，u (1)>0，∴－1<a ≤1，即若命题q 真，则－1<a ≤1. 若命题“p ∨q ”是真命题，则a >－1.(理)探求关于x 的方程x 2＋2mx ＋12－m ＝0两根都大于2的充要条件． [解析] 设两根为x 1，x 2，则⎩⎪⎨⎪⎧x 1>2，x 2>2，而⎩⎪⎨⎪⎧x 1>2，x 2>2，⇔⎩⎪⎨⎪⎧Δ≥0，x 1－x 2－，x 1－＋x 2－，⇔⎩⎪⎨⎪⎧4m 2－－m ，－m －－2m ＋4>0，－2m －4>0，⇔⎩⎪⎨⎪⎧m ≥3或m ≤－4，m >－163，m <－2，⇔－163<m ≤－4.∴方程两根都大于2的充要条件为－163<m ≤－4.1．(2011·福州月考)下列有关命题的说法正确的是( ) A ．命题“若x 2＝1，则x ＝1”的否命题为：“若x 2＝1，则x ≠1” B ．“x ＝－1”是“x 2－5x －6＝0”的必要不充分条件C ．命题“∃x ∈R ，使得x 2＋x ＋1<0”的否定是：“∀x ∈R ，均有x 2＋x ＋1<0” D ．命题“若x ＝y ，则cos x ＝cos y ”的逆否命题为真命题 [答案] D[解析] A 中，否命题应为若x 2≠1，则x ≠1；B 中，x ＝－1⇒x 2－5x －6＝0，反之则不成立，应为充分不必要条件；C 中，命题的否定应为∀x ∈R ，均有x 2＋x ＋1≥0.2．(2011·浙江省台州市调研)给出下列命题，其中错误的是( )A ．命题“若x 2－3x －4＝0，则x ＝4”的逆否命题为“若x ≠4，则x 2－3x －4≠0” B ．“x 2－3x －4＝0”是“x ＝4”的必要不充分条件 C ．若p ∧q 是假命题，则p ，q 都是假命题D ．命题p ：∃x ∈R ，使得x 2＋x ＋1<0，则綈p ：∀x ∈R ，都有x 2＋x ＋1≥0 [答案] C[解析] 选项A 根据逆否命题的写法，是正确的；选项B“x 2－3x －4＝0”不能推出“x ＝4”，但是“x ＝4”能推出“x 2－3x －4＝0”所以B 正确；选项C 中若p ∧q 是假命题，只需要其中一个是假命题即可，故选项C 错误．根据特称命题与全称命题的否定，选项D 正确．3．下列命题中的假命题是( ) A ．∀x >0且x ≠1，都有x ＋1x>2B ．∀a ∈R ，直线ax ＋y ＝a 恒过定点(1,0)C ．∃m ∈R ，使f (x )＝(m －1)·xm 2－4m ＋3是幂函数 D ．∀φ∈R ，函数f (x )＝sin(2x ＋φ)都不是偶函数 [答案] D[解析] ∵x ＋1x≥2等号在x ＝1时成立，∴A 真；将x ＝1，y ＝0代入直线方程ax ＋y ＝a中成立，∴B 真；令m －1＝1得m ＝2，此时f (x )＝x －1是幂函数，故C 真；当φ＝π2时，f (x )＝sin ⎝⎛⎭⎪⎫2x ＋π2＝cos2x 为偶函数，故D 假． 4．已知命题p ：“∀x ∈[1,2]，x 2－a ≥0”，命题q ：“∃x ∈R ，使x 2＋2ax ＋2－a ＝0.”若命题“p ∧q ”是真命题，则实数a 的取值范围是( )A ．{a |a ≤－2或a ＝1}B ．{a |a ≤－2或1≤a ≤2}C ．{a |a ≥1}D ．{a |－2≤a ≤1}[答案] A[解析] “p ∧q ”为真，即p 、q 同为真．对于命题p ，∀x ∈[1,2]，x 2－a ≥0恒成立，只需12－a ≥0成立，即a ≤1；对于命题q ，∃x ∈R ，使x 2＋2ax ＋2－a ＝0成立，只需保证判别式Δ＝4a 2－4(2－a )≥0，∴a ≤－2或a ≥1，∴选A.5．(2011·南昌模拟)给出以下三个命题：①若ab ≤0，则a ≤0或b ≤0；②在△ABC 中，若sin A ＝sin B ，则A ＝B ；③在一元二次方程ax 2＋bx ＋c ＝0中，若b 2－4ac <0，则方程有实数根．其中原命题、逆命题、否命题、逆否命题全都是真命题的是( )A ．①B ．②C ．③D ．②③ [答案] B[解析] 对命题①，其原命题和逆否命题为真，但逆命题和否命题为假；对命题②，其原命题、逆命题、否命题、逆否命题全部为真；对命题③，其原命题、逆命题、否命题、逆否命题全部为假．6．已知动圆C 过点A (－2，0)，且与圆M ：(x －2)2＋y 2＝64相内切． (1)求动圆C 的圆心C 的轨迹方程；(2)设直线l ：y ＝kx ＋m (其中k ，m ∈Z )与(1)中所求轨迹交于不同两点B ，D ，与双曲线x 24－y 212＝1交于不同两点E ，F ，问是否存在直线l ，使得向量DF →＋BE →＝0，若存在，指出这样的直线有多少条？若不存在，请说明理由．[解析] (1)圆M ：(x －2)2＋y 2＝64的圆心M 的坐标为(2,0)，半径R ＝8. ∵|AM |＝4<R ，∴点A (－2,0)在圆M 内．设动圆C 的半径为r ，圆心为C (x ，y )，依题意得r ＝|CA |，且|CM |＝R －r ，即|CM |＋|CA |＝8>|AM |.∴圆心C 的轨迹是中心在原点，以A 、M 两点为焦点，长轴长为8的椭圆，设其方程为x 2a 2＋y 2b2＝1(a >b >0)，则a ＝4，c ＝2，∴b 2＝a 2－c 2＝12. ∴所求动圆的圆心C 的轨迹方程为x 216＋y 212＝1.(2)由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 216＋y 212＝1，消去y 化简整理得：(3＋4k 2)x 2＋8kmx ＋4m 2－48＝0，设B (x 1，y 1)，D (x 2，y 2)，则x 1＋x 2＝－8km3＋4k 2Δ1＝(8km )2－4(3＋4k 2)(4m 2－48)>0①由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24－y212＝1，消去y 化简整理得：(3－k 2)x 2－2kmx －m 2－12＝0.设E (x 3，y 3)，F (x 4，y 4)，则x 3＋x 4＝2km 3－k 2，Δ2＝(－2km )2＋4(3－k 2)(m 2＋12)>0②∵DF →＝(x 4－x 2，y 4－y 2)，BE →＝(x 3－x 1，y 3－y 1)，且DF →＋BE →＝0，∴(x 4－x 2)＋(x 3－x 1)＝0，即x 1＋x 2＝x 3＋x 4，∴－8km 3＋4k 2＝2km3－k 2，∴km ＝0或－43＋4k 2＝13－k 2.解得k ＝0或m ＝0.当k ＝0时，由①、②得－23<m <23， ∵m ∈Z ，∴m 的值为－3，－2，－1,0,1,2,3；当m ＝0时，由①、②得－3<k <3，∵k ∈Z ，∴k ＝－1,0,1.∴满足条件的直线共有9条．。

高考数学总复习第一章第2课时命题与量词、基本逻辑联结词课件新人教版

例1 写出由下列各组命题构成的“p或q” 、“p且q”、“非p”形式的复合命题,并判断真假. (1)p：平行四边形的对角线相等; q：平行四边形的对角线互相垂直; (2)p:方程x2＋x－1＝0的两实根符号相同; q：方程x2＋x－1＝0的两实根的绝对值相等.
【思路分析】 (1)利用“或”、“且 ”、“非”把两个命题联结成新命题; (2)根据命题p和命题q的真假判断复合命题的真假.
考向瞭望•把脉高考
命题预测从近几年的高考题来看,全称命题、存在性命题的否定、真假的判断及逻辑联结词是高考的热点,常与其他知识相结合命题.题型一般为选择题,
属容易题,尤其全称命题、存在性命题为新课标新增内容,在课改区高考中有升温的趋势,应引起重视. 预测2013年高考仍将以全称命题、存在性命题的否定和真假判断为主要考点, 重点考查学生的逻辑推理能力.
2.逻辑联结词中,较难理解含义的是“或”, 应从以下两个方面来理解概念：(1)逻辑联结词中的“或”与集合中的“或”含义的一致性.(2)结合实例,剖析生活中的“或”与逻辑联结词中的“或”之间的区别.生活中的“或”一般指“或此或彼只必具其一,但不可兼而有之”,而逻辑联结词中的“或” 具有“或此或彼或兼有”三种情形.
【解】 (1)p∨q：平行四边形的对角线相等或互相垂直.假命题. p∧q：平行四边形的对角线相等且互相垂直.假命题. ¬p ：有些平行四边形的对角线不相等 . 真命题.
(2)p∨q：方程x2＋x－1＝0的两实根符号相同或绝对值相等.假命题. p∧q：方程x2＋x－1＝0的两实根符号相同且绝对值相等.假命题. ¬p：方程x2＋x－1＝0的两实根符号不相同.真命题.
函数单调递减,故 p2 是假命题.由此可知,q1 真,q2 假,q3 假,q4 真.故选 C. 法二： p1 是真命题同法一 ; 由于 2x ＋ 2 － x≥2 2x·2－x＝2,故函数 y＝2x＋2－x 在 R 上存在最小值,故这个函数一定不是 R 上的单调函数,故 p2 是假命题.由此可知,q1 真,q2 假,q3 假,q4 真.故选 C.

高考数学(理)人教B版一轮复习考点探究课件：第一章第二节命题与量词、基本逻辑联结词

核心考点互动探究
题组练通
1．(2018·西安质检)已知命题 p：∃x0∈R，log2(3x0＋1)≤0，则( B ) A．p 是假命题；綈 p：∀x∈R，log2(3x＋1)≤0 B．p 是假命题；綈 p：∀x∈R，log2(3x＋1)＞0 C．p 是真命题；綈 p：∀x∈R，log2(3x＋1)≤0 D．p 是真命题；綈 p：∀x∈R，log2(3x＋1)＞0 ∵3x＞0，∴3x＋1＞1，则 log2(3x＋1)＞0，∴p 是假命题：綈 p：
答案：D
6．若命题“对∀x∈R，kx2－kx－1＜0”是真命题，则 k 的取值范围是__(－__4,_0]___．解析：“对∀x∈R，kx2－kx－1＜0”是真命题，当 k＝0 时，则有－1＜0；当 k≠0 时，则有 k＜0 且 Δ＝(－k)2－4×k×(－ 1)＝k2＋4k＜0，解得－4＜k＜0，综上所述，实数 k 的取值范围是(－4,0]．
•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/62021/9/6Monday, September 06, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/62021/9/62021/9/69/6/2021 11:31:25 AM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/62021/9/62021/9/6Sep-216-Sep-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/62021/9/62021/9/6Monday, September 06, 2021
A．p∧(綈 q)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.2 命题与量词、基本逻辑联结词一、选择题1．下列命题中的假命题是( )． A ．∃x 0∈R ，lg x 0＝0 B ．∃x 0∈R ，tan x 0＝1 C ．∀x ∈R ，x 3＞0D ．∀x ∈R,2x ＞0解析对于A ，当x 0＝1时，lg x 0＝0正确；对于B ，当x 0＝π4时，tan x 0＝1，正确；对于C ，当x ＜0时，x 3＜0错误；对于D ，∀x ∈R,2x ＞0，正确．答案 C2. 已知命题p ：函数f (x )＝⎝ ⎛⎭⎪⎫12x －log 13x 在区间⎝⎛⎭⎪⎫0，13内存在零点，命题q ：存在负数x 使得⎝ ⎛⎭⎪⎫12x >⎝ ⎛⎭⎪⎫13x .给出下列四个命题：①p 或q ；②p 且q ；③p 的否定；④q 的否定．其中真命题的个数是( )A ．1B ．2C ．3D ．4 解析命题p 为假命题，命题q 也为假命题．利用真值表判断．答案 B3．命题“∀x ＞0，x 2＋x ＞0”的否定是( )． A ．∃x 0＞0，x 20＋x 0＞0 B ．∃x 0＞0，x 20＋x 0≤0 C ．∀x ＞0，x 2＋x ≤0D ．∀x ≤0，x 2＋x ＞0解析根据全称命题的否定是特称命题，可知该命题的否定是：∃x 0＞0，x 20＋x 0≤0. 答案 B4．已知p ：|x －a |＜4；q ：(x －2)(3－x )＞0，若非p 是非q 的充分不必要条件，则a 的取值范围为( )． A ．a ＜－1或a ＞6 B ．a ≤－1或a ≥6 C ．－1≤a ≤6D ．－1＜a ＜6解析解不等式可得p ：－4＋a ＜x ＜4＋a ，q ：2＜x ＜3，因此非p ：x ≤－4＋a 或x ≥4＋a ，非q ：x ≤2或x ≥3，于是由非p 是非q 的充分不必要条件，可知2≥－4＋a 且4＋a ≥3，解得－1≤a ≤6. 答案 C5．若函数f (x )＝－x e x ，则下列命题正确的是( )A ．∀a ∈⎝⎛⎭⎪⎫－∞，1e ，∃x ∈R ，f (x )>aB ．∀a ∈⎝ ⎛⎭⎪⎫1e ，＋∞，∃x ∈R ，f (x )>aC ．∀x ∈R ，∃a ∈⎝⎛⎭⎪⎫－∞，1e ，f (x )>a D ．∀x ∈R ，∃a ∈⎝ ⎛⎭⎪⎫1e ，＋∞，f (x )>a解析 f ′(x )＝－e x(x ＋1)，由于函数f (x )在(－∞，－1)上递增，在(－1，＋∞)上递减，故f (x )max ＝f (－1)＝1e ，故∀a ∈⎝⎛⎭⎪⎫－∞，1e ，∃x ∈R ，f (x )>a .答案 A6．若函数f (x )＝x 2＋ax(a ∈R )，则下列结论正确的是( )． A ．∀a ∈R ，f (x )在(0，＋∞)上是增函数 B ．∀a ∈R ，f (x )在(0，＋∞)上是减函数 C ．∃a ∈R ，f (x )是偶函数 D ．∃a ∈R ，f (x )是奇函数解析对于A 只有在a ≤0时f (x )在(0，＋∞)上是增函数，否则不成立；对于B ，如果a ≤0就不成立；对于D 若a ＝0，则f (x )为偶函数了，因此只有C 是正确的，即对于a ＝0时有f (x )＝x 2是一个偶函数，因此存在这样的a ，使f (x )是偶函数．答案 C7．已知p ：∃x 0∈R ，mx 20＋2≤0.q ：∀x ∈R ，x 2－2mx ＋1＞0，若p ∨q 为假命题，则实数m 的取值范围是( )． A ．[1，＋∞) B ．(－∞，－1] C ．(－∞，－2]D ．[－1,1]解析 (直接法)∵p ∨q 为假命题，∴p 和q 都是假命题．由p ：∃x 0∈R ，mx 20＋2≤0为假，得∀x ∈R ，mx 2＋2＞0，∴m ≥0.①由q ：∀x ∈R ，x 2－2mx ＋1＞0为假，得∃x 0∈R ，x 20－2mx 0＋1≤0，∴Δ＝(－2m )2－4≥0⇒m 2≥1⇒m ≤－1或m ≥1.② 由①和②得m ≥1. 答案 A【点评】本题采用直接法，就是通过题设条件解出所求的结果，多数选择题和填空题都要用该方法，是解题中最常用的一种方法. 二、填空题8．若命题“∃x 0∈R,2x 20－3ax 0＋9＜0”为假命题，则实数a 的取值范围是________．解析因为“∃x 0∈R,2x 20－3ax 0＋9＜0”为假命题，则“∀x ∈R,2x 2－3ax ＋9≥0”为真命题．因此Δ＝9a 2－4×2×9≤0，故－22≤a ≤2 2. 答案－22≤a ≤2 29．已知命题p ：x 2＋2x －3＞0；命题q ：13－x＞1，若非q 且p 为真，则x 的取值范围是________．解析因为非q 且p 为真，即q 假p 真，而q 为真命题时，x －2x －3＜0，即2＜x ＜3，所以q 假时有x ≥3或x ≤2；p 为真命题时，由x 2＋2x －3＞0，解得x ＞1或x ＜－3，由⎩⎨⎧x ＞1或x ＜－3，x ≥3或x ≤2，得x ≥3或1＜x ≤2或x ＜－3，所以x 的取值范围是x ≥3或1＜x ≤2或x ＜－3. 故填(－∞，－3)∪(1,2]∪[3，＋∞)．答案 (－∞，－3)∪(1,2]∪[3，＋∞) 10．已知命题p ：f (x )＝1－2mx在区间(0，＋∞)上是减函数；命题q ：不等式(x－1)2>m 的解集为R .若命题“p ∨q ”为真，命题“p ∧q ”为假，则实数m 的取值范围是________．解析由f (x )＝1－2m x 在区间(0，＋∞)上是减函数，得1－2m >0，即m <12，由不等式(x －1)2>m 的解集为R ，得m <0.要保证命题“p ∨q ”为真，命题“p ∧q ”为假，则需要两个命题中只有一个正确，而另一个不正确，故0≤m <12.答案 0≤m <12 8．令p (x )：ax 2＋2x ＋a ＞0，若对∀x ∈R ，p (x )是真命题，则实数a 的取值范围是________．解析 ∵对∀x ∈R ，p (x )是真命题． ∴对∀x ∈R ，ax 2＋2x ＋a ＞0恒成立，当a ＝0时，不等式为2x ＞0不恒成立，当a ≠0时，若不等式恒成立，则⎩⎨⎧a ＞0，Δ＝4－4a 2＜0，∴a ＞1.答案 a ＞111. 已知定义在R 上的函数f(x),写出命题”若对任意实数x 都有f(-x)=f(x),则f(x)为偶函数”的否定: . 解析所给命题是全称命题,其否定为存在性命题.答案若存在实数0x ,使得00()()f x f x -≠,则f(x)不是偶函数12．已知命题“∀x ∈R ，x 2－5x ＋152a ＞0”的否定为假命题，则实数a 的取值范围是________．解析由“∀x ∈R ，x 2－5x ＋152a ＞0”的否定为假命题，可知命题“∀x ∈R ，x 2－5x ＋152a ＞0”必为真命题，即不等式x 2－5x ＋152a ＞0对任意实数x 恒成立．设f (x )＝x 2－5x ＋152a ，则其图象恒在x 轴的上方．故Δ＝25－4×152a ＜0，解得a ＞56，即实数a 的取值范围为⎝ ⎛⎭⎪⎫56，＋∞. 答案 ⎝ ⎛⎭⎪⎫56，＋∞三、解答题13．已知命题p ：∀x ∈[1,2]，x 2－a ≥0，命题q ：∃x 0∈R ，x 20＋2ax 0＋2－a ＝0，若“p 且q ”为真命题，求实数a 的取值范围．解析由“p 且q ”为真命题，则p ，q 都是真命题．p ：x 2≥a 在[1,2]上恒成立，只需a ≤(x 2)min ＝1，所以命题p ：a ≤1；q ：设f (x )＝x 2＋2ax ＋2－a ，存在x 0∈R 使f (x 0)＝0，只需Δ＝4a 2－4(2－a )≥0，即a 2＋a －2≥0⇒a ≥1或a ≤－2，所以命题q ：a ≥1或a ≤－2.由⎩⎨⎧a ≤1，a ≥1或a ≤－2得a ＝1或a ≤－2∴实数a 的取值范围是a ＝1或a ≤－2. 14．写出下列命题的否定，并判断真假． (1)q ：∀x ∈R ，x 不是5x －12＝0的根； (2)r ：有些质数是奇数； (3)s ：∃x 0∈R ，|x 0|＞0.解析 (1)非q ：∃x 0∈R ，x 0是5x －12＝0的根，真命题． (2)非r ：每一个质数都不是奇数，假命题． (3)非s ：∀x ∈R ，|x |≤0，假命题．15．设命题p ：函数f (x )＝x 3－ax －1在区间[－1,1]上单调递减；命题q ：函数y ＝ln(x 2＋ax ＋1)的值域是R .如果命题p 或q 为真命题，p 且q 为假命题，求a 的取值范围．解析 p 为真命题⇔f ′(x )＝3x 2－a ≤0在[－1,1]上恒成立⇔a ≥3x 2在[－1,1]上恒成立⇔a ≥3.q 为真命题⇔Δ＝a 2－4≥0恒成立⇔a ≤－2或a ≥2. 由题意p 和q 有且只有一个是真命题． p 真q 假⇔⎩⎨⎧a ≥3，－2<a <2⇔a ∈∅；p 假q 真⇔⎩⎨⎧a <3，a ≤－2或a ≥2⇔a ≤－2或2≤a <3.综上所述：a ∈(－∞，－2]∪[2,3)．16.已知m ∈R ,命题p:对任意[08]x ∈,,不等式log 13(1)x +≥23m m -恒成立;命题q:对任意x ∈R ,不等式|1+sin2x-cos2x|2m ≤|cos ()4x π-|恒成立.(1)若p 为真命题,求m 的取值范围;(2)若p 且q 为假,p 或q 为真,求m 的取值范围.解析 (1)令f(x)=log 13(x+1),则f(x)在(1)-,+∞上为减函数.因为[08]x ∈,,所以当x=8时min ()(8)2f x f ,==-.不等式log 132(1)3x m m +≥-恒成立,等价于223m m -≥-,解得12m ≤≤.(2)不等式|1+sin2x-cos2x|2m ≤|cos ()4x π-|,即|2sinx(sinx+cosx)|≤|sinx+cosx|,所以m ≥即命题q:m ≥若p 且q 为假,p 或q 为真,则p 与q 有且只有一个为真.若p 为真,q 为假,那么12m m ≤≤,⎧⎪⎨<⎪⎩则1m ≤<若p 为假,q 为真,那么12m m m <>,⎧⎪⎨≥⎪⎩或则m>2.综上所述1m ,≤<m>2. 故m的取值范围是[1(2)⋃,+∞.。