无限深势阱 势垒
16-3 一维势阱和势垒问题
]
ψ1 = A1 e + B1 e
ik1x
−ik1x
− ik 2 x
1
( x < 0)
( x > a)
U
通解: 通解
ψ 2 = A2 e
ik 2 x
1
+ B2 e
(0 ≤ x ≤ a )
U0
ψ 3 = A3 eik x + B3 e − ik x
处无反射波: 由 x > a 处无反射波: B 3 = 0 令 A1 = 1(以入射波强度为标准) 以入射波强度为标准) 由波函数的 标准条件得 O 可解得
§16-3 一维势阱和势垒问题
一、一维无限深方势阱 模型的建立:微观粒子被局限于某区域中, 模型的建立:微观粒子被局限于某区域中,并在该 区域内可以自由运动的问题 →简化模型。 →简化模型 简化模型。 例如: 例如: 金属中自由电子 受规则排列的晶格点阵作用 简化:交换动量) 简 相互碰撞 (简化:交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 无限深势阱
2 2πx p = ∫ |ψ | d x = ∫ sin dx a a 0 0
4 4 2 a a
2a πx 2 πx = ∫ sin d( ) aπ a a 0
4
a
1 πx 1 2 2 2π x = ( − sin ) π a 4 a
a
4
= 9.08 × 10 −2
0
练习: 练习
已知: 已知:
ψ = cx ( L − x )
A A2 ∞ 2 dx = ∫ dx = A arctg x − ∞ = A2π = 1 ∫∞ 1 + ix 1 + x2 − −∞
一维对称无限深方势阱的波函数表达式

一维对称无限深方势阱的波函数表达式在量子力学中,一维对称无限深方势阱是一种经典的势阱模型,它在研究粒子在受限空间内的运动和能级结构等方面有很好的应用。
对于一维对称无限深方势阱来说,波函数的表达式是非常重要的,它可以帮助我们理解粒子在势阱内的行为以及计算其能级。
1. 势阱模型的基本假设一维对称无限深方势阱模型假设了以下几点:势阱的宽度为a,势阱内部的势能为0,而在势阱外部势能为无穷大,这意味着粒子在势阱内运动自由,在势阱外不能存在。
这是一个理想化的模型,但对于研究粒子在受限空间内的行为却是非常有用的。
2. 薛定谔方程的求解根据薛定谔方程,我们可以求解一维对称无限深方势阱中的波函数。
薛定谔方程的一般形式为:-ħ²/2m * d²Ψ/dx² + V(x)Ψ = EΨ其中,ħ是普朗克常数,m是粒子的质量,V(x)是势能函数,Ψ是波函数,E是能量。
对于无限深方势阱来说,势能函数V(x)在势阱内为0,在势阱外为无穷大,因此薛定谔方程可以简化为:-ħ²/2m * d²Ψ/dx² = EΨ4. 波函数的边界条件在一维对称无限深方势阱中,波函数的边界条件非常明确,因为势能在势阱外为无穷大,粒子无法透过势垒逃逸出去,故波函数在势阱外为0。
而在势阱内部,波函数要满足Ψ(0) = Ψ(a) = 0,这是因为势阱的边界为0。
5. 波函数的表达式根据边界条件,我们可以求解出一维对称无限深方势阱中的波函数表达式。
在势阱内部,波函数的一般形式为:Ψ(x) = Asin(kx) + Bcos(kx)其中,A和B是待定系数,k是波数,根据波函数的边界条件,我们可以求解出波函数的具体形式。
在势阱内部,波函数的波数k为:k = sqrt(2mE) / ħ对于一维对称无限深方势阱,能级是分立的,即E = n²π²ħ² / (2ma²),其中n为正整数。
势阱中的粒子

由此解得最大值得位置为 例如
n = 1, N = 0 n = 2 , N = 0 , 1,
最大值位置 最大值位置
x= Hale Waihona Puke a 23 x= 1a,4a 4
n = 3 , N = 0 ,1, 2 , 最大值位置
3 x = 1 a , 6 a, 5 a, 6 6
可见,概率密度最大值的数目和量子数 相等 相等。 可见,概率密度最大值的数目和量子数n相等。
T=
ψ3 (a)
A
2
2
≈e
−2 a 2m(U0 −E) h
贯穿概率与势垒的宽度与高度有关。 贯穿概率与势垒的宽度与高度有关。
三、谐振子
谐振子的势能为
薛定谔方程为
1 2 1 2 2 U = kx = mω x 2 2 2 d ψ 2m 1 2 2 + 2 (E − mω x )ψ = 0 2 dx h 2
例题2试求在一维无限深势阱中粒子概率密度的最大 例题 试求在一维无限深势阱中粒子概率密度的最大 值的 位置。 位置。 解: 一维无限深势阱中粒子的概率密度为
2 φn (n) = a sin2 nπ x a 2
n = 1,2,3,L
将上式对x求导一次, 将上式对 求导一次,并令它等于零 求导一次
d φn ( x ) dx
0 U(x) = ∞
0< x <a
x ≤ 0, x ≥ a
∞
∞
o
a
x
dU(x) 保守力与势能之间的关系: 保守力与势能之间的关系: F = − dx 在势阱边界处,粒子要受到无限大、 在势阱边界处,粒子要受到无限大、指向阱内的 表明粒子不能越出势阱, 力,表明粒子不能越出势阱,即粒子在势阱外的概 率为0 率为0。 势阱内的一维定态薛定谔方程为 薛定谔方程为: 势阱内的一维定态薛定谔方程为:
163一维势阱和势垒问题

0,
mn mn
克罗内克符号
二、势垒穿透和隧道效应
有限高的方形势垒
数学形式:
U
(
x)
0,
U 0 ,
图形形式:
x 0(P区),x a(S区) 0 x a(Q区)
U
考虑粒子的动能 E小于势垒高
U0
度 U0的情况。( E < U0 )
E
PQ S
o ax
U (x) 0, x 0和x a
1
(0 x a)
(x 0及x a)
2
势阱内 0 < x < a
d 2 1
dx2
2E
2
1
0
势阱外 x ≤ 0 ;x ≥a
2 0
理由:因为势壁无限高,所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d 2
d x2
2E
2
0
E是粒子的总能量,E > 0,令 k
定态薛定谔方程变为
d 2
一维无限深方势阱的图形表达形式 :
∞∞
U(x)
粒子只能在宽为 a 的两个无限 高势壁间运动,这种势称为一 维无限深方势阱。
0
ax
因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。
2
2
2
U
(r)
(r )
E
(r )
————定态薛定谔方程
①列出各区域的定态薛定谔方程
若在样品与针尖之间
加一微小电压Ub电子 就会穿过电极间的势
垒形成隧道电流。
隧道电流对针尖与样品间的距离十分敏感。 若控制隧道电流不变,则探针在垂直于样品 方向上的高度变化就能反映样品表面的起伏。
量子力学中的无限深势阱问题

量子力学中的无限深势阱问题量子力学是描述微观世界的物理学理论,它在解释和预测微观粒子行为方面具有重要的作用。
其中,无限深势阱问题是量子力学中的一个经典问题,它帮助我们理解波函数的性质以及粒子在势场中的行为。
无限深势阱问题是指一个粒子被限制在一个势能在某个区域内为无限大,在区域外为零的势场中运动。
这个问题可以用一维的情况来描述,假设势阱的宽度为L,那么势阱内的势能函数可以表示为:V(x) = 0, 0 < x < LV(x) = ∞, x < 0 或者 x > L在经典力学中,粒子在势场中的运动是由牛顿第二定律描述的,而在量子力学中,粒子的运动状态由波函数来描述。
波函数是量子力学中的基本概念,它是一个复数函数,可以用来描述粒子的位置和动量。
对于无限深势阱问题,我们可以使用定态薛定谔方程来求解。
定态薛定谔方程可以表示为:-ħ²/2m * d²ψ(x)/dx² + V(x)ψ(x) = Eψ(x)其中ħ是普朗克常数的约化形式,m是粒子的质量,E是粒子的能量,ψ(x)是粒子的波函数。
在势阱内部,势能V(x)为零,因此定态薛定谔方程可以简化为:-ħ²/2m * d²ψ(x)/dx² = Eψ(x)这是一个简化的定态薛定谔方程,可以通过求解这个方程来得到粒子在势阱内部的波函数。
根据边界条件,当x=0或者x=L时,势能V(x)为无穷大,因此波函数必须为零。
这意味着在势阱的两个边界处,波函数的值为零。
根据上述条件,我们可以得到波函数的一般形式为:ψ(x) = A * sin(kx)其中A是归一化常数,k是波数,可以通过边界条件来确定。
当x=0时,波函数为零,因此有sin(0) = 0,这意味着kx = 0,即k = 0。
当x=L时,波函数为零,因此有sin(kL) = 0,这意味着kL = nπ,其中n是一个整数。
通过边界条件,我们可以得到k的取值为:k = nπ/L由于波函数必须是归一化的,我们可以通过归一化条件来确定归一化常数A。
16-3一维势阱和势垒问题解读
x a
a x
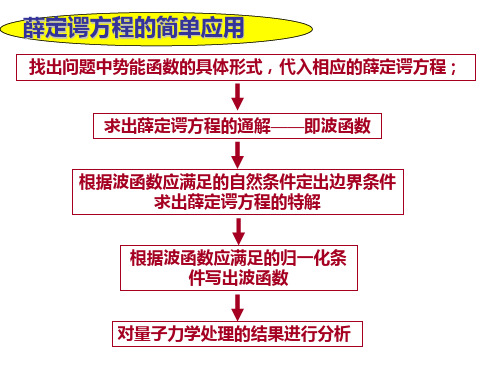
第k激发态(n=k+1)有k个节点。
(2)一维无限深势阱 的粒子位置概率密度 分布
1
2
n 1
0 2 2 n 2 a
2
x
0 无数峰:量子 经典均匀分布 0
a a n 1,x 处,几率最大 0 3 2 b n ,峰数 ,当n 时,
4
U0
II
III
o
a
x
而在微观粒子的情形,却会发生反射。
ቤተ መጻሕፍቲ ባይዱ
(2)E<U0 从解薛定谔方程的结果来看,在 势垒内部存在波函数2。即在势垒内 部找出粒子的概率不为零,同时,在 x>a区域也存在波函数,所以粒子还 I 可能穿过势垒进入x>a区域。
V
V0
II
III
o
a
x
粒子在总能量E小于势垒高度时仍能贯穿势垒的 现象称为隧道效应。
式中 A和α是待定常数,由边界条件和归一化条 件确定。
( x) A sin( kx )
从物理上考虑,粒子不可能透过阱壁,因而按照波 函数的统计诠释,要求在阱壁上和阱外波函数为0。 考虑波函数在阱壁上等于零的情况,即
(0) 0, (a) 0
————边界条件
(0) 0
这说明:并非任何 E值所对应的波函数都能满足一维 无限深方势阱所要求的边界条件,只有当能量取上式 给出的那些分立的值 En(体系的能量本征值)时, 相应的波函数才是物理上有意义的,即本问题中体系 的能量是量子化的,亦即体系的能谱是分立的。
2
2
2 2 2
( x) A sin kx
nx n ( x) A sin( ) a
量子力学-无限深势井

当粒子在势场U(x,y,z) 中运动时,其定态Schrö dinger 方程为:
令 ψ(x,y,z) = X(x) Y(y) Z(z) E = Ex + Ey + Ez 于是S-方程化为三个常微分方程:
一维运动就是指在某 一方向上的运动。
4
第二章
(二)一维无限深势阱
0, U ( x) | x | a | x | a
n 1,2,3,
(1)n = 1, 基态,
2 2 E1 8a
与经典粒子不同,粒子的最低能量不为零,这个最低能 量称为 “零点能”,这是量子效应,微观粒子具有波动 性的表现。从波的角度是可以理解的,因为“静止的波” 没有意义。
13
第二章 (2)n = 0 , E = 0, ψ = 0,态不存在,无意义。
1 A , a
能量最低的态称为基态,其上为第一激发态、第二激发态依次类 推。 11
第二章
(三)宇称
(1)空间反射:空间矢量反向的操作。 r r (r , t ) ( r , t ) ( r , t ) (r , t ) (2)此时如果有: ( r , t ) (r , t ) 称波函数具有正宇称(或偶宇称); ( r , t ) (r , t ) 称波函数具有负宇称(或奇宇称); ( r , t ) (r , t ) (3)如果在空间反射下, 则波函数没有确定的宇称。
2 d 2 [ U 1 ( x )]X ( x ) E x X ( x ) 2 dx2 2 d 2 [ U 2 ( y )] ( y ) E yY ( y ) Y 2 dy2 [ d U 3 ( z )]Z ( z ) E z Z ( z ) 2 dz2
16-3 一维势阱和势垒问题
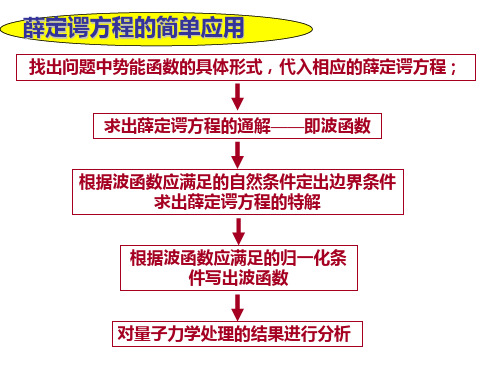
ψ(x) = Asinkx
nπx ψn(x) = Asin ( ) a
ka = nπ , n = 1,2,3,......
(0< x < a) n =12,3 , ,...
与能量本征值E 与能量本征值 n相对应的本征波函数ψn (x)为:
利用归一化条件
∫
2
ψn(x) dx = ∫ ψn(x) dx =1 0 −∞
ψ2 =0
理由:因为势壁无限高 所以粒子不能穿透势壁 理由 因为势壁无限高,所以粒子不能穿透势壁 故势 因为势壁无限高 所以粒子不能穿透势壁,故势 阱外的 波函数为零
定态薛定谔方程为
d ψ 2µ E + 2 ψ =0 2 dx ℏ
2
E是粒子的总能量,E > 0,令 是粒子的总能量, 是粒子的总能量 , 定态薛定谔方程变为
ℏ
V
U0
0≤ x≤a
I II III
O a
x
ℏ
d2ψ1(x) 2 + k ψ1(x) = 0, x ≤0 2 dx 三个区间的薛定 2 谔方程简化为: 谔方程简化为: d ψ 2 ( x) − γ 2ψ ( x) = 0, 0≤ x≤a 2 2 dx d 2ψ3 (x) 2 + k ψ3 (x) = 0, x≥a 2 dx
一维无限深方势阱的数学表达形式 :
U (x ) =
0
(0 < x < a )
∞ ( x ≤ 0 及x ≥ a )
一维无限深方势阱的图形表达形式 : ∞
U(x)
∞ 粒子只能在宽为 a 的两个无 限高势壁间运动, 限高势壁间运动,这种势称为 一维无限深方势阱。
0
a
x
因为系统的势能与时间无关, 因为系统的势能与时间无关,因此这是一个定 态问题,可以用定态薛定谔方程进行求解。 态问题,可以用定态薛定谔方程进行求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
薛定谔方程应用举例 (一维问题) 一维问题)
求解问题的思路: 求解问题的思路: 1. 写出具体问题中势函数U(r)的形式代入方程 2. 用分离变量法求解 3. 用归一化条件和标准条件确定积分常数 只有E取某些特定值时才有解
本征值 本征函数
一、一维无限深势阱 模型的建立: 微观粒子被局限于某区域中, 模型的建立 :微观粒子被局限于某区域中 ,并在该 区域内可以自由运动的问题 →简化模型 简化模型。 。 例如: 例如: 金属中自由电子 受规则排列的晶格点阵作用 简 相互碰撞 (简化: 简化:交换动量) 交换动量) 化 只考虑边界上突然升高的势 能墙的阻碍 —— 势阱 认为金属中自由电子不能逸出表面 ——无限深势阱 可解释金属导热、 可解释金属导热、导电、 导电、顺磁性…...
ik1 x
+ B3e
− ik1 x
d 2 ψ 2m + ( E − U 0 )ψ = 0 d x 2 ℏ2
第一项: 第一项: 向x方向传播的波 第二项: 第二项: 向-x方向传播的波
]
(0 ≤ x ≤ a )
E −i (k1x+ t ) ℏ
]
3
通解: 通解:
ψ 1 = A1eik x + B1e − ik x
(0 < x < a)
x
o
a
2. 求解波函数
①
d2ψ 2m + 2 ( E − ∞ )ψ = 0 d x2 ℏ
代入一维定态薛定谔方程的一般形式
d2ψ 2m + (E − U )ψ = 0 d x2 ℏ2
该方程只有解Ψ 该方程只有解Ψ=0 即粒子不能逸出势阱) x ≤ 0, x ≥ a ψ = 0 (即粒子不能逸出势阱)
最小能量 E 1即零点能 ,
粒子不可能静止不动, 粒子不可能静止不动,
x
注意: 注意: 解为驻波 解为驻波形式 驻波形式
由
E=
k 2ℏ 2 n 2π 2 ℏ 2 = = n 2 E1 2m 2ma 2
( n = 1,2,3,...)
2) 粒子在势阱中的概率分布 经典: 粒子匀速直线运动 经典: 势阱中U = 0,粒子匀速直线运动 粒子在势阱内各处出现的概率相等 量子: 量子:
由归一化条件
∫ |ψ
−∞
∫ψ ⋅ψ
∞
*
d x = ∫ A sin 2
2 0
A=
2 a
4.讨论解的物理意义 讨论解的物理意义 1) 无限深势阱中粒子的能量量子化 nπ 由 k 2 = 2mE k= 2 a ℏ 2 2 2 2 2 k ℏ nπ ℏ 得 E= = = n 2 E1 ( n = 1,2,3,...) 2m 2ma 2
1 1
U
U
U0 入射波+反射波
U0 透射波
ψ 2 = A2 e
ψ 3 = A3e
ik 2 x
+ B2 e
+ B3e
−k1 x
由 x > a 处无反射波: 处无反射波: B 3 = 0 令 A 1 = 1(以入射波强度为标准) 以入射波强度为标准)
ψ 1(0) = ψ 2 (0) dψ 1 dψ 2
练习:
解:
解:
|ψ |2 =
a 4
2 2πx sin a a
区间发现粒子的概率。 。 求:0 ~ L 区间发现粒子的概率 3
L L
由归一化条件
2 2 2 2 ∫ |ψ | dx = ∫ c x ( L − x) dx = 0 0
2 πx p = ∫ |ψ |2 d x = ∫ sin 2 dx a a 0 0
1 ψ (x ) = π (1 + ix )
∞
得:
x=0
即在 x = 0 处粒子的概率密度最大。 处粒子的概率密度最大。
得:
A =
π
二. 势垒 隧道效应
模型: 模型:金属表面的势能墙不是无限高, 金属表面的势能墙不是无限高,而是有限值 势函数: 势函数:
U ( x) =
令
k12 =
2mE ℏ2
2 k2 =
于是: 于是:
2 nπ x sin ψ ( x) = a a
2 nπ x sin ⋅e a a
i − Et ℏ
(n = 1,2,3,...)
(n = 1,2,3⋯)
E只能取一系列分离值n 2 E1
式中
E n=4 n=3 n=2 n=1
E1 =
π 2ℏ 2
2ma 2
o 满足不确定关系 a
Ψ ( x, t ) =
2 nπx − ℏ Et sin e a a 2 nπx 概率密度 | Ψ ( x , t ) |2 =|ψ ( x ) |2 = sin 2 a a
波函数 Ψ ( x, t ) = x
(n = 1,2,3,...)
波函数为驻波形式, 波函数为驻波形式,势阱中不同位置强度不等, 势阱中不同位置强度不等,粒 子出现的概率不相同。 。 子出现的概率不相同
4
a
1 2 5 c L =1 30
a
=
∫ a π sin
0
4
2a
2
πx
a
d(
πx
a
)
4
得
L
−2
c=
30 L5
2
ψ=
L
1 πx 1 2 2π x = ( 2 − sin ) π a 4 a
a
30 x( L − x ) L5
= 9.08 × 10
0
p=
∫ |ψ |
0
3
dx =
∫L
0
3
30
5
x 2 ( L − x ) 2 dx =
罗雷尔( 罗雷尔(瑞士) 瑞士) (Heinich Rohrer,1933-)
(获1986年诺贝尔物理奖 1986年诺贝尔物理奖) 年诺贝尔物理奖)
样品表面 探针表面
由于隧道效应逸出的电子, 由于隧道效应逸出的电子,“电子云” 电子云”
加电压形成隧穿电流——对表面间距异常敏感 通过探测物质表面的隧道电流来分辨其表面特征
U
U
o
U
a
∞
4. 讨论解的物理意义, 讨论解的物理意义, 得出粒子在空间的概率分布。 即求|Ψ |2,得出粒子在空间的概率分布 得出粒子在空间的概率分布。
o
a
求解问题的步骤: 求解问题的步骤: 1. 写出具体问题中势函数U(r)的形式, 的形式,代入一维定态 薛定谔方程的一般形式, 薛定谔方程的一般形式,得本问题中的薛定谔方程。 得本问题中的薛定谔方程。
设粒子在一维无限深势阱运动 势函数 U(x) =
得本问题中的薛定谔方程:
得本问题中的薛定谔方程: 得本问题中的薛定谔方程:
d 2 ψ 2m Eψ = 0 + d x 2 ℏ2
d 2 ψ 2m (E − ∞ )ψ = 0 + d x2 ℏ2
U
∞
0<x<a
x ≤ 0, x ≥ a
x
o
a
U
∞
0
∞
( x ≤ 0, x ≥ a )
17 = 0 .21 81
A 方向运动,其波函数为 ψ (x) = 1 + ix P.247 设粒子沿 x 方向运动, 1.将此波函数归一化; 将此波函数归一化; 17-6 2.求出粒子按坐标的概率分布函数; 求出粒子按坐标的概率分布函数; 练习: 3.在何处找到粒子的概率最大? 在何处找到粒子的概率最大?
既透射, 既透射,也反射
( B1 ≠ 0 )
( A3 ≠ 0 )
(a )
E < U0
既透射, 既透射,也反射
U
入射波+反射 波
U0
3. 扫描隧穿显微镜( 扫描隧穿显微镜(STM)
透射波 ——具有原子级高分辨率, 具有原子级高分辨率,继光学显微镜、 继光学显微镜、 电子显微镜之后的第三代显微镜。 。 电子显微镜之后的第三代显微镜
4
k= nπ a
x
o
a
( n = 1, 2 , 3 ⋯ )
思考: 思考:n为什么不取零和负数? 为什么不取零和负数?
ψ ( x ) = A sin
nπ x a
( n = 1,2,3,...)
1
ψ ( x ) = A sin
nπ x a
∞ −∞
a
(n = 1,2,3,...)
|2 d x = 1
nπ x d x =1 a
2m ( E −U0 ) ℏ2
( x < 0 , x > a)
0
x < 0,
x>a
U
d2 ψ + k12ψ = 0 d x2
d2 ψ 2 + k2 ψ =0 d x2
1
U0
(0 ≤ x ≤ a )
1
U0
代入 得
0≤ x≤a
d 2 ψ 2m + 2 ( E − U )ψ = 0 d x2 ℏ
d ψ 2mE + 2 ψ =0 d x2 ℏ
2.
概率密度为: 概率密度为:
p 2 = ψ (x ) = dx
3. 令:
1 1 = π (1 + x 2 ) π (1 + ix )
2
解: 1. 由归一化条件
d 2 ψ (x ) = 0 dx
−∞
∫ 1 + ix
∞
A
2
dx =
∞
−∞
∫ 1+ x
1
A2
2
dx = A2arctg x − ∞ = A2π = 1
2
ψ1 = A1eik x + B1e−ik x ( x < 0)
