三年级奥数一、巧填竖式
三年级奥数(1)-第七讲--简单加减法竖式

13
例题4
如图,用0,1,2,3,4,5,6,7,8,9这十个数字各一次,完成下面竖式,已经给出3个数字。
1
9
7
练习4
如图,用0,1,2,3,4,5,6,7,8,9这十个数字各一次,完成下面竖式,已经给出5个数字。
64
28
3
例题5
在下面竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字,求出每 个汉字代表什么数字?
简单加减法竖式--进位与借位
教师:巨人龙老师
张老师把红、白、蓝各一个气球分别送给三位小朋 友。根据下面三句话,请你猜一猜,他们分到的各 是什么颜色的气球?
(1)小春说:“我分到的不是蓝气球。” (2)小宇说:“我分到的不是白气球。” (3)小华说:“我看见张老师把蓝气球和红气球分给 上面两位小朋友了。” 小春分到( )气球。小宇分到( )气球。小华分到( ) 气球。
14 9 2
练习2
在竖式的各个方格内,分别填入恰当的数字,使竖式成立,所填数字之和最小是多 少?最大是多少?
16 9 7
例题3
如图所示,在竖式的各个方格内填入合适的数字,使得竖式成立,那么6个数字之 和最大是多少?
862
练习3
如图所示,在竖式的各个方格内填入合适的数字,使得竖式成立,那么7个数字之 和最小是多少?
行程问题: (1)三个基本概念 (2)三个基本公式:
(3)相遇问题的公式变形:
(4)追及问题的公式变形:来自题1--线段图的用法在竖式中填入合适的数字,使得竖式成立。
38
2
7
3
4
练习1
完成竖式
9 576
2
1
91 6 0
例题2
在竖式的各个方格内,分别填入恰当的数字,使竖式成立,所填数字之和最大是多 少?
三年级奥数竖式数字迷

竖式数字迷知识集锦解答竖式数字谜时,应注意以下几点:(1)数字谜空格中只能填写0,1,2,3,4,5,6,7,8,9,而且最高位不能为0;(2)进位要留意,不能漏掉了;(3)答案有时不唯一;(4)两数字相加,最大进位为1,三个数字相加最大进位为2;(5)两数字相乘,最大进位为8;(6)相同的字母(汉字或符号)代表相同的数字,不同的字母(汉字或符号)代表不同的数字。
例题集合例1下面的算式中,只有5个数字已经写出,请补上其他的数字。
6+练习1 在下面竖式的空格内,各填入一个合适的数字,使竖式成立。
35+0 6例2 内各填入一个合适的数字,使算式成立。
0 0- 5 0 99 3练习2 在下面竖式的空格内,各填入一个合适的数字,使竖式成立。
5 8- 2 79 4例3 下面是一个六位数乘以一个一位数的算式,不同的汉字表示不同的数,相同的汉字表示相同的数,其中的六位数是。
小学希望杯赛×赛9 9 9 9 9 9练习3 下面是一道题的乘法算式,请问:式子中,A、B、C、D、E分别代表什么数字?1 A B C D E× 3A B C D E 1例4 里填上合适的数字,使算式成立。
4 A 4 B× 6 思考:× C 61 058 8练习4 里填上合适的数字,使算式成立。
7 6×1 83 1 0例5 里填上合适的数字,使算式成立。
9 45 53 7练习5 里填上合适的数字,使算式成立。
7课堂练习一、填空题。
1)。
+1 9 82)。
-2 93中的数字之和为()。
× 64、要使下面的竖式成立,则A+B+C=()。
5 7 8- A B CA B C二、选择题。
5、右边竖式中x为()时,竖式才可能成立。
3 2 5A.1B.2 - x 8 yC.3D.7 3 z6、右边竖式中的乘数应该是(),才可能使竖式成立。
A.4B.6 ×C.2D.5 9 4 07、右边竖式的x、y为()时,竖式才能成立。
小学三年级奥数讲解.竖式数字谜

竖式数字谜第1部分:加、减法竖式数字谜这一部分主要讲加、减法竖式的数字谜问题。
解加、减法数字谜问题的基本功,在于掌握好上一讲中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是通过综合观察、分析,找出解题的“突破口”。
题目不同,分析的方法不同,其“突破口”也就不同。
这需要通过不断的“学”和“练”,逐步积累知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数都是两位数,从第一个加数个位是5与和的个位数是9,可以推断第二个加数的个位数必定是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数都是9,这样,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只知道其中两个加数的个位分别是7、5,而和的个位却是8,肯定是进位造成的。
从7+5+?=□8,可判断另一个加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:这个减法算式,只告知了减数是1,被减数、减数都不知道!全式应有八个数字,其中七个都是未知数,初看是比较难解的。
但是认真分析一下减法算式各部分的数位,便可以找到突破口。
被减数有四位,减去1后,差却成了三位数,只有相减时连续退位,才会如此。
那么,什么数减去1需要向高位借数呢?只有“0”!而最高位退1后成了0,表明被减数的最高位就是“1”。
这样,就可以断定被减数是1000。
知道了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
那么,?-8=9,可知被减数十位上是7。
再看百位,因为被减数是四位数。
(完整)三年级奥数乘除法竖式迷
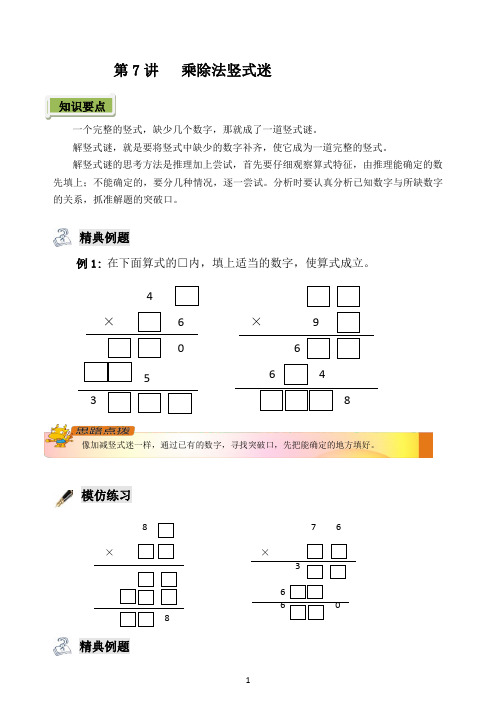
1第7讲 乘除法竖式迷知识要点一个完整的竖式,缺少几个数字,那就成了一道竖式谜。
解竖式谜,就是要将竖式中缺少的数字补齐,使它成为一道完整的竖式。
解竖式谜的思考方法是推理加上尝试,首先要仔细观察算式特征,由推理能确定的数先填上;不能确定的,要分几种情况,逐一尝试。
分析时要认真分析已知数字与所缺数字的关系,抓准解题的突破口。
精典例题例1: 在下面算式的□内,填上适当的数字,使算式成立。
模仿练习精典例题像加减竖式迷一样,通过已有的数字,寻找突破口,先把能确定的地方填好。
4× 6 053× 9 6 6 4 88×87 6× 3 66 0例2: 在方框里填入合适的数字,使竖式成立。
模仿练习精典例题例3: 下面竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请求出这些汉字所代表的数字。
模仿练习除法在寻找突破口时,还需要注意有没有余数,而且余数要比除数小。
在有汉字或字母的竖式迷中,要利用不同的汉字或字母表示不同的数字这一规则来做8 2 9 )16 4 )228 ) 5 6 22 8 07 )6奥运× 奥 运8北 京 好 运科 学 × 学 科 1 1 4甲乙 丙 丁× 43甲=( ) 乙=( )科=( ) 学=( ) 丙=( ) 丁=( )精典例题例4: 在下面竖式的□里,各填入一个合适的数字,使算式成立。
模仿练习家庭作业1. 在方框里填上合适的数字,让竖式成立。
被除数和除数都不知道,可以先通过余数先确定除数的范围,再根据已知的数来确定除数。
4427(2)52962504(1)2.下面是一道题的乘法算式,请问:式子中,A,B,C,D,E 分别代表什么数字?131A B C D E ABCDE× 6 11 9 0 46 ) 3 844 )425A=( ) B=( ) C=( ) D=( ) E=( )3.在右式中,“我”、“爱”、“数”、“学”分别代表什么数时,乘法竖式成立?爱数学 4× 3我爱数学我=( ) 爱=( ) 数=( ) 学=( )4.“我”、“们”、“爱”、“祖”、“国”各代表一个不同的数字,它们各等于多少时,右边的乘法竖式成立?国祖爱们我× 4我们爱祖国我=( ) 们=( ) 爱=( ) 祖=( ) 国=( )5。
三年级奥数(1)第六讲--简单加减法竖式

2 37
6
6
8
练习4
完成减法竖式。
8
7
例题5
下面是一个加减混合的算式,请完成它。
1 9 9
5
练习5
在图中方格中填入合适的数,使竖式成立。 1
9
91
思考题
在空格内填入互不相同的数字,使算式成立, 请写出两种填法。
66 6 6
感谢您的观看
9
81 5 4
69
3
2
练习2
完成下面两个竖式 7
9 78
3
4
23 4 0
例题3
在图中空格处填入合适的数字,使竖式成立
9
9
1
9
11 1 1
练习3
将下面两个竖式填写完整。
8
6
7
4
5 48
7
21
7
4
知识预讲(复习)
下面几个竖式中,哪些数是确定的?
知识预讲(复习)
下面几个竖式中,哪些数是确定的?
例题4
知识预讲(复习)
竖式计算的顺序:
例题1
在下面的竖式中填入恰当数字,使
在下面的竖式中填入恰当数字,使竖式成立。
1
4
9
6
9 5 47
4
6
41
知识预讲(复习)
加法进位的讨论:
2个数字相加,最多进1;3个数字相加最多进2;4个数字相加最多进3.
例题2
在图中空格处填入恰当的数字,使竖式成立。
三年级奥数(1)
简单加减法竖式 (竖式填空格)
教师:巨人龙老师
课前热身
有一天,某一珠宝店被盗走了一块贵重的钻石。经侦破,查明作案人肯定在甲、乙、丙、丁之中。于 是,对这四个重大嫌疑犯进行审讯。审讯所得到的口供如下:
小学三年级奥数第1课速算与巧算1试题附答案-精品

小学三年级上册数学奥数知识点讲解第1课《速算与巧算1》试题附答案一、加法中的巧算1.什么叫“补数”?两个数相加,若能恰好凑成整十、整百、整千、整万…,就把其中的一个数叫做另一个数的“补数”。
如:1+9=10,3+7=10,2+8=10,4+6=10,5+5=10。
又如:11+89=100,33+67=100,22+78=100,44+56=100,55+45=100,在上面算式中,1叫9的“补数”;89叫11的“补数”,11也叫89的“补数”也就是说两个数互为“补数”。
对于一个较大的数,如何能很快地算出它的“补数”来呢?一般来说,可以这样“凑”数:从最高位凑起,使各位数字相加得9,到最后个位数字相加得10。
如:87655f12345,46802—53198,87362—12638,…下面讲利用“补数”巧算加法,通常称为“凑整法”。
2.互补数先加。
例1巧算下面各题:①36+87+64②99+136+101③1361+972+639+283.拆出补数来先加。
例2①188+873②548+996③9898+2034.竖式运算中互补数先加。
6 8\ 2+12 3%91 622 9 8 3如:二、减法中的巧算1.把几个互为“补数”的减数先加起来,再从被减数中减去。
例3①300-73-27②1000-90-80-20-102.先减去那些与被减数有相同尾数的减数。
例4①4723-(723+189)②2356-159-2563.利用“补数”把接近整十、整百、整千…的数先变整,再运算(注意把多加的数再减去,把多减的数再加上)。
例5①506-397②323-189③467+9970987-178-222-390三、加减混合式的巧算1.去括号和添括号的法则在只有加减运算的算式里,如果括号前面是“十”号,则不论去掉括号或添上括号,括号里面的运算符号都不变;如果括号前面是“/号,则不论去掉括号或添上括号,括号里面的运算符号都要改变,“+”变变“+”,即:a+(b+c+d)=a+b+c+da-(b+a+d)=a-b-c-da-(b-c)=a-b+c例6①100+(10+20+30)②100-(10+20+30)③1()0-(30-10)例7计算下面各题:①100+10+20+30②100-10-20-30③100-30+102.带符号“搬家”例8计算325+46-125+543.两个数相同而符号相反的数可以直接“抵消”掉例9计算9+2-9+34.找“基准数”法几个比较接近于某一整数的数相加时,选这个整数为“基准数”。
三年奥数 巧填竖式

三年奥第十七讲巧填竖式(一张卷)
一、在□里填上合适的数,使竖式成立(109页例1、111页例4)
二、在□里填上合适的数,使竖式成立(114页2、115页3)
三、在□里填上合适的数,使竖式成立(114页2、115页3)
四、下面竖式中每一个汉字代表一个数字,不同汉子代表不同数字,
当它们各代表什么数字时竖式成立(115页5)
一、求面积,(141页例1)
图
二、有一块长方形菜地,长29米,宽15米,菜地中间横、竖各有一条宽1米的路,正好把菜地4等分,每块菜地的面积是多少?把小路铺上边长为10分米的方砖,需要多少块?每块砖11元,需要多少元?
图(1)
(2) (3)
三、两个完全一样的正方形部分重叠后成为一个长方形,这个长方形的长16厘米,重叠部分8厘米,求长方形的面积
(图)
一、用4个完全相同的长方形拼成一个面积为100平方厘米的正方形(包括中
间部分)每个小长方形的周长是多少?(147页8)
(图)
二、用两张长方形纸片和一个正方形纸片拼成一个大正方形,两个长方形的面
积分别为64平方厘米和48平方厘米,求小正方形的面积(147页9)(图)
三、下图是一个大正方形,里面两个阴影部分是小正方形,已知两个阴影小正
方形的周长和是64米,求大正方形的面积(148页12)
四、(不画图)一个较大长方形的3/16与一个较小长方形的3/4相等,较大长方
形的面积是较小长方形的几倍?(自编)。
(完整)小学三年级奥数讲解.竖式数字谜

(完整)小学三年级奥数讲解.竖式数字谜竖式数字谜第1部分:加、减法竖式数字谜这一部分要紧说加、减法竖式的数字谜咨询题。
解加、减法数字谜咨询题的基本功,在于掌握好上一说中介绍的运算规则(1)(2)及其推演的变形规则,另外还要掌握数的加、减的“拆分”。
关键是经过综合观看、分析,找出解题的“突破口”。
题目别同,分析的办法别同,其“突破口”也就别同。
这需要经过别断的“学”和“练”,逐步积存知识和经验,总结提高解题能力。
例1:在下列各竖式的□中填上适当的数字,使竖式成立解:加数基本上两位数,从第一具加数个位是5与和的个位数是9,能够判断第二个加数的个位数必然是4。
即5+?=9。
从和的百位数与十位数是18,可断定,两个加数的十位数基本上9,如此,谜便揭开了.例2:在下列各竖式的□中填上适当的数字,使竖式成立解:三个加数,只懂其中两个加数的个位分不是7、5,而和的个位却是8,确信是进位造成的。
从7+5+?=□8,可推断另一具加数的个位必为6,十位上5+□+7=□7,可断定:□加上个位进上来的1是5,去掉进上来的1应是4。
百位上2+□=6,可知:□=4,去掉进上来的1,□=3。
例3:在下列各竖式的□中填上适当的数字,使竖式成立解:那个减法算式,只告知了减数是1,被减数、减数都别懂!全式应有八个数字,其中七个基本上未知数,初看是比较难解的。
然而仔细分析一下减法算式各部分的数位,便能够找到突破口。
被减数有四位,减去1后,差却成了三位数,惟独相减时延续退位,才会这样。
这么,啥数减去1需要向高位借数呢?惟独“0”!而最高位退1后成了0,表明被减数的最高位算是“1”。
如此,就能够断定被减数是1000。
懂了被减数和减数,差就迎刃而解了!例4:在下列各竖式的□中填上适当的数字,使竖式成立解:个位上,被减数是7,差是6,可知减数是1。
十位上,减数是8,差是9,可知被减数必小于8,借位后才使差比减数大的。
这么,?-8=9,可知被减数十位上是7。
