苏教版八年级数学下册教案--8.3 频率与概率 (2)
最新苏教版八年级数学下册8.3频率与概率公开课优质教案(2)
结果如下：
n
0 0 0 0 00 炼 学 生 地
每批粒数
n
10 30 40 60 10 20 30 0 0 0 0 00 20 00
发芽地频
数m
28 34 55 94 口 头 表 达 96
3 4 2 8 能力，通
发芽地频
数m
发芽地频
28 34 55 94 19 28 96
3 4 2 8 12 48
发芽地频 率m
8.3 频率与概率 (2)
教学目标
教学重点 教学难点
1．认识到在实际生活中，人们常把试验次数很大时，事件发生地频 率作为概率地估计值； 2．初步体会到出现机会地均等与试验结果是否具有等可能性地关系； 3．通过试验，加深对频率与概率地关系地理解． 用频率地稳定值去估计概率． 1．经历试验过程，培养随机观念；
升华地作 用．
作为其概率地估计值．例如，根据统计学 出现“正面朝上” 与出现“反 动 中 ， 培
家历次做“抛掷质地均匀地硬币试验”地 面朝上” 地机会就均等， 试验地 养 学 生 合
结果中，可以估计“正面朝上”地概率为 结果具有等可能性； 在“掷图钉 作 交 流 和
0.5 ；根据“某批足球产品质量检验结果” ， 试验”中，显然钉帽地质量较大， 发 散 思 维
形成过
活动二 某种绿豆在相同条件下发芽试验地 结果如下：
程，让学
生对知识
地认识由
感性上升
到理性．
小组讨论， 合作交流， 代表
通过
回答：
小组合
每批粒数 2 5 1 5 1 5 1 1 作 ， 提 高
每批粒数
n
发芽地频
数m
112 3
n
15
苏科版数学八年级下册8.3《频率与概率》说课稿2
苏科版数学八年级下册8.3《频率与概率》说课稿2一. 教材分析《频率与概率》是苏科版数学八年级下册第8.3节的内容。
本节课的主要内容是让学生理解频率与概率的概念，掌握频率与概率之间的关系，并通过实例让学生学会如何运用频率估计概率。
教材通过引入频率这一概念，引导学生从实际问题中发现概率的规律，从而培养学生的数学思维能力和解决问题的能力。
二. 学情分析学生在学习本节课之前，已经学习了概率的基本概念，对概率有一定的认识。
但学生对频率与概率之间的关系可能还不够清晰，需要通过实例来进一步理解和掌握。
此外，学生可能对如何从实际问题中提出概率模型并运用频率估计概率还存在一定的困难。
三. 说教学目标1.知识与技能目标：让学生理解频率与概率的概念，掌握频率与概率之间的关系，学会如何运用频率估计概率。
2.过程与方法目标：通过实例分析，培养学生从实际问题中提出概率模型的能力，培养学生的数学思维能力和解决问题的能力。
3.情感态度与价值观目标：激发学生对数学学习的兴趣，培养学生的团队合作意识和交流表达能力。
四. 说教学重难点1.重点：频率与概率的概念，频率与概率之间的关系。
2.难点：如何从实际问题中提出概率模型并运用频率估计概率。
五. 说教学方法与手段1.教学方法：采用问题驱动法、案例教学法和小组合作学习法。
2.教学手段：利用多媒体课件进行教学，通过实例和动画演示帮助学生直观地理解频率与概率的概念和关系。
六. 说教学过程1.导入新课：通过一个简单的实例，引导学生思考频率与概率之间的关系。
2.讲解概念：介绍频率与概率的定义，并通过实例帮助学生理解这两个概念。
3.分析关系：引导学生分析频率与概率之间的关系，让学生明白频率是概率的近似值。
4.应用实例：通过具体的实例，让学生学会如何从实际问题中提出概率模型并运用频率估计概率。
5.总结提高：让学生总结本节课的主要内容和收获，提高学生对频率与概率的理解和应用能力。
七. 说板书设计板书设计主要包括频率与概率的定义、频率与概率之间的关系以及如何从实际问题中提出概率模型并运用频率估计概率的步骤。
八年级数学下册第8章认识概率8.3频率与概率教案苏科版
8.3 频率与概率教学目标：1．理解随机事件发生的可能性有大有小，概率的定义；2．概率是随机事件自身的属性，它反映随机事件发生的可能性大小；3．在多次重复试验中，体会频率的稳定性．教学重点：频率稳定性的理解．教学难点：频率稳定性的理解．教学过程：一、情境创设飞机失事会给旅客造成意外伤害．一家保险公司要为购买机票的旅客进行保险，应该向旅客收取多少保费呢？为此，保险公司必须精确计算出飞机失事的可能性有多大．类似这样的问题在我们的日常生活中也经常遇到．例如：抛掷1枚均匀硬币，正面朝上．在装有彩球的袋子中，任意摸出的1个球恰好是红球．明天将会下雨．抛掷1枚均匀骰子，6点朝上．……随机事件发生的可能性有大有小．一个事件发生可能性大小的数值，称为这个事件的概率．若用A表示一个事件，则我们就用P（A）表示事件A发生的概率．通常规定，必然事件发生的概率是1，记作P（A）＝1；不可能事件发生的概率为0，记作P（A）＝0；随机事件发生的概率是0和1之间的一个数，即0＜P（A）＜1．（要求：认真理解，积极参与思考，激发学习内驱力．归纳引出概念：一个随机事件发生的概率是由这个随机事件自身决定的，并且是客观存在的．概率是随机事件自身的属性，它反映这个随机事件发生的可能性大小．）二、探索活动活动一、做“抛掷质地均匀的硬币试验”，每人10次．分别汇总5人、10人、15人……的试验结果，并将试验数据汇总填入下表：（要求：互相讨论，踊跃回答：观察上面的折线统计图，你发现了什么规律？请与同学交流． 下表是小明抛硬币试验获得的数据（折线图在教材P45）： 抛掷次数50100150200250300350400450500正面朝上的频数20537098115156169202219244正面朝上的频率0.40.530.470.490.460.520.480.510.490.49活动二、观察教材P45折线统计图，当抛掷硬币次数很大时，正面朝上的频率是否比较稳定？下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据．观察此表，你发现了什么？（要求：学生畅所欲言，勇于发表自己的看法，小组推选出代表回答．从上表可以看出：“正面朝上”的频率总在21附近波动，而且近似等于21．） 活动三、表2是某批足球产品质量检验获得的数据． 抽取的足球数n50 100 200 500 1000 2000 优等品频数m46 93 194 472 953 1903 优等品频数nm （1）填写表中的空格；（2）画出优等品频率的折线统计图；（3）当抽取的足球数很大时，你认为优等品的频率会在哪个常数附近摆动？（要求：讨论后共同归纳．从表1可以看到，当抽查的足球数很多时，抽到优等品的频率n m 接近于某一个常数，并在它附近摆动．通常，在多次重复试验中，一个随机事件发生的频率会在某一个常数附近摆动，并且趋于稳定．这个性质称为频率的稳定性．）三、小结你在本节课中的感悟是什么？你还有什么疑惑？（要求：学生自由地想，大胆地说，表达自己的情感．）。
八年级数学下册8.3频率与概率学案(新版)苏科版
八年级数学下册8.3频率与概率学案（新版）苏科版学习重点知道随机事件随实验次数的增加而逐渐趋稳的事实、学习难点对实验结果的分析、教学流程预习导航1、某啤酒厂搞捉销活动,一箱啤酒(每箱24瓶)中有4瓶的盖内印有“奖”字,•小明的爸爸买了一箱这种品牌的啤酒,但是连续打开4瓶均未中奖,•这时小明在剩下的啤酒中任意拿出一瓶,那么他拿出的这瓶啤酒中奖的机会是( )A、B、C、D、无法确定2、一只小狗在如图的方砖上走来走去，若最终停在阴影方砖上，则甲胜，否则乙胜，那么甲的成功率是（）A、B、C、D、合作探究一情景创设飞机失事会给旅客造成意外伤害。
一家保险公司要为购买机票的旅客进行保险，应该向旅客收取多少保费呢？为此保险公司必须精确计算出飞机失事的可能性有多大。
类似这样的问题在我们的日常生活中也经常遇到。
例如：抛掷1枚均匀硬币，正面朝上、在装有彩球的袋子中，任意摸出的1个球恰好是红球、明天将会下雨。
抛掷1枚均匀骰子，6点朝上、……二、新知探究：随机事件发生的可能性有大有小、一个事件发生可能性大小的数值，称为这个事件的概率（）、若用表示一个事件，则我们就用表示事件发生的概率、通常规定，必然事件发生的概率是1，记作；不可能事件发生的概率为0，记作；随机事件发生的概率是0和1之间的一个数，即0＜＜1、任一随机事件，它发生的概率是由它自身决定的，且是客观存在的，概率是随机事件自身的属性。
它反映这个随机事件发生的可能性大小、。
三、例题分析：抛掷硬币试验：1、分别汇总5人，10人，15人，…，50人的试验结果，并将试验数据汇总填入下表：2、根据上表，完成下面的折线统计图：3、观察上面的折线统计图，你发现了什么规律？请与同学交流、四、展示交流：下表是小明抛硬币试验获得的数据（折线图在课本P45：）观察课本P45折线统计图，当抛掷硬币次数很大时，正面朝上的频率是否比较稳定？观察此表，你发现了什么？从上表可以看出：“正面朝上”的频率总在附近波动，而且近似等于、人们在抛掷硬币、骰子之类的游戏中发现：在充分多次试验中，一个随机事件的频率一般会在一个定值附近摆动，而且试验次数越多，摆动幅度越小。
八年级数学下册第八章认识概率8.3频率与概率2苏科版38
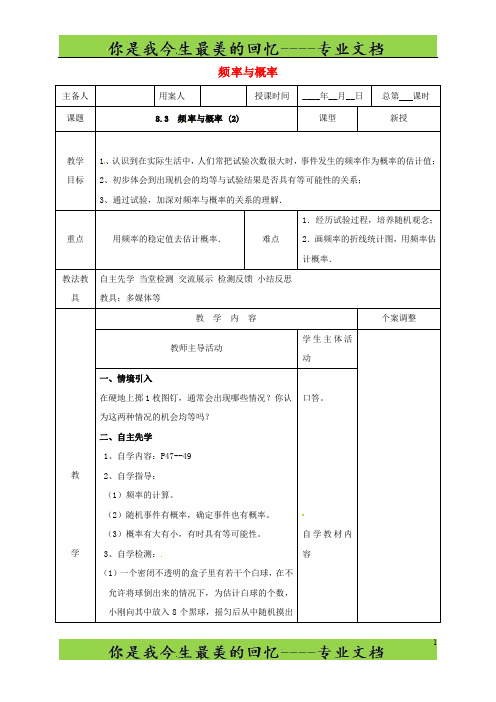
（2）下列说法：
①甲同学在玩掷骰子游戏时说：“6，6，6……啊！真的是6！你只要一直想要某个数，就会掷出那个数！”②乙同学在玩掷骰子游戏时说：“我发现我越是想要某个数就越得不到这个数，倒是不想它反而会掷出那个数。”③丙同学说：“ 中奖率为 的彩票，买1000张一定会中将！”其中，正确的说法是（）
2、自学指导：
（1）频率的计算。
（2）随机事件有概率，确定事件也有概率。
（3）概率有大有小，有时具有等可能性。
3、自学检测：
（1）一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球（ ）
2、一个人随意翻书三次，三次都翻到了偶数页，我们能否说翻到偶数页的可能性就大？
3、袋子里装有红、白两种颜色的小球，质地、大小、形状一样，小明从中随机摸出一个球，然后放回，如果小明5次摸到红球，能否断定袋子里红球的数量比白球多？怎样做才能判断哪种颜色的球数量较多？
4、已知地球表面陆地面积与海洋面积的比均 为3：7。如果宇宙中飞来一块陨石落在地球上，“落在海洋里”与“落在陆地上”哪个可能性更大？
A.①B .②C.③D.都不正确
（3）质疑问难，提出学习中存在的问题。
三、交流展示
（一）展示一
分组展示自主先学中的问题，归纳所学知识。
1频率的计算。概率有大有小，有时具有等可能性。
2、随机事件有概率，确定事件也有概率。
3、概率有大有小，有时具有等可能性。
（二）展示二（例题）
例1、判断下列说法对不对？请说明理由。
苏教版八年级数学下册教案--8.3 频率与概率 (2)
频率与概率主备人用案人授课时间____年__月__日总第课时课题8.3 频率与概率 (2) 课型新授教学目标1、认识到在实际生活中，人们常把试验次数很大时，事件发生的频率作为概率的估计值；2、初步体会到出现机会的均等与试验结果是否具有等可能性的关系；3、通过试验，加深对频率与概率的关系的理解．重点用频率的稳定值去估计概率．难点1．经历试验过程，培养随机观念；2．画频率的折线统计图，用频率估计概率．教法教具自主先学当堂检测交流展示检测反馈小结反思教具：多媒体等教学过教学内容个案调整教师主导活动学生主体活动一、情境引入在硬地上掷1枚图钉，通常会出现哪些情况？你认为这两种情况的机会均等吗？二、自主先学1、自学内容：P47--492、自学指导：（1）频率的计算。
（2）随机事件有概率，确定事件也有概率。
（3）概率有大有小，有时具有等可能性。
3、自学检测：（1）一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出口答。
自学教材内容程教一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球（）A、28个B、30个C、36个D、42个（2）下列说法：①甲同学在玩掷骰子游戏时说：“6，6，6……啊！真的是6！你只要一直想要某个数，就会掷出那个数！”②乙同学在玩掷骰子游戏时说：“我发现我越是想要某个数就越得不到这个数，倒是不想它反而会掷出那个数。
”③丙同学说：“中奖率为11000的彩票，买1000张一定会中将！”其中，正确的说法是（）A.①B.②C.③D.都不正确（3）质疑问难，提出学习中存在的问题。
三、交流展示（一）展示一分组展示自主先学中的问题，归纳所学知识。
1频率的计算。
概率有大有小，有时具有等可能性。
2、随机事件有概率，确定事件也有概率。
3、概率有大有小，有时具有等可能性。
（二）展示二（例题）例1、判断下列说法对不对？请说明理由。
【最新苏科版精选】苏科初中数学八下《8.3 频率与概率》word教案 (4).doc
频率与概率 (2)学习目标：1．认识到在实际生活中，人们常把试验次数很大时，事件发生的频率作为概率的估计值；2．初步体会到出现机会的均等与试验结果是否具有等可能性的关系； 3．通过试验，加深对频率与概率的关系的理解．3．让学生感受数学学习中，从猜想→实验（验证）的过程和感受从实验→结果（估计）的过程重点、难点：1．经历试验过程，培养随机观念； 2．画频率的折线统计图，用频率估计概率． 一.【预学指导】预习47、48页 二.【问题探究】问题1.活动一数学实验室：在硬地上掷1枚图钉，通常会出现两种情况：钉尖着地，钉尖不着地； （1）任意掷1枚图钉，你认为是“钉尖着地”的可能性大，还是“钉尖不着地”的可能性大？（2）做“掷图钉试验”，每人掷1枚图钉20次，分别汇总5人、10人、15人、…、50人……的试验结果，并将试验数据填入下表：（3）根据上表，完成下面的折线统计图：（4）观察所画的折线统计图，你发现了什么？并与同学交流．三.三、【拓展提升】 问题2. 活动二某种绿豆在相同条件下发芽试验的结果如下：钉尖不着地的频100 200 300 400 600 500 700 800 900 100发芽的频数m（2）画出绿豆发芽频率的折线统计图；（3）这种绿豆发芽的概率的估计值是多少？四.【课堂小结】通过这节课的学习，你有什么收获呢？五.【当堂反馈】1、事件“同一枚硬币抛50次，没有一次正面朝上”是（）A、必然事件B、不可能事件C、随机事件D、何种事件不能肯定2、一枚均匀的硬币抛200次，若正面朝上的次数为102次，那么反面朝上的频率是_______3、一个事件经过5000次试验，它的频率是0.32，那么它的概率估计值是 _______4、如图所示是一个可以自由转动的转盘，转1次得到1个数，利用这种转盘，可能得到的最大三位数是，可能得到最小三位数是，哪一个出现的可能性大？为什么？ 10、一个圆形转盘的半径为2cm，现将圆盘分成若干个扇形，并分别相间涂上红、黄两种颜色，转盘转动10000次，指针指向红色部分为2500次。
苏科版初二下册数学 8.3 频率与概率 教案(教学设计)
8..3 频率与概率教学目标：1．理解随机事件发生的可能性有大有小，概率的定义；2．概率是随机事件自身的属性，它反映随机事件发生的可能性大小；3．在多次重复试验中，体会频率的稳定性．教学重点：频率稳定性的理解．教学难点：频率稳定性的理解．教学过程：一、情境创设飞机失事会给旅客造成意外伤害．一家保险公司要为购买机票的旅客进行保险，应该向旅客收取多少保费呢？为此，保险公司必须精确计算出飞机失事的可能性有多大．类似这样的问题在我们的日常生活中也经常遇到．例如：抛掷1枚均匀硬币，正面朝上．在装有彩球的袋子中，任意摸出的1个球恰好是红球．明天将会下雨．抛掷1枚均匀骰子，6点朝上．……随机事件发生的可能性有大有小．一个事件发生可能性大小的数值，称为这个事件的概率．若用A表示一个事件，则我们就用P（A）表示事件A发生的概率．通常规定，必然事件发生的概率是1，记作P（A）＝1；不可能事件发生的概率为0，记作P（A）＝0；随机事件发生的概率是0和1之间的一个数，即0＜P（A）＜1．（要求：认真理解，积极参与思考，激发学习内驱力．归纳引出概念：一个随机事件发生的概率是由这个随机事件自身决定的，并且是客观存在的．概率是随机事件自身的属性，它反映这个随机事件发生的可能性大小．）二、探索活动活动一、做“抛掷质地均匀的硬币试验”，每人10次．分别汇总5人、10人、15人……的试验结果，并将试验数据汇总填入下表：（要求：互相讨论，踊跃回答：观察上面的折线统计图，你发现了什么规律？请与同学交流． 下表是小明抛硬币试验获得的数据（折线图在教材P45）：抛掷次数50100150200250300350400450500正面朝上的频数20537098115156169202219244正面朝上的频率0.40.530.470.490.460.520.480.510.490.49活动二、观察教材P45折线统计图，当抛掷硬币次数很大时，正面朝上的频率是否比较稳定？下表是自18世纪以来一些统计学家进行抛硬币试验所得的数据．观察此表，你发现了什么？（要求：学生畅所欲言，勇于发表自己的看法，小组推选出代表回答．从上表可以看出：“正面朝上”的频率总在21附近波动，而且近似等于21．） 活动三、表2是某批足球产品质量检验获得的数据．抽取的足球数n 50 100 200 500 1000 2000 优等品频数m 46 93 194 472 953 1903 优等品频数nm（1（2）画出优等品频率的折线统计图；（3）当抽取的足球数很大时，你认为优等品的频率会在哪个常数附近摆动？（要求：讨论后共同归纳．从表1可以看到，当抽查的足球数很多时，抽到优等品的频率nm接近于某一个常数，并在它附近摆动．通常，在多次重复试验中，一个随机事件发生的频率会在某一个常数附近摆动，并且趋于稳定．这个性质称为频率的稳定性．） 三、小结你在本节课中的感悟是什么？你还有什么疑惑？（要求：学生自由地想，大胆地说，表达自己的情感．）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
频率与概率
主备人用案人授课时间____年__月__日总第课时课题8.3 频率与概率 (2) 课型新授
教学目标1、认识到在实际生活中，人们常把试验次数很大时，事件发生的频率作为概率的估计值；
2、初步体会到出现机会的均等与试验结果是否具有等可能性的关系；
3、通过试验，加深对频率与概率的关系的理解．
重点用频率的稳定值去估计概率．难点1．经历试验过程，培养随机观念；2．画频率的折线统计图，用频率估计概率．
教法教具自主先学当堂检测交流展示检测反馈小结反思教具：多媒体等
教学过
教学内容个案调整教师主导活动
学生主体活
动
一、情境引入
在硬地上掷1枚图钉，通常会出现哪些情况？你认
为这两种情况的机会均等吗？
二、自主先学
1、自学内容：P47--49
2、自学指导：
（1）频率的计算。
（2）随机事件有概率，确定事件也有概率。
（3）概率有大有小，有时具有等可能性。
3、自学检测：
（1）一个密闭不透明的盒子里有若干个白球，在不
允许将球倒出来的情况下，为估计白球的个数，
小刚向其中放入8个黑球，摇匀后从中随机摸出
口答。
自学教材内
容
程教
一个球记下颜色，再把它放回盒中，不断重复，
共摸球400次，其中88次摸到黑球，估计盒中大
约有白球（）
A、28个
B、30个
C、36个
D、42个
（2）下列说法：
①甲同学在玩掷骰子游戏时说：“6，6，6……
啊！真的是6！你只要一直想要某个数，就会
掷出那个数！”②乙同学在玩掷骰子游戏时说：
“我发现我越是想要某个数就越得不到这个
数，倒是不想它反而会掷出那个数。
”③丙同学
说：“中奖率为
1
1000
的彩票，买1000张一定
会中将！”其中，正确的说法是
（）
A.①
B.②
C.③
D.都不正
确
（3）质疑问难，提出学习中存在的问题。
三、交流展示
（一）展示一
分组展示自主先学中的问题，归纳所学知识。
1频率的计算。
概率有大有小，有时具有等可能性。
2、随机事件有概率，确定事件也有概率。
3、概率有大有小，有时具有等可能性。
（二）展示二（例题）
例1、判断下列说法对不对？请说明理由。
（1）抛一枚质量分布均匀的硬币，是“正”是“反”
无法预测，全凭运气，因此抛1000次的话
也许只有200次“正”，也许有700次“正”，
没有什么规律；
（2）抛一枚质量分布均匀的硬币，出现“正面”
完成检测题
交流问难
学过程
教
和出现“反面”的机会均等，因此抛1000
次的话，一定会有500次“正”， 500次“反”。
（三）展示三（拓展）
. 一个口袋中有10个黑球和若干个白球，从口
袋中随机摸出一球记下其颜色，再把它放回口袋
中摇匀，重复上述过程，共实验100次，其中有
75次摸到白球，由此请你估计袋中的白球数。
四、检测反馈
1、一个袋子里装有20个形状、质地、大小一
样的球，其中4个白球，2个红球，3个黑球，其它
都是黄球，从中任摸一个，摸中哪种球的可能性最
大？
2、一个人随意翻书三次，三次都翻到了偶数页，
我们能否说翻到偶数页的可能性就大？
3、袋子里装有红、白两种颜色的小球，质地、
大小、形状一样，小明从中随机摸出一个球，然后
放回，如果小明5次摸到红球，能否断定袋子里红
球的数量比白球多？怎样做才能判断哪种颜色的球
数量较多？
4、已知地球表面陆地面积与海洋面积的比均为
3：7。
如果宇宙中飞来一块陨石落在地球上，“落在
海洋里”与“落在陆地上”哪个可能性更大？
五、小结反思
1、有什么收获？
2、有什么疑惑和遗憾？
分组展示板
演并讲解学
生讲解
试试看。
试着去估计
一下。
学
过程按照要求完成检测练习。
谈谈自己今天的收获。