03-均匀各向同性湍流
恒星讲义5

第五章 恒星内部的对流运动第一节 对流运动的一般特征由于流体内部温度变化而产生的流动,称为对流运动。
一种特殊情况是自由对流,它是由浮力产生的流动。
在重力场中,流体不同部分的温度差导致密度差,由此产生出浮力,驱动流体运动。
于是,热的流体趋向于上升,冷的流体趋向于下降。
考虑一个充满于两无限大水平平板中间的流体层,板间距离为d ,下面板的温度T 2大于上面板的温度T 1。
于是,冷的重流体位于热的轻流体之上。
这种位形是可以处于平衡状态的,即控制方程存在静止解,但是这种平衡却是不稳定的。
如果冷的重流体向下运动,而热的轻流体向上运动,就会有势能放出,给运动提供动能。
显然,出现这种运动的一个明显的准则是:12T T >在一般流体中,不稳定性受到粘性摩擦作用的对抗,同时还存在热传导作用的对抗。
只有当温度差的失稳作用大到足以克服上述这些对抗因素时,运动才会发生。
于是出现运动的判据是所谓的Rayleigh 数判据,即:crit Ra TT T d g Ra >-=123 νκδ其中g 是重力加速度,δ、ν、κ分别是流体的膨胀指数、运动粘性系数和热扩散系数。
临界值Ra crit 一般在1600~1700。
Rayleigh 数在临界值以下,流体保持静止;在临界值之上,流体开始运动。
当流体的Rayleigh 数刚好高于临界值时,流体中会形成若干热的上升区和冷的下降区,同时在顶部和底部出现水平运动以保持连续性。
上升流体接触冷的顶部时被冷却,使得它转变为冷的重流体而向下运动;而下降流体在接触热的底部时被加热,转变为热的轻流体而向上运动。
在底部的加热和在顶部的冷却提供给流体势能,而连续释放的势能和运动造成的机械能的粘性耗散相平衡,从而使得流动形成稳定的图案。
从热力学的观点看,这个过程实际就是一个热机。
流动的状态和流体的Rayleigh数密切相关。
当Rayleigh数高于临界值不太多时,运动首先以尺度可以达到流动区域特征尺度(如距离d)的长卷筒形式的上升和下降流动出现。
湍流简史

湍流简史精选已有 3889 次阅读2012-9-22 10:40|个人分类:学术探讨|系统分类:科研笔记|关键词:湍流简介湍流理论发展简史:N-S方程的导出:描述粘性不可压缩流体动量守恒的运动方程,简称N-S方程。
因1821年由C.-L.-M.-H.纳维(基于分子运动)和1845年由G.G.斯托克斯(基于连续介质假定)分别导出而得名。
后人在此基础上又导出适用于可压缩流体的N-S方程。
N-S方程包含两个假设:第一连续介质假定;第二是所有涉及到的场,全部是可微的假定。
N-S方程和连续方程共同构成了一个闭合的非线性方程组。
该方程组是质量守恒定律和牛顿运动定律在流体力学中的一种应用形式,由于其高度非线性,因此很难求得其解析解。
一般认为无论流体运动多么复杂,方程组都能够描述流体的运动。
湍流的发现:1839年,G.汉根在实验中首次观测到了流动由层流向紊流的转变。
层流向湍流转变的雷诺实验:1883年英国科学家雷诺(Reynolds)通过实验研究并展示了液体在流动中存在两种内部结构完全不同的流态:层流和紊流。
雷诺揭示了重要的流体流动机理,即根据流速的大小,流体有两中不同的形态,并提出了著名的层流向紊流转变的雷诺数(包括分层流动的情况)。
当流体流速较小时,流体质点只沿流动方向作一维的运动,与其周围的流体间无宏观的混合即分层流动这种流动形态称为层流或滞流。
流体流速增大到某个值后,流体质点除流动方向上的流动外,还向其它方向作随机的运动,即存在流体质点的不规则脉动,这种流体形态称为湍流。
并在1885年提出了著名的雷诺平均方法。
湍动能串级过程:1922年Richardson发现湍动能串级过程。
大尺度涡流脉动犹如一个很大的蓄能池,它不断从外界获得能量并输出给小尺度涡能量;小尺度湍流就像一个耗能机械,从大尺度湍流涡输出来的动能在这里全部耗散掉,流体的惯性犹如一个传送机械,把大尺度脉动传给小尺度脉动。
流动的雷诺数越大,蓄能的大尺度和耗能的小尺度之间的惯性区域越大。
中国湍流研究的发展史_中国科学家早期湍流研究的回顾

中国湍流研究的发展史I 中国科学家早期湍流研究的回顾黄永念北京大学力学与工程科学系,湍流与复杂系统国家重点实验室,北京,100871摘要总结了二十世纪三十年代到六十年代中国老一辈科学家(包括物理学家,力学家)周培源、王竹溪、张国藩、林家翘、谢毓章、张守廉、黄授书、胡宁、柏实义、陈善模、庄逢甘、陆祖荫、李政道、蔡树棠、是勋刚、李松年、谈镐生、包亦和等诸位先生的湍流研究工作。
介绍他们对流体力学中最为困难的湍流问题所作出的努力和贡献。
关键词湍流统计理论,能量衰变规律,均匀各向同性湍流,剪切湍流。
引言湍流一直被认为是物理学中最难而又久未解决的基础理论研究的一个课题。
从1883年Reynolds圆管湍流实验研究算起已经跨越了两个世纪,湍流问题仍未得到解决。
在跨入二十一世纪时,很多从事湍流研究工作的科学家都在思考这样的问题:二十世纪的湍流研究留给我们哪些宝贵财富?二十一世纪又应该如何面对这个老大难问题?Yaglom在2000年法国举行的一次湍流讲习班上回顾了二十世纪的湍流理论发展过程[1],指出了其中两个最重要的成就:一个是Kolmogorov的局部均匀各向同性湍流理论,另一个是von Karman的湍流平均速度的对数分布律。
同时又一次向世人介绍著名科学家Lamb在临终前对解决湍流问题的悲观看法。
由于中国与世界各国在文字和语言上的差异和长期缺乏国际间的交流,历次湍流研究工作的总结和回顾中,人们往往忽略了中国科学家的作用。
只有周培源教授在1995年流体力学年鉴上发表了“中国湍流研究50年”才打破了这种隔阂[2]。
但是这篇文章也只局限于周培源教授率领的北京大学研究组所做的系列研究工作。
实际上有很多中国科学家在上一世纪中做了非常出色的工作。
本文仅就半个世纪前的三十年代到六十年代他们的湍流研究工作做一个简单的介绍,目的是要引起大家关注中国科学家的湍流研究和对湍流研究所做的贡献。
中国科学家的湍流研究工作可以分成两个方面,一是在国内极其困难的条件下坚持开展的研究工作,这方面的工作国际上鲜为人知。
8第八章湍流简介

利用前面推导建立的瞬时函数求时均时的性质,可建立雷诺方程为:
注意Leabharlann 是一个张量:称雷诺应力张量,反映的是湍流涡团所输运动量,可以证明是一个对称 张量,记 ,有 ,由于湍流涡团的尺度远比分子制度大,湍 流涡团脉动运动的尺度也远比分子运动自由程大。所以一般雷诺应力远 大于粘性应力。更为关键的是引入的雷诺应力是未知的,我们尚无法描 述,这样在雷诺方程组中就多出来了六个未知数,使的原来封闭的N-S方 程变的不封闭了。这也是百余年来湍流研究的困难所在。
一、湍流的连续方程
二、湍流的平均动量方程—雷诺方程
认为湍流特征时间的尺度远小于非定常过程的特征时间尺度,这样用 时均法同样可以描述湍流的非定常过程,而时间平均也是雷诺最早使用的 概念。
湍流的N-S方程可以写成(瞬时值流场):
由于
,所以不可压N-S方程可写成:
其中:
对N-S方程求时均:
结论:湍流雷诺应力大于粘性应 力,湍流阻力大于层流阻力。
由于涡的诱导作用,流向涡向下 游突出部分被抬起,被抬起部分 进入速度较高的区域,使这种扰 动进一步被放大,使涡丝出现峰 与谷的不同部分。在速度剖面上 形成一个拐点,造成剪切层的不 稳定。当上抬涡峰被进一步拉伸 时,很快会导致层流状态的崩溃。 这种崩溃首先是形成“湍斑”, 其周围被层流包围,产生后即被 携往下游。由于“湍斑”前部以 0.9U移动,后部以0.5U移动,致 使逐渐发展成剪头状并与原生点 成22.5°夹角。随着湍斑区域扩大 并互相合并,最终发展成完全湍 流状态。这一过程称为猝发。
湍流与分子运动论的比较
项目 1.基元数 2.基元数性质 3.基元数数目 4.特征长度 5.基元数速率 6.运动性质 7.边界影响 8.驰豫时间 分子运动论 分子 稳定,大小一定 常数 平均自由程,只随温压改变 平均速率只随温度变化,不 是空间位置的显函数 随机运动 分子形状与数目不随边界形 状改变 短,没有记忆 湍流 旋涡 大小不一定,不稳定 变数 混合长度,随边界形状改变 涨落速度随空间位置不同起 伏很大 有拟序结构 旋涡结构、形状和数目随边 界形状急剧改变 长,有记忆
第三章-湍流模型
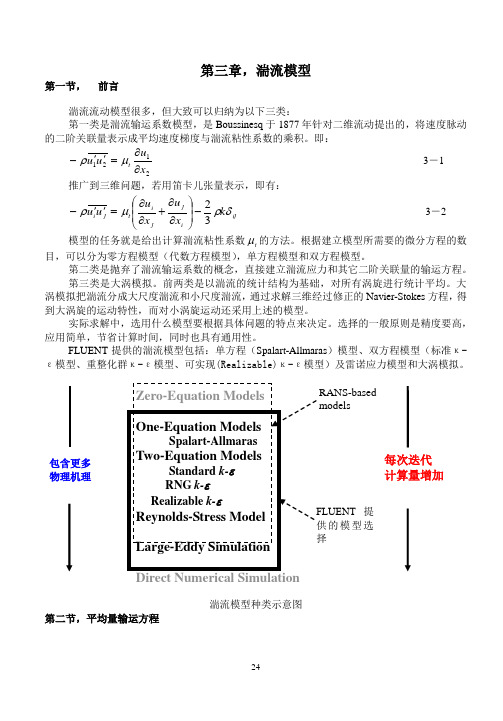
第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图第二节,平均量输运方程包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。
第三章,湍流模拟

主对角线上的三个分量,和称为湍流正应力,其余的六个分量称 为湍流切应力。三个湍流正应力之和是湍流脉动动能的两倍
u3 ui u u2 ui 2k
2 1 2 2 i 1
D7 热科学与能源工程系
3
计算流体与传热传质
湍流模型
湍流应力
若以主对角线上的三个分量作为对称轴,则对称的两个切应力分 量是相等的,很显然,这是一个对称的二阶张量。很容易可以证 明,在各向同性湍流中,湍流正应力的三个分量相等,即
D4
热科学与能源工程系
计算流体与传热传质
湍流模型
湍流模拟的方法
直接数值模拟(DNS)只适合低雷诺数流动。 求解雷诺平均的 Navier-Stokes (RANS) 方程:
Rij Ui p 2Ui Uk xk xi x jx j x j
其中
(定常, 不可压缩流动 有/无 体 积力) (雷诺应力)
ui u j 2 ul ij uiu j x x x 3 x j i l j
上面两个方程称为雷诺平均的Navier-Stokes(RANS)方程。
uiu j
如果要求解该方程,必须模拟该项以封闭方程。
D10
热科学与能源工程系
计算流体与传热传质
湍流模型
需要作出选择
物理流体 计算资源
湍流模型 和 近壁处理
计算网格
精度要求
计算时间要求
D11
热科学与能源工程系
计算流体与传热传质
湍流模型
湍流模型
Zero-Equation Models
基于雷诺平均 (RANS)的模型
湍流流动模型-带作业

•
在工程上, 我们最感兴趣的是各种流体力学量的平
均值, 以及它们在平均值周围的变化范围, 有时也须
知道各种量之间的关联大小。然而这些量的平均值
如何确定, 这在湍流中是一个有争议的间题。
4-1-3平均量输运方程
• 现在着手建立平均量输运方程, 为容易理解起见,
首先讨论不可压缩流体。把各种参数都分解为平
4-4 双方程模型
• 为了考虑对流和扩散对湍流尺度的影响, 除了湍流动能方
程以外, 还须建立湍流尺度的微分方程。在双方程模型中,
假定式(4-27)和式(4-37)成立。初期人们尝试了各种各样
的湍流尺度的微分方程, 但在使用中都不很成功。
• 后来发现, 用各向同性耗散率作为变量, 建立微分
方程, 并用耗散率模拟式
还增加了密度脉动、速度脉动的二阶关联量和三阶关联量, 这
些量反映了密度的变化在湍流中起相当大的作用, 方程变的很
复杂。
作业: 推导上述平均方程。
• 与式(4-18)比较可看出, 在用法夫雷平均得到的输运方程
中, 没有出现与密度脉动有关的项, 使方程得到了很大的
简化, 且平均参数的物理意义有时也比简单时间平均值清
成不封闭了。
• 从瞬时参数的守恒方程出发, 可以推出各种二阶
关联量的输运方程。但很快就发现, 在这些二阶
关联量的输运方程中, 又出现了三阶关联量, 同样,
在三阶关联量的方程中, 出现四阶关联量, 如此等
等。
• 很明显, 从基本的方程出发, 无法解决不封闭问题。
• 目前, 我们一般都采用模型封闭的办法, 即用量纲
• 测量表明, 当流动雷诺数较大时, 湍流的涡旋尺寸分布可
以明显地区分为含能涡旋区、惯性区和耗散区。
[工学]湍流流动
![[工学]湍流流动](https://img.taocdn.com/s3/m/c0afecf27f1922791688e8e5.png)
τ
y
τ
二是流层的波动。在流动着的流体中,如果由于某种原因,流层 发生轻微的波动,则流层凸起的地方将因微小流束截面的减小而 使流速增大;反之,在凹入的地方,将因微小流束截面的增大而 使流速减小。根据柏努利方程,流速的增大将引起压力的减小, 而流速的减小将引起压力的增大。这样一来,轻微波动的流层就 将承受横向压力。
(5-42)
(3)湍流主体(y+≥30)
u 2.5ln y 5.5
(5-43)
式(5-41)~式(5-43)即为光滑圆管湍流时的通用速度分布方程。这是一个 半经验半理论公式,它存在明显的局限和不足,例如用式(5-43)计算 得到的管中心速度梯度并不为零,而实际在管中心的速度梯度等于零。 尽管如此,上述通用速度分布方程仍然能够满足工程计算的要求。
此外,圆管中稳态湍流的速度分布亦可用如下形式的经验公 式近似地表示
y u umax ri
1/ n
r umax 1 ri
1/ n
4×104<Re<1.1×105时,n=6; 式中,指数 n 随Re数的变化而变化。 1×105<Re<3.2×106时,n=7; Re>3.2×106时,n=10 。 流体输送中较常遇到的Re值范围在~105左右,故1/7次方定律应用的较 为普遍。但它只是近似的,特别是不能表达壁面处的情况。因为在壁 面处其速度梯度→∞ ,这显然与实际不符。
u y l
d ux dy
将脉动速度表达式带入(5-12)中,有
引入比例系数c1
r yx
dux 2 l ( ) dy
2
r yx c1 l 2 (
dux 2 ) dy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质疑的核心:湍动能耗散率不是一个常数
浙江大学航空航天学院流体工程研究所
24
局部各向同性湍流的结构函数(5)
标度律
Kolmogorov的修正
层次结构标度律-佘振苏
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
25
局部各向同性湍流的结构函数(6)
随机函数的增量
大尺度的脉动相互抵消
脉动速度增量的统计矩
IFE , Zhejiang University
二阶 结构 函数
三阶 函数
浙江大学航空航天学院流体工程研究所
18
局部各向同性湍流的结构函数(补充)
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
19
不可压缩均匀各向同性湍 流
− − − − 动力学方程 卡门-霍华斯方程 卡门-霍华斯方程应用 能量传输链
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
2
均匀各向同性的相关函数谱张量(1)
均匀各向同性湍流
均匀湍流
均匀各向同性湍流
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
14
不可压缩均匀各向同性湍流(8)
能量传输链
能量谱方程
记
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
15
不可压缩均匀各向同性湍流(9)
能量传输链
特征尺度
惯性区
IFE , Zhejiang University
惯性子区 耗散区
标度律
− 由卡门-霍华斯方程,Kolmogorov首先推导了结构函数的方程
结构函数的动力学方程
− 对耗散区
IFE , Zhejiang University
− 对惯性子区
浙江大学航空航天学院流体工程研究所
26
相关函数的简化
三阶函数的简化
IFE , Zhejiang University
对于不可压缩流动
浙江大学航空航天学院流体工程研究所
7
不可压缩均匀各向同性湍流(1)
动力学方程
谱方程
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
8
不可压缩均匀各向同性湍流(2)
10
不可压缩均匀各向同性湍流(4)
卡门-霍华斯方程
二阶函数方程的简化
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
11
不可压缩均匀各向同性湍流(5)
卡门-霍华斯方程的应用
洛强斯基不变量
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
Kolmogorov标度律
湍流耗散率为常数
IFE , Zhejiang University
小尺度特征速度与耗散率和粘性有关
浙江大学航空航天学院流体工程研究所
22
局部各向同性湍流的结构函数(3)
结构函数
− 量级
Kolmogorov标度律
− 对小尺度速度,由于距离很小
IFE , Zhejiang University
− 对于惯性子区,结构函数与粘性无关,仅与耗散率有关
浙江大学航空航天学院流体工程研究所
23
局部各向同性湍流的结构函数(4)
结构函数
− 更一般的,在惯性子区,对于任意阶的结构函数
Kolmogorov标度律
称为Kolmogorov的p/3标度律
Landau的质疑
IFE , Zhejiang University
IFE , Zhejiang University
湍动能耗散率
浙江大学航空航天学院流体工程研究所
5
均匀各向同性的相关函数谱张量(4)
相关函数的简化
二阶函数的简化
IFE , Zhejiang University
对于不可压缩流动
浙江大学航空航天学院流体工程研究所
6
均匀各向同性ห้องสมุดไป่ตู้相关函数谱张量(5)
浙江大学航空航天学院流体工程研究所
16
不可压缩均匀各向同性湍流(10)
能量传输链
− 假定 小尺度统计特性由耗散率和流体粘性确定
Kolmogorov-5/3幂次律
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
17
局部各向同性湍流的结构函数(1)
结构函数
局部各向同性湍流的结构函数(补充)
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
20
局部各向同性湍流的结构函数(补充)
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
21
局部各向同性湍流的结构函数(2)
结构函数
− 假定 在雷诺数足够大时,小尺度区是局部各向同性的
浙江大学航空航天学院流体工程研究所
3
均匀各向同性的相关函数谱张量(2)
相关函数和谱张量的性质
相关函数-二阶函数
不可压缩流中的二阶函数
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
4
均匀各向同性的相关函数谱张量(3)
相关函数和谱张量的性质
不可压缩流中的拟涡能
动力学方程
谱方程的简化
IFE , Zhejiang University
忽略非线性项,得到粘性耗散的作用规律
浙江大学航空航天学院流体工程研究所
9
不可压缩均匀各向同性湍流(3)
卡门-霍华斯方程
二阶函数方程(雷诺应力)
IFE , Zhejiang University
浙江大学航空航天学院流体工程研究所
12
不可压缩均匀各向同性湍流(6)
卡门-霍华斯方程的应用
湍动能耗散方程及微尺度
IFE , Zhejiang University
其中 令
浙江大学航空航天学院流体工程研究所
泰勒微尺度
13
不可压缩均匀各向同性湍流(7)
卡门-霍华斯方程的应用
湍流的后期衰变
其中必须有
IFE , Zhejiang University
高等流体力学
第三讲 均匀各向同性湍流
张凌新
浙江大学航空航天学院 流体工程研究所 Institute of Fluid Engineering
内容
均匀各向同性湍流的相关 函数和谱张量
− 均匀各向同性湍流 − 相关函数和谱张量的性质 − 相关函数的简化
局部各向同性湍流的结构 函数
− 结构函数 − Laudau的质疑 − 标度律
