质心运动守恒定理
质心运动定律

mi ai
i
N
m
质点系的质心运动
质心与质心运动定律
质点系质心运动
质心的特点与求法 质心系
5
质心的求法
(1) 分立质点系的质心
rC
mi ri
i 1
N
m
在直角坐标系下可以表示为:
xC
m x
i
i i
m
, yC
m y
i i
i
m
, zC
m z
i
i i
m
6
D 三质点在某一时刻的位置坐标 B、 例4.1.2-1 A 、
N i
N
ac
Fi
i
质心位置矢量:
rC Biblioteka mi ri m应用: 运动员、炮弹等的轨迹 筛选法(大小土豆) F 0 ,自然界如没摩擦力 的情形设想……
4
质心速度:
drC vC dt
2
mi vi
i
N
m
d rC 质心加速度: a C 2 dt
(4) 多个规则形状物体组成系统的质心
多个规则形状物体组成系统的质心,可先找到每 个物体的质心,再用分立质点系质心的求法,求出公
共质心。
例4.1.2-3 如例4.1.2-3图所示,半径为 R 、质量为 m 、
R 质量分布均匀的圆盘,沿某半径方向挖去半径为 2 的小圆
盘,求大圆盘剩余部分的质心位置。
0, yC y边 ,则系统的质心为:
1 1 R Yc yC dm y边 (2 x边 dy边 ) m m 0
dy边
1 R 4R 2 2 y边 (2 R y边 dy边 ) m 0 3π
质心系动量定理

质心系动量定理
质心系动量定理,是在物理学中常常使用的一个定理,它是描述一个系统动量守恒的定理。
在物理学中,质心系是一个非常有用的概念,它可以帮助我们更好地理解物体的运动状态。
首先,让我们来了解一下什么是质心。
质心是一个物体所有质点的平均位置,它是一个重要的物理量。
在物理学中,我们经常使用质心来描述一个物体的运动状态。
接下来,我们来了解一下什么是动量。
动量是一个物体的运动状态的量度,它是一个矢量量。
在物理学中,我们使用动量来描述一个物体的运动状态。
在物理学中,质心系动量定理是指:在一个封闭系统中,系统质心的速度等于系统所有质点动量之和除以系统总质量。
这个定理可以用来证明一个系统的动量守恒。
举个例子来说,假设有两个质点A和B,它们的质量分别为m1和m2,速度分别为v1和v2。
那么这个系统的总质量为
m1+m2,总动量为m1v1+m2v2。
根据质心系动量定理,这个系统的质心速度为(m1v1+m2v2)/(m1+m2)。
当然,在实际应用中,我们可能会遇到更加复杂的系统,但是质心系动量定理的原理是一样的:系统质心的速度等于系统所有质点动量之和除以系统总质量。
总之,质心系动量定理是一个非常重要的物理定理,在物理学中有着广泛的应用。
它可以帮助我们更好地理解物体的运动状态,并且可以用来证明一个系统的动量守恒。
06-6质心力学定理

V M
C O
的速度) 对 的速度 又 ∵ v ≈ v ′ ( v ′是m对M的速度 1 ∴ m υ ′ 2 + ∆E引 = 0 2 地球参考系不是惯性系⇒ • 地球参考系不是惯性系⇒ 动量守恒不成立 地球参考系仍可正确表示系统的功能 功能关系 • 地球参考系仍可正确表示系统的功能关系
03/2006 S.H.Deng
12
质点组总动能等于质心动能与相对质心动能之和. 质点组总动能等于质心动能与相对质心动能之和. S.H.Deng
理学院 邓胜华
第6章 质心力学定理
二.重力势能与质心势能
定义: 定义:E C = Mgh C
E =
i i i
——质心重力势能 质心重力势能
质点组重力势能 ∑ m gh ——质点组重力势能 M =∑m ∑m h E = ∑ m gh = g ∑ m h = g ∑m ∑m
× m i v iC ) + ∑ (riC × m i v C )
i
S.H.Deng
i
OiBiblioteka C03/200614
理学院 邓胜华
第6章 质心力学定理
L = rC × ∑ m i v C + ∑ (riC × m i v iC ) + rC × ∑ (m i v iC ) i i i + ∑ (m i riC ) × v C
质心动量的改变量等于和外力的冲量. 质心动量的改变量等于和外力的冲量.
dv C = 又:M dt
∑F
i
i
即 M aC =
∑F
i
i
——质心运动定理 质心运动定理
质点组总质量与质心加速度的乘 积等于质点组所受到的合外力. 积等于质点组所受到的合外力. S.H.Deng 03/2006
3.2质点系的动量定理

v0
dm 时间内的火箭受喷射燃料的 火箭受喷射燃料的推进力 dt 时间内的火箭受喷射燃料的推进力 F = u dt
3.2 质点系的动量定理及动量守恒 3.2质点系的动量定理及动量守恒
神舟六号待命飞天
注:照片摘自新华网
3.2 质点系的动量定理及动量守恒 3.2质点系的动量定理及动量守恒
神舟六号点火升空
要增大v 需要提高火箭的质量比 要增大v:需要提高火箭的质量比 或增大喷气速度u 推动力:以喷出的燃料d 2 推动力:以喷出的燃料dm为研究对象 时间内的动量变化率为燃料受火箭力 dt 时间内的动量变化率为燃料受火箭力
dm[(υ − u ) − υ ] dm F= = −u dt dt
m0 火箭速度v v m dm ∫v0 d v = − u ∫m0 m
3.2 质点系的动量定理及动量守恒 3.2质点系的动量定理及动量守恒
6.当质点之间有相对运动时, 6.当质点之间有相对运动时,应运用伽利 当质点之间有相对运动时 略速度变换建立相对于同一惯性系的动量 定理。 定理。 7.质点系的动量守恒定律是自然界一切物理 7.质点系的动量守恒定律是自然界一切物理 质点系的动量守恒定律是 过程的基本定律, 最普遍、 过程的基本定律,是最普遍、最基本的定律 之一.在宏观和微观领域均适用。 之一.在宏观和微观领域均适用。
v v t′ 所以: 所以:I = ∫ ( ∑ Fi )dt = ∑
t i i
∫
t′
t
v v Fi dt = ∑ I i
i
质点所受外力的总冲量等于各分力冲量之和
3.2 质点系的动量定理及动量守恒 3.2质点系的动量定理及动量守恒
t2 r r 再看内力冲量之和 ∑∫ Fint,tdt = ∫ (∑Fint,t )dt i t1 t1 i r 因为内力之和为零: 因为内力之和为零:∑ Fint,t = 0 i t2 r 结论 内力的冲量之和为零 ∑ ∫ Fint,t dt = 0 t2
3-2质心运动定理、角动量守恒
L
O
●
rA r
●
A α m
●
v
证明: 不受外力,质点将做 匀速直线运动。 m在某一时刻经过A点时, 其对固定点O的角动量为
L rA mv rAmvsin r m v
固定点O到轨迹直线的垂直距离只有一 个值,所以角动量的大小恒定。 而角动量的方向恒垂直于固定点O和运动 轨迹所决定的平面。 所以m对任意固定点的角动量矢量保持不变。
力矩的大小:
力矩的方向: 角动量定理:
M r F rF sin
也由右螺旋法则确定。
dL M dt
质点所受的合外力矩等于它的角动量对时间的 变化率。 M 注意:定理中的力矩和角 动量是对惯性系中地同一 固定点而言的。
o
●
r
F
r
α
m
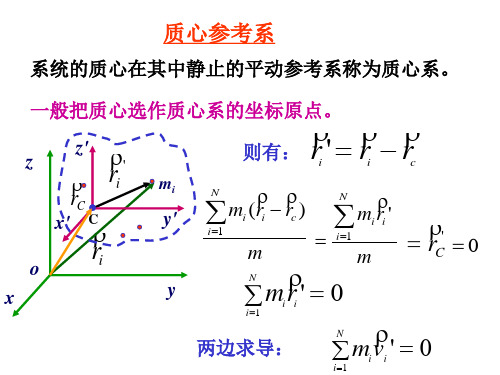
§3.7 角动量守恒定律
给上式两边同时乘以系统质量m
rC
mi ri
i
则:
mvc mi vi p
dvc dp p mvc 两边求导得: m mac dt dt dp F m a c dt
——质心运动定理
i
不管物体的质量如何分布,也不管外力作用在 物体的什么位置上,质心的运动就象是物体的质量 全部都集中于此,而且所有外力也都集中于此的一 个质点的运动一样。 实际上在质心位置处可能既无质量,又未受力。
i 1
m
' rC
0
两边求导:
'0 mv i i
N i 1
z
z'
x'
o
rC
' ri
3-5质心和质心运动定理

2 内力不能使质心产生加速度,当质点
系所受外力为零时,系统动量守恒。
物体中质心的运动是竖直上抛. 物体中质心的运
动是斜上抛.
大学物理学
m i ri
rc
=
i =1 N
∑ mi
= i =1 m
z
i =1
∑
xc =
mi xi M
∑
y
c
=
mi yi M
x
∑
z
c
=
mi zi M
rc
ri
mi
y
对连续分布的物质,可将其分为N个小质元
x
c
=
∫
xdm M
y
c
=
∫
ydm M
zc
=
∫
zdm M
说明:
1心运动定律
质心
对于多个质点组成的系统,为简化问题
引入特殊点-----质心。设系统有N个质点, 其中第i个质点的位矢位ri ,则定义系统的质
量中心简称质心C 的位矢定义为
N
N
∑ ∑ mi ri
m i ri
rc
=
i =1 N
∑ mi
= i =1 m
i =1
N个粒子系统的质心:
N
N
∑ ∑ mi ri
2 质心与重心是不同概念。
质心运动定律
N
∑ ∑ ∑ P =
N
p i
i =1
=
N m i dri i =1 dt
d m i ri = i =1
dt
=
d( mrc ) dt
= m drc dt
= mvc
F = dP ⇒ F = mac
3-9 质心 质心运动定律1

y
d
O
H
52.3
o
o
C
d
H
x
52.3
o
第三章 动量守恒和能量守恒
6
物理学
第五版
3-9 质心
质心运动定律
解
xC
yC=0
i i
m x m
i 1 i
n
mH d cos52.3o mO 0 mH d cos52.3o mH mO mH
12
xC 6.8 10 m 12 rC 6.8 10 mi
第三章 动量守恒和能量守恒
n
i 1
d( pi )
i 1
n
dt
9
物理学
第五版
n dpi ex 根据质点系动量定理 Fi i 1 dt i 1 n in (因质点系内 Fi 0 ) i 1 ex dvC F m' m' aC dt
n
以上质心问题只是了解一下就可以了,不要 求掌握。
第三章 动量守恒和能量守恒
11
物理学
第五版
3-9 质心
质心运动定律
本章结束语:
本章内容中有许多是中学接触过的,学习 过程中应该特别注意其概念和方法的扩展。 例如,变力的冲量,功的概念的扩展,变 力的功的计算,保守力与势能的相互关系, 机械能守恒条件的一般表述,以及划分阶段 求解综合性问题等。
8
物理学
第五版
3-9 质心
质心运动定律
m 'rC mi ri
i 1
n
上式两边对时间 t 求一阶导数,得
n drC dri m' mi dt dt i 1
质点力学第7讲变质量问题质心和质心运动定理质点的角动量定理和角动量守恒定律

z
C× rc
mi
ri
xC
mi xi
m
yC
mi
m
yi
zC
mi zi
m
0
y
x
质心位置是质点位置以
质量为权重的平均值。
6
几种系统的质心
● 两质点系统
· · m1
C× m2
r1
r2
m1 r1 = m2 r2
● 连续体
z
dm
rC
rdm m
r
×C
rc m
xC
xdm m
0
y
……
x
7
例1 任意三角形的每个顶点有一质量m,
4
(二)火箭所受的反推力 研究对象:喷出气体 dm dt内喷出气体所受冲量 F箭对气dt = dm(v + d v - u) - vdm
火箭所受燃气的反推力为
dm FF气 对箭udt
5
二、质心运动定理
(一)质心的概念
定义质心C 的位矢为:
···· ···· rC
mi ri(
m
mmi )
移动多少距离?
y
xc
1 2
F M
t2
o
x
13
三、质点的角动量
(一) 质点的角动量
质点m对固定点 O的
L
p
·O
r
m
角动量定义为:
L r p r (m v )
L rs pin rm vsin
单位: kgm2/s 或 Js
14
(二)质点的角动量定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质心运动守恒定理
质心运动守恒定理,也称为质心运动定理,是物理学中的一个重要定理,用于描述系统总质量的质心在不受外力作用时的运动特性。
质心是一个系统的所有质点的质量加权平均位置。
在不受外力作用的情况下,质心的运动有一个重要的特性:系统的质心以恒定的速度直线运动。
质心运动守恒定理的表述如下:
在一个封闭系统中,如果系统内部没有外力作用,那么系统的质心将以恒定的速度沿着直线运动。
这意味着,如果一个系统内部没有物体离开或进入,系统的总质量保持不变,而且系统的质心在运动过程中不会改变速度或方向。
质心运动守恒定理是一个非常有用的工具,特别在研究大规模物体组成的系统时,如行星运动、天体运动等。
需要注意的是,如果系统受到外力作用,那么质心运动守恒定理将不再适用,质心的运动将会受到外力的影响。
因此,在具体问题中,需要根据情况来判断是否可以应用质心运动守恒定理。
1/ 1。
