质心系动量定理
质心运动定理

Newton 第三定律和动量守恒Newton 第二定律给出了任何物体的加速度与作用在它上面的力之间的关系,在这个基础上,原则上可以解决任何力学问题。
例如,为了确定几个粒子的运动,人们可以利用前面一节中所展开的数值方法。
但是我们有充分的理由来进一步研究Newton 定律。
首先,有一些十分简单的运动不仅可以用数值方法分析,也可以直接进行数学分析。
比如:虽然我们可以按数值方法计算简谐振子的位置,但是分析这个运动并找到一般解cos x t =,则更令人满意。
同样,一个行星由引力决定的绕太阳的运行固然可以用上一节的数值解法逐点地加以计算,从而找到轨道的一般形状,但能够得到准确的形状——分析表明这是一个完整的椭圆——就更好了。
因此,当存在一种简单而又更为精确的方法以得出结果时,再去用一系列麻烦的算术运算就毫无必要了。
遗憾的是,只有很少问题能够以分析方法精确求解。
例如就简谐振子来说,如果弹簧力不是正比于位置,而是更为复杂的话,人们就只得又回到数值解法上来。
或者,假如有两个天体绕太阳运行,使天体的总数是三个,那么分析法就无法得出一个简单的运动公式,实际上这个问题只能作数值解。
这就是有名的三体问题,今天,它已作为常规计算准确地按上一节所描述的方式进行充分的演算后,加以解决了。
十分有趣的是,人们曾经化了那么长时间才领悟到也许数学分析的能力是有限的,因而使用数值解法是必要的这个事实。
然而,也有一些两种方法都失效的情况:对简单的问题我们可以用分析方法,对适当困难的问题可以用数值和算术方法;但是对非常困难的问题则这两种方法都不能用了。
例如:两辆汽车的碰撞,或者甚至气体中分子的运动,就是一种复杂的问题。
在一立方厘米的气体中有数不清的粒子,而试图用这么许多变量(约个——即一万亿亿个)来作计算将是荒谬的。
任何问题,如果不是只有二、三个行星绕太阳运行,而是诸如象气体、木块、铁块中的分子或原子的运功,或在球状星团中许多恒星的运动之类这样的问题,我们就不能直接去解,因此只好借助于其他手段。
06-6质心力学定理

V M
C O
的速度) 对 的速度 又 ∵ v ≈ v ′ ( v ′是m对M的速度 1 ∴ m υ ′ 2 + ∆E引 = 0 2 地球参考系不是惯性系⇒ • 地球参考系不是惯性系⇒ 动量守恒不成立 地球参考系仍可正确表示系统的功能 功能关系 • 地球参考系仍可正确表示系统的功能关系
03/2006 S.H.Deng
12
质点组总动能等于质心动能与相对质心动能之和. 质点组总动能等于质心动能与相对质心动能之和. S.H.Deng
理学院 邓胜华
第6章 质心力学定理
二.重力势能与质心势能
定义: 定义:E C = Mgh C
E =
i i i
——质心重力势能 质心重力势能
质点组重力势能 ∑ m gh ——质点组重力势能 M =∑m ∑m h E = ∑ m gh = g ∑ m h = g ∑m ∑m
× m i v iC ) + ∑ (riC × m i v C )
i
S.H.Deng
i
OiBiblioteka C03/200614
理学院 邓胜华
第6章 质心力学定理
L = rC × ∑ m i v C + ∑ (riC × m i v iC ) + rC × ∑ (m i v iC ) i i i + ∑ (m i riC ) × v C
质心动量的改变量等于和外力的冲量. 质心动量的改变量等于和外力的冲量.
dv C = 又:M dt
∑F
i
i
即 M aC =
∑F
i
i
——质心运动定理 质心运动定理
质点组总质量与质心加速度的乘 积等于质点组所受到的合外力. 积等于质点组所受到的合外力. S.H.Deng 03/2006
3-2质心运动定理、角动量守恒
L
O
●
rA r
●
A α m
●
v
证明: 不受外力,质点将做 匀速直线运动。 m在某一时刻经过A点时, 其对固定点O的角动量为
L rA mv rAmvsin r m v
固定点O到轨迹直线的垂直距离只有一 个值,所以角动量的大小恒定。 而角动量的方向恒垂直于固定点O和运动 轨迹所决定的平面。 所以m对任意固定点的角动量矢量保持不变。
力矩的大小:
力矩的方向: 角动量定理:
M r F rF sin
也由右螺旋法则确定。
dL M dt
质点所受的合外力矩等于它的角动量对时间的 变化率。 M 注意:定理中的力矩和角 动量是对惯性系中地同一 固定点而言的。
o
●
r
F
r
α
m
§3.7 角动量守恒定律
给上式两边同时乘以系统质量m
rC
mi ri
i
则:
mvc mi vi p
dvc dp p mvc 两边求导得: m mac dt dt dp F m a c dt
——质心运动定理
i
不管物体的质量如何分布,也不管外力作用在 物体的什么位置上,质心的运动就象是物体的质量 全部都集中于此,而且所有外力也都集中于此的一 个质点的运动一样。 实际上在质心位置处可能既无质量,又未受力。
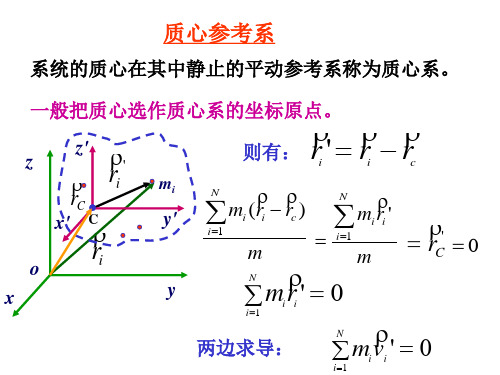
i 1
m
' rC
0
两边求导:
'0 mv i i
N i 1
z
z'
x'
o
rC
' ri
质心运动定理动量定理

2. 质心的速度如何确定? mvC mivCi
2
3. 质心的加速度如何确定? maC miaCi
3
(二)质心运动定理
对每个质点
mi
d 2ri dt 2
Fi
1
求和
mi
d 2ri dt 2
Fi
2
左边
d2 dt 2
miri
d2 dt 2
mrC
m
d 2rC dt 2
maC
右边
垂直,另一端刚连一重W3的小球。设电动机轴以匀角速ω转
动,求螺栓和基础作用于电动机的最大总水平力及铅直力。
解: 1.取坐标系oxy
2.任意时刻质心坐标
xc
W2
l 2
sint
W3 l
sint
W1 W2 W3
yc
W2
l 2
cos
t
W3l
cos
t
W1 W2 W3
Fy
例2:电动机重W1,外壳用螺栓固定在基础上,如图所示。另 有一均质杆,长l,重W2,一端固连在电动机轴上,并与机轴
第一节 质心运动定理
质点系在力的作用下,其运动状态不但与各 质点的质量有关,而且与质量的分布情况有关。
质量中心是反映质点系质量分布特征的物理量之一。
(一)质量中心(质心)
rC
mi ri mi
问题:
xC
mi xi mi
yC
mi yi mi
zC
mi zi mi
1系.系统统质由心几如个何刚确体定构?成,每个m刚rC体质心位m置irC已i 知,1
2maA F
A
C
F
例1:图示机构,地面光滑,初始时刻系统静止。问
动量定理 质心运动定理

动量定理质心运动定理动量定理质心运动定理质点的动量定理可以表述为:质点动量的微分,等于作用于质点上力的元冲量。
用公式d(mv),Fdt表达为 (17-7)d(mv),Fdt (17-8)tptp2211设时刻质点系的动量为,时刻质点系的动量为,将(17-8)式积分,积分区tt21间为从到,得t2p,p,Fdt21,t 1 (17-9)t2Fdt,I,tttF211记,称为力在到时间间隔内的冲量。
式(17-9)为质点系动量定理的积分形式,它表明质点系在某时间间隔内的冲量的改变量,等于作用在质点系上的外力主矢在该时间间隔内的冲量。
(e)(i)MFFiii对于质点系而言,设为质点所受到的外力,为该质点所受到的质点系内力,根据牛顿第二定律得dv(e)(i)im,F,F(e)(i)iiima,F,Fdtiiii 即mi除了火箭运动等一些特殊情况,一般机械在运动中可以认为质量不变。
如果质点的质量不dmv()(e)(i)ii,F,Fiidt变,则有上式对质点系中任一点都成立,n个质点有n个这样的方程,把这n个方程两端相加,得ndm(v),iinn()()ei,1i,,FF,,iidt,1,1iinn(e)(i)FF,,iii,1i,1 质点系的内力总是成对地出现,内力的矢量和等于零。
上式中是质点dp(e),F(e)RFdtR系上外力的矢量和,即外力系的主矢,记作,则上式可写为(17-10)1这就是质点系动量定理的微分形式,它表明:质点系的动量对时间的导数等于作用在质点系上外力的矢量和。
(e)dp,Fdt 将式(17-10)写成微分形式 Rtptptt222111 设时刻质点系的动量为,时刻质点系的动量为,上式从到积分,得t2(e)p,p,Fdt21R,t,I1 (17-11)p,p0 当外力主矢为零时,由上式可推出质点系的动量是一常矢量,即这表明当作用在质点系上的外力的矢量和为零时,质点系的动量保持不变,这就是质点系的动量守恒定理。
3-2 质点系动量定理和质心运动定理

解:
dm = 2xσdx
a/ 2
y a
三角形质心坐标x 三角形质心坐标 c是
xc
∫ xdm = ∫ = ∫ dm ∫
0
a/
0
2 a = 2 3 2σxdx
2σx dx
2
O x dx
x
这个结果和熟知的三角形重心位置一致。 这个结果和熟知的三角形重心位置一致。
11
三、质心运动定理 右边: 右边:
r d 据质点系动量定理: 据质点系动量定理 ∑ F = (∑m v ).
质点系动量定理:在一段时间内, 质点系动量定理:在一段时间内,作用于质点系的 外力矢量和的冲量等于质点系动量的增量. 外力矢量和的冲量等于质点系动量的增量
1
v d n v 微分形式) Fi = (∑mivi ) (微分形式) ∑ dt i=1 i=1
n
其分量式
Fixdt = ∑mi vix − ∑mi vi 0x ∫t0 ∑ t ∫t0 ∑Fiydt = ∑miviy − ∑mivi0 y t Fizdt = ∑mi viz − ∑mi vi 0z ∫t0 ∑
z
dm ( x , y , z )
体分布 面分布 线分布
dm = ρdV
r r
x o
M
dm = σdS dm = λdl
y
dm ρ= dτ dm σ= ds dm λ= dl
dm:宏观小,微观大 宏观小,
xc =
r rc =
∫ ∫
xdm M ydm M
注意: 注意:
1.质心的坐标值与坐标系的选取有关; 2.质量分布均匀、形状对称的实物,质 心位于其几何中心处; 3.不太大的实物,质心与重心相重合。
质心 质心运动定理

y
d
C 0.64R
dm
x
解: 建坐标系如图
取 dl
o
M M Rd d dm dl R
x R cos y R sin
M d 0.
R sin 0 M
xc
x dm
M
R cos 0 M
说明: 质点系动量等于总质量与质心速度的积
dP 质点系动量定理 F外 d t
2. 质心的加速度及其动力学规律
质点系动量 P mv c 说明: (1)质心运动状态只取决于外力,与内力无关 (2)若 F外 0 则 ac 0 vc 常矢量
dvc F外 m mac dt
质心 质心运动定理
一、 质心(the center of mass) 质心位矢 坐标
xc
rc
mi r i m
i i
z
mi
mx
ri
rc
r1
m1
m2
yc
m mi y i
o
y
m
i i
zc
mz m
x
对于质量连续分布的系统 rc
rdm m
例: 已知一半圆环半径为 R,质量为m ,
M
d 0
二、质心运动定理(theorem of the motion of center of mass) 1. 质心的速度 dri m dr i miv i d mi ri c d t ( ) vc m dt m m dt mv c mi v i P 质点系动量 P mv c
理论力学PPT课件第5章 动量定理、质点系动量定理、质点系动量矩定理

A
o
G
B
x
2020年4月20日
15
偏心电机
e m2
F Oy
FOx
思考:偏心电机转动时,支座的动约束力为多大?
2020年4月20日
16
3.动量守恒与质心运动守恒
动量守恒 若:FRe=0 则:p = 常矢量 若:FRex=0 则:px = 常量
质心运动守恒(不动)
1) 若 FRe 0
ac 0
由动量矩定理:
dLOz dt
M
e Oz
d d t(2 W gr2A2 W gr2 BW gvC2 r)M W 2 r
2 W gr2A2 W gr2BW g2raCM 2 W r
2020年4月20日
49
2 W gr2A2 W gr2BW g2raCM 2 W r
补充运动学方程
aCrArB
2W graCW g2raCM2Wr
LA ri'm ivi' vi'— 相对速度
(3)绝对动量矩与相对动量矩的关系 LAL'AAC (mA), v c为质心,
当AC=0,即,动点为质心C时 LC=LC —对质心的绝对与 量相 矩对 相动 等
2020年4月20日
34
3.刚体的动量矩(对定点A)
(1)平移刚体的动量矩
L A r i ' m iv c A (C v m c ) A P C
Mce 0,Lc守恒 .
O
FT
C
GV
2020年4月20日
52
思考:猴子爬绳比赛,已 m A 知 m B ,vA rv B.r
答:若不计绳与滑轮的质量,则 v1a v2a
若考虑绳与滑轮的质量,则 m AvArm BvBrJoω
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质心系动量定理
质心系动量定理,是在物理学中常常使用的一个定理,它是描述一个系统动量守恒的定理。
在物理学中,质心系是一个非常有用的概念,它可以帮助我们更好地理解物体的运动状态。
首先,让我们来了解一下什么是质心。
质心是一个物体所有质点的平均位置,它是一个重要的物理量。
在物理学中,我们经常使用质心来描述一个物体的运动状态。
接下来,我们来了解一下什么是动量。
动量是一个物体的运动状态的量度,它是一个矢量量。
在物理学中,我们使用动量来描述一个物体的运动状态。
在物理学中,质心系动量定理是指:在一个封闭系统中,系统质心的速度等于系统所有质点动量之和除以系统总质量。
这个定理可以用来证明一个系统的动量守恒。
举个例子来说,假设有两个质点A和B,它们的质量分别为m1和m2,速度分别为v1和v2。
那么这个系统的总质量为
m1+m2,总动量为m1v1+m2v2。
根据质心系动量定理,这个系统的质心速度为(m1v1+m2v2)/(m1+m2)。
当然,在实际应用中,我们可能会遇到更加复杂的系统,但是质心系动量定理的原理是一样的:系统质心的速度等于系统所有质点动量之和除以系统总质量。
总之,质心系动量定理是一个非常重要的物理定理,在物理学中有着广泛的应用。
它可以帮助我们更好地理解物体的运动状态,并且可以用来证明一个系统的动量守恒。
