物体的质心和惯性力
第20讲义章惯性力

M IzM z(F Iit) m ir i r i ( m ir i2 ) J z 14
第二十章 惯性力
综上所述,惯性力系向转轴上一点O简化的主矩为
M IOM IxiM IyjM Izk
如果刚体有质量对称平面,切该平面与转轴z垂直,简化中 心O取为 此平面与转轴的交点,则有
F IR P gaCP g(aAaC t )A F Ie F Ir
式中
FIeP gaA,FIrP gaC t A
惯性力系向质心简化得主矩为
M IC
J C
1 12
P l 2
g
1P
12
g
la A
方向如图所示。
B
F Ie C
O
F
t Ir
M IC
q
A aA
21
第二十章 惯性力
再向O点简化, 主矢不变
P F IR g a C
M I O r i ( m i a i ) (m i r i ) a C m r C a C
若选质心C为简化中心,则 rC=0,有: MIC 0
故平移刚体的惯性力系可以简化
为通过质心的合力,其力大小等
于刚体质量与加速度的乘积,合
力的方向与加速度方向相反。
12
第二十章 惯性力
2、定轴转动刚体 如图示定轴转动刚体,考 虑质点i,以O为简化中。 有
29
第二十章 惯性力
由前面所得,即有
F Ix mC a x0, F Iy mC a y0
置静止落下。求开始落下时杆AB的角加速度及A点支座反力。
解: 选杆AB为研究对象
虚加惯性力系:
FIt
ml
2
F Inmna 0,M IAJA m 3 2l
惯性半径计算公式

惯性半径计算公式
惯性半径计算公式是指以米和克为单位计算质心距离的一种计算方法。
它可以用来测定物体的质心,以及物体的惯性量。
它也被用来测量物体的惯性力,以及物体的质量分布。
惯性半径计算公式的基本原理是,以物体的质心为原点,将物体的质量分布想象成一个球体,然后计算球体的半径。
这个半径就是惯性半径。
惯性半径计算公式的具体计算步骤如下:
1. 首先,计算物体的质心,即物体的重心,也就是物体的所有质点的重心位置;
2. 然后,计算物体所有质点到质心的距离;
3. 求出这些距离的平方和;
4. 最后,用总距离的平方和除以物体的质量,就得到了物体的惯性半径。
惯性半径计算公式的应用非常广泛,它可以用来测量物体的惯性量,以及物体的质量分布。
它也可以用来测量物体的惯性力,以及物体的重心距离。
另外,惯性半径的计算结果还可以用来计算物体的惯性矩,以及物体的动量。
总之,惯性半径计算公式是一种重要的物理计算方法,它可以帮助我们测量物体的质量分布,以及物体的惯性量,以及物体的惯性力等。
因此,惯性半径计算公式在物理学中有着重要的地位,它可以帮助我们更好地理解物体的性质和特性。
惯性力 动量定理 质心运动定理精品PPT课件
上页
下页
(一)直线加速运动参照系中的惯性力和动力学方程:
1. 惯性力:
F惯 ma0
a0
F惯
惯性力大小等于质点的 质 量与非惯性系加 速度a0 的 乘积,方向与a0方向相反。
注意: 1.惯性力不是真实力,是非惯性系中的观察者假 想出来的力,只有在非惯性系中才能观察得到;
2.惯性力不是物体间的相互作用,不存在惯性力
Fx2
F
2 y
此力与水平方向夹角为
tan Fy
Fx
代值求解得 F 8.1 103 N
300
上页
下页
例2、质量为2.5g的乒乓 球以10m/s的速率飞来, 被板推挡后,又以20m/s 的速率飞出。设两速度在 垂直于板面的同一平面内, 且它们与板面法线的夹角 分别为45o和30o,求: (1)乒乓球得到的冲量; (2)若撞击时间为0.01s, 求板施于球的平均冲力的 大小和方向。
间内合力的冲量。(单位:N·S )
(1)式为质点动量定理的微分形式,表示:
积合分 力的(元1)冲式量:等tt0 于F 质dt点 动P 量 的P0微 分mv。
m
v0
(2)
左侧积分表示在t0 到 t 这段时间
内合外力的冲量,用I 表示
t
I t0 Fdt
上页
下页
(2)式可表示为: I P P0
上页
下页
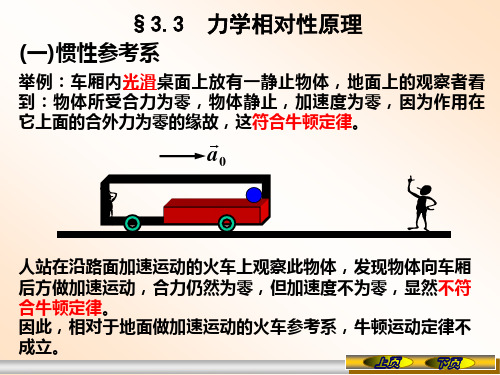
力学相对性原理:在一切惯性系中,力学定律 具有完全相同的表达形式。
由力学相对性原理可知,在研究力学规律时,所 有的惯性系都是等价的。我们在惯性系中所做的任何 力学实验,都不能确定该惯性系相对于其他惯性系是 否在运动。
力学相对性原理也称为伽利略相对性原理。
§3.4 非惯性系中的动力学
理论力学第十一章 达朗贝尔原理(动静法)

讨论:1)脱离角α与滚筒的角速度和滚筒半径有关,而与钢球质量无关。
2)
筒壁。此时转筒
的转速称为临界转速,对球磨机而言,要求n小于nL,否则球磨机就不能工作。
§11-2 刚体惯性力系的简化
刚体平移时惯性力系的简化
当刚体平移时,任一瞬时体内各点的加速度相等。若记某瞬 时刚体质心加速度为aC,则该瞬时体内任一质量为m的质点 的加速度ai=aC,虚加在该点上的惯性力Fgi=-miai=-miaC 。 刚体内每一点都加上相应的惯性力,由静力学知,该空间平 行力系可简化为过质心的合力,即
式中,Fgτ=-maτ,称为切向惯性力 Fgn=-man称为法向惯性力(也称离心力)
负号表示它们分别与切向加速度和法向加速度的方向相反。
§11-1 惯性力与质点的达朗贝尔原理
质点系的动静法
对由n个质点组成的非自由质点系,设其中任一质点的质量 为mi,某瞬时加速度为ai,作用其上的主动力F,约束反力 Fni,假想在该质点上加上惯性力Fgi=-mai,由质点达朗贝 尔原理,则
=- maC
该力偶的力偶矩等于惯性力系对刚体惯性力系的简化
结论 当刚体有质量对称面,且绕垂直于质量对称面的定轴 转动时,惯性力系可以简化为对称面内的一个力和一个力偶。 该力等于刚体的质量与质心加速度的乘积,方向与质心加速 度方向相反,且力的作用线通过转轴;
该力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘 积,其转向与角加速度转向相反。惯性力系向点O简化的结 果如图b)所示。
Fg=-m a
质点的达朗伯原理:质点在运动的每一瞬时,作用 于质点上的主动力、约束反力与假想地在质点上 的惯性力,在形式上构成一平衡力系。
§11-1 惯性力与质点的达朗贝尔原理
基本物理学问题中的惯性力和惯性质量

基本物理学问题中的惯性力和惯性质量一、引言惯性力和惯性质量是基础物理学中的重要概念,它们在描述物体运动时具有至关重要的作用。
这两个概念在物理学中的地位,类似于数学中的基本运算符号,是基本、必不可少的。
二、惯性力在描述物体运动时,有时候会遇到力的作用方向与物体方向不一致的情况。
这时候就需要引入惯性力。
惯性力是物体由于其惯性而产生的一种力,这种力与物体运动的状态有关。
比如,当我们在车上突然刹车时,我们的身体会向前倾,这是因为我们的身体具有惯性。
当车突然停止,身体仍然具有向前的惯性,导致身体向前倾。
这时,我们会感觉到一个向后的推力,这就是惯性力。
惯性力的大小与物体的质量、加速度以及惯性系的参考系有关。
在不同的参考系下,一个物体所受的惯性力是不同的。
三、惯性质量惯性质量是用来衡量物体惯性大小的物理量。
它描述了物体对力的反应能力,也就是说,物体的惯性越大,它所能受到的力也就越大,这就是惯性质量和力的关系。
惯性质量与物体的质量密切相关,但并不完全相同。
惯性质量是描述物体惯性大小的一个物理量,而物体的质量描述的是它的质量大小。
比如,一个小石头和一个大石头在相同的力作用下,根据牛顿第二定律,它们所受到的加速度应该是不同的。
这是因为它们具有不同的惯性质量。
尽管它们的质量相同,但是惯性质量不同,因此所受到的力也不同。
四、结论惯性力和惯性质量是描述物体运动时必不可少的概念。
惯性力描述了物体由于惯性而产生的一种力,而惯性质量则描述了物体对力的反应能力。
在实际中,我们常常需要考虑惯性力和惯性质量对物体运动的影响,在设计机器、运动模拟等方面,有重要的应用价值。
哲学家牛津在《人性困境》中指出:我们感知的世界,总是是以惯性的形式出现的。
这一点在物理学中也同样有体现。
物体的惯性力和惯性质量,是我们理解物体运动时必须要了解的重要概念,同时也是深入理解物理学的关键之一。
知识资料理论力学(十四)(新版)(1)

五、达朗伯原理达朗伯原理是一种解决非自由质点系动力知识题的普遍主意。
这种主意将质点系的惯性力虚加在质点系上,使动力知识题可以应用静力学写平衡方程的主意来求解,故称为动静法,动静法在工程技术中得到广泛的应用。
(一)惯性力当质点受到其他物体的作用而改变其本来运动状态时,因为质点的惯性产生对施力物体的反作使劲,称为质点的惯性力。
惯性力的大小等于质点的质量与其加速度的乘积,方向与加速度的方向相反,并作用在施力物体上。
惯性力的表达式为(二)达朗伯原理在非自由质点M运动中的每一瞬时,作用于质点的主动力F、约束反力N和该质点的惯性力FI构成一假想的平衡力系。
这就是质点达朗伯原理,其表达式为在非自由质点系运动中的每一瞬时,作用于质点系内每一质点的主动力Fi、约束反力N,和该质点的惯性力FiI构成一假想的平衡力系。
这就是质点系达朗伯原理。
即(三)刚体运动时惯性力系的简化对刚体动力知识题,可以将刚体上每个质点惯性力组成惯性力系,使劲系简化的主意,得出简化结果。
这些简化结果与刚体的运动形式有关。
详细结果见表4-3-9。
(四)动静法按照达朗伯原理,在质点或质点系所受的主动力、约束反力以外,假想地加上惯性力或惯第1 页/共7 页性力系的简化结果,则可用静力学建立平衡方程的主意求解动力知识题,这种求解动力知识题的主意称为动静法。
必须指出,动静法只是解决动力知识题的一种主意,它并不改变动力知识题的性质,因为惯性力并不作用在质点或质点系上,质点或质点系也不处于平衡状态。
动静法中“平衡”只是形式上的平衡,并没有实际意义。
应用动静法列出的平衡方程,实质上就是运动微分方程。
(五)例题[例4—3—13] 长方形匀质薄板重W,以两根等长的软绳支持如图4—3—37所示。
设薄板在图示位无初速地开始运动,图中α=30°。
求此时绳子中的拉力。
[解](1)对象以平板的为研究对象。
(2)受力分析运动开始时板受重力w、软绳约束反力T1、T2。
动力学中的质心与惯性矩阵计算

动力学中的质心与惯性矩阵计算动力学是研究物体在力作用下的运动规律的学科,它是力学的一个重要分支。
其中,质心和惯性矩阵是动力学中的两个重要概念,在计算系统的运动时起着关键的作用。
一、质心的概念与计算方法质心是一个物体或者物体系统几何形状的一个重要属性,它是物体所有质点的集中体现。
质心的位置可以通过质量的加权平均来计算,即质心的位置横纵坐标分别为所有质点质量加权平均后的坐标值。
对于一个由N个质点组成的物体系统,质心的位置坐标可以用如下公式计算:Xc = (m1x1 + m2x2 + ... + mNxN) / (m1 + m2 + ... + mN)Yc = (m1y1 + m2y2 + ... + mNyN) / (m1 + m2 + ... + mN)其中,Xc和Yc分别是质心的横纵坐标,m1、m2、...、mN是各个质点的质量,x1、x2、...、xN和y1、y2、...、yN是各个质点的横纵坐标。
通过这样的计算方法,可以获得一个物体系统的质心位置。
二、惯性矩阵的概念与计算方法惯性矩阵描述了物体在各个轴向上的惯性特性,它反映了物体对于旋转运动的抵抗程度。
对于一个刚体系统,惯性矩阵是一个3x3的矩阵,其元素分别表示物体在x、y、z三个轴向上的惯性。
对于一个由N个质点组成的刚体系统,该刚体相对于某个坐标系的惯性矩阵可以通过如下公式计算:[I] = Σ[(ri^2 - rci^2)Ii + mi⋅(R^2⋅Ii - ri⋅ri^T)]其中,[I]是惯性矩阵,ri是第i个质点相对于坐标系原点的位置矢量,rci是第i个质点相对于质心的位置矢量,Ii是第i个质点相对于质心的惯性矩阵,mi是第i个质点的质量,R是质心相对于坐标系原点的位置矢量,^T表示矩阵的转置。
通过这样的计算方法,可以得到一个刚体系统相对于某个坐标系的惯性矩阵。
三、质心与惯性矩阵在动力学中的应用质心和惯性矩阵是动力学中非常重要的概念,它们在分析物体或者物体系统的运动过程中起到关键的作用。
达朗伯原理

解:以整个系统为研究对象
FB
作受力图(包括惯性力)
B
FI ma
M IO
J
J
a R
mg FI
FI ma
M IO J
J
a R
α
M IO
O FA
对系统应用动静法
MB 0
mgl2 FIl2 Pl3 MIO FAl1 l2 0
Fy 0
l3
FB FA FB mg P F1 0
偏心状态
r FRA 1
FI1
m
FRB
A r2 m B
FI 2
r1 r2
FI1 FI2
FRA 0 FRB 0
偏角状态
FI1
m
A r1
FRB
r FRA 2
B
r1 r2
FI1 FI2
m FI 2
FRA 0 FRB 0
既偏心又偏角状态
FI1
A r1
m FRB
r FRA 2
m
r1 r2
FIRn
maCn
(3)转轴通过质心,且为
匀速转动 FIR 0
FIRn 0
M IO 0
四、刚体作平面运动
刚体平面运动 = 随质心的平移 + 绕质心的转动
将惯性力系向质心简化:
平移部分的惯性力系
合力
FIR maC
绕质心转动的惯性力系
合力偶 M IC=-JC
结论:
刚 通体 过作 质平 心面的运合动力时F,I R惯性力m系a简C化为,一以个及 一个合力偶: M IC=-JC
主矢和主矩和加速度、角加速度的方向相反
4、列出静平衡方程求解
FIR
在m静a平C 衡方程F中IRn ,惯m性a力Cn不加负号M,I直O=接J代z入
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物体的质心和惯性力
质心和惯性力是物理学中重要的概念。
质心是物体的一个特殊点,惯性力则是物体在运动过程中表现出的一种力。
在本文中,我们将探讨物体的质心和惯性力的概念、性质和应用。
一、质心的概念和性质
质心是一个抽象的概念,指的是物体所有质点的集中点。
对于均匀物体而言,质心位于物体的几何中心。
质心的坐标可以用物体不同部分的质量与其对应坐标的乘积之和除以物体总质量来表示。
质心的性质有以下几个方面。
首先,质心是一个物体的内禀性质,与物体的形状、大小和材质无关。
其次,质心可以用来描述物体的整体运动状态。
例如,当一个均匀杆在空中旋转时,在质心处施加的力矩为零,因此质心保持静止,整个杆绕质心旋转。
最后,质心具有稳定性,即使外力作用于物体的其他部分,质心的位置也不会改变。
二、惯性力的概念和性质
惯性力是物体在惯性参考系中由于加速度而产生的一种力。
牛顿第一定律告诉我们,物体在没有外力作用时会保持匀速直线运动或静止。
然而,在非惯性参考系中观察物体时,我们会看到物体受到了似乎无法解释的额外力,这就是惯性力。
惯性力的性质主要有以下两个方面。
首先,惯性力的大小与物体的质量和加速度成正比。
根据牛顿第二定律,物体的加速度与施加于物体上的力成正比,因此惯性力也会随之增加。
其次,惯性力的方向与物体的加速度相反。
这是因为惯性力的作用是为了使物体在参考系中保持惯性状态。
三、质心和惯性力的应用
质心和惯性力在物理学中有许多重要的应用。
其中一个应用是在力的分析中使用质心定理。
根据质心定理,可以将一个物体的复杂运动简化为质心的运动。
这极大地简化了力的计算和分析过程。
另一个应用是在静力学中使用质心概念。
当物体处于平衡状态时,质心位于物体的支撑位置上。
这使得我们可以通过控制质心位置来控制物体的平衡状态,例如在建筑物设计中。
惯性力的应用也非常广泛。
一个常见的应用是在转弯时的离心力。
当我们在转弯时,惯性力会将我们推向转弯的外侧。
这是因为我们的身体想要保持直线运动状态,而车辆转弯造成了向心加速度,所以我们会感受到向外的惯性力。
除此之外,惯性力还在航天领域的人造卫星和空间飞船中起着重要作用。
在这些运输工具中,惯性力被用来模拟地球引力,保持乘员和设备的重力感应。
总结
质心和惯性力是物理学中的重要概念。
质心是物体的集中点,可以用来描述物体的整体运动状态和稳定性。
惯性力是由于加速度而产生的一种额外力,大小与物体质量和加速度成正比,方向与加速度相反。
质心和惯性力的应用广泛,对于力的计算和分析以及物体的平衡和运动控制都有重要作用。
