高等数学(工本)自考教材
000230000高等数学(工本)课程考试说明

000230000 高等数学(工本)课程考试说明一、本课程使用的教材、大纲高等数学(工本)课程指定使用的教材为:(1)《高等数学(工专)》(附大纲),全国高等教育自学考试指导委员会组编,吴纪桃、漆毅主编,北京大学出版社,2006版(2)《高等数学(工本)》(附大纲),全国高等教育自学考试指导委员会组编,陈兆斗、高瑞主编,北京大学出版社,2006版二、本课程的试卷题型及试题难易程度1.试卷题型结构表2.试卷分别针对识记、领会、简单应用、综合应用四个认知及能力层次命制试题,四个层次在试卷中所占的比例大致为识记占20%,领会占30%,简单应用占30%,综合应用占20%。
3.试卷难易度大致可分为容易、中等偏易、中等偏难、难四个等级,根据课程的特点,试卷中不同难易度试题所占的分数比例,大致依次为容易占30分,中等偏易占30分,中等偏难占20分,难占20分。
三、各章内容分数的大致分布根据自学考试大纲的要求,试卷在命题内容的分布上,兼顾考核的覆盖面和课程重点,力求点面结合。
教材具体各章所占分值情况如下:四、考核重点及难点1.高等数学(工专)教材部分第一章函数重点:基本初等函数、函数的特性。
难点:函数的复合。
第二章极限与连续重点:极限概念、极限运算、两个重要极限、连续性及间断点分类。
难点:两个重要极限及相应的各种变形形式。
第三章导数与微分重点:导数定义、微分概念、导数的几何意义、导数的物理意义、各种求导法则。
难点:复合函数求导、几类特殊函数的求导方法。
第四章微分中值定理与导数的应用重点:三个中值定理的内容、洛必达法则、函数的单调性、凹凸性、极值、最值之判定和实际应用。
难点:综合运用中值定理、函数的特征证明一些不等式或等式。
第五章一元函数积分学重点:不定积分、定积分概念及运算、定积分应用。
难点:不定积分的综合运算和变上限积分的求导数。
2. 高等数学(工本)教材部分第一章空间解析几何与向量代数重点:向量的运算、平面、直线、柱面、椭球面、圆锥面、旋转抛物面的标准方程及其图形。
高等数学工本 自考教程

高等数学工本自考教程1. 高等数学工本自考教程简介高等数学是大学数学的重要基础课程,对于理工科学生来说尤为重要。
通过自考学习高等数学,可以帮助学生建立扎实的数学基本功,为后续学习其他高级数学课程打下坚实的基础。
2. 自考教程的编排自考教程通常包括以下内容:- 第一章:数列与极限介绍数列的定义、性质以及极限的概念和运算法则。
- 第二章:函数与极限介绍函数的概念、性质以及极限的计算方法和相关定理。
- 第三章:连续与导数介绍连续函数和导数的概念,掌握连续函数和可导函数的性质和计算方法。
- 第四章:微分学应用介绍微分学在曲线的切线、法线、极值、凹凸性及应用问题中的应用方法。
- 第五章:积分学介绍不定积分和定积分的概念、性质、求法以及应用。
- 第六章:多元函数微分学介绍多元函数的概念、偏导数、全微分与全微分公式以及最值和极值的判定方法。
- 第七章:多元函数积分学介绍多重积分的概念、性质、计算方法以及应用。
3. 自考教程的特点- 知识点全面:自考教程会对高等数学的各个知识点进行详尽的讲解,让学生能够全面掌握每个知识点的概念和运算方法。
- 实例讲解:教程中通常会给出大量的实例来帮助学生理解和应用所学的数学知识。
- 习题提供:教程通常会提供大量的习题和答案,供学生进行自测和巩固知识。
- 考试指导:教程还会提供考试指导,包括考试形式、重点、难点和解题技巧等信息,帮助学生备考。
4. 自考教程的选择和使用自考教程可以通过购买纸质教材、在线教育平台或自考培训班等途径获取。
在选择教程时,可以参考教材的内容、作者的资历和口碑,以及其他学生的评价来进行判断。
使用教程时,建议按照教程的编排顺序进行学习,结合教材的理论讲解、实例分析和习题练习来进行学习。
同时,可以结合相关的参考书和网上资源来扩充学习内容,提高学习效果。
自考高等数学工本教材

自考高等数学工本教材高等数学是大学数学的基础课程之一,对于学习理工科的学生而言非常重要。
自考高等数学工本教材作为自考专用教材,内容详实全面,涵盖了高等数学的各个方面,适合自学或者补习使用。
一、教材的编写背景和目的自考高等数学工本教材是根据自考科目设置以及学生自学需求编写的。
自考考试相对于常规高校教育,学生一般需要更加独立地进行学习,教材的编写旨在为自考学生提供一个全面系统的学习资料,以确保他们能够全面准确地掌握高等数学的相关知识和技能。
二、教材的内容安排自考高等数学工本教材内容涵盖了常规高等数学的各个分支,包括但不限于微积分、数列与级数、多元函数与偏导数、重积分与曲线积分等。
每个分支都以相应的理论知识为基础,结合大量的例题和习题,以帮助学生理解和掌握知识。
1. 微积分微积分是高等数学的核心内容,教材以微积分为起点,通过引入函数、极限以及导数等概念,逐步展开微积分的基本理论。
教材注重理论与实践的结合,通过典型例题和习题的讲解,让学生掌握微积分的基本思想和方法。
2. 数列与级数数列与级数是高等数学的重要内容,教材对数列与级数的定义、性质以及求和公式进行了详细讲解,并通过典型例题和习题引导学生理解数列与级数的概念和运算方法。
3. 多元函数与偏导数多元函数与偏导数是高等数学的一项重要内容,教材对多元函数的概念、偏导数与全微分的计算方法进行了详细介绍,并通过实例引导学生理解与运用。
4. 重积分与曲线积分教材对重积分与曲线积分的定义、性质以及计算方法进行了详细讲解,并通过实例让学生掌握计算重积分与曲线积分的步骤和技巧。
三、教材的特点与优势自考高等数学工本教材具有以下特点与优势:1. 系统全面:教材内容覆盖了高等数学的各个分支,构成一个系统完整的学习体系。
2. 知识点突出:教材对每个知识点进行了详细的讲解和拓展,帮助学生充分理解和掌握。
3. 理论与实践结合:教材以理论为基础,通过典型实例的引导,让学生将所学知识应用于实际问题中。
全国高等教育自学考试课程代码及选用教材
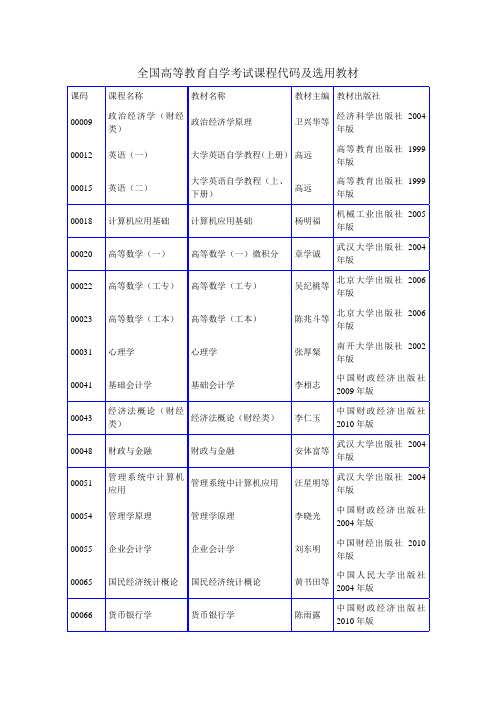
朱根娣
上海科技文献出版社2008年版
01759
药物化学(二)
药物化学
郑虎
人民卫生出版社2009年第6版
01761
药剂学(二)
药剂学
崔福德
人民卫生出版社2009年第6版
01763
药事管理学(二)
药事管理学
吴蓬
人民卫生出版社2008年第4版
02009
抽象代数
近世代数基础
张禾瑞
康士勇
中国人民大学出版社2008年版
00169
房地产法
房地产法
程信和等
北京大学出版社2006年版
00182
公共关系学
公共关系学
廖为建
高等教育出版社2011年版
00186
国际商务谈判
国际商务谈判
刘园
中国人民大学出版社2008年版
00189
旅游与饭店会计
基础会计学
李相志
中国财经出版社2009年版
00190
数量方法
数量方法
钱小军等
高等教育出版社2000年版
00800
经济学
经济学
刘凤良等
高等教育出版社2000年版
00801
会计学
会计学
耿建新
高等教育出版社2000年版
00803
财务管理
财务管理
黄慧馨等
高等教育出版社2001年版
00806
财务报表分析
财务报表分析
荆新
高等教育出版社2001年版
00807
金融概论
辽宁师范大学出版社2002年版
00399
学前游戏论
学前儿童游戏
自考高等数学教材目录

自考高等数学教材目录一、函数与极限1.1 实数及其运算1.2 映射与函数1.3 极限的概念与性质1.4 无穷小量与无穷大量1.5 极限运算法则1.6 极限存在准则1.7 函数的连续性二、导数与微分2.1 导数的概念与性质2.2 基本初等函数的导数2.3 反函数与隐函数的导数2.4 高阶导数2.5 微分的概念与性质2.6 微分中值定理与Taylor公式2.7 函数的单调性与曲线的凹凸性三、一元函数的应用3.1 函数的极值与最值3.2 函数与曲线的画法3.3 高次函数与附图3.4 弧长与曲线3.5 曲线的面积与旋转体的体积 3.6 微分中值定理的应用3.7 不定积分与定积分四、一元函数积分学4.1 不定积分4.2 定积分的概念与性质4.3 定积分的计算法4.4 定积分的应用4.5 反常积分五、多元函数微分学5.1 二元函数的极限与连续性 5.2 偏导数5.3 隐函数与参数方程的求导 5.4 方向导数与梯度5.5 多元复合函数的求导法则 5.6 多重积分5.7 曲线的弧长与曲面的面积六、重积分与曲线积分6.1 二重积分的概念与性质6.2 二重积分的计算法6.3 二重积分的应用6.4 三重积分的概念与性质6.5 三重积分的计算法6.6 曲线积分的概念与性质6.7 曲线积分的计算法七、无穷级数与幂级数7.1 数项级数的概念与性质7.2 正项级数的审敛法及其应用 7.3 幂级数的概念与性质7.4 幂级数的收敛域7.5 幂级数的求和八、常微分方程8.1 常微分方程的基本概念8.2 一阶微分方程的解法8.3 二阶线性微分方程8.4 高阶线性微分方程8.5 线性微分方程组与矩阵以上是自考高等数学教材的目录,涵盖了高等数学的各个知识点和章节。
这些内容从最基础的实数及运算开始,逐渐深入到函数与极限、导数与微分、一元函数的应用、一元函数积分学、多元函数微分学、重积分与曲线积分、无穷级数与幂级数以及常微分方程等方面。
通过学习这些内容,可以建立对高等数学的系统性理解和应用能力。
高等数学自考本科教材内容

高等数学自考本科教材内容高等数学是大学本科阶段的一门重要课程,涉及到微积分、线性代数等多个方面的知识。
本文将为您详细介绍高等数学自考本科教材内容,帮助您对这门学科有更为全面的了解。
1. 微积分微积分是高等数学中的基础部分,包括导数、积分和微分方程等内容。
自考本科教材通常会从导数开始,介绍函数的变化率和极限的概念。
接着,会深入讲解各种函数的导数计算方法,并引入微分的概念。
积分部分则包括不定积分和定积分,以及它们的应用,如曲线长度、面积计算等。
最后,会介绍常微分方程,包括一阶和二阶常微分方程的基本概念和解法。
2. 线性代数线性代数是另一个重要的组成部分,主要涉及到向量、矩阵和线性方程组等内容。
自考本科教材通常会从向量开始,详细介绍向量的性质、加法和数量积等运算。
接着,会引入矩阵的概念,包括矩阵的运算、逆矩阵、行列式等。
线性方程组是线性代数的重点内容,会介绍线性方程组的消元法、矩阵表示、解的存在性和唯一性等。
3. 空间解析几何空间解析几何是高等数学的一个分支,主要涉及到点、直线、平面和空间曲线等内容。
自考本科教材通常会从三维空间的基本概念开始,如点的坐标表示和距离公式。
接着,会介绍直线和平面的方程表示,以及它们的相交关系。
空间曲线包括参数方程表示和求曲线的切线等内容。
4. 多元函数多元函数是指具有多个自变量的函数,自考本科教材会介绍多元函数的极限、连续性和偏导数等概念。
接着,会讲解多元函数的方向导数和梯度,以及它们在几何和物理问题中的应用。
此外,还会介绍多元函数的二阶导数、泰勒展开和条件极值等内容。
5. 无穷级数无穷级数是数学中一个重要的概念,自考本科教材会介绍级数的概念和收敛性判定方法。
接着,会深入讲解各种常见级数的性质和求和方法,如等比级数、幂级数和傅里叶级数等。
此外,还会介绍级数在数学和物理问题中的应用。
以上是高等数学自考本科教材内容的主要内容,通过自学和实践,能够掌握这些知识,对于进一步学习相关专业课程和应用数学都是有帮助的。
高等数学自学教材推荐书目

高等数学自学教材推荐书目自学高等数学是提高数学能力和培养数学思维的重要途径之一。
选择一本好的教材对自学者的学习效果至关重要。
下面是一些高等数学自学教材的推荐书目,以供参考。
1.《数学分析》(尚敬泽著)《数学分析》是中国高等数学界的经典教材之一。
全书涵盖了高等数学分析的基本内容,包括数列与级数、函数与极限、导数与微分、微分中值定理、不定积分与定积分、多元函数与多重积分等。
该教材以其简明扼要的叙述、严谨的证明和对数学思想的深入解读,深受广大数学学习者的喜爱。
2.《高等数学》(郑光远、江维杰著)《高等数学》是一本系统全面的高等数学教材。
该书从基础概念出发,逐步展开高等数学的各个分支,包括数列与级数、函数与极限、导数与微分、积分与常微分方程等。
该书的特点是理论与实践相结合,注重理解与应用的统一,并附有大量的例题和习题,有助于读者巩固和提高自己的数学能力。
3.《数学分析教程》(张贤亮、徐杏蓉著)《数学分析教程》是面向高等院校学生编写的教材,但也非常适合自学高等数学。
该书系统地介绍了高等数学基础知识,包括函数与极限、导数与微分、积分与反常积分、无穷级数等。
每章都配有大量的例题和习题,涵盖各种难度和类型,有助于读者加深对数学知识的理解和掌握。
4.《高等数学辅导教程》(邵新建、乔明安著)《高等数学辅导教程》是一本针对高等数学考试辅导的教材,也适合自学使用。
该书以考试所需的知识和技巧为导向,分析了常见的考试题型,并提供了解题思路和解题方法。
该教材内容全面、结构清晰,能够帮助自学者迅速掌握高等数学的关键概念和解题技巧。
5.《高等数学导论》(毛寿龙、田春艳著)《高等数学导论》是一本面向大学生和研究生的高等数学教材。
该书内容丰富,包括数列与级数、函数与极限、导数与微分、积分与微积分基本公式、线性代数等。
同时,该书注重引入数学背后的思想和概念,使读者更好地理解数学的本质和应用。
总结:自学高等数学需要选择一本适合自己的教材,通过系统的学习和反复的练习,掌握并灵活运用数学的基本概念、方法和技巧。
高等数学自学教材推荐

高等数学自学教材推荐高等数学是一门重要的学科,对于理工类专业的学生来说,它是一门必修课程。
由于高等数学内容较为抽象和复杂,学生在学习过程中可能会遇到困难。
为了帮助学生更好地自学高等数学,下面将推荐几本优秀的自学教材。
一、《高等数学》(同济大学出版社)这本教材是同济大学出版社出版的经典教材,深受学生和教师的喜爱。
该教材以数学分析为基础,全面系统地讲解了高等数学的各个重要概念和定理。
同时,该书在理论讲解的基础上,注重实际问题的引入和应用,并提供了大量的习题和解答,供学生进行巩固和练习。
二、《高等数学》(人民教育出版社)这本教材是人民教育出版社出版的权威教材之一,广泛应用于高校和中等职业学校。
该教材结构清晰,内容详细,适合初学者自学。
书中所附习题有不同难度,从基础到深入,供学生选择自己的学习进度。
此外,该教材还配有电子辅助教学资源,学生可以通过扫描二维码或登录官方网站,获取更多习题和教学视频。
三、《高等数学导学与习题解析》(清华大学出版社)作为清华大学出版社推出的教材,该书内容全面,讲解深入。
与传统的教材不同,该书以导学方式引导学生,通过一系列实例和习题解析,帮助学生更好地理解和掌握高等数学的知识。
该教材还加入了一些案例和思维拓展题,培养学生的创新思维和问题解决能力。
四、《高等数学辅导教程》(高教出版社)这本教材是高教出版社推出的辅助教材,内容简明扼要,适用于复习和巩固高等数学知识。
该书突出重点和难点,重点讲解高等数学中的重要概念和常用定理,同时提供大量的习题和解析,供学生进行巩固和强化。
此外,该教材还附有一张光盘,内含教学视频和练习题答案,方便学生自主学习。
以上所推荐的教材都是经过广泛使用和验证的,具有权威性和可靠性。
每本教材都有其特点和适用对象,学生可以根据自己的实际情况和学习风格选择适合自己的教材。
在自学高等数学的过程中,学生应该结合教材提供的习题和解析进行练习,及时解决自己的疑惑,并在解题过程中培养自己的逻辑思维能力和问题解决能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学(工本)自考教材
高等数学(工本)自考教材
高等数学是大学数学中的一门重要课程,对于理工类专业的学生尤为重要。
掌握高等数学的基本理论和方法,不仅有助于理解和应用其他学科的知识,还为进一步学习相关专业奠定了坚实的基础。
本文将针对高等数学(工本)自考教材进行详细讨论和分析。
一、教材概述
高等数学(工本)自考教材以系统、全面地介绍高等数学的知识为主线,包含了数列、极限、微分学、积分学等多个重要章节,涵盖了高等数学所需的基本概念、理论和方法。
教材内容丰富,层次分明,适合自学和复习使用。
二、教材特点
1. 理论与实践相结合:教材既讲述了高等数学的基本理论,又通过大量的例题和习题,引导学生将理论应用于实际问题中,培养解决问题的能力。
2. 知识体系完整:教材将高等数学的各个分支知识有机地融合在一起,形成一个完整的知识体系。
从数列到极限,再到微分和积分,层层推进,层层深入,使学生能够系统地理解和掌握高等数学的核心内容。
3. 理论与实例并重:教材中穿插了大量的例题和习题,既展示了理论的应用,又提供了学生自我检测和巩固知识的机会。
学生在解题过程中能够不断地反复思考和总结,巩固理论知识。
三、教学方法
高等数学(工本)自考教材适用于自学和复习,教学方法需要根据个人情况和学习进度来选择。
以下是几种常用的教学方法:
1. 理论与实践相结合:在学习教材的过程中,要注重理论的学习,同时通过例题和习题的实际操作,加深对理论知识的理解和应用。
2. 多角度思考问题:在学习高等数学时,可以从不同的角度考虑问题,拓宽思维,培养解决问题的能力。
3. 合理规划学习时间:高等数学的学习需要一定时间和精力投入,因此要合理规划学习时间,保持学习的连续性和专注度。
四、学习建议
1. 注重基础知识的学习:高等数学是建立在基础数学知识之上的,所以在学习过程中,要注重对基础概念和定理的理解和掌握。
只有打好基础,才能更好地理解和应用高等数学的知识。
2. 制定学习计划:制定一个合理的学习计划对于高等数学的学习非常重要。
学习计划可以帮助你规划学习时间,合理安排每个章节的学习进度,确保学习的有序进行。
3. 多做题和总结:在学习过程中,要多做例题和习题,尤其是一些经典题目和难题。
通过不断地练习和总结,可以提高解题能力和对知识的掌握程度。
4. 寻求帮助和交流:如果在学习的过程中遇到问题,可以寻求他人的帮助和交流。
可以向同学、老师或者通过线上的学习平台和论坛进行交流,共同解决问题,提高学习效果。
五、总结
高等数学(工本)自考教材是一本系统、全面的教材,对于学习高等数学的学生来说具有重要的参考价值。
在学习过程中,需要注重理论和实践的结合,培养解决问题的能力,并合理规划学习时间。
通过多角度思考问题、注重基础知识的学习以及多做题和总结,可以提高学习效果,更好地掌握高等数学的知识和方法。
