散布图
品质七大手法(C5)-散布图

Xmax=90 Ymax=75 Xmin=10 Ymin=23
3)画出x-y轴坐标,取适当刻度
100 80 60 40
20
0
20
40
60
80
100
4)将数据点绘于x-y轴中
100 80 o 60 o 40 o o o o o o o
20
0
20
1、散布图的概念
1.2散布图的基本概念 将因果关系所对应变化的数据分别 描绘再x-y轴坐标系上,以掌握两个变量 之间是否相关及相关的程度如何,这种 图形叫“散布图”,也称作“相关 图”。,
1、散布图的概念
1.3散布图的分类 1)正相关:当变量x增大时,另一变量y也增大。 相关性强:如马力与载重的关系; 相关性中:如收入与消费的关系; 相关性弱:如体重与身高的关系。 2)负相关:当变量x增大时,另一变量y却减少。 相关性强:如投资率与失业率的关系; 相关性中:如举重力与年龄的关系; 相关性弱:如举重力与身高的关系。
2.1散布图的制作步骤 1)确定要调查的两个变量,收集成对的数据 (x1,y1),(x2,y2)….,整理成数据表; 至少30足以上。
No 1 x x1 y y1
2
3 4
x2
x3 x4
y2
y3 y4
….
….
….
2、散布图的制作
2.1散布图的制作步骤 2)找出两个变量x,y的最大值及最小值; 3)以x,y的最大值及最小值建立x-y坐标,并决定适 当的刻度便于描点; 4)将相对应的两个变量x,y以点的形式描在x-y坐标 中; 5)记入图名、制作者、制作时间等项目; 6)判读散布图的相关性与相关程度。
散布图

nⅢ
n
Ⅳ
Q X
六、注意事项:
数据的性质要相同,否则会导致不真实的判断结果;
散布图的相关规律的运用范围一般局限于观测值数据的范围 内,不能任意扩大相关推断范围; 散布图中出现的个别偏离分布趋势的异常点,应当查明原因 予以剔除;
七、实例解析:
某酒厂要判定中间产品酒中的酸度喝酒度2个变量之间有无关系, 存在什么关系?(搜集到的数据如下表)
Y
Y
Y
Y
Y
X
(a)正相关(强)
X (b)正相关(中)
X
(c)正相关(弱)
Y
序号 酸度 x 酒度 y 序号 酸度 x 酒度 y
1
2 3 4 5 6 7 8 9 10 11 12 13
0.5
0.9 1.2 1.0 0.9 0.7 1.4 0.9 1.3 10. 1.5 0.7 1.3
6.3
5.8 4.8 4.6 5.4 5.8 3.8 5.7 4.3 5.3 4.4 6.6 4.6
X (g)负相关(强) (h)负相关(中)
X
X (i)负相关(弱)
三、散布图的用途:
散布图可以用来发现两组相关数据之间的关系,并确认两组 相关数据之间预期的关系; 分析两组相关数据之间的关系主要是确认其相关性质,即正 相关和负相关;相关程度,即强相关和弱相关。电子云的形 态可以反映出相关的性质和程度;
7.散布图
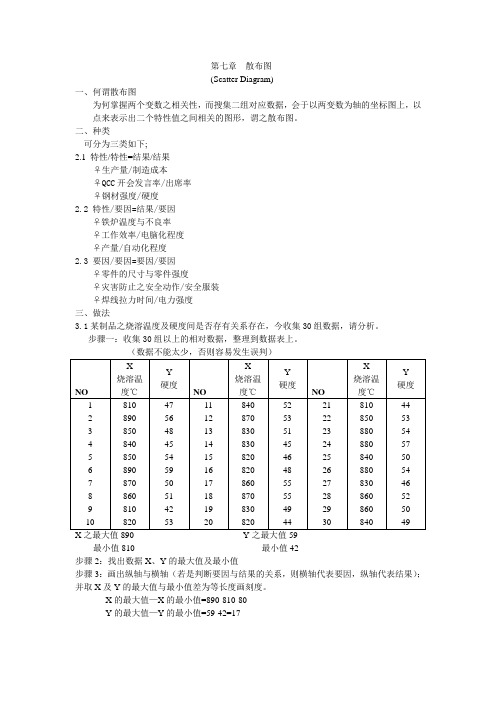
第七章散布图(Scatter Diagram)一、何谓散布图为何掌握两个变数之相关性,而搜集二组对应数据,会于以两变数为轴的坐标图上,以点来表示出二个特性值之间相关的图形,谓之散布图。
二、种类可分为三类如下;2.1 特性/特性=结果/结果♀生产量/制造成本♀QCC开会发言率/出席率♀钢材强度/硬度2.2 特性/要因=结果/要因♀铁炉温度与不良率♀工作效率/电脑化程度♀产量/自动化程度2.3 要因/要因=要因/要因♀零件的尺寸与零件强度♀灾害防止之安全动作/安全服装♀焊线拉力时间/电力强度三、做法3.1某制品之烧溶温度及硬度间是否存有关系存在,今收集30组数据,请分析。
步骤一:收集30组以上的相对数据,整理到数据表上。
(数据不能太少,否则容易发生误判)X之最大值890 Y之最大值59最小值810 最小值42步骤2:找出数据X、Y的最大值及最小值步骤3:画出纵轴与横轴(若是判断要因与结果的关系,则横轴代表要因,纵轴代表结果);并取X及Y的最大值与最小值差为等长度画刻度。
X的最大值—X的最小值=890-810-80Y的最大值—Y的最小值=59-42=17800 810 820 830 840 850 860 870 880 890烧溶温度℃X步骤4:将各组对数据点在坐标上。
横轴与纵轴的数据交汇处点上“·”二组数据重复在同一点上时,划上二重圆记号“◎”三组数据重复在同一点上时,划上三重圆记号“⊙”605856 NO.154 (X=890,Y=58)硬52度50 NO.1Y48 (X=810,Y=47) 图:数据打点法46444240800 810 820 830 840 850 860 870 880 890烧溶温度℃X60 n=3058 时间=9/25~9/29硬56度54Y52 制品名:SA-5050 单位:压延课48 绘图者:林武东46 绘制日:444240800 810 820 830 840 850 860 870 880 890图:钢的烧溶温度与硬度散布图步骤5:记入必要事项数据数、采取时间、目的、制品名、工程名、绘图者、绘制日期、、、、、、、均要说明。
散布图

二.散布图的实施步骤 1.确定要调查的两个变量,收集相关的最新数 确定要调查的两个变量, 确定要调查的两个变量 至少30个以上。 30个以上 据,至少30个以上。 2.找出两个变量的最大值与最小值,将两个变 找出两个变量的最大值与最小值, 找出两个变量的最大值与最小值 量描入X轴与Y 量描入X轴与Y轴。 3.将相对应两个变量,以点的形式标上坐标系。 将相对应两个变量, 将相对应两个变量 以点的形式标上坐标系。 4.记入图名、制作者、制作时间等项目。 记入图名、 记入图名 制作者、制作时间等项目。 5.判读散布图的相关性与相关程度。 判读散布图的相关性与相关程度。 判读散布图的相关性与相关程度
为确认马达连续运转之后,速度是否发生改变,经试验获得以下数据。 为确认马达连续运转之后,速度是否发生改变,经试验获得以下数据。
3.无相关(点子分布无向上或下倾向者): 无相关(点子分布无向上或下倾向者): 无相关 a.X与Y之间看不出有何相关关系。 与 之间看不出有何相关关系 之间看不出有何相关关系。 b.X增大时(或Y), 并不改变(或X)。 增大时( ),Y并不改变 增大时 ), 并不改变( )。 以上两种情形均称之为无相关,如下图 以上两种情形均称之为无相关,如下图h—j
4.曲线相关(点子分布不是呈直线倾向,而是 曲线相关(点子分布不是呈直线倾向, 曲线相关 弯曲变化者) 弯曲变化者) X开始增大时,Y也随之增大,但达到某一值 开始增大时, 也随之增大 也随之增大, 开始增大时 则当X值增大时 值增大时, 反而减少 反而减少, 后,则当 值增大时,Y反而减少,反之亦 称为同曲线相关。如下图K—L 然,称为同曲线相关。如下图
散布图的原理及应用

散布图的原理及应用1. 简介散布图(Scatter plot)是一种用于展示两个变量之间关系的图表。
它通过将每个数据点绘制为二维平面上的一个点,用点的位置表示两个变量的值,从而可以观察到变量之间的相关性、分布情况以及异常值等信息。
2. 原理散布图的原理非常简单,将两个变量的值分别映射到平面的X轴和Y轴上,并将每个数据点绘制为对应的点。
通过观察这些点的分布情况,我们可以得到以下信息:•相关性:散布图可以反映两个变量之间的相关性。
当散布图呈现出一条明显的趋势线时,表示两个变量之间存在一定程度的线性相关性。
如果趋势线是上升的,则表示正相关;如果趋势线是下降的,则表示负相关;如果趋势线接近水平,则表示无相关性。
•分布情况:散布图可以显示数据点的分布情况。
如果数据点紧密地聚集在某一区域,表示两个变量之间存在着较强的相关关系。
如果数据点局部散布较广,则表示两个变量之间相关性较弱。
•异常值:散布图可以帮助我们检测和识别异常值。
如果散布图中存在与主要分布趋势不一致的数据点,那么这些数据点很可能是异常值。
通过观察这些异常值,我们可以进一步分析其原因以及对数据分析结果的影响。
3. 应用散布图在数据分析和数据可视化领域有着广泛的应用。
以下是散布图常见的几种应用场景:3.1. 相关性分析散布图可以帮助我们分析两个变量之间的相关性。
通过观察散布图的趋势线,我们可以判断出两个变量之间的关系是正相关、负相关还是无相关。
这对于统计分析、市场调研等领域非常有价值。
3.2. 群组发现散布图可以帮助我们发现数据中的群组。
如果在散布图上存在多个独立的聚集点,那么可以认为这些聚集点代表了不同的群组。
这对于人群分析、社交网络分析等领域非常有用。
3.3. 异常检测散布图可以帮助我们检测和识别数据中的异常值。
通过观察散布图中与主要分布趋势不一致的数据点,我们可以识别出潜在的异常值。
这对于数据清洗、异常检测等领域非常重要。
3.4. 聚类分析散布图可以被用来进行聚类分析。
QC(旧)七大手法之六——散布图

QC(旧)七大手法之六——散布图(scatter diagram)第一小节散布图的观察分析一.定义散布图,也称散点图、相关图,散布图法又称为相关图法,QC要掌握的是平面散布图,是指通过分析研究两种因素的数据(成对出现)之间的关系,来控制影响产品质量的相关因素的一种有效方法(图示技术)。
散布图是研究成对出现的两组数据之间关系的图示技术。
在生产实际中,往往是一些变量共处于一个统一体中,它们相互联系、相互制约,在一定条件下又相互转化。
有些变量之间存在着确定性的关系,它们之间的关系,可以用函数关系来表达,如圆的面积S=πr2,有些变量之间却存在相关关系(即统计关系),即这些变量之间既有关系,但又不能由一个变量的数值精确地求出另一个变量的数值,如钢铁材料强度与含碳量之间的关系,车间的照明度与IPQC的测量误差之间的关系,人的身高与体重之间的关系等,这种统计关系只能用统计技术去研究,即将这两种有关的数据列出,用点子打在坐标图上,然后观察这两种因素之间的关系,这种图就是散布图或相关图,对散布图的分析称为相关分析。
散布图中所分析的两种数据之间的关系,一般有三种:可以是特性与原因的关系,即特性——原因(结果——原因);也可以是某一特性与另一特性的关系,即特性——特性(结果——结果);还可以是同一特性的两个原因之间的关系,即原因——原因。
散布图分析法,是适用范围较广的一种数理统计方法。
只要生产或试验中,存在着一些变量共处于一个共同体中,并且它们的关系又是不能用函数表示的非确定性关系,就可以运用散布图法来分析其是否具有相关关系以及这种关系的密切程度(即相关系数大小)。
若同时存在的不只是两个变量,而是多个变量,则可以两两分别作散布图来加以分析。
当然,也可用正交试验设计方法来对多变量(因素)之间的关系进行分析,并求得它们之间的最优配合。
注:用相关图法,可以应用相关系数r、回归分析等进行定量的分析处理,确定各种因素对产品质量的影响程度。
散布图

散布图作业方法
1.概念:
散布图是指:研究成对(如X、Y,每组为一点)出现的两组相关数据之间的关系的简单图示。
又名散点图或相关图。
2.目的:发现和显示两类相关数据之间的关系,确认两类相关数据之间的预期关系。
3.作图方法
3.1识别要测试的关系;
3.2收集成对数据(X、Y),至少要有25组关于这两个变量的数据;
3.3分别在X轴和Y轴对这两个变量标注和画出刻度。
如果认为一个因素影响另一个因素(称因变量),把它标在X轴(横轴)上,把被影响因素标在Y轴(纵轴)上。
3.4把所收集的数据组在图上描出对应的点。
3.5分析点子云的形态、相关关系的类型和强度。
4.点子云的形态与相关关系的类型和强度的判定准则
4.1模式1:正相关。
点子云从左下角向右上角方向伸展,说明当一个变量增大时另一个变量也增大。
点子分散程度小时,称为强正相关;点子分散程度大时,称为弱正相关;4.2模式2:负相关。
点子云从左上角向右下角方向伸展,说明当一个变量增大时另一个变量减少。
点子分散程度小时,称为强负相关;点子分散程度大时,称为弱负相关;4.3模式3:无相关。
散布图

散布图散布图又称相关图,是用来表示一组成对的数据之间是否有相关性,进而控制影响产品质量的相关因素的一种有效方法。
产品质量是以一系列的特性表现出来的,而这些特性又与各种因素相关联,通过散布图将两种有关的数据列出,用点子打在坐标图上,然后观察两种因素之间的关系。
绘制散布图的方法如下:(1)收集数据。
收集不少于30组(量小不易发现趋势)的数据,并按一一对应关系列成数据表。
(2)画出坐标图X轴、Y轴,并标出刻度。
X轴、Y轴的极限长度最好取基本相等的长度,以便分析相关性。
若两组数据是特性和原因关系(如价格与成本),X轴表示原因数据(成本),Y轴表示特性数据(价格);若两组数据是特性关系(如身体健康状况与遗传基因),则常用X轴表示易测定的特性(身体健康状况),Y轴表示难测定的特性(遗传基因)。
(3)描点。
将一一对应的数据描绘到图上,若有两组或多组数据完全相同,则可用圈(○)表示。
(4)判断。
研究点子的分布状况,确定其相互关系的类型及密切程度。
根据测量的两组数据绘成散布图后,即可从图上点子分布状况来分析两组数据间的关系及密切程度。
数据关系通常有六种基本形状:(1)强正相关。
即X增大,Y也显著增大。
对此,一般控制了X,Y也能得到相应的控制。
(2)弱正相关。
即X增大,Y也增大,但增大不明显。
对此,除考虑X因素外,还要分析是否有其他因素的影响。
可进行分层处理,寻找工序以外的其他影响因素。
(3)强负相关。
即X增大,Y显著减小。
对此,一般控制了X,Y也能得到相应的控制。
(4)弱负相关。
即X增大,Y减小,但不明显。
对此的处理与弱正相关相同。
(5)不相关。
即X与Y两个因素不存在相关关系。
(6)非线性相关。
即X增大,Y也增大(或减小),但当X增大到一定程度时,X再增大,Y反而减小(或增大)。
对此,在某一数值前,按正(负)相关处理;超过该数值后,按负(正)相关处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、散布图的相关检验
2、符号检验法(中值法)
◆令:n1+n3=n+ ; n2+n4=n- ; s=Min(n+,n-),即s为n+、n-之中的最小值。
◆查符号检验表得判断值Sα。
在符号检验表中查得与n和α相对应的判断值Sα。 其中:n点数的总和(恰好在中位线上的点子不计算): n=n++n-。
α:显著水平α,也称作风险度,是与置信度β相对应的参数α+ β=1。 α:一般取0.01、0.05,意谓着判断错误的风险率是0.01(1%)和0.05(5%)
达。 ②相关关系:变量之间存在密切关系,但又不能由一个(或几 个)变量的数值精确地求另一变量的数值,称这类变量的关系 为相关关系。
③不相关:事物之间没有关系。
一、散布图概述
3、散布图的用途:
①用来发现和确认两组数据之间的关系并确定两组相
关数据之间预期的关系。
②通过确定两组数据、两个因素之间的相关性,有助
四、散布图的相关检验
2、符号检验法(中值法)
散布图中位线 Y (%)
93 92
Ⅱ n2=5
● ●
P
● ● ● ●
Ⅰ n1=10
● ●
91
90 89 88 87 86 85
● ● ● ● ●
●
● ● ●
●
● ● ● ●
Q
● ● ●
●
● ●
n3 =10
8.0 8.5 9.0
Ⅲ
●
Ⅳ n4 =5
9.5
X(g)
异常值
三、作散布图的注意事项
3、分层的必要性
在下图中,从全体座标点看不至相关,然而,从“*”与 “×”将座标点分层,则发现各自皆有相关。 反之,整体好像相关,而分层后层内没有相关的情况存在, 所以作散布图前应考虑分层,且以不同的记号表示分层后的座 标点。
三、作散布图的注意事项
4、假相关
有时存在这样的情况,观察散布图明明有相关,但从技术 上看,直接提出的原因与结果之间都没有关系。 比如,可能与民列原因之外的原因相关,而错误的认为与 所列原因相关,这就叫假相关。
总判断:结合的判断结 论作出总判断。 对于上表的案例:
S=10,
查右表知:Sα=9, 因为S>Sα,所以添加 剂”A“的重量和产出 率是弱正相关。
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
五、相关系数及其检验
1、相关系数的定义。 相关系数:表示两个变量x与y的相关程度。 ( X X )(Y Y ) r= (X X ) (Y Y )
● ● ● ● ● ●● ● ● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ●● ● ● ● ● ● ●● ● ●● ● ●● ● ● ●● ● ● ● ● ●● ● ● ● ●● ●● ● ● ● ● ● ●● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ● ● ●● ● ● ●● ● ● ● ● ● ● ●● ●● ● ● ● ● ● ● ● ● ●● ● ●● ● ●● ●● ● ●● ● ● ● ● ● ● ● ●● ● ● ● ● ●
X以外的因素)。
y
● ● ● ● ● ● ● ● ●
● ● ● ● ● ● ●
(e)不相关
x
● ● ●
不相关。 X与Y无任何关系。 不存在相关系数R。
y
● ●
● ● ● ● ● ● ● ● ● ● ● ●
非线性相关。
(f)非线性相关
x
四、散布图的相关检验
2、符号检验法(中值法)
符合检验法是利用“符号检验表”检查点子云的形态, 以判断相关关系及其程度的一种定性分析方法。符号检验 法的分析结果要比对照典型图法准确。 符号检验法分析步骤(结合下表来说明) ①在散布图中作一条平行于X轴的中位线Q,平分散布图中 所有的点子,使上下点子数基本相等。 ②在散布图中作一条平行于Y轴的中位线P,平分散布图中 所有的点子,使左右点子数基本相等。
r 接近 -1
三、作散布图的注意事项
2、异常值的处理
在散布图上如果出现下图所示的偏离集体很远的点,则该 点可认为是异常值,有必要追究其原因。 作为异常值的原因,除了测量差错或记录的疏忽外,常常 是操作条件的变化造成的,由此可找到工序改进的线索。
● ● ● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ●● ● ● ● ● ● ●● ● ●● ● ●● ● ● ●● ● ● ● ● ●● ● ● ● ●● ●● ● ● ● ● ● ●● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ● ● ●● ● ● ●● ● ● ● ● ● ● ●● ●● ● ● ● ● ● ● ● ● ● ● ●● ● ●● ● ● ● ●● ●● ● ● ●● ● ● ● ● ● ● ● ● ●● ● ● ● ● ●
二、散布图的绘图步骤
1、选定分析对象
分析对象的选定,可以是质量特性值与因素之间的关系、 质量特性值与质量特性值之间的关系、因素与因素之间的 关系。 本例选定的分析对象是添加剂的重量与产出率的关系, 它们是因素与质量特性值之间的关系。
2、收集数据,填入数据表。
数据一般要在30组以上,且数据必须是对应的,并记录 收集数据的日期、取样方法、测量方法等有关事项。 案例收集了30组对应数据
四、散布图的相关检验
表4 常见的散布图形状与分析
图 形
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
X与Y的关系 强正相关。 X变大,Y也变大。 强负相关。 X变大,Y变小;X变 小,Y变大。
说
明
y
(a)强正相关
x
X、Y之间可以用直线表示。一般 只要控制住X,Y就会行到相应控 制。
散布图(Scatter Diagram)
目录
一、散布图概述 二、散布图的绘图步骤
三、作散布图的注意事项
四、散布图的相关检验
五、相关系数及其检验
六、练习
一、散布图概述
1、定义:
描述两个因素之间相关关系的图形,称为散布图,又叫相关图
2、相关的概念:变量之间存在的关系,有下列几种还情况。
①完全相关关系:这种关系一般可用一个不变的数学公式来表
四、散布图的相关检验
绘出散布图后,应对其观察和分析,来判 断两个变量之间的相关关系。散布图的定性分 析一般有两种方法: 1、对照典型图法
对照典型图法是散布图分析中最粗略的分析法,把绘好的 散布图与典型图对照,可判断出两个变量之间的相关关系。 利用对照典型图法,可判断出案例添加剂“A”的重量与产 出率之间存在着弱正相关关系。
y
● ● ● ● ● ● ● ● ● ● ● ● ●
● ●
(b)强负相关
x x
y
●
● ● ● ● ● ● ● ● ● ● ●
弱正相Y外,还要考虑其他 因素(一般可进行分层处理,寻找
(C)弱正相关
y
● ●
● ● ●
● ● ● ● ● ● ● ● ●
(d)弱负相关
x
弱负相关。 X变大,Y大致变小。
于寻找问题的可能原因。
二、散布图的绘图步骤
案例:表1-6 列出了添加剂的重量与产出率的数据,请根据这 些数据描绘出散布图并进行分析。
表1 添加剂“A”的重量和相应的产出率
Å ú º Å 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Ì í ¼ Ó ¼ Á ¡ °A” £ ¨g£ © 8.7 9.2 8.6 9.2 8.7 8.7 8.5 9.2 8.5 8.3 8.6 8.9 8.8 8.4 8.8 ú ³ ² ö Â Ê £ ¨%£ © 88.7 91.1 91.2 89.5 89.6 89.2 87.7 88.5 86.6 89.6 88.9 88.4 87.4 87.4 89.1 ú º Å Å 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 í ¼ Ì Ó ¼ Á ¡ °A” £ ¨g£ © 8.4 8.2 9.2 8.7 9.4 8.7 8.3 8.9 8.9 9.3 8.7 9.1 8.7 8.8 8.9 ú ³ ² ö Â Ê £ ¨%£ © 89.4 86.4 92.2 90.9 90.5 89.6 88.1 90.8 88.6 92.8 87.2 92.5 91.2 88.2 90.4
二、散布图的绘图步骤
3、在坐标纸上建立直角坐标系
①为便于分析相关关系,两个坐标数值的最大值与最小值 之间的范围应基本相等。见表2。 ②若分析对象的关系,属于因素与质量特性值之间的关系, 则X轴表示因素,Y轴表示质量特性值。
表2 散布图的横、纵坐标的范围应基本相等
Y
应基本相等
Y的数 据范围
X的数据范围
8.5
9.0
9.5
添加剂“A”,g
表3:此散布图示出了添加剂“A”的质量与产出率之间存在着弱正相关的关系。
二、散布图的绘图步骤
4、描点
当散布图上出现明显偏离其他数据点的异常点时,应查 明原因,以便决定是否删除或校正。所谓异常点就是散布 图上出现远离群点的点。对于这种点的出现,要查明原因。 一般来说产生这种现象的原因是由于测量的误差、数据记 录错误或操作条件的变化等。 如查清确实属于上述等原因造成的,则应将这些点删 除。如果原因不明,就不能删除,变量之间很可能包含着 我们认识不到的规律。
5、记入必要信息
填写散布图标题、数据来源及其它必要事项。
三、作散布图的注意事项
