平面直角坐标系中求面积( 全)
人教版初一数学下册平面直角坐标系中求三角形的面积
在直角坐标系中求图形的面积图形的面积可以利用相应的面积公式求得，但是在平面直角坐标系内的求面积问题，往往不直接给出边或高之类的条件，而是给出一些点的坐标。
我们常常会遇到在平面直角坐标系中求三角形面积和一些不规则图形面积的问题，解题时我们要注意其中的解题方法和解题技巧。
现对这类题目的解法举例说明如下：一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y 轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C （-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD ×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.。
平面直角坐标系求面积1
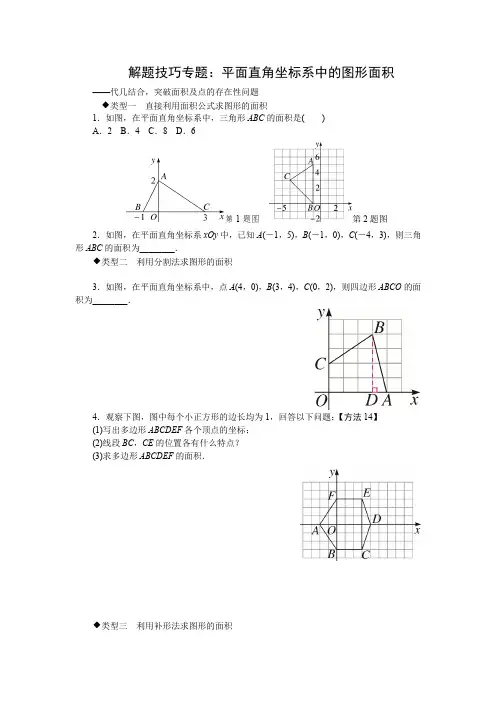
解题技巧专题：平面直角坐标系中的图形面积
——代几结合，突破面积及点的存在性问题
◆类型一直接利用面积公式求图形的面积
1．如图，在平面直角坐标系中，三角形ABC的面积是()
A．2 B．4 C．8 D．6
第1题图第2题图2．如图，在平面直角坐标系xOy中，已知A(－1，5)，B(－1，0)，C(－4，3)，则三角形ABC的面积为________．
◆类型二利用分割法求图形的面积
3．如图，在平面直角坐标系中，点A(4，0)，B(3，4)，C(0，2)，则四边形ABCO的面积为________．
4．观察下图，图中每个小正方形的边长均为1，回答以下问题：【方法14】
(1)写出多边形ABCDEF各个顶点的坐标；
(2)线段BC，CE的位置各有什么特点？
(3)求多边形ABCDEF的面积．
◆类型三利用补形法求图形的面积
5．在如图所示的正方形网格中，每个小正方形的边长均为1，三角形ABC的三个顶点恰好是正方形网格的格点．【方法14】
(1)写出三角形ABC各顶点的坐标；
(2)求出此三角形的面积．
◆类型四与图形面积相关的点的存在性问题
6．(2017·定州市期中)如图，A(－1，0)，C(1，4)，点B在x轴上，且AB＝3.
(1)求点B的坐标；
(2)求三角形ABC的面积；
(3)在y轴上是否存在点P，使以A，B，P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．。
向量叉积求平面直角坐标系三角形面积
向量叉积求平面直角坐标系三角形面
积
在平面直角坐标系中，可以使用向量叉积来计算三角形的面积。
假设三角形的三个顶点分别是$(x_1,y_1)$、$(x_2,y_2)$、$(x_3,y_3)$，则可以将两个向量$\overrightarrow{AB}$和$\overrightarrow{AC}$表示为：
$\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$，$\overrightarrow{AC}=(x_3-x_1,y_3-y_1)$
然后计算两个向量的叉积：
$\overrightarrow{AB}\times\overrightarrow{AC}=|(x_2-x_1)(y_3-y_1)-(y_2-y_1) (x_3-x_1)|$
这个叉积的结果就是三角形的面积的两倍。
因此，三角形的面积可以表示为：
$S=\dfrac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|=\dfrac{1}{2}| (x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1)|$
这个公式可以用于计算任意平面上的三角形面积，不仅限于直角坐标系。
需要注意的是，如果三角形的三个顶点共线，那么它的面积为0。
平面直角坐标系中的面积问题
∴OA=4， yB =3
∴ S△AOB
1 OA OB 2
=1 43 2
6 【典型例题】 类型 1 有一边在坐标轴上
∴ S△AOB
1 OA 2
yB
=1 43 2
6
例 1 如图 1，△ABC 的三个顶点的坐标分别是 A(4，0)，B(-2，0)，C(2，4)，求△ ABC 的面积.
山东大学附属中学初二数学组 张永坤整理
【点拨】（1）“补”的思想；（2）三角形的面积公式：
“底乘高除以 2”.
图5
山东大学附属中学初二数学组 张永坤整理
例 6 如图 6，已知△ABC 中，A（4，1），B（4，5），C（-1，2），求△ABC 的 面积.
图6 【分析】采用“补”的思想，将△ABC 补成一个正方形或者梯形. 【方法】
例 7 如图 7，以 OA 为边的△OAB 的面积为 2，试找出符合条件得且顶点是第一象 限格点的点 C，你能找出几个这样的点？
【分析】要求三角形的面积，需要分别求出底边及其高.由图 1 可知，△ABC 的边 AB 在 x 轴上，容易求得 AB 的长，而 AB 边上的高，恰好是 C 点到 x 轴的距离，也就是 C 点的纵坐标的绝对值.
解：∵A(4，0)，B(-2，0)，
∴AB=4-（-2）=6.
∵C 点坐标为(2，4)，
∴C 点到 x 轴的距离为 4，
【分析】明确底和高，以及利用平行线之间的距 离处处相等进行面积转化.【同底等高模型】
【方法】
图7
山东大学附属中学初二数学组 张永坤整理
例 8 如图所示，已知：A（0，1），B（2，0），C（4，3）. （1）在坐标系中描出各点，画出△ABC． （2）求△ABC 的面积； （3）设点 P 在坐标轴上，且△ABP 与△ABC 的面积相等，求点 P 的坐标． 【分析】（1）确定出点 A、B、C 的位置，连接 AC、 CB、AB 即可； （2）过点 C 向 x、y 轴作垂线，垂足为 D、E， S△ABC = S 四边形 DOEC -S△ACE -S△BCD -S△AOB； （3）当点 P 在 x 轴上时，由 S△ABP =4，求得：BP=8， 故此点 P 的坐标为（10，0）或（﹣6，0）；当点 P 在 y 轴 上时，S△ABP =4，解得：AP=4．所以点 P 的坐标为（0，5） 或（0，﹣3）． 【解答】 解：（1）如图所示：△ABC 即为所求．
如何求平面直角坐标系中三角形的面积
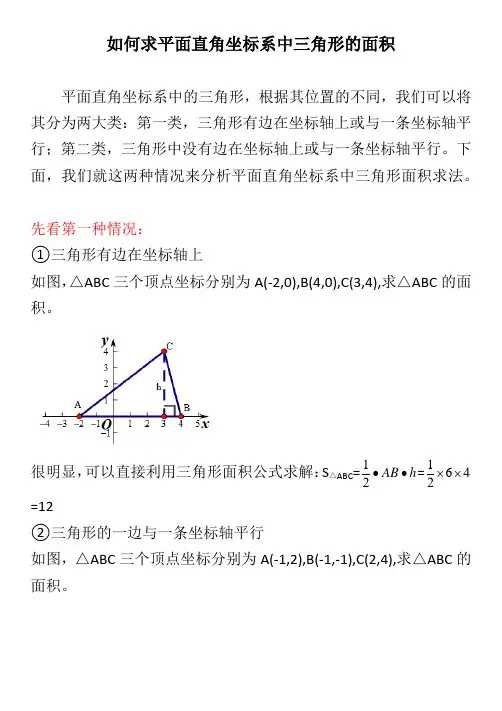
如何求平面直角坐标系中三角形的面积平面直角坐标系中的三角形，根据其位置的不同，我们可以将其分为两大类：第一类，三角形有边在坐标轴上或与一条坐标轴平行；第二类，三角形中没有边在坐标轴上或与一条坐标轴平行。
下面，我们就这两种情况来分析平面直角坐标系中三角形面积求法。
先看第一种情况：①三角形有边在坐标轴上如图，△ABC 三个顶点坐标分别为A(-2,0),B(4,0),C(3,4),求△ABC 的面积。
很明显，可以直接利用三角形面积公式求解：S △ABC =h AB ••21=4621⨯⨯=12②三角形的一边与一条坐标轴平行如图，△ABC 三个顶点坐标分别为A(-1,2),B(-1,-1),C(2,4),求△ABC 的面积。
这种情形，与①相比，只需利用顶点坐标求出底边AB 长及AB 边上的高h 的值，再代入三角形面积公式求解即可：S △ABC =h AB ••21=293321=⨯⨯以上①与②是坐标系中求三角形面积问题的基础。
位置无此特殊性的三角形可转化为该情况后再求解。
再看第二种情况：三角形中没有边在坐标轴上或与一条坐标轴平行。
例1：已知△ABC 三个顶点的坐标分别为：A(1,2)，B(4,6)，C(2,21)，求这个三角形的面积。
分析：如果用三角形面积公式进行求解，知道点的坐标，容易求得线段的长度，底的问题解决了，但底边上的高呢？有点麻烦。
我们不妨试试下面的方法。
分别过点A 、B 、C 作x 轴、y 轴的平行线，则所求三角形的面积S △ABC =S 矩形BDEF -S △ADB -S △AEC -S △BCF =4172112212312143212113=⨯⨯-⨯⨯-⨯⨯-⨯过点C 作y 轴的平行线交AB 边于点M ，将原三角形化作有边与一条坐标轴平行的问题来解决。
易知所求三角形面积S △ABC =S △AMC +S △BMC =)(2121212121h h MC h MC h MC +••=••+••=PQ MC ••21 其中，线段PQ 的长度可由A 、B 两点的横坐标求得，线段MC 的长度需知道点M 与点C 的纵坐标，所以，接下来主要是求得点M 的坐标的问题。
平面直角坐标系中三角形面积的求法(例题及对应练习)
例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。
例析平面直角坐标系中三角形面积的求法
例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为〔－3，0〕，〔0，3〕，〔0，－1〕，你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC ＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-〔-1〕=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A〔4，1〕，B〔4，5〕，C〔-1，2〕，求三角形ABC的面积.分析：由A〔4，1〕，B〔4，5〕两点的横坐标一样，可知边AB与y轴平行，因而AB 的长度易求.作AB边上的高CD，那么D点的横坐标与A点的横坐标一样，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标一样，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，那么D点的横坐标为4，所以CD=4-〔-1〕=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，点A〔-3，-1〕，B〔1，3〕，C〔2，-3〕，你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想方法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形〔长方形〕的上下底〔长〕与其中一坐标轴平行，高〔宽〕与另一坐标轴平行.这样，梯形〔长方形〕的面积容易求出，再减去围在梯形〔长方形〕边缘局部的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，那么四边形ADEC为梯形.因为A〔-3，-1〕，B〔1，3〕，C〔2，-3〕，所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=〔AD+CE〕×DE-AD×DB-CE×BE=×〔4+6〕×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题〔提高篇〕“割补法〞的应用一、点的坐标，求图形的面积。
坐标系中如何求三角形的面积
坐标系中如何求三角形的面积
问题描述
在平面直角坐标系中，给定三角形的三个顶点坐标 A(x1, y1), B(x2, y2), C(x3,
y3)，如何通过坐标计算出这个三角形的面积呢？
基本原理
要计算三角形的面积，我们可以利用向量的知识来求解。
设向量AB为向量a，向量AC为向量b。
则向量a的坐标为 (x2 - x1, y2 - y1)，向量b的坐标为 (x3 - x1,
y3 - y1)。
具体步骤
1.计算向量a和向量b的叉乘，即 a × b = x1y2 + x2y3 + x3y1 - x1y3 -
x2y1 - x3y2。
2.三角形的面积等于叉乘结果的绝对值的一半，即 area = |a × b| / 2。
3.最终得出的结果即为这个三角形的面积。
例子
例子：
假设三角形ABC的三个顶点坐标为A(1, 2), B(4, 5), C(3, 7)。
计算过程如下：
向量a = AB = (4 - 1, 5 - 2) = (3, 3)
向量b = AC = (3 - 1, 7 - 2) = (2, 5)
叉乘结果为 a × b = 15 + 42 + 33 - 17 - 45 - 32 = 5 + 8 + 9 - 7 - 20 - 6 = -1
三角形的面积为 area = |-1| / 2 = 0.5
所以，三角形ABC的面积为0.5。
结论
通过向量的方法，我们可以方便地在坐标系中计算三角形的面积。
这种方法简
单直观，可以很好地应用于实际问题中。
专题4.1 平面直角坐标系中图形面积的求法(4大类型)(原卷版)
专题4.1 平面直角坐标系中图形面积的求法（4大类型）【典例1】如图，△ABC是由△A1B1C1向右平移2个单位，再向上平移1.5个单位所得．已知A（2，1），B（5，3），C（3，4）．（1）直接写出△A1B1C1三个顶点的坐标．（2）求△ABC的面积．【变式1-1】（2022春•五华区期末）在平面直角坐标系中，△ABC经过平移得到三角形△A′B′C′，位置如图所示：（1）分别写出点A、A'的坐标：A，A'；（2）若点M（m，n）是△ABC内部一点，则平移后对应点M'的坐标为；（3）求△ABC的面积．【变式1-2】（2022春•宜城市期末）如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）．（1）画出三角形ABC，并求其面积；（2）如图，△A′B′C′是由△ABC经过怎样的平移得到的？（3）已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标（，）．【典例2】如图，已知在平面直角坐标系中，四边形各顶点的坐标分别为A（0，0），B（9，0），C（7，4），D（2，8），求四边形ABCD的面积．【变式2-1】如图，在平面直角坐标系中，图中的网格是由边长相等的小正方形组成，点A、B、C的坐标分别为（﹣5，4），（﹣4，0）．（﹣5，﹣3）．（1）请写出点D、E、F、G的坐标；（2）求图中阴影部分（多边形ABCDEFG）的面积．【变式2-2】如图，四边形ABCD各顶点的坐标分别是A（0，0），B（8，0），C（6，4），D（3，6），求出四边形ABCD的面积．【典例3】如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足，过C作CB⊥x轴于B．（1）求△ABC的面积．（2）在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．（3）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．【变式3-1】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B的对应点C，D，连接AC，BD，CD．（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；（2）在y轴上是否存在一点P，连接P A，PB，使S△P AB ＝S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由．6．平面直角坐标系中，将点A、B先向下平移3个单位长度，再向右平移2个单位后，分别得到点A′（3，﹣2）、B′（2，﹣4）．（1）点A坐标为，点B坐标为，并在图中标出点A、B；（2）若点C的坐标为（2，﹣2），求△ABC的面积；（3）在（2）的条件下，点D为y轴上的点，且使得△ABD面积与△ABC的面积相等，求D点坐标．【变式3-2】在平面直角坐标系中，O为原点，点A（0，2），B（﹣2，0），C （4，0）．（Ⅰ）如图①，则三角形ABC的面积为；（Ⅱ）如图②，将点B向右平移7个单位长度，再向上平移4个单位长度，得到对应点D．①求三角形ACD的面积；②点P（m，3）是一动点，若三角形P AO的面积等于三角形CAO的面积．请直接写出点P坐标．【变式3-3】综合与探究：如图1，在平面直角坐标系中，O为原点，点A、B在坐标轴上，其中A（0，a），B（b，0）、C（c，O）满足将点B向右平移7个单位长度，再向上平移4个单位长度，得到对应点D ，如图2所示．（1）点A 的坐标为 ，点B 的坐标为 ，点C 的坐标为 ．（2）写出点D 的坐标，并求出△ACD 的面积；（3）点P （m ，4）是坐标平面内一点，若S △P AD ＝S △AOC ，请直接写出点P 的坐标．【变式3-4】如图，在直角坐标系中，已知A （0，a ），B （b ，0），C （b ，c ）三点，其中a ，b ，c 满足关系式，|a +b ﹣5|+＝0，（c ﹣4）2≤0．（1）求a ，b ，c 的值；（2）在直线BC 上是否存在点Q ，使△ABQ 的面积是△ABC 面积的？若存在，求出点Q 的坐标；若不存在，请说明理由；（3）如果在第二象限内有一点P （m ，），是否存在点P ，使四边形ABOP 的面积与△ABC 的面积相等？若存在，求出点P 的坐标；若不存在，请说明理由．【变式3-5】如图1，在平面直角坐标系中，点A 、B 的坐标分别为A （a ，0）、B （b ，0），且a 、b 满足，现同时将点A 、B 分别向上平移3个单位长度，再向右平移1个单位长度，得到点A 、B 的对应点D 、C ，连接AD 、BC 、CD ．（1）求a、b的值，并直接写出点A、点B、点C、点D的坐标；（2）如图2，点P是线段DC上的一个动点，连接P A、PB，当点P在线段DC上移动时，△ABP的面积是否变化？若不变，请求出△ABP的面积；若变化，请说明理由；（3）在x轴上是否存在一点M，使△MBD的面积与△ACD的面积相等？若存在，请直接写出点M的坐标，若不存在，请说明理由．【典例4】如图，在平面直角坐标系中，点A、B的坐标分别为（﹣2，0）、（4，0），现在把线段AB向上平移2个单位长度，再向右平移2个单位长度，得到线段CD，连接AC、BD．（1）请直接写出点C、点D的坐标；（2）在x轴上是否存在一点P，使得△CDP的面积是△BDP面积的2倍？若存在，求出点P的坐标；若不存在，请说明理由．【变式4-1】已知：如图，在平面直角坐标系中，三角形ABC的三个顶点坐标分别是A（1，0），B（﹣2，3），C（﹣3，0）．（1）线段AC的中点的坐标为，三角形ABC的面积是；（2）若点A、C的位置不变，当点P在y轴上时，且三角形ACP的面积等于三角形ABC的面积的2倍，则P的坐标是；（3）若点B、C的位置不变，当点Q在x轴上时，且三角形BCQ的面积等于三角形ABC的面积的2倍，求点Q的坐标；（4）若点M（m，0）是三角形ABC的AC边上的一点，直接写出三角形ABC 向右平移3个单位，向下平移2个单位后，点M的对应点M1的坐标（用含m 的代数式表示）．【变式4-2】如图，在平面直角坐标系中，已知点A（0，4），B（8，0），C（8，6）三点．（1）求△ABC的面积；（2）如果在第二象限内有一点P（m，1），且四边形ABOP的面积是△ABC 的面积的两倍；求满足条件的P点的坐标．【变式4-3】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（a，0），B（b，0），C（1，3），且（a+5）2+|2b﹣6|＝0．（1）直接写出A、B两点坐标；（2）若点M在x轴上运动，且△BCM的面积是△ABC面积的，求点M的坐标；（3）过点C作AB的平行线，交y轴于点D，连接AD．将线段AD沿x轴向右平移至BE，再作EG⊥x轴于G．动点P从D出发，沿DE→EG方向运动，速度为每秒1个单位长度，设运动时间为t秒，当△PBD的面积为9时，求t 的值．【变式4-4】如图，在平面直角坐标系xOy中，A（6，0），B（8，6），将线段OA平移至CB，连接OC，AB，OC∥AB，点D在x轴上运动（不与点O，A 重合），连接CD，BD．（1）直接写出点C的坐标；（2）在点D运动的过程中，是否存在三角形ODC的面积是三角形ADB面积的3倍？如果存在，请求出点D的坐标；如果不存在，请说明理由．【变式4-5】如图在直角坐标系中，已知A（0，a），B（b，0）C（3，c）三点，若a，b，c满足关系式：|a﹣2|+（b﹣3）2+＝0．（1）求a，b，c的值．（2）求四边形AOBC的面积．（3）是否存在点P（x，﹣x），使△AOP的面积为四边形AOBC的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．。
平面直角坐标系中的面积问题
突破数学压轴题解题策略平面直角坐标系中的面积问题解题策略1【专题攻略】面积问题是初中常考内容，一般应用以下几种方法解决：一是“直接法〞，即套用求面积的公式.二是常用“割补法〞.割：分割，把图形分割成几局部容易求解的图形，分别求解，然后相加即可.补：补齐，把图形补成一个容易求解的图形，然后再减去补上的那些局部.三是“平行线转化法〞，即利用平行线之间的距离处处相等，同底等高模型转化面积来解决.在平面直角坐标系中求面积时，必然会用到线段长度，这里会涉及到利用两点之间的距离公式来求距离.在平面直角坐标系中有两点A〔x1,y1〕、B〔x2,y2〕，那么AB2=〔x1-x2〕2+ 〔y1–y2〕2.假设两点平行于坐标轴，那么两点之间的距离可以直接用横或纵坐标的差来求.【复习回忆】：y >6 - 5 - D4 - 3 - 2 - 1 -x-1 01 2 3 4 5 6 7 -1- -2 - 图4类型1有一边在坐标轴上例1如图ΔABC 的三个顶点的坐标分别是A 〔4，0〕，B 〔-2，0〕，C 〔2，4〕，求ΔABC 的面积.例2如图2，点C 为平面直角坐标系中的任意一点，点A 〔-5，0〕，点B 〔3, 0〕Δ ABC 的面积为12，试说明点C 的坐标特点.类型2有一边与坐标轴平行例3如图Δ ABC 三个顶点的坐标分别为A 〔4，1〕，B 〔4，5〕，C 〔-1，2〕，求Δ ABC 的面积.例4如图4，在四边形ABCD 中，A 、B 、C 、D 的四个点的坐标分别为〔0，2〕，〔1，0〕，〔6，2〕〔2, 4〕求四边形ABCD 的面积.图5y,:4(1)〆o123 4 1类型3 三边均不与坐标轴平行例5在图5的直角坐标系中，Δ ABC的顶点都在网格点上，其中，A点坐标为〔2，一1〕，那么Δ ABC的面积为.例6如图，Δ ABC中，A〔4，1〕，B〔4，5〕，C〔-1，2〕，求Δ ABC的面积.例7如图，以O A为边的ΔOAB的面积为2，试找出符合条件得且顶点是第一象限格点的点C，你能找出几个这样的例8：A〔0,1〕,B〔2,0〕,C〔4，3〕.〔1〕在坐标系中描出各点，画出ΔABC〔2〕求ΔABC的面积；〔3〕设点P在坐标轴上，且ΔABP与ΔABC的面积相等，求点P的坐标.。
平面直角坐标系中三角形面积的求法(例题及对应练习)
例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题我们要注意其中的解题方法和解题技巧.现一、有一边在坐标轴上例1如图1，平面直角坐标系中，△ ABC的顶点坐标分别为(— 3 , 0),(0, 3),( 0,—1),你能求岀三角形ABC的面积吗？1~.解题时丄丄丄 1 1(AD+CE X DE- 2 ADX DB-M CE X BE= X( 4+6)X 5 —2 X4X 4—X^6 X 1 = 14.平面直角坐标系中的面积问题(提高篇)4、在平面直角坐标系中，△ ABC的顶点坐标分别为A (1, -1) , B (-1 ,4), C (-3 , 1), (1)求厶ABC 的面积；(2)将厶ABC先向下平移2个单位长度,再向右平移3个单位长度，求线段AB扫过的面积。
“割补法”的应用-、已知点的坐标，求图形的面积。
1、在平面直角坐标系中，△ ABC的顶点坐标分别为A (-2, -2), B (0 , -1) , C ( 1 , 1),求厶ABC 的面积。
分析：根据三个顶点的坐标特征可以看岀，△ ABC的边y轴上,由图形可得BC= 4,点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3,然后根据三角形的面积公式求解解：因为B(0,3),C(0,-1), 所以BC=3- (-1 ) =4.因为A(-3,0), 所以A点到y轴的距离，即BC边上的高为3,S iAiC=-BC^AO =丄汀恋二6二、有一边与坐标轴平行例2 如图2,三角形ABC三个顶点的坐标分别为A(4, 1), B (4, 5), C (-1 , 2), 求三角形ABC的面积.2、在平面直角坐标系中，四边形ABCD (-4, -2) B (4, -2) C (2, 2) D (-2 , 3)分析：由A (4 , 1), B (4, 5)两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的咼CD,则D点的横坐标与A点的横坐标相同，也是4,这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A, B两点的横坐标相同，所以边AB// y轴，所以AB=5-1=4.作AB边上的咼CD,则D点的横坐标为4,所以<y—X4X5 = 10所以.三、三边均不与坐标轴平行例3如图2,平面直角坐标系中，已知点A (-3，-1)，B( 1，3)，C(2,-3)，你能求岀三角形ABC的面积吗？CD=4- (-1 ) =5，TFh-llH丿丄i—『J-l]bJnNJ・rE3分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形(长方形)的上下底(长)与其中一坐标轴平行，高(宽)与另一坐标轴平行.这样，梯形(长方形)的面积容易求岀，再减去围在梯形(长方形)内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D E,则四边形ADEC为梯形.因为A (-3 , -1 ), B (1,1*7 —3) , C (2, -3 )，所以AD= 4, CE=6, DB=4, BE=1, DE= 5.所以亠-=-ABC的面积为12,求点C的坐标的各个顶点的坐标分别为A求这个四边形的面积。
(完整版)平面直角坐标系中的面积问题
陈玲萍
问题1 已知平面直角坐标系中，点A（1，-2）， B（-4，-2），C（1,3）.
则①线段AB与x轴的位置关系 平行，线段 AB的长度为 5 ； ②线段AC与y轴的位置关系 平行 ，线段 AC的长度为 5 。
平行x轴的直线上的AB两点间的距离为：AB= xA xB 平行y轴的直线上的AC两点间的距离为：AC= yA yC
AD
44 2
8
（2）A（0,5），B（0,3），C（3,1）；
如图，过点C做CD⊥AB
∵A（0,5），B（0,3），C（3,1）
∴CD=3，AB=2
∴
SABC
1 ABCD 1 23 3
2
2
小结
平面直角坐标系中，求三角形的面积， 关键在于找到平行x轴或平行y轴的线 段作为规则图形的底和高。
F
∴BE=3,CF=3
∴ SABC SABD SACD
1 AD• BE 1 AD• CF
E
2
2
1 33 1 33
2
2
9
F
E
补
补
割
问题4
在平面直角坐标系中，四边形OABC的顶点 坐标分别为O(0，0)，A(5，0)，B(3，4)， C(0，3),计算这个四边形的面积。
方法总结
割
割
割
补
补
问题2
• 求下列三角形的面积： • （1）A（1,4），B（0,0），C（4,0）； • （2）A（0,5），B（0,3），C（3,1）；
（1）A（1,4），B（0,0），C（4,0）； 由图，过点A作AD⊥BC
∵A（1,4），B（0,0），C（4,0）
∴AD=4，BC=4
(完整版)平面直角坐标系中的面积问题-专题练习
O
1 234
x
图（4）
SOAB2
1 2
2
2
2
Y
4
3
B3 (2,3)
2
1
பைடு நூலகம்
A(2,1)
O
1
234
X
图（5）
SOAB3
1 2
2
2
2
y
4
B4 (4,4)
3
2
1
A(2,1)
O
1
2 3 4x
图（6）
y
4
N
B4 (4,4)
方
3
法
1
2
1
A(2,1)
O
1
2M 3 4 x
图（7）
S S S OAB4
OAC
AC B4
S S VA1B1C1
梯形DEC1B1
S S VA1B1D
VA1C1E
-4
-5 -6 -7
1 (2.5 2) 3 2
1 1 2 1 2 2.5
2
2
6.75 1 2.5
3.25
谈谈我们的收获
1.等积变换
方法
2.割补法求面积
化复杂为简单
转化
化未知为已知
作业
»书P80 第9题
4
5
6
x
-2
-3 -4
B
C
-5
-6
解 :点A1(2, 2) 点B1(3, 0) 点C1(0. 0.5)
-7
y 7
（2）求出三角形 A1B1C1
6
的面积。
5 4
分析:可把它补成一个梯形减去
DA1
3 2E
平面直角坐标系中的面积问题(提高篇)
平面直角坐标系中的面积问题（提高篇）一、已知点的坐标，求图形的面积。
1、在平面直角坐标系中，△ABC的顶点坐标分别为A（-2，-2），B（0，-1），C（1，1），求△ABC 的面积。
2、在平面直角坐标系中，四边形ABCD的各个顶点的坐标分别为A（-4，-2）B（4，-2）C（2，2）D（-2，3）。
求这个四边形的面积。
二、已知面积（可以求面积），求点的坐标3、在平面直角坐标系中，A（-5，0），B（3，0），点C在y轴上，且△ABC的面积为12，求点C的坐标。
4、已知，点A（-2，0）B（4，0）C（2，4）（1）求△ABC的面积；（2）设P为x轴上一点，若12APC PBCS S=，试求点P的坐标。
5、在平面直角坐标系中，P（1，4），点A在坐标轴上，4PAOS=，求点P的坐标三、点的存在性问题（运动性）6、在平面直角坐标系中，点A、B的坐标分别为（-1，0），（3，0），现同时将点A、B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B的对应点C、D，连接AC、BD。
（1）求点C、D的坐标及四边形ABDC的面积；（2）在y轴上是否存在一点P，连接PA、PB ，使12APB ABDCS S=四，若存在这样的点，求出点P的坐标，若不存在，试说明理由。
7、如图，已知长方形ABCO中，边AB=8，BC=4。
以O为原点，OAOC所在的直线为y轴和x轴建立直角坐标系。
（1）点A的坐标为（0，4），写出B、C两点的坐标；（2）若点P从C点出发，以2单位/秒的速度向CO方向移动（不超过点O）,点Q从原点O出发，以1单位/秒的速度向OA方向移动（不超过点A），设P、Q两点同时出发，在他们移动过程中，四边形OPBQ的面积是否发生变化？若不变，求其值；若变化，求变化的范围。
专题05平面直角坐标系中求图形面积(解析版)
专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图，在平面直角坐标系中，点()0,4A b 为y 轴正半轴上一点，点()3,0B b 是x 轴正半轴上一点，其中b 满足()316b +=．（1）求点A ，B 的坐标．（2）点C 为x 轴上一点，且ABC 的面积为12，求C 点的坐标．【答案】（1）()0,4A ，()3,0B ；（2）点C 的坐标为()3,0-或()9,0【解析】（1）由()316b +=得1b =，∴()04A ，，()30B ，．（2）设点C 的坐标为()0x ，，则3BC x =-，由1（）可知4OA =，∴1432ABC S x =⨯⨯-= 12，解得：9x =或3-．∴点C 的坐标为()30-，或()90，．【变式训练1】在平面直角坐标系中，已知点(),0A a ，(),0B b ，a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩，（1）求A 、B 两点的坐标；（2）C 为y 轴正半轴上一点，且6ABC S = ，请求出C 的坐标．【答案】（1）A （-3，0），B （1，0）；（2）C （0，3）【解析】（1）解方程组24a b a b +=-⎧⎨-=-⎩，解得：31a b =-⎧⎨=⎩，∴A （-3，0），B （1，0）；（2）由（1）可知：AB =4，∵S △ABC =12AB •OC =6，∴12×4×OC =6，解得OC =3，∴C （0，3）．故答案为：（1）A （-3，0），B （1，0）；（2）C （0，3）类型二、割补法求面积例1.如图，三角形ABC 的面积等于（）A ．12B ．1122C ．13D ．1132【答案】D【解析】过点A 作AD x ⊥轴于D ，如图所示：由题意可得，3BO =，3OC =，6AD =，3CD =，∴6OD =，∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=，即272ABC S ∆=，故选：D ．【变式训练1】如图，连接AB 、BC 、AC ，则△ABC 的面积是（）A ．312B ．3C ．212D ．2【答案】C【解析】长方形AGDE 的面积为：3×2=6，AGC 的面积：3×1÷2=1.5，CDB △的面积：2×1÷2=1，ABE △的面积：2×1÷2=1，故ABC 的面积为：6-1.5-1-1=2.5，故答案为：C ；【变式训练2】如图，三角形ABO 中，()2,3A --，()2,1B -，A B O ''' 是ABO 平移之后得到的图形，并且O 的对应点O '的坐标为()5,4．（1）作出ABO 平移之后的图形A B O ''' ，并写出A '、B '两点的坐标分别为A '______，B '_____；（2）()00,P x y 为ABO 中任意一点，则平移后对应点P 的坐标为______．（3）求ABO 的面积；【解析】（1）如图，△A 'B 'O '即为所求，A '、B '两点的坐标分别（3，1），（7，3）．故答案为：（3，1），（7，3）．（2）点P '的坐标为（x 0+5，y 0+4）．故答案为：（x 0+5，y 0+4）．（3）S △ABO =3×4-12×2×3-12×1×2-12×4×2=4．【变式训练3】在平面直角坐标系xoy 中，△ABC 的位置如图所示，点A ，B ，C 都在格点上．（1）分别写出下列顶点的坐标：A ________；B ________；（2）请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′；（3）计算出△ABC 的面积．【答案】（1）(-1,6)，(-2,0)；（2）见解析；（3）152【解析】（1）由图知，点A 的坐标为(-1,6)，点B 的坐标为(-2,0)，故答案为：(-1,6)，(-2,0)（2）由图得，点C 的坐标为(-4,3)，则点A 、B 、C 关于y 轴的对称点A ′，B ′，C ′坐标分别为(1,6)，(2,0)，(4,3)，依次连接A ′，B ′，C ′，即得△A ′B ′C ′，所得图形如图所示（3）过A 、C 作x 轴的垂线，垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图，在平面直角坐标系中，点B ，C 的坐标分别为(),2a a -、()3,2a a ，其中0a >，点A 为BC 的中点，若4BC =，解决下列问题：（1）BC 所在直线与x 轴的位置关系是；（2）求出a 的值，并写出点A ，C 的坐标；（3）在y 轴上是否存在一点P ，使得三角形PAC 的面积等于5？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）平行；（2）()1,2A ，()3,2C ；（3）存在，P 点坐标为()0,3-或()0,7【解析】（1）∵点B ，C 的坐标分别为(),2a a -、()3,2a a ，∴BC 所在直线与x 轴的位置关系是平行．故答案为：平行．（2）∵4BC =，∴()34a a --=，∴1a =，∴B （-1，2），C （3，2），∵A 为BC 的中点，∴()1,2A ．（3）存在点P ．设()0,P m ，∵2AC =，∴12252m ⨯⨯-=，∴3m =-或7.∴P 为()0,3-或()0,7．【变式训练1】如图，在直角坐标系中，已知()0,2A ，()3,0B ，()3,4C 三点．（1）求四边形AOBC 的面积；（2）是否存在点()0.5P x x ,，使2ABC AOBC S S = 四边形？若存在，求出点P 的坐标．若不存在，请说明理由．【答案】（1）9；（2）存在，()189P --,或(18,9)【解析】如图，∵34C （，），∴33CD ==．∵()34C ，，30B （，），∴404CB =-=，∴4312DCBO S =⨯=四边形．∵()04D ，，()02A ，，∴422DA =-=，∴11236322DCA S =⨯⨯=⨯= ．∵DCA AOBC DCBO S S S =- 四边形四边形，∴1239AOBC S =-=四边形．（2）由（1）得1239AOBC S =-=四边形设存在点()0.5P x x ，，使△AOP 的面积为四边形AOBC 的面积的两倍．∵△AOP 的面积=122x x ⨯⨯=，∴29x =⨯，∴18x =±∴存在点P （18，9）或（-18，-9），使△AOP 的面积为四边形AOBC 的面积的两倍．【变式训练2】如图，A （0，3）是直角坐标系y 轴上一点，动点P 从原点O 出发，沿x 轴正半轴运动，速度为每秒2个单位长度，以P 为直角顶点在第一象限内作等腰Rt △APB ．设P 点的运动时间为t 秒．（1）若AB ∥x 轴，求t 的值；（2）如图2，当t ＝2时，坐标平面内有一点M （不与A 重合）使得以M 、P 、B 为顶点的三角形和△ABP 全等，请直接写出点M 的坐标．【答案】（1）t 的值为1.5；（2）点M 的坐标为（3，7），（8，﹣3），（11，1）．【解析】（1）过点B 作BC ⊥x 轴于点C ，如图所示．∵AO⊥x轴，BC⊥x轴，且AB∥x轴，∴四边形ABCO为矩形，∴AO=BC=3，∵△APB为等腰直角三角形，∴AP=BP，∠PAB=∠PBA=45°，∴∠OAP=90°-∠PAB=45°，∴△AOP为等腰直角三角形，∴OA=OP=3，∴t=3÷2=1.5（秒），故t的值为1.5；（2）当t=2时，OP=4，①如图3，若△ABP≌△MBP，则AP=PM，过点M作MD⊥OP于点D，∵∠AOP=∠PDM，∠APO=∠DPM，∴△AOP≌△MDP（AAS），∴OA=DM=3，OP=PD=4，∴M（8，-3）；②如图，若△ABP≌△MPB，连接AM，则AP=PB=BM，∠APB=∠MBP=90︒，∴AP∥MB，且AP=MB，∴四边形APBM是平行四边形，y轴于点E，又∠APB=∠MBP=90︒，∴四边形APBM是正方形，∴AP=AM，过点M作ME⊥同理可证△AOP≌△MEA（AAS），∴OA=EM=3，OP=AE=4，∴M（3，7）；③如图，若△ABP≌△MPB，则AP=BP=BM，过点M 、B 分别作x 轴的垂线，垂足分别为点F 、G ，过点M 作MH ⊥BF 于点H ，∴四边形FGMH 是矩形，∴MH =FG ，MG =HF ，同理可证△AOP ≌△PFB ≌△BHM （AAS ），∴OA =PF =BH =3，OP =BF =MH =4，∴MG =HF =BF -BH =1，OG =OP +PF +FG =11，∴M （11，1）；综合以上可得点M 的坐标为（3，7），（8，-3），（11，1）．【变式训练3】在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为()1,0，点D 的坐标为()0,2．延长CB 交x 轴于点1A ，作第1个正方形111A B C C ；延长11C B 交x 轴于点2A ，作第2个正方形2221A B C C ，…，按这样的规律进行下去，第2021个正方形的面积是______．【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ，1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C，1113222A B A C ∴====⨯同理可得：22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为：404235.2⎛⎫⨯ ⎪⎝⎭。
平面直角坐标系中的面积计算(专题)
平面直角坐标系中的面积计算
一、
例1：平面直角坐标系中，A(4，-4)，B(1，0)，C(6，0). 求△ABC的面积.
例2：平面直角坐标系中，A(0，3)，B(0，-3)，C(2，1). 求△ABC的面积.
x
变式1.若A、B两点的坐标和△ABC的面积均保持不变，且C点坐标为（2，y）,求y.
变式2.若A、B两点的坐标保持不变，△ABC的面积为9，且C点坐标为(x，1),求x的值. 二、
例3：平面直角坐标系中，A(-2，3)，B(-2，-3)，C(2，1). 求△ABC的面积
.
x
三、
变式1.保持A 、C 不动，改变点B 的位置：B (0，-3), 求△ABC 的面积.
x
x
x
变式2.保持A 、C 不动，再次改变点B 的位置：B (3，-3), 求△ABC 的面积.
x
x
例4：在平面直角坐标系中，已知A(-5, 4)，B(-2, -2)，C(0, 2).若点P 在坐标y 轴上，
且△PBC 和△ABC 的面积相等.求点P 的坐标.
思考题：
1.平面直角坐标系中，A(-3，-2)，B(3，-2)，C(1，3)，D(-2，1)，求四边形
ABCD 的面积.
2.已知点O(0,0)，B(1,2)，点A 在坐标轴上，且2OAB S ∆=，求满足条件的点A 的坐标. 坐标轴上，且2=∆OAB S ，求满足条件的点A 的坐标.。
平面直角坐标系下图形面积的计算
19
谈谈我们的收获
1、在平面直角坐标系下，计算图形的面积可以 运用什么方法？
割补法求面积
平移
2、今天我们学习了什么数学思想？
转化思想
化复杂为简单
20
C （-14 ， 0 ）
E
D
0 D
X
如图，四边形ABCD各个顶点的坐标分别为 （– 2，8），（– 11，6），（– 14，0），（0，0）。 （1）确定这个四边形的面积，你是怎么做的? （2）如果把原来ABCD各个顶点纵坐标保持不变，横坐标 增加2，所得的四边形面积又是多少？ 5
（2）已知A（－1，0），B（3，0），C（2，－3），
3
例1 平面直角坐标系内,A(2,3),B(4,3),C(3,-5),试求△ABC的面积.
y
4 3 2 1 -5 -4 -3 -2 -1 0 -1 -2 -3 -4 -5
1
2 3
x
平面直角坐标系中求三角形的面积时以与 坐标轴重合或平行于坐标轴的边为底.
4
y
A （-2 ， 8 ） （-11 ， 6 ） B
2
复习：
1. 已知P(a,b)， 则点P到X轴的距离是 |b| ， 到y轴的距离是 |a| 。 2. 若A(a,0)，B(b,0) ，则AB= |a-b| ；
若A(0,a)，B(0,b) ，则AB=|a-b| 。
3. 若A(a,c)，B(b,c) ，则AB= |a-b| ； 若A(c,a)，B(c,b) ，则AB= |a-b| 。
C(1,3)
E(6,3)
4 F(-1,3) 3 2 1
B(6,2)
A(-1,-2)
-2
x
17
-2
-1 O -1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
1
一、自主学习 1、（1）已知点P在x轴上，且到y轴的距离为2，
则 点P的坐标为(_-_2_,_0_)_(_2_,_0_) （2）已知点P到x轴的距离为3，到y轴的距离为4，则
点P的坐标为_(_4_,_3_)_(_-_4_,_3_)_(_4_,_-_3_)_(_-_4_,_-_3_)_ （3）若A（-1,0），B（4,0），则线段AB的长为_5___ （4）若A（0,5），B（0,3），则线段AB的长为__2___ （5）若A（-3，-2），B（-5，-2），则线段AB的长
B(6,2)
x
-2 2O 1 2 3 4 5
-1 -1 6 7 8
1
A(-1,-2)
D(6,-2)
-
2
a
17
题型四
❖与图形面积相关的点的存在 性问题
a
18
例1.已知，△ABC 三个顶点A、B、C的坐标分别为A（-2，4），B（2，
0），C（2，5）。
（1）在所给的平面直角坐标系xoy中画出△ABC，并求△ABC的面积。
∴ S四边形ABCD= S△AOD+ S梯形ABED+S△BEC
= 1 OD·AD+ 1 (BE+AD)·DE +1 ·EC ·BE
2
2
2
=
1 2
×1×4+ 1
2
×6×4+
1 2
×1×2
= 15
a
14
已知△ABC中，A(-1,-2),B(6,2),C(1,3), 求△ABC(1,3)
a
20
（2）点P在x轴上，且△ABP的面积等于△ABC的面积，求点P的坐标。
y
7
6
A
5 4
C
3
2
Pꞌ
1
P
-6 -5 -4 -3 -2 -1-1 01 2B3 4 5 6 7x
-2
-3
-4
-5
-6
a
19
-7
总结
平面直角坐标系中求面积
方法一：一边在坐标轴上三角形面积的求法 方法二：一边平行于坐标轴的三角形面积的求法 方法三：利用割补法求图形的面积 方法四：与图形面积相关的点的存在性问题
求四边形ABCO的面积。
A (1,4)
4
●
3
B (5,2)
F2
●
1
●
-5 -4 -3 -2 -1O
1D 2
-1
C (6,0)
●
x 3 4E 5 6
-2
-3
-4
a
13
解：过点A作AD⊥X轴于点D，过点B作BE⊥X轴于点E
则D(1,0) E(5,0)，由点的坐标可知
AD=4 BE=2 OD=1 DE=4 CE=1
3
2
1
B(6,2)
-2 -1O -1
1
2 3 4 56 7 8
x
A(-1,-2)-2
-3
a
15
y
5 F(-14,3) C(1,3)
3
方法1
E(6,3)
B(6,2)
-2 2O 1 2 3 4 5
-1 -1 6 7 8
1
A(-1,-2)
D(6,-2)
x
-
2
a
16
y
5
4
C(1,3)
3
方法2
E(6,3)
∴ S△ABC = 1 ·BC·AD= 1 ×6×5=15
2
2
a
7
练习. １．已知A(1,4),
B(-4,0),C(2,0). △ABC的面积是＿12＿＿．
y
A (1,4)
２.若BC的坐标不变,
B (-4,0) O
△ABC的面积为6,点A
y
的横坐标为-1,那么
A
点A的坐标为_(_-1,2)或(-1_,.-2)
坐标系xoy中画出△ABC，并求△ABC的面积。
y
7
6
A
5 4
C
3
2
1
-6 -5 -4 -3 -2 -1-1 01 2B3 4 5 6 7x
-2
-3
-4
-5
-6
a
11
-7
题型三
❖利用割补法求图形的面积
a
12
例1、探究展示
如图，四边形ABCO在平面直角坐标系中，
且A（1,4），B（5,2），Cy（6,0）， O（0,0），
2
1
A (4,0)
O
1
234
x
图（2）
a
5
2、如图所示，A(-4,-5),B(-2,0),C(4,0), 求△ABC的面积。
y
4
3
2
1
DB
C
●
●
-5 -4 -3 -2 -1O -1
12 345
x
-2
-3
-4
A●
-5
a
6
解：过点A作AD⊥X轴于点D
∵A(-4,-5)
∴D(-4,0)
由点的坐标可得 AD=5 BC=6
为__2___ （6）若A（3,2），B（3，-3），则线段AB的长为_5__
a
2
题型一
❖一边在坐标轴上三角形 面积的求法
a
3
问题1 如图（1）， △AOB的面积是多少？
y
4
B (0,3)
3
2
1
A (4,0)
O
1
234
x
图（1）
a
4
（2）这个△AOB的面积是多少，你会求吗？
y
4
B (3,3)
3
(-4,0B)
C (2,0x)
(2,0)
Cx
a
8
题型二
❖一边平行于坐标轴的三 角形面积的求法
a
9
例1：三角形ABC三个顶点的坐标分别为 A（4，1），B（4，5），C（-1，2）， 求三角形ABC的面积.
a
10
例2.已知，△ABC 三个顶点A、B、C的坐标分别为A（-
2，4），B（2，0），C（2，5）。在所给的平面直角