五年级地方试卷14下2
2019-2020学年青岛版(六三制)小学五年级下册期末考试数学试卷(二)(解析版)

2019-2020学年青岛版(六三制)小学五年级下册期末考试数学试卷一.选择题(共10小题)1.下列说法中错误的是()A.0是最小的数B.直线上﹣3在﹣1的左边C.负数比正数小2.两根同样长的铁丝,一根用去了,另一根用去了米,剩下的铁丝相比,()A.第一根长B.第二根长C.同样长D.无法比较哪根长3.能表示出意义的算式是()A.﹣=B.1﹣=C.﹣=4.小刚放学回家时往西南方向走,那么他上学时应该往()方向走.A.东北B.西北C.东南D.西南5.图中物体形状是正方体的有()A.A B.A和C C.C D.A和D6.下面四幅图中,()不是正方体的展开图.A.B.C.D.7.与点(6,5)挨着的点是()A.(5,5)B.(6,3)C.(8,5)8.+可以直接相加,是因为两个加数()A.分子相同B.分数单位相同C.都是真分数D.都是最简分数9.小兵和小花一起喝一瓶果汁,小兵喝了这瓶果汁的,小花喝的比小兵多一些,小花喝了这瓶果汁的()A.B.C.D.10.从如图的统计图中可知道,甲车间2018年平均每季度的产值是()万元.A.37.5B.55C.91.5二.填空题(共8小题)11.甲乙两人进行120米的滑板比赛,乙让甲先滑10秒.他们两人滑的路程与时间的关系如下图.(1)乙在滑完全程中,每秒钟滑行米;(2)乙滑完全程时两人相距米.12.桑植白茶远近闻名,茶香四海.为了提高桑植白茶的品质,工厂准备定制一款长与宽是20厘米、高为10厘米的精美长方体茶叶盒,制作这样一款茶叶盒至少需要平方分米的材料,这款茶叶盒的容积是升.13.和的公分母是,两个数相减的结果是.14.在﹣﹣﹣﹣里填上“>”“<”或“=”.1﹣15.把2m长的铁丝平均分成三段,每段是全长的,每段长m.16.王红在教室的位置用数对表示为(3,5),表示她在第列第行,她的同桌李华的位置用数对表示可能是(,)或(,).17.东东从0点向东行70米,表示为+70米,那么从0点向西行30米,表示为米;如果他先向东行60米,再向西行40米,这时东东的位置表示为米.18.把36升水倒入一个长8分米,宽2.5分米的长方体水箱内,正好倒满,这个水箱深分米.(水箱的厚度忽略不计)三.判断题(共5小题)19.(判断对错)(改正)20.在﹣4、﹣9、﹣1、0.1这四个数中,最大的数是﹣9.(判断对错)21.一张油饼分给两个人吃,每人吃了油饼的.(判断对错)22.以学校为参照点,甲乙二人到学校的距离相等.他们一定在同一地方.(判断对错)23.将一个正方体钢坯锻造成长方体,正方体和长方体的体积相等.(判断对错).四.计算题(共2小题)24.求下列立体图形的表面积和体积.(单位:厘米)(1)(2)25.怎样简便就怎样计算.①+++②﹣(+)③++五.应用题(共7小题)26.某食品包装袋上有“500±5g”字样,那么这种食品的正常含量应在什么范围?27.一个底面是正方形的长方体铁桶,把它的侧面展开正好得到一个边长为40厘米的正方形.如果铁桶内装半桶水,与水接触的面积是多少平方厘米?28.学校星期一用水吨,星期二用水0.35吨,星期三用水吨.29.在一幅1:500000地图上量得甲乙两地之间的距离是7厘米,一列火车以每小时200千米的速度从甲地开往乙地,需要行驶多长时间到达乙地?30.某地4月1﹣8日的气温统计如下表.(单位:℃)日期1日2日3日4日5日6日7日8日最高气温1818161925232524最低气温1112121314141516请画出折线统计图,再回答下面的问题.(1)这几天中,哪天的温差最大?哪天的温差最小?(2)这几天的最高气温是怎样变化的?最低气温呢?31.小林骑自行车去郊游,去时平均每小时行12km,小时到达.原路返回时只用了小时,返回时平均每小时行多少千米?32.一个分数约分后是,如果约分前的分子与分母的和是66,这个分数约分前是多少?参考答案与试题解析一.选择题(共10小题)1.【分析】0不是最小的数,没有最小的数,A错误;直线上﹣3<﹣1,所以﹣3在﹣1的左边,B正确;负数比所有正数都小,C正确.【解答】解:说法中错误的是“0是最小的数”.故选:A.【点评】此题考查了正负数的大小比较方法,要熟练掌握.2.【分析】可以分三种情况考虑:(1)总长小于1米时,第一根铁丝剩下:全长×,第二根剩的:总长﹣,第一根剩的长;(2)总长等于1米时,第一根剩的长度为:1×=(米);第二根剩的是:1﹣=(米),两根一样长;(3)大于1米时,第一根剩的长度:全长×;第二根剩的;全长﹣,第二根剩的长.【解答】解:分三种情况:(1)总长小于1米时,假设全长为米,则第一根剩:×=(米),第二根剩的:﹣=(米),>,第一根剩的长;(2)总长等于1米时,第一根剩的长度为:1×=(米);第二根剩的是:1﹣=(米),两根一样长;(3)总长大于1米时,假设为3米时,第一根剩的长度为:3×=2(米);第二根剩的:3﹣=(米),2<,第二根剩的长.所以无法比较.故选:D.【点评】主要考察解决实际问题时要分情况考虑,最后综合下结论.3.【分析】把一个长方形的面积看作单位“1”,平均分成6份,每份是,表示其中的5份是,减去其中的2份,就是减去,还剩下3份,就是,据此解答.【解答】解:根据题意与分析可得:能表示出意义的算式是:﹣=故选:C.【点评】考查了分数的意义以及分数减法的意义的灵活运用.4.【分析】“小刚放学回家时往西南方向走”,说明她家在学校的西南面,所以学校在她家的东北面.【解答】解:小刚放学回家时往西南方向走,那么他上学时该往东北方向走;故选:A.【点评】本题主要考查方向的辨别,注意找准观察点.5.【分析】正方体的每个面都是相同的正方形,据此选择即可.【解答】解:图中物体形状是正方体的有A、C.B是长方体,D是正方形.故选:B.【点评】此题考查了正方体的特征,要熟练掌握.6.【分析】A和C都属于正方体展开图的1﹣4﹣1型,能够折成一个正方体;D图属于正方体展开图的2﹣2﹣2型,也能够折成一个正方体;只有B不能,因为同侧的两个正方形在折的过程中会重叠,所以不是正方体展开图.【解答】解:根据分析可得:A、D、C这三个图属于正方体展开图,能够折成一个正方体;而B图不是正方体展开图.故选:B.【点评】本题重在培养学生的空间想象能力,在解答时要掌握正方体展开图的几个基本的类型,然后据此调整即可判断.7.【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,点(6,5)在第6列,第5行,与点(6,5)挨着的点要么与列,要么行与点(6,5)挨着(相差1).【解答】解:如图与点(6,5)挨着的点是(5,5).故选:A.【点评】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行.8.【分析】同分母分数相加(减),分子进行相加(减)得数作分子,分母不变;异分母分数相加(减),必须先通分,然后,按照同分母分数相加(减)的法则进行运算.【解答】解:+可以直接相加,是因为两个加数同分母,即分数单位相同.故选:B.【点评】此题重点考查学生对分数加减法的计算能力,同时注意计算的灵活性.9.【分析】把这瓶果汁看作单位“1”,小兵喝了这瓶果汁的,还剩下这杯果汁的1﹣=,再根据小花喝的比小兵多一些,也就是比多一些,由于大于,所以,小花喝了这瓶果汁的,据此解答.【解答】解:1﹣=;>答:小花喝了这瓶果汁的.故选:C.【点评】本题关键是把这瓶果汁看作单位“1”,根据分数的意义,求出剩下的分率,然后再根据分数大小的比较方法的进行解答.10.【分析】通过观察折线统计图可知,纵轴每格表示10万元,2018年甲车间第一季度的产值是10万元,第二季度的产值是40万元,第三季度的产值是80万元,第四季度的产值是90万元,根据求平均数的方法,用甲车间全年的产值除以4即可.【解答】解:(10+40+80+90)÷4=220÷4=55(万元)答:甲车间2018年平均每季度的产值是55万元.故选:B.【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.二.填空题(共8小题)11.【分析】(1)根据折线统计图可知,虚线代表乙,实线代表甲,乙滑完120米用了55秒,甲用了65秒,根据速度=路程÷时间即可解答;(2)先求出15秒后平均速度,再用求出的平均速度乘以甲滑完全程多用的时间;即可进行解答.【解答】解:(1)120÷(55﹣10)=120÷45=2(米);答:乙在滑完全程中,每秒钟滑行2米.(2)(120﹣40)÷(65﹣15)×(65﹣55)=80÷50×10=1.6×10=16(米);答:乙滑完全程时两人相距16米.故答案为:2,16.【点评】本题主要考查了学生根据统计图分析数量关系解答问题的能力.12.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体容积公式:V=abh,把数据分别代入公式解答.【解答】解:(20×20+20×10+20×10)×2=(400+200+200)×2=800×2=1600(平方厘米)1600平方厘米=16平方分米20×20×10=4000(立方厘米)4000立方厘米=4升答:制作这样一款茶叶盒至少需16平方分米的材料,这款茶叶盒的容积是4升.故答案为:16、4.【点评】此题主要考查长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式.13.【分析】先求出6和8的公倍数(一般选用最小公倍数)就是这个两个分数的公分母,然后通分,变成同分母的分数,再根据分母不变,分子相减,求出算式的结果.【解答】解:6=2×38=2×2×26和8的最小公倍数是:2×2×2×3=24和的公分母是24;﹣=﹣=两个数相减的结果是.故答案为:24,.【点评】本题考查了异分母分数加减法的计算方法:异分母分数相加减,先通分,变成同分母的分数相加减,再计算.14.【分析】根据分数加减法的计算方法以及分数混合运算的顺序与运算定律,分别求出各个算式的结果,再比较解答.【解答】解:(1)=,=,>;所以,>;(2)=1+=1=+()=+1=11<1;所以,<;(3)1﹣=1﹣()=1﹣===<;所以,1﹣<.故答案为:>,<,<.【点评】含有算式的大小比较,先求出它们的结果,然后再按照分数大小比较的方法进行解答.15.【分析】把这根铁丝的长度看作单位“1”,把它平均分成三段,每段是全长的;求每段长,用这根铁丝的长度除以平均分成的段数.【解答】解:1÷3=2÷3=(m)答:每段是全长的,每段长m.故答案为:,.【点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称.16.【分析】根据数对确定位置的方法:先列后行,确定王红的数对即可;因为同桌与她同一行,只是列加1或减1,据此确定李华的位置即可.【解答】解:3﹣1=23+1=4答:王红的位置是第3列第5行;李华的位置可能是(2,5)或(4,5).故答案为:3,5;2,5;4,5.【点评】此题考查了数对的写法,即先看在第几列,这个数就是数对中的第一个数;再看在第几行,这个数就是数对中的第二个数.17.【分析】此题主要用正负数来表示具有意义相反的两种量:向从0点向东记为正,则从0点向西就记为负,直接得出结论即可,先向东再西是先加后减通过计算即可.【解答】解:根据题意可知向东为正,向西30米就表示﹣30米;先向东60米是+60,再向西40米是﹣40,所以此时的位置是+20米;故答案为:﹣30米、+20米.【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负.18.【分析】根据长方体的体积(容积)公式:V=abh,那么h=V÷ab,把数据代入公式解答.【解答】解:36升=36立方分米36÷(8×2.5)=36÷20=1.8(分米)答:这个水箱深1.8分米.【点评】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算.三.判断题(共5小题)19.【分析】异分母分数相加,必须先通分,然后按照同分母分数加法的计算法则进行计算,本题没有通分,所以错误,然后改正即可.【解答】解:原题计算错误;改正:=+=故答案为:=+=.【点评】解答本题关键是掌握异分母分数加法的计算法则.20.【分析】正数>0>负数,负数大小比较就是看负号后面的数字,数字越大的反而越小,跟正数恰好相反,据此解答即可.【解答】解:因为﹣9<﹣4<﹣1<0.1,所以在﹣4、﹣9、﹣1、0.1这四个数中,最大的数是0.1.故题干的说法是错误的.故答案为:×.【点评】此题主要考查了正、负数、0的大小比较,要熟练掌握.21.【分析】一张油饼平均分给两个人吃,求每人吃油饼几分之几,平均分的是单位“1”,求的是分率;用除法计算.但此题没有“平均”两个字,所以错误.【解答】解:1÷2=但是由于没有“平均”两个字,每人吃的或多或少,就不一定是.故原题说法错误;故答案为:×.【点评】此题关键是理解分数的意义是建立在平均分的基础上的.22.【分析】到一个固定点的距离相等的点有无数个,所以以学校为参照点,甲乙二人到学校的距离相等,他们不一定在同一地方,这样的点不确定,由此判断即可.【解答】解:以学校为参照点,到学校的距离相等的点有无数个,所以以学校为参照点,甲乙二人到学校的距离相等.他们一定在同一地方,说法错误;【点评】明确到一个固定点的距离相等的点有无数个,是解答此题的关键.23.【分析】根据体积的意义,物体所占空间的大小叫做物体的体积.将一个正方体钢坯锻造成长方体,只是形状变了,但是正方体和长方体的体积相等.据此判断.【解答】解:将一个正方体钢坯锻造成长方体,只是形状变了,但是正方体和长方体的体积相等.因此,将一个正方体钢坯锻造成长方体,正方体和长方体的体积相等.这种说法是正确的.故答案为:√.【点评】此题考查的目的是理解掌握体积的意义及应用.四.计算题(共2小题)24.【分析】(1)长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据分别代入公式解答.(2)根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据分别代入公式解答.【解答】解:(1)(8×6+8×3+6×3)×2=(48+24+18)×2=90×2=180(平方厘米)8×6×3=144(立方厘米)答:这个长方体的表面积是180平方厘米,体积是144立方厘米.(2)5×5×6=150(平方厘米)5×5×5=125(立方厘米)答:这个正方体的表面积是150平方厘米,体积是125立方厘米.【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式.25.【分析】①根据加法结合律和结合律进行简算;②根据减法的性质进行简算;③根据加法交换律进行简算.【解答】解:①+++=(+)+(+)=1+1=2②﹣(+)=﹣﹣=1﹣=③++=++=1+=1【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算.五.应用题(共7小题)26.【分析】先分别计算出净重的最大值和最小值,再确定合格范围,即可得出答案.【解答】解:净重的最大值是500+5=505(g);净重的最小值是500﹣5=495(g);这种食品的净重在495g~505g之间都是合格的.【点评】本题考查了正数和负数的知识,要能读懂题意,正确理解500±5克的实际意义,分别计算最大值和最小值来确定合格范围.27.【分析】它的侧面是一个边长40厘米的正方形,它的边长既是这个长方体的高,也是底面周长;再用底面周长除以4,求出底面的边长,进而求出长方体铁桶的表面积,再除以2就是与水接触的面积.【解答】解:底面边长:40÷4=10(厘米)10×10×2+40×10×4=200+1600=1800(平方厘米)1800÷2=900(平方厘米)答:与水接触的面积是900平方厘米.【点评】此题主要考查长方体的表面积公式的灵活运用,关键是求出底面边长.28.【分析】在、0.35和三个数中,其中两个分数都能化为有限小数,所以把它们化为小数进行比较大小即可.【解答】解:,,因为0.4>0.35>0.3,所以星期三用水最多.答:星期三用水最多.【点评】本题主要考查了分数大小的比较,如果分数都能化为有限小数,通常化为小数比较大小.29.【分析】此题应先求出甲、乙两地的实际距离,根据实际距离=图上距离÷比例尺即可求出;要求火车从甲地开往乙地,需要几小时,就是用距离除以速度即可.【解答】解:甲、乙两地的距离:7÷=3500000(厘米)=35(千米)从甲地开往乙地,需要:35÷200=0.175(小时)答:从甲地开往乙地,需要0.175小时.【点评】此题考查了比例尺的实际应用,以及对“时间=路程÷速度”这一关系式的掌握情况.30.【分析】根据折线统计图的绘制方法,先根据统计表中的数据分别描出各点,然后顺次连接各点即可.(1)通过观察统计表可知,5日的温差最大,3日的温差最小.(2)这几天的最高气温,1日、2日温度相同,3日有所下降,4日到5日气温呈上升趋势,6日有所下降,7日比6日有所上升,8日有下降.最低气温呈逐渐上升趋势.【解答】解:作图如下:(1)5日的温差最大,3日的温差最小.(2)这几天的最高气温,1日、2日温度相同,3日有所下降,4日到5日气温呈上升趋势,6日有所下降,7日比6日有所上升,8日有所下降.最低气温整体看呈逐渐上升趋势.【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图表提供的信息,解决有关的实际问题.31.【分析】首先根据速度×时间=路程,用去时的速度乘以用的时间,求出两地之间的距离是多少;然后用它除以返回用的时间,求出返回时平均每小时行多少千米即可.【解答】解:12×÷=18÷=24(千米/时)答:返回时平均每小时行24千米.【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握,解答此题的关键是求出两地之间的距离是多少.32.【分析】根据约分后的分数是,可知分子与分母的比为5:6,分别求出分子、分母各占分子与分母和的几分之几,用乘法计算即可.【解答】解:66×=3066×=36答:这个分数约分前是.【点评】此题主要利用分数的基本性质和按比例分配解决问题.。
新课标标准实验版2021-2022年五年级下册数学期末考试试卷(II)卷

新课标标准实验版2021-2022年五年级下册数学期末考试试卷(II)卷姓名:________ 班级:________ 成绩:________亲爱的小朋友们,这一段时间的学习,你们收获怎么样呢?今天就让我们来检验一下吧!一、填空。
(共15题;共39分)1. (2分)单位换算。
平方米=________平方分米日=________小时。
2. (2分) (2018五下·云南期中) 1m3=________cm3 , 1dm3=________L。
A.1 B.10 C.1000 D.10000003. (2分) (2020五上·雁塔期末) 把3米长的绳子平均分成5份,每份占全长的________,每份长有________米.4. (2分)比________少1,吨比吨多________吨。
5. (1分) A,B,C各代表________时,下面的算式才能成立?(按A,B,C的顺序填写)6. (3分) (2019五下·南京月考) 三个连续的自然数,最小的一个是n,其他两个分别是________和________,这三个数的和是________.7. (5分)6÷________= ________=________%=0.75=________:32=________折8. (2分) (2020四上·朔州期末) 算式54×600的积的末尾有________个0;若a×b=50,那么(a×3)×b=________。
9. (1分)(2020·南通) 如图,陀螺的上面是圆柱,下面是圆锥.经过测试,当圆锥的高是圆柱高的75%时,陀螺才能旋转得又稳又快。
照着这个标准做了一个陀螺,其中圆柱的底面直径是6厘米,高是6厘米。
这个陀螺的体积是________立方厘米。
10. (2分) (2021四上·鼓楼期末) 下边的物体是由________个小正方体摆成的.在它上面至少再添________个小正方体,就可以摆成一个长方体。
完整版五年级下学期期中考试数学试卷(2)
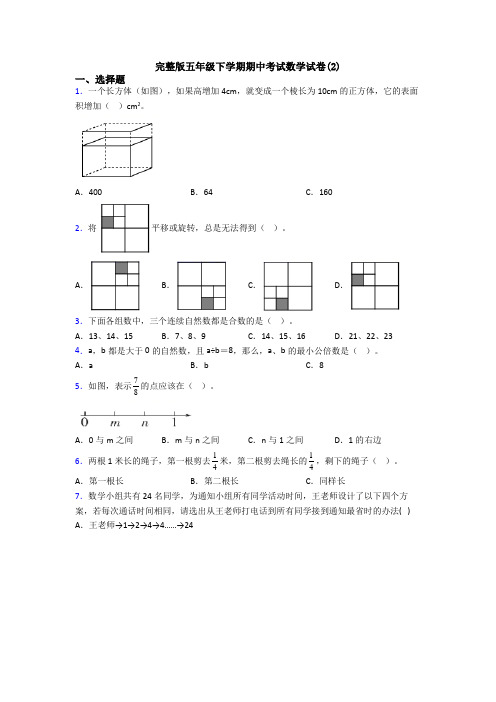
完整版五年级下学期期中考试数学试卷(2)一、选择题1.一个长方体(如图),如果高增加4cm,就变成一个棱长为10cm的正方体,它的表面积增加()cm2。
A.400 B.64 C.1602.将平移或旋转,总是无法得到()。
A.B.C.D.3.下面各组数中,三个连续自然数都是合数的是()。
A.13、14、15 B.7、8、9 C.14、15、16 D.21、22、23 4.a,b都是大于0的自然数,且a÷b=8,那么,a、b的最小公倍数是()。
A.a B.b C.85.如图,表示78的点应该在()。
A.0与m之间B.m与n之间C.n与1之间D.1的右边6.两根1米长的绳子,第一根剪去14米,第二根剪去绳长的14,剩下的绳子()。
A.第一根长B.第二根长C.同样长7.数学小组共有24名同学,为通知小组所有同学活动时间,王老师设计了以下四个方案,若每次通话时间相同,请选出从王老师打电话到所有同学接到通知最省时的办法( ) A.王老师→1→2→4→4……→24B.C.D.8.李阿姨喝一整杯酒,分四次喝完。
第一次喝了这杯酒的16,觉得味道太重了,就加满了雪碧,第二次喝了13,还是觉得味道重,再一次加满了雪碧,第三次喝了半杯后又加满了雪碧,最后一次李阿姨把整杯都喝完,请问李阿姨喝的()。
A.红酒多B.雪碧多C.一样多二、填空题9.3.85立方米=(______)立方分米 4.04L (______)L(______)mL10.分数单位是18的最大真分数是(________),最小假分数是(________),最小带分数是(________),最小的带分数再加上(________)个分数单位就是最小的质数。
11.25□,要使这个数既是2的倍数,又是3的倍数,□里可以填(______),(有几个填几个),5□□,要使这个数是2、3、5的倍数,这个数是(______),(有几个填几个)。
12.x,y都表示非0自然数,y是x的14。
2019-2020学年小学五年级下册期末考试数学试卷(二)(解析版)

2019-2020学年沪教版小学五年级下册期末考试数学试卷(二)一.选择题(共10小题)1.0°C读作()A.零上0摄氏度B.零下0摄氏度C.0摄氏度D.正0摄氏度2.在直线上,点A表示的数是()A.﹣0.1B.C.D.0.83.一个三角形的面积是y平方米,如果把它的底和对应的高都扩大到原来的3倍,得到的新三角形的面积是()平方米.A.3y B.4.5y C.6y D.9y4.正方体的棱长缩小到原来的,它的表面积就缩小到原来的()A.B.C.D.5.布袋里放了5个球:〇〇〇●●,任意摸一个再放回,小明连续摸了4次都是白球.如果再摸一次,认为下面说法正确的是()A.可能摸到黑球B.一定能摸到黑球C.摸到黑球的可能性大D.不可能再摸到白球6.小明植了40棵树,比小华植的棵数的2倍少4,小华植了多少棵树?设小华植了x棵树,则下面方程错误的是()A.2x﹣40=4B.40﹣4=2x C.2x=40+47.正方体的棱长扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的()倍.A.2B.4C.6D.88.已知方程4x+6=14,则2x+2=()A.4B.6C.89.一个无盖的正方体纸盒,下底标有字母“M”,沿图中加粗的线将其剪开,展开后的平面图是()A.B.C.10.不计算,你能判断下面()与“0.524÷0.01÷(4×0.5)的计算结果不同吗?A.5.24÷0.1÷(4×0.5)B.52.4÷10÷(4×0.5)C.0.524÷0.01÷4÷0.5D.0.524×100÷(4×0.5)二.填空题(共8小题)11.计算长方体容器容积时,要从容器量长、宽、高.12.在﹣3,0,3,5,﹣2,9,120,,﹣1,7,中,正数有个,负数有个,既不是正数也不是负数的有个.13.元旦期间,沃尔玛超市进行购物有奖活动,规定凡购物满58元者均可参加抽奖,设一等奖2名,二等奖5名,三等奖10名,纪念奖100名.妈妈购物70元,她去抽奖,最有可能抽中奖.14.星辰小学本学期转入48人,转出24人,现在一共有学生836人.星辰小学上学期有学生多少人?根据题意可知,题中的等量关系式是,如果设星辰学上学期有学生x人,则可列方程为.15.写出直线上点A,B,C,D,E表示的数.A;B;C;D;E.16.如果x+4=7,那么3x+12=.17.一个三角形的三个角的度数分别是40°,80°和x°,可以列出方程为.18.一个正方体的棱长是3厘米,放在地面上占地面积是平方厘米.三.判断题(共5小题)19.x=5是方程x+10=15的解.(判断对错)20.5℃比﹣2℃的温度高3℃.(判断对错)21.盒子里有12个白球,8个黄球,摸到黃球的可能性大.(判断对错)22.把一个表面积是18平方分米的正方体切成两个完全相同的长方体,表面积增加了3平方分米.(判断对错)23.五年级参加“故事大王”比赛的有67人,比六年级人数的3倍还多4人.六年级有多少人参加比赛?(判断对错)解:设六年级有x人参加比赛.(1)3x﹣67=4(2)3x+4=67(3)3x﹣4=67(4)3x=67﹣4(5)67﹣3x=4(6)x÷3﹣4=67.四.计算题(共3小题)24.计算图形的表面积和体积.25.解方程5.8x﹣0.4=170.6(x+1.5)=4.26.8×3﹣7x=5.71.44÷4x=1.226.看图列方程,并求出方程的解.五.应用题(共6小题)27.做一个底面周长是18cm,高是4cm的长方体铁丝框架.至少需要多少厘米的铁丝?28.甲乙两筐苹果,甲筐苹果的个数比乙筐的2.4倍多45个,两筐苹果一共300个,原来两筐苹果各有多少个?(列方程解答)29.商店做了一个如图所示的展示柜,展示柜的上、下面是木板,其他各面都是玻璃.做这样一个展示柜,不计损耗,需要木板和玻璃各多少平方米?30.某商人设计了一个如图所示的转盘游戏,游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母A,则收费2元;若指针指向字母B,则奖3元;若指针指向字母C,则奖1元.一天,前来游戏的人转动转盘80次.你认为商人盈利的可能性大还是亏损的可能性大?为什么?31.用边长30厘米的正方形地板砖铺一段长12米、宽6米的人行道路面至少需要多少块这样的地砖?32.一辆公共汽车从起点站开出后,途中还要停靠5个车站,最后到达终点站.下表记录了这辆公共汽车全程载客数量的变化情况.停靠站起点站途中第一站途中第二站途中第三站途中第四站途中第五站终点站上下车人数+30﹣6﹣3﹣20﹣17+40+8+6+1(1)从起点站到终点站中间,第几站没人上车?第几站没人下车?(2)公共汽车从第三站开出时车上有多少人?从第四站开出时车上有多少人?(3)终点站有多少人下车?参考答案与试题解析一.选择题(共10小题)1.【分析】读取温度数值时,先要明确温度值在零上还是零下,℃读作摄氏度,然后依次读出即可.【解答】解:0°C读作0摄氏度;故选:C.【点评】此题考查了温度的读法,注意平时基础知识的积累.2.【分析】由数轴得出:每一大段是1,数轴上0的左面是负数,右边是正数,把1平均分成3份,一份就是,所以A点表示的数是;由此解答即可.【解答】解:在直线上,点A表示的数是;故选:C.【点评】解决本题的关键是根据题意判断把一个单位长度平均分成的份数.3.【分析】三角形的面积=底×高,根据积的变化规律,一个因数不变,另一个因数扩大几倍,积也扩大几倍.所以底和高都扩大到原来的3倍,面积就扩大3×3=9倍.据此解答即可.【解答】解:y×3×3=y×9=9y(平方米)答:它的面积是9y平方米.故选:D.【点评】解答本题要掌握三角形的面积公式,要用积的变化规律解答.4.【分析】根据正方体的表面积公式:S=6a2,再根据因数与积的变化规律,积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积.据此解答.【解答】解:=所以,正方体的棱长缩小到原来的,它的表面积就缩小到原来的.故选:C.【点评】此题考查的考查的目的是理解掌握正方体的表面积公式及应用,因数与积的变化规律及应用.5.【分析】因为袋子里放了5个球,有黑球,也有白球,其中黑球2个,白球3个,两种都有摸到的可能,只是摸到白球的可能性较大,摸到黑球的可能性较小;据此解答即可.【解答】解:布袋里放了材质大小都一样的3个白球2个黑球,任意摸一个再放回,小明连续摸了4次都是白球后袋子里面仍然有黑球和白球,所以再摸一次,黑球、白球都有可能;所以,如果再摸一次,摸到的球可能是黑球.故选:A.【点评】此题应根据事件的确定性和不确定性进行解答.6.【分析】根据题意可知,小华植树棵数×2﹣小明植树的棵数=4棵或小华植树的棵数×2=小明植树的棵数+4棵,设小华植了x棵树,据此列方程解答.【解答】解:设小华植了x棵树,2x﹣40=42x﹣40+40=4+402x=442x÷2=44÷2x=22或2x=40+42x=442x÷2=44÷2x=22答:小华植了22棵树.所以方程错误的是:40﹣4=2x.故选:B.【点评】解答此题,首先弄清题意,分清已知与所求,再找出基本数量关系,由此列方程解答.7.【分析】根据因数与积的变化规律:正方体体积扩大的倍数是棱长扩大倍数的立方,据此解答.【解答】解:一个正方体棱长扩大2倍,则体积扩大2×2×2=8倍.答:体积扩大到原来的8倍.故选:D.【点评】此题主要根据因数与积的变化规律和正方体的体积公式进行解答.8.【分析】根据等式的性质,方程4x+6=14的两边同时减6,然后同时除以4,即可得到x的值,然后将x的值代入2x+2,计算即可解答本题.【解答】解:4x+6=14,4x+6﹣6=14﹣64x=84x÷4=8÷4x=22x+2=2×2+2=4+2=6故选:B.【点评】本题考查方程的解和解方程,明确解方程的方法是解答本题的关键.9.【分析】剪成的是正方体展开图的“1﹣4﹣1”少一个“1”,且另一个“1”为底,底与侧面形成一个“L”形.【解答】解:如图一个无盖的正方体纸盒,下底标有字母“M”,沿图中加粗的线将其剪开,展开后的平面图是:.故选:A.【点评】解答上题时,可按图操作一下,即可解答问题.关键是看明白,展开后,底与四个侧面组成的长方形一边齐.10.【分析】把各个选项通过除法的性质,商的变化规律、以及除以一个不为0的数等于乘这个数的倒数,变形后与“0.524÷0.01÷(4×0.5)”比较,找出相等的即可.【解答】解:5.24÷0.1÷(4×0.5)=(5.24÷10)÷(0.1÷10)÷(4×0.5)=0.524÷0.01÷(4×0.5)A选项与原算式结果相等;52.4÷10÷(4×0.5)=(52.4÷100)÷(10÷100)÷(4×0.5)=0.524÷0.1÷(4×0.5)≠0.524÷0.01÷(4×0.5)B选项与原算式结果不相等;根据除法的性质可知:0.524÷0.01÷4÷0.5=0.524÷0.01÷(4×0.5)C选项与原算式结果相等;0.524÷0.01=0.524×100所以:0.524×100÷(4×0.5)=0.524÷0.01÷(4×0.5)D选项与原算式结果相等;故选:B.【点评】解决本题根据“除法的性质,商的变化规律”进行求解.二.填空题(共8小题)11.【分析】根据容积的意义,某容器所能容纳别的物体的体积,叫做容器的容积,所以计算长方体容器的容积时,要从容器的里面量长、宽、高.据此解答.【解答】解:计算长方体容器的容积时,要从容器的里面量长、宽、高.故答案为:里面.【点评】此题考查的目的是理解掌握容积的意义及应用.12.【分析】根据正数的意义,以前学过的1、2、3、…这样的数叫做正数,正数前面也可以加“+”号;根据负数的意义,为了表示两种相反意义的量,这里出现了一种新的数,像﹣1、﹣2、﹣3、…这样的数叫做负数;0即不是正数也不是负数.【解答】解:在﹣3,0,3,5,﹣2,9,120,,﹣1,7,中,正数有:3、5、9、120、、7,共6个,负数有:﹣3、﹣2、﹣1、,共4个,既不是正数也不是负数的有0,只有1个;故答案为:6,4,1.【点评】本题是考查正、负数的意义,明确正数、负数的含义,是解答此题的关键.13.【分析】因为奖券的总数不变,所以数量最多的摸到的可能性就最大,数量最少的可能性就最小.据此解答即可.【解答】解:100>10>5>2答:她去抽奖,最有可能抽中纪念奖.故答案为:纪念.【点评】此题主要考查可能性的大小,根据各种奖券总数不变,数量多的摸到的可能性就大,数量少的可能性就小.14.【分析】根据题意,设星辰学上学期有学生x人,有关系式:上学期的学生数+转入的学生数﹣转出的学生数=现有学生数=现有学生数,列方程求解即可.【解答】解:设星辰学上学期有学生x人,x+48﹣24=836x=836+24﹣48x=812答:星辰小学上学期有学生812人.【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.15.【分析】在数轴上,原正左边的为负数,右边的为正数,原点用0表示,A在原点左边3个单位长度,表示﹣3,B在原点左边2个单位长度,表示﹣2,C在原点左边,1到2之间分成3等份,点C表示的数占2等份,又在1的左边,因此点C表示的数是1+,所以表示的数是﹣;同理点D表示的数是﹣;点E在原点右边两个长度单位加上,表示2;据此解决.【解答】解:【点评】本题的解题关键是知道数轴上以0为原点,0的右边表示正数,左边表示负数.16.【分析】首先把3x+12化成3(x+4),然后把x+4=7代入3(x+4),求出算式的值是多少即可.【解答】解:因为x+4=7,所以3x+12=3(x+4)=3×7=21故答案为:21.【点评】此题主要考查了方程的解和解方程,要熟练掌握,解答此题的关键是把所求的算式灵活变形.17.【分析】根据题意可得等量关系式:三个角的和=三角形的内角和180度,设未知角的度数是x度,然后列方程解答即可.【解答】解:40+80+x=180120+x=180x=60答:未知角的度数是60度.故答案为:40+80+x=180.【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.18.【分析】根据正方形的面积公式:S=a2,把数据代入公式解答.【解答】解:3×3=9(平方厘米)答:它的占地面积是9平方厘米.故答案为:9.【点评】此题考查的目的是理解掌握正方体的特征,以及正方形面积公式的灵活运用,关键是熟记公式.三.判断题(共5小题)19.【分析】依据等式的性质,方程两边同时减去10,求出题干中方程的解,再与x=5比较即可解答.【解答】解:x+10=15x+10﹣10=15﹣10x=5所以题干的解答是正确的.故答案为:√.【点评】依据等式的性质解方程是本题考查知识点.20.【分析】这是一道有关温度的运算题目,用零下5℃减去零下2℃;据此解答解即可.【解答】解:5﹣(﹣2)=5+2=7(℃)答:5℃比﹣2℃的温度高7℃.;所以原题说法错误.故答案为:×.【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负.21.【分析】首先根据盒子里装有12个白球和8个黄球,比较出黄球、白球的数量的大小,然后根据它们数量的多少,判断出摸到哪一种球的可能性大即可.【解答】解:盒子里装有12个白球和8个黄球,12>8,白球的数量大于黄球的数量,所以摸出白球的可能性大,故本题说法错误,故答案为:×.【点评】解决此类问题的关键是分两种情况:(1)需要计算可能性的大小的准确值时,根据求可能性的方法:求一个数是另一个数的几分之几,用除法列式解答即可;(2)不需要计算可能性的大小的准确值时,可以根据各种球数量的多少,直接判断可能性的大小.22.【分析】把一个表面积是18dm2的正方体,切成两个完全相同的长方体,表面积增加了两个正方体的面,根据正方体的表面积是6个面的和,用18除以6可求出一个面的面积,进而解答即可.【解答】解:18÷6×2=3×2=6(平方分米)即表面积增加了6平方分米;所以原题说法错误.故答案为:×.【点评】本题的重点是求出正方体一个面的面积,进而求出增加的面积.23.【分析】根据题意,可得到等量关系式:六年级人数×3+4=五年级参加的人数,设六年级的参加的有x人,把未知数代入等量关系式进行分析即可.【解答】解:设六年级的参加的有x人,3x+4=67,或67﹣3x=4,或3x=67﹣4.所以:(1)3x﹣67=4×(2)3x+4=67√(3)3x﹣4=67×(4)3x=67﹣4√(5)67﹣3x=4√(6)x÷3﹣4=67×故答案为:×,√,×,√,√,×.【点评】解答此题的关键是找准等量关系式,然后再根据等量关系式进行演变即可.四.计算题(共3小题)24.【分析】通过观察图形可知,在长方体的顶点处拿掉一个小正方体,因为这个小正方体原来外露3个面,拿掉后有露出与原来相同的3个面,所以表面积不变,体积减少了,根据长方体的表面积公式:S =(ab+ah+bh)×2,长方体的体积公式:V=abh,正方体的体积公式:V=a3,把熟记代入公式解答.【解答】解:1.5分米=15厘米(15×10+15×8+10×8)×2=(150+120+80)×2=350×2=700(平方厘米)15×10×8﹣6×6×6=1200﹣216=984(立方厘米)答:它的表面积是700平方厘米,体积是984立方厘米.【点评】此题主要考查长方体的表面积公式、体积公式、正方体的体积公式的灵活运用,关键是熟记公式.25.【分析】(1)首先根据等式的性质,两边同时加上0.4,然后两边再同时除以5.8即可.(2)首先根据等式的性质,两边同时除以0.6,然后两边再同时减去1.5即可.(3)首先根据等式的性质,两边同时加上7x,然后两边再同时减去5.7,最后两边同时除以7即可.(4)首先根据等式的性质,两边同时乘4x,然后两边再同时除以4.8即可.【解答】解:(1)5.8x﹣0.4=175.8x﹣0.4+0.4=17+0.45.8x=17.45.8x÷5.8=17.4÷5.8x=3(2)0.6(x+1.5)=4.20.6(x+1.5)÷0.6=4.2÷0.6x+1.5=7x+1.5﹣1.5=7﹣1.5x=5.5(3)6.8×3﹣7x=5.720.4﹣7x=5.720.4﹣7x+7x=5.7+7x5.7+7x=20.45.7+7x﹣5.7=20.4﹣5.77x=14.77x÷7=14.7÷7x=2.1(4)1.44÷4x=1.21.44÷4x×4x=1.2×4x4.8x=1.444.8x÷4.8=1.44÷4.8x=0.3【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等.26.【分析】(1)根据题意可知,3个面包的钱数+2瓶饮料的钱数=12元,设每瓶饮料x元,据此列方程解答.(2)根据题意可知,一袋面粉的钱数+3袋大米的钱数=256元,设每袋大米x元,据此列方程解答.【解答】解:(1)设每瓶饮料x元,2×3+2x=126+2x=126+2x﹣6=12﹣62x=62x÷2=6÷2x=3答:每瓶饮料3元.(2)设每袋大米x元,64+3x=25664+3x﹣64=256﹣643x=1923x÷3=192÷3x=64答:每袋大米64元.【点评】解决这类问题主要找出题里面蕴含的等量关系,设出未知数,由此列出方程解决问题.五.应用题(共6小题)27.【分析】求至少需要多少厘米长的铁丝就是求长方体棱长和,长方有12条棱,12条棱包括:下底面的4条棱和上底面的4条棱和4条高,上下底面的4条棱的和都是18厘米,即2个18厘米再加上4个4厘米就是所求的问题.【解答】解:18×2+4×4=36+16=52(厘米)答:至少需要52厘米长的铁丝.【点评】此题主要考查长方体的特征以及棱长总和的求法.28.【分析】这道题的等量关系非常明显:甲筐苹果的个数+乙筐苹果的个数=300,甲筐苹果的个数=乙筐苹果的个数×2.4+45,由此设出乙筐苹果的个数为x个,列出方程解答即可.【解答】解:设乙筐苹果的个数为x个,则甲筐有(2.4x+45)个,则:(2.4x+45)+x=3003.4x+45=3003.4x=255x=752.4×75+45=225(个)答:甲筐苹果有225个,乙筐苹果有75个.【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题.29.【分析】根据题意可知,这个展示柜的6个面都是长方形,展示柜的上、下面是木板,上、下面的长是2.5米,宽是0.8米,其他各面都是玻璃.也就是这个长方体的前后、左右4个面是玻璃,前后面的长是2.5米,宽是1.2米,左右面的长是1.2米,宽是0.8米,根据长方形的面积公式:S=ab,把数据代入公式解答.【解答】解:2.5×0.8×2=4(平方米)(2.5×1.2+0.8×1.2)×2=(3+0.96)×2=3.96×2=7.92(平方米)答:需要木板4平方米,需要玻璃7.92平方米.【点评】此题考查的目的是理解掌握长方体的特征,以及长方形面积公式的灵活运用,关键是熟记公式.30.【分析】根据几何概率的定义,面积比即概率.图中A,B,C所占的面积与总面积之比即为A,B,C 各自的概率,算出相应的可能性,乘钱数,比较即可.【解答】解:80×50%×2=40×2=80(元)80×12.5%×3=10×3=30(元)80×37.5×1=30×1=30(元)80元>30元+30元所以商人盈利的可能性大.【点评】考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=所求情况数与总情况数之比.31.【分析】要求需要这样的地砖多少块,就要用地面的面积除以每块地砖的面积,地面是长方形的,根据长方形的面积公式S=ab可求出地面的面积,地砖是正方形的可根据正方形的面积公式S=a2求出地砖的面积,据此解答.【解答】解:30厘米=0.3米0.3×0.3=0.09(平方米)12×6=72(平方米)72÷0.09=800(块)答:至少需要800块这样的地砖.【点评】本题的关键是让学生走出要用地面的面积除以地砖的边长的误区,要除以地砖的面积.32.【分析】(1)哪个车站没有“+”的就表示没有上车人数;没有“﹣”就表示没有下车人数;(2)(3)“+”表示上车人数,“﹣”表示下车人数,根据表格代入计算求解.【解答】解:(1)从起点站到终点站中间,第二站没人上车,第四站没人下车;(2)30﹣6+4﹣3+0﹣2+8=31(人)31﹣0+6=37(人)答:公共汽车从第三站开出时车上有31人,从第四站开出时车上有37人.(3)37﹣17+1=21(人)答:终点站有21人下车.【点评】本题考查了简单的统计表,要学会统计表获取信息,进一步认识负数的意义,掌握正负数的意义是解决本题的关键.。
新都区小学五年级调考试卷

新都区小学五年级调考试卷一、选择题(每题2分,共20分)1. 下列哪个选项是正确的成语使用?A. 画蛇添足B. 画龙点睛C. 画虎不成反类犬D. 画龙点睛(错别字)2. “不入虎穴,焉得虎子”这句话的意思是:A. 不去冒险就得不到成功B. 只有深入虎穴才能得到虎子C. 只有亲自去虎穴才能了解虎子D. 虎穴是危险的地方,不能去3. 以下哪个词组搭配不当?A. 学习知识B. 学习技能C. 学习运动D. 学习兴趣4. 在数学中,一个数的平方根是它自身的数是:A. 0B. 1C. -1D. 25. 下列哪个句子使用了“虽然...但是...”的句式?A. 他虽然很努力,但是成绩还是不理想。
B. 他很努力,成绩很好。
C. 他虽然很努力,成绩很好。
D. 他很努力,但是成绩还是不理想。
二、填空题(每空1分,共20分)6. 请填写下列成语的后半部分:一言既出,__________。
7. 圆的周长公式是C=2πr,其中π是圆周率,r是圆的半径。
如果一个圆的半径是3厘米,那么它的周长是__________厘米。
8. 请写出一个含有“海”字的诗句:__________。
9. 请写出一个含有“山”字的成语:__________。
10. 请写出一个含有“水”字的成语:__________。
三、判断题(每题1分,共10分)11. 地球是太阳系中最大的行星。
()12. 植物通过光合作用制造氧气。
()13. 所有的昆虫都有六条腿。
()14. 人类的DNA与大猩猩的DNA有99%相似。
()15. 一年有365天。
()四、简答题(每题5分,共10分)16. 请简述光合作用的过程。
17. 请简述为什么说“书籍是人类进步的阶梯”。
五、阅读理解(每题5分,共20分)阅读以下短文,回答问题。
短文一:小明的家乡是一个美丽的小山村,那里有清澈的溪流,郁郁葱葱的树林,还有一片片金黄的稻田。
每当春天来临,小明就会和家人一起去山上采摘新鲜的竹笋,夏天则去溪边捉小鱼,秋天则是收获的季节,一家人会一起收割稻谷,冬天则围坐在火炉旁,听爷爷讲述古老的故事。
五年级下数学月考试题综合考练(2)_1415广西人教新课标

2021-2021学年广西百色市隆林县猪场乡五年级〔下〕第一次月考数学试卷一、填空1.在①8﹣X=7 ②X+22 ③4×9=32 ④Y÷61=1.7 ⑤4X>12 ⑥39X 中,方程有,等式有〔填序号〕.2.在横线上填上“>〞、“<〞或“=〞.〔1〕当x=36时,136﹣x100;〔2〕当x=0.9时,x÷30.3.3.解方程x+5.2=12时,方程左右两边应同时 5.2.解方程5x=6.5时,方程左右两边应同时5.4.求方程中未知数的值的过程,叫做.5.车上原来有X人,中途有6人下车,如今车上有人.6.24×﹣×15=18.7.小明和他的爸爸相差28岁.小明X岁,爸爸42岁.请用方程表示他们父子的数量关系.8.甲乙丙三个百米比赛,丙用X秒,甲比丙多用1.5秒,乙比丙少用1.5秒.三人中,是冠军.二、请你当小裁判.9.等式两边都乘或除以一个数,等式仍成立..〔判断对错〕10.X=10是方程..〔判断对错〕11.含有未知数的式子叫方程..〔判断对错〕12.因为x+8.7=y+7.8,所以x>y.〔判断对错〕三、选择题13.解方程X÷10=5时,方程两边都应〔〕A.加10B.减10C.乘10D.除以1014.当a=5 b=6 c=7时,bc﹣ac的值是〔〕A.1B.7C.乘12D.无法计算15.小明比小芳大,小明今年a岁,小芳今年b岁.三年后,小明比小芳大〔〕岁.A.3B.a﹣bC.a﹣b+3D.无法计算16.方程1.8+x=3的解是〔〕A.x=2.2B.x=1.2C.x=4.817.x=2.5是方程〔〕中未知数的值.A.X÷2.5=2.5B.2.5﹣x=1C.2.5÷x=1四、解答题〔共1小题,总分值18分〕18.解方程x+36=67 12÷ⅹ=0.3 4x﹣3×9=2942x+25x=134 7.9x﹣x=8.97ⅹ+18﹣25=43.五、解答题〔共1小题,总分值12分〕19.看图列式计算.六、用方程解决问题.〔1~5每题6分,6题10分〕20.某市居民用电每千瓦•时的价格是0.52元,芳芳家上个月付电费23.4元,用电多少千瓦•时?21.一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇.客车的速度是95千米/时,货车的速度是多少千米/时?22.两个相邻自然数的和是85,这两个自然数分别是多少?23.少先队员参加植树活动,六年级植树的棵数是五年级的1.5倍,五年级比六年级少植树24棵,两个年级各植树多少棵?24.学校印制画册一共用去2240元,画册的印刷费是3.6元本,其余费用是800元.学校印制了多少本画册?25.以下是9~15届亚运会中国和韩国获金牌情况如下表:9 10 11 12 13 14 15中国61 94 183 137 129 150 165韩国28 93 54 63 65 96 58你能根据表中的数据,接着完成下面的折线统计图吗?看图讨论下面的问题:〔1〕中国和韩国分别在哪一届亚运会上获得的金牌数量最多?〔2〕哪一届亚运会两国金牌数量相差最少?〔3〕根据统计图,简单分析两面国在历届亚运会上的表现〔4〕你还能提出什么问题?2021-2021学年广西百色市隆林县猪场乡五年级〔下〕第一次月考数学试卷参考答案与试题解析一、填空1.在①8﹣X=7 ②X+22 ③4×9=32 ④Y÷61=1.7 ⑤4X>12 ⑥39X 中,方程有①③④,等式有①④〔填序号〕.【考点】方程需要满足的条件.【分析】等式是指用“=〞连接的式子,方程是指含有未知数的等式;据此进展分类.【解答】解:等式有:①、③、④,因为它们是用“=〞号连接的式子,方程有:①、④,因为它们是含有未知数的等式.故答案为:①③④,①④.2.在横线上填上“>〞、“<〞或“=〞.〔1〕当x=36时,136﹣x=100;〔2〕当x=0.9时,x÷3=0.3.【考点】含字母式子的求值.【分析】〔1〕当x=36时,求出算式136﹣x的值,然后把它和100比拟大小即可;〔2〕当x=0.9时,求出算式x÷3的值,然后把它和0.3比拟大小即可.【解答】解:〔1〕当x=36时,136﹣x=136﹣36=100,所以当x=36时,136﹣x=100;〔2〕当x=0.9时,x÷3=0.9÷3=0.3,所以当x=0.9时,x÷3=0.3.故答案为:=、=.3.解方程x+5.2=12时,方程左右两边应同时减 5.2.解方程5x=6.5时,方程左右两边应同时除以5.【考点】方程的解和解方程.【分析】解方程X+5.2=12时,由等式的性质可得方程左右两边应同时减去5.2;解方程5X=6.5时,由等式的性质可得方程左右两边应同时除以5.【解答】解:x+5.2=12x=12﹣5.2=6.8所以解方程X+5.2=12时,由等式的性质可得方程左右两边应同时减去5.2;5x=6.5x=6.5÷5x=1.3所以解方程5X=6.5时,由等式的性质可得方程左右两边应同时除以5.故答案为:减,除以.4.求方程中未知数的值的过程,叫做解方程.【考点】方程的意义.【分析】解方程是指求方程中未知数的值的过程;据此解答.【解答】解:求方程中未知数的值的过程,叫做解方程.故答案为:解方程.5.车上原来有X人,中途有6人下车,如今车上有x﹣6人.【考点】用字母表示数.【分析】求如今车上有多少人,用车上原来的人数减去中途下去的人数即可.【解答】解:x﹣6〔人〕答:如今车上有x﹣6人.故答案为:x﹣6.6.24×2﹣2×15=18.【考点】运算定律与简便运算.【分析】根据乘法分配律,设这个数为x,可得方程24x﹣15x=18,解此方程即可.【解答】解:设这个数为x,由题意得:24x﹣15x=18〔24﹣15〕x=189x=189x÷9=18÷9x=2.故答案为:2,2.7.小明和他的爸爸相差28岁.小明X岁,爸爸42岁.请用方程表示他们父子的数量关系42﹣x=28.【考点】用字母表示数.【分析】他们父子的数量关系可以写成:爸爸的岁数﹣小明的岁数=相差的岁数,据此列出含字母的式子得解.【解答】解:42﹣x=28.故答案为:42﹣x=28.8.甲乙丙三个百米比赛,丙用X秒,甲比丙多用1.5秒,乙比丙少用1.5秒.三人中,乙是冠军.【考点】用字母表示数;小数大小的比拟.【分析】由题意得:甲的时间=丙+1.5,乙的时间=丙﹣1.5,所以甲的时间>丙的时间>乙的时间,路程一样,用的时间最少的是冠军.据此解答即可.【解答】解:由题意得:甲的时间=丙+1.5,乙的时间=丙﹣1.5,所以甲的时间>丙的时间>乙的时间,所以乙是冠军.故答案为:乙.二、请你当小裁判.9.等式两边都乘或除以一个数,等式仍成立.×.〔判断对错〕【考点】等式的意义.【分析】等式的性质:等式的两边同时加上、同时减去、同时乘上或同时除以一个数〔0除外〕,等式的左右两边仍相等;据此进展判断.【解答】解:等式的两边只有同时加上、同时减去、同时乘上或同时除以一个数〔0除外〕,等式的左右两边仍相等;所以等式两边都乘或除以一个数,等式仍成立的说法是错误的.故答案为:×.10.X=10是方程.√.〔判断对错〕【考点】方程的意义.【分析】方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进展选择.【解答】解:x﹣=10,既含有未知数又是等式,具备了方程的条件,因此是方程;故答案为:√.11.含有未知数的式子叫方程.×.〔判断对错〕【考点】方程的意义.【分析】根据方程的概念,首先是等式,再就是含有未知数,举例子进一步说明可得出答案.【解答】解:例如4x+6是含有未知数的式子,4+5=9是等式,可它们都不是方程,而5+x=9就是方程.故答案为:错误.12.因为x+8.7=y+7.8,所以x>y×.〔判断对错〕【考点】小数大小的比拟.【分析】根据两数和相等,8.7>7.8,一个加数越大另一个加数越小,从而可以得出x和y 的关系.【解答】解:因为x+8.7与y+7.8的和相等,而且8.7>7.8,所以x<y.故答案为:×.三、选择题13.解方程X÷10=5时,方程两边都应〔〕A.加10B.减10C.乘10D.除以10【考点】方程的解和解方程.【分析】解方程x÷10=5时,方程的两边同时乘10即可得到未知数值.【解答】解:x÷10=5x×10÷10=5×10x=50所以方程的两边同时乘以10即可求解.应选:C.14.当a=5 b=6 c=7时,bc﹣ac的值是〔〕A.1B.7C.乘12D.无法计算【考点】含字母式子的求值.【分析】把a=5,b=6,c=7代入bc﹣ac,求出算式bc﹣ac的值是多少即可.【解答】解:bc﹣ac=6×7﹣5×7=42﹣35=7所以bc﹣ac的值是7.应选:B.15.小明比小芳大,小明今年a岁,小芳今年b岁.三年后,小明比小芳大〔〕岁.A.3B.a﹣bC.a﹣b+3D.无法计算【考点】用字母表示数.【分析】两人的年龄差是一定的,不会随着年龄的增长而有变化,根据小明比小芳大的岁数=小明岁数﹣小芳岁数即可解答.【解答】解:小明比小芳大,小明今年a岁,小芳今年b岁.三年后,小明比小芳大〔a﹣b〕岁.应选:B.16.方程1.8+x=3的解是〔〕A.x=2.2B.x=1.2C.x=4.8【考点】方程的解和解方程.【分析】根据题意,等式的左边减去1.8,由等式的性质,等式的右边也要减去1.8,然后再进一步解答即可;【解答】解:1.8+x=31.8+x﹣1.8=3﹣1.8x=1.2应选:B.17.x=2.5是方程〔〕中未知数的值.A.X÷2.5=2.5B.2.5﹣x=1C.2.5÷x=1【考点】方程的解和解方程.【分析】将x=2.5分别代入A、B、C三个选项,再进展选择即可.【解答】解:A、2.5÷2.5=1≠2.5,故本选项错误;B、2.5﹣2.5=0≠1,故本选项错误;C、2.5÷2.5=1,故本选项正确.应选:C.四、解答题〔共1小题,总分值18分〕18.解方程x+36=67 12÷ⅹ=0.3 4x﹣3×9=2942x+25x=134 7.9x﹣x=8.97ⅹ+18﹣25=43.【考点】方程的解和解方程.【分析】①解方程x+36=67时,根据等式的性质可得方程左右两边应同时减去36;②解方程12÷ⅹ=0.3时,根据等式的性质可得方程左右两边应同时乘x,把方程改写为0.3x=12,然后再根据等式的性质可得方程左右两边应同时除以0.3即可;③解方程4x﹣3×9=29时,可先把方程改写成4x﹣27=29,根据等式的性质可得方程左右两边应同时加27,然后再方程两边同时除以4即可;④解方程42x+25x=134时,可先把方程改写成67x=134,根据等式的性质可得方程左右两边应同时除以67即可;⑤解方程7.9x﹣x=8.97时,可先把方程改写成6.9x=8.97,根据等式的性质可得方程左右两边应同时除以6.9即可;⑥解方程ⅹ+18﹣25=43时,根据等式的性质可得方程左右两边应同时加上25,然后再减去18即可.【解答】解:①x+36=67x=67﹣36x=31;②12÷ⅹ=0.30.3x=12x=12÷0.3x=40;③4x﹣3×9=294x﹣27=294x=56x=14;④42x+25x=13467x=134x=2;⑤7.9x﹣x=8.976.9x=8.97x=1.3;⑥ⅹ+18﹣25=43ⅹ+18﹣25+25﹣18=43+25﹣18x=50.五、解答题〔共1小题,总分值12分〕19.看图列式计算.【考点】图文应用题.【分析】〔1〕由图知,4个x是36,可得4x=36,解方程即可;〔2〕由图知,一本书共250页,看了x页,还剩110页,根据看的+剩下的=总页数列方程解答即可;〔3〕根据平行四边形的面积=底×高列方程解答即可;〔4〕根据总页数﹣已看的页数=剩下的页数列方程解答即可.【解答】解:〔1〕4x=364x÷4=36÷4x=9;〔2〕x+110=250x+110﹣110=250﹣110x=140;〔3〕2.4x=122.4x÷2.4=12÷2.4x=5;〔4〕x﹣38=64x﹣38+8=64+38x=102.六、用方程解决问题.〔1~5每题6分,6题10分〕20.某市居民用电每千瓦•时的价格是0.52元,芳芳家上个月付电费23.4元,用电多少千瓦•时?【考点】整数、小数复合应用题.【分析】根据除法的包含意义:用芳芳家付的电费的总钱数除以每千瓦•时的电价即可求解.【解答】解:23.4÷0.52=45〔千瓦•时〕答:用电45千瓦•时.21.一辆客车和一辆货车同时从相距540千米的两地出发,相向而行,经过3小时相遇.客车的速度是95千米/时,货车的速度是多少千米/时?【考点】简单的行程问题.【分析】首先根据路程÷时间=速度,用两地之间的间隔除以两车相遇的时间,求出两车的速度之和;然后用两车的速度之和减去客车的速度,求出货车的速度是多少千米/时即可.【解答】解:540÷3﹣95=180﹣95=85〔千米/时〕答:货车的速度是85千米/时.22.两个相邻自然数的和是85,这两个自然数分别是多少?【考点】和差问题.【分析】此题要求,可设较小的自然数为x,那么另一个自然数为〔x+1〕,根据题意,列出方程x+〔x+1〕=85,解方程即可.【解答】解:设较小的自然数为x,那么另一个自然数为〔x+1〕,由题意得:x+〔x+1〕=852x+1=852x=84x=42x+1=42+1=43.答:这两个自然数分别是42、43.23.少先队员参加植树活动,六年级植树的棵数是五年级的1.5倍,五年级比六年级少植树24棵,两个年级各植树多少棵?【考点】差倍问题.【分析】把五年级植树的棵数看作1倍数,六年级植树的棵数是五年级的1.5倍,六年级植树的棵数比五年级植树的棵数多〔1.5﹣1〕倍,又知五年级比六年级少植树24棵,用除法即可得五年级植树的棵数,再求六年级植树的棵数即可.【解答】解:24÷〔1.5﹣1〕=24÷0.5=48〔棵〕48+24=72〔棵〕答:五年级植树48棵,六年级植树72棵.24.学校印制画册一共用去2240元,画册的印刷费是3.6元本,其余费用是800元.学校印制了多少本画册?【考点】整数、小数复合应用题.【分析】根据题意,可用2240减去800计算出印刷画册的钱数,然后再除以3.6进展计算即可得到答案.【解答】解:÷3.6=1440÷3.6=400〔本〕答:学校印制了400本画册.25.以下是9~15届亚运会中国和韩国获金牌情况如下表:9 10 11 12 13 14 15中国61 94 183 137 129 150 165韩国28 93 54 63 65 96 58你能根据表中的数据,接着完成下面的折线统计图吗?看图讨论下面的问题:〔1〕中国和韩国分别在哪一届亚运会上获得的金牌数量最多?〔2〕哪一届亚运会两国金牌数量相差最少?〔3〕根据统计图,简单分析两面国在历届亚运会上的表现〔4〕你还能提出什么问题?【考点】统计图表的填补;从统计图表中获取信息.【分析】根据统计表中提供的数据,在折线统计图上找出各对应点,再把各个点描起来即可;〔1〕根据统计表判断中国和韩国分别在哪一届亚运会上获得的金牌数量最多即可.〔2〕分别求出届亚运会两国金牌数量相差多少,然后比拟大小即可.〔3〕根据统计图,简单分析两国在历届亚运会上的表现即可.〔4〕可以提问题:第9﹣14届亚运会中国一共获金牌多少枚?【解答】解:根据第9﹣14届亚运会中国和韩国获金牌情况,绘制折线统计图如下:〔2〕61﹣28=33〔枚〕94﹣93=1〔枚〕183﹣54=129〔枚〕137﹣63=74〔枚〕129﹣65=64〔枚〕150﹣96=54〔枚〕所以第十届亚运会两国金牌数量相差最少.答:第十届亚运会两国金牌数量相差最少.〔3〕第9届亚运会上中国获得的金牌数是韩国的2倍还多;第10届,中国只比韩国多一枚金牌,说明韩国进步较大;第11届,由于在北京举办,中国队与韩国金牌数差异最大;从12届、13届、14届中韩两国金牌数之差分别是74枚、64枚、54枚,逐渐变小,说明韩国进步较大.〔4〕可以提问题:第9﹣14届亚运会中国一共获金牌多少枚?61+94+183+137+129+150=754〔枚〕答:第9﹣14届亚运会中国一共获金牌754枚.2021年7月15日。
苏教版五年级科学下册单元测试卷及答案(全册)

苏教版五年级科学下册单元测试卷及答案·最新说明:文档整理了苏教版五年级科学下册各单元测试卷的内容,试卷内容涵盖教育大纲内容,突出了重点知识的检测,对所学内容进行了拓展和延伸,望对同仁有所借鉴。
目录苏教版小学科学五年级下册第一单元测试卷 (3)苏教版小学科学五年级下册第一单元测试卷:参考答案 (8)苏教版小学科学五年级下册第二单元测试卷 (10)苏教版小学科学五年级下册第二单元测试卷:参考答案 (14)苏教版小学科学五年级下册第三单元测试卷 (16)苏教版小学科学五年级下册第三单元测试卷:参考答案 (21)苏教版小学科学五年级下册第四单元测试卷 (23)苏教版小学科学五年级下册第四单元测试卷:参考答案 (28)苏教版小学科学五年级下册期末测试卷 (31)苏教版小学科学五年级下册期末测试卷:参考答案 (36)苏教版小学科学五年级下册第一单元测试卷(时间:60分钟总分:100分)一、选择题(每题 2分,共40分)1.下面的细菌对人类有益的是()。
A.乳酸菌B.结核杆菌C.双球菌2.馒头发霉的条件是()。
A.温暖、干燥B.寒冷、潮湿C.温暖、潮湿3.构成生命体的“积木”是一种微小的结构,胡克把它命名为()。
A.细菌B.病毒C.细胞轴4.霉烂的水果、蔬菜,多是()造成的。
A .细菌 B.病毒 C.真菌5.在显微镜下观察的物体,制作的装片必须是()。
A.一般物体B.可厚可薄C.透明的D.薄而透明的物体6.下列是显微镜下观察到的几种微生物,其中草履虫是()。
A. B. C.7.实验中,我们采集微生物的主要场所是()。
A.鱼缸、池塘的水中B.盐水中C.碘酒中8.草履虫、变形虫等原生动物都是由()细胞组成。
A.一个B.多个C.无数个9.靠尾部发光器互相联系,找到对衣藻、草履虫是通过()与外界环境进行物质交换的。
A.细胞膜B.细胞质C.细胞核D.鞭毛和纤毛10.对于微生物的特点,下列叙述不正确的是()。
A.种类繁多B.生长繁殖慢C.分布广泛11.( )是构成大多数生物体的基本单位。
五年级下册数学抽考试卷加油站(14)_人教新课标

五年级下册数学抽考试卷加油站(14)_人教新课标当x=2.5,y=1.5时,2x﹣3y= .【答案】0.5【解析】试题分析:把x=2.5,y=1.5代入2x﹣3y运算即可.解:当x=2.5,y=1.5时,2x﹣3y=2×2.5﹣3×1.5=5﹣4.5=0.5.故答案为:0.5.【点评】本题考查了含字母式子求值,关键是把x和y的值代入运算.当 a 比15 多b 时,用等式表示是.【答案】a=b+15.(答案不唯独)【解析】试题分析:当a 比15 多b 时,a=b+15,据此解答即可.解:a=b+15,故答案为:a=b+15.(答案不唯独)【点评】关键是依照题意,得出数量关系等式.假如(3,2)表示第3列第二排,那么(2,1)表示第排,第7列第8排,能够表示为.【答案】1,(7,8).【解析】试题分析:数对表示位置的方法是:第一个数字表示列,从左向右数;第二个数字表示行,从下向上数,同时列与行之间用“,”隔开,由此即可解答.解:假如(3,2)表示第3列第二排,那么(2,1)表示第1排,第7列第8排,能够表示为(7,8).故答案为:1,(7,8).【点评】此题考查了数对的写法,即先看在第几列,那个数确实是数对中的第一个数;再看在第几行,那个数确实是数对中的第二个数.小伟今年10岁,爸爸今年x岁,5年后,爸爸比小伟大岁,爸爸岁.【答案】(x﹣10),(x+5).【解析】试题分析:因为不管通过多长时刻,爸爸与亲小孩的年龄差是不变的,今年相差x﹣10岁,因此5年后爸爸和小伟仍相差(x﹣10)岁,用爸爸今年的岁数加5,即可得5年后爸爸的岁数.解:x﹣10(岁);x+5(岁)答:5年后,爸爸比小伟大(x﹣10)岁,爸爸(x+5)岁.故答案为:(x﹣10),(x+5).【点评】此题应抓住年龄差不变来求解,因为不管通过多长时刻,二人增长的时刻是一样的,故差不变.三个连续的偶数,假如中间一个数是X,则其中最小的数是,最大的数是.【答案】X﹣2,X+2.【解析】试题分析:因为连续的2个偶数相差2,因此中间的一个数是X,则最小的一个是X﹣2,最大的是X+2.解:三个连续的偶数中间一个是X,最小的一个数是X﹣2,最大的一个数是X+2;故答案为:X﹣2,X+2.【点评】解题关键是明确连续的两个偶数相差2,据此表示出两个偶数.5个连续的自然数和是60,中间的数是,最小的数是,最大的数是.【答案】12,10,14.【解析】试题分析:依照自然数的意义明白,每相邻的两个自然数相差1,因此用60÷5求出5个数的平均数,确实是这5个数中的中间的数,然后用中间的数加上2即可求出最大的数.据此解答.解:60÷5=12,12+2=14,12﹣2=10;答:中间的数是12,最小的数是10,最大的数是14;故答案为:12,10,14.【点评】灵活利用自然数的意义与平均数的意义是解答此题的关键.用数对表示位置时,一样用一个数字表示,用第二个数表示;列一样是从从往数,行一样是从往数.【答案】列,行,左,右,下,上.【解析】试题分析:数对表示位置的方法是:第一个数字表示列,从左向右数;第二个数字表示行,从下向上数,同时列与行之间用“,”隔开,由此即可解答.解:用数对表示位置时,一样用一个数字表示列,用第二个数表示行;列一样是从左从往右数,行一样是从下往上数.故答案为:列,行,左,右,下,上.【点评】此题要紧考查数对表示位置的方法.要修一条长a千米的路,修了4天后,还剩b千米没有修,平均每天修千米.【答案】(a﹣b)÷4.【解析】试题分析:用全长减去剩下的长度运算出差不多修的长度,再除以修的天数即可运算出平均每天修的长度.解:(a﹣b)÷4(千米),答:平均每天修(a﹣b)÷4千米.故答案为:(a﹣b)÷4.【点评】此题要紧考查平均数的运算,关键是运算出与修的天数对应的长度.超市原有苹果a千克,又运进8筐,每筐X千克,现在超市有苹果千克.【答案】(8X+a).【解析】试题分析:先求出运进多少千克苹果,即8X千克,再加上原有的重量即可得到现在的重量.解:X×8+a=8X+a(千克)答:现在超市有苹果(8X+a)千克.故答案为:(8X+a).【点评】本题关键求出运进的重量,运用乘法进行解答,然后进一步解决问题即可.二、判定题:求方程找中未知数的值的过程,叫做方程的解(判定对错)【答案】×【解析】试题分析:解方程是指求方程中未知数的值的过程;方程解的意义是:使方程两边左右相等的未知数的值叫做方程的解,据此解答.解:求方程找中未知数的值的过程,叫做方程的解的说法是错误的,应该是解方程.故答案为:×.【点评】此题考查解方程的意义,要与方程的解区分开.2x=19 方程两边同时除以a,所得结果仍旧是方程(判定对错)【答案】×【解析】试题分析:等式两边同时乘或除以同一个不为0的数,等式仍旧成立;据此解答.解:依照等式的性质可知,2x=19 方程两边同时除以a(a≠0),所得结果仍旧是方程,但本题没有说明a≠0,因此说法错误.故答案为:×.【点评】此题考查了等式性质的运用.等式两边同时加上(或减去)同一个数,或者等式两边同时乘或除以同一个不为0的数,等式的值不变.方程x﹣28.6=15 的解是x=13.6 (判定对错)【答案】×【解析】试题分析:依照等式的性质,两边同时加上28.6,即可判定得解.解:x﹣28.6=15x﹣28.6+28.6=15+28.8x=43.8因此方程x﹣28.6=15 的解是x=13.6的说法是错误的,应该是x=43. 8.故答案为:×.【点评】在解方程时应依照等式的性质,即等式两边同加上、同减去、同乘上或同除以某一个数(0除外),等式的两边仍相等,同时注意“=”上下要对齐.3x+8是方程.(判定对错)【答案】×【解析】试题分析:依照方程的意义:含有未知数的等式才是方程;据此进行判定.解:3x+8,只是含有未知数的式子,不是等式,因此不是方程;故判定为:×.【点评】此题要紧考查方程的意义,方程具备两个条件:一含有未知数,二必须是等式.方程一定是等式,等式也一定是方程..(判定对错)【答案】×【解析】试题分析:方程是指含有未知数的等式,因此方程一定是等式是正确的;等式是指用“=”号连接的式子,等式中不一定含有未知数,因此等式不一定是方程,它只是等式的一部分.据此判定.解:因为方程是指含有未知数的等式,等式是指用“=”号连接的式子,等式中不一定含有未知数,因此方程一定是等式,等式不一定是方程.故判定为:×.【点评】此题考查方程与等式的关系:所有的方程差不多上等式,但等式不一定是方程.三、选择题(将正确答案的序号填入括号内)一块三角形菜地,面积是160平方米,假如底是40米,高是x米,错误的方程是()A.40x÷2=6 B.x=160÷2÷40 C.40x=160×2【答案】AB【解析】试题分析:三角形的面积=底×高÷2,得出高=2三角形的面积÷底,菜地的面积和底边长已知,代入公式即可求解.解:依照三角形的面积公式,得:40x÷2=160(A错误)40x÷2×2=160×240x=160×2(C正确)40x÷40=160×2÷40x=160×2÷40(B错误)x=8故选:A、B.【点评】此题要紧考查三角形的面积公式的灵活应用.李明的妈妈今年36岁,正好相当于李明年龄的3倍,假设李明的年龄为x岁,那么列方程正确的是()A.3x=36 B.x÷3=36 C.x÷36=3 D.x+3x=36【答案】A【解析】试题分析:第一依照题意,可得妈妈的年龄等于小明的年龄乘3,然后依照:小明的年龄×3=36,求出方程,求出小明今年多少岁即可.解:假设李明的年龄为x岁,由题意,得:3x=363x÷3=36÷3x=12故选:A.【点评】此题要紧考查了一元一次方程的应用,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键.18比x的三倍少10,列方程是()A.3x+10=18 B.3x﹣10=18 C.3x=18﹣10【答案】B【解析】试题分析:依照题意18比x的3倍少10,题目中的等量关系式应是1 8比X的三倍少10,列方程是,据此可列出方程.解:18比x的三倍少10,列方程是3x﹣10=18故选:B.【点评】考查学生分析题意找出等量关系式来列方程,关键是找出等量关系式,这是用方程解应用题和文字题的关键.[来源:学*科*网]甲数比乙数的2倍少6,乙数是x,甲数()A.x÷2=6 B.(x﹣6)÷2 C.2x﹣6【答案】C【解析】试题分析:依照题意明白,甲数=乙数×2﹣6,由此即可得出答案.解:甲数:2×x﹣6=2x﹣6故选:C.【点评】关键是把给出的字母当做已知数,再依照差不多的数量关系解决问题;注意字母与数相乘时要简写,即省略乘号,把数写在字母的前面.下列各式中,是方程的是()A.x﹣16<9 B.4x﹣3=0 C.2.5+3=5.5【答案】B【解析】试题分析:方程是指含有未知数的等式.因此方程必须具备两个条件:①含有未知数;②等式.由此进行选择.解:A、x﹣16<9,尽管含有未知数,但它是不等式,也不是方程.B、4x﹣3=0,既含有未知数又是等式,具备了方程的条件,因此是方程;C、2.5+3=5.5,只是等式,不含有未知数,不是方程;故选:B.【点评】此题考查方程的辨识:只有含有未知数的等式才是方程.四、先找出错误,再改正.先找出错误,再改正.(1)x+65=100解:x=100+65x=165(2)x﹣20=120解:x=120﹣20x=100(3)x÷1.2=1.2x=1.2×1.2x=14.4(4)3x=96x=96×3x=288.【答案】(1)错误在于:方程两边应该同时减65,而不是加65;x=35(2)错误在于:方程两边应该同时加20,而不是方程两边边减20;x=140(3)错误在于:运算结果错误,结果是1.44,而不是14.4;x=1.44(4)错误在于:方程两边应该同时除以3,而不是乘3;x=32[来源:]【解析】试题分析:(1)错误在于:方程两边应该同时减65,而不是加65,解答时应:依据等式的性质,方程两边同时减65即可解答;(2)错误在于:方程两边应该同时加20,而不是方程两边边减20,解答时应:依据等式的性质,方程两边同时加20即可解答;(3)错误在于:运算结果错误,结果是1.44,而不是14.4;(4)错误在于:方程两边应该同时除以3,而不是乘3;解答时应:依据等式的性质,方程两边同时除以3即可解答.解:(1)错误在于:方程两边应该同时减65,而不是加65;x+65=100x+65﹣65=100﹣65x=35(2)错误在于:方程两边应该同时加20,而不是方程两边边减20;x﹣20=120x﹣20+20=120+20x=140(3)错误在于:运算结果错误,结果是1.44,而不是14.4;x÷1.2=1.2x÷1.2×1.2=1.2×1.2x=1.2×1.2x=1.44(4)错误在于:方程两边应该同时除以3,而不是乘3;3x=963x÷3=96÷3x=32【点评】正确判定解方程的方法是否正确,并能运用等式的性质解方程,是本题考查知识点.五、解方程解方程2x﹣4×3=2015x﹣6x=270x﹣5.3+10=15.42(x﹣0.5)=4.6x÷0.4=12.5.【答案】(1)x=16;(2)x=30;(3)x=10.7;(4)x=2.8;(5)x=5.【解析】试题分析:(1)先化简方程,再依照等式的性质,方程两边同时加上1 2,再两边同时除以2求解;(2)先化简方程,再依照等式的性质,方程两边同时除以9求解;(3)依照等式的性质,方程两边同时减去10,再两边同时加上5.3求解;(4)依照等式的性质,方程两边同时除以2,再两边同时加上0.5求解;(5)依照等式的性质,方程两边同时乘以0.4求解.解:(1)2x﹣4×3=202x﹣12+12=20+122x=322x÷2=32÷2x=16;(2)15x﹣6x=2709x=2709x÷9=270÷9x=30;(3)x﹣5.3+10=15.4x﹣5.3+10﹣10=15.4﹣10x﹣5.3=5.4x﹣5.3+5.3=5.4+5.3x=10.7;(4)2(x﹣0.5)=4.62(x﹣0.5)÷2=4.6÷2x﹣0.5=2.3x﹣0.5+0.5=2.3+0.5x=2.8;(5)x÷0.4=12.5x÷0.4×0.4=12.5×0.4x=5.【点评】在解方程时应依照等式的性质,即等式两边同加上、同减去、同乘上或同除以某一个数(0除外),等式的两边仍相等,同时注意“=”上下要对齐.六、列方程求解列方程求解(1)x的8倍与x的5倍的和等于169,求x.(2)x的 4.6 倍是23,x 是多少?(3)x除以0.7 的商是9,x是多少?【答案】x=13;x=5;x=6.3;【解析】试题分析:(1)x的8倍是8x,x的5倍是5x,x的8倍与x的5倍的和等于等于169,依据题意可列方程:8x+5x=169,依据等式的性质求解即可;(2)依照题意,x的4.6倍是4.6x,x的4.6 倍是23,即4.6x=23,然后再依据等式的性质求解即可;(3)x除以0.7 的商是9,依据题意可列方程:x÷0.7=9,依据等式的性质求解即可.解:(1)8x+5x=16913x=16913x÷13=169÷13x=13;答:x是13.(2)4.6x=234.6x÷4.6=23÷4.6x=5;答:x是5.(3)x÷0.7=9x÷0.7×0.7=9×0.7x=6.3;答:x是6.3.【点评】列方程解决问题,先找出等量关系,然后列出方程进行解答.学校合唱队中有女队员58名,女队员的人数比男队员的2倍还多4名,学校合唱队有男队员多少名?(列方程解答)【答案】27名【解析】试题分析:设学校合唱队有男队员x名,依照等量关系:男队员的人数×2+4名=女队员的人数,列方程解答即可.解:设学校合唱队有男队员x名,2x+4=582x=54x=27答:学校合唱队有男队员27名.【点评】本题考查了列方程解应用题,关键是依照等量关系:男队员的人数×2+4名=女队员的人数,列方程.3个连续自然数的和是99,中间的数是X,你能列方程求X的值吗?其余两个数分别是几?【答案】X的值是33,其余两个数分别是32、34.【解析】试题分析:连续的3个自然数,中间的自然数是X,那么另外两个自然数分别是X﹣1和X+1,进而依照连续3个自然数的和是99,列出方程并求得方程的解.解:中间的自然数是X,另外两个自然数分别是X﹣1和X+1,由题意得X﹣1+X+X+1=993X=993X÷3=99÷3X=33.中间的自然数是33.33﹣1=3233+1=34答:能列方程求X的值,X的值是33,其余两个数分别是32、34.【点评】此题考查用字母表示数,先用含字母的式子表示出两外两个自然数,进而写出方程并求得方程得解.甲,乙两个小组要在6天合作加工1608个零件,甲组每天加工144个,乙组每天加工多少个?【答案】124个[来源:学§科§网]【解析】试题分析:第一依照工作量÷工作时刻=工作效率,求出甲、乙两个小组的工作效率和.然后减去甲组的工作效率即可.解:1608÷6﹣144=268﹣144=124(个);答:乙组每天加工124个零件.【点评】此题要紧考查工作时刻、工作效率、工作总量三者之间的数量关系,搞清每一步所求的问题与条件之间的关系,选择正确的数量关系解答.一个服装厂原先做一套衣服用2.2米布改进裁剪方法后,每套节约0.2米,原先做1500套衣服的布,现在可做多少套?【答案】1650套【解析】试题分析:先依据布的总长度=每套衣服用布长度×套数,求出布的总长度,再求显现在每套衣服用布长度,最后依照套数=总长度÷每套用布长度即可解答.解:(2.2×1500)÷(2.2﹣0.2)=3300÷2=1650(套)[来源:ZXXK]答:现在可做1650套.【点评】本题属于比较简单应用题,只要明确数量间的等量关系,再依照它们之间的关系,代入数据即可解答.一个梯形的面积72.9平方厘米,上底是10.6厘米,下底5.8厘米,高是多少厘米?(列方程解答)[来源:]【答案】8.89厘米【解析】试题分析:设梯形的高为h厘米,依据梯形的面积S=(a+b)×h÷2即可列方程求解即可.解:设梯形的高为h厘米,依题意有:(10.6+5.8)×h÷2=72.98.2h=72.9h≈8.89答:高约是8.89厘米.【点评】此题考查了梯形的面积公式的实际应用.李老师的商店买了3副等价的羽毛球拍,给售货员50员钱,找回3.2元,每副羽毛球拍的售价是多少元?【答案】15.6元.【解析】试题分析:先求出3副等价的羽毛球拍的价格:50﹣3.2=46.8元,再依照“总价÷数量=单价”即可得解.解:(50﹣3.2)÷3=46.8÷3=15.6(元)答:每副羽毛球拍的售价是15.6元.【点评】本题要紧考查关系式“总价÷数量=单价”的应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013---2014学年下学期五年级地方期末试卷
一、 填空 (3×20=60分)
1、1900年,沙俄在黑龙江边制造了( )惨案。
2、1931年9月18日发生了( )。
3、“黑色的金子”指的是( )。
4、1960年我国发现了( )油田。
5、“石油之子”是( )。
6、12世纪,( )建立了金朝,曾统治了北起( )南至( )的广大地区。
7、( )后期,( )来到黑龙江地区,强行在这里 建立据点。
1968年,清政府同沙俄政府在尼布楚签订了中俄( ),正式划定了两国的东北边界。
8、( )年,在黑龙江省发现了( )油田。
9、1956年我国科学家在新疆准噶尔盆地发现了( )油田。
10、( )是新中国的( )石油钻探工人。
11、在我国,女孩子在( )岁左右,男孩子在( )岁左右,就会进入人生的第二生长高峰期----------青春期。
14、在社会生活中,为了让我们的生活更方便、更安全、人们制定了各种各样的( ) 16、传染病会威胁我们的健康甚至( )。
二、判断 (2×10=20分) 1、石油与我们的生活息息相关。
( ) 2、“铁人精神”就是“大庆精神”。
( ) 3、夏季为痢疾流行季节。
( )
4、人不能没有倾诉,也不能没有聆听,因此人不能没有互慰方方面面( )
5、我们日常生活中,喝生水、吃生或半生的食品。
( )
6、饭前、便后不洗手。
( )
7、传染病不会威胁我们的健康和生命。
( ) 8、不要对着别人打喷嚏。
( )
9、我们要善于网上学习,不浏览不良信息.( ) 10、刘胡兰是抗日英雄。
( ) 三、简答题:(20分) 1、怎样才能文明安全的上网呢?
2、预防传染病,你知道哪些预防措施?(至少写4条)
装
订
线
(
装
订
线
内 不
要
答
题 )
姓 名
班 级。
