固体物理补充习题05
固体物理补充习题

固体物理补充习题(十四系用)1. 将半径为R 的刚性球分别排成简单立方(sc )、体心立方(bcc )和面心立方(fcc )三种结构,在这三种结构的间隙中分别填入半径为r p 、r b 和r f 的小刚球,试分别求出r p /R 、r b /R 和r f /R 的最大值。
提示:每一种晶体结构中都有多种不同的间隙位置,要比较不同间隙位置的填充情况。
2. 格常数为a 的简单二维密排晶格的基矢可以表为 1a =G a i2122a a =−+G a i j (1)求出其倒格子基矢1G b 和2G b , 证明倒格子仍为二维密排格子;(2)求出其倒格子原胞的面积Ωb 。
3. 由N 个原子(或离子)所组成的晶体的体积V 可以写为V =Nv = N βr 3,其中v 为平均一个原子(或离子)所占的体积,r 为最近邻原子(或离子)间的距离,β是依赖于晶体结构的常数,试求下列各种晶体结构的β值:(1) sc 结构 (2) fcc 结构 (3) bcc 结构(4) 金刚石结构 (5) NaCl 结构。
4. 设两原子间的相互作用能可表示为()m nu r r r αβ=−+ 其中,第一项为吸引能;第二项为排斥能;α、β、n 和m 均为大于零的常数。
证明,要使这个两原子系统处于稳定平衡状态,必须满足n > m 。
5. 设晶体的总相互作用能可表示为()m n A B U r r r=−+ 其中,A 、B 、m 和n 均为大于零的常数,r 为最近邻原子间的距离。
根据平衡条件求:(1)平衡时,晶体中最近邻原子的间距r 0和晶体的相互作用能U 0;(2)设晶体的体积可表为V =N γr 3,其中N 为晶体的原子总数,γ为体积因子。
若平衡时 晶体的体积为V 0,证明:平衡时晶体的体积压缩模量K 为 009mn U K V = 。
6. 设有一由2N 个离子组成的离子晶体,若只计入作近邻离子间的排斥作用,设两个离子间的势能具有如下的形式: 式中,λ和ρ为参数;R 为最近邻离子间距。
《固体物理学》基础知识训练题及其参考答案

《固体物理》基础知识训练题及其参考答案说明:本内容是以黄昆原著、韩汝琦改编的《固体物理学》为蓝本,重点训练读者在固体物理方面的基础知识,具体以19次作业的形式展开训练。
第一章作业1:1.固体物理的研究对象有那些?答:(1)固体的结构;(2)组成固体的粒子之间的相互作用与运动规律;(3)固体的性能与用途。
2.晶体和非晶体原子排列各有什么特点?答:晶体中原子排列是周期性的,即晶体中的原子排列具有长程有序性。
非晶体中原子排列没有严格的周期性,即非晶体中的原子排列具有短程有序而长程无序的特性。
3.试说明体心立方晶格,面心立方晶格,六角密排晶格的原子排列各有何特点?试画图说明。
有那些单质晶体分别属于以上三类。
答:体心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体的体心位置还有一个原子。
常见的体心立方晶体有:Li,Na,K,Rb,Cs,Fe等。
面心立方晶格:除了在立方体的每个棱角位置上有1个原子以外,在该立方体每个表面的中心还都有1个原子。
常见的面心立方晶体有:Cu, Ag, Au, Al等。
六角密排晶格:以ABAB形式排列,第一层原子单元是在正六边形的每个角上分布1个原子,且在该正六边形的中心还有1个原子;第二层原子单元是由3个原子组成正三边形的角原子,且其中心在第一层原子平面上的投影位置在对应原子集合的最低凹陷处。
常见的六角密排晶体有:Be,Mg,Zn,Cd等。
4.试说明, NaCl,金刚石,CsCl, ZnS晶格的粒子排列规律。
答:NaCl:先将错误!未找到引用源。
两套相同的面心立方晶格,并让它们重合,然后,将一套晶格沿另一套晶格的棱边滑行1/2个棱长,就组成Nacl晶格;金刚石:先将碳原子组成两套相同的面心立方体,并让它们重合,然后将一套晶格沿另一套晶格的空角对角线滑行1/4个对角线的长度,就组成金刚石晶格;Cscl::先将错误!未找到引用源。
组成两套相同的简单立方,并让它们重合,然后将一套晶格沿另一套晶格的体对角线滑行1/2个体对角线的长度,就组成Cscl晶格。
(整理)固体物理课后习题与答案

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。
固体物理+胡安版+部分习题答案

[
]
p 是 (k + l ), (l + h ), (h + k ) 的最大公约数。 的最大公约数。
可得到元胞坐标系下的晶面指数: 已知晶面密勒指数 ( hlk ),可得到元胞坐标系下的晶面指数:
( h 1 h 2 h 3 ) == 1 p
{(k
+ l )(l + h
)(h
+ k
)}
补充习题2 补充习题2
A=0
出现消光 4、hkl 中有两个指数分量为奇数,其余为偶数时, 中有两个指数分量为奇数,其余为偶数时,
A=0
出现消光
补充习题1 补充习题1
a 晶胞基矢: 晶胞基矢: = ai , b = aj , c = ak
a =b =c
与晶胞坐标系对应的倒格子基矢: 与晶胞坐标系对应的倒格子基矢:
2π 2π 2π i ,b∗ = j,c∗ = k a a a a a1 = ( j + k ) 2 a a 2 = (i + k ) a1 = a2 = a3 元胞基矢 2 a a3 = (i + j ) 2 a∗ =
2 2
∗
⋅c∗ )
(a )
∗ 2
4 2π , b∗ = 3 a
2
( )
2
( 2π ) 4 2π ∗ 2 = , (c ) = 3 a c2
(a
(
∗
⋅b∗
)
)
2 2π = 3 a
2
b∗ ⋅c∗ = 0
a∗ ⋅ c ∗ ) = 0 (
4 2π 2 4 2π 2 2π 2 4 2π = h + k + l + hk 3 a 3 a c 3 a
《固体物理学》房晓勇主编教材-习题解答参考pdf05第五章_金属电子论基础

8.45
×1022
⎤1/ ⎦
3
=
5.2 限制在边长为 L 的正方形的 N 个电子,单电子能量为
( ) ( ) E kx, ky
=
2
k
2 x
+
k
2 y
2m
(1)求能量 E 到 E+dE 之间的状态数; (2) 求绝对零度时的费米能量。 解:(参考中南大学 4.6,王矜奉 6.2.2,林鸿生 1.1.83,徐至中 5-2) (1)如《固体物理学》图 5-1 所示,每个状态点占据的面积为
G′(E) = 2 dZ ⋅ dk = 2 L2 k • dk dE 2π
m = L2m 2k π 2
得二维金属晶体中自由电子的状态密度为:
…………………………(4)
g(E)
=
G′(E) S
=
1 L2
L2m π2
=
m π2
………………………(5)
(2)根据《固体物理学》式 金属的电子浓度
3
∫ ∫ n =
2π i 2π = (2π )2
Lx Ly
L2
所以每个单位
k
空间面积中应含的状态数为
L2
(2π )2
,
d k 面积元中应含有的状态数为
dZ
=
L2
(2π )2
d
k
而单电子能量为
( ) ( ) E kx, ky
=
2
k
2 x
+
k
2 y
2m
= 2k2 2m
E+dE E
可见在 k 空间中等能曲线为一圆,如图所示,在 E——E+dE 两个等能圆之间的
2
固体物理补充习题05

固体物理补充习题(十四系用)1. 将半径为R 的刚性球分别排成简单立方(sc )、体心立方(bcc )和面心立方(fcc )三种结构,在这三种结构的间隙中分别填入半径为r p 、r b 和r f 的小刚球,试分别求出r p /R 、r b /R 和r f /R 的最大值。
提示:每一种晶体结构中都有多种不同的间隙位置,可填充小刚球的大小也各不相同。
2. 格常数为a 的简单二维密排晶格的基矢可以表为a 1 = a ia 2 = -12a i + 32a j (1)求出其倒格子基矢b 1 和b 2 , 证明倒格子仍为二维密排格子;(2)求出其倒格子原胞的面积Ωb 。
3. 由N 个原子(或离子)所组成的晶体的体积V 可以写为V =Nv = N βr 3,其中v 为平均一个原子(或离子)所占的体积,r 为最近邻原子(或离子)间的距离,β是依赖于晶体结构的常数,试求下列各种晶体结构的β值:(1) sc 结构 (2) fcc 结构 (3) bcc 结构(4) 金刚石结构 (5) NaCl 结构。
4. 设两原子间的相互作用能可表示为()m nu r r r αβ=-+ 其中,第一项为吸引能;第二项为排斥能;α、β、n 和m 均为大于零的常数。
证明,要使这个两原子系统处于稳定平衡状态,必须满足n > m 。
5. 设晶体的总相互作用能可表示为()m n A B U r r r=-+ 其中,A 、B 、m 和n 均为大于零的常数,r 为最近邻原子间的距离。
根据平衡条件求:(1)平衡时,晶体中最近邻原子的间距r 0和晶体的相互作用能U 0;(2)设晶体的体积可表为V =N γr 3,其中N 为晶体的原子总数,γ为体积因子。
若平衡时 晶体的体积为V 0,证明:平衡时晶体的体积压缩模量K 为 009mn U K V = 。
6. 设有一由2N 个离子组成的离子晶体,若只计入作近邻离子间的排斥作用,设两个离子间的势能具有如下的形式: 式中,λ和ρ为参数;R 为最近邻离子间距。
固体物理习题解答

《固体物理学》习题解答( 仅供参考)参加编辑学生柯宏伟(第一章),李琴(第二章),王雯(第三章),陈志心(第四章),朱燕(第五章),肖骁(第六章),秦丽丽(第七章)指导教师黄新堂华中师范大学物理科学与技术学院2003级2006年6月第一章晶体结构1. 氯化钠与金刚石型结构是复式格子还是布拉维格子,各自的基元为何?写出这两种结构的原胞与晶胞基矢,设晶格常数为a。
解:氯化钠与金刚石型结构都是复式格子。
氯化钠的基元为一个Na+和一个Cl-组成的正负离子对。
金刚石的基元是一个面心立方上的C原子和一个体对角线上的C原子组成的C原子对。
由于NaCl和金刚石都由面心立方结构套构而成,所以,其元胞基矢都为:123()2()2()2a a a ⎧=+⎪⎪⎪=+⎨⎪⎪=+⎪⎩a j k a k i a i j 相应的晶胞基矢都为:,,.a a a =⎧⎪=⎨⎪=⎩a ib jc k2. 六角密集结构可取四个原胞基矢123,,a a a 与4a ,如图所示。
试写出13O A A '、1331A A B B 、2255A B B A 、123456A A A A A A 这四个晶面所属晶面族的晶面指数()h k l m 。
解:(1).对于13O A A '面,其在四个原胞基矢上的截矩分别为:1,1,12-,1。
所以,其晶面指数为()1121。
(2).对于1331A A B B 面,其在四个原胞基矢上的截矩分别为:1,1,12-,∞。
所以,其晶面指数为()1120。
(3).对于2255A B B A 面,其在四个原胞基矢上的截矩分别为:1,1-,∞,∞。
所以,其晶面指数为()1100。
(4).对于123456A A A A A A 面,其在四个原胞基矢上的截矩分别为:∞,∞,∞,1。
所以,其晶面指数为()0001。
3. 如将等体积的硬球堆成下列结构,求证球体可能占据的最大体积与总体积的比为: 简立方:6π;体心立方:8;面心立方:6;六角密集:6;金刚石:16。
固体物理习题及答案
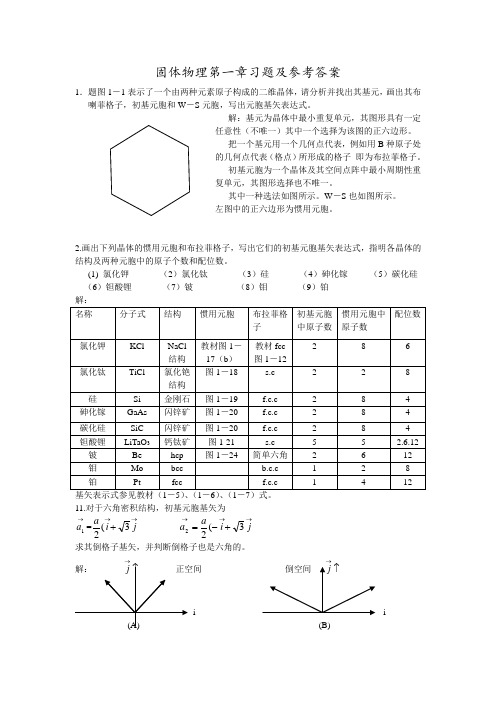
固体物理第一章习题及参考答案1.题图1-1表示了一个由两种元素原子构成的二维晶体,请分析并找出其基元,画出其布喇菲格子,初基元胞和W -S 元胞,写出元胞基矢表达式。
解:基元为晶体中最小重复单元,其图形具有一定任意性(不唯一)其中一个选择为该图的正六边形。
把一个基元用一个几何点代表,例如用B 种原子处的几何点代表(格点)所形成的格子 即为布拉菲格子。
初基元胞为一个晶体及其空间点阵中最小周期性重复单元,其图形选择也不唯一。
其中一种选法如图所示。
W -S 也如图所示。
左图中的正六边形为惯用元胞。
2.画出下列晶体的惯用元胞和布拉菲格子,写出它们的初基元胞基矢表达式,指明各晶体的结构及两种元胞中的原子个数和配位数。
(1) 氯化钾 (2)氯化钛 (3)硅 (4)砷化镓 (5)碳化硅 (6)钽酸锂 (7)铍 (8)钼 (9)铂 解:基矢表示式参见教材(1-5)、(1-6)、(1-7)式。
11.对于六角密积结构,初基元胞基矢为→1a =→→+j i a 3(2 →→→+-=j i a a 3(22求其倒格子基矢,并判断倒格子也是六角的。
倒空间 ↑→ji i (B)由倒格基失的定义,可计算得Ω⨯=→→→3212a a b π=a π2)31(→→+j i →→→→→+-=Ω⨯=j i a a a b 31(22132ππ→→→→=Ω⨯=k ca ab ππ22213正空间二维元胞(初基)如图(A )所示,倒空间初基元胞如图(B )所示(1)由→→21b b 、组成的倒初基元胞构成倒空间点阵,具有C 6操作对称性,而C 6对称性是六角晶系的特征。
(2)由→→21a a 、构成的二维正初基元胞,与由→→21b b 、构成的倒初基元胞为相似平行四边形,故正空间为六角结构,倒空间也必为六角结构。
12.用倒格矢的性质证明,立方晶格的(hcl )晶向与晶面垂直。
证:由倒格矢的性质,倒格矢→→→→++=321b l b k b h G hkl 垂直于晶面(h 、k 、l )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
固体物理补充习题(十四系用)1. 将半径为R 的刚性球分别排成简单立方(sc )、体心立方(bcc )和面心立方(fcc )三种结构,在这三种结构的间隙中分别填入半径为r p 、r b 和r f 的小刚球,试分别求出r p /R 、r b /R 和r f /R 的最大值。
提示:每一种晶体结构中都有多种不同的间隙位置,可填充小刚球的大小也各不相同。
2. 格常数为a 的简单二维密排晶格的基矢可以表为a 1 = a ia 2 = -12a i +32a j(1)求出其倒格子基矢b 1 和b 2 , 证明倒格子仍为二维密排格子; (2)求出其倒格子原胞的面积Ωb 。
3. 由N 个原子(或离子)所组成的晶体的体积V 可以写为V =Nv = N βr 3,其中v 为平均一个原子(或离子)所占的体积,r 为最近邻原子(或离子)间的距离,β是依赖于晶体结构的常数,试求下列各种晶体结构的β值:(1) sc 结构 (2) fcc 结构 (3) bcc 结构 (4) 金刚石结构 (5) NaCl 结构。
4.设两原子间的相互作用能可表示为()mnu r rrαβ=-+其中,第一项为吸引能;第二项为排斥能;α、β、n 和m 均为大于零的常数。
证明,要使这个两原子系统处于稳定平衡状态,必须满足n > m 。
5. 设晶体的总相互作用能可表示为()mnA B U r rr=-+其中,A 、B 、m 和n 均为大于零的常数,r 为最近邻原子间的距离。
根据平衡条件求: (1)平衡时,晶体中最近邻原子的间距r 0和晶体的相互作用能U 0;(2)设晶体的体积可表为V =N γr 3,其中N 为晶体的原子总数,γ为体积因子。
若平衡时 晶体的体积为V 0,证明:平衡时晶体的体积压缩模量K 为009m n U K V =。
6. 设有一由2N 个离子组成的离子晶体,若只计入作近邻离子间的排斥作用,设两个离子间的势能具有如下的形式:式中,λ和ρ为参数;R 为最近邻离子间距。
若晶体的Madelung 常数为α,最近邻的离子数为Z ,求平衡时晶体总相互作用势能的表达式。
7. 由N 个原子组成的一维单原子晶体,格波方程为()cos n x A t naq ω=-,若其端点固定,(1)证明所形成的格波具有驻波性质,格波方程可表为()sin sin n x A naq t ω'=;(最近邻间) (最近邻以外)±er2λρeeRR --/2()u r =(2)利用边界条件x N = 0,求q 的分布密度和波数的总数;(3)将所得结果与周期性边界条件所得的结果进行比较并讨论之。
8. 由2N 个(设N 很大)带电荷±q 的正负离子相间排列的一维晶体链,最近邻之间的排斥能为B/R n ,(1)试证在平衡时,晶体链的互作用能为()20002ln 2114N q U R R n πε⎛⎫=-- ⎪⎝⎭;(2)若晶体被压缩,使()001R R δ→-,设δ 1,证明在晶体被压缩过程中,外力对 每一个离子所做的功的主项平均为212c δ,其中,()2001ln 24n q c R πε-=。
9. 由N 个原子组成的一维单原子链,原子间的相互作用能可表为()1264u r x x σσε⎡⎤⎛⎫⎛⎫=-⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦,其中x 为原子间距。
试求(1)平衡时的原子间距x 0与相互作用能u 0;(2)若只考虑近邻原子间的相互作用,求原子链的弹性模量K 。
10. 若一维单原子链的格波方程取为()n x Acon t naq ω=-,证明:(1)格波的总能量为()22111E m 22n n n n n dx x x dt +⎛⎫=+β- ⎪⎝⎭∑∑,这里m 为原子质量,β为恢复力系数,求和指标n 遍及所有原子; (2)每个原子的时间平均总能量22112E m Aω=。
11. 质量分别为M 和m (设M > m )的两种原子以a 和13a 相间排成如图所示的一维晶体链,若只考虑近邻原子间的弹性相互作用,设相邻原子间的恢复力系数同为β,(1)写出每种原子的动力学方程式; (2)写出格波方程式;(3)导出色散关系式。
12. 在坐标纸上画出二维正方晶格的前五个布里渊区图形。
13. 由N 个原子组成的一维(链长为L)、二维(面积为S)和三维(体积为V)简单晶格晶体,设格波的传播速度为c ,应用Debye 模型分别计算: (1)晶格振动的模式密度g(ω); (2)截止频率ωm ; (3)Debye 温度ΘD ; (4)晶格热容C V ;(5)晶体的零点振动能E 0 (用N 和ωm 表示)。
14. 由N 个质量为m 的原子组成的一维单原子链,近邻原子间距为a ,相互作用的力常数为β,用格波模型求:(1)晶格振动的模式密度g(ω); (2)晶体的零点能E 0;a 1M μn-1 νn-1 μnνn μn+1 νn+1(3)晶格的热容量C V ; 15. 在高温下(k B T ωm ),试用Debye 模型求三维简单晶格频率从0到ωm 中总的平均声子数 (已知晶体体积为V ,格波的传播速度为c )。
16. 在高温下(T ΘD ),根据Debye 理论证明由N 个原子组成的d 维晶体的晶格热容为(1)一维: C V = Nk B 11362-⎛⎝⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥ΘD T ; (2)二维: C V = 2Nk B 11242-⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥ΘD T ; (3)三维: C V = 3Nk B 11202-⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥ΘD T 。
17. Grüneisen 常数(1)证明频率为ωi 的声子模式的自由能为ln 22i B B k T sh k T ω⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦ ;(2)以∆表示体积相对改变,那么单位体积晶体的自由能可以表为()21E ,ln 222i B i B TB k T sh k T ω⎡⎤⎛⎫∆=∆+⎢⎥ ⎪⎝⎭⎣⎦∑其中B 为体积弹性模量。
假设ωi (q)与体积的依赖关系为δω/ω = - γ∆,其中γ为Grüneisen常数。
如果将γ看作与模式无关,证明当122i i iB B cth k T ωγω⎛⎫∆= ⎪⎝⎭∑时,F 相对于∆为极小。
18. 已知三维晶体在q ≈ 0附近一支光学波的色散关系为()()2220x x y y z z q A q A q A q ωω=-++其中A x 、A y 、A z 为大于零的常数,试求这支光学波的模式密度g(ω)的表达式。
19. 在Debye 近似下证明T =0时,三维晶体中一个原子的均方位移为222338DR cωπρ=其中ρ为晶体的质量密度,c 为声速,ωD 为Debye 截止频率。
提示:一个格波的平均能量可参考补充题10(2)及T =0时一个格波的能量()12E ωω= 。
20. 对于Cu ,形成一个Schottky 空位所需的能量为1.2 eV ,形成一个间隙原子的能量为4 eV 。
在接近熔点时(1300 K),试估算晶体中空位的浓度和间隙原子的浓度,并比较这两种浓度的数量级差。
21. 若晶体中原子的总数为N ,间隙位置的总数为N’,形成一个Frenkel 缺陷所需的能量为u f 。
在一定的温度下,平衡时晶体中有n f 个Frenkel 缺陷,试由∂∂F n f T⎛⎝⎫⎭⎪= 0 导出平衡时Frenkel 缺陷数目的表达式,设n f N ,N’ 。
22. 已知1100︒C 时,碳在γ-Fe 中的扩散系数D =6.7×10 –7 cm 2/s 。
若保持表面处碳的浓度不变,要得到d = 1 mm 厚的渗碳层(碳的浓度为表面处的一半),问在此温度下需要扩散多长时间?(erf(0.500) = 0.52050,erf(0.477) = 0.50005)23. 设有某种简单立方晶体,熔点为800︒C ,由熔点结晶后,晶粒大小为L =1 μm 的立方体,晶格常数a = 4⨯10 –10 m 。
求结晶后每个晶粒中的空位数,已知空位的形成能为1 eV 。
若晶体在高温形成的空位,降到室温后聚集到一个晶面上,形成一个空位园片,以致引起晶体内部的崩塌,结果将转变为何种形式的晶格缺陷?求出此时每个晶粒中的位错密度。
24. 证明在T =0 K 时,金属中自由电子气的状态方程为 PV 5/3= const . , 这里P 为电子气的压强,V 为金属的体积。
已知Cu 的电子密度n = 8.45×1022 cm –3,计算Cu 中电子气的压强为多少个大气压。
(提示:利用热力学第一定律) 25. 证明T =0时自由电子气的体积弹性模量109U K V=,这里U 为自由电子的总能量,V 为金属的体积。
若已知钾的电子密度为1.4×1022 cm –3,求钾的体积弹性模量。
26. 在长为L 的一维金属链中共有N 个自由电子,在T =0 K 时,求:(1)电子的能态密度N(E); (2)晶体链的费米能级E F 0;(3)一个电子的平均能量E 。
27. 假设每个铜原子贡献一个自由电子,试计算室温(300 K )下电子气体的热容量,并将所得结果与铜的总热容量24 J/mol ·K 的数值进行比较。
已知铜的原子量为63.5,密度为8.9 g/cm 3。
28. 证明电子密度为n 的二维自由电子气的化学势可由下式给出()μπTk T n m k T B B =⎛⎝ ⎫⎭⎪-⎡⎣⎢⎢⎤⎦⎥⎥l n exp 21 ,其中m 为电子质量。
29. 在低温下,金属钾摩尔热容量的实验结果可表为C = ( 2.08T+2.57T 3 ) ×10 –3 J/mol.K ,试求:(1)钾的Debye 温度ΘD ; (2)Fermi 温度T F ;(3)在Fermi 面上一摩尔金属的电子能态密度N(E F 0)。
30. 已知Cu 的电子密度为n = 8.45×1022 cm –3,Debye 温度ΘD = 315 K 。
(1)求当T 为何值时,电子热容等于晶格热容?(2)计算T =300 K 时一摩尔Cu 的电子顺磁磁化率χ 。
31. 利用Sommerfeld 展开式证明,在k B T E F 0时一个自由电子的平均动能近似为⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+=22125153FFT T E E π 。
32. 已知Na 为bcc 结构,晶格常数为a = 4.28×10 –10 m ,(1)用自由电子模型计算其Hall 系数R H ; (2)设有一长方形Na 晶片,长为 ,宽为5 mm ,厚为1 mm 。
若沿晶片长边方向通以100 mA 的电流,并将其置于0.1 T 的磁场中(磁场方向垂直于晶片),求Hall 电压V H 的大小。
