07-7第三十九讲渐开线直齿圆柱齿轮的啮合传动
渐开线直齿圆柱齿轮的啮合传动

∙正确啮合的条件渐开线齿轮正确啮合的条件是:两轮的模数和压力角应分别相等。
∙外啮合齿轮传动的中心距1 、确定中心距时应满足的两点要求:i) 保证两轮的齿侧间隙为零。
为了避免轮齿间的冲击,齿侧间隙一般都很小,通常是由制造公差来保证。
ii) 保证两轮的顶隙为标准值。
2 、标准中心距如图7-5-1所示,当顶隙为标准值时,两轮的中心距为称此中心距为标准中心距,即两轮的标准中心距a 等于两轮分度圆半径之和。
3 、安装中心距安装中心距为一对齿轮安装后啮合时的实际中心距,其值等于两啮合齿轮节圆半径之和,a'=r 1 '+r 2 ' 。
4 、标准安装:把标准齿轮按标准中心距进行的安装称为标准安装,此时两齿轮的分度圆相切。
5 、标准安装的特点i) 按标准中心距安装时,两轮的节圆与各自的分度圆重合,顶隙为标准值。
其传动比为图7-5-1ii) 在按标准中心距安装时,能满足无齿侧间隙的要求。
6 、分度圆和节圆的区别节圆:齿轮啮合传动时在节点处相切的一对圆。
对于一个单一的齿轮来说是不存在节圆的。
而且两齿轮节圆的大小显然是随其中心距的变化而变化的。
分度圆:齿轮的分度圆是一大小完全确定的圆,不论这个齿轮是否与另一齿轮啮合,也不论两轮的中心距如何变化,每个齿轮都有一个唯一的大小完全确定的分度圆。
∙啮合角齿轮传动的啮合角:指两轮传动时其节点P 的速度方向与啮合线之间所夹的锐角。
通常用表示。
啮合角就等于节圆压力角。
对于标准中心距安装时,由于节圆与分度圆重合,故啮合角也等于分度圆压力角。
图7-5-2 图7-5-3∙非标准安装的情况:即两轮的实际中心距不等于标准中心距。
这时节圆与分度圆不重合,节圆半径也不等于分度圆半径,其啮合角也不等于分度圆的压力角,如图7-5-2。
此时标准中心距为而实际中心距为于是可推得中心距与啮合角的关系为∙齿轮与齿条啮合传动(如图7-5-3)标准安装:指齿轮分度圆与齿条分度线相切。
此时齿轮的节圆与分度圆重合,齿条的节线与分度线重合。
渐开线直齿圆柱齿轮啮合传动设计

1 设计应满足的条件1. 正确啮合条件一对渐开线齿廓能保证定传动比传动,但这并不表明任意两个渐开线齿轮都能搭配起来正确啮合传动。
为了正确啮合,还必须满足一定的条件。
图示一对渐开线齿轮同时有两对齿参加啮合,两轮齿工作侧齿廓的啮合点分别为K和K'。
为了保证定传动比,两啮合点K和K'必须同时落在啮合线N1N2上;否则,将出现卡死或冲击的现象。
这一条件可以表述为。
和分别为齿轮1和齿轮2相邻同侧齿廓沿公法线上的距离,称为法向齿距,用pn1、pn2表示。
因此,一对齿轮实现定传动比传的正确啮合件为两轮的法向齿距相等。
又由渐开线性质可知,齿轮法向齿距与基圆齿距相等,则该条件又可表述为两轮的基圆齿距相等,即将和代入上式得式中m1、m2和α1、α2分别为两轮的模数和压力角。
由于齿轮的模数和压力角都已标准化,要使上式成立,可以取来保证两轮的法向齿距相等。
因此,渐开线直齿圆柱齿轮的正确啮合条件最终表述为:两轮的模数和压力角分别相等。
2. 连续传动的条件(1)啮合传动过程齿轮传动是通过其轮齿交替啮合而实现的。
图所示为一对轮齿的啮合过程。
主动轮1顺时针方向转动,推动从动轮2作逆时针方向转动。
一对轮齿的开始啮合点是从动轮齿顶圆η2与啮合线N1N2的交点B2,这时主动轮的齿根与从动轮的齿顶接触,两轮齿进入啮合。
随着啮合传动的进行,两齿廓的啮合点将沿着啮合线向左下方移动。
一直到主动轮的齿顶圆η1与啮合线的交点B1,主动轮的齿顶与从动轮的齿根即将脱离接触,两轮齿结束啮合,B1点为终止啮合点。
线段为啮合点的实际轨迹,称为实际啮合线段。
当两轮齿顶圆加大时,点B1、B2分别趋于点N1、N2,实际啮合线段将加长。
但因基圆内无渐开线,故点B1、B2不会超过点N1、N2,点N1、N2称为极限啮合点。
线段是理论上最长的实际啮合线段,称为理论啮合线段。
2)连续传动条件连续传动条件为保证齿轮定传动比传动的连续性,仅具备两轮的基圆齿距相等的条件是不够的,还必须满足≥Pb。
渐开线直齿圆柱齿轮正确啮合的条件

渐开线直齿圆柱齿轮正确啮合的条件篇一:哎呀呀,你们知道渐开线直齿圆柱齿轮正确啮合的条件吗?这可太有意思啦!就好像我们玩拼图,得把每一块都放对位置才能拼成完整的图案,渐开线直齿圆柱齿轮要正确啮合,也有它的“规则”呢!先来说说第一个条件,那就是两齿轮的模数必须相等。
啥是模数?简单说,模数就像是齿轮的“标准尺码”。
如果一个齿轮的模数大,另一个齿轮的模数小,那不就像一只大脚穿小鞋,或者一只小脚穿大鞋,怎么能走得顺呢?再瞧瞧第二个条件,两齿轮的压力角也要相等。
压力角就像是齿轮工作时的“用力方向”。
要是两个齿轮的压力角不一样,一个往东用力,一个往西用力,那还不得乱套啦?我们可以想象一下,齿轮们就像一群小伙伴在合作完成一项大任务。
如果它们不遵守这些条件,就好比小伙伴们各有各的想法,谁也不听谁的,那能把事情做好吗?肯定不能呀!有一次,我在工厂里看到师傅们在修理机器,就是因为齿轮没正确啮合,机器发出“嘎吱嘎吱”的怪声,差点就出大问题啦!这就告诉我们,渐开线直齿圆柱齿轮正确啮合真的超级重要!所以说呀,渐开线直齿圆柱齿轮正确啮合的条件,咱们可得牢牢记住,不然机器就会闹脾气,工作就会出乱子!你们说是不是这个理儿?篇二:哎呀,说起渐开线直齿圆柱齿轮正确啮合的条件,这可真是个超级有趣的知识呢!你们知道吗?就好像两个好朋友要一起玩耍,得有一些特定的条件才行。
渐开线直齿圆柱齿轮也是这样的呀!想象一下,两个齿轮就像两个舞者,要在舞台上完美配合,跳出优美的舞蹈。
首先,它们的模数得一样才行!模数就像是它们的脚步大小,如果一个齿轮迈大步,一个齿轮迈小步,那不是乱套啦?这不就像跑步比赛,大家步子大小不一样,怎么能一起跑整齐呢?还有呢,压力角也得相同哟!压力角就好像是它们跳舞的节奏,如果节奏都不一样,一个快一个慢,那能跳得好吗?咱再想想,要是齿轮的齿数不合适,那也不行呀!这就好比玩拼图,块数不对,怎么能拼得完整漂亮呢?“哎呀,这渐开线直齿圆柱齿轮正确啮合的条件也太重要了吧!要是不符合条件,那机器还不得乱套啦?”总之呢,模数相同、压力角相同,齿数匹配,这三个条件就像是三把神奇的钥匙,只有同时拥有它们,渐开线直齿圆柱齿轮才能完美地啮合在一起,为我们的各种机器正常运转发挥巨大的作用!我的观点就是:渐开线直齿圆柱齿轮正确啮合的条件是非常关键的,必须严格满足这些条件,才能保证机器的高效稳定运行!篇三:哇塞!今天老师给我们讲了渐开线直齿圆柱齿轮正确啮合的条件,这可太有意思啦!一开始,我看到那些齿轮的图片,心里还在犯嘀咕:这小小的齿轮能有啥大讲究?结果一听课,才发现这里面的学问可大了去了!老师说,渐开线直齿圆柱齿轮要正确啮合,就像两个人手拉手跳舞,得步伐一致才行。
机械原理(2015春)渐开线直齿圆柱齿轮的啮合传动下
ea
=
B1B2 pb
=
PB1 + PB2
pm cosa
PB1 = N1B1 - PN1 = rb1 tanaa1 - rb1 tana '
=
mz1 2
cosa
(tan a
a1
-
tan a
'
)
PB2
=
N2B2
-
PN2
=
rb2
tanaa2
-
rb2
tana '
=
mz2 2
cosa(tanaa2
渐开线直齿圆柱齿轮的啮合传动—连续传动条件
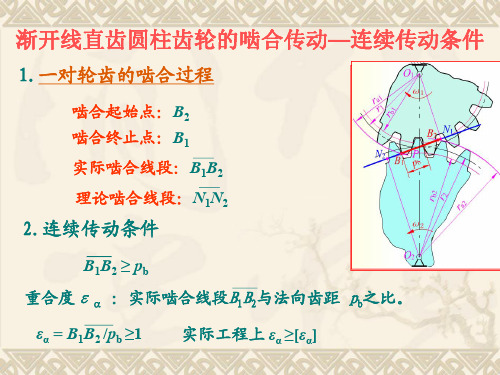
1.一对轮齿的啮合过程
啮合起始点:B2 啮合终止点:B1 实际啮合线段:B1B2 理论啮合线段:N1N2
2.连续传动条件
B1B2 ≥ pb
重合度εα :实际啮合线段B1B2与法向齿距 pb之比。
εα = B1B2 /pb ≥1
实际工程上 εα ≥[εα]
3.重合度的计算及影响因素
渐开线直齿圆柱齿轮的啮合传动—连续传动条件
1.一对轮齿的啮合过程 2.连续传动条件 3.#39; )
ea
=
z1(tgaa1 - tga ') + z2 (tgaa2 2p
- tga ')
εα与模数无关,随着齿数的增多而加大。
2)重合度的物理意义
重合度的大小表明了同时参与啮合的 轮齿对数。 CD段为单齿啮合区,B1D和B2C为 双齿啮合区。 如εα=1.4,双齿啮合区的长度为0.8pb, 单齿啮合区的长度为0.6pb。
渐开线直齿圆柱齿轮

渐开线直齿圆柱齿轮
渐开线直齿圆柱齿轮是渐开线齿轮中,一种非常常用的齿轮形式,其形状同时又类似
于普通圆柱齿轮。
它主要由一组正交配合的、渐开线形状的圆柱齿条组成,各齿分布在整
个节圆上,均匀分布,形成左右两侧分位一部分齿条,称为节圆、棱圆或节圆棱圆。
渐开线直齿圆柱齿轮主要应用于静恒速轴系中,它能满足减不平行旋转运动的柔性传
动要求,也就是使啮合齿轮的动轴同比例对准,旋转角度差不及动轴方向的要求,能提供
良好的动力传递性能,并保持良好的精度。
此外,渐开线直齿圆柱齿轮的几何结构也十分优美,在它的整体齿廓上,有均匀的齿
条划分,由于它的简单结构,可以使用自动检测机检测,以及配合优秀的服饰加工方法来
得到高精度的制造件。
渐开线直齿圆柱齿轮在传动机械系统中的应用也非常的广泛,如行星齿轮减速器、分
度盘、旋转机构等。
前进器中使用了直角齿圆柱齿轮,两个小轮的螺旋槽齿形,可以极大
地提升传动效率。
另外,渐开线直齿圆柱齿轮基于其制造时所采用的对模分度特性,制造过程中要求大
量的精度,因此,要依据传动技术要求,进行合理优化设计。
而且,为了满足应用要求,
获得更好的传动效率,还要考虑齿轮改性处理,以及使用优质的材料来改善齿轮的耐磨性。
自动控制系统中,渐开线直齿圆柱齿轮也是一种很常用的传动件,机械传动整体性能
要求高的应用比较多,比如机床送料系统、合页压力机液压驱动系统等。
此外,除了传动
件以外,在数控设备中,其也被称为型轮,用于准确的位置识别,为其它部件作有效的同
步和调节。
第三十九讲渐开线直齿圆柱齿轮的啮合传动
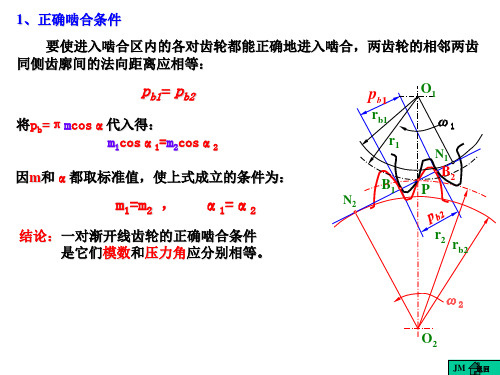
在主动轮顶圆与N1N2 线交点处B1脱离啮合。
B1B2 -实际啮合线
NN22
N1N2 :理论上可能的最长啮合线段 ——理论啮合线段
N1、N 2 ——啮合极限点
阴影线部分——齿廓的实际工作段。
O1 ω1 ra1
B2 NN11 P B1
ra2 rb2
ω2
O2
JM 返回
4、连续传动条件 为保证连续传动,要求: 实际啮合线段B1B2≥pb (齿轮的法向齿距),
r1’ = r1 α’=α
节线与分度线不重合
ra1
r1
rf1
O1
ω1
1
N1
B2 N2 B1P v2
α’=α
2
ra1
r1
rf1
O1
ω1
1
B2 N1 α’=α
N2
P
B1
v2
2
JM 返回
3、一对轮齿的啮合过程
轮齿在从动轮顶圆与N1N2 线交点B2处进入啮合,
主动轮齿根推动从动轮齿顶。
rb1
随着传动的进行,啮合点沿N1N2 线移动。
∴εα =[z1(tgαa1-tgα’) + z2(tgαa2-tgα’)]/2π
O1
ra1 B1
α’ rb1
αa1
P B2N1
N2 ra2
rb2 αa2
α’
O2
JM 返回
②齿轮齿条传动:
εα= B1B2/pb =(PB1+P B2)/πmcosα PB1 =z1mcosα(tgαa1-tgα’)/2 PB2=h*am/sinα
1、正确啮合条件
要使进入啮合区内的各对齿轮都能正确地进入啮合,两齿轮的相邻两齿 同侧齿廓间的法向距离应相等:
#标准渐开线齿轮直齿圆柱齿轮啮合传动

4.3 标准渐开线齿轮直齿圆柱齿轮啮合传动一、啮合过程和正确啮合条件图1 图2图中B2点是从动轮2齿顶圆与啮合线N1N2的合传动的进行,两齿廓的啮合点沿着啮合线移交点B1时,两轮齿即将脱离接触,B1点为轮从一对轮齿的啮合过程来看,啮合点实际走,称为实际啮合线。
当两轮齿顶圆加大时,点B2和B1将分别趋因基圆内无渐开线,所以实际啮合线不会超过啮合线。
从动画中可以看出,在两轮轮齿的啮合过程中,并非全部渐开线齿廓都参加工作,而是图中阴影线所示的部分。
实际参与啮合的这段齿廓称为齿廓工作段。
一对齿轮啮合时齿廓工作段的求法:三个图中的齿轮都是渐开线齿轮,但图1和图2中的主动轮只能带动从动轮转过一个小角度就动从动轮整周转动,看来并不是任意两个渐开线齿轮都能正确地进行啮合,而是必须满足一定的条是什么?从图3中可以看出:两个渐开线齿轮在啮合过程中,参加啮合的轮齿的工作一侧齿廓的啮合点都工作一侧齿廓的啮合点H不在啮合线N1N2上,这就是两轮卡死的原因。
从图3中可以看出是齿轮1的法向齿矩,是齿轮2的法向齿矩,亦即:这个式子就是一对相啮合齿轮的轮齿分布要满足的几何条件,称为正确啮合条件。
由渐开线性质可知,法向齿距与基圆齿距相等,故上式也可写成将和代入式中得:因为模数m和压力角均已标准化,不能任意选取,所以要满足上式必须使:结论:一对渐开线齿轮,在模数和压力角取标准值的情况下,只要它们分度圆上的模数和压力角二、齿轮传动的正确安装条件1、齿侧间隙为了避免齿轮在正转和反转两个方向的传动中齿轮发生撞击,要求相啮合的轮齿的齿侧没有间隙。
齿侧间隙沿两轮的节圆来测量,无测隙要求:,即无齿侧间隙啮合条件为:一个齿轮节圆上的槽宽等于另一个齿轮节圆上的齿厚。
2、标准安装如图所示为满足正确啮合条件的一对外啮合标准直齿圆柱齿轮,它的中心距是两轮分度圆半径之和,此中心距称为标准中心距。
啮合线N1N2与O1O2的交点C是啮合节点,而两轮分度圆也相切于C 点,所以分度圆与节圆重合为一个圆。
渐开线标准直齿圆柱齿轮的啮合传动

渐开线直齿圆柱齿轮
图10-5 渐开线齿轮传动的啮合特性
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1.传动比的恒定性 由图10-5,可推得齿轮传动的瞬时传动比
i12
1 2
vK1 / O1K vK 2 / O2 K
O1和O2为圆心,过节点P作两个相切的圆,称为节圆。节圆半径r'1=
O1P,r'2= O2P。所以
i12
1 2
rb 2 rb1
r2 ' r1 '
(10-11)
即一对渐开线齿轮传动的瞬时传动比也等于两节圆半径的反比。
2.啮合角的不变性
一对齿轮通过齿廓的直接接触来传递运动和动力,所有啮合点
都在啮合线上。当不计摩擦时,其齿廓间的正压力将沿接触点的公
B2 B1 1
(10-15)
pb
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1.4 安装中心距和标准安装中心距
一对外啮合渐开线标准齿轮传动的安装中心距a'是两齿轮节圆
半径之和,即a'=r1'+ r2'。由式(10-1)可得 r'= rb/cosα',式中α'是节
1.2 渐开线齿轮的正确啮合条件
如图10-6a所示,设相邻两齿同侧齿廓与啮合线(也是公法线)
N1N2的交点分别为K1和K2,线段K1K2的长度称为齿轮的法向齿距。 要使两轮正确啮合,它们的法向齿距必须相等。由渐开线的性质可
知,法向齿距等于两轮基圆上的齿距。因此,要使两轮正确啮合,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比较得:
2.2齿轮齿条传动 标准安装: 节圆与分度圆重合,节线与分度线重合,α’=α 非标准安装: N1N2 线与齿廓垂直,故节点位置不变,且
r1 ’ = r1
ra1 r1
α’ =α
O1
节线与分度线不重合
O1 ra1 r1 rf1 B2 N2 B1 P v2
ω1
rf1
ω1
1
N1
α’=α
1
N1 α’=α B2
单齿啮合区
设一对轮齿从B2点进入啮合到B1点退出啮合的时间为T, 则双齿啮合所占时间的百分比为:
T双/ T =2(B1B2-pb)/ B1B2 =2-2/ε
单齿啮合所占时间的百分比为:
α
T单/ T =[B1B2-2(B1B2-pb)]/ B1B2 =(2pb - B1B2)/B1B2 = 2/ε
α-1
rb2
1
1 B3 2 P
1 B2 B4 2 2
N1
B1
N2 当第二对齿从B4点运动到B3点时; 第三对正好在B2点进入啮合。 开始一个新的循环。 单齿啮合区长度: L1= ε αP b -2(ε α-1) P b = (2-ε α) P b
双齿啮合区长度: L2= 2(ε α-1) P b
3
rb2
双齿啮合区 双齿啮合区
O1
α’ αa1
PB1 =z1mcosα(tgαa1-tgα’)/2 PB2=h*am/sinα
代入得:ε
α =[ z1
(tgαa1-tgα’ )]/2π + h*a /π cosαsinα
B2 N1 h* a m B1 P
α’
③内啮合传动
ε
α=
B1B2/pb
=(PB1+P B2)/π mcosα N2
pb1=pb2
O2
ω2
pb1>pb2 m1>m2
O2 不能正确啮合!
ω2
不能正确啮合!
能正确啮合!
1、正确啮合条件
要使进入啮合区内的各对齿轮都能正确地进入啮合,两齿轮的相邻两齿 同侧齿廓间的法向距离应相等:
pb1= pb2
将pb=π mcosα代入得: m1cosα1=m2cosα2 因m和α都取标准值,使上式成立的条件为:
ε pb B1
双
α
pb pb
B2
单
双
分析:ε
α
=[Z1(tgαa1-tgα’)+Z2(tgαa2-tgα’)]/2π
→平稳性、承载能力↑
O1 rb1 B2 P B2 rb2
ε
α↑
→啮合齿对↑
α的因素:
影响ε ①ε
ra1
N2 O1 ra1
α↑
α与z,
ha*,α’,α有关而与m无关。
B1
N1
αa=arccos(rb/ra) =arccos(db/da)
啮合角α’:N1N2 线与VP 之间的夹角,即节圆压力角。 O1 O1 ra1 r r1 ω1 b1
N1
ra1
α’=α
ra1 ω1 r’ r1 rb1 1
N1
α’>α
N2
P rb2 r2
c
N2
P
a
r'2
rb2 r2 rf2
a’ > a
rf2
rf2
ω2
O2 标准安装时:α’=α, 非标准安装时: O2
N2
B1
P
v2
2
2
3、一对轮齿的啮合过程
O1
轮齿在从动轮顶圆与N1N2 线交点B2处进入啮合, 主动轮齿根推动从动轮齿顶。
随着传动的进行,啮合点沿N1N2 线移动。
rb1
ω1 ra1 B2 P B1 ra2 rb2 ω2 O2
N N11
在主动轮顶圆与N1N2 线交点处B1脱离啮合。
B1B2 -实际啮合线 N1N2 :理论上可能的最长啮合线段 ——理论啮合线段 N1、N 2 ——啮合极限点 阴影线部分——齿廓的实际工作段。 N 22 N
标准中心距 显然:
a=ra1+c+rf2 =r1+ha
*m+c*m
+ r2-(ha
*m+c*m)
a =r1+ r2
=r1+ r2 =m(z1+z2)/2
两轮节圆总相切: a=r’1+ r’2 两轮的传动比: i12 = r’2 /r’1
=r1+ r2 = r2 /r1
r’1 = r1 节圆与分度圆重合 r’2 = r2
pb 1
rb1 r1 B1
O1 ω1
N1
B2 P r2
m1=m2 ,
α1 =α2
N2
结论:一对渐开线齿轮的正确啮合条件 是它们模数和压力角应分别相等。
rb2
ω2
O2
2、中心距a及啮合角α’ 2.1外啮合传动 对标准齿轮,确定中心距a时,应满足两个要求:
1)理论上齿侧间隙为零。
2 )顶隙c为标准值。
使用场合
[ε
α
一般机械制造业
1.4
汽车拖拉机
1.1~1.2
金属切削机床
1.3
]
重合度ε
α 计算公式:
O1
α’ rb1 αa1
①外啮合传动 ε
α=
B1B2/pb =(PB1+P B2) /π mcosα N2
ra1
B1
其中:PB1=B1 N1-PN1=rb1tgαa1 - rb1tgα’ =z1mcosα(tgαa1-tgα’)/2
P
B1 ra1
PB1 =B1 N1- PN1 =rb1tgαa1 -r tgα’ b1
=z1mcosα(tgαa1-tgα’)/2 同上
N1 αa1
B2
rb1
rb2
ra2α
’
α’ O1
PB2=PN2 - B2 N2 =rb2tgα’ - rb2tgαa2
=- z2mcosα(tgαa2-tgα’)/2 ∴ε ε
=arccos[mzcosα/(mz+2ha* m)] =arccos[zcosα/(z+2ha*)] ② ha
*↑
ra2
ra2
→α a ↑ →ε
α↑
O2
α’
③ z↑
→ da↑ →B1B2↑ →ε
α↓
④α’↑ →B1B2 ↓ →ε
B2
B1 B1 ra2
B2
α’
⑤ α ↓ →α a ↑ →ε
α↑
α ’ > α’
P
B2 ra2
N1
rb2
αa2 α’
PB2=B2 N2-PN2 =rb2tgαa2 - r tgα’ b2
=z2mcosα(tgαa2-tgα’)/2
∴ε
α
=[z1(tgαa1-tgα’) + z2(tgαa2-tgα’)]/2π
O2
②齿轮齿条传动:
ε
α=
B1B2/pb =(PB1+P B2)/π mcosα
O1
ω1
4、连续传动条件 pb
B2
为保证连续传动,要求:
实际啮合线段B1B2≥pb (齿轮的法向齿距), N2
B1
N1
K
即:
令ε
α
B1B2/pb≥1
= B1B2/pb
,
ω2 ε
α
为一对齿轮的重合度
α
ε 一对齿轮的连续传动条件是:
≥1
α
O2 ≥[ε
α
为保证可靠工作,工程上要求:ε [ε
α
]
]的推荐值:
ω2
rb1+rb2 = (r1 +r2)cosα = a cosα
由于a’>a ,两分度圆将分离, 此时α’ >α。
标准安装时: rb1+rb2= a cosα
非标准安装时:由于a’>a,两分度圆将分离,此时α’ >α
但基圆不变: rb1+rb2 = (r1’+r2’)cosα =’ a’cosα’ a’cosα’ = a cosα
B1B2 < B1B2 O
当Z1,,Z2 →∞时 ,ε
α→ε αmax
PB1=PB2 =ha*m/sinα ε
αmax=(PB1+PB2
)/pb =2 ha*m/(sinαπ mcosα)
=4 ha*/π sin2α
取:α=20°, ha*=1
ε
αmax
=1.981,
B2 h* a m B1 P
α
第三十九讲 渐开线直齿圆柱齿轮的啮合传动
一对齿轮传动时,所有啮合点都在啮合线N1N2上。
pb1 rb1 r1
B1
O1
ω1
N1
pb 1
rb1 r1 B1
O1 ω1
N1
pb1
rb1 r1
O1 ω1
N1
B2
N2
N2
P r2
B2
P r2
N2
B2
B1
P r2
rb2
rb2
rb2
pb1<pb2 m1<m2
O2
ω2
α=[Z1(tgαa1-tgα ’)-Z 2(tgαa2-tgα ’)]/2π
αa2O2Fra bibliotekαa2<α’
α的物理意义:
表示同时参与啮合的轮齿对数的平均值。
ε
α
= 1.45d的意义:
B1B2=ε αP b = 1.45 Pb 第一对齿在B2点进入啮合 第一对齿从B2运动到B3点时; 第二对齿在B2点恰好进入啮合。 第一对齿从B3运动到B1点时; 第二对齿从B2运动到B4点时。 第一对齿在B1点脱离啮合后; 只有第二对齿处于啮合状态。
