标准直齿圆柱齿轮传动强度计算
标准直齿圆柱齿轮传动的强度计算

标准直齿圆柱齿轮传动的强度计算一、轮齿的受力分析图6-6所示为齿轮啮合传动时主动齿轮的受力情况,不考虑摩擦力时,轮齿所受总作用力f n将沿着啮合线方向,f n称为法向力。
f n在分度圆上可分解为切于分度圆的切向力f t和沿半径方向并指向轮心的径向力f r 。
圆周力f t=n径向力 f r= f t tg n (6-1)法向力 f n=n式中:d1为主动轮分度圆直径,mm;为分度圆压力角,标准齿轮=20°。
设计时可根据主动轮传递的功率p1(kw)及转速n1(r/min),由下式求主动轮力矩t1=9.55×106×(n mm)(6-2)根据作用力与反作用力原理,f t1=-f t2,f t1是主动轮上的工作阻力,故其方向与主动轮的转向相反,f t2是从动轮上的驱动力,其方向与从动轮的转向相同。
同理,f r1=-f r2,其方向指向各自的轮心。
二、载荷与载荷系数由上述求得的法向力f n 为理想状况下的名义载荷。
由于各种因素的影响,齿轮工作时实际所承受的载荷通常大于名义载荷,因此,在强度计算中,用载荷系数k 考虑各种影响载荷的因素,以计算载荷f nc 代替名义载荷f n 。
其计算公式为(6-3)式中:k 为载荷系数,见表6-3。
表6-3 载荷系数k二、齿根弯曲疲劳强度计算齿根处的弯曲强度最弱。
计算时设全部载荷由一对齿承担,且载荷作用于齿顶,将轮齿看作悬臂梁,其危险截面可用30o 切线法确定,即作与轮齿对称中心线成30o 夹角并与齿根过渡曲线相切的两条直线,连接两切点的截面即为齿根的危险截面,如图6-7所示。
运用材料力学的方法,可得轮齿弯曲强度校核的公式为= ≤或σf =≤(6-4)或由上式得计算模数m的设计公式m≥ (6-5)式中:=b/d1称齿宽系数(b为大齿轮宽度),由表6-4查取;称为齿形系数,由图6-8查取;[]为弯曲许用应力,由式6-8计算。
表6-4齿宽系数=b/d1三、齿面接触疲劳强度计算齿面接触疲劳强度计算是为了防止齿间发生疲劳点蚀的一种计算方法,它的实质是使齿面节线处所产生的最大接触应力小于齿轮的许用接触应力,齿面接触应力的计算公式是以弹性力学中的赫兹公式为依据的,对于渐开线标准直齿圆柱齿轮传动,其齿面接触疲劳强度的校核公式为≤或≤ (6-6)将上式变换得齿面接触疲劳强度的设计公式d1≥ (6-7)式中:“±”分别用于外啮合、内啮合齿轮;z e为齿轮材料弹性系数,见表6-5;z h为节点区域系数,标准直齿轮正确安装时z h =2.5;[σh]为两齿轮中较小的许用接触应力,由式6-9计算;u为齿数比,即大齿轮齿数与小齿轮齿数之比。
15直齿圆柱齿轮传动的强度计算
二、齿轮传动的强度计算
齿轮传动的强度计算是根据轮齿可能出现的失效形式和 设计准则来进行的,由于轮齿的主要失效形式是齿面疲劳点 蚀和轮齿疲劳折断,因此只讨论齿面接触疲劳强度和齿根弯 曲疲劳强度的计算
1.齿面接触疲劳强度计算 1.齿面接触疲劳强度计算
针对齿面点蚀失效进行的 齿面点蚀是因为接触应力过大引起的。 接触应力过大引起的 齿面点蚀是因为接触应力过大引起的。齿轮啮合可看 作是分别以接触处的曲率半径ρ 作是分别以接触处的曲率半径ρl、ρ2为半径的两个圆柱 赫兹应力公式计算 体的接触,其最大接触应力可由赫兹应力公式计算, 体的接触,其最大接触应力可由赫兹应力公式计算,即
10.10 直齿圆柱齿轮传动的强度计算 一、轮齿的受力分析与计算载荷
轮齿的受力分析
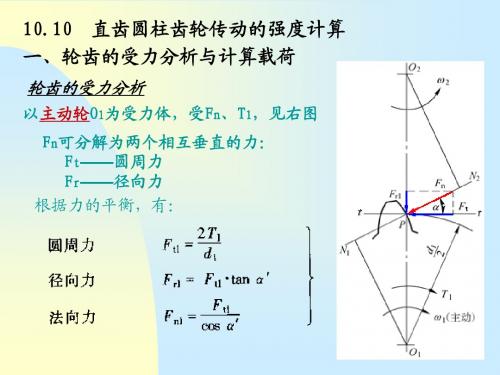
以主动轮O1为受力体,受Fn、T1,见右图 主动轮O 为受力体, 可分解为两个相互垂直的力: Fn可分解为两个相互垂直的力: Ft——圆周力 圆周力 Fr——径向力 径向力 根据力的平衡,有:
其中: 其中: 主动轮传递的转矩N mm T1 -主动轮传递的转矩N·mm 主动轮分度圆直径mm; mm;非标准时用节圆直径代替 d1 -主动轮分度圆直径mm;非标准时用节圆直径代替
对于斜齿圆柱齿轮传动从前端面进入啮合到后端面脱离啮合其在啮合线上的长度比直齿圆柱齿轮增加了btg斜齿圆柱齿轮的啮合面斜齿圆柱齿轮传动的重合度端面重合度附加重合度附加重合度是由于齿的倾斜而产生它随齿宽b和的增大而增大这是斜齿轮传动平稳承载能力较高的原因之一当量齿轮及当量齿数在研究斜齿轮法面齿形时可以虚拟一个与斜齿轮的法面齿形相当的直齿轮称这个虚拟的直齿轮为该斜齿的当量齿轮其齿数则称四斜齿圆柱齿轮的当量齿数和最小齿数在进行强度计算和用成形法加工齿轮选择铣刀时必须知道斜齿轮的法面齿形通常用近似的方法来分析做法如图所示过斜齿轮分度圆柱上齿廓的任一点c作齿的法面nn该法面与分度圆柱面的交线为一椭圆椭圆的长半轴为
标准直齿圆柱齿轮传动的强度计算

6.3 标准直齿圆柱齿轮传动的强度计算 (一)轮齿的受力分析 进行齿轮的强度计算时,首先要知道齿轮上所受的力,这就需要对齿轮传动作受力分析。
当然,对齿轮传动进行力分析也是计算安装齿轮的轴及轴承时所必需的。
齿轮传动一般均加以润滑,啮合轮齿间的摩擦力通常很小,计算轮齿受力时,可不予考虑。
垂直于齿面,为了计算方便,将法向 沿啮合线作用在齿面上的法向载荷Fn在节点P处分解为两个相互垂直的分力,即圆周力F t与径向力F r, 。
由此载荷Fn得F t=2T1/d1; F r=F t tanα ; FF t/cosα (a)n=—小齿轮传递的转矩,N·mm; 式中:T1—小齿轮的节圆直径,对标准齿轮即为分度圆直径,mm; d1 α—啮合角,对标准齿轮,α=20°。
(二)齿根弯曲疲劳强度计算 轮齿在受载时,齿根所受的弯矩最大 ,因此齿根处的弯曲疲劳强度最弱。
当轮齿在齿顶处啮合时,处于双对齿啮合区,此时弯矩的力臂虽然最大,但力并不是最大,因此弯矩并不是最大。
根据分析,齿根所受的最大弯矩发生在轮齿啮合点位于单对齿啮合区最高点。
因此,齿根弯曲强度也应按载荷作用于单对齿啮合区最高点来计算。
由于这种算法比较复杂,通常只用于高精度的齿轮传动(如6级精度以上的齿轮传动)。
对于制造精度较低的齿轮传动(如7,8,9级精度),由于制造误差大,实际上多由在齿顶处啮合的轮齿分担较多的载荷,为便于计算,通常按全部载荷作用于齿顶来计算齿根的弯曲强度。
当然,采用这样的算法,齿轮的弯曲强度比较富余。
右边动画所示为齿轮轮齿啮合时的受载情况。
动画演示为齿顶受载时,轮齿根部的应力图。
下一页 在齿根危险截面AB处的压应力σc仅为弯曲应力σF的百分之几,故可忽略,仅按水平分力p c a cosγ所产生的弯矩进行弯曲强度计算。
假设轮齿为一悬臂梁,则单位齿宽(b=1)时齿根危险截面的弯曲应力为 取,并将(a)式代入。
对直齿圆柱齿轮,齿面上的接触线长L即为齿宽b(mm),得 令 Y Fa是一个无量纲系数,只与齿轮的齿廓形状有关,而与齿的大小(模数m)无关。
标准直齿圆柱齿轮传动强度

标准直齿圆柱齿轮传动的强度可以根据以下步骤进行计算:
1.确定齿轮上所受的力。
这包括圆周力(Ft)、径向力(Fr)和法向力
(Fn)。
2.根据圆周力和齿轮的节圆直径(d1),计算出转矩(T1)。
转矩可以用公
式T1 = 2 × Ft × tanα来表示,其中α是啮合角,通常取值为20°。
3.根据转矩和齿宽,计算出弯曲应力。
弯曲应力可以用公式σ= Ft/Wb来表
示,其中Wb是齿宽。
4.根据齿根处的弯曲应力,计算出弯曲疲劳强度系数。
这个系数通常由实验
确定,也可以通过查阅相关设计手册获得。
5.根据弯曲疲劳强度系数和弯曲应力,计算出弯曲疲劳极限。
弯曲疲劳极限
可以用公式σHlim = k × Wb × Ft来表示,其中k是弯曲疲劳强度系数。
6.根据弯曲疲劳极限,计算出安全系数。
安全系数可以用公式H=σHlim/σH
来表示,其中σH是工作应力。
7.根据安全系数和弯曲应力,计算出许用弯曲应力。
许用弯曲应力可以用公
式σH=σHlim/S来表示,其中S是安全系数。
以上是标准直齿圆柱齿轮传动强度的计算步骤,希望能对您有所帮助。
标准直齿圆柱齿轮的传动设计计算

标准直齿圆柱齿轮的传动设计计算:
一.齿轮的受力分析:
圆周力Ft=Ft1=Ft2=2T1/d1=2T2/d2;
径向力Fr=Fr1=Fr2=Ft.tanа;
法向力Fn=Fn1= Fn2=Ft/COSа;式中:T1、T2为两齿轮的转距,N.mm;d1、d2为两齿轮的分度圆直径,mm;а为压力角,а=20°。
若P为传递的功率,KW;n1为小齿轮的转速,r/min;可得转矩:T1=9.55*106P/n1.式中T1的单位为N.mm。
二.轮齿的计算载荷:
上式分析的法向力Fn是作用在轮齿上的理想状况下的载荷,称为名义载荷,在强度计算时,需引用载荷系数K(新国标中用使用系数、动载系数、分布系数、分配系数等考虑多种因素的影响,本处为简化计算,仅用载荷系数表示。
)则计算载荷Fnc=KFn;载荷系数K值可根据载荷特性查设计手册表中所得。
三.齿面接触疲劳强度计算:
四.齿面疲劳强度计算的目的是为了防止齿面点蚀失效。
防止齿面点蚀的强度条件为:节点
处的计算接触应力应该小于齿轮材料的许用接触应力,即:σH≤〖σH〗。
齿面最大的计算接触应力,可用赫兹应力公式计算:
式中:σH的单位为Mpa;Fn为作用在轮齿上的法向力,N;b为轮齿的宽度,mm;ρ1,ρ2为两轮齿廓在节点处的曲率半径,mm;μ1,μ2为两轮材料的泊松比;E1、E2为两轮材料的弹性模量,Mpa;正号用于外啮合,负号用于内啮合。
令ZE=
ZE称为齿轮材料的弹性系数,
普通圆柱蜗杆的传动效率η=(100-3.5i)%。
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
10-05 标准直齿圆柱齿轮传动的强度计算

受载分析及应力计算公式
当齿顶受载时,轮齿根部
的应力如图。载荷 pca 对危险 截面产生的应力有弯曲应力和 压应力。 注意:在齿根危险截面处
的压应力仅为弯曲应力的百分
之几,故可忽略。计算时仅考 虑水平分力产生的弯曲应力。
受载分析及应力计算公式
取h = Khm,S = KSm,并将
代入,得:
齿形系数YFa及应力校正系数YFs
YFa是一个无量纲系数,它只与轮齿的齿廓形状有关,而与 齿的大小(模数m)无关。 在实际计算时,还应计入齿根危险截面处的过渡圆角所引 起的应力集中作用以及弯曲应力以外对齿根应力的影响,因此, 引入应力校正系数YSa。 齿根弯曲疲劳强度校核计算公式 :
齿形系数YFa及应力校正系数YSa 表
齿根弯曲疲劳强度公式
10-5 标准直齿圆柱齿轮传动的强度计算
(1)轮齿的受力分析
(2)齿根弯曲疲劳强度计算
(3)齿面接触疲劳强度计算
(4)齿轮传动的强度计算说明
轮齿的受力分析
• 法向载荷Fn • 圆周力Ft • 径向力Fr
T1——小齿轮传递的转矩,N.mm; d1——小齿轮的节圆直径,对标准齿轮即为分 度圆直径,mm; α——啮合角,对标准齿轮,α=20°。
齿根弯曲疲劳强度校核计算公式 :
按齿根弯曲疲劳强度设计齿轮的计算公式:
按齿根弯曲疲劳强度设计时,[σ]F1/(YFa1YSa1)或 [σ]F2/(YFa2YSa2)中较小的数值代入设计公式进行计算。
齿宽系数
装置 状况 φd 两支承相对小 齿轮对称布置 0.9-1.4 (1.2-1.9) 两支承相对小齿 轮不对称布置 0.7-1.15 (1.1-1.65) 小齿轮作 悬臂布置 0.4-0.6
直齿圆柱齿轮传动的弯曲强度计算.
危险截面
危险截面:用30°切线法确定。 作与轮齿对称中线成30°角并 与齿根过渡圆角相切的切线, 通过两切点作平行于轴线的截 面即为危险截面(左图所示)。
d1
3
2KT1 1 Z E Z H d H
2
mm
2KTY 2KTY 1 FaYSa 1 FaYSa F [ F ] 2 bmd1 bm z1
MPa
硬齿面闭式齿轮传动: 按弯曲强度进行设计,按接触强度校核 :
2 KT1 YFaYsa m . 2 d Z1 [ ]F
hF 6( ) cos F F KFt m bm ( sF ) 2 cos m
∵hF和SF与模数m相关, 故YF与模数m无关。 对于标准齿轮, YFa仅取决于齿数Z,取值见图11-8。
考虑在齿根部有应力集中,引入应力集中系数Ysa,图形11-9
轮齿弯曲强度计a 1 FaYSa F [ F ] 2 bmd1 bm z1
MPa
以b=φd1代入得
2 KT1 YFaYsa . 得设计公式: m 2 d Z1 [ ]F
3
mm
二. 说明
1.一般YFa1 ≠ YFa2, 故[σF1 ] ≠ [σF2]
YFa1YSa1 YFa 2YSa 2 2.计算时取: [ F1 ] [ F 2 ]
较大者.
3.对于传递动力的齿轮模数一般应大于1.5~2mm。 4.对于开式传动,为考虑齿面磨损,可将算得模 数值加大10%~ 15%。
§11-6 直齿圆柱齿轮传动的弯曲强度计算
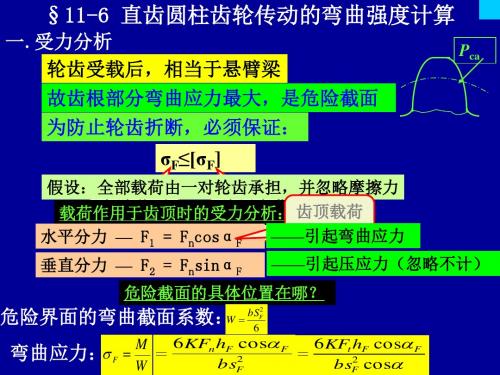
一.受力分析 轮齿受载后,相当于悬臂梁
Pca
故齿根部分弯曲应力最大,是危险截面
为防止轮齿折断,必须保证: σF≤[σF]
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8-5 标准直齿圆柱齿轮传动的强度计算一.齿轮传动承载能力计算依据轮辐、轮缘、轮毂等设计时,由经验公式确定尺寸。
若设计新齿,可参《工程手册》20、22篇,用有限元法进行设计。
轮齿的强度计算:1.齿根弯曲强度计算:应用材料力学弯曲强度公式WMb =σ进行计算。
数学模型:将轮齿看成悬臂梁,对齿根进行计算,针对齿根折断失效。
险截面上,γcos ca p --产生剪应力τ,γsin ca p 产生压应力σc ,γcos .h p M ca =产生弯曲应力σF 。
分析表明,σF 起主要作用,若只用σF 计算齿根弯曲疲劳强度,误差很小(<5%),在工程计算允许范围内,所以危险剖面上只考虑σF 。
单位齿宽(b=1)时齿根危险截面的理论弯曲应力为220cos .66*1cos .S h p S h p W M ca ca F γγσ===令αcos ,,b KF L KF p m K S m K h tn ca S h ====,代入上式,得()αγαγσcos cos 6.cos cos ..6220S h t S h t F K K bm KF m K b m K KF ==令 αγc o sc o s 62S h Fa K K Y =Fa Y --齿形系数,表示齿轮齿形对σF 的影响。
Fa Y 的大小只与轮齿形状有关(z 、h *a 、c *、α)而与模数无关,其值查表10-5。
齿根危险截面理论弯曲应力为 bmY KF Fat F =0σ 实际计算时,应计入载荷系数及齿根危险剖面处的齿根过渡曲线引起的应力集中的影响。
bmY Y KF SaFa t F =σ式中:Sa Y --考虑齿根过渡曲线引起的应力集中系数,其影响因素同Fa Y ,其值可查表10-5。
2.齿根弯曲疲劳强度计算校核公式 []F Fa Sa Sa Fa t F Y Y bmd KT bm Y Y KF σσ≤==112 MPa令1d bd =φ,d φ--齿宽系数。
将111,mz d d b d ==φ代入上式 设计公式 [])(.23211mm Y Y z KT m FSaFa d σφ≥往往齿根面先发生点蚀,然后才扩展到齿顶面,即齿顶面比齿根面具有较高的接触疲劳强度。
因此,虽然此时接触应力大,但对大齿轮不一定会构成威胁。
由右图可看出,大齿轮在节点处的接触应力较大,同时,大齿轮单对齿啮合的最低点(D 点)处接触应力也较大。
按理应分别对小齿轮和大齿轮节点与单对齿啮合的最低点处进行接触强度计算。
但按单对齿啮合的最低点计算接触应力比较麻烦,并且当小齿轮齿数z 1≥20时,按单对齿啮合的最低点计算所得的接触应力与按节点啮合计算得的接触应力极为相近。
为了计算方便,通常以节点啮合为代表进行齿面的接触强度计算。
2)齿面接触应力计算二齿轮在节点处啮合,曲率半径为αραρsin 2sin 2222111d P N d P N ====P 点的当量曲率为:⎪⎪⎭⎫⎝⎛±=±=±=∑121122112211111ρρρρρρρρρρρρ 齿数比 小大z z u =与关系为:增速传动 iu 1=减速传动 i u =uu d u u u z z d d 1.sin 21.1111121212±=±=∴===∑αρρρρ节点处只有一对齿啮合,b L =将以上二式代入赫兹公式并考虑载荷系数uu bd KT E E u u d b KF E E uu d b KF E E t n H 1.2.cos .sin 2.1111.sin 2.cos .1111.sin 2..11121122212112221211222121±⎪⎪⎭⎫ ⎝⎛-+-=±⎪⎪⎭⎫⎝⎛-+-=±⎪⎪⎭⎫⎝⎛-+-=ααμμπααμμπαμμπσ令⎪⎪⎭⎫⎝⎛-+-=222121111E E z E μμπ,ααcos .sin 2=H zuu bd KT z z HE H 1.2211±=σ MPa 式中:E z --弹性系数,仅与齿轮材料特性有关,其值查表10-6。
H z --节点区域系数,考虑节点位置的齿廓曲率半径等因素对接触应力的影响,标准直齿轮020=α时,H z =2.5。
+--外啮合;—--内啮合。
2.齿面接触疲劳强度计算 校核公式[]H HE H uu bd KT z z σσ≤±=1.2211 MPa 将1d b d φ=代入上式设计公式 []32111..2u u z z KT d H HE d ±⎪⎪⎭⎫⎝⎛≥σφ mm 由上式可知:在一定的使用条件和寿命下,当b 、u 、齿轮材料及其热处理规范一定时,齿轮传动的接触疲劳强度取决于d 1(中心距a)。
配对齿轮的21H H σσ=,但[]1H σ不一定等于[]2H σ,所以设计或校核时,应以[]1H σ、[]2H σ中较小者代入上式。
一对标准钢制齿轮[]H EH uu bd KT z σσ≤±=1.25.2211 MPa []32111..32.2u u z KT d H Ed ±⎪⎪⎭⎫⎝⎛≥σφ mm 六.齿轮传动的强度计算说明1. 当配对齿轮均为硬齿面时,两轮的材料、热处理方法及硬度均可取成一样的。
设计时,可分别按齿根弯曲疲劳强度及齿面接触疲劳强度的设计公式进行计算,并取其中较大者作为设计结果。
2. 当用设计公式初步计算齿轮的分度圆直径d 1(或模数m n )时,动载系数K v 、齿间载荷分布系数K α及齿向载荷分布系数K β不能预先确定,此时可试选一载荷系数K t ,则计算出来的分度圆直径(或模数)也是一个试算值d 1t (或m nt ),然后按d 1t 值计算齿轮的圆周速度,查取动载系数K v 、齿间载荷分布系数K α及齿向载荷分布系数K β,计算载荷系数K 。
若算得的K 值与试选的值K t 相差不多,就不必修改原计算;若二者相差较大时,应按下式校正 试算所得的分度圆直径d 1t (或m nt ):3311//tnt n t t K K m m K K d d ==§8-6 齿轮传动的设计参数、许用应力与精度选择一.齿轮传动设计参数的选择1.压力角α由《机械原理》可知,增大压力角α,轮齿的齿厚及节点处的齿廓曲率半径亦随之增加,有利于提高齿轮传动的弯曲强度及接触强度。
我国对一般用途的齿轮传动规定的标准压力角α=200。
为增强航空齿轮用齿轮传动的弯曲强度及接触强度,规定α=250的标准压力角。
对重合度接近2的高速齿轮传动,推荐采用齿顶高系数为1~1.2,压力角为160~180的齿轮,可增加轮齿的柔性,降低和动载荷。
2.小齿轮齿数z 1若齿轮传动的中心距不变,增加齿数z 1---增大重合度、改善传动平稳性---减小模数、降低齿高---减少金属切削量,节省制造费用。
降低齿高---减小滑动速度---减少磨损及减小胶合的可能性。
但模数小---齿厚减薄---降低轮齿的弯曲强度。
对闭式齿轮传动,传动尺寸主要取决于齿面接触疲劳强度,齿根弯曲疲劳强度较充裕,此时,在保持齿轮传动尺寸不变的前提下,为提高传动的平稳性,减小冲击振动,齿数多一些,z 1=20~40。
开式(半开式)齿轮传动,由于轮齿主要为磨损失效,为使轮齿不致过小,齿数取少一些,z 1=17~20。
3.模数m模数值必须取标准系列值。
模数m 越大---轮齿尺寸越大---在齿宽b 、齿数z 相同的条件下---轮齿弯曲疲劳强度越高。
但模数m 越小---中心距不变的条件下,齿数z 越多---重合度越大---传动越平稳;且模数m 越小---齿高越小m h h a a *=---齿顶圆越小---节省材料---切齿时切去的金属量少---提高效率。
所以,在满足齿根弯曲疲劳强度的条件下,模数m 取小一些。
4.齿宽系数φd轮齿越宽---承载能力越高---轮齿不宜过窄;但轮齿越宽---齿面上载荷分布更不均匀—轮齿不宜过宽。
φd 荐用值见表10-7。
对于标准圆柱齿轮减速器,()u d b a b a +==15.01φ,对外啮合齿轮传动()a d u d bφφ+==15.01φa 的值规定为0.2,0.25,0.30,0.40,0.50,0.60,0.80,1.0,1.2。
运用设计公式时,对标准减速器,先选定φa 后再计算出相应的φd 值。
计算齿宽1d b d ϕ=,圆整。
为防止两齿轮因装配后轴向稍有错位而导致啮合齿宽减小,常把小齿轮的齿宽在计算齿宽的基础上人为加宽约5~10mm 。
二.齿轮传动的许用应力本书荐用的齿轮疲劳极限是用m=3~5mm ,α=200,b=10~50mm ,v=10m/s ,齿面粗糙的度为0.8的直齿付试件,失效概率为1%,经持久疲劳实验确定。
一般齿轮传动,因绝对尺寸、表面粗糙度、速度及润滑对实际齿轮疲劳极限影响不大,不预考虑,只考虑N 对疲劳极限的影响。
[]SK N limσσ=式中:S---疲劳强度安全系数。
对接触疲劳强度计算,点蚀破坏发生后,只引起、振动,不立即导致不能继续工作的后果,所以1=H S 。
若一旦发生断齿,会发生严重事故,所以5.1~25.1=F S 。
K N ---寿命系数。
K FN ---图10-18;K HN ---图10-19。
h njL N 60=式中:n---齿轮转速,rpm ;j---每转一圈,同侧齿面的啮合次数。
h L ---工作寿命,h 。
lim σ---齿轮疲劳极限。
弯曲:ST F FE FE Y .,lim lim σσσσ==(ST Y ---实验齿轮应力校正系数),图10-20;点蚀:lim lim H σσ=,图10-21。
lim σ---取中间偏下值,即在MQ 及ML 中间选值。
若齿面硬度超出图中荐用范围,可大体按外插法查相应的FE σ、lim H σ。
图10-20为脉动循环的FE σ,对称循环的极限应力值仅为脉动循环应力的70%。
三.齿轮精度的选择各类机器所用齿轮传动的精度等级范围参表10-8,按载荷及速度推荐的齿轮传动精度等级如图10-22。
四.直齿圆柱齿轮传动的设计 1.齿轮传动的基本要求 (1)传动准确、平稳;(2)在尺寸小、重量轻的前提下,承载能力高。
2.已知条件(1)齿轮传动的工作条件,P 、n 、i ;原动机、工作机的工作特性等;(2)结构要求;(3)工艺条件;(4)使用要求;(5)环境条件。
3.承载能力计算---根据计算准则 闭式软齿面齿轮传动:(1)应用齿面接触疲劳强度设计公式求d1;(2)由参数选择原则及几何关系确定z、m及其它;(3)校核齿根弯曲疲劳强度。
闭式硬齿面齿轮传动及开式齿轮传动(1)应用齿根弯曲疲劳强度设计公式求m,开式传动将求得的m增大10~20%,以补偿磨损对轮齿的削弱;(2)由参数选择原则及几何关系确定z、d1及其它;(3)校核齿面接触疲劳强度(开式不需)。
