江苏省盐城中学2018届高三考前热身2试题及答案解析
最新-盐城市高三英语试题 精品

盐城市2018/2018学年度高三年级第二次调研考试英语试题第一部分听力(共两节,满分20分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. When will the man see the headmaster?A. At 9:30.B. At 11:45.C. At 12:40.2. Why does the man want to keep the window shut?A. Because he is ill.B. Because he wants to open it himself.C. Because the air inside is fresh enough.3. What is Mike?A. A teacher.B. A student.C. A writer.4. What has made working at home possible?A. Personal computers.B. Communication industry.C. Living far from companies.5. Where is the woman?A. In a soap factory.B. At the shop.C. In her house.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
2018届江苏省南京市、盐城市高三第二次模拟考试 英语 (解析版)

南京市盐城市2018 届高三年级第二次模拟考试(解析版)英语2018.03本卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),满分120分。
考试时间120分钟。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1分,满分5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What's wrong with the man?A. He is sick.B. He is thirsty.C. He is tired.2. What will the speakers discuss?A. A paper.B. A new computer.C. A new viewpoint.3. Why does the man make the phone call?A. To book a room.B. To apply for a job.C. To put an advertisement.4. How much time did the man spend on the exam?A. One hour and 20 minutes.B. One hour and 40 minutes.C. Two hours and 20 minutes.5. Where does the conversation probably take place?A. In a bookstore.B. In a museum.C. In a library.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
推荐-江苏省盐城中学2018届高三第二次模拟考试数学试题 精品

江苏省盐城中学2018届高三年级第二次模拟考试数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第一卷从第1页到第2页,第二卷从2页到第3页.考试结束后,将答题卡和答题纸一并交回.满分150分.考试时间120分钟.第一卷 (选择题,共50分)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号填写在答题卡上.用2B 铅笔将答题卡试卷类型(A )填涂在答题卡上.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知{|1}A x x =<,}0))(2(|{≤--=a x x x B ,若1≤a 则=B A (A ){|2}x x ≤ (B ){|1}x x ≤ (C ) {|2}x x ≥ (D ){|1}x x ≥2.设21cos ),0,2(=-∈απα,则=+)6tan(πα (A )3 (B )33 (C )3- (D )33- 3.设等差数列}{n a 的前n 项和是n S ,且0864=++a a a ,则6S 与5S 的大小关系是 (A )56S S < (B ) 56S S > (C ) 56S S = (D )无法确定 4.设b a 、表示直线,βα、表示平面,则βα//的充分条件是 (A )b a b a //,,βα⊂⊂ (B )βα⊥⊥b a b a ,,// (C )αββα//,//,,b a b a ⊂⊂ (D )αβ⊥⊥⊥b a b a ,,5.与直线34-=x y 平行的曲线23-+=x x y 的切线方程是(A )04=-y x (B )044=--y x(C )024=--y x (D )04=-y x 或044=--y x6.将函数x y 2cos =的图象沿向量a平移得到函数1)62sin(--=πx y 的图象,则向量a可以是 (A ))1,3(-π(B ))1,6(π (C ))1,3(--π (D ))1,6(π-7.若实数y x 、满足:⎩⎨⎧≤+≥+1022y x y x ,则y x +2的最小值是 (A )2-(B )22-(C )5- (D )52- 8.某水电站的蓄水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.已知某天0点到6点进行机组试运行,且该水池的蓄水量与时间(时间单位:小时)的关系如图丙所示:丙乙甲给出以下三个判断:①0点到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水不出水. 则上述判断中一定正确的是(A )① (B )② (C )①③ (D )②③ 9.设函数xxx x f -+⋅=11ln)(,若)()(21x f x f >,则下列不等式必定成立的是 (A )21x x > (B )21x x < (C )2221x x > (D )2221x x < 10.已知数列{}n a 的通项公式是)193)(72(10--=n n a n ,则该数列的最大项和最小项的和为 (A )73- (B )75- (C )79- (D )1-第二卷 (非选择题,共100分)注意事项:1. 请用书写黑色字迹的0.5毫米的签字笔在答题纸上指定区域内作答,在试题上作答一律无效.2. 作图题可先用2B 铅笔作答。
2018年江苏省盐城中学高考数学热身试卷(J)

2018年江苏省盐城中学高考数学热身试卷(J)副标题题号一二总分得分一、填空题(本大题共14小题,共14.0分)1.已知集合M+{x|−1<x<3},N={x|−2<x<1},则M∩N=______.【答案】{x|−1<x<1}【解析】解:∵M={x|−1<x<3},N={x|−2<x<1},∴M∩N={x|−1<x<1},故答案为:{x|−1<x<1}根据M与N,找出两集合的交集即可.此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.2.i是虚数单位,复数z满足(z−2i)(2−i)=5,则z=______.【答案】2+3i【解析】解:复数z满足(z−2i)(2−i)=5,可得z=52−i +2i=5(2+i)(2−i)(2+i)+2i=2+3i.故答案为:2+3i.直接利用复数的除法的运算法则化简求解即可.本题考查复数的代数形式混合运算,考查计算能力.3.某中学有高中生3500人,初中生1500人.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为______.【答案】100【解析】解:分层抽样的抽取比例为703500=150,总体个数为3500+1500=5000,∴样本容量n=5000×150=100.故答案为:100.计算分层抽样的抽取比例和总体个数,利用样本容量=总体个数×抽取比例计算n值.本题考查了分层抽样方法,熟练掌握分层抽样方法的特征是关键.4.执行如图所示的流程图,则输出s的值为______.【答案】19【解析】解:模拟程序的运行,可得k=2,s=0满足条件k<10,执行循环体,s=2,k=3满足条件k<10,执行循环体,s=5,k=5满足条件k<10,执行循环体,s=10,k=9满足条件k<10,执行循环体,s=19,k=17此时,不满足条件k<10,退出循环,输出s的值为19.故答案为:19.由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量s的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.5.已知tanθ=2,则sinθcosθ=______.【答案】25【解析】解:由tanθ=2,则sinθcosθ=sinθcosθsin2θ+cos2θ=tanθtan2θ+1=24+1=25.故答案为:25.利用同角三角函数的基本关系,求得sinθcosθ的值.本题主要考查同角三角函数的基本关系,属于基础题.6.用半径为2cm的半圆形纸片卷成一个圆锥筒,则这个圆锥筒的高为______cm.【答案】√3【解析】解:半径为2的半圆弧长为2π,圆锥的底面圆的周长为2π,其轴截面为等腰三角形如图:圆锥的底面半径为:1∴圆锥的高ℎ=√22−12=√3.故答案是√3.先求半圆的弧长,就是圆锥的底面周长,求出底面圆的半径,然后利用勾股定理求出圆锥的高.本题考查圆锥以及侧面展开图的知识,考查学生的运算能力.7.从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只一个被选取的概率为______.【答案】23【解析】解:从甲,乙,丙,丁4个人中随机选取两人,共有(甲乙),(甲丙),(甲丁),(乙丙),(乙丁),(丙丁)六种,其中甲乙两人中有且只一个被选取,则(甲丙),(甲丁),(乙丙),(乙丁),共4种, 故甲乙两人中有且只一个被选取的概率为46=23, 故答案为:23根据古典概型的概率公式即可得到结论.本题主要考查概率的计算,利用列举法是解决本题的关键.8. 已知F 1(−c,0),F 2(c,0)为椭圆x 2a 2+y 2b 2=1(a >b >0)的两个焦点,P 为椭圆上一点且PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =c 2,则此椭圆离心率的取值范围是______.【答案】[√33,√22]【解析】解:由椭圆定义可得|PF 1|+|PF 2|=2a ,① ∵PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅PF 2⃗⃗⃗⃗⃗⃗⃗ =c 2,∴|PF 1||PF 2|cos∠F 1PF 2=c 2,②由余弦定理可得|PF 1|2+|PF 2|2−2|PF 1||PF 2|cos∠F 1PF 2=4c 2,③ 由①②③得cos∠F 1PF 2=c 22a 2−3c 2≤1,|PF 1||PF 2|=2a 2−3c 2,∴e ≤√22, ∵|PF 1||PF 2|≤14(|PF 1|+|PF 2|)2=a 2, ∴2a 2−3c 2≤a 2, ∴e ≥√33, ∴此椭圆离心率的取值范围是[√33,√22].故答案为:[√33,√22].利用椭圆的定义、余弦定理、向量的数量积公式,结合基本不等式,即可求出椭圆离心率的取值范围.本题考查椭圆离心率的取值范围,考查椭圆的定义、余弦定理、向量的数量积公式、基本不等式,属于中档题.9. 设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2a 4=1,S 3=7,则S 5=______. 【答案】314【解析】解:由题意可得a 2a 4=a 32=1,∴a 3=1, 设{a n }的公比为q ,则q >0,∴S 3=1q 2+1q +1=7,解得q =12或q =−13(舍去),∴a 1=1q 2=4,∴S 5=4×(1−125)1−12=314故答案为:314由等比数列的性质易得a3=1,进而由求和公式可得q=12,再代入求和公式计算可得.本题考查等比数列的通项公式和求和公式,属基础题.10.从边长为10cm×16cm的矩形纸板的四角截去四个相同的小正方形,作成一个无盖的盒子,则盒子容积的最大值为______cm3.【答案】144【解析】解:设小正方形的变长为xcm(0<x<5),则盒子的容积V=(10−2x)(16−2x)x=4x3−52x2+160x(0<x<5),,当0<x<2时,0'/>,当2<x<5时,,∴x=2时V取得极大值,也为最大值,等于(10−4)(16−4)×2=144(cm3),故答案为:144.设小正方形的变长为xcm(0<x<5),可表示出盒子的容积,利用导数可求得其最大值.本题考查导数在解决实际问题中的应用,考查学生的阅读理解能力及利用数学知识解决问题的能力.11.已知正实数a,b满足1a+b +1a−b=1,则3a+2b的最小值为______.【答案】3+√5【解析】解:根据题意,1a+b +1a−b=2a(a+b)(a−b)=1,又由a、b为正实数,则a−b>0,则3a+2b=5(a+b)+(a−b)2=12×[5(a+b)+(a−b)]×[1a+b+1a−b]=12×[6+5(a+b)a−b+a−b a+b ]≥3+√5(a+b)a−b×a−ba+b=3+√5;故答案为:3+√5.根据题意,将1a+b +1a−b变形分析可得a−b>0,据此有3a+2b=5(a+b)+(a−b)2=1 2×[5(a+b)+(a−b)]×[1a+b+1a−b]=12×[6+5(a+b)a−b+a−ba+b],由基本不等式的性质分析可得答案.本题考查基本不等式的性质以及应用,关键是对3a+2b的变形.12.若斜率互为相反数且相交于点P(1,1)的两条直线被圆O:x2+y2=4所截的弦长之比为√62,则这两条直线的斜率之积为______.【答案】−9或−19【解析】解:设这两条直线的斜率分别为k、−k,则这两条直线的方程分别为m:y−1=k(x−1),n:y−1=−k(x−1),即m:kx−y+1−k=0,n:kx+y−1−k=0.圆心O到直线m的距离为d=√k2+1=√k2+1,可得弦长为2√4−(k−1)2k2+1.圆心O到直线n的距离为d′=√k2+1=√k2+1,可得弦长为2√4−(k+1)2k2+1.再由弦长之比为2√4−(k−1)2k 2+12√4−(k+1)2k 2+1=√62,即√3k 2+2k+33k 2−2k+3=√62,可得3k 2−10k +3=0.求得k =3,或k =13,∴当k =3时,这两条直线的斜率之积为3×(−3)=−9; 当k =13 时,两条直线的斜率之积为13×(−13)=−19, 故答案为:−9或−19.设这两条直线的斜率分别为k 、−k ,利用点斜式求得两条弦所在的直线方程,求出各自的弦心距,再结合弦长之比为√62得到关于k 的一元二次方程,求出k 的值,即可求得方程的两根之积.本题主要考查直线和圆相交的性质,点到直线的距离公式,韦达定理,弦长公式,属于中档题.13. 在△ABC 中,AB ⊥AC ,AB =1t ,AC =t ,P 是△ABC 所在平面内一点,若AP ⃗⃗⃗⃗⃗ =4AB ⃗⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗⃗|+AC⃗⃗⃗⃗⃗ |AC⃗⃗⃗⃗⃗ |,则△PBC 面积的最小值为______. 【答案】32【解析】解:由题意建立如图所示的坐标系, 可得A(0,0),B(1t ,0),C(0,t),∵AP ⃗⃗⃗⃗⃗ =4AB⃗⃗⃗⃗⃗⃗ |AB ⃗⃗⃗⃗⃗⃗ |+AC ⃗⃗⃗⃗⃗ |AC ⃗⃗⃗⃗⃗ |=(4,0)+(0,1)=(4,1), ∴P(4,1);又|BC|=√t 2+(1t)2,BC 的方程为tx +yt =1,∴点P 到直线BC 的距离为d =|4t+1t−1|√t +(1t)2,∴△PBC 的面积为S =12⋅|BC|⋅d =12⋅√t 2+(1t )2⋅|4t +1t −1|√t 2+(1t)2=12|4t +1t −1|≥12⋅|2√4t ⋅1t −1|=32, 当且仅当4t =1t ,即t =12时取等号, ∴△PBC 面积的最小值为32.故答案为:32.建立直角坐标系,由向量的坐标运算得出P 的坐标, 利用基本不等式求得△PBC 面积的最小值.本题考查了平面向量数量积的运算以及函数的最值和基本不等式的运用问题,是中档题.14. 已知函数f(x)={4x −x 2,x ≥03x,x <0,若函数g(x)=|f(x)|−3x +b 有三个零点,则实数b 的取值范围为______. 【答案】(−∞,−6)∪(−14,0]【解析】解:函数f(x)={4x −x 2,x ≥03x ,x <0,若函数g(x)=|f(x)|−3x +b 有三个零点,就是ℎ(x)=|f(x)|−3x 与y =−b 有3个交点,ℎ(x)={x −x 2,0≤x ≤4x 2−7x,x >4−3x−3x,x <0,画出两个函数的图象如图:,当x <0时,−3x −3x ≥6,当且仅当x =−1时取等号,此时−b >6,可得b <−6; 当0≤x ≤4时,x −x 2≤14,当x =12时取得最大值,满足条件的b ∈(−14,0]. 综上,b ∈(−∞,−6)∪(−14,0]. 故答案为:(−∞,−6)∪(−14,0].求出函数|f(x)−3x 的解析式,画出函数的图象,利用函数的极值,转化求解即可.| 本题考查函数的零点个数的判断,考查数形结合以及计算能力.二、解答题(本大题共12小题,共12.0分)15. 已知向量a ⃗ =(sinθ,2),b ⃗ =(cosθ,1),且a ⃗ ,b ⃗ 共线,其中θ∈(0,π2).(1)求tan(θ+π4)的值;(2)若5cos(θ−φ)=3√5cosφ,0<φ<π2,求φ的值.【答案】证明:(1)∵a⃗//b⃗ ,∴sinθ−2cosθ=0,即tanθ=2,∴tan(θ+π4)=1+tanθ1−tanθ=1+21−2=−3;(2)由(1)知tanθ=2,又θ∈(0,π2),∴sinθ=2√55,cosθ=√55,∴5cos(θ−ϕ)=3√5cosϕ∴5(cosθcosϕ+sinθsinϕ)=3√5cosϕ,即√5cosϕ+2√5sinϕ=3√5cosϕ,∴cosϕ=sinϕ,即tanϕ=1又0<ϕ<π2,∴ϕ=π4.【解析】(1)根据向量共线建立方程关系求出tanθ的值,结合两角和差的正切公式进行求解即可.(2)由两角和差的余弦公式展开进行求解即可.本题主要考查三角函数的化简和求解,利用两角和差的正切公式和余弦公式是解决本题的关键.16.已知在如图的多面体中,AE⊥底面BEFC,AD//EF//BC,BE=AD=EF=12BC= 2,G是BC的中点.(1)求证:AB//平面DEG;(Ⅱ)求证:EG⊥平面BDF;(Ⅲ)若AE=BE=EG,求BD与平面DEG所成角的正弦值.【答案】解:(Ⅰ)证明:∵AD//EF ,EF//BC , ∴AD//BC ,又∵BC =2AD ,G 是BC 的中点,∴AD//BG ,且AD =BG ;∴四边形ADGB 是平行四边形, ∴AB//DG ,又AB ⊄平面DEG ,DG ⊂平面DEG ,∴AB//平面DEG ;(Ⅱ)证明:连接GF ,四边形ADFE 是矩形,∴DF ⊥EG ,AE ⊥底面BEFC , ∴DF ⊥平面BCFE , 又EG ⊂平面BCFE , ∴DF ⊥EG ,又EF//BG ,且EF =BG ,EF =BE ,∴四边形BGFE 为菱形, ∴BF ⊥EG ,又BF ∩DF =F ,BF ⊂平面BFD ,DF ⊂平面BFD , ∴EG ⊥平面BDF ; (Ⅲ)设BF ∩EG =O ,连接OD , 由几何图形的对称性知,∠BDO 是BD 与平面DEG 所成的角,BE =2,∴EO =1,OB =√3,BD =√22+(2√3)2=4,OD =√(2√2)2−12=√7; ∴cos∠BDO =2√7)2√3)22×4×√7=5√714; ∴sin∠BDO =1−(5√714)=√2114, ∴BD 与平面DEG 所成角的正弦值为√2114.【解析】(Ⅰ)由题意证明四边形ADGB 是平行四边形,得出AB//DG ,从而证明AB//平面DEG ;(Ⅱ)证明DF ⊥平面BCFE ,得出DF ⊥EG ,再由四边形BGFE 为菱形,得出BF ⊥EG ,从而证明EG ⊥平面BDF ;(Ⅲ)设BF ∩EG =O ,连接OD ,得出∠BDO 是BD 与平面DEG 所成的角,利用余弦定理求得cos∠BDO ,再由同角的三角函数关系求得sin∠BDO 的值. 本题考查了空间中的平行与垂直关系的应用问题,也考查了直线与平面所成角的计算问题,是综合题.17. 如图,在P 地正西方向8km 的A 处和正东方向1km 的B 处各有一条正北方向的公路AC 和BD ,现计划在AC 和BD 路边各修建一个物流中心E 和F ,为缓解交通压力,决定修建两条互相垂直的公路PE 和PF ,设∠EPA =α(0<α<π2). (1)为减少对周边区域的影响,试确定E ,F 的位置,使△PAE 与△PFB 的面积之和最小;(2)为节省建设成本,试确定E,F的位置,使PE+PF的值最小.【答案】(1)在Rt△PAE中,由题意可知∠APE=α,AP=8,则AE=8tanα.所以S△APE=12PA×AE=32tanα.…(2分)同理在Rt△PBF中,∠PFB=α,PB=1,则BF=1tanα所以S△PBF=12PB×BF=12tanα.…(4分)故△PAE与△PFB的面积之和为32tanα+12tanα…(5分)32tanα+12tanα≥2√32tanα⋅12tanα=8当且仅当32tanα=12tanα,即tanα=18时取等号,故当AE=1km,BF=8km时,△PAE与△PFB的面积之和最小.…(6分) (2)在Rt△PAE中,由题意可知∠APE=α,则PE=8cosα同理在Rt△PBF中,∠PFB=α,则PF=1sinα令f(α)=PE+PF=8cosα+1sinα,0<α<π2…(8分)则f′(α)=8sinαcos2α−cosαsin2α=8sin3α−cos3αsin2αcos2α(10分)f′(α)=0得tanα=12所以tanα=12,f(α)取得最小值,…(12分)此时AE=AP⋅tanα=8×12=4,BF=BPtanα=2当AE为4km,且BF为2km时,PE+PF的值最小.…(14分)【解析】(1)借助三角函数求出△PAE与△PFB的面积,利用基本不等式性质,求出E,F的位置;(2)借助三角函数求出PE+PF,利用导数求出当AE为4km,且BF为2km时,PE+PF 的值最小.本题考查了学生解三角形的能力,基本不等式的性质和导数的应用,本题对学生的综合应用知识的能力有较高的要求.18.给定椭圆C:x2a2+y2b2=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为√32,且经过点(0,1).(1)请求出椭圆C的标准方程;(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2√2,求实数m的值.【答案】解:(1)记椭圆C的半焦距为c,由题意,得b=1,ca =√32,c2=a2+b2,解得a=2,b=1,故椭圆C的标准方程为:x24+y2=1.(2)由(1)知,椭圆C的方程为x24+y2=1,圆C1的方程为x2+y2=5.显然直线l的斜率存在.设直线l的方程为y=kx+m,即kx−y+m=0.因为直线l与椭圆C有且只有一个公共点,故方程组{y=kx+mx24+y2=1(∗)有且只有一组解.由(∗)得(1+4k2)x2+8kmx+4m2−4=0.从而△=(8km)2−4(1+4k2)(4m2−4)=0.化简,得m2=1+4k2.①因为直线l被圆x2+y2=5所截得的弦长为2√2,所以圆心到直线l的距离d=√5−2=√3.即2=√3.②由①②,解得k2=2,m2=9.因为m>0,所以m=3.【解析】(1)记椭圆C的半焦距为c.由题意,得b=1,ca =√32,由此能求出a,b.(2)由(1)知,椭圆C的方程为x24+y2=1,圆C1的方程为x2+y2=5.设直线l的方程为y=kx+m,由{y=kx+mx24+y2=1,得(1+4k2)x2+8kmx+4m2−4=0.由此利用根的判别式、弦长公式、圆心到直线的距离,结合知识点能求出m.本题主要考查实数值的求法,考查直线与椭圆、圆等知识,同时考查解析几何的基本思想方法和运算求解能力,属于中档题.19.已知函数f(x)=e x−c,g(x)=13ax3+12bx2+cx(a,b,c∈R).(1)若ac<0,求证:函数y=g(x)有极值;(2)若a=b=0,且函数y=f(x)与y=g(x)的图象有两个相异交点,求证:c>1.【答案】证明:(1)由g(x)=13ax 3+12bx 2+cx 得g′(x)=ax 2+bx +c ,∵ac <0,∴△>0且a ≠0. …(4分)∴函数g′(x)有两个零点,则可设为g′(x)=a(x −α)(x −β)∴若x 1<α<x 2<β<x 3,则g′(x 1)g′(x 2)<0,g′(x 2)g′(x 3)<0. ∴g(x)有极值. …(6分)(2)由e x −c =cx ,得e x −cx −c =0, 记ℎ(x)=e x −cx −c ,则ℎ′(x)=e x −c ,由函数y =f(x)与y =g(x)的图象有两个相异交点知函数ℎ(x)有两互异零点…(9分) 若c ≤0,ℎ(x)单调递增,则ℎ(x)最多1个零点,矛盾. …(11分) ∴c >0.此时,令ℎ′(x)=0,则x =lnc . 列表:min 【解析】(1)求导数,函数g′(x)有两个零点,则可设为g′(x)=a(x −α)(x −β),利用零点存在定理,即可证明结论;(2)记ℎ(x)=e x −cx −c ,则ℎ′(x)=e x −c ,由函数y =f(x)与y =g(x)的图象有两个相异交点知函数ℎ(x)有两互异零点,即可得出结论.本题考查导数知识的综合运用,考查函数的极值,考查学生分析解决问题的能力,属于中档题.20. 已知数列{a n }中a 1=1,a n+1={13a n +n a n −3n(n 为偶数)(n 为奇数).(1)是否存在实数λ,使数列{a 2n −λ}是等比数列?若存在,求λ的值;若不存在,请说明理由;(2)若S n 是数列{a n }的前n 项和,求满足S n >0的所有正整数n . 【答案】解:(1)设b n =a 2n −λ, 因为b n+1b n=a 2n+2−λa 2n −λ=13a 2n+1+(2n+1)−λa 2n −λ=13(a 2n−6n)+(2n+1)−λa 2n −λ=13a 2n+1−λa 2n −λ…2分若数列{a 2n −λ}是等比数列,则必须13a 2n+1−λa 2n −λ=q(常数),即(13−q)a 2n +(q −1)λ+1=0,即{13−q =0(q −1)λ+1=0⇔{q =13λ=32…5分此时b 1=a 2−32=13a 1+1−32=−16≠0,所以存在实数λ=32,使数列{a 2n −λ}是等比数列…6分 (2)由(1)得{b n }是以−16为首项,13为公比的等比数列, 故b n =(−16)⋅(13)n−1=−12⋅(13)n ,即a 2n =−12⋅(13)n +32…8分由a 2n =13a 2n−1+(2n −1)得a 2n−1=3a 2n −3(2n −1)=−12⋅(13)n−1−6n +152, (10)分所以a 2n−1+a 2n =−12[(13)n−1+(13)n ]−6n +9=−2⋅(13)n −6n +9,S 2n =(a 1+a 2)+(a 3+a 4)+⋯+(a 2n−1+a 2n ) =−2[13+(13)2+⋯+(13)n ]−6(1+2+⋯+n)+9n=−2⋅13[1−(13)n ]1−13−6⋅n(n +1)2+9n =(13)n −1−3n 2+6n =(13)n −3(n −1)2+2…12分 显然,当n ∈N ∗时,{S 2n }单调递减,又当n =1时,S 2=73>0,当n =2时,S 4=−89<0,所以当n ≥2时,S 2n <0; S 2n−1=S 2n −a 2n =32⋅(13)n −52−3n 2+6n .同理,当且仅当n =1时,S 2n−1>0,综上,满足满足S n >0的所有正整数n 为1和2…16分 【解析】(1)设b n =a 2n −λ,依题意,可得b n+1b n=a 2n+2−λa 2n −λ=13a 2n+1−λa 2n −λ,若数列{a 2n −λ}是等比数列,则必须13a 2n+1−λa 2n −λ=q(常数),整理得{13−q =0(q −1)λ+1=0,求得{q =13λ=32,于是存在实数λ=32,使数列{a 2n −λ}是等比数列;(2)由(1)得{b n }是以−16为首项,13为公比的等比数列,于是a 2n−1+a 2n =−12[(13)n−1+(13)n ]−6n +9=−2⋅(13)n −6n +9,利用分组求和的方法,分别用等比数列的求和公式与等差数列的求和公式即可求得S 2n =(13)n −3(n −1)2+2,分n =1与2讨论,计算即可得到答案.本题考查数列递推关系式的应用,综合考查等比数列的性质、分组求和,考查分类讨论思想及抽象思维、逻辑思维、综合运算能力,属于难题.21. 如图,已知AB 是圆O 的直径,P 是上半圆上的任意一点,PC 是∠APB 的平分线,E 是AB ⏜的中点.求证:直线PC 经过点E . 【答案】证明:∵AB 是圆O 的直径,P 是上半圆上的任意一点,PC 是∠APB 的平分线,E 是AB ⏜的中点, ∴AE⏜=BE ⏜, ∴∠APE =∠BPE ,∵PC 是∠APB 的平分线, ∴直线PC 经过点E .【解析】由AE⏜=BE ⏜,得到∠APE =∠BPE ,由此能证明直线PC 经过点E . 本题考查角平分线的证明,是基础题,解题时要认真审题,注意圆、直线方程、圆周角定理的合理运用.22. 已知矩阵M =[0ab 0]满足:M a i ⃗⃗⃗ =λi a i ⃗⃗⃗ ,其中λi (i =1,2)是互不相等的实常数,a i ⃗⃗⃗ (i =1,2)是非零的平面列向量,λ1=1,a 2⃗⃗⃗⃗ =[11],求矩阵M . 【答案】解:由题意,λ1,λ2是方程f(λ)=∣∣∣λ−a −b λ∣∣∣=λ2−ab =0的两根, 因为λ1=1,所以ab =1;又因为Ma 2=λ2a 2,所以[0a b 0]⋅[11]=λ2[11], 从而{b =λ2a=λ2,所以λ22=ab =1,因为λ1≠λ2,所以λ2=−1,从而a =b =−1, 故矩阵M =[0−1−10]. 【解析】由题意λ1,λ2是方程f(λ)=∣∣∣λ−a −b λ∣∣∣=λ2−ab =0的两根, 由λ1=1得ab =1,由Ma 2=λ2a 2得[0a b]⋅[11]=λ2[11], 求得λ22=ab =1,再由λ1≠λ2求得a 、b 的值即可.本题考查了矩阵变换的应用问题,是基础题.23. 已知两个动点P ,Q 分别在两条直线l 1:y =x 和l 2:y =−x 上运动,且它们的横坐标分别为角θ的正弦,余弦,θ∈[0,π].记OM ⃗⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +OQ⃗⃗⃗⃗⃗⃗ ,求动点M 的轨迹的普通方程. 【答案】解:设M(x,y),则{y =sinθ−cosθx=sinθ+cosθ…(2分) 两式平方相加得x 2+y 2=2. …(5分) 又x =√2sin(θ+π4),y =√2sin(θ−π4),θ∈[0,π],所以x ∈[−1,√2],y ∈[−1,√2].…(8分)所以动点M 轨迹的普通方程为x 2+y 2=2(x,y ∈[−1,√2]).…(10分)【解析】设M(x,y),根据OM ⃗⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +OQ ⃗⃗⃗⃗⃗⃗ ,可得{y =sinθ−cosθx=sinθ+cosθ两式平方相加得动点M 的轨迹的普通方程.本题考查了轨迹方程的求法,考查了数学转化思想方法,比较基础.24. 已知a >0,b >0,证明:(a 2+b 2+ab)(ab 2+a 2b +1)≥9a 2b 2. 【答案】证明:因为a >0,b >0,所以a 2+b 2+ab ≥3√a 2⋅b 2⋅ab 3=3ab >0,(当且仅当a =b 时,取等号) ab 2+a 2b +1≥3√ab 2⋅a 2b ⋅13=3ab >0,(当且仅当a =b =1时,取等号) 所以(a 2+b 2+ab)(ab 2+a 2b +1)≥9a 2b 2.【解析】运用基本不等式,即可证明结论.本题考查不等式的证明,考查基本不等式的运用,属于中档题.25. 一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的A ,B ,C ,D ,E 五种商品有购买意向.已知该网民购买A ,B 两种商品的概率均为34,购买C ,D 两种商品的概率均为23,购买E 种商品的概率为12.假设该网民是否购买这五种商品相互独立.(1)求该网民至少购买4种商品的概率;(2)用随机变量η表示该网民购买商品的种数,求η的概率分布和数学期望. 【答案】解:(1)记“该网民购买i 种商品”为事件A i ,i =4,5,则:P(A 5)=34×34×23×23×12=18,P(A 4)=34×34×23×23×(1−12)+C 2134×(1−34)×23×23×12+C 2123×(1−23)×34×34×12=13,…(2分) 所以该网民至少购买4种商品的概率为 P(A 5)+P(A 4)=18+13=1124. 答:该网民至少购买4种商品的概率为1124.…(3分) (2)随机变量η的可能取值为0,1,2,3,4,5,P(η=0)=(1−34)×(1−34)×(1−23)×(1−23)×(1−12)=1288,P(η=1)=C 2134×(1−34)×(1−23)×(1−23)×(1−12)+C 2123×(1−23)×(1−34)×(1−34)×(1−12)+12×(1−34)×(1−34)×(1−23)×(1−23)=11288,P(η=2)=34×34×(1−23)×(1−23)×(1−12)+23×23×(1−34)×(1−34)×(1−12)+C 21(1−23)×23×(1−34)×(1−34)×12+C 2134×(1−34)×(1−23)×(1−23)×12+C 2134×(1−34)×C 2123×(1−23)×(1−12)=47288,P(η=3)=1−P(η=0,1,2,4,5)=1−1288−11288−47288−13−18=97288,P(η=4)=P(A 4)=13,P(η=5)=P(A 5)=18.…(8分) 所以:随机变量η的概率分布为:故Eη=0×1288+1×11288+2×47288+3×97288+4×13+5×18=103.…(10分)【解析】(1)记“该网民购买i 种商品”为事件A i ,i =4,5,由互斥事件概率加法公式能求出该网民至少购买4种商品的概率.(2)随机变量η的可能取值为0,1,2,3,4,5,分别求出相应的概率,由此能求出η的概率分布和数学期望.本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合的合理运用,是中档题.26. 设n 个正数a 1,a 2,…,a n 满足a 1≤a 2≤⋯≤a n (n ∈N ∗且n ≥3).(1)当n =3时,证明:a 1a 2a 3+a 2a 3a 1+a 3a 1a 2≥a 1+a 2+a 3; (2)当n =4时,不等式a 1a 2a 3+a 2a 3a 4+a 3a 4a 1+a 4a 1a 2≥a 1+a 2+a 3+a 4也成立,请你将其推广到n(n ∈N ∗且n ≥3)个正数a 1,a 2,…,a n 的情形,归纳出一般性的结论并用数学归纳法证明.【答案】(1)证明:因为a n (n ∈N ∗且n ≥3)均为正实数, 左−右=12(a 1a 3a 2+a 1a 2a 3−2a 1)+12(a 2a 3a 1+a 1a 2a 3−2a 2)+12(a 2a 3a 1+a 1a 3a 2−2a 3)≥12(2√a 1a 3a 2×a 1a 2a 3−2a 1)+12(2√a 2a 3a 1×a 1a 2a 3−2a 2)+12(2√a 2a 3a 1×a 1a 3a 2−2a 3)=0,所以,原不等式a 2a 3a 1+a 1a 3a 2+a 1a 2a 3≥a 1+a 2+a 3成立. …(4分)(2)解:归纳的不等式为:a 1a 2a 3+a 2a 3a 4+⋯+a n−2a n−1a n+a n−1a n a 1+a n a 1a 2≥a 1+a 2+⋯+a n (n ∈N ∗且n ≥3).…(5分) 记F n =a 1a 2a 3+a 2a 3a 4+⋯+a n−2a n−1a n+a n−1a n a 1+a n a 1a 2−(a 1+a 2+⋯+a n ),当n =3(n ∈N ∗)时,由(1)知,不等式成立; 假设当n =k(k ∈N ∗且k ≥3)时,不等式成立,即F k =a 1a 2a 3+a 2a 3a 4+⋯+a k−2a k−1a k+a k−1a k a 1+a k a 1a 2−(a 1+a 2+⋯+a k )≥0.则当n =k +1时,F k+1=a 1a 2a 3+a 2a 3a 4+⋯+a k−2a k−1a k+a k−1a k a k+1+a k a k+1a 1+a k+1a 1a 2−(a 1+a 2+⋯+a k +a k+1) =F k +a k−1a k a k+1+a k a k+1a 1+a k+1a 1a 2−a k−1a k a 1−a k a 1a 2−a k+1…(7分)=F k +a k−1a k (1a k+1−1a 1)+a k+1(a k a 1−1)+a 1a 2(a k+1−a k )≥0+a k 2(1a k+1−1a 1)+a k+1(a k a 1−1)+a 1a k(a k+1−a k )=(a k+1−a k )(a k a 1+a 1a k−a k+1+a k a k+1),因为a k+1≥a k ,ak a 1+a1a k ≥2,a k+1+a k a k+1≤a k+1+a k+1a k+1=2,所以F k+1≥0,所以当n =k +1,不等式成立. …(9分) 综上所述,不等式a 1a 2a 3+a 2a 3a 4+⋯+a n−2a n−1a n+a n−1a na 1+a n a 1a 2≥a 1+a 2+⋯+a n (n ∈N ∗且n ≥3)成立.…(10分)【解析】(1)利用作差法证明即可; (2)归纳的不等式为:a 1a 2a 3+a 2a 3a 4+⋯+a n−2a n−1a n+a n−1a n a 1+a n a 1a 2≥a 1+a 2+⋯+a n (n ∈N ∗且n ≥3),再用数学归纳法进行证明.本题考查等式的证明,数学归纳法的证明方法的应用,考查计算能力与逻辑推理能力.。
南京市盐城市届高三年级第二次模拟考试含解析.doc

南京市、盐城市2018届高三年级第二次模拟考试物 理2018.3本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.满分120分,考试时间100分钟.第I 卷(选择题共31分)一、单项选择题:本题共5小题,每小题3分,共15分.每小题只有一个选项符合题 意. 1.在国际单位制(SI )中,力学和电学的基本单位有m (米)、kg (千克)、s (秒)、A (安培).库仑定律F = k^中k 的单位用上述基本单位可表示为()A. kg ・ n?・ A 2 • s 1B. kg ・ m'・ A ?・ s 2C. kg • m 3 • A 2 • s 'D. kg • • A ? • s 42•如图甲所示为某公司研制的“双动力智能型救援机器人”(又被网友称为“麻辣小龙 虾”),其长长的手臂前端有两个对称安装的“铁夹”.在某次救援活动中,“麻辣小龙虾” 用铁夹恰好竖直抓取到重量为G 的长方形水泥制品,水泥制品在空中处于静止状态,如图乙所示,贝9()A. 水泥制品受到的摩擦力大小一定等于GB. 水泥制品受到的摩擦力方向可能竖直向下C. 若铁夹的位置稍向上移,水泥制品受到的摩擦力变大D. 若增大铁夹对水泥制品的挤压,水泥制品受到的摩擦力变大3. 在体育课上,某同学练习投篮,他站在罚球线处用力将篮球从手中投出,如图所示, 篮球约以1 m/s 的速度撞击篮筐.己知篮球质量约为0.6 kg,篮筐离地高度约为3 m,则该 同学投篮时对篮球做的功约为()A. 1 JB.10JC. 30 JD. 50 J甲 乙4.如图所示,理想变压器的原、副线圈的匝数比为2: 1,在原、副线圈的回路中分别接有阻值相同的电阻R,原线圈一侧接有电压为220 V的正弦交流电源,设副线圈回路中电阻两端的电压为U,原、副线圈冋路屮电阻R上消耗的功率之比为k,则()A.U=110 VB. U=440VC. k=|D. k=45.如图所示,在磁感应强度为B,范圉足够大的水平匀强磁场内,固定着倾角为。
2018南京市盐城市届高三年级第二次模拟考试含解析
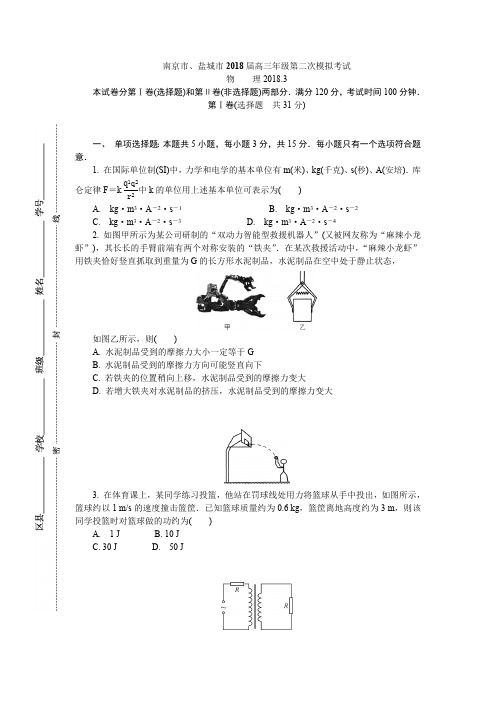
南京市、盐城市2018届高三年级第二次模拟考试物 理2018.3本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分120分,考试时间100分钟.第Ⅰ卷(选择题 共31分)一、 单项选择题:本题共5小题,每小题3分,共15分.每小题只有一个选项符合题意.1. 在国际单位制(SI)中,力学和电学的基本单位有m(米)、kg(千克)、s(秒)、A(安培).库仑定律F =k 中k 的单位用上述基本单位可表示为( ) q 1q 2r 2A. kg ·m 3·A -2·s -1 B. kg ·m 3·A -2·s -2C. kg ·m 3·A -2·s -3D. kg ·m 3·A -2·s -42. 如图甲所示为某公司研制的“双动力智能型救援机器人”(又被网友称为“麻辣小龙虾”),其长长的手臂前端有两个对称安装的“铁夹”.在某次救援活动中,“麻辣小龙虾”用铁夹恰好竖直抓取到重量为G 的长方形水泥制品,水泥制品在空中处于静止状态,如图乙所示,则( )A. 水泥制品受到的摩擦力大小一定等于GB. 水泥制品受到的摩擦力方向可能竖直向下C. 若铁夹的位置稍向上移,水泥制品受到的摩擦力变大D. 若增大铁夹对水泥制品的挤压,水泥制品受到的摩擦力变大3. 在体育课上,某同学练习投篮,他站在罚球线处用力将篮球从手中投出,如图所示,篮球约以1 m/s 的速度撞击篮筐.已知篮球质量约为0.6 kg ,篮筐离地高度约为3 m ,则该同学投篮时对篮球做的功约为( )A. 1 JB. 10 JC. 30 JD. 50 J4. 如图所示,理想变压器的原、副线圈的匝数比为2∶1,在原、副线圈的回路中分别接有阻值相同的电阻R ,原线圈一侧接有电压为220 V 的正弦交流电源,设副线圈回路中电阻两端的电压为U ,原、副线圈回路中电阻R 上消耗的功率之比为k ,则( )A. U =110 VB. U =440 VC. k =D. k =4 145. 如图所示,在磁感应强度为B ,范围足够大的水平匀强磁场内,固定着倾角为θ的绝缘斜面,一个质量为m 、电荷量为-q 的带电小物块以初速度v 0沿斜面向上运动,小物块与斜面间的动摩擦因数为μ.设滑动时电荷量不变,在小物块上滑过程中,其加速度大小a 与时间t 的关系图象,可能正确的是( )二、 多项选择题:本题共4小题,每小题4分,共16分.每小题有多个选项符合题意,全部选对的得4分,选对但不全的得2分,错选或不答的得0分.6. 光敏电阻是用硫化镉或硒化镉等半导体材料制成的特殊电阻器,其电阻值会随光照强度的增大而减小,光敏电阻的这种特殊性能,在科技生活中得到广泛应用.某应用电路如图所示,R 1、R 2为定值电阻,L 为小灯泡,R 3为光敏电阻,当照射光强度增大时( )A. 电压表的示数增大B. R 2中电流减小C. 小灯泡的功率增大D. R 3的功率增大7. 某试验卫星在地球赤道平面内一圆形轨道上运行,每5天对某城市访问一次,下列关于该卫星的描述中正确的是( )A. 角速度可能大于地球自转角速度B. 线速度可能大于第一宇宙速度C. 高度一定小于同步卫星的高度D. 向心加速度一定小于地面的重力加速度8. 如图所示,虚线a 、b 、c 是电场中的三个等势面,相邻等势面间的电势差相等,即U ab =U bc ,实线为一个带负电的质点仅在电场力作用下的运动轨迹,P 、Q 是轨迹上的两点.下列说法中正确的是( )A. 三个等势面中,等势面a 的电势最低B. 质点通过Q 点时的电势能比通过P 点时小C. 质点通过Q 点时的加速度比通过P 点时大D. 质点通过Q 点时的加速度的方向一定与等势面a 垂直9. 如图所示,两质量相等的物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑.弹簧开始时处于原长,运动过程中始终处在弹性限度内,在物块A上施加一个水平恒力F,A、B从静止开始运动到第一次速度相等的过程中,下列说法中正确的有( )A. A的加速度先增大后减小B. B的加速度一直增大C. 当A、B的速度相等时,弹簧的弹性势能最大D. 当A、B的加速度相等时,两者的动能之差最大第Ⅱ卷(非选择题 共89分)三、简答题:本题分必做题(第10、11题)和选做题(第12题)两部分,共42分.请将解答填写在相应的位置.【必做题】10. (8分)在探究物体质量一定时加速度与力的关系实验中,小明同学做了如图甲所示的实验改进,在调节桌面水平后,添加了用力传感器来测细线中的拉力.(1) 关于该实验的操作,下列说法正确的是________.A. 必须用天平测出砂和砂桶的质量B. 一定要保证砂和砂桶的总质量远小于小车的质量C. 应当先释放小车,再接通电源D. 需要改变砂和砂桶的总质量,打出多条纸带(2) 实验得到如图乙所示的纸带,已知打点计时器使用的交流电源的频率为50 Hz,相邻两计数点之间还有四个点未画出,由图中的数据可知,小车运动的加速度大小是________m/s2.(计算结果保留三位有效数字)(3) 由实验得到小车的加速度a与力传感器示数F的关系如图丙所示.则小车与轨道的滑动摩擦力F f=________N.(4) 小明同学不断增加砂子质量重复实验,发现小车的加速度最后会趋近于某一数值,从理论上分析可知,该数值应为________m/s2.11. (10分)某同学欲测量一卷粗细均匀的、阻值约为100 Ω的金属漆包线的长度,备选器材如下:A. 量程为5 mA、内阻r1=50 Ω的电流表B. 量程为0.6 A、内阻r2=0.2 Ω的电流表○,A2)C. 量程为6 V、内阻r3约为15 kΩ的电压表○,V)D. 最大阻值为15 Ω、最大允许电流为2 A的滑动变阻器E. 定值电阻R1=5 ΩF. 电动势E=6 V、内阻很小的直流电源G. 开关一个、导线若干H. 螺旋测微器(1) 已知做成这种漆包线芯的金属丝的电阻率为ρ,若金属丝的电阻用R表示,直径用d表示,则这一卷漆包线的长度L=________.(2) 该同学用螺旋测微器测金属丝的直径如图甲所示,则螺旋测微器的示数d=________mm.(3) 为了尽可能精确地测量该金属丝的电阻,电流表应选用________(选填“A”或“B”),请在方框中画出实验原理电路图.(4) 若该同学在测量金属丝直径时没有去除漆包线表面的绝缘漆,这会使实验测得该漆包线的长度与真实值相比________(选填“偏大”或“偏小”).12. 【选做题】本题包括A、B、C三小题,请选定其中两题作答.若三题都做,则按A、B两小题评分.A. (选修模块33)(12分)(1) 下列说法中正确的是________.A. 空气中PM2.5颗粒的无规则运动属于分子热运动B. 某物体温度升高,组成该物体的分子的平均动能一定增大C. 云母片导热性能各向异性,是由于该物质的微粒在空间的排列不规则D. 空气相对湿度越大,则空气中水蒸气压强越接近饱和汽压(2) 两分子间的作用力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0,甲分子固定在坐标原点O,乙分子在分子力作用下从图中a点由静止开始运动.在r>r0阶段,乙分子的动能________(选填“增大”“减小”或“先增大后减小”),两分子的势能________(选填“增大”“减小”或“先减小后增大”).(3) 如图所示,一圆柱形绝热汽缸竖直放置,通过绝热活塞封闭着一定质量的理想气体,活塞的质量为m ,横截面积为S ,与气缸底部相距h ,此时封闭气体的温度为T.现通过电热丝缓慢加热气体,当气体吸收热量Q 时,气体温度上升到1.5T.已知大气压强为p 0,重力加速度为g ,不计活塞与汽缸的摩擦.求:① 加热后活塞到汽缸底部的距离;② 加热过程中气体的内能增加量.B. (选修模块3-4)(12分)(1) 我国成功研发的反隐身先进米波雷达堪称隐身飞机的克星,它标志着我国雷达研究创新的里程碑.米波雷达发射无线电波的波长在1~10 m 范围内,则对该无线电波的判断正确的有________.A. 必须依靠介质传播B. 频率比厘米波的频率低C. 比可见光更容易产生衍射现象D. 遇到厘米波有可能产生干涉现象(2) 如图所示为频率f =1 Hz 的波源产生的横波.图中虚线左侧为A 介质,右侧为B 介质,则该波在A 、B 两种介质中传播的速度大小之比v A ∶v B =________;若图示时刻为t =0时刻,且此时x =14 m 处的质点振动方向向上,则t =1.75 s 时,处于x =6 m 的质点位移为________cm.(3) 两束平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图所示.已知其中一条光线沿直线穿过玻璃,它的入射点是O ;另一条光线的入射点为A ,穿过玻璃后两条光线交于P 点.已知玻璃截面的圆半径为R ,OA =,OP =R ,光在真空中传播的速R 23度为c.求:① 玻璃材料的折射率;② 入射点为A 的激光在玻璃中传播的时间.。
江苏省盐城中学2018届高三上学期期末考试英语试题Word版含答案

江苏省盐城中学2018届高三上学期期末考试英语试题第一部分听力(共两节,满分20分)第一节(共5小题;每小题1分,满分5分)听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19. 15.B. £9. 18.C. £9.15.答案是C。
1. Why does the man need a map?A. To tour Manchester.B. To find a restaurant.C. To learn about China.2. What does the woman want to do for vacation?A. Go to the beach.B. Travel to Colorado.C. Learn to snowboard.3. What will the man probably do?A. Take the job.B. Refuse the offer.C. Change the working hours.4. What does the woman say about John?A. He won’t wait for her.B. He won’t come home today.C. He won’t be on time for dinner.5. What will the speakers probably do next?A. Order some boxes.B. Go home and rest.C. Continue working.第二节(共15小题;每小题1分,满分15分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
江苏省盐城中学2018届高三上学期期末考试数学试题(PDF版)

3 ,1 2
10. 设 m, n 是两条不同的直线, , , 是三个不同的平面,给出下列四个命题,其中正 确命题的序号是 ▲ .①② ②若 ∥ , ∥ , m ⊥ ,则 m ⊥ ④若 m , n , m ∥ n ,则 ∥ . ①若 m ⊥ , n ∥ ,则 m ⊥ n ③若 , ,则 ;
DE 6 sin A 2 sin A
BC CD ,又∠BDC=2A,得 sin BDC sin B
在 BCD 中
证明:(1)略 (2)∵ PC ⊥底面 ABCD , AC 底面 ABCD ∴ PC ⊥ AC
D
2 CD 3 6 3 2 ,∴ CD ∴ CD 解得 cos A ,所以 A = 4 sin 2 A sin 2 A 2 sin A sin 2 A 2 sin 3 17.我校为丰富师生课余活动,计划在一块直角三角形 ABC 的空地上修建一个占地面积 为 S (平方米)的矩形 AMPN 健身场地.如图,点 M 在 AC 上,点 N 在 AB 上,且 P 点在斜边 BC 上.已知 ACB 60 , | AC | 30 米, AM = x 米, x [10,20 ] .设矩
P 向 圆 C2 所 作 的 两 条 切 线 PA, PB 且 APB 60 , 则 椭 圆 C1 的 离 心 率 的 取 值 范 围 是
▲ .
a aq aq 2 , 2 2 5 1 5 1 ,又 得 q 2 2 2 2 1 q q aq aq a,
a 2 2a 1 ,解得 3 a 1 . 4
8.若 log 4 (a 4b) log 2 ab ,则 a b 的最小值是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省盐城中学2018届高三考前热身2数学试题一、填空题1.已知集合}31|{<<-=x x M ,}12|{<<-=x x N ,则=N M . 2.设复数z 满足5)2)(2(=--i i z ,则=z .3.某中学有高中生3500人,初中生1500人.为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n 的样本,已知从高中生中抽取70人,则n 为 . 4.执行如图所示的流程图,则输出S 的值为 .5.已知2tan =θ,则=θθcos sin .6.应半径为2cm 的半圆形纸片卷成一个圆锥筒,则这个圆锥筒的高为 cm .7.从甲、乙、丙、丁4个人中随机选取两人,则甲、乙两人中有且只有一个被选取的概率为 .8.已知)0,(),0,(21c F c F -为椭圆)0(12222>>=+b a by a x 的两个焦点,P 为椭圆上一点,且221c PF =⋅,则此椭圆离心率的取值范围是 .9.设{}n a 是由正数组成的等比数列,n S 为其前n 项和,已知142=a a ,73=S ,则=5S . 10.从边长为10cm 16cm ⨯的矩形纸板的四角截去四个相同的小正方形,作成一个无盖的 盒子,则盒子容积的最大值为 3cm .11.已知正实数b a ,满足111=-++ba b a ,则b a 23+的最小值为 . 12.若斜率互为相反数且相交于点)1,1(P 的两条直线被圆O :422=+y x 所截得的弦长之比为26,则这两条直线的斜率之积为 . 13.在△ABC 中,AC AB ⊥,tAB 1=,t AC =,P 是△ABC 所在平面内一点,若||||AC AB AP =△PBC 面积的最小值为 . 14.已知函数⎪⎩⎪⎨⎧<≥-=0,30,4)(2x xx x x x f ,若函数b x x f x g +-=3|)(|)(有三个零点,则实数b的取值范围为 . 二、解答题15.已知向量)1,(cos ),2,(sin θθ==,且,共线,其中π2(0,)θ∈. (1)求)4tan(πθ+的值;(2)若ϕϕθcos 53)cos(5=-,20πϕ<<,求ϕ的值.16.在如图多面体中,⊥AE 底面BEFC ,BC EF AD ////,BC EF AD BE 21===,G是BC 的中点.(1)证明://AB 平面DEG ; (2)证明:⊥EG 平面BDF .17.如图,在P 地正西方向km 8的A 处和正东方向km 1的B 处各一条正北方向的公路AC 和BD ,现计划在AC 和BD 路边各修建一个物流中心E 和F .为缓解交通压力,决定修建两条互相垂直的公路PE 和PF .设)20(παα<<=∠EPA .(1)为减少周边区域的影响,试确定F E ,的位置,使PAE ∆与PFB ∆的面积之比最小; (2)为节省建设成本,试确定F E ,的位置,使PF PE +的值最小.18.给定椭圆C :22221(0)x y a b a b+=>>,称圆22221:b a y x C +=+为椭圆C 的“伴随圆”.已知椭圆C 的离心率为23,且经过点)1,0(.(1)求实数b a ,的值;(2)若过点),0(m P (0>m )的直线l 与椭圆C 有且只有一个公共点,且l 被椭圆C 的伴随圆1C 所截得的弦长为22,求实数m 的值.19.已知函数),,(2131)(,)(23R c b a cx bx ax x g c e x f x∈++=-=. (1)若0<ac ,求证:函数)(x g y =有极值;(2)若0==b a ,且函数)(x f y =与)(x g y =的图象有两个相异交点,求证:1>c .20.已知数列{}n a 中,⎪⎩⎪⎨⎧-+==+)(3)(31,111为偶数为奇数n n a n n a a a n n n .(1)是否存在实数λ,使数列}{2λ-n a 是等比数列?若存在,求λ的值;若不存在,请说明理由;(2)若n S 是数列}{n a 的前n 项和,求满足0>n S 的所有正整数n .数学Ⅱ(附加题)21.【选做题】在A ,B ,C ,D 四小题中只能选做两题.......解答时应写出文字说明、证明过程 或演算步骤.A .选修4—1:几何证明选讲已知AB 为圆O 的直径,P 是上半圆上的任意一点,PC 是APB ∠的平分线,E 是下半圆的中点.求证:直线PC 经过点E .B .选修4—2:矩阵与变换 已知矩阵⎥⎦⎤⎢⎣⎡=00a b M 满足:i i i a Ma λ=,其中)2,1(=i i λ是互不相等的实常数,)2,1(=i a i 是非零的平面列向量,11=λ,⎥⎦⎤⎢⎣⎡=112a ,求矩阵M .C .选修4—4:坐标系与参数方程已知两个动点Q P ,分别在两条直线x y l =:1和x y l -=:2上运动,且它们的横坐标分别为角θ的正弦,余弦,],0[πθ∈,记+=,求动点M 的轨迹的普通方程.D .选修4—5:不等式选讲已知0,0>>b a ,证明:2222229)1)((b a b a ab ab b a ≥++++.【必做题】第22题、第23题,每题10分,共计20分.解答时应写出文字说明、证明过程 或演算步骤.22.一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的E D C B A ,,,,五种商品有购买意向.已知该网民购买B A ,两种商品的概率均为43,购买D C ,两种商品的概率为32,购买E 种商品的概率为21.假设该网民是否购买这五种商品相互独立. (1)求该网民至少购买4种商品的概率;(2)用随机变量η表示该网民购买商品的种数,求η的概率分布和数学期望.23.设n 个正数n a a a ,,,21 满足*21(N n a a a n ∈≤≤≤ 且)3≥n . (1)当3=n 时,证明:321213132321a a a a a a a a a a a a ++≥++; (2)当4=n 时,不等式4321214143432321a a a a a a a a a a a a a a a a +++≥+++也成立,请你将其推广到n *(N n ∈且)3≥n 个正数n a a a ,,,21 的情形,归纳出一般性的结论并用数学归纳法证明.【参考答案】一、填空题1.)1,1(- 2.i 32+ 3.100 4.19 5.52 6.3 7.32 8.]22,33[ 9.431 10.14411.53+ 12.9-或91- 13.23 14.]0,41()6,(---∞ 二、解答题15.解:(1)∵//,∴0cos 2sin =-θθ,即2tan =θ ∴)4tan(πθ+32121tan 1tan 1-=-+=-+=θθ(2)由(1)知2tan =θ,又)2,0(πθ∈,∴55cos ,552sin ==θθ, ∴ϕϕθcos 53)cos(5=-∴ϕϕθϕθcos 53)sin sin cos (cos 5=+,即ϕϕϕcos 53sin 52cos 5=+, ∴ϕϕsin cos =,即1tan =ϕ 又<0ϕ2π<,∴4πϕ=.16.证明:(1)∵BC EF EF AD //,//, ∴BC AD //又∵CD Bc 2=,G 是BC 的中点, ∴BG AD //,∴四边形ADGB 是平行四边形, ∴DG AB //.(2)连接GF ,四边形ADFE 是矩形, ∵AE DF //,⊥AE 底面BEFC , ∴⊥DF 平面BCFE ,⊂EG 平面BCFE , ∴EG DF ⊥∵BG EF //,BE EF =, ∴四边形BGFE 为菱形, ∴EG BF ⊥,又F DF BF = ,⊂BF 平面BFD ,⊂DF 平面BFD , ∴⊥EG 平面BDF .17.解:(1)在PAE Rt ∆中,由题意可知α=∠APE ,8=AP ,则αtan 8=AE所以αtan 3221=⨯=∆AE PA S APE 同理在PBF Rt ∆中,1,==∠PB PFB α,则αtan 1=BF , 所以αtan 2121=⨯=∆BF PB S PBF 故PAE ∆与PEB ∆的面积之和为8tan 21tan 322tan 21tan 32=⨯≥+αααα,当且仅当ααtan 21tan 32=,即81tan =α时,取“=”故当1=AE km ,8=BF km 时,PAE ∆与PEB ∆的面积之和最小. (2)在PAE Rt ∆中,由题意可知α=∠APE ,则αcos 8=PE 同理在PBF Rt ∆中,α=∠PFB ,则αsin 1=PF 令αααsin 1cos 8)(+=+=PF PE f ,20πα<<, 则ααααααααα223322cos sin cos sin 8sin cos cos sin 8)('-=-=f , 令0)('=αf ,得21tan =α,记21tan 0=α,, 当),0(0αα∈时,0)('<αf ,)(αf 单调减; 当)2,(0παα∈时,0)('>αf ,)(αf 单调增;所以21tan =α时,)(αf 取得最小值,此时4218tan =⨯=⋅=αAP AE ,2tan ==αBPBF 所以当AE 为km 4,且BF 为km 2时,PF PE +的值最小.18. 解:(1)记椭圆C 的半焦距为c , 由题意,得1=b ,23=a c ,222b ac += 解得1,2==b a(2)由(1)知椭圆C 的方程为1422=+y x ,圆1C 的方程为522=+y x 显然直线l 的斜率存在,设直线l 的方程为m kx y +=,即0=+-m y kx因为直线l 与椭圆C 有且只有一个公共点,故方程组⎪⎩⎪⎨⎧=++=1422y x m kx y (*)有且只有一组解由(*)得0448)41(222=-+++m kmx x k从而0)44)(41(4)8(222=-+-=∆m k km 化简得2241k m +=① 因为直线l 被圆522=+y x 所截得的弦长为22, 所以圆心到直线l 的距离325=-=d ,即31||2=+k m ②由①②,解得9,222==m k .因为0>m ,所以3=m . 19. 解:(1)cx bx ax x g ++=232131)(得c bx ax x g ++=2)(', ∵0<ac ,∴042>-=∆ac b 且0≠a∴函数)('x g 有两个零点,则可设为))(()('βα--=x x a x g ,(βα<) ∴若321x x x <<<<βα,则0)(')(',0)(')('3221<⋅<⋅x g x g x g x g ∴)(x g 有极值.(2)由cx c e x =-,得0=--c cx e x,记c cx e x h x --=)(,则c e x h x-=)(',由函数)(x f y =与)(x g y =的图象有两个相异交点知函数)(x h 有两互异零点 若)(,0)('0x h x h c >⇒≤单调递增,则)(x h 最多1个零点,矛盾 ∴0>c ,此时,令0)('=x h ,则c x ln =,列表:∴0ln )(ln )(min <-==c c c h x h ,∴1>c .20. 解:(1)设λ-=n n a b 2,因为λλλλλ---++=--=++++n n n n n n n a a n a a a b b 222122221)12(31λλλλ--+=--++-=n n n n a a a n n a 2222131)12()6(31 若数列}{2λ-n a 是等比数列,则必须有q a a n n =--+λλ22131(常数), 即01)1()31(2=+-+-λq a q n ,即⎪⎩⎪⎨⎧=+-=-01)1(031λq q ⎪⎪⎩⎪⎪⎨⎧==⇔2331λq , 此时0612313123121≠-=-+=-=a a b 所以存在实数23=λ,使数列}{2λ-n a 是等比数列. (2)由(1)得}{n b 是以61-为首项,31为公比的等比数列 故232-=n n a b 1)31(61--=n n )31(21⋅-=,即23)31(212+⋅-=n n a 由)12(31122-+=-n a a n n ,得2156)31(21)12(331212+-⋅-=--=--n n a a n n n , 所以96)31(296])31()31[(211212+--=+-+-=+--n n a a n n n n n ,)()()(2124321n n n a a a a a a S ++++++=-n n n n 92)1(6])31()31(31[22++⋅-+++-= 2)1(3)31(631)31(22+--==+--=n n n n n 显然当*N n ∈时,}{2n S 单调递减,又当1=n 时,0372>=S ,当2=n 时,0984<-=S ,所以当2≥n 时,02<n S ; n n a S S n n n n 6325)31(2322212+--=-=-, 同理,当且仅当1=n 时,012>-n S综上,满足0>n S 的所有正整数n 为1和2.附加题21.A 证明:连结OE BE AE ,,,则090=∠=∠BOE AOE因为APE ∠是圆周角,AOE ∠同弧上的圆心角 所以04521=∠=∠AOE APE 同理可得045=∠BPE ,所以PE 是APB ∠的平分线又PC 也是APB ∠的平分线,APB ∠的平分线有且只有一条,所以PC 与PE 重合,所以直线PC 经过点E .21.B 解:由题意,21,λλ是方程0)(2=-=--=ab b a f λλλλ的两根 因为11=λ,所以1=ab又因为222a Ma λ=,所以⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡1111002λb a ,从而⎩⎨⎧==22λλb a 所以122==ab λ因为21λλ≠,所以12-=λ,从而1-==b a ,故矩阵⎥⎦⎤⎢⎣⎡--=0110M 21.C 解:设),(y x M ,则⎩⎨⎧-=+=θθθθcos sin cos sin y x , 两式平方相加得222=+y x 又],0[),4sin(2),4sin(2πθπθπθ∈-=+=y x , 所以]2,1[],2,1[-∈-∈y x所以动点M 轨迹的普通方程为222=+y x (]2,1[,-∈y x ).21.D 证明:因为0,0>>b a 所以03332222>=⋅⋅≥++ab ab b a ab b a 0313132222>=⋅⋅≥++ab b a ab b a ab所以2222229)1)((b a b a ab ab b a ≥++++.22. 解(1)记“该网民购买i 种商品”为事件5,4,=i A i ,则 812132324343)(5=⨯⨯⨯⨯=A P ,31214343)321(32213232)431(43)211(32324343)(12124=⨯⨯⨯-⨯+⨯⨯⨯-⨯+-⨯⨯⨯⨯=C C A P , 所以该网民至少购买4种商品的概率为24113181)()(45=+=+A P A P . 答:该网民至少购买4种商品的概率为2411. (2)随机变量η的可能取值为0,1,2,3,4,52881)211()321()321()431()431()0(=-⨯-⨯-⨯-⨯-==ηP , 28811)321()321()431()431(21)211()431()431()321(32)211()321()321()431(43)1(1212=-⨯-⨯-⨯-⨯+-⨯-⨯-⨯-⨯+-⨯-⨯-⨯-⨯==C C P η28847)211()321()431(4321)321()321()431(4321)431()431(32)321()211()431()431(3232)211()321()321(4343)2(12121212=-⨯-⨯⨯-⨯+⨯-⨯-⨯-⨯+⨯-⨯-⨯⨯⨯-⨯+-⨯-⨯-⨯⨯+-⨯-⨯-⨯⨯==C C C C P η 288978131288472881128811)5,4,3,2,1,0(1)3(=-----==-==ηηP P , 31)()4(4===A P P η, 81)()5(5===A P P η. 所以随机变量η的概率分布列为故31081531428897328847228811128810=⨯+⨯+⨯+⨯+⨯+⨯=ηE . 23.(1)证明:因为n a (*N n ∈且3≥n )均为正实数,左-右21=)2(21)2(21)2(332113223211321213321a a a a a a a a a a a a a a a a a a a a a -++-++-+ 0)22(21)22(21)22(21323113223211321321231=-⨯+-⨯+-⨯≥a a a a a a a a a a a a a a a a a a a a a所以原不等式321213132321a a a a a a a a a a a a ++≥++成立. (2)解:归纳的不等式为:n n n n n n n a a a a a a a a a a a a a a a a a a +++≥+++++--- 21211112432321(*N n ∈且3≥n ) 记)(21211112432321n n n n n n n n a a a a a a a a a a a a a a a a a a F +++-+++++=--- , 当*N n ∈且3≥n 时,由(1)知,不等式成立;假设当k n =(*N k ∈且3≥k )时,不等式成立,即0)(21211112432321≥+++-+++++=---k k k k k k k k a a a a a a a a a a a a a a a a a a F 则当1+=k n 时,))(()()1()11(0)()1()11()(111111111112121111111211121111111212111111124323211+--++++-+-+-+++-++++---++-+-=-+-+-+≥-+-+-+=---+++=++++-++++++=k k k k k k k k k kk k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k a a a a q a a a a a a a a a a a a a a a a a a a a a a a a a F a a a a a a a a a a a a a a a a F a a a a a a a a a a a a a a a a a a a a a a F 因为,1k k a a ≥-2,21111111=+≤+≥+++++-k k k k k k k k a a a a a a a q a a 所以01≥+k F ,所以当1+=k n ,不等式成立综上所述,不等式n n n n n n n a a a a a a a a a a a a a a a a a a +++≥+++++--- 21211112432321(*N n ∈且3≥n )成立.。
