最新人教版高中数学选修2-1第二章《椭圆的几何性质》自我小测
人教A版高中数学高二(A)选修2-1试题 椭圆的简单几何性质

2.2.2椭圆的简单几何性质双基限时练(十一)1.椭圆x 2m +y 24=1的焦距是2,则m 的值为( ) A .5 B .8 C .5或3D .8或5解析 当焦点在x 轴上时,m =4+1=5;当焦点在y 轴上时,4=m +1,∴m =3,综上知,m =5或3.答案 C2.椭圆x 225+y 29=1与x 29-k +y 225-k =1(0<k <9)的关系为( )A .有相等的长轴B .有相等的短轴C .有相同的焦点D .有相等的焦距解析 当0<k <9时,(25-k )-(9-k )=25-9=16=c 2,∴c =4,而焦点一个在x 轴上,一个在y 轴上,∴两椭圆的焦点不同,因此,有相同的焦距,故选D.答案 D3.已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于( )A.13B.33C.12D.32解析 依题意2a =4b ,即a =2b ,又a 2=b 2+c 2,∴a 2=14a 2+c 2,即34a 2=c 2,∴c 2a 2=34,∴e =c a =32. 答案 D4.若椭圆x 216+y 2m =1的离心率为13,则m 的值为( ) A.1289 B.1289或18 C .18D.1283或6解析 当焦点在x 轴上时,a 2=16,b 2=m ,∴c 2=a 2-b 2=16-m ,∴e 2=c 2a 2=16-m 16=⎝ ⎛⎭⎪⎫132,∴m =1289,当焦点在y 轴上时,同理可求得m =18.综上知m 的值为1289或18. 答案 B5.直线y =x +1被椭圆x 24+y 22=1所截得的线段的中点坐标为( )A.⎝ ⎛⎭⎪⎫23,53B.⎝⎛⎭⎪⎫43,73 C.⎝⎛⎭⎪⎫-23,13 D.⎝⎛⎭⎪⎫-132,-172解析由⎩⎨⎧y =x +1,x 2+2y 2=4消去y ,得3x 2+4x -2=0.设直线与椭圆的交点A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-43, ∴y 1+y 2=x 1+x 2+2=23.∴AB 中点的坐标为⎝ ⎛⎭⎪⎫-23,13.答案 C6.已知F 1,F 2是椭圆x 2k +2+y 2k +1=1的左、右焦点,弦AB 过点F 1,若△ABF 2的周长是8,则椭圆的渐近线方程为________________________.解析 由题意得4k +2=8,∴k =2.∴椭圆方程为x 24+y 23=1,其渐近线方程为y =±32x .答案 y =±32x7.人造地球卫星的运行轨道是以地心为一个焦点的椭圆,设地球半径为R ,卫星近地点、远地点离地面的距离分别为r 1、r 2,则卫星运行轨道的离心率是__________.解析由题意得⎩⎨⎧a +c =r 2+R ,a -c =r 1+R ,∴2a =2R +r 1+r 2,2c =r 2-r 1. ∴e =ca =r 2-r 12R +r 1+r 2.答案 r 2-r 12R +r 1+r 28.在平面直角坐标系xOy 中,设椭圆x 2a 2+y 2b 2=1(a >b >0)的焦距为2c .以点O 为圆心,a 为半径作圆M ,若过点P (a 2c ,0)所作圆M 的两条切线互相垂直.则该椭圆的离心率为________.解析 如图,切线PA ,PB 互相垂直,又半径OA 垂直于PA ,所以△OAP 为等腰直角三角形.∴a 2c =2a ,∴e =c a =22.答案 229.椭圆y 2a 2+x 2b 2=1(a >b >0)的两焦点为F 1(0,-c ),F 2(0,c )(c >0),离心率e =32,焦点到椭圆上点的最短距离为2-3,求椭圆的方程.解 ∵椭圆的长轴的一个端点到焦点的距离最短, ∴a -c =2- 3. 又e =c a =32, ∴a =2,c = 3.∴b 2=1.∴椭圆的方程为y 24+x 2=1.10.直线l 过点M (1,1),与椭圆x 24+y 23=1相交于A ,B 两点,若AB 的中点为M ,求直线l 的方程.解 设A (x 1,y 1),B (x 2,y 2), 则x 214+y 213=1,①x 224+y 223=1,②①-②得(x 1-x 2)(x 1+x 2)4+(y 1-y 2)(y 1+y 2)3=0, ∴y 1-y 2x 1-x 2=-34·x 1+x 2y 1+y 2. 又M (1,1)为AB 的中点, ∴x 1+x 2=2,y 1+y 2=2. ∴直线l 的斜率为-34.∴直线l 的方程为y -1=-34(x -1), 即3x +4y -7=0.11.椭圆过点(3,0)点,离心率e =63,求椭圆的标准方程. 解 当椭圆焦点在x 轴上时,则a =3,c a =63,∴c = 6. ∴b 2=a 2-c 2=3.故椭圆的方程为x 29+y 23=1. 当椭圆的焦点在y 轴上时, 则b =3,又c a =63, ∴a 2-b 2a =63,∴a 2=27, 故椭圆的方程为x 29+y 227=1.∴所求椭圆的方程为x 29+y 23=1或x 29+y 227=1.12.在平面直角坐标系xOy 中,点P 到两点(0,-3),(0,3)的距离之和等于4,设点P 的轨迹为C .(1)求C 的方程;(2)设直线y =kx +1与C 交于A ,B 两点,k 为何值时OA →⊥OB →?此时|AB |的值是多少.解 (1)设P (x ,y ),由椭圆的定义知,点P 的轨迹C 是以(-3,0),(3,0)为焦点,长半轴长为2的椭圆,它的短半轴长b =22-(3)2=1.故曲线C 的方程为x 24+y 2=1.(2)设A (x 1,y 1),B (x 2,y 2),其坐标满足⎩⎨⎧y =kx +1,x 2+4y 2=4.消去y ,并整理,得(k 2+4)x 2+2kx -3=0.由根与系数的关系得x 1+x 2=-2k k 2+4,x 1x 2=-3k 2+4.若OA →⊥OB →,则x 1x 2+y 1y 2=0.∵y 1y 2=(kx 1+1)(kx 2+1)=k 2x 1x 2+k (x 1+x 2)+1, ∴x 1x 2+y 1y 2=-3k 2+4-3k 2k 2+4-2k 2k 2+4+1=-4k 2-1k 2+4=0,∴k =±12.当k =±12时,x 1+x 2=∓417,x 1x 2=-1217. ∴|AB |=(x 1-x 2)2+(y 1-y 2)2=(1+k 2)(x 1-x 2)2.而(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=42172+4×1217=43×13172,∴|AB |=54×43×13172=46517.。
高中数学 专题2.2.2 椭圆的简单的几何性质(2)测试(含解析)新人教A版高二选修2-1数学试题

椭圆的简单的几何性质(2)(时间:25分,满分55分)班级 姓名 得分一、选择题1.椭圆x 212+y 23=1的一个焦点为F 1,点P 在椭圆上,如果线段PF 1的中点M 在y 轴上,那么点M 的纵坐标是( ) A .±34 B .±32C .±22D .±34答案:A2.如图所示,直线l :x -2y +2=0过椭圆的左焦点F 1和一个顶点B ,该椭圆的离心率为( )A.15B.25C.55D.255解析:由条件知:F 1(-2,0),B (0,1),所以b =1,c =2, 所以a =22+12=5,所以e =c a=25=255.答案:D3.直线y =kx -k +1与椭圆x 29+y 24=1的位置关系为( )A .相切B .相交C .相离D .不确定解析:选B 直线y =kx -k +1可变形为y -1=k(x -1),故直线恒过定点(1,1),而该点在椭圆x29+y24=1内部,所以直线y =kx -k +1与椭圆x29+y24=1相交,故选B .4.过椭圆x 2+2y 2=4的左焦点作倾斜角为π3的弦AB ,则弦AB 的长为( )A.67B.167C.716D.76答案:B5.已知F 是椭圆x 225+y 29=1的一个焦点,AB 为过其中心的一条弦,则△ABF 的面积最大值为( )A .6B .15C .20D .12解析:S =12|OF |·|y 1-y 2|≤12|OF |·2b =12.答案:D6.椭圆mx 2+ny 2=1与直线y =1-x 交于M ,N 两点,过原点与线段MN 中点所在直线的斜率为22,则m n的值是( ) A .22B .233C .922D .2327解析:选A 由⎩⎪⎨⎪⎧mx 2+ny 2=1,y =1-x 消去y 得,(m +n )x 2-2nx +n -1=0.设M (x 1,y 1),N (x 2,y 2),MN 中点为(x 0,y 0), 则x 1+x 2=2n m +n ,∴x 0=n m +n, 代入y =1-x 得y 0=mm +n.由题意y 0x 0=22,∴m n =22,选A . 二、填空题7.已知动点P (x ,y )在椭圆x 225+y 216=1上,若A 点坐标为(3,0),|AM |=1,且PM ·AM =0,则|PM |的最小值是________.解析:易知点A(3,0)是椭圆的右焦点.∵PM ·AM =0, ∴AM ⊥PM .∴|PM |2=|AP |2-|AM |2=|AP |2-1,∵椭圆右顶点到右焦点A 的距离最小,故|AP |min =2,∴|PM |min =3. 答案: 38.已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为32,且G 上一点到G 的两个焦点的距离之和为12,则椭圆G 的方程为____________________.9.若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点,点P 为椭圆上的任意一点,则OP ·FP 的最大值为________.解析:由x24+y23=1可得F(-1,0).设P(x ,y),-2≤x≤2,则OP ·FP =x2+x +y2=x2+x +31-x24=14x2+x +3=14(x +2)2+2,当且仅当x =2时,OP ·FP 取得最大值6. 答案:610.已知椭圆C :x 22+y 2=1的右焦点为F ,直线l :x =2,点A ∈l ,线段AF 交C 于点B ,若FA →=3FB →,则|AF→|=________.解析:设点A (2,n ),B (x 0,y 0). 由椭圆C :x 22+y 2=1知a 2=2,b 2=1,所以c 2=1,即c =1,所以右焦点F (1,0). 所以由FA →=3FB →得(1,n )=3(x 0-1,y 0). 所以1=3(x 0-1)且n =3y 0. 所以x 0=43,y 0=13n .将x 0,y 0代入x 22+y 2=1,得12×⎝ ⎛⎭⎪⎫432+⎝ ⎛⎭⎪⎫13n 2=1.解得n 2=1,所以|AF →|=(2-1)2+n 2=1+1= 2.答案: 2 三、解答题11.已知直线l :y =kx +1与椭圆x 22+y 2=1交于M 、N 两点,且|MN |=423.求直线l 的方程.解:设直线l 与椭圆的交点M (x 1,y 1),N (x 2,y 2),由⎩⎪⎨⎪⎧y =kx +1,x 22+y 2=1,消y 并化简,得(1+2k 2)x 2+4kx =0, 所以x 1+x 2=-4k 1+2k2,x 1x 2=0.由|MN |=423,得(x 1-x 2)2+(y 1-y 2)2=329,所以(1+k 2)(x 1-x 2)2=329,所以(1+k 2)[(x 1+x 2)2-4x 1x 2]=329.即(1+k 2)⎝ ⎛⎭⎪⎫-4k 1+2k 22=329. 化简,得k 4+k 2-2=0,所以k 2=1,所以k =±1. 所以所求直线l 的方程是y =x +1或y =-x +1.12.已知中心在坐标原点,焦点在x 轴上的椭圆过点P (2,3),且它的离心率e =12.(1)求椭圆的标准方程;(2)与圆(x +1)2+y 2=1相切的直线l :y =kx +t 交椭圆于M ,N 两点,若椭圆上一点C 满足OM →+ON →=λOC →,求实数λ的取值范围.(3+4k 2)x 2+8ktx +(4t 2-48)=0. 设M (x 1,y 1),N (x 2,y 2),则有x 1+x 2=-8kt3+4k2, y 1+y 2=kx 1+t +kx 2+t =k (x 1+x 2)+2t =6t 3+4. 因为,λOC →=(x 1+x 2,y 1+y 2), 所以C ⎝⎛⎭⎪⎫-8kt (3+4k 2)λ,6t (3+4k 2)λ. 又因为点C 在椭圆上,所以,4k 2t 2(3+4k 2)2λ2+3t2(3+4k 2)2λ2=1⇒λ2=t 23+4k2=1⎝ ⎛⎭⎪⎫1t 22+⎝ ⎛⎭⎪⎫1t 2+1.因为t 2>0,所以⎝ ⎛⎭⎪⎫1t 22+⎝ ⎛⎭⎪⎫1t 2+1>1, 所以0<λ2<1,所以λ的取值范围为(-1,0)∪(0,1).。
人教版数学选修2-1第2章 第1课时椭圆的简单几何性质学业分层测评

学业分层测评(建议用时:45分钟)[学业达标]一、选择题1.焦点在x 轴上,短轴长为8,离心率为35的椭圆的标准方程是( ) A.x 2100+y 236=1 B.x 2100+y 264=1 C.x 225+y 216=1D.x 225+y 29=1【解析】 由题意知2b =8,得b =4,所以b 2=a 2-c 2=16,又e =c a =35,解得c =3,a =5,又焦点在x 轴上,故椭圆的标准方程为x 225+y 216=1,故选C.【答案】 C2.椭圆的短轴的一个顶点与两焦点组成等边三角形,则它的离心率为( ) A.12 B.13 C.14D.22【解析】 由题意知a =2c ,∴e =c a =c 2c =12. 【答案】 A3.曲线x 225+y 29=1与x 29-k +y 225-k=1(0<k <9)的关系是( )【导学号:37792055】A.有相等的焦距,相同的焦点B.有相等的焦距,不同的焦点C.有不等的焦距,不同的焦点D.以上都不对【解析】 曲线x 225+y 29=1的焦距为2c =8,而曲线x 29-k +y 225-k=1(0<k <9)表示的椭圆的焦距也是8,但由于焦点所在的坐标轴不同,故选B.【答案】 B4.如图2-2-4,直线l:x-2y+2=0过椭圆的左焦点F1和一个顶点B,该椭圆的离心率为()图2-2-4A.15 B.25C.55 D.255【答案】 D5.已知O是坐标原点,F是椭圆x24+y23=1的一个焦点,过F且与x轴垂直的直线与椭圆交于M,N两点,则cos∠MON的值为()A.513 B.-513C.21313 D.-21313【解析】由题意,a2=4,b2=3,故c=a2-b2=4-3=1.不妨设M(1,y0),N(1,-y0),所以124+y203=1,解得y0=±32,所以|MN|=3,|OM|=|ON|=12+⎝⎛⎭⎪⎫322=132.由余弦定理知cos∠MON=|OM|2+|ON|2-|MN|22|OM||ON|=⎝⎛⎭⎪⎫1322+⎝⎛⎭⎪⎫1322-322×132×132=-513.【答案】 B 二、填空题6.已知长方形ABCD ,AB =4,BC =3,则以A ,B 为焦点,且过C 、D 的椭圆的离心率为________.【导学号:37792056】【解析】 如图,AB =2c =4,∵点C 在椭圆上,∴CB +CA =2a =3+5=8,∴e =2c 2a =48=12.【答案】 127.设AB 是椭圆x 2a 2+y 2b 2=1的不垂直于对称轴的弦,M 为AB 的中点,O 为坐标原点,则k AB ·k OM =________.【解析】 设A (x 1,y 1),B (x 2,y 2),则中点坐标M ⎝ ⎛⎭⎪⎫x 1+x 22,y 1+y 22,得k AB=y 2-y 1x 2-x 1, k OM =y 2+y 1x 2+x 1,k AB ·k OM =y 22-y 21x 22-x 21,b 2x 21+a 2y 21=a 2b 2,b 2x 22+a 2y 22=a 2b 2, 得b 2(x 22-x 21)+a 2(y 22-y 21)=0,即y 22-y 21x 22-x 21=-b 2a 2.【答案】 -b 2a 28.已知P (m ,n )是椭圆x 2+y 22=1上的一个动点,则m 2+n 2的取值范围是________.【解析】 因为P (m ,n )是椭圆x 2+y 22=1上的一个动点,所以m 2+n 22=1,即n 2=2-2m 2,所以m 2+n 2=2-m 2,又-1≤m ≤1,所以1≤2-m 2≤2,所以1≤m 2+n 2≤2.【答案】 [1,2] 三、解答题9.(1)求与椭圆x 29+y 24=1有相同的焦点,且离心率为55的椭圆的标准方程;(2)已知椭圆的两个焦点间的距离为8,两个顶点坐标分别是(-6,0),(6,0),求焦点在x 轴上的椭圆的标准方程.【解】 (1)∵c =9-4=5,∴所求椭圆的焦点为(-5,0),(5,0). 设所求椭圆的方程为x 2a 2+y 2b 2=1(a >b >0). ∵e =c a =55,c =5, ∴a =5,b 2=a 2-c 2=20, ∴所求椭圆的方程为x 225+y 220=1. (2)因为椭圆的焦点在x 轴上,所以设它的标准方程为x 2a 2+y 2b 2=1(a >b >0), ∵2c =8,∴c =4, 又a =6,∴b 2=a 2-c 2=20. ∴椭圆的方程为x 236+y 220=1.10.设椭圆x 2a 2+y 2b 2=1(a >b >0)与x 轴交于点A ,以OA 为边作等腰三角形OAP ,其顶点P 在椭圆上,且∠OPA =120°,求椭圆的离心率.【导学号:37792057】【解】 不妨设A (a,0),点P 在第一象限内,由题意知,点P 的横坐标是a2,设P ⎝ ⎛⎭⎪⎫a 2,y ,由点P 在椭圆上,得⎝ ⎛⎭⎪⎫a 22a 2+y 2b 2=1,y 2=34b 2,即P ⎝ ⎛⎭⎪⎫a 2,32b ,又∠OPA =120°,所以∠POA =30°,故tan ∠POA =32b a 2=33,所以a =3b ,所以e =ca =a 2-b 2a=(3b )2-b 23b=223. [能力提升]1.设椭圆的两个焦点分别为F 1,F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是( )A.22B.2-1C.2- 2D.2-12【解析】 设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0), 由题意得|PF 2|=b 2a =2c , 即a 2-c 2a =2c ,得离心率e =2-1,故选B. 【答案】 B2.“m =3”是“椭圆x 24+y 2m =1的离心率为12”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件【解析】 椭圆x 24+y 2m =1的离心率为12, 当0<m <4时,4-m 2=12,得m =3, 当m >4时,m -4m=12,得m =163,即“m =3”是“椭圆x 24+y 2m =1的离心率为12”的充分不必要条件. 【答案】 A3.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若AP →=2PB →,则椭圆的离心率是________.【解析】 由AP →=2PB →,得|AO |=2|FO |(O 为坐标原点),即a =2c , 则离心率e =12. 【答案】 124.已知点A ,B 分别是椭圆x 236+y 220=1的左、右顶点,点F 是椭圆的右焦点,点P 在椭圆上,且位于x 轴上方,PA ⊥PF .(1)求点P 的坐标;【导学号:37792058】(2)设M 是椭圆长轴AB 上的一点,且M 到直线AP 的距离等于|MB |,求椭圆上的点到点M 的距离d 的最小值.【解】 (1)由已知可得A (-6,0),B (6,0),F (4,0), 设点P 的坐标是(x ,y ),则AP →=(x +6,y ),FP →=(x -4,y ).由已知得⎩⎨⎧x 236+y 220=1,(x +6)(x -4)+y 2=0,则2x 2+9x -18=0,解得x =32或x =-6. 由于y >0,所以只能取x =32,于是y =52 3. 所以点P 的坐标是⎝ ⎛⎭⎪⎫32,523.(2)直线AP 的方程是x -3y +6=0. 设点M 的坐标是(m,0),则M 到直线AP 的距离是|m +6|2,又B (6,0), 于是|m +6|2=|m -6|, 又-6≤m ≤6,解得m =2,设椭圆上的点(x ,y )到点M 的距离为d ,有 d 2=(x -2)2+y 2=x 2-4x +4+20-59x 2 =49⎝ ⎛⎭⎪⎫x -922+15,由于-6≤x ≤6,所以当x =92时,d 取最小值为15.。
人教新课标版-数学-高二-数学人教B版选修2-1自我小测 2.2.1椭圆的标准方程

自我小测1.化简方程x 2+(y +3)2+x 2+(y -3)2=10为不含根式的形式是( )A.x 225+y 216=1B.x 225+y 29=1C.x 216+y 225=1D.x 29+y 225=1 2.椭圆x 225+y 29=1上的一点M 到焦点F 1的距离为2,N 是MF 1的中点,则|ON |(O 是坐标原点)的值是( )A .4B .2C .8 D.323.若△ABC 的两个顶点坐标为A (-4,0),B (4,0),△ABC 的周长为18,则顶点C 的轨迹方程为( )A.x 225+y 29=1B.y 225+x 29=1(y ≠0)C.x 216+y 29=1(y ≠0)D.x 225+y 29=1(y ≠0) 4.已知椭圆x 210-m +y 2m -2=1的焦点在y 轴上,若焦距为4,则m =( ) A .4 B .5 C .7 D .85.设F 1,F 2是椭圆x 216+y 212=1的焦点,P 为椭圆上的一点,则△PF 1F 2的周长为( ) A .10 B .12 C .16 D .不确定6.“m >n >0”是“方程mx 2+ny 2=1表示焦点在y 轴上的椭圆”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.椭圆x 24+y 2m=1的焦距为2,则m =__________. 8.P 是椭圆x 24+y 23=1上任意一点,F 1,F 2是焦点,那么∠F 1PF 2的最大值是__________. 9.已知椭圆C :x 22+y 2=1的两焦点为F 1,F 2,点P (x 0,y 0)满足0<x 202+y 20<1,则|PF 1|+|PF 2|的取值范围为______.10.已知圆A :(x +3)2+y 2=1及圆B :(x -3)2+y 2=81,动圆P 与圆A 外切,与圆B 内切,求动圆圆心P 的轨迹方程.11.已知x 轴上一定点A (1,0),Q 为椭圆x 24+y 2=1上任意一点,求AQ 的中点M 的轨迹方程.12.如图,已知椭圆的方程为x24+y23=1,若点P在第二象限,且∠PF1F2=120°,求△PF1F2的面积.参考答案1.解析:由题意可知,方程表示点(x ,y )与两个定点(0,3)和(0,-3)之间的距离之和为10,又两定点之间的距离为6,6<10,它符合椭圆的定义,即2a =10,2c =6,从而可求得b 2=16.答案:C2.解析:设另一个焦点为F 2,则|MF 1|+|MF 2|=10,又|MF 1|=2,所以|MF 2|=8.而ON为△MF 1F 2的中位线,所以|ON |=12|MF 2|=4. 答案:A3.解析:因为|AC |+|BC |+|AB |=18,所以|CA |+|CB |=10>|AB |=8.所以点C 的轨迹是以A ,B 为焦点的椭圆,其方程为x 225+y 29=1,且y ≠0. 答案:D4.解析:因为焦点在y 轴上,所以⎩⎪⎨⎪⎧ m -2>0,10-m >0,m -2>10-m⇒6<m <10.又焦距2c =4,所以m -2-10+m =22⇒m =8.答案:D5.答案:B6.答案:C7.解析:分两种情况:焦点在x 轴上或焦点在y 轴上.答案:3或58.解析:当点P 为(0,3)或(0,-3)时∠F 1PF 2最大,此时|PF 1|=|PF 2|=2,|F 1F 2|=2,故△PF 1F 2为等边三角形.答案:60°9.解析:因为点P (x 0,y 0)满足0<x 202+y 20<1, 所以点P 在椭圆内且不过原点,所以2c ≤|PF 1|+|PF 2|<2a .又因为a 2=2,b 2=1,所以a =2,b =1,c 2=a 2-b 2=1,即c =1,所以2≤|PF 1|+|PF 2|<2 2.答案:hslx3y3h2,22)10.分析:利用椭圆的定义先判断出动圆圆心P 的轨迹是椭圆,再求其方程. 解:设动圆P 的半径为r .由所给圆的方程知,A (-3,0),B (3,0),由题意,可得|PA |=r +1,|PB |=9-r ,故|PA |+|PB |=r +1+9-r =10>|AB |=6.由椭圆的定义知动点P 的轨迹是椭圆.其中2a =10,2c =6,即a =5,c =3,所以b 2=16.故动圆圆心P 的轨迹方程为x 225+y 216=1. 11.解:设中点M 的坐标为(x ,y ),点Q 的坐标为(x 0,y 0),利用中点公式,得⎩⎪⎨⎪⎧x =x 0+12,y =y 02,所以⎩⎪⎨⎪⎧x 0=2x -1,y 0=2y .因为Q (x 0,y 0)在椭圆x 24+y 2=1上, 所以x 204+y 20=1. 将x 0=2x -1,y 0=2y 代入上式,得(2x -1)24+(2y )2=1. 故所求AQ 的中点M 的轨迹方程是⎝⎛⎭⎫x -122+4y 2=1. 12.解:由已知得a =2,b =3,所以c =a 2-b 2=4-3=1, 所以|F 1F 2|=2c =2.在△PF 1F 2中,由余弦定理,得|PF 2|2=|PF 1|2+|F 1F 2|2-2|PF 1||F 1F 2|cos 120°, 即|PF 2|2=|PF 1|2+4+2|PF 1|.① 由椭圆定义,得|PF 1|+|PF 2|=4, 即|PF 2|=4-|PF 1|.②把②代入①解得|PF 1|=65. 所以12PF F S =12|PF 1|·|F 1F 2|·sin 120°=12×65×2×32=335, 即△PF 1F 2的面积是353.。
人教新课标版数学高二选修2-1限时练 椭圆的简单几何性质(二)

2.2.2 椭圆的简单几何性质(二)一、选择题1.线段|AB |=4,N 为AB 的中点,动点P 满足条件|P A |+|PB |=6,当P 点在同一平面内运动时,|PN |的最大值M ,最小值m 分别是( )A .M =4,m = 3B .M =3,m = 5C .M =5,m = 5D .M =3,m = 32.直线y =x +1被椭圆x 24+y 22=1所截得的弦的中点坐标是( ) A.⎝⎛⎭⎫23,53B.⎝⎛⎭⎫43,73C.⎝⎛⎭⎫-23,13D.⎝⎛⎭⎫-132,-172 3.已知椭圆mx 2+4y 2=1的离心率为22,则实数m 等于( ) A .2B .2或83C .2或6D .2或84.已知F 1,F 2是椭圆x 24+y 2=1的两个焦点,P 为椭圆上一动点,则使|PF 1|·|PF 2|取最大值的点P 为( )A .(-2,0)B .(0,1)C .(2,0)D .(0,1)或(0,-1)5.已知椭圆:x 24+y 2b2=1(0<b <2),左,右焦点分别为F 1,F 2,过F 1的直线l 交椭圆于A ,B 两点,若|BF 2|+|AF 2|的最大值为5,则b 的值是( )A .1B. 2C.32D. 3 6.已知圆C 1:x 2+2cx +y 2=0,圆C 2:x 2-2cx +y 2=0,c >0,椭圆C :x 2a 2+y 2b2=1(a >b >0),且c 2=a 2-b 2.若圆C 1,C 2都在椭圆内,则椭圆离心率的取值范围是( )A .[12,1) B .(0,12] C .[22,1) D .(0,22] 7.已知椭圆mx 2+ny 2=1与直线x +y =1相交于A ,B 两点,M 为AB 的中点,O 为坐标原点,若直线OM 的斜率为2,则n m的值为( ) A.22 B.12C. 2 D .2 二、填空题8.人造地球卫星的运行是以地球中心为一个焦点的椭圆,近地点距地面p 千米,远地点距地面q 千米,若地球半径为r 千米,则运行轨迹的短轴长为____________.9.若直线mx +ny =4与圆x 2+y 2=4没有交点,则过点P (m ,n )的直线与椭圆x 29+y 24=1的交点个数为________.10.设椭圆中心在坐标原点,A (2,0),B (0,1)是它的两个顶点,直线y =kx (k >0)与线段AB 相交于点D ,与椭圆相交于E 、F 两点.若ED =6DF ,则k 的值为________.三、解答题11.已知椭圆C 1:x 24+y 2=1,椭圆C 2以C 1的长轴为短轴,且与C 1有相同的离心率. (1)求椭圆C 2的方程;(2)设O 为坐标原点,点A ,B 分别在椭圆C 1和C 2上,OB =2OA ,求直线AB 的方程.12.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的两个焦点分别为F 1(-2,0),F 2(2,0),离心率为63.过点F 2的直线l (斜率不为0)与椭圆C 交于A 、B 两点,线段AB 的中点为D ,O 为坐标原点,直线OD 交椭圆于M ,N 两点.(1)求椭圆C 的方程;(2)当四边形MF 1NF 2为矩形时,求直线l 的方程.13.椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点(1,32),离心率为12,左,右焦点分别为F 1,F 2,过F 1的直线交椭圆于A 、B 两点.(1)求椭圆C 的方程;(2)当△F 2AB 的面积为1227时,求直线的方程.参考答案1.B [由|P A |+|PB |=6>|AB |=4,∴P 的轨迹是以A 、B 为焦点,N 为中心的椭圆.则M =|PN |max =a =3,m =|PN |min =b =a 2-c 2=9-4= 5.]2.C [把y =x +1代入椭圆方程,整理得3x 2+4x -2=0,所以弦的中点坐标(x 0,y 0)满足x 0=x 1+x 22=-23,y 0=x 0+1=-23+1=13.] 3.D [显然m >0且m ≠4,当0<m <4时,椭圆长轴在x 轴上, 则1m -141m =22, 解得m =2;当m >4时,椭圆长轴在y 轴上, 则14-1m 14=22, 解得m =8.]4.D [由椭圆定义得|PF 1|+|PF 2|=2a =4,∴|PF 1|·|PF 2|≤(|PF 1|+|PF 2|2)2=4, 当且仅当|PF 1|=|PF 2|=2,即P (0,-1)或(0,1)时,取“=”.]5.D [由题意知a =2,所以|BF 2|+|AF 2|+|AB |=4a =8,因为|BF 2|+|AF 2|的最大值为5,所以|AB |的最小值为3,当且仅当AB ⊥x 轴时,取得最小值,此时A ⎝⎛⎭⎫-c ,32,B ⎝⎛⎭⎫-c ,-32,代入椭圆方程得c 24+94b 2=1,又c 2=a 2-b 2=4-b 2,所以4-b 24+94b 2=1,即1-b 24+94b2=1,所以b 24=94b 2,解得b 2=3, 所以b = 3.]6.B [圆C 1,C 2都在椭圆内等价于圆C 2的右顶点(2c,0),上顶点(c ,c )在椭圆内部,∴只需⎩⎪⎨⎪⎧ 2c ≤a ,c 2a 2+c 2b 2≤1,可得⎩⎪⎨⎪⎧e ≤12,e 4-3e 2+1≥0,结合e ∈(0,1),可得0<e ≤12.] 7.A [设A (x 1,y 1),B (x 2,y 2),线段AB 的中点M (x 0,y 0),由题意可得y 1+y 2x 1+x 2=y 0x 0=2,y 2-y 1x 2-x 1=-1,① 因为A ,B 在椭圆上,所以mx 21+ny 21=1,mx 22+ny 22=1, 两式相减可得m (x 1-x 2)(x 1+x 2)+n (y 1-y 2)(y 1+y 2)=0.②所以y 1-y 2x 1-x 2=-m (x 1+x 2)n (y 1+y 2),即-1=-m (x 1+x 2)n (y 1+y 2), 所以-1=-m n ·22,即n m =22.] 8.2(p +r )(q +r )解析 ∵⎩⎪⎨⎪⎧p +r =a -c ,q +r =a +c , ∴b 2=a 2-c 2=(a +c )(a -c )=(q +r )(p +r ),∴2b =2(p +r )(q +r ).9.2解析 因为直线mx +ny =4与圆x 2+y 2=4没有交点, 所以|-4|m 2+n 2>2,所以m 2+n 2<4, 即点P (m ,n )在以原点为圆心,以2为半径的圆内,故过点P (m ,n )的直线与椭圆x 29+y 24=1有两个交点.10.23或38解析 依题意得椭圆的方程为x 24+y 2=1, 直线AB ,EF 的方程分别为x +2y =2,y =kx (k >0).如图,设D (x 0,kx 0),E (x 1,kx 1),F (x 2,kx 2),其中x 1<x 2,则x 1,x 2满足方程(1+4k 2)x 2=4,故x 2=-x 1=21+4k 2.由ED =6DF 知x 0-x 1=6(x 2-x 0),得x 0=17(6x 2+x 1)=57x 2=1071+4k 2.由D 在直线AB 上知,x 0+2kx 0=2,x 0=21+2k ,所以21+2k =1071+4k 2,化简得24k 2-25k +6=0,由此解得k =23或k =38. 11.解 (1)由已知可设椭圆C 2的方程为y 2a 2+x 24=1(a >2), 其离心率为32,故a 2-4a =32,解得a =4. 故椭圆C 2的方程为y 216+x 24=1. (2)方法一 A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ),由OB =2OA 及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入x 24+y 2=1中, 得(1+4k 2)x 2=4,所以x 2A =41+4k 2. 将y =kx 代入y 216+x 24=1中,得(4+k 2)x 2=16,所以x 2B =164+k 2. 又由OB =2OA ,得x 2B =4x 2A ,即164+k 2=161+4k 2, 解得k =±1.故直线AB 的方程为y =x 或y =-x .方法二 A ,B 两点的坐标分别记为(x A ,y A ),(x B ,y B ),由OB =2OA 及(1)知,O ,A ,B 三点共线且点A ,B 不在y 轴上,因此可设直线AB 的方程为y =kx .将y =kx 代入x 24+y 2=1中,得(1+4k 2)x 2=4, 所以x 2A =41+4k 2,y 2A =4k 21+4k 2. 由OB =2OA ,得x 2B =161+4k 2,y 2B =16k 21+4k 2. 将x 2B ,y 2B 代入y 216+x 24=1中,得4+k 21+4k 2=1,即4+k 2=1+4k 2, 解得k =±1.故直线AB 的方程为y =x 或y =-x .12.解 (1)由题意可知⎩⎪⎨⎪⎧ c =2,c a =63,a 2=b 2+c 2,解得a =6,b = 2.故椭圆C 的方程为x 26+y 22=1. (2)由题意可知直线l 的斜率存在.设其方程为y =k (x -2),点A (x 1,y 1),B (x 2,y 2),M (x 3,y 3),N (-x 3,-y 3),由⎩⎪⎨⎪⎧ x 26+y 22=1,y =k (x -2),得(1+3k 2)x 2-12k 2x +12k 2-6=0,则x 1+x 2=12k 21+3k 2,则y 1+y 2=k (x 1+x 2-4)=-4k 1+3k 2, 所以AB 的中点D 的坐标为(6k 21+3k 2,-2k 1+3k 2), 因此直线OD 的方程为x +3ky =0(k ≠0).由⎩⎪⎨⎪⎧ x +3ky =0,x 26+y 22=1, 解得y 23=21+3k 2,x 3=-3ky 3, 因为四边形MF 1NF 2为矩形,所以2F M ·2F N =0.即(x 3-2,y 3)·(-x 3-2,-y 3)=0,所以4-x 23-y 23=0,所以4-2(9k 2+1)1+3k 2=0.解得k =±33. 故直线l 的方程为y =±33(x -2). 13.解 (1)因为椭圆C :x 2a 2+y 2b 2=1(a >b >0)过点(1,32), 所以1a 2+94b2=1.① 又因为离心率为12,所以c a =12,所以b 2a 2=34.② 解①②得a 2=4,b 2=3.所以椭圆C 的方程为x 24+y 23=1. (2)当直线的倾斜角为π2时, A (-1,32),B (-1,-32), 2ABF S =12|AB |×|F 1F 2|=12×3×2=3≠1227. 当直线的倾斜角不为π2时,设直线方程为y =k (x +1), 代入x 24+y 23=1得(4k 2+3)x 2+8k 2x +4k 2-12=0.设A (x 1,y 1)、B (x 2,y 2),则x 1+x 2=-8k 24k 2+3,x 1x 2=4k 2-124k 2+3, 所以2ABF S=12|y 1-y 2|×|F 1F 2| =|k |(x 1+x 2)2-4x 1x 2 =|k | (-8k 24k 2+3)2-4·4k 2-124k 2+3=12|k |k 2+14k 2+3=1227, 所以17k 4+k 2-18=0,解得k 2=1(k 2=-1817舍去), 所以k =±1,所以所求直线的方程为x -y +1=0或x +y +1=0.。
数学人教B版选修1-1自我小测 2-1-2椭圆的几何性质 含

自我小测1.已知k <0,则曲线x 29+y 24=1和x 29-k +y 24-k =1有相同的( )A .顶点B .焦点C .离心率D .长轴长2.椭圆的对称轴为坐标轴,若它的长轴长与短轴长之和为18,焦距为6,则椭圆的标准方程为( )A.x 29+y 216=1B.x 225+y 216=1C.x 225+y 216=1或x 216+y 225=1D.x 216+y 225=1 3.中心在原点,焦点在坐标轴上,离心率为32,且过点(2,0)的椭圆的方程是( ) A.x 24+y 2=1 B.x 24+y 2=1或x 2+y 24=1 C .x 2+4y 2=1D .x 2+4y 2=4或4x 2+y 2=164.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( ) A.45B.35C.25D.155.设F 1,F 2是椭圆C :x 28+y 24=1的焦点,在曲线C 上满足1PF ·2PF =0的点P 的个数为( )A .0B .2C .3D .46.若椭圆的焦距长等于它的短轴长,则椭圆的离心率等于______.7.已知椭圆的一个焦点将长轴分成长度比为3∶2的两段,则其离心率e 为__________.8.在x 轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6的椭圆的标准方程为__________.9.已知椭圆x 2a 2+y 2b 2=1(a >b >0)过点⎝⎛⎭⎫1,32,且离心率e =12,求此椭圆的方程. 10.已知椭圆的焦点在x 轴上,椭圆上一点的横坐标等于右焦点的横坐标,且纵坐标的长等于短半轴长的23,求该椭圆的离心率.11.已知F 1,F 2是椭圆的两个焦点,P 为椭圆上一点,∠F 1PF 2=60°. (1)求椭圆的离心率的取值范围;(2)求证:△F1PF2的面积只与椭圆的短轴长有关.参考答案1. 解析:c 21=9-4=5,且焦点在x 轴上;c 22=(9-k )-(4-k )=5,且焦点在x 轴上. 答案:B2. 答案:C3. 解析:若焦点在x 轴上,则a =2.又e =32,所以c = 3. 所以b 2=a 2-c 2=1.所以方程为x 24+y 2=1,即x 2+4y 2=4;若焦点在y 轴上,则b =2. 又e =32, 所以b 2a 2=1-34=14,所以a 2=4b 2=16.所以方程为x 24+y 216=1,即4x 2+y 2=16.答案:D4. 解析:依题意有2×2b =2a +2c ,即2b =a +c ,所以4b 2=a 2+2ac +c 2.因为b 2=a 2-c 2,所以4a 2-4c 2=a 2+2ac +c 2,所以3a 2-2ac -5c 2=0,两边同除以a 2,即有5e 2+2e -3=0,解得e =35或e =-1(舍去).故选B.答案:B5. 解析:因为1PF ·2PF =0,所以PF 1⊥PF 2. 所以点P 即为以线段F 1F 2为直径的圆与椭圆的交点,且半径为c =8-4=2. 又b =2,所以点P 为短轴的两个端点. 答案:B6. 解析:椭圆的焦距长等于它的短轴长,即2b =2c ,则有a 2=b 2+c 2=2c 2,解得a =2c ,所以e =c a =22.答案:227. 解析:由题意,得(a +c )∶(a -c )=3∶2,即1+e 1-e =32,解得e =5-2 6.答案:5-2 68. 解析:如图,根据题意可知F 1B 1⊥F 1B 2,|OF 1|=3.可知|OB 2|=|OB 1|=3, 所以b =c =3,a 2=b 2+c 2=18. 所以椭圆的标准方程为x 218+y 29=1.答案:x 218+y 29=19. 分析:由椭圆的离心率可得a ,c 的关系,从而知道b ,c 的关系,再由点在椭圆上,代入方程即可求得椭圆的标准方程.解:由题意知椭圆的离心率e =c a =12,所以a =2c ,所以b 2=a 2-c 2=3c 2,所以椭圆的方程为x 24c 2+y 23c2=1.又点⎝⎛⎭⎫1,32在椭圆上, 所以14c 2+⎝⎛⎭⎫3223c 2=1,所以c 2=1,所以椭圆的方程为x 24+y 23=1.10. 解法一:设椭圆方程为x 2a +y 2b =1(a >b >0),焦点坐标为F 1(-c,0),F 2(c,0).依题意设M 点坐标为⎝⎛⎭⎫c ,23b , 在Rt △MF 1F 2中,|F 1F 2|2+|MF 2|2=|MF 1|2, 即4c 2+49b 2=|MF 1|2,所以|MF 1|+|MF 2|=4c 2+49b 2+23b =2a .整理得3c 2=3a 2-2ab . 又c 2=a 2-b 2, 所以3b =2a ,b 2a 2=49,所以e 2=c 2a 2=a 2-b 2a 2=1-b 2a 2=59,所以e =53. 解法二:设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),由已知条件设M ⎝⎛⎭⎫c ,23b , 依题意得c 2a 2+4b 29b 2=1,所以c 2a 2=59,c a =53,即e =53.11. (1)解:不妨设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),由余弦定理得cos 60°=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=(|PF 1|+|PF 2|)2-2|PF 1|·|PF 2|-|F 1F 2|22|PF 1|·|PF 2|,所以|PF 1|·|PF 2|=4a 2-2|PF 1|·|PF 2|-4c 2, 所以3|PF 1|·|PF 2|=4b 2, 所以|PF 1|·|PF 2|=4b 23.又因为|PF 1|·|PF 2|≤⎝⎛⎭⎫|PF 1|+|PF 2|22=a 2,所以3a 2≥4(a 2-c 2), 所以c a ≥12,所以e ≥12.又因为椭圆中0<e <1,所以所求椭圆的离心率的取值范围是12≤e <1.(2)证明:由(1)可知|PF 1|·|PF 2|=43b 2,S △F 1PF 2=12|PF 1|·|PF 2|sin 60°=12×43b 2×32=33b 2. 所以△F 1PF 2的面积只与椭圆的短轴长有关.。
2021年高中数学 2.2.2椭圆及其简单几何性质练习新人教版选修2-1

2021年高中数学 2.2.2椭圆及其简单几何性质练习新人教版选修2-1一、选择题(共6个小题,每小题只有一个正确答案)1.若椭圆经过点P(2,3),且焦点为F1(-2,0), F2 (2,0),则这个椭圆的离心率等于()A.22B.13C.12D.322. 已知椭圆的对称轴是坐标轴,离心率为,长轴长为12,则椭圆方程为()A. 或B.C. 或D. 或3.已知、是椭圆的两个焦点,满足的点总在椭圆内部,则椭圆离心率的取值范围是()A. B. C. D.4.已知椭圆的左焦点为,右顶点为,点在椭圆上,且轴,直线交轴于点.若,则椭圆的离心率是()A.B.C.D.5.如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点处进入以月球球心为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在变点第二次变轨进入仍以月球球心为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在点第三次变轨进入以为圆心的圆形轨道Ⅲ绕月飞行,若用和分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用和分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:①; ②; ③; ④<.其中正确式子的序号是()A. ①③B. ②③C. ①④D. ②④6.过椭圆()的左焦点作轴的垂线交椭圆于点,为右焦点,若,则椭圆的离心率为()A.B.C.D.二、填空题(共4个小题)7.巳知椭圆的中心在坐标原点,长轴在轴上,离心率为,且上一点到的两个焦点的距离之和为12,则椭圆的方程为.8.如果一个椭圆的长轴长是短轴长的两倍,那么这个椭圆的离心率为 .9.已知地球运行的轨道是长半轴长km,离心率的椭圆,且太阳在这个椭圆的一个焦点上,则地球到太阳的最大和最小距离分别为, .10.在平面直角坐标系中,椭圆1( 0)的焦距为2,以O为圆心,为半径的圆,过椭圆准线与轴的交点作圆的两切线互相垂直,则离心率= .三、解答题(共1个小题)11.设、分别是椭圆的左、右焦点,是该椭圆上的一个动点.(1)求的最大值和最小值;(2)求的最大值和最小值.33096 8148 腈38007 9477 鑷25059 61E3 懣22826 592A 太 35159 8957 襗23273 5AE9 嫩27653 6C05 氅29524 7354 獔VP32480 7EE0 绠OV7。
最新人教版高中数学选修2-1第二章《椭圆的简单几何性质》梳理探究
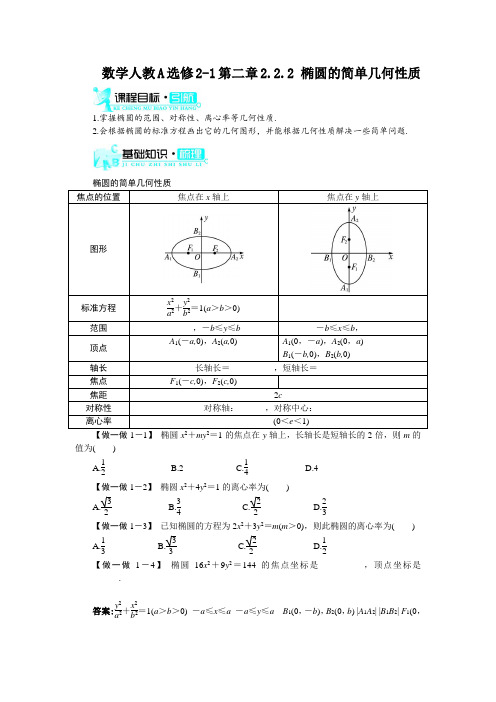
数学人教A 选修2-1第二章2.2.2 椭圆的简单几何性质1.掌握椭圆的范围、对称性、离心率等几何性质.2.会根据椭圆的标准方程画出它的几何图形,并能根据几何性质解决一些简单问题.x 2a 2+y 2b 2=1(a >b >0) __________ ______,-b ≤y ≤b -b ≤x ≤b ,______A 1(-a,0),A 2(a,0) __________ ,-a ),A 2(0,a ) 0),B 2(b,0),短轴长=____________________【做一做1-1】 椭圆x +my =1的焦点在y 轴上,长轴长是短轴长的2倍,则m 的值为( )A.12B.2C.14 D.4 【做一做1-2】 椭圆x 2+4y 2=1的离心率为( ) A.32 B.34 C.22 D.23【做一做1-3】 已知椭圆的方程为2x 2+3y 2=m (m >0),则此椭圆的离心率为( ) A.13 B.33 C.22 D.12【做一做1-4】 椭圆16x 2+9y 2=144的焦点坐标是__________,顶点坐标是__________.答案:y 2a 2+x 2b2=1(a >b >0) -a ≤x ≤a -a ≤y ≤a B 1(0,-b ),B 2(0,b ) |A 1A 2| |B 1B 2| F 1(0,-c ),F 2(0,c ) 坐标轴 原点(0,0) e =ca【做一做1-1】 C 椭圆x 2+my 2=1的标准形式为x 2+y 21m=1,∵焦点在y 轴上,且长轴长是短轴长的2倍, ∴1m =4,∴m =14. 【做一做1-2】 A 化为标准形式x 2+y 214=1,则a 2=1,b 2=14,c 2=34,∴c a =32.【做一做1-3】 B 化为标准方程为x 2m 2+y 2m 3=1(m >0),∵a 2=m 2,b 2=m 3,∴c 2=m 6.∴c 2a 2=13,∴e =33. 【做一做1-4】 (0,±7) (3,0),(-3,0),(0,4),(0,-4)1.椭圆的离心率剖析:椭圆的焦距与长轴长的比,称作椭圆的离心率.记作e =2c 2a =ca .由a >c >0,知0<e <1.e 越接近1,则c 越接近a ,从而b =a 2-c 2越小,因此椭圆越扁;反之e 越接近于0,c 就越接近于0,从而b 越接近于a ,这时椭圆就越接近于圆;当且仅当a =b 时,c =0,这时两个焦点重合,图形变成圆,方程为x 2+y 2=a 2.2.直线与椭圆的位置关系剖析:(1)直线与椭圆有三种位置关系:①相交——直线与椭圆有两个不同的公共点; ②相切——直线与椭圆有且只有一个公共点; ③相离——直线与椭圆没有公共点. (2)直线与椭圆的位置关系的判断:我们把直线与椭圆的位置关系问题转化为直线和椭圆的公共点问题,而直线与椭圆的公共点问题,又可以转化为它们的方程所组成的方程组的解的问题,而它们的方程所组成的方程组的解的问题又可以转化为一元二次方程解的问题,一元二次方程解的问题可以通过判别式来判断;因此,直线和椭圆的位置关系,可由相应的一元二次方程的判别式来判断.判断方法:将直线方程和椭圆的方程联立,消去一个未知数,得到一个一元二次方程,若Δ>0,则直线与椭圆相交;若Δ=0,则直线与椭圆相切;若Δ<0,则直线与椭圆相离.3.弦长公式剖析:设直线方程为y =kx +m ,椭圆方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0),直线与椭圆的两个交点为A (x 1,y 1),B (x 2,y 2),则|AB |=(x 1-x 2)2+(y 1-y 2)2=(x 1-x 2)2+(kx 1+m -kx 2-m )2 =(x 1-x 2)2·(1+k 2)=1+k 2·|x 1-x 2| =1+k 2·(x 1+x 2)2-4x 1x 2, 或者|AB |=(x 1-x 2)2+(y 1-y 2)2 =⎝⎛⎭⎫y 1-m k-y 2-m k 2+(y 1-y 2)2=1+1k 2·|y 1-y 2| =1+1k2·(y 1+y 2)2-4y 1y 2. 当k =0时,直线平行于x 轴, 所以|AB |=|x 1-x 2|.由弦长公式可知,求弦长时无需求出交点坐标,只需将方程联立,整理成关于x (或y )的一元二次方程,再根据一元二次方程根与系数的关系求出x 1+x 2,x 1·x 2(或y 1+y 2,y 1·y 2),代入弦长公式即可.题型一 由方程求椭圆的几何性质【例题1】 求椭圆25x 2+y 2=25的长轴和短轴的长及其焦点和顶点坐标.分析:本题可先把椭圆方程化成标准方程,再确定a ,b ,c 的值,从而求得椭圆的几何性质.反思:已知椭圆的方程讨论其几何性质时,应先把椭圆的方程化成标准形式,找准a 与b ,才能正确地写出其相关性质.在求顶点坐标和焦点坐标时,应注意焦点所在的坐标轴.题型二 利用椭圆的几何性质求标准方程【例题2】求适合下列条件的椭圆的标准方程.(1)长轴长是6,离心率是23;(2)焦点在x 轴上,且一个焦点与短轴的两个端点的连线互相垂直,焦距为6.分析:因为要求的是椭圆的标准方程,故可以先设出椭圆的标准方程,再利用待定系数法求参数a ,b ,c .反思:利用性质求椭圆的标准方程,通常采用待定系数法.而其关键是根据已知条件去构造关于参数的关系式,利用解方程(组)求得参数.题型三 求椭圆的离心率【例题3】 在△ABC 中,AB =BC ,cos B =-718.若以A ,B 为焦点的椭圆经过点C ,则该椭圆的离心率e =__________.反思:求椭圆的离心率的常见思路:一是先求a ,c ,再计算e ;二是依据条件中的关系,结合有关知识和a ,b ,c 的关系,构造关于e 的方程,再求解.注意e 的范围:0<e <1.题型四 直线与椭圆的位置关系【例题4】 (2010福建高考,理17)已知中心在坐标原点O 的椭圆C 经过点A (2,3),且点F (2,0)为其右焦点.(1)求椭圆C 的方程;(2)是否存在平行于OA 的直线l ,使得直线l 与椭圆C 有公共点,且直线OA 与l 的距离等于4?若存在,求出直线l 的方程;若不存在,说明理由.反思:直线与椭圆之间有相交、相切、相离三种位置关系,即直线与椭圆有两个不同公共点、惟一一个公共点、没有公共点,相应地,直线与椭圆方程联立的方程组有两组解、一组解、无解,消元后的一元二次方程对应的有∆>0、∆=0、∆<0三种情况.题型五 易错辨析【例题5】 若椭圆x 2k +8+y 29=1的离心率e =12,则k 的值为__________.错解:由已知a 2=k +8,b 2=9,又e =c a =12,故e 2=c 2a 2=a 2-b 2a 2=k -1k +8=14,解得k =4.答案:【例题1】 解:把已知方程化成标准方程为y 225+x 2=1,这里a =5,b =1,所以c =25-1=2 6.因此,椭圆的长轴和短轴的长分别是2a =10和2b =2,两个焦点分别是F 1(0,-26),F 2(0,26),椭圆的四个顶点是A 1(0,-5),A 2(0,5),B 1(-1,0)和B 2(1,0).【例题2】 解:(1)设椭圆方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0).由已知得2a=6,∴a =3.又e =c a =23,∴c =2.∴b 2=a 2-c 2=9-4=5.∴椭圆的标准方程为x 29+y 25=1或y 29+x 25=1.(2)由题意知焦点在x 轴上,故可设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0),且两个焦点分别为F ′(-3,0),F (3,0).如图所示,△A 1F A 2为等腰直角三角形,OF 为斜边A 1A 2的中线,且|OF |=c ,|A 1A 2|=2b , ∴c =b =3.∴a 2=b 2+c 2=18.∴所求椭圆的标准方程为x 218+y 29=1.【例题3】 38 ∵以A ,B 为焦点的椭圆过点C ,∴椭圆的离心率e =ABAC +BC .∵AB =BC ,∴e =ABAC +AB.又∵cos B =AB 2+BC 2-AC 22AB ·BC =-718,即2AB 2-AC 22AB 2=-718,得AC 2=259AB 2, ∴AC =53AB .∴e =AB 53AB +AB =38.【例题4】 解:(1)依题意,可设椭圆C 的方程为x 2a 2+y 2b 2=1(a >b >0),且可知左焦点为F ′(-2,0),从而有⎩⎪⎨⎪⎧c =2, 2a =|AF |+|AF ′|=3+5=8,解得⎩⎪⎨⎪⎧c =2, a =4.又a 2=b 2+c 2,所以b 2=12.故椭圆C 的方程为x 216+y 212=1.(2)假设存在符合题意的直线l ,其方程为y =32x +t .由⎩⎨⎧y =32x +t ,x 216+y212=1,得3x 2+3tx +t 2-12=0.因为直线l 与椭圆C 有公共点, 所以∆=(3t )2-4×3(t 2-12)≥0. 解得-43≤t ≤4 3.另一方面,由直线OA 与l 的距离d =4, 可得|t |94+1=4,从而t =±213. 由于±213∉[-43,43], 所以符合题意的直线l 不存在.【例题5】 错因分析:错解中忽视了椭圆的焦点位置的不确定性,应分焦点在x 轴和y 轴上两种情况进行讨论.正解:(1)若焦点在x 轴上,即k +8>9时,a 2=k +8,b 2=9,e 2=c 2a 2=a 2-b 2a 2=k -1k +8=14,解得k =4.(2)若焦点在y 轴上,即0<k +8<9时,a 2=9,b 2=k +8,e 2=c 2a 2=a 2-b 2a 2=1-k 9=14,解得k =-54.综上所述,k =4或k =-54.1 (2012浙江名校联考,文9)已知P 是椭圆22221x y a b+=(a >b >0)上的一动点,且P 与椭圆长轴两顶点连线的斜率之积为-12,则椭圆离心率为( )C.12答案:B 设P (x 0,y 0),则000012y y x a x a =--+ ,化简得22002221x y a a +=,又P 在椭圆上,所以2220021x y a b+=,所以a 2=2b 2,故e.2 已知椭圆中心在原点,一个焦点为(0),且长轴长是短轴长的2倍,则该椭圆的标准方程是( )A.24x +y 2=1B.x 2+24y =1C.23x +y 2=1 D.x 2+23y =1答案:A ∵一个焦点为(0), ∴焦点在x 轴上且c又∵长轴长是短轴长的2倍,即2a =2×2b ,a =2b .故选A.3 (2010广东高考,文7)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )A.45 B.35 C.25 D.15答案:B 由2a,2b,2c 成等差数列,得2b =a +c . 又b 2=a 2-c 2,所以(a +c )2=4(a 2-c 2), 所以a =53c .所以e =3.5c a = 4 “嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月球飞行,之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月球飞行,最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月球飞行.若用2c 1和2c 2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:①a 1+c 1=a 2+c 2;②a 1-c 1=a 2-c 2;③c 1a 2>a 1c 2;④1212c c a a <.其中正确的是( ) A.①③ B.②③ C.①④ D.②④ 答案:B 在椭圆Ⅰ中,|PF |=a 1-c 1,e 1=11c a ;在椭圆Ⅱ中|PF |=a 2-c 2,e 2=22ca ,故②正确.由图知轨道Ⅰ比轨道Ⅱ扁,即e 1>e 2,故③正确.应选B.5 (一题多解)椭圆ax 2+by 2=1与直线x +y -1=0相交于A ,B 两点,C 是AB 的中点,若|AB |=OC的斜率为2,求椭圆的方程. 5.答案:解:方法一:设A (x 1,y 1),B (x 2,y 2),代入椭圆方程,得22111ax by +=,① 22121ax by +=.②②-①,得a (x 1+x 2)(x 2-x 1)+b (y 2+y 1)(y 2-y 1)=0. 而2121y y x x --=k AB =-1,21212OC y y k x x +==+b. 又∵|AB ||x 2-x 1|x 2-x 1|= ∴|x 2-x 1|=2.又由221,1,ax by x y ⎧+=⎨+=⎩得(a +b )x 2-2bx +b -1=0, ∴x 1+x 2=2b a b +,x 1x 2=1b a b-+.∴|x 2-x 1|2=(x 1+x 2)2-4x 1x 2=2b a b ⎛+⎫⎪⎝⎭2-4·1b a b -+=4.将b 代入,得a =13,b=3.∴所求的椭圆方程为221.33x y +=方法二:由直线方程和椭圆方程联立,得221,1,ax by x y ⎧+=⎨+=⎩得(a +b )x 2-2bx +b -1=0. 设A (x 1,y 1),B (x 2,y 2).则|AB |∵|AB |=1=.①设C (x ,y ),则x =122x x b a b +=+,y =1-x =aa b+.∵OC a b .代入①,得a =13,b .∴椭圆方程为22 1.33x y +=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自我小测
1.如果一个椭圆的长轴长是短轴长的2倍,那么这个椭圆的离心率为( )
A .4
B .2
C .
2 D .12 2.已知焦点在x 轴上的椭圆的离心率为
12
,且它的长轴长等于圆C :x 2+y 2-2x -15=0的半径,则椭圆的标准方程是( ) A .22=143x y + B .22
=11612
x y + C .22=14x y + D .22
=1164
x y + 3.过椭圆22
22=1(0)x y a b a b
+>>的左焦点F 1作x 轴的垂线交椭圆于点P ,F 2为右焦点,若∠F 1PF 2=60°,则椭圆的离心率为( )
A B .2
C .3
D .2
4.若方程22
2=1x y a a
-表示焦点在y 轴上的椭圆,则a 的取值范围是( ) A .a <0 B .-1<a <0
C .a <1
D .无法确定
5.(2010·广东高考,文7)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )
A .
45 B .35
C .25
D .15
6.如果椭圆
22
=1
89
x y
k
+
+
的离心率为
1
2
,则k=__________.
7.则其离心率为__________.
8.直线x+2y-2=0经过椭圆
22
22
=1(0)
x y
a b
a b
+>>的一个焦点和一个顶点.则该椭
圆的离心率等于__________.
9.已知椭圆
22
22
=1(0)
x y
a b
a b
+>>过点
3
1,
2
⎛⎫
⎪
⎝⎭
,且离心率
1
2
e=,求此椭圆的方程.
10.已知椭圆
22
22
=1(0)
x y
a b
a b
+>>的离心率e=
形的面积为4,求椭圆的方程.
参考答案1.答案:B
2.答案:A由x2+y2-2x-15=0,知r=4=2a a=2.又
1
==
2
c
e
a
,c=1.故b2=a2
-c2=4-1=3.故选A.
3.答案:C在Rt△PF1F2中,设|PF1|=m
,由已知得
12
|F F,|PF2|=2m
,则
12
12
2
===
2+||3
F F
c
e
a PF PF
.
4.答案:B方程
22
2
=1
x y
a a
-表示焦点在y轴上的椭圆,所以2
0,0,
10
10
a a
a
a
a a
<<
⎧⎧
⇒⇒-<<
⎨⎨
-<<
<-⎩
⎩
.
5.答案:B依题意有2×2b=2a+2c,即2b=a+c,
∴4b2=a2+2ac+c2.
∵b2=a2-c2,∴4a2-4c2=a2+2ac+c2,
∴3a2-2ac-5c2=0,两边同除以a2,即有5e2+2e-3=0,解得
3
5
e=或e=-1(舍).故选B.
6.答案:4或
5
4
-当焦点在x轴上,即k>1时,b=3
,a
∴c=
1
2
=,解得k=4.符合k>1,∴k=4;
当焦点在y轴上,即-8<k<1时,a=3
,b=
∴c==
1
2
=,解得
5
4
k=-,符合-8<k<1,
∴
5
4
k=-.综上得k=4或
5
4
-.
7.答案
:5-由题意
得():(
a c a c
+-,
即
1
1
e
e
+
=
-
,解得
5e =-
8.
由题意知椭圆的焦点在x 轴上,又直线x +2y -2=0与x 轴,y 轴的交点分别为(2,0),(0,1),它们分别是椭圆的焦点和顶点,所以b =1,c =2
,从而a
c e a ==. 9. 答案:分析:由椭圆的离心率可得a ,c 的关系,从而知道b ,c 的关系,再由点在椭圆上,代入方程即可,从而求得椭圆的标准方程.
解:由题意知,椭圆的离心率12e =
, ∴12
c a =,∴a =2c ,∴b 2=a 2-c 2=3c 2, ∴椭圆的方程为22
22=143x y c c
+, 又点31,2⎛⎫ ⎪⎝⎭在椭圆上,∴2
22312=143c c ⎛⎫ ⎪⎝⎭+, ∴c 2=1,∴椭圆的方程为22
=143x y +. 10. 答案:分析:
由离心率c e a ==及a 2=b 2+c 2可得a =2b ,由菱形面积为4,可得ab =2,两式联立可求得a ,b ,从而得到椭圆的方程.
解:
由2
c e a ==,得3a 2=4c 2.再由c 2=a 2-b 2,解得a =2b .由题意可知12242
a b ⨯⨯=,即ab =2. 解方程组2,2,a b ab =⎧⎨=⎩得2,1.a b =⎧⎨=⎩
所以椭圆的方程为2
2+=14
x y .。
