第13课时直通中考
中考数学复习第13课时《反比例函数》说课稿

中考数学复习第13课时《反比例函数》说课稿一. 教材分析《中考数学复习第13课时》这一课时,是在学生已经掌握了比例函数的基础上进行教学的。
本课时主要让学生了解反比例函数的定义、性质及其图象,能够熟练运用反比例函数解决实际问题。
教材通过丰富的实例,引导学生探究反比例函数的图象和性质,培养学生的观察能力、思维能力和创新能力。
二. 学情分析初中生在学习反比例函数时,已经具备了一定的函数基础,对比例函数的概念和图象有一定的了解。
但学生在学习过程中,可能会对反比例函数的定义和性质产生混淆,特别是在解决实际问题时,不知道如何运用反比例函数。
因此,在教学过程中,我要注重引导学生理解反比例函数的定义,掌握其性质,并能运用到实际问题中。
三. 说教学目标1.知识与技能目标:让学生掌握反比例函数的定义、性质及其图象,能够熟练运用反比例函数解决实际问题。
2.过程与方法目标:通过观察、实验、探究等方法,让学生了解反比例函数的图象和性质,培养学生的观察能力、思维能力和创新能力。
3.情感态度与价值观目标:激发学生学习反比例函数的兴趣,培养学生的团队合作意识,使学生感受到数学在生活中的应用价值。
四. 说教学重难点1.教学重点:反比例函数的定义、性质及其图象。
2.教学难点:反比例函数在实际问题中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、小组合作学习法等,引导学生主动探究、积极参与。
2.教学手段:利用多媒体课件、反比例函数图象软件等,直观展示反比例函数的图象和性质,提高学生的学习兴趣。
六. 说教学过程1.导入:通过复习比例函数的知识,引出反比例函数的概念,激发学生的学习兴趣。
2.新课导入:讲解反比例函数的定义,让学生通过实例理解反比例函数的概念。
3.性质探究:引导学生观察反比例函数的图象,总结反比例函数的性质。
4.应用拓展:通过实际问题,让学生运用反比例函数解决问题,巩固所学知识。
5.练习环节:布置一些有关反比例函数的练习题,让学生独立完成,检测学习效果。
中考思想品德第13课时 中考命题点梳理

点拨中考思想品德第13课时全面建成小康社会实现共同理想考点一我国社会发展不平衡的现状命题点1:当前我国城乡、区域发展不平衡的表现(1)经济发展速度差距大。
(2)基本公共服务水平的差距较大。
(3)教育公平问题突出。
(4)医疗服务、社会保障体系不够完善。
(5)东南沿海地区发展较快,中西部地区发展较慢。
命题点2:国家采取措施推进城乡协调发展的意义(1)有利于提高农民的社会地位,逐步缩小城乡居民之间的差距。
(2)有利于提高农民的生活质量,让农民生活得更加幸福、更有尊严。
(3)有利于促进农村社会的进步,实现城乡和谐发展。
命题点3:如何改善我国城乡、区域发展不平衡的现状(1)完善社会主义分配制度。
(2) 不断提高中低收入者的收入水平。
(3)完善社会保障体系。
(4)制定符合初级阶段国情的方针和政策,有效地调控合理水平范围内的差距。
考点二共同理想命题点1:共同理想和最高理想(1)共同理想:在社会主义初级阶段,把我国建设成为富强民主文明和谐的社会主义现代化国家。
(2)最高理想:实现共产主义。
共产主义社会将是物质财富极大丰富,人民精神境界极大提高,每个人自由而全面发展的社会。
命题点2:艰苦奋斗精神的内涵及其在新时期的集中表现(1)内涵:艰苦奋斗不仅是一种勤俭节约、艰苦朴素,反对铺张浪费、奢侈挥霍的生活作风和道德品质,也是一种不畏艰险、坚忍不拔、奋发图强、顽强拼搏的精神状态和高尚情操,是成就任何事业必不可少的精神力量和崇高美德。
(2)集中表现:艰苦奋斗在新时期集中表现为创业精神,创业实践需要创业精神的支持和鼓舞。
命题点3:新的历史时期,我们要发扬艰苦奋斗精神的原因(1)艰苦奋斗是中华民族的传统美德,是民族精神的重要内容,是中华民族代代相传的精神。
几千年来,正是依靠这种艰苦奋斗精神,中华民族才历经沧桑而不衰,巍然屹立于世界民族之林。
(2)为了巩固和提高目前达到的小康水平,为了实现各族人民的共同理想,我们还需要进行长期的艰苦奋斗。
福建省中考历史中国近代史第13课时中华民族的抗日战争课堂讲本课件

候,如今又遭到更大的浩劫。”“六年前的三千万流
民”产生的原因是 ( B )
A. 甲午中日战争
B. 九一八事变
C. 七七事变
D. 南京大屠杀
2. 【2018·福建·2 分】蒋介石电文:“此次台儿庄之捷,
幸赖我前方将士之不惜牺牲,后方同胞之共同奋斗,
乃获此初步之胜利。”材料说明台儿庄大捷的原因是
(A)
七 大
容
(3) 大会选举产生了中央领导机关,毛泽东在七届一中 全会上当选为中共中央主席;
(4) 大会确立毛泽东思想为中国共产党的指导思想并写
入党章
中共 意 为争取抗日战争的最后胜利准备了条件,并为 七大 义 中国共产党和中国人民指明了战后的奋斗方向
抗日 战争 的胜 利
日 本
(1) 1945 年8 月15 日,日本天皇被迫宣布无条
(2)阅读以上材料,围绕其主题提炼一个观点,并结合 材料和所学中国近代史知识加以论述。(要求:观 点明确,史论结合,条理清楚)(8 分)
示例一:观点:长征的胜利打开了中国革命的新局面。 论述:遵义会议开始确立以毛泽东为主要代表的马克思 主义正确路线在中共中央的领导地位,是中国共产党历 史上一个生死攸关的转折点。
注意区别:台儿庄战役是抗战以来中国正面战场 取得的最大的一场胜仗;百团大战是中国共产党 领导的军队在敌后战场上发动的大规模战役。
课标5 中共七大和抗日战争的胜利
课标要求:知道中国共产党第七次全国代表大会的主要内 容;了解日本投降的史实;(识记)探讨抗日战 争胜利的原因及历史意义。( 运用)
中共 七大
场 战 概 下,组织100 多个团,在华北广阔的地域对日
况 军发动了一场大规模进攻,历时数月,战果辉
煌
人教版(北京)化学中考复习课件【第13课时】气体的制取与净化(28页)

考点聚焦
京考探究
第13课时┃ 气体的制取与净化
2.装置
图13-2 发生装置:固+液不加热型,装置图如图13-2中a、b所示。 向上 排空气法,装置图如图c。 收集装置:________
考点聚焦
京考探究
第时┃ 气体的制取与净化
①用 b 装置制取 CO2 时, 长颈漏斗要伸到液面 以下形成“液封” ,以防气体逸出。 ②伸入到反应容器中的导管稍露出橡胶塞即可, 不宜 太长,否则不利于气体导出。 ③集气瓶内的导管应伸入到集气瓶底部, 利于排尽空 气。
考点聚焦
京考探究
第13课时┃ 气体的制取与净化
净化气体所用的试剂应根据气体的性质来 选定。吸收的试剂只能吸收杂质气体,不能吸收待净 化的气体。
考点聚焦
京考探究
第13课时┃ 气体的制取与净化
3.所用装置
图13-1
考点聚焦 京考探究
第13课时┃ 气体的制取与净化 考点3 氧气的制法
1.实验室制法 反应 原理
考点聚焦
京考探究
第13课时┃ 气体的制取与净化
在二氧化碳的实验室制法中, 不能用稀硫酸与块状 石灰石反应来制取 CO2,这是因为稀硫酸与 CaCO3 反应生成 微溶的 CaSO4,它会覆盖在 CaCO3 的表面,阻碍反应的进行。 若用浓盐酸与石灰石反应来制取 CO2, 会导致浓盐酸中的氯化 氢气体混入产生的 CO2 内,造成制取的气体不纯。
考点聚焦
京考探究
第13课时┃ 气体的制取与净化
氧气
二氧化碳
制 取 装 置
适用②(要在试管口加棉花)
适用①
考点聚焦 京考探究
第13课时┃ 气体的制取与净化
氧气
二氧化碳
收 集 方 法 排水法 向上排空气法 (不易溶于水) (密度比空气略大) 向上排空气法 (密度比空气大)
中考数学一轮复习:第13课时反比例函数的综合应用课件

2. (202X莆田5月质检10题4分)如图,点A,B分别在反比例函数y=1 (x>0),y
=
a x
(x<0)的图象上,若OA⊥OB,OOBA
=2,则a的值为(
A)
x
A. -4
B. 4
C. -2
D. 2
第2题图
3. (202X福建16题4分)已知矩形ABCD的四个顶点均在反比例函数y= 1 的图象
15
12
.
x
设OC=a,点B在直线y=x上,∴点B(a,a).
又∵BC⊥x轴,∴△BOC为等腰直角三角形.
返回目录
No
第13课时 反比例函数的综合应用
∵AB⊥l,AD⊥BC,
∴△ABD为等腰直角三角形.
设BD=b,则AD=b,
∴点A(a+b,a-b).
将点A(a+b,a-b)代入y=12,得 x
a-b=a1+2b,
x
(1)如图①,过点A分别作x轴,y轴的垂线,垂足分别为B,C.若四边形OBAC的
面积为2,则k的值为___2_____;
例题图①
No
第13课时 反比例函数的综合应用
(2)过点A作x轴的垂线,垂足为B. ①如图②,点C是y轴上任意一点.若S△ABC=1,则k的值为__2______; ②点A与点C关于原点对称. (i)如图③,若S△ABC=2,则k的值为___2_____;
第13课时 反比例函数的综合应用
返回目录
第13课时 反比例函数的综合应用
No
思维导图
返回目录
利用k的几何意义 确定反比例函数
的解析式
反比例函数 的综合应用
反比例函数 系数k的几何意义
k的几何意义
计算与双曲线 y
2023年生物中考一轮复习第13课时 人体的呼吸(鲁科版)
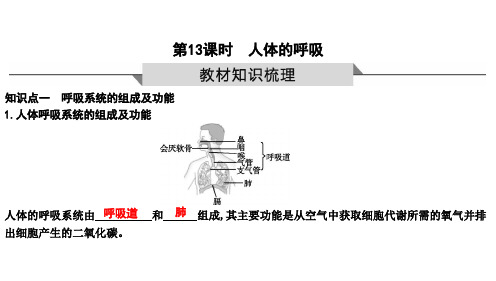
知识点一 呼吸系统的组成及功能 1.人体呼吸系统的组成及功能
人体的呼吸系统由 呼吸道 和 肺 组成,其主要功能是从空气中获取细胞代谢所需的氧气并排 出细胞产生的二氧化碳。
组成器官
结构特点和功能
注意事项
鼻
鼻毛可 清洁 空气;黏膜分泌黏液可清洁、 湿润 空气;丰富的毛细血管可 温暖 空气
知识点二 发生在肺内的气体交换 1.肺与外界的气体交换(肺的通气) (1)原理:肺与外界的气体交换是通过 呼吸运动 来实现的。胸廓(由胸骨、肋骨和胸椎构成)有 节律地扩大和缩小的过程称为呼吸运动,包括吸气和呼气两个动作。
(2)过程:(下图为吸气过程,呼气过程与之相反)
方法技巧 (1)图示法理解膈肌运动与吸气和呼气过程的关系
【秒判正误】(正确的填“√”,错误的填“×”) (1)吸气、呼气取决于肺内与外界的气压差。( √ ) (2)呼吸运动是通过呼吸肌的收缩和舒张完成的,需要消耗能量。( √ ) (3)在人体内,二氧化碳和氧气含量最高的地方分别是肺泡、组织细胞。( × ) (4)呼出的气体中,二氧化碳浓度比氧气浓度高。( × ) (5)气体扩散是指某种气体总是从浓度高的地方流向浓度低的地方,不需要消耗能量。( √ )
名师点拨 (1)咽既是食物的通道,也是气体的通道。食物和气体不能同时通过咽,呼吸和吞咽不能同时进行。 呼吸时,喉口开放,空气畅通无阻;吞咽时,会厌软骨盖住喉口,以免食物进入气管。“食不言寝不 语”,如果在吃饭时随意说笑,吞咽时会厌软骨可能来不及盖住喉口,食物会进入气管,引起剧烈的 咳嗽。
(2)外界气体进入肺内的过程:鼻→咽→喉→气管→支气管→肺。
(1)通过呼吸运动(包括吸气和呼气两个动作)实现了肺与外界的气体交换(肺的通气)。 (2)人体内的气体交换包括肺泡内的气体交换和组织里的气体交换,其原理是气体的扩散作用。 4.呼吸的意义 进入血液的氧,通过血液循环输送到全身各处的组织细胞里,氧在组织细胞的 线粒体 中参与呼吸 作用,分解有机物,释放出生命活动所需的 能量 。这些能量一部分用于各项生命活动,还有一 部分用于 维持体温 。
中考总复习冀教英语13-第13课时 九年级 Units1-2(精练册)

having a PE lesson in the playground.
A. somebody B. anybody
C. nobody D. everybody
6. Their parents don’t allow them ____C_____in the river because it’s really
tell them that we can do as much as the normal
D. health B. manager D. master B. which D. whom
people, and maybe we can even do better!” 一 二 三 四 五 六 七
三、阅读理解 (2022•金华)
Su believes the sky is the limit. “Find the thing you love, believe in yourself and do your very best. Finally, your dream will come true.”
D. woke up
pronounce each word correctly.
一二三四五六七
Through her hard work, she 7 Jilin
University with a high score of 615 marks in ( B ) 7. A. left
B. entered
named her Mengnan which means “dream and (D ) 4. A. sister
south”. Her parents wished that their 4 would
福建省生物中考复习:考点梳理篇第13课时人的生殖和发育知识点总结与复习

12. 【2021•百色】下图为人的生殖和胚胎发育简图,请你 运用所学的生物学知识回答下列问题。
(1)我们每个人都是从一个__受__精__卵__发育而来的。甲表示 正在受精的卵细胞,受精过程是在母体内的__输__卵__管__处 完成的。
(2)丁是由乙经过细胞的__分__裂____和___分__化___等复杂过程 逐渐发育形成的。丁通过____胎__盘__从母体血液获得氧气 和养料,并将代谢废物排到母体内。
7.【2020·漳州质检·2分】营养物质由孕妇到达胎儿体内的过程 是( )D
A.脐带→胎盘→母体→胎儿 B.母体→脐带→胎盘→胎儿 C.胎盘→脐带→母体→胎儿 D.母体→胎盘→脐带→胎儿
8.【2020·南平质检·2分】人体分泌雌性激素的器官是( C ) A.输卵管 B.子宫 C.卵巢 D.胎盘
基础梳理篇
从母体阴道产出体外,这个过程叫做__分__娩____。 (5)早期胚胎需要的营养来自__卵__黄____,胚胎和胎儿发育需
要的营养通过____胎__盘__和_____脐__带_从母体获得。
【方法点拨】 胎儿和母体进行的物质交换:
【特别提醒】 “试管婴儿”是由受精卵发育而来的,属于有 性生殖。
2 重点突破
【点拨】本题考查胚胎发育的有关知识,重点是了解胎盘 的功能。位于子宫中的胎儿,通过胎盘和脐带从母体获得 营养并排出代谢废物。
【答案】D
3 福建5年中考聚焦
01
02
03
04
05
06
07
08
1.【2021·福建·2分】人体中产生卵细胞的器官是( B )
A.子宫
B.卵巢
C.胎盘
D.输卵管
2.【2020·福建·2分】胎儿与母体进行物质交换的结构
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分 系统复习知能提升第三单元 函数及其图象 第13课时 二次函数的应用一、选择题1.(2013·湖南株洲)二次函数y =2x 2+mx +8的图象如图所示,则m 的值是( )A .-8B .8C .±8D .6解析:由图可知,抛物线与x 轴只有一个交点,∴Δ=m 2-4×2×8=0.解得m =±8.∵对称轴为直线x =-m2×2<0,∴m >0.∴m 的值为8.答案:B2.(2012·天津)若关于x 的一元二次方程(x -2)(x -3)=m 有实数根x 1,x 2,且x 1≠x 2,有下列结论:①x 1=2,x 2=3;②m >-14;③二次函数y =(x -x 1)(x -x 2)+m 的图象与x 轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )A .0B .1C .2D .3解析:一元二次方程(x -2)(x -3)=m 化为一般形式得x 2-5x +6-m =0.∵方程有两个不相等的实数根x 1,x 2,∴b 2-4ac =(-5)2-4(6-m )=4m +1>0.解得m >-14.故结论②正确;∵一元二次方程实数根分别为x 1,x 2,∴x 1+x 2=5,x 1x 2=6-m .而结论①中x 1=2,x 2=3,只有在m =0时才能成立,故结论①错误;二次函数y =(x -x 1)(x -x 2)+m =x 2-(x 1+x 2)x +x 1x 2+m =x 2-5x +(6-m )+m =x 2-5x +6=(x -2)(x -3),令y =0,得(x -2)(x -3)=0.解得x =2或3.∴抛物线与x 轴的交点为(2,0)或(3,0),故结论③正确.综上所述,正确的结论有2个:②③.答案:C3.(2012·四川资阳)如图是二次函数y =ax 2+bx +c 的部分图象,由图象可知不等式ax 2+bx +c <0的解集是( )A .-1<x <5B .x >5C .x <-1且x >5D .x <-1或x >5解析:由图象得,对称轴是x =2,其中一个点的坐标为(5,0).∴图象与x 轴的另一个交点坐标为(-1,0).利用图象可知,ax 2+bx +c <0的解集即是y <0的解集.∴x <-1或x >5.答案:D4.(2011·江苏无锡)如图,抛物线y =x 2+1与双曲线y =kx 的交点A 的横坐标是1,则关于x 的不等式kx+x 2+1<0的解集是( )A .x >1B .x <-1C .0<x <1D .-1<x <0解析:∵抛物线y =x 2+1与双曲线y =k x 的交点A 的横坐标是1,∴x =1时,kx =x 2+1.再结合图象当0<x <1时,k x >x 2+1,∴-1<x <0时,|k x |>x 2+1.∴kx +x 2+1<0.∴关于x的不等式kx+x 2+1<0的解集是-1<x <0.答案:D 二、填空题5.(2013·湖北黄石)若关于x 的函数y =kx 2+2x -1的图象与x 轴仅有一个公共点,则实数k 的值为________.解析:令y =0,则kx 2+2x -1=0.∵关于x 的函数y =kx 2+2x -1的图象与x 轴仅有一个公共点,∴关于x 的方程kx 2+2x -1=0只有一个根.①当k =0时,2x -1=0,即x =12,∴原方程只有一个根.∴k =0符合题意;②当k ≠0时,Δ=4+4k =0,解得k =-1.综上所述,k =0或-1.答案:0或-16.(2012·浙江绍兴)教练对小明推铅球的录像进行技术分析,发现铅球行进高度y (m)与水平距离x (m)之间的关系为y =-112(x -4)2+3,由此可知铅球推出的距离是________m.解析:令函数解析式y =-112(x -4)2+3中,y =0时,解得x 1=10,x 2=-2(舍去).∴铅球推出的距离是10m.答案:107.(2013·浙江衢州)某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一颗树,平均每棵树就会少结5个橘子.设果园增种x 棵橘子树,果园橘子总个数为y 个,则果园里增种________棵橘子树,橘子总个数最多.解析:假设果园增种x 棵橘子树,那么果园共有(x +100)棵橘子树,∵每多种一棵树,平均每棵树就会少结5个橘子,∴这时平均每棵树就会少结5x 个橘子,则平均每棵树结(600-5x )个橘子.∵果园橘子的总产量为y ,∴则y =(x +100)(600-5x )=-5x 2+100x +60000.∴当x =-b 2a =-1002×(-5)=10(棵)时,橘子总个数最多.答案:10 三、解答题8.(2012·山东青岛)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (个)与销售单价x (元/个)之间的对应关系如图所示:(1)试判断y 与x 之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w (元)与销售单价x (元/个)之间的函数关系式;(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.分析:(1)观察可得该函数图象是一次函数,设出一次函数解析式,把其中两点代入即可求得该函数解析式,进而把其余两点的横坐标代入看纵坐标是否与点的纵坐标相同;(2)销售利润=每个许愿瓶的利润×销售量;(3)根据进货成本可得自变量的取值,结合二次函数的关系式即可求得相应的最大利润.解:(1)y 是x 的一次函数,设y =kx +b , ∵图象过点(10,300),(12,240),∴⎩⎪⎨⎪⎧ 10k +b =300,12k +b =240,解得⎩⎪⎨⎪⎧k =-30,b =600.∴y =-30x +600.当x =14时,y =180;当x =16时,y =120.∴点(14,180),(16,120)均在函数y =-30x +600图象上. ∴y 与x 之间的函数关系式为y =-30x +600; (2)w =(x -6)(-30x +600)=-30x 2+780x -3600, ∴w 与x 之间的函数关系式为 w =-30x 2+780x -3600;(3)由题意,得6(-30x +600)≤900.解得x ≥15. w =-30x 2+780x -3600图象的对称轴为 x =-b 2a =-7802×(-30)=13.∵a =-30<0,∴抛物线开口向下. 当x ≥15时,w 随x 增大而减小.∴当x =15时,w 最大=1350,即以15元/个的价格销售这批许愿瓶可获得最大利润1350元.9.(2012·辽宁锦州)某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x 元时(x 为正整数),月销售利润为y 元.(1)求y 与x 的函数关系式并直接写出自变量x 的取值范围; (2)每件玩具的售价定为多少元时,月销售利润恰为2520元?(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?分析:(1)根据题意知一件玩具的利润为(30+x-20)元,月销售量为(230-10x),然后根据月销售利润=一件玩具的利润×月销售量即可求出函数关系式;(2)把y=2520时代入y =-10x2+130x+2300中,求出x的值即可;(3)把y=-10x2+130x+2300化成顶点式,求得当x=6.5时,y有最大值,再根据0<x≤10且x为正整数,分别计算出当x=6和x=7时y的值即可.解:(1)根据题意,得y=(30+x-20)(230-10x)=-10x2+130x+2300,自变量x的取值范围是0<x≤10且x为正整数;(2)当y=2520时,得-10x2+130x+2300=2520.解得x1=2,x2=11(不合题意,舍去) .当x=2时,30+x=32(元),∴每件玩具的售价定为32元时,月销售利润恰为2520元.(3)根据题意,得y=-10x2+130x+2300=-10(x-6.5)2+2722.5.∵a=-10<0,∴当x=6.5时,y有最大值为2722.5.∵0<x≤10且x为正整数,∴当x=6时,30+x=36,y=2720(元).当x=7时,30+x=37,y=2720(元).∴每件玩具的售价定为36元或37元时,每个月可获得最大利润,最大的月利润是2720元.10.(2013·湖北咸宁)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?分析:(1)把x=20代入y=-10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;(2)由利润=销售价-成本价,得w=(x-10)(-10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;(3)令-10x2+600x-5000=3000,求出x 的值,结合图象求出利润的范围,然后设政府每个月为他承担的总差价为p 元,根据一次函数的性质求出总差价的最小值.解:(1)当x =20时,y =-10x +500=-10×20+500=300,300×(12-10)=300×2=600,即政府这个月为他承担的总差价为600元. (2)依题意,得w =(x -10)(-10x +500) =-10x 2+600x -5000=-10(x -30)2+4000, ∵a =-10<0,∴当x =30时,w 有最大值4000. ∴当销售单价定为30元时,每月可获得最大利润4000.(3)由题意,得-10x 2+600x -5000=3000. 解得x 1=20,x 2=40.∵a =-10<0,抛物线开口向下,∴结合图象可知,当20≤x ≤40时,w ≥3000. 又∵x ≤25,∴当20≤x ≤25时,w ≥3000. 设政府每个月为他承担的总差价为p 元, ∴p =(12-10)×(-10x +500)=-20x +1000. ∵k =-20<0,∴p 随x 的增大而减小. ∴当x =25时,p 有最小值500.∴销售单价定为25元时,政府每个月为他承担的总差价最少为500元.1.已知二次函数y =x 2-3x +m (m 为常数)的图象与x 轴的一个交点为(1,0),则关于x 的一元二次方程x 2-3x +m =0的两实数根是( )A .x 1=1,x 2=-1B .x 1=1,x 2=2C .x 1=1,x 2=0D .x 1=1,x 2=3解析:∵二次函数的解析式是y =x 2-3x +m (m 为常数),∴该抛物线的对称轴是x =32.又∵二次函数y =x 2-3x +m (m 为常数)的图象与x 轴的一个交点为(1,0),∴根据抛物线的对称性质知,该抛物线与x 轴的另一个交点的坐标是(2,0),∴关于x 的一元二次方程x 2-3x +m =0的两实数根分别是x 1=1,x 2=2.答案:B2.如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为()A.-1≤x≤9 B.-1≤x<9C.-1<x≤9 D.x≤-1或x≥9解析:由图形可以看出,抛物线y2=ax2+bx+c(a≠0)和一次函数y1=kx+n(k≠0)的交点的横坐标分别为-1,9.当y1≥y2时,x的取值范围正好在两交点之内(包括两交点),即-1≤x≤9.答案:A3.如图,小浩从二次函数y=ax2+bx+c(a≠0)的图象中得到如下信息:①ab<0 ;②4a+b=0 ;③当y=5时只能得x=0;④关于x的一元二次方程ax2+bx+c=10有两个不相等的实数根.你认为其中正确的有()A.1个B.2个C.3个D.4个解析:∵抛物线开口向下,∴a<0.∵抛物线的对称轴为直线x=-b2a=2,∴b=-4a.∴b>0,b+4a=0.∴①②正确;∵抛物线的对称轴为直线x=2,∴(0,5)和(4,5)是抛物线上两对称点.∴x=0或4时,y=5.∴③错误;∵抛物线的顶点坐标为(2,9),∴y的最大值为9.∴ax2+bx+c≤9.∴一元二次方程ax2+bx+c=10无实数解.∴④错误.答案:B4.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线x =12;④在对称轴左侧,y 随x 增大而增大.解析:根据图表,当x =-2,y =0时,根据抛物线的对称性,当x =3时,y =0,即抛物线与x 轴的交点为(-2,0)和(3,0);∴抛物线的对称轴是直线x =3-52=12.根据表中数据得到抛物线的开口向下,∴当x =12时,函数有最大值,而不是x =0或1对应的函数值6,并且在直线x =12的左侧,y 随x 增大而增大.∴①③④正确,②错.答案:①③④5.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y =ax 2+bx .小强骑自行车从拱梁一端O 沿直线匀速穿过拱梁部分的桥面OC ,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC 共需________秒.解析:设在10秒时到达A 点,在26秒时到达B ,∵10秒时和26秒时拱梁的高度相同,∴A ,B 关于对称轴对称.∵从A 到B 需要16秒,∴从A 到D 需要8秒.∴从O 到D 需要10+8=18秒.∴从O 到C 需要2×18=36秒.答案:366.(1)请在坐标系中画出二次函数y =x 2-2x 的大致图象;(2)根据方程的根与函数图象的关系,将方程x 2-2x =1的根在图上近似的表示出来(描点);(3)观察图象,直接写出方程x 2-2x =1的根.(精确到0.1)解析:(1)确定顶点坐标和函数图象与x轴,y轴交点,作出图形;(2)方程x2-2x=1的根就是二次函数y=x2-2x的函数值为1时的横坐标x的值;(3)观察图象可知交点即为方程的根.解:(1)如图,y=x2-2x=(x-1)2-1,作出顶点,作出与x轴的交点,用平滑的曲线连接三点画出函数图象;(2)正确作出点M,N;(3)写出方程的根为-0.4,2.4.7.如图,有一座抛物线形拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m 时,水面CD的宽是10m.(1)建立如图所示的直角坐标系,求此抛物线的解析式;(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地,已知甲地距此桥280km(桥长忽略不计).货车正以每小时40km的速度开往乙地,当行驶1小时时,忽然接到紧急通知:前方连降暴雨,造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处,当水位达到拱桥最高点O时,禁止车辆通行),试问:如果货车按原来速度行驶,能否安全通过此桥?若能,请说明理由;若不能,要使货车安全通过此桥,速度应超过每小时多少千米?分析:(1)结合题意和图所示的直角坐标系,我们可以得到D(5,-h),B(10,-h-3),即可求出抛物线的解析式;(2)根据时间和车到桥的距离即可求出车安全过桥的最低速度.解:(1)设抛物线的解析式为y =ax 2(a 不等于0),拱桥最高点O 到水面CD 的距离为h米.则D (5,-h ),B (10,-h -3).∴⎩⎪⎨⎪⎧25a =-h ,100a =-h -3.解得⎩⎪⎨⎪⎧a =-125,h =1.∴抛物线的解析式为y =-125x 2.(2)水位由CD 处涨到点O 的时间为1÷0.25=4(小时);货车按原来速度行驶的路程为40×1+40×4=200<280,∴货车按原来速度行驶不能安全通过此桥. 设货车速度提高到x 千米/时, 当4x +40×1=280时,x =60.∴要使货车安全通过此桥,货车的速度应超过60千米/时.。
