【学习课件】第六章气体动理论习题
气体动理论习题课
5 E氧 = ν RT 2
2 ε 转动 = ν RT 2
12/13
9 .某理想气体定压摩尔热容为 29.1J ⋅ mol −1 ⋅ K −1 。求它 某理想气体定压摩尔热容为 在温度为273 K时分子平均转动动能. = 1.38 × 10 −23 J ⋅ K −1 时分子平均转动动能. 在温度为 时分子平均转动动能 k
2/13
五、理想气体压强、温度的统计意义 理想气体压强、
2 P = nε k 3
εk
1 3 2 = m v = kT 2 2
p = nkT
六、三种速率
v =
2
3 kT = m
3 RT M
2kT 2 RT vp = = m M
v ≈ 1 . 60
kT = 1 . 60 m
RT M
3/13
七、理想气体自由度数目
i E = ν RT 2
pV氧 = ν 氧 RT
E氧 = ν 氧
5 RT 2
E氦 = ν 氦
3 RT 2
pV氦 = ν 氦 RT
2. 压强为 、体积为 的氢气(视为刚性分子理想气体)内能为: 压强为p、体积为V的氢气 视为刚性分子理想气体)内能为: 的氢气( (A)
5 PV 2 3 (B) PV 2
i C P = CV + R = R + R 2
2(C P − R ) CP i= = 2 − 1 = 5 R R
可见是双原子分子。 可见是双原子分子。只有两个转动自由度
2 ε r = kT = kT = 3.77 × 10 − 21 J 2
13/13
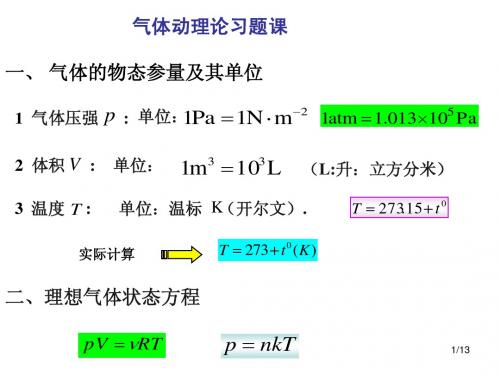
气体动理论习题课 一、 气体的物态参量及其单位
1 气体压强 2 体积 V : 3 温度 T :
气体动理论练习题

气体动理论练习题练习1一、选择题1. 在一密闭容器中,储有A 、B 、C 三种理想气体,处于平衡状态。
A 种气体的分子数密度为n 1,它产生的压强为p 1,B 种气体的分子数密度为2n 1,C 种气体的分子数密度为3n 1,则混合气体的压强p 为 ( )A. 3p 1;B. 4p 1;C. 5p 1;D. 6p 1.2. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻 尔兹曼常量,R 为普适气体常量,则该理想气体的分子数为 ( )A. pV m ⁄;B. pV kT ⁄;C. pV RT ⁄;D. pV mT ⁄。
3. 一定量某理想气体按pV 2=恒量的规律膨胀,则膨胀后理想气体的温度( )A. 将升高;B. 将降低;C. 不变;D. 升高还是降低,不能确定。
二、填空题1. 解释下列分子动理论与热力学名词:(1) 状态参量: ;(2) 微观量: ;(3) 宏观量: 。
2. 在推导理想气体压强公式中,体现统计意义的两条假设是:(1) ;(2) 。
练习2一、选择题1. 一个容器内贮有1摩尔氢气和1摩尔氦气,若两种气体各自对器壁产生的压强分别为p1和p2,则两者的大小关系是( )A. p1>p2; B. p1<p2; C. p1=p2; D. 不能确定。
2. 两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数为n,单位体积内的气体分子的总平动动能为E kV⁄,单位体积内的气体质量为ρ,分别有如下关系( )A. n不同,E k V⁄不同,ρ不同;B. n不同,E k V⁄不同,ρ相同;C. n相同,E k V⁄相同,ρ不同;D. n相同,E k V⁄相同,ρ相同。
3. 有容积不同的A、B两个容器,A中装有刚体单原子分子理想气体,B中装有刚体双原子分子理想气体,若两种气体的压强相同,那么,这两种气体的单位体积的内能E A和E B的关系( )A. E A<E B;B. E A>E B;C. E A=E B;D.不能确定。
普通物理学第五版第6章气体动理论答案(精品课件)

解:
μ gh
M gh
P = P0 e kT =P0 e RT
ln
P P0
=
Mg h RT
h=
RT Mg
ln P P0
=
8.31×273 28×10-3×9.8
ln
0.75
= 2.3km
结束 目录
6-15 求压强为1.013×105Pa、质量为 2×10-3kg、容积为1.54×10-3m3的氧气的 分子的平均平动动能。
结束 目录
解:P = ( h1 h2)d =(0.76 0.60)×1.33×105 Pa
V = 0.28×2.0×10-4 =5.6×10-4 m3
T = 273+27=300 K
M = 0.004 kg/mol
PV
=
m M
RT
m
=
M PV RT
=
0.04×0.16×1.33×105×5.6×10-4 8.31×300
提示:
2 p
01e- x2dx =0.847
2 p
0∞e- x2dx =1
结束 目录
解:(1)
v=
v0pv dN vp dN
0
=
vp 0
v
3e
vp 0
v
2e
dv v 2
v
2
p
dv v 2
v
2
p
令
x=
v vp
dv= vp dx
v
=
vp
1 0
1 0
x 3e-x
2 dx
x 2e-x 2 dx
结束 目录
6-3 一封闭的圆筒,内部被导热的不漏 气的可移动活塞隔为两部分。最初,活塞位 于筒中央,圆筒两侧的长度 l1= l2。 当两侧 各充以T1、p1,与T2、p2的相同气体后,问 平衡时活塞将在什么位置上( 即 l1/l2 是多 少)?已知 p1=1.013×105Pa, T2= 680K, p2 = 2.026×105Pa, T2 =280K。
气体分子动理论习题解PPT课件

1 mv2 3 kT,可得
2
2
N 1 mv2 3 NkT
2
2
即
N
1 2
mv2
3 2
RTN
/(Nd m)
3 (M 2
/
M mol )RT
3 2
(RT
/
M mol )V
7.31106
E
1 2
(M
/
M mol )iRT
(V
/
M mol )
1 2
iRT
4.16104
J
(v2 )1/2
(v
2 2
)1/
2
(v21)1/2
(1) 气体分子的平动动能总和. (2) 混合气体的压强. (普适气体常量R=8.31 J·mol-1·K-1 )
3 kT 8.281021 J
2
Ek
N
( N1
N2)
3 kT 2
4.14105 J
p nkT 2.76 105 Pa
第6页/共10页
17.一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为 = 6.21×10-21
[B]
8.速率分布函数f(v)的物理意义为:
(A) 具有速率v的分子占总分子数的百分比.
(B) 速率分布在v附近的单位速率间隔中的分子数占总分子数的百分比.
(C) 具有速率v的分子数.
(D) 速率分布在v附近的单位速率间隔中的分子数.
[B ]
9.设某种气体的分子速率分布函数为f(v),则速率在v 1─v 2区间内的分子的平均速
4.一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,
而且它们都处于平衡状态,则它们
(A) 温度相同、压强相同.
第六章气体动理论基础

§1 讨论题1.黄绿光的波长是 A 5000(m 10A 110-=)。
理想气体在标准状态下,以黄绿光的波长为边长的立方体内有多少个分子?(玻尔兹曼常量123K J 1038.1--⋅⨯=k )2.容积为L 0.20的瓶子以速率1s m 200-⋅=v 匀速运动,瓶子中充有质量为g100的氦气。
设瓶子突然停止,且气体的全部定向运动动能都变为气体分子热运动的动能,瓶子与外界没有热量交换,求热平衡后氦气的温度、压强、内能及氦气分子的平均动能各增加多少?(摩尔气体常量11K m ol J 31.8--⋅⋅=R ,玻尔兹曼常量123K J 1038.1--⋅⨯=k ) 3.有 3-3m 102⨯刚性双原子分子理想气体,其内能为J 106.752⨯。
(1)试求气体的压强;(2)设分子总数为22105.4⨯个,求分子的平均平动动能及气体的温度。
(玻尔兹曼常量123K J 1038.1--⋅⨯=k )4.一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为J 1021.621-⨯=w 。
试求:(1)氧气分子的平均平动动能和方均根速率;(2)氧气的温度。
(阿伏伽德罗常量123m ol 10022.6-⨯=A N ,玻尔兹曼常量123K J 1038.1--⋅⨯=k )5.某理想气体的定压摩尔热容为11K m ol 29.1J --⋅⋅。
求它在温度为K 273时分子平均转动动能。
(玻尔兹曼常量123K J 1038.1--⋅⨯=k )6.容器内有kg 66.2=M 氧气,已知其气体分子的平动动能总和是J 1014.45⨯=k E ,求:(1)气体分子的平均平动动能;(2)气体温度。
(阿伏伽德罗常量123m ol 10022.6-⨯=A N ,玻尔兹曼常量123K J 1038.1--⋅⨯=k )7.容积3m 1=V 的容器内混有251100.1⨯=N 个氢气分子和252100.4⨯=N 个氧气分子,混合气体的温度为K 400,求:(1)气体分子的平动动能总和;(2)混合气体的压强。
气体动理论(附答案)

气体动理论一、填空题1.(本题3分)某气体在温度为T = 273 K时,压强为p=1.0×10-2atm,密度ρ = 1.24×10-2 kg/m3,则该气体分子的方均根速率为____________。
(1 atm = 1.013×105 Pa)答案:495m/s2.(本题5分)某容器内分子密度为1026m-3,每个分子的质量为3×10-27kg,设其中1/6分子数以速率v=200m/s垂直向容器的一壁运动,而其余5/6分子或者离开此壁、或者平行此壁方向运动,且分子与容器壁的碰撞为完全弹性的。
则(1)每个分子作用于器壁的冲量ΔP=_____________;(2)每秒碰在器壁单位面积上的分子数n0=___________;(3)作用在器壁上的压强p=_____________;答案:1.2×10-24kgm/s×1028m-2s-14×103Pa3.(本题4分)储有氢气的容器以某速度v作定向运动,假设该容器突然停止,气体的全部定向运动动能都变为气体分子热运动的动能,此时容器中气体的温度上升0.7K,则容器作定向运动的速度v=____________m/s,容器中气体分子的平均动能增加了_____________J。
(普适气体常量R=8.31J·mol-1·K-1,波尔兹曼常k=1.38×10-23J·K-1,氢气分子可视为刚性分子。
)答案::1212.4×10-234.(本题3分)体积和压强都相同的氦气和氢气(均视为刚性分子理想气体),在某一温度T下混合,所有氢分子所具有的热运动动能在系统总热运动动能中所占的百分比为________。
答案:62.5%5.(本题4分)根据能量按自由度均分原理,设气体分子为刚性分子,分子自由度为i,则当温度为T时,(1)一个分子的平均动能为_______。
(完整版)《大学物理》习题册题目及答案第6单元 气体动理论

第6单元 气体动理论 序号 学号 姓名 专业、班级一 选择题[ C ]1.在标准状态下, 若氧气(视为刚性双原子分子的理想气体)和氦气的体积比2121=V V ,则其内能之比21/E E 为: (A) 1/2 (B) 5/3 (C) 5/6 (D) 3/10[ B ]2.若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻耳兹曼常量,R 为摩尔气体常量,则该理想气体的分子数为(A) pV/m (B) pV/(kT)(C) pV/(RT) (D) pV/(mT)[ D ]3.若)(v f 为气体分子速率分布函数,N 为分子总数,m 为分子质量,则 )(21221v Nf mv v v ⎰ d v 的物理意义是 (A) 速率为v 2的各分子的总平均动能与速率为v 1的各分子的总平均动能之差。
(B) 速率为v 2的各分子的总平动动能与速率为v 1的各分子的总平动动能之和。
(C) 速率处在速率间隔v 1~ v 2之内的分子的平均平动动能。
(D) 速率处在速率间隔v 1~ v 2之内的分子平动动能之和。
[ D ]4.在一密闭容器中,储有A 、B 、C 三种理想气体,处于平衡状态,A 种气体的分子数密度为 1n ,它产生的压强为 1p ,B 种气体的分子数密度为 12n ,C 种气体的分子数密度为3n 1,则混合气体的压强p 为(A)31p (B)41p(C)51p (D)61p二 填空题1.在定压下加热一定量的理想气体,若使其温度升高1K 时,它的体积增加了0.005倍,则气体原来的温度是_________200k__________。
2.用总分子数N 、气体分子速率v 和速率分布函数f(v),表示下列各量:(1)速率大于0v 的分子数= ⎰∞0)(v dv v Nf ;(2)速率大于0v 的那些分子的平均速率=⎰⎰∞∞00)()(v v dv v f dv v vf ;(3)多次观察某一分子的速率,发现其速率大于0v 的概率=⎰∞0)(v dv v f 。
气体动理论ppt课件

对一定质量 的同种气体
p1V1 p2V2
T1
T2
理想气体物 态方程
pV m RT M
摩尔气体常量 R 8.31J mol 1 K1
8
第六章 气体动理论
pV NkT
归一化条件
i 概率 粒子在第 格中出
现的可能性大小 .
i
i
Ni iN
1
15
第六章 气体动理论
7-3 理想气体的压强公式
一 理想气体的微观模型
1)分子可视为质点; 线度
间距 r ~ 109 m, d r;
d ~ 10 10 m,
2)除碰撞瞬间, 分子间无相互作用力;
3)弹性质点(碰撞均为完全弹性碰撞); 4)分子的运动遵从经典力学的规律 .
v 450m/s ~ 107 m; z ~ 1010次 / s
13
第六章 气体动理论
对于由大 量分子组成的 热力学系统从 微观上加以研 究时,必须用 统计的方法 .
............ ........... ............ ........... ............ ........... ............
16
第六章 气体动理论
二 理想气体压强公式
设 边长分别为 x、y 及 z 的长方体中有 N 个全同的
质量为 m 的气体分子,计算 A1壁面所受压强 .
y
A2 o
z
- mmvvvxx
x
v y A1 y
o
z x v z
v v x
