期中复习(四)
晋教版地理 七年级上册 期中复习串讲 第四章 天气和气候——地球大气的风云变化 专题 (解析版)

晋教版地理七年级上册期中复习串讲第四章天气和气候——地球大气的风云变化知识梳理一、气温概念:指大气的冷暖程度单位:℃(读作摄氏度)测量仪器:温度计气温日平均气温表示月平均气温年平均气温二、气温时间变化日变化最高气温:午后2点左右最低气温:日出前后气温年变化(北半球)气温最高月:7月(陆地)气温最低月:1月(陆地)三、气温的空间分布【规律总结】1、世界1月平均气温分布特点是从赤道地区向南北两极地区递减;北半球等温线弯曲且密集,气温差异大;南半球等温线较平直且稀疏,气温差异小,主要是因为南半球的海洋面积广阔。
2、世界7月平均气温的分布特点是从赤道地区向南北两极地区递减;除南极洲外,全球大部分地区的平均气温多在0℃以上。
3、气温随海拔的升高而下降,海拔每上升100米,气温约降低0.6℃。
等温线:在地图上将气温相同的各点连接起来的线——等温线图。
气温不同纬度地区:低纬——高纬(气温逐渐降低)(纬度位置)的空分夏季陆地气温高,海洋气温低间分布同纬度地区海陆分布布规冬季陆地气温低,海洋气温高律山地:海拔升高,气温低(地形因素)四、降水和降水的分布【规律总结】日降水量的计算方法:将每天8时和20时观测到的降水量数值相加。
含义:从大气中降落到地面的液态水和固态水形式:雨、雪、冰雹等降水单位:毫米(㎜)表示:多年的平均降水量五、降水的季节变化同一地区的不同季节降水量不同降水全年多雨型的季不同地区的不同季节全年少雨型节变降水量不同夏季多雨型化冬季多雨型六、降水的空间分布【规律总结】世界年降水量的分布特点是:赤道地区降水多,两极地区降水少;亚欧大陆沿海地区降水多,内陆地区降水少;回归线附近的大陆东岸降水多,西岸降水少。
等降水量线:在地图上把降水量相同的各点连起来的线。
降水分赤道地区降水多,两极地区降水少(纬度位置)的空布亚欧大陆的沿海地区降水多,内陆地区降水少(海陆分布)间分规南、北回归线附近的大陆东岸降水多,西案降水少律山地迎风坡降水多,背风坡降水少(地形因素)七、天气天气概念:指一个地方短时间内大气的风雨、冷热、阴晴等状况特点:短时间、多变的天气和我们天气人类生产、生活八、常用天气符号1、常见天气符号2、风向与风级的表示概括总结:风向是指风的来向;风速越快风力越大,反之风力越大风速则越快。
部编版语文四年级下册 期中专项复习:04常识 练习(含答案)

部编版四年级下期中专项复习:常识姓名:__________ 班级:__________考号:__________一、单选题1.下列说法有误的是()A. 屈原,战国时期楚国诗人,中国历史上第一位伟大的爱国诗人。
B. 孟浩然,唐代著名的山水田园派诗人。
后人把孟浩然与王维并称为“王孟”。
C. 杜甫,唐代伟大的现实主义诗人,与李白合称“大李杜”。
杜甫在中国古典诗歌中的影响非常深远,被后人称为“诗仙”,他的诗被称为“诗史”。
D. 韩愈,唐代杰出的文学家、思想家、哲学家,政治家。
韩愈被后人尊为“唐宋八大家”之首,与柳宗元并称“韩柳”。
2.下列关于《十万个为什么》的说法正确的一项是()A. 它的作者是英国作家米·伊林。
B. 作者在这本书中,带着我们进行了一次屋内旅行。
C. 这本书向读者提出了十万个问题。
D. 这是一本内容有趣、语言生动的小说。
二、填空题3.选词填空。
猛烈激烈剧烈(1)针对“什么是爱国”这个话题,同学们进行了________辩论。
(2)饭后不能做________运动,这是常识。
(3)海风________地吹,澎湃的波涛把海里的泥沙卷到岸边。
4.我们学习时,遇到不懂的问题怎么解决呢?正确的序号________。
①联系上下文解决问题。
②结合生活经验解决问题。
③不管它。
④向别人请教。
其他的方法:________、________5.选择正确的词语填空。
A.领头羊B.百灵鸟C.老黄牛D.应声虫(1)这位民歌手歌声动听,真是________啊!(2)他在工作上任劳任怨,几十年如一日,简直就是________。
(3)有了班长这个________,我们班每周都被评为文明班级。
(4)妹妹是个________,姐姐说什么她就跟着说什么。
6.选择搭配自行车________ A.贝尔电报________ B.贝尔德电视________ C.马可民电话________ D.德来斯7.填空。
(1)《繁星》的作者是________,原名________,她被称作“________”(2)《绿》作者是________,他是继________、________等人之后推动一代诗风的重要诗人。
2022-2023学年浙教版数学八上期中复习专题4 三角形全等的性质与判定(学生版)
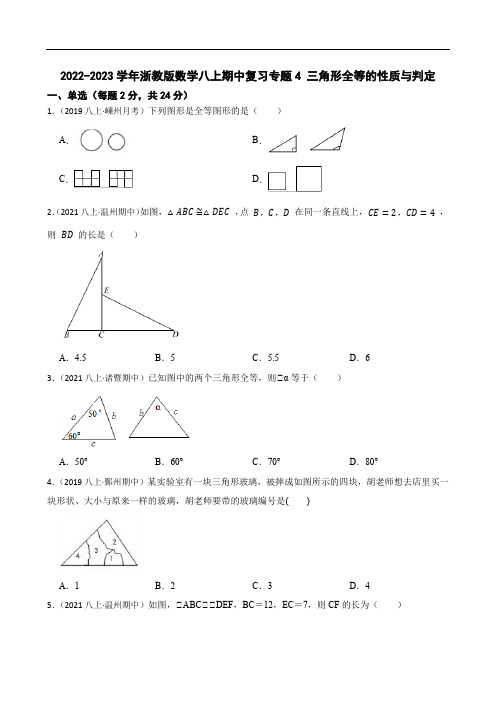
2022-2023学年浙教版数学八上期中复习专题4 三角形全等的性质与判定一、单选(每题2分,共24分)1.(2019八上·嵊州月考)下列图形是全等图形的是()A.B.C.D.2.(2021八上·温州期中)如图,△ABC≅△DEC,点B,C,D在同一条直线上,CE=2,CD=4,则BD的长是()A.4.5B.5C.5.5D.63.(2021八上·诸暨期中)已知图中的两个三角形全等,则∠α等于()A.50°B.60°C.70°D.80°4.(2019八上·鄞州期中)某实验室有一块三角形玻璃,被摔成如图所示的四块,胡老师想去店里买一块形状、大小与原来一样的玻璃,胡老师要带的玻璃编号是()A.1B.2C.3D.45.(2021八上·温州期中)如图,∠ABC∠∠DEF,BC=12,EC=7,则CF的长为()A.5B.6C.7D.86.(2021八上·义乌期中)如图,已知∠OAB∠∠OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是()A.∠BDO=62°B.∠BOC=21°C.CD∠OA D.OC=47.(2021八上·温州期中)下列命题是假命题的是()A.等底等高的两个三角形面积相等B.两个全等三角形的面积相等C.面积相等的两个三角形全等D.等腰三角形底边上的高线和中线互相重合8.(2021八上·温州期中)如图,BP平分∠ABC,D为BP上一点,点E,F分别在BA,BC上,且满足DE=DF.若∠BED=140°,则∠BFD的度数是()A.40°B.50°C.60°D.70°9.(2021八上·鄞州期末)如图,在OA,OB上分别截取OD,OE使OD=OE,再分别以点D、E为圆心,大于12DE长为半径作弧,两弧在∠AOB内交于点C,射线OC就是∠AOB的角平分线.理由是连结CD,CE,证∠COD∠∠COE得∠COD=∠COE.证∠COD∠∠COE的条件是()A.SAS B.AAS C.ASA D.SSS10.(2022八上·柯桥期末)如图,已知AB=AD,AC=AE,若要判定∠ABC∠∠ADE,则下列添加的条件中正确的是()A.∠1=∠DAC B.∠B=∠D C.∠1=∠2D.∠C=∠E 11.(2021八上·台州期中)如图,已知∠1=∠2,添加一个条件,使得△ABC∠ △ADC,下列条件添加错误的是()A.∠B=∠D B.BC=DC C.AB=AD D.∠3=∠4 12.(2021八上·诸暨期中)下列条件中,不能判定两个三角形全等的是()A.有一个锐角相等和一组边相等的直角三角形B.底边和底边上高线对应相等的等腰三角形C.顶角和底边相等的等腰三角形D.一条直角边和一条斜边对应相等的直角三角形二、解答题(共12题,共84分)13.(2019八上·余姚期中)如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:∠涂黑部分的面积是原正方形面积的一半;∠涂黑部分成轴对称图形.如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)14.(2020八上·吴兴期中)图①和图②是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的长均为1.请分别画出符合要求的图形,所画图形的各顶点必须与方格纸中的小正方形的顶点重合.(1)请在图①中出一个面积为3的等腰三角形;(2)请在图②中画出一个与∠ABC全等的三角形ABD.15.(2021八上·温州期中)已知:如图,在∠ABC、∠ADE中,∠BAC=∠DAE=50°,AB=AC,AD =AE,连结BD、CE,BD所在直线交CE、AC分别于点F、G.(1)求证:∠BAD∠∠CAE;(2)求∠BFC的度数.16.(2021八上·余杭月考)如图∠ADF∠∠BCE,∠B=40°,∠F=22°,BC=2cm,CD=1cm.求:(1)∠1的度数;(2)AC的长.17.(2021八上·拱墅期中)已知:点O到∠ABC的两边AB、AC所在直线的距离OE、OF相等,且OB=OC.(1)如图,若点O在边BC上,求证:AB=AC;(2)如图,若点O在∠ABC的内部,则(1)中的结论还成立吗?若成立,请证明;若不成立,说明理由;(3)若点O在∠ABC的外部,则(1)的结论还成立吗?请画图表示.18.(2021八上·鹿城期中)问题情境:如图1,在直角三角形ABC中,∠BAC=90°,AD∠BC于点D,可知:∠BAD=∠C(不需要证明);(1)特例探究:如图2,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF∠AE于点F,BD∠AE于点D.证明:∠ABD∠∠CAF;(2)归纳证明:如图3,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD 上,∠1、∠2分别是∠ABE、∠CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:∠ABE∠∠CAF;(3)拓展应用:如图4,在∠ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F 在线段AD上,∠1=∠2=∠BAC.若∠ABC的面积为3,则∠ACF与∠BDE的面积之和为. 19.(2021八上·瑞安期中)已知:如图,点D在∠ABC的外部,点C在DE边上,BC与AD交于点O.∠1=∠2=∠3,AB=AD.求证:∠ACE是等腰三角形.证明:∵∠1=∠3(),∴∠1+∠CAD=∠3+∠CAD,即∠BAC=∠_▲_.∵∠1=∠2,∠▲_=∠COD,∴180°﹣∠1﹣∠AOB=180°﹣∠2﹣∠COD,即∠B=∠D.又∵AB=AD,∴∠ABC∠∠ADE(),∴AC=AE(),∴∠ACE是等腰三角形().20.(2021八上·绍兴期中)已知:如图1,线段AD=5,点B从点A出发沿射线AD方向运动,以AB为底作等腰∠ABC,使得AC=BC=35AB.(1)如图2,当AB=10时,求证:CD∠AB;(2)当∠BCD是以BC为腰的等腰三角形时,求BC的长;(3)当AB>5时,在线段BC上是否存在点E,使得∠BDE与∠ACD全等,若存在,求出BC的长;若不存在,请说明理由;(4)作点A关于直线CD的对称点A′,连结CA′当CA′∠AB时,求CA′=(请直接写出答案).21.(2021八上·绍兴期中)【问题情境】在等边∠ABC的两边AB,AC上分别有两点M,N,点D为∠ABC外一点,且∠MDN=60°,∠BDC =120°,BD=DC.【特例探究】如图1,当DM=DN时,(1)∠MDB=度;(2)MN与BM,NC之间的数量关系为;(3)【归纳证明】如图2,当DM≠DN时,猜想MN与BM,NC之间的数量关系,并加以证明.(4)【拓展应用】∠AMN的周长与∠ABC的周长的比为.22.(2021八上·萧山期中)已知:如图1,在等边三角形ABC的BC,AC边上各取一点P,Q,使BP=CQ,AP,BQ相交于点O.(1)求证:∠ABP∠∠BCQ;(2)求∠BOP的度数;(3)如图2,沿AB将∠ABC折叠得到∠ABD连结OD交AB于点H,求∠BOD的度数;(4)请你直接写出DO、AO、BO之间的数量关系.23.(2021八上·金东期中)如图1,已知直线l垂直线段AB于点B,点P是直线l上异于点B的一个动点,线段AP绕点P顺时针旋转90°得到线段CP,线段BP绕点P逆时针旋转90°得到线段DP,连结AC,BD,CD,CD与直线l交于点E,AB=4.(1)如图2,过点C作直线l的垂线,垂足为F.①求证:△ABP≌△PFC.②求PE的长.(2)在点P的运动过程中,点P,E,B三点中,是否存在其中一点恰是另外两点为端点的线段的中点,若存在,求出相应CD的长.若不存在,说明相应理由.24.(2021八上·温州期中)问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD∠BC于点D,可知:∠BAD=∠C(不需要证明);(1)特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC,CF∠AE于点F,BD∠AE于点D.证明:∠ABD∠∠CAF;(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是∠ABE、∠CAF的外角.已知AB=AC,∠1=∠2=∠BAC.求证:∠ABE∠∠CAF;(3)拓展应用:如图④,在∠ABC中,AB=AC,A B>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若∠ABC的面积为3,则∠ACF与∠BDE的面积之和为.答案解析部分1.【答案】C【知识点】全等图形【解析】【解答】解:A、两个圆不一样大,不是全等图形,不符合题意;B、两个三角形最大角分别是直角和钝角,不符合题意;C、两个图形放置的方位不一致,但图形的大小一样,形状相同,是全等图形,符合题意;D、两个正方形的大小不一样,不是全等图形;故答案为:C .【分析】只有形状相同,大小相等的两个图形才全等, 据此分别分析和判断.2.【答案】D【知识点】三角形全等及其性质【解析】【解答】解:∵△ABC≅△DEC,∴BC=EC=2,AC=CD=4,∴BD=BC+CD=2+4=6.故答案为:D.【分析】由全等三角形的性质可得BC=EC=2,AC=CD=4,然后根据BD=BC+CD进行计算. 3.【答案】C【知识点】三角形内角和定理;三角形全等及其性质【解析】【解答】解:∵两个三角形全等,∴∠α=180°﹣50°﹣60°=70°.故答案为:C.【分析】根据全等三角形的对应角相等以及内角和定理进行求解.4.【答案】B【知识点】全等三角形的应用【解析】【解答】解:第一块,仅保留了原三角形的部分边,故该块不行;第二块,不但保留了原三角形的两个角还保留了其中一个边,所以符合ASA判定,所以应该拿这块去;第三块,仅保留了原三角形的一部分边,所以该块不行;第四块,仅保留了原三角形的一个角和部分边,不符合任何判定方法;故答案为:B.【分析】显然第②块中保留了原三角形的三个完整条件,根据ASA可以证出所买的三角形与原三角形全等.5.【答案】A【知识点】三角形全等及其性质【解析】【解答】解:∵∠ABC∠∠DEF,∴BC=EF,又BC=12,∴EF=12,∴EC=7,∴CF=EF﹣EC=12﹣7=5.故答案为:A.【分析】由全等三角形的性质可得BC=EF=12,然后根据CF=EF-EC进行计算.6.【答案】C【知识点】三角形内角和定理;三角形全等及其性质;等腰三角形的性质【解析】【解答】解:∵∠OAB∠∠OCD,∴OA=OC=4,OB=OD,故D不符合题意;∴∠AOB=∠DOC=35°,∵OA=OC,∴∠ACO=∠OAC=62°,∴∠AOC=180°-∠ACO-∠OAC=180°-62°-62°=56°,∴∠BOC=∠AOC-∠AOB=56°-35°=21°,故B不符合题意;∴∠BOD=∠DOC+∠BOC=35°+21°=56°;∵OB=OD∴∠BDO=∠OBD=(180°-56°)÷2=62°,故A不符合题意;∠DCO≠∠COA,∴CD不平行于OA,故C符合题意;故答案为:C.【分析】利用全等三角形的性质可求出OC的长及∠DOC的度数,可对D作出判断;同时可证得OA=OC,OB=OD,利用等腰三角形的性质可得到∠ACO=∠OAC=62°,利用三角形的内角和定理求出∠AOC的度数,即可得到∠BOD的度数,可对B作出判断;再求出∠BDO的度数,可对A作出判断;利用已知不能证明∠DCO≠∠COA,可对C作出判断.7.【答案】C【知识点】三角形的面积;三角形全等及其性质;三角形全等的判定;等腰三角形的性质;真命题与假命题【解析】【解答】解:A、根据三角形面积公式可知,等底等高的两个三角形面积相等,正确;B、∵两个全等三角形等大,∴两个全等三角形的面积相等,正确;C、面积相等的两个三角形不一定全等,如同底等高的直角三角形和等边三角形面积相等,但不全等,错误;D、等腰三角形三线合一,即底边上的高、中线和顶角平分线重合,正确;综上,C是假命题.故答案为:C.【分析】等底同高的两个三角形面积显然相等;等大的两个三角形面积显然相等;根据同底等高两三角形面积相等举一个反例,即可判断C;根据等腰三角形的性质判断D.8.【答案】A【知识点】直角三角形全等的判定(HL);角平分线的性质【解析】【解答】解:过点D作DM∠BC于点M,DG∠AB于点G,∴∠EGD=∠FMD=90°,∵BP平分∠ABC,∴DG=DM,在Rt∠EGD和∠FMD中,{DE=DFDG=DM∴Rt∠EGD∠∠FMD(HL)∴∠DEG=∠BFD∵∠BED+∠DEG=140°,∴∠DEG=180°-140°=40°,∴∠BFD=40°.故答案为:A.【分析】过点D作DM∠BC于点M,DG∠AB于点G,利用垂直的定义可证得∠EGD=∠FMD=90°,利用角平分线的性质可知DG=DM;利用HL证明Rt∠EGD∠∠FMD,利用全等三角形的性质可得到∠DEG=∠BFD;然后利用补角的性质可求出∠BFD的度数.9.【答案】D【知识点】三角形全等的判定(SSS)【解析】【解答】解:在∠COE和∠COD中,{OC=OC OE=OD CE=CD,∴∠COE∠∠COD(SSS).故答案为:D.【分析】由作图步骤可知:CE=CD,根据已知条件可知OE=OD,然后结合全等三角形的判定定理进行解答.10.【答案】C【知识点】三角形全等的判定(SAS)【解析】【解答】解:∵AB=AD,AC=AE,则可通过∠1=∠2,得到∠BAC=∠DAE,利用SAS证明∠ABC∠∠ADE.故答案为:C.【分析】根据角的和差关系可得∠BAC=∠DAE,然后根据全等三角形的判定定理进行解答. 11.【答案】B【知识点】三角形全等的判定【解析】【解答】解:A、在∠ABC和∠ADC中,{∠1=∠2∠B=∠DAC=AC,∴∠ABC∠∠ADC(AAS),正确,不符合题意;B、ASS两三角形不一定全等,错误符合题意;C 、在∠ABC 和∠ADC 中,{AB =AD∠1=∠2AC =AC ,∴∠ABC∠∠ADC (SAS ),正确,不符合题意;D 、在∠ABC 和∠ADC 中,{∠3=∠4AC =AC ∠1=∠2,∴∠ABC∠∠ADC (ASA ),正确,不符合题意.故答案为:B.【分析】三角形全等的判定定理有:边角边、角角边、角边角和边边边定理,逐项分析即可判断.12.【答案】A【知识点】三角形全等的判定【解析】【解答】解:当等腰三角形的底边与底边上的高对应相等时,由勾股定理可得腰长相等,则根据SSS 可判断:底边和底边上高线对应相等的等腰三角形全等,故B 不满足题意;当顶角相等时,根据等腰三角形的性质和内角和定理可得底角相等,根据ASA 或AAS 可判断C 中两个三角形全等,故C 不满足题意;利用HL 可知: 一条直角边和一条斜边对应相等的两个直角三角形全等,故D 不满足题意. 故答案为:A.【分析】根据全等三角形的判定定理进行判断.13.【答案】解:(答案不唯一)【知识点】全等图形;轴对称图形【解析】【分析】(1)抓住已知条件:涂黑部分的面积是原正方形面积的一半,只需涂黑8个三角形即可。
八年级政治上册期中复习资料第四课

第四课社会生活讲道德(一)尊重他人1.什么是尊重他人?尊重即尊敬、重视。
尊重他人是一个人内在修养的外在表现。
社会生活中,我们应该尊重他人的人格、权利等。
2.为什么要尊重他人?(1)尊重他人是一个人内在修养的外在表现,我们要尊重他人的人格、权利等。
(2)每个人都是有尊严的个体,都希望得到他人的尊重和社会的尊重。
(3)尊重使社会生活和谐融洽。
3.尊重他人对个人的影响是什么?受到他人尊重能够增强自尊、自信,产生良好的心理体验,如满足感、成就感等。
相反,如果得不到他人的尊重与认可,往往会产生自卑感、挫败感等。
4.尊重他人对社会的影响是什么?尊重使社会生活和谐融洽。
尊重是维系良好人际关系的前提,是文明社会的重要特征。
尊重能够减少摩擦,消除隔阂,增进信任,形成互敬互爱的融洽关系,从而促进社会进步,提高社会文明程度。
5.如何尊重他人?(1)积极关注、重视他人。
对他人的疑惑给予细致的解答,对他人的请求给予热情的帮助。
(2)平等对待他人。
对所有人要一视同仁,不能以家庭、身体、智能、性别等原因而轻视、歧视他人。
(3)学会换位思考。
要设身处地为他人着想,不把自己的意志强加给他人,体会他人的感受,理解他人的难处,包容他人。
(4)学会欣赏他人。
我们要善于发现他人的优点和长处,真诚的欣赏和赞美他人,给予他人积极的评价。
(二)以礼待人1.礼的含义是什么?礼包括礼貌和礼仪。
礼体现一个人的尊重、谦让、与人为善等良好品质。
社会生活中,礼主要表现在语言文明、仪表端庄、举止文明等方面。
2.为什么要文明有礼?(1)文明有礼是人立身处世的前提。
文明有礼会使人变得优雅可亲,更容易赢得他人的尊重和认可。
(2)文明有礼促进社会和谐。
文明有礼有助于人们友好交往,增进人们的团结友爱,有利于形成安定有序、文明祥和的社会。
(3)文明有礼体现国家形象。
我们的一言一行都体现了国家形象,我们举行的各种仪式,体现了民族的尊严和国家的形象。
3.如何做文明有礼的人?(1)做文明有礼的人,要态度谦和,用语文明。
人教版七年级上册数学课堂作业同步期中复习:数轴与一元一次方程综合(四)

人教版七年级上册数学课堂作业同步期中复习:数轴与一元一次方程综合(四)1.已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a﹣b|.(1)数轴上有理数x与有理数﹣2所对应两点之间的距离可以表示为;(2)|x+6|可以表示数轴上有理数x与有理数所对应的两点之间的距离;若|x+6|=|x﹣2|,则x=;(3)若a=1,b=﹣2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数表示的点P重合;(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:,N:;(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.2.如图,数轴上A,B两点对应的数分别﹣4,8.有一动点P从点A出发第一次向左运动1个单位长度;然后在新的位置第二次运动,向右运动2个单位长度;在此位置第三次运动,向左运动3个单位长度,…按照如此规律不断地左右运动(1)当运动到第2018次时,求点P所对应的有理数.(2)点P会不会在某次运动时恰好到达某一个位置,使点P到点B的距离是点P到点A 的距离的3倍?若可能请求出此时点P的位置,若不可能请说明理由.3.已知数轴上两点A,B对应的数分别为a,b,点M为数轴上一动点,其中a,b满足(a+2)2+|b﹣7|=0.(1)写出点A表示的数是;点B表示的数是.(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是[A,B]的好点.①若点M到运动到原点O时,此时点M[A,B]的好点(填是或者不是)②若点M以每秒1个单位的速度从原点O开始运动,当M是[A,B]的好点时,求点M所表示的数.(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.4.已知数轴上两点A、B,点A在点B的左边,A点表示的数为a,点B表示的数为b,且A、B两点的距离是6.(Ⅰ)当a=﹣2时,b=;当|b|=4时,a=;(Ⅱ)当a取何值时,|a|+|b|的值最小?最小值是多少;(Ⅲ)若|a+b|=|a|+|b|,求a的取值范围.5.一辆出租车从甲地出发,在一条东西走向的街道上往返行驶,每次行驶的路程(记向东为正),记录如下表(12<X<23,单位:km):第1次第2次第3次第4次x x﹣12 2(10﹣x)(1)说出这辆出租车每次行驶的方向;(2)这辆出租车共行驶了多少路程?6.如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a、b、c、d.(1)若c与d互为相反数,则a=;(2)若d﹣2b=8,那么点C对应的数是;(3)若abcd<0,a+b>0,求|a﹣2b|+|b+c|﹣3+|c﹣7|+|d﹣a|的取值范围.7.如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合.(提示:圆的周长C=2πr,结果保留π的形式)(1)把圆片沿数轴向右滚动1周,点Q到达数轴上点A的位置,点A表示的数是;(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣5,﹣1①第几次滚动后,Q点距离原点最远?②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?8.已知:在一条东西向的双轨铁路上迎面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD=4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向右方向为正方向画数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是c,且|a+8|与(c﹣16)2互为相反数.(忽略两辆火车的车身及双铁轨的宽度.)(1)求此时刻快车头A与慢车头C之间相距单位长度.(2)从此时刻开始,若快车AB以6个单位长度/秒的速度向右匀速继续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,再行驶秒两列火车的车头A、C 相距8个单位长度.(3)在(2)中快车、慢车速度不变的情况下,此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟內,他的位置P到两列火车头A、C的距离和加上到两列火车尾B、D的距离和是一个不变的值(即PA+PC+PB+PD为定值).则这段时间t是秒,定值是单位长度.9.点A、B在数轴上分别表示数a,b,A、B两点之间的距离表示为|AB|.数轴上A、B两点之间的距离|AB|=|a﹣b|.回答下列问题:(1)数轴上表示﹣1和﹣4的两点之间的距离是;(2)数轴上表示x和﹣1的两点A和B之间的距离是,如果|AB|=2,那么x的值是;(3)若x表示一个有理数,且﹣1<x<3,则|x﹣3|+|x+1|=;(4)若x表示一个有理数,且|x﹣1|+|x+2|>3,则有理数x的取值范围是.10.如图在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b﹣4|=0;(1)点A表示的数为;点B表示的数为;(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),①当t=1时,甲小球到原点的距离=;乙小球到原点的距离=;当t=3时,甲小球到原点的距离=;乙小球到原点的距离=;②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.参考答案1.解:(1)数轴上有理数x与有理数﹣2所对应两点之间的距离可以表示为|x+2|;(2)|x+6|可以表示数轴上有理数x与有理数﹣6所对应的两点之间的距离;若|x+6|=|x﹣2|,则x=(﹣6+2)÷2=﹣2;(3)∵a=1,A点与﹣7表示的点重合,∴对称中心为(﹣7+1)÷2=﹣3,∵b=﹣2,∴B点与数﹣2﹣2×(﹣2+3)=﹣4表示的点P重合;(4)11÷2=5.5,﹣3﹣5.5=﹣8.5,﹣3+5.5=2.5.故M、N两点表示的数分别是:M:﹣8.5,N:2.5;(5)∵A:1,B:﹣2,P:﹣4,∴B向右移动0.5个单位,或向右移动8个单位,或向左移动7个单位,或P向右移动3.5个单位,或向右移动8个单位,或向左移动1个单位,能使相邻两点间距离相等.故答案为|x+2|;﹣6,﹣2;﹣4;﹣8.5,2.5.2.解:(1)﹣4﹣1+2﹣3+4﹣5+6﹣…﹣2017+2018=﹣4+1009=1005.故点P所对应的有理数是1005.(2)①当P点在A点的左边时,∵PB=3PA,∴AB=2PA,∴PA=6,∴P点对应的数为﹣10,﹣4﹣1+2﹣3+4﹣5+6﹣7+8﹣9+10﹣11=﹣10,∴可以;②当P点在AB之间时,∵PB=3PA,∴AB=4PA,∴PA=3,∴P点对应的数为﹣1,﹣4﹣1+2﹣3+4﹣5+6=﹣1,∴可以.∴点P对应的数为﹣10或﹣1.3.解:(1)∵(a+2)2+|b﹣7|=0,∴a+2=0,b﹣7=0,∴a=﹣2,b=7;(2)①AM=2,BM=7,2×2=4≠7,故点M不是【A,B】的好点;②当点M在点B的右侧时,t+2=2(t﹣7),解得t=16;当点M在点A与B之间时,t+2=2(7﹣t),解得t=4;当点M在点A的左侧时,﹣2+t=2(7+t),解得t=﹣16(不合题意舍去).故点M的运动方向是向右,运动时间是4或16秒;(3)线段BM与AM的差即BM﹣AM的值发生变化,理由是:设点M对应的数为c,由BM=|c﹣7|,AM=|c+2|,则分三种情况:当点M在点B的右侧时,BM﹣AM=c﹣7﹣c22=﹣9;当点M在点A与B之间时,BM﹣AM=7﹣c﹣c﹣2=5﹣2c,当点M在点A的左侧时,BM﹣AM=7﹣c+c+2=9.故答案为:﹣2,7,不是.4.解:(Ⅰ)当a=﹣2时∵点A在点B的左边,且A、B两点的距离是6∴b=4;当|b|=4时b=﹣4或b=4当b=﹣4时,a=﹣10;当b=4时,a=﹣2故答案为:﹣10或﹣2.(Ⅱ)当原点在点A和点B之间(包括A、B两点)时,A,B到原点的距离和最小,∴﹣6≤a≤0时,|a|+|b|的值最小,最小值是6.(Ⅲ)当a、b同号或至少有一个为0时,|a+b|=|a|+|b|成立即点A在原点及原点右边或点B在原点及原点左边∴a≥0或a≤﹣6.∴a的取值范围为a≥0或a≤﹣6.5.解:(1)第一次向东行驶x千米,第二次向西行驶x千米,第三次向东行驶(x﹣12)千米,第四次向西行驶2(10﹣x)千米,(2)|x|+|﹣x|+|x﹣12|+|2(10﹣x|=x+x+x﹣12+2x﹣20=x﹣32,答:这辆出租车共行驶了(x﹣32)千米.6.解:(1)如图所示:∵c与d互为相反数,∴CD=4,O为原点,∴|OA|=8,∴a=﹣8;(2)如图2所示:∵BD=7,d﹣2b=8,∴b=﹣1,∴点B向右移动一个单位长度是原点,又∵OC=2,点C在原点的右侧,c=2(3)如图3所示:若abcd<0,a+b>0,求|a﹣2b|+|b+c|﹣3+|c﹣7|+|d﹣a|的取值范围.∵a+b>0,∴b>0>a,且|b|>|a|,﹣1.5<a<0,∴a﹣2b<0,又∵abcd<0,∴d>c>b>0>a,∴b+c>0,c﹣7<0,d﹣a>0.由图可知:b=a+3,c=a+6,d=a+10,|a﹣2b|+|b+c|﹣3+|c﹣7|+|d﹣a|=2b﹣a+b+c﹣3+7﹣c+d﹣a=3b﹣2a+d+4=3(a+3)﹣2a+(a+10)+4=2a+23,∵﹣1.5<a<0,∴20<2a+23<23.7.解:(1)∵2πr=2×π×1=2π,∴点A表示的数是2π,故答案为:2π;(2)①∵(+2)+(﹣1)+(+3)=4,∴第3次滚动后,Q点距离原点最远;②∵|+2|+|﹣1|+|+3|+|﹣5|+|﹣1|=12,∴12×2π×1=24π,∴当圆片结束运动时,Q点运动的路程共有24π,∵2﹣1+3﹣5﹣1=﹣2,∴﹣2×2π×1=﹣4π,∴此时点Q所表示的数是﹣4π.8.解:(1)∵|a+8|与(b﹣16)2互为相反数,∴|a+8|+(b﹣16)2=0,∴a+8=0,b﹣16=0,解得a=﹣8,b=16.∴此时刻快车头A与慢车头C之间相距16﹣(﹣8)=24单位长度;故答案为:24;(2)(24﹣8)÷(6+2)=16÷8=2(秒).或(24+8)÷(6+2)=4(秒)答:再行驶2秒或4秒两列火车行驶到车头AC相距8个单位长度;故答案为:2或4;(3)∵PA+PB=AB=2,当P在CD之间时,PC+PD是定值4,t=4÷(6+2)=4÷8=0.5(秒),此时PA+PC+PB+PD=(PA+PB)+(PC+PD)=2+4=6(单位长度).故这个时间是0.5秒,定值是6单位长度.故答案为:0.5,6.9.解:(1)数轴上表示﹣1和﹣4的两点之间的距离是:|﹣1﹣(﹣4)|=3;故答案为:3;(2)数轴上表示x和﹣1的两点A之和B之间的距离是:|x﹣(﹣1)|=|x+1|;如果|AB|=2,|x+1|=2,∴x+1=2,x+1=﹣2,∴x=1或﹣3.故答案为:|x+1|,1或﹣3;(3)∵﹣1<x<3,∴x﹣3<0,x+1>0,∴|x﹣3|+|x+1|=3﹣x+x+1=4;故答案为:4;(4)∵|x﹣1|+|x+2|>3表示数轴上到﹣2和1的距离之和大于3的数,∴x<﹣2或x>1.故答案为:(4)x<﹣2或x>1.10.解:(1)∵|a+2|+|b﹣4|=0;∴a=﹣2,b=4,∴点A表示的数为﹣2,点B表示的数为4,故答案为:﹣2,4;(2)①当t=1时,∵一小球甲从点A处以1个单位/秒的速度向左运动,∴甲小球1秒钟向左运动1个单位,此时,甲小球到原点的距离=3,∵一小球乙从点B处以2个单位/秒的速度也向左运动,∴乙小球1秒钟向左运动2个单位,此时,乙小球到原点的距离=4﹣2=2,故答案为:3,2;当t=3时,∵一小球甲从点A处以1个单位/秒的速度向左运动,∴甲小球3秒钟向左运动3个单位,此时,甲小球到原点的距离=5,∵一小球乙从点B处以2个单位/秒的速度也向左运动,∴乙小球2秒钟向左运动2个单位,此时,刚好碰到挡板,改变方向向右运动,再向右运动1秒钟,运动2个单位,∴乙小球到原点的距离=2.②当0<t≤2时,得t+2=4﹣2t,解得t=;当t>2时,得t+2=2t﹣4,解得t=6.故当t=秒或t=6秒时,甲乙两小球到原点的距离相等.故答案为:5,2.。
人教版九年级上册数学课堂作业同步期中复习:一元二次方程应用题(四)

人教版九年级上册数学课堂作业同步期中复习:一元二次方程应用题(四)31.从5月份开始,水蜜桃和夏橙两种水果开始上市,根据市场调查,水蜜桃售价为20元/千克,夏橙售价为15元/千克.(1)某水果商城抓住商机,开始销售这两种水果.若第一周水蜜桃的平均销量比夏橙的平均销量多100千克,要使该水果商城第一周销售这两周水果的总销售额不低于9000元,则第一周至少销售水蜜桃多少千克?(2)若该水果商城第一周按照(1)中水蜜桃和夏橙的最低销量销售这两种水果,并决定第二周继续销售这两种水果.第二周水蜜桃售价降低了,销量比第一周增加了2a%,夏橙的售价保持不变,销量比第一周增加了a%.结果两种水果第二周的总销售额比第一周增加了,求a的值.32.巴蜀中学在厦天到来之际,很多学生需要更换夏季校服,欲购买校服T恤.男生的T恤每件价格50元,女生的T恤每件价格45元,第一批共购买600件.(1)第一批购买的校服的总费用不超过28000元,求女生T恤最少购买多少件?(2)箅二批购买校服,男女生购买校服的件数比为3:2,价格保持第一批的价格不变;第三批购买男生的价格在第一批购买的价格上每件减少了元,女生的价格比第一批购买的价格上每件增加了元,男生T恤的数量比第二批增加了m%,女生T恤的数量比第二批减少了m%,第二批与第三批购买校服的总费用相同,求m的值.33.手机下载一个APP、缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行,共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、推车下河、大卸八块等毁坏共享单车的行为也层出不穷•某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.(1)一月份该公司投入市场的自行车至少有多少辆?(2)二月份的损坏率为20%•进入三月份,该公司新投入市场的自行车比二月份增长4a%,由于媒体的关注,毁坏共享单车的行为点燃了国民素质的大讨论,三月份的损坏率下降为,三月底可使用的自行车达到7752辆,求a的值.34.中秋节前夕,某公司的李会计受公司委派去超市购买若干盒美心月饼,超市给出了该种月饼不同购买数量的价格优惠,如图,折线ABCD表示购买这种月饼每盒的价格y(元)与盒数x(盒)之间的函数关系.(1)当购买这种月饼盒数不超过10盒时,一盒月饼的价格为 元;(2)求出当10<x<25时,y与x之间的函数关系式;(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼?35.“谁言寸草心,报得三春晖”,每年5月的第二个星期日为母亲节,某礼品商城经营A、B两种母亲节礼盒,礼盒A售价为每份200元,礼盒B售价为每份150元.(1)已知礼盒A的进价为120元,礼盒B的进价为100元,该礼品盒商城五月份第一周准备购进两种礼盒共200份,若将两种礼盒全部销售,要使总利润不低于13600元,求最多购进礼盒B多少份?(2)为了获得更多利润,根据销售情况和市场分析,该礼品商城第二周决定将礼盒A的售价下调%,礼盒B的售价保持不变,结果与(1)中获得最低利润时的销售量相比,礼盒A的销售量增加了2a%,而礼盒B的销售量增加了a%,最终第二周的销售额比第一周的销售额增加了a%,求a的值.36.4月份,重庆市果桑(俗称桑泡儿)将进入采摘期,预计持续1个月左右,届时全市25个成规模的果桑采摘园将陆续开园迎客,某区有一果园占地250亩,育有56个品种的果桑,其中台湾超长果桑因果形奇特、口感佳而大面积种植,售价30/斤,其它各个品种售价均为20元/斤(1)清明节当天,该果园一共售出500斤果桑,其中售出其它品种的果桑总重量不超过售出台湾超长果桑重量的3倍,问至少售出台湾超长果桑多少斤?(2)为了提高台湾超长果桑的知名度,商家对台湾超长果桑进行广告宣传,4月14日售出其它品种的果桑总重量是售出台湾超长果桑重量的2倍.4月15日起果园推出优惠政策,台湾超长果桑每斤降价a%,其余品种果桑价格保持不变,当日售后统计台湾超长果桑销售数量在前一日的基础之上增加了2a%,其余果桑销售数量在前一日基础之上减少了a%,若当日总销售额与前一日总销售额持平,求a的值.37.如图所示,学校准备在教学楼后面搭建一简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为18m),另外三边利用学校现有总长38m的铁栏围成.(1)若围成的面积为180m2,试求出自行车车棚的长和宽;(2)能围成的面积为200m2自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.38.某地2014年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2016年投入资金2880万元.(1)从2014年到2016年,该地投入异地安置资金的年平均增长率为多少?(2)在2016年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?39.长沙市市政绿化工程中有一块面积为160m2的矩形空地,已知该矩形空地的长比宽多6m.(1)请算出该矩形空地的长与宽;(2)规划要求在矩形空地的中间留有两条互相垂直且宽度均为1m的人行甬道(其中两条人行甬道分别平行于矩形空地的长和宽),其余部分种上草.如果人行甬道的造价为260元/m2,种草区域的造价为220元/m2,那么这项工程的总造价为多少元?40.2016年5月29日,中超十一轮,重庆力帆将主场迎战河北华夏幸福,重庆“铁血巴渝”球迷协会将继续组织铁杆球迷到现场为重庆力帆加油助威.“铁血巴渝”球迷协会计划购买甲、乙两种球票共500张,并且甲票的数量不少于乙票的3倍.(1)求“铁血巴渝”球迷协会至少购买多少张甲票;(2)“铁血巴渝”球迷协会从售票处得知,售票处将给予球迷协会一定的优惠,本场比赛球票以统一价格(m+20)元出售给该协会,因此协会决定购买的票数将在原计划的基础上增加(m+10)%,购票后总共用去56000元,求m的值.参考答案31.解:(1)设第一周夏橙销售量为x千克.则水蜜桃销售量为(x+100)千克,根据题意得:20(x+100)+15x≥9000,解得:x≥200,∴x+100≥300.答:第一周至少销售水蜜桃300千克.(2)根据题意得:20(1﹣a%)×300(1+2a%)+15×200(1+a%)=9000(1+ a%),令t=a%,原方程整理为5t2﹣t=0,解得:t1=,t2=0,∴a1=20,a2=0(舍去).答:a的值为20.32.解:(1)设购买女生T恤x件,则购买男生T恤(600﹣x)件,根据题意得:45x+50(600﹣x)≤28000,解得:x≥400.答:女生T恤最少购买400件.(2)设第二批购进女生T恤2y件,则购进男生T恤3y件,根据题意得:45×2y+50×3y=(45+m)×2y(1﹣m%)+(50﹣m)×3y (1+m%),整理得:m2﹣50m=0,解得:m1=0(舍去),m2=50.答:m的值为50.33.解:(1)设一月份该公司投入市场的自行车x辆,x﹣(7500﹣1200)≥10%x,解得,x≥7000,答:一月份该公司投入市场的自行车至少有7000辆;(2)由题意可得,[7500×(1﹣20%)+1200(1+4a%)](1﹣a%)=7752,化简,得a2﹣250a+4600=0,解得:a1=230,a2=20,∵a%<20%,解得,a<80,∴a=20,答:a的值是20.34.解:(1)∵当0≤x≤10时,y=240.故答案为:240.(2)当10<x<25时,设y=kx+b(其中k、b为常数且k≠0),将B(10,240)、C(25,150)代入y=kx+b中,得:,解得:,∴当10<x<25时,y=﹣6x+300.(3)∵3600÷240=15(盒),3600÷150=24(盒),∴收费标准在BC段.根据题意得:(﹣6x+300)x=3600,解得:x1=20,x2=30(不合题意,舍去).答:李会计买了20盒这种月饼.35.解:(1)设购进礼盒Bx份,则购进礼盒A(200﹣x)份,根据题意得:(200﹣120)(200﹣x)+(150﹣100)x≥13600,解得:x≤80.答:最多购进礼盒B80份.(2)根据题意得:200(1﹣a%)(200﹣80)(1+2a%)+150×80(1+a%)=[200×(200﹣80)+150×80]×(1+a%),令m=a%,则原方程整理得:5m2﹣2m=0,解得:m1=0,m2=,∴a1=0(不合题意,舍去),a2=40.答:a的值为40.36.解:(1)设售出台湾超长果桑x斤,则其它品种售出(500﹣x)斤,根据题意得:500﹣x≤3x,解得:x≥125.答:至少售出台湾超长果桑125斤.(2)设4月14日售出的台湾超长果桑y斤,则售出其它品种果桑2y斤,根据题意得:30(1﹣a%)y(1+2a%)+20×2y(1﹣a%)=30y+20×2y,令a%为m,则原方程整理得:4m2﹣m=0,解得:m1=0,m2=,∴a1=0(不合题意,舍去),a2=25.答:a的值为25.37.解:(1)设AB=x,则BC=38﹣2x;根据题意列方程的,x(38﹣2x)=180,解得x1=10,x2=9;当x=10,38﹣2x=18(米),当x=9,38﹣2x=20(米),而墙长18m,不合题意舍去,答:若围成的面积为180m2,自行车车棚的长和宽分别为18米,10米;(2)根据题意列方程的,x(38﹣2x)=200,整理得出:x2﹣19x+100=0;△=b2﹣4ac=361﹣400=﹣39<0,故此方程没有实数根,答:因此如果墙长18m,满足条件的花园面积不能达到200m2.38.解:(1)设该地投入异地安置资金的年平均增长率为x,根据题意得:1280(1+x)2=2880解得:x1=,x2=﹣(不合题意,应舍去),答:从2014年到2016年,该地投入异地安置资金的年平均增长率为50%;(2)设今年该地有a户享受到优先搬迁租房奖励,根据题意得:1000×8×400+(a﹣1000)×5×400≥5000000解得:a≥1900答:今年该地至少有1900户享受到优先搬迁租房奖励.39.解:(1)设该矩形空地的长为x m,则宽为(x﹣6)m,由题意可得:x(x﹣6)=160.化简得:x2﹣6x﹣160=0,解得x1=16,x2=﹣10(不合题意,舍去)当x=16时,x﹣6=16﹣6=10(m).答:该矩形空地的长为16 m,宽为10 m;(2)由题意可得:(16﹣1)(10﹣1)=135(m2),160﹣135=25(m2),135×220+25×260=29700+6500=36200(元),答:这项工程的总造价为36200元.40.解:(1)设:购买甲票x张,则购买乙票(500﹣x)张.由条件得:x≥3(500﹣x)∴x≥375,故:“铁血巴渝”球迷协会至少购买375张甲票.(2)由条件得:500[1+(m+10)%](m+20)=56000∴m2+130m﹣9000=0∴m1=50,m2=﹣180<0(舍)故:m的值为50.。
四年级下册语文期中复习专题 04病句
四年级下册语文期中复习专题: 04病句姓名:__________ 班级:__________考号:__________一、单选题(共2题;共4分)1.(2分)下列句子中,没有语病的一项是()。
A.《雨巷》的作者是著名诗人戴望舒写的。
B.冰心眼里,充满纯真童趣的世界才是人间最美的情感。
C.通过本次综合性学习,使我们进一步了解诗歌,感受诗歌的魅力。
D.朗读诗歌时,不但要表情自然,而且要用恰当的语气读出诗歌表达的情感。
2.(2分)下面句子有语病的一句是_____A.这白鹅,是一位将要远行的朋友送给我的。
B.我亲自抱了这雪白的大鸟回家。
C.它(大白鹅)伸长了颈,左顾右盼。
D.每逢它(大白鹅)吃饭的时候,就躲在篱边窥伺。
二、判断题(共1题;共2分)3.(2分)我们阅读课外书,可以增长知识和写作水平。
三、填空题(共1题;共20分)4.(20分)按要求写句子。
(1)(5分)青、红的瓜,碧绿的藤和叶,构成了一道别有风趣的装饰。
(缩句)(2)(5分)这是一幅自然和谐的田园风景画。
(改为感叹句)(3)(5分)屋子就黑得像地洞里似的。
(用下划线的词语造句)(4)(5分)乡下人在屋顶上面挖一个小方洞,装一块玻璃,叫做天窗。
(修改病句)四、语言表达(共21题;共229分)5.(5分)按要求写句子。
①我们必须认真改正并检查作业中的错误。
(修改病句)②白发三千丈,缘愁似个长。
(仿写句子)③小小的天窗会使你的想象活跃起来。
(改成反问句)6.(5分)用修改符号修改病句。
①一幢幢高大的高楼拔地而起。
②我们参观了科技馆,开阔了眼界和知识。
7.(5分)修改下面的病句①我想起过去的往事就激动不已。
②我已经将要升入五年级了。
③老师讲的知识,我基本全懂了。
8.(5分)用修改符号修改病句。
①老师讲的知识,我全部完全都懂了。
②我打扫教室干干净净。
③读了《雷锋的故事》后,受到了深刻的教育。
④我提高了良好的学习习惯。
9.(5分)改病句。
①教室里传来了雷鸣般的掌声。
2021年部编版小学语文六年级下册期中考试复习精选题(四)(含答案)
统编版语文六年级下册期中考试复习精选题(四)一、选择题1.加点字的注音全对的一组是()A.徘徊.(huái)膝.盖(qī)萦.绕(yíng)蜜饯.(jiàn)B.蚂蚁.(yi)唠叨.(dāo)绽.放(chàn)唾.沫(tuò)C.亲吻.(wěn)搓.手(cuō)依偎.(wēi)皎.洁(jiǎo)D.珍藏.(cáng)蒸.汽(zhēng)挪.移(luó)聊.天(liáo)2.下列词语没有错别字的一组是()。
A.肿胀染缸鞭炮万不得己B.抛弃简陋野蛮翻箱到柜C.倾覆念叨搀扶焉知非福D.瞻仰耽误收敛精兵减政3.下列句子中有病句的一项是()A.各班班长,请听到广播后立即到校学生会办公室开会。
B.腊月初八这天,家家熬腊八粥。
C.下一站,香港路。
现在开始检票,买票了的请出示,没有买票的请准备好零钱。
D.他年纪不算大,可满头乌发的头上长出了不少白发。
4.下列句中加点的词语使用错误的一项是()A.巫女的面具是半黑半白,象征其两面三刀....的性格。
B.蜜蜂整日不辞辛苦....地劳动着。
C.她的歌唱得非常动听,随心所欲....。
D.民间剪纸绚丽多彩乡亲们见了都赞叹不已....。
5.下列诗句中描写中秋节的一项是()A.爆竹声中一岁除,春风送暖入屠苏。
B.春城无处不飞花,寒食东风御柳斜。
C.家家乞巧望秋月,穿尽红丝几万条。
D.今夜月明人尽望,不知秋思落谁家?6.下列选项中,不是劝诫人们珍惜时间的一项是()A.世人若被明日累,春去秋来老将至。
B.一年之计在于春,一日之计在于晨。
C.不饱食以终日,不弃功于寸阴。
D.燕雀安知鸿鹄之志。
7.下列四组词语中,依次填入句中横线上最恰当的一组是()有人说,我们这个时代不缺机会,所以也势必会让每个人面临很多选择,那么,是遵从自己的内心,还是_____;是直面挑战还是_____;是选择喧嚣一时的功利,还是_____的善良。
2023年春学期七年级语文下册期中复习检测试卷(四)及答案解析
2023年春学期七年级语文下册期中复习检测试卷(四)(考试时间:120分钟,总分:120分)一、积累与运用(28分)1.下列加点字注音完全正确的一项是()(2分)A.萦带(yínɡ) 收敛(lián) 目不窥园(kuī)B.殷红(yān) 挚友(zhì) 义愤填膺(yīnɡ)C.疙瘩(ɡé) 阖眼(hè) 慷慨淋漓(kǎi)D.朔气(sù) 污秽(suì) 妇孺皆知(rú)2.下列词语书写有误的一项是()(2分)A.积攒瞬息波澜壮阔来势汹汹B.澎湃怪诞深恶痛绝锲而不舍C.元勋迭起无遐及此大庭广众D.锁闭衰微锋芒毕露鞠躬尽瘁3.下列加点成语使用有误的一项是()(2分)A.我们不要把精力全放在微不足道的小事上,而要从大局出发,大处着眼,统筹规划。
B.闻一多先生还有另外一个方面……这个方面,情况就迥乎不同,而且一反既往了。
C.吃水不忘挖井人,生活在幸福和平年代的我们不能忘本,不能忘记那兀兀穷年里发生的感人故事。
D.当时,他是美国家喻户晓的人物,因为他曾成功地领导战时美国的原子弹制造。
4.下列句子没有语病的一项是()(2分)A.在比赛中,无论遇到怎样的困难,选手却能勇敢面对。
B.在列车长粗暴的干涉下,使爱迪生在火车上边卖报边做实验的愿望破灭了。
C.中国残疾人艺术团在香港演出大型音乐舞蹈《我的梦》,受到观众的热烈欢迎。
D.为了防止疫情不再反弹,市领导要求各单位进一步加强管理,制定严密的防范措施。
5.下列各句标点符号使用不规范的一项是()(2分)A.如何让古典音乐走进普通人的生活并深入人们的内心?一些艺术家分享了自己工作中的经验与感悟。
B.文艺工作者只有真正深入生活并紧跟时代步伐,才可能创作出有温度、有深度、有高度的优秀作品。
C.原始人类阅读的对象就是大自然:山峦在蔚蓝的天空下寂静绵延,野鹿在蜿蜒的溪流旁边悠闲漫步。
D.历史正剧往往庄重严整,因为它倾向于真实再现,历史传奇常常灵动丰盈,因为它有较多理想色彩。
期中复习 第四单元自然界的水
一、选择题1.下列关于水净化过程中常用方法的说法正确的是()A.明矾可以促进水中悬浮物的沉降B.过滤能除去天然水中的所有杂质C.活性炭的吸附作用可使海水转化成淡水D.过滤或加热均能使硬水转化成软水2.小明收集到一瓶浑浊的长江水,拟定如图所示的净化流程,有关说法错误的是()A.步骤I中加入的试剂X可以是明矾B.Y试剂可以是活性炭C.高铁酸钾消毒杀菌发生了化学变化D.得到的净化水是纯净物3. 在进行过滤操作时,下列仪器不会使用到的是( )4. 生活饮用水的水质必须达到国家规定的相应指标。
下列指标可通过过滤达到的是( ) A.澄清 B.无异色 C.无异味 D.无细菌和病毒5.震后灾区人民须将河水净化成生活用水,常见的净水操作有①过滤、②加明矾吸附、③蒸馏、④消毒杀菌。
应选用的净化顺序为( )A.①②③④ B.②④①③ C.②①④ D.①③④6. 下列关于水的净化过程描述错误的是( )A.加入明矾使小颗粒凝聚而沉淀 B.通入氯气杀菌、消毒C.通过过滤装置除去钙、镁离子 D.通过蒸馏获得蒸馏水7.有关水的电解实验,下列说法正确的是( )。
A.证明了水是由氢元素和氧元素组成B.证明了水是由氢气和氧气组成C.证明了水中含有氢、氧两种物质D.证明了水中含有氢、氧两种分子8.河水净化的主要步骤如下图所示。
有关说法错误..的是( )。
A.步骤Ⅰ可除去难溶性杂质 B.X试剂可以是活性炭C.步骤Ⅲ可杀菌、消毒 D.净化后的水是纯净物9.某物质的化学式为R2O3,其中R元素的质量分数为70%,则R2O3的相对分子质量为( D )。
A.56B.112C.48D.16010.地震过后,防疫部门常用到一种高效安全灭菌消毒剂,该消毒剂可表示为RO2,主要用于饮用水消毒。
实验测得该氧化物中R与O的质量比为71∶64,则RO2的化学式为( D ) A.CO2 B.NO2 C.SO2 D.ClO211.已知某种氮的氧化物中氮、氧元素的质量之比为7∶12,则该氧化物中氮元素的化合价为( B )A.+2B.+3C.+4D.+512.有一可能含下列物质的硝酸铵样品,经分析知道其中氮元素的质量分数为20%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
展示题。 1、填空题 (1)用一个因数乘另一个因数十位上的数时, 所得的积的末位要和因数的( )位对齐。
(2)求一个数的近似数时,一般采用( ) 法。 (3)两个最小的两位数的积是( ),最大的两位数 和最小的两位数的积是( )。 (4)22x38的积是( )位数,积大约是( )。 (5)计算18x(86-27)时,应先算( ),再算( ), 结果是( )。 (6)一捆电线长150米,第一次用去18米,第二次用 去的是第一次的3倍,还剩( )米。
归纳总结: 说一说本节课复习了哪些知识点?
巩固提升 一、列式计算(12分) (1)85的14倍是多少?
(2)两个22相乘得多少?
(3)甲数是35,乙数是甲数的26倍, 甲、乙两数的和是多少?
二、应用题(20分) 1.学校买来12个排球,15个足球,每个排球65元, 每个足球74元。
(1)足球和排球各用了多少钱?
2、判断题。
(1)最大的一位数乘最小的两位数,积是 1089。( ) (2)在乘法算式中,一个因数中间有“0”, 积的中间一定有“0”。 (3)两位数乘两位数的积最多是四位数。 () (4)39省略最高位后面尾数后,得到的近似 数是30。( ) (5)284≈300,读作“284约等于300”( ) (6)30x50的积的末尾有两个0。( ) (7)一个数乘以10,只要在这个数的末尾加 上一个0就可以。( )
3、计算题。 直接写出得数。 12×10= 30×40= 16×50= 4×5×20= 13×12= 25×40= 列式计算。 45×37= 24×15= 76×45= 19×37= 26×15= 182×4=
3.脱式计算。(8分) 28×28+13×26 30×(234÷9)
18×(313-259) 16×17+398
期中复习(四)
复习目标:
1、我能熟练掌握两位数乘两位数的笔算、口 算和估算的方法。 2、我能运用所学知识解决问题,并能发现规 律并运用规律。复习指导:
浏览课本38----50页内容,重点看例 题的解法,梳理知识点。
1、回忆两位数乘两位数的笔算、口算和估算的方法。 2、两位数乘两位数计算时,应注意什么?
(2)一共用了多少钱? (3)排球比足球少用了多少钱?
2.甲地到乙地的距离是2100米,一辆自行车从甲地 到乙地,平均每分钟行使95米。走了13分钟后,距 离乙地还有多少米?
