平行线的判定和性质的综合运用(习题课)
平行线的判定与性质证明题

平行线的判定和性质1.如图,已知:AB∥CD,∠B=∠D,求证:BC∥AD .2.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.3.如图,已知AB∥CD,∠1=∠2,求证:BE∥CF.4.已知:如图所示,C,P,D三点在同一条直线上,∠BAP+∠APD=180°,∠E=∠F,求证:∠1=∠2.5.如图,已知AC∥ED,EB平分∠AED,∠1=∠2,求证:AE∥BD.6.如图,已知∠C=∠D,DB∥EC.AC与DF平行吗?试说明你的理由.7.已知:如图,∠1=∠2,∠A=∠F,则∠C与∠D 相等吗?试说明理由.8.如图,在四边形ABCD中,∠A=∠C=90°,∠1=∠2,∠3=∠4,求证:BE∥DF.9.如图,在△ABC中,CD⊥AB,垂足为D,点E 在BC上,EF⊥AB,垂足为F .(1)CD与EF平行吗?为什么?(2)如果∠1=∠2,DG∥BC吗?为什么?10.如图,已知∠1=∠A,∠2=∠B,那么MN与EF平行吗?如果平行,请说明理由.11.已知:如图,AD⊥BC,EF⊥BC,∠1=∠2.求证:AB∥GF.12.已知:如图,∠C=∠1,∠2和∠D互余,BE⊥FD 于点G.求证:AB∥CD.13.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.14.如图,AD⊥BC于点D,∠1=2,∠CDG=∠B,请你判断EF与BC的位置关系,并加以证明,要求写出每步证明的理由.15、如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的正确性。
结论:(1)________________(2)_______________(3)________________(4)_______________选择结论:____________,说明理由。
素养集训:平行线的判定和性质综合应用的五种常用方法

解:AB∥CD.理由如下: 如图,过点F作FH∥AB, ∴∠MFH=∠2=50°. ∵MF⊥NF,∴∠NFH=90°-∠MFH=40°. ∵∠1=140°,∴∠1+∠NFH=180°. ∴FH∥CD. 又∵FH∥AB,∴AB∥CD.
5.如图,∠B+∠BCD+∠D=360°. 求证:∠1=∠2.
2.如图,∠BEF=70°,∠B=70°,∠DCE=140°,且CD∥AB.求∠CEF的度数.
解:∵∠BEF=70°,∠B=70°,∴∠BEF=∠B.∴AB∥EF. 又∵CD∥AB,∴EF∥CD. ∴∠DCE+∠CEF=180°. 又∵∠DCE=140°, ∴∠CEF=180°-140°=40°.
素养集训
第七章 平行线的证明
平行线的判定和性质综合应用的五种常用方法
答案显示
1
2
3
4
提示:点击 进入习题
5
见习题
见题
见习题
见习题
见习题
1.如图,在△ABC中,EF⊥AB,CD⊥AB,DG∥BC.试判断∠1,∠2的数量关系,并说明理由.
解:∠1=∠2.理由如下: ∵EF⊥AB,CD⊥AB,∴EF∥CD.∴∠1=∠BCD. ∵DG∥BC,∴∠2=∠BCD. ∴∠1=∠2.
3.如图,∠BED=80°,∠B=30°,∠D=50°. 求证:AB∥CD.
证明:如图,过点E作EF∥AB, ∴∠BEF=∠B=30°. ∵∠BED=80°,∴∠FED=50°. 又∵∠D=50°,∴∠FED=∠D. ∴EF∥CD.∴AB∥CD.
4.如图,MF⊥NF于点F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°.试判断AB和CD的位置关系,并说明理由.
证明:如图,过点C作CP∥AB, ∴∠B+∠5=180°. 又∵∠B+∠BCD+∠D=360°, ∴∠6+∠D=180°.∴CP∥ED. 又∵CP∥AB,∴AB∥ED. ∴∠3=∠4. ∵∠1+∠3=180°,∠2+∠4=180°, ∴∠1=∠2.
平行线的判定及性质 例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (2)平行公理的推论:平行于同一条直线的两条直线. (3)在同一平面内,垂直于同一条直线的两条直线. (4)同位角相等,两直线平行. (5)内错角相等,两直线平行.(6)同旁内角互补,两直线平行.3、平行线的性质(1)两直线平行,同位角相等. (2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.二、【例题精讲】专题一:余角、补角、对顶角与三线八角例题1:∠A的余角与∠A的补角互为补角,那么2∠A是()A.直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中,下列判断正确的是()A.4对同位角,2对内错角,4对同旁内角B.4对同位角,2对内错角,2对同旁内角C.6对同位角,4对内错角,4对同旁内角D.6对同位角,4对内错角,2对同旁内角【活学活用2】如图2-82,下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是()A.对顶角B.互余C.互补D相等例题2:如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角分别是_______.【活学活用4】如图,∠AOC +∠DOE +∠BOF = .专题二:平行线的判定例题3:如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行,那么这样的平行棱共有 ( )A .9对B .16对 C.18对 D .以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图2-97,已知:∠1=∠2=,∠3=∠4,∠5=∠6.求证:AD ∥BC.4、如图2—101,若要能使AB ∥ED ,∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ,若a ∥b ,a ⊥c ,b ⊥d ,则c 、d 的位置关系为( ) A.互相垂直 B .互相平行 C.相交 D .没有确定关系专题三:平行线的性质1、如图,110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行,则BOC ∠= . 2、如图,AB //CD ,BC //DE ,则∠B+∠D = .3、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE .若60DOE ∠=,则∠AOC 的度数是 .4、 如图,175,2120,375∠=∠=∠=,则4∠= .13 425、如图,//AB CD ,直线EF 分别交AB 、CD 于E 、F ,ED 平分BEF ∠,若172∠=,则2∠= .【例题讲解】例1:如图,已知:AD ∥BC, ∠AEF=∠B,求证:AD ∥EF 。
平行线的判定和性质练习题
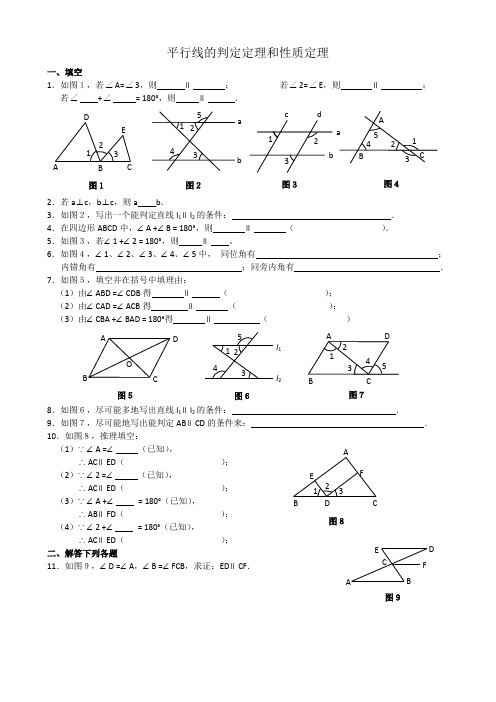
平行线的判定定理和性质定理一、填空1.如图1,若∠A=∠3,则 ∥ ; 若∠2=∠E ,则 ∥ ; 若∠ +∠ = 180°,则 ∥ .2.若a ⊥c ,b ⊥c ,则a b .3.如图2,写出一个能判定直线l 1∥l 2的条件: .4.在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( ).5.如图3,若∠1 +∠2 = 180°,则 ∥ 。
6.如图4,∠1、∠2、∠3、∠4、∠5中, 同位角有 ; 内错角有 ;同旁内角有 .7.如图5,填空并在括号中填理由:(1)由∠ABD =∠CDB 得 ∥ ( );(2)由∠CAD =∠ACB 得 ∥ ( );(3)由∠CBA +∠BAD = 180°得 ∥ ( )8.如图6,尽可能多地写出直线l 1∥l 2的条件: .9.如图7,尽可能地写出能判定AB ∥CD 的条件来: .10.如图8,推理填空:(1)∵∠A =∠ (已知), ∴AC ∥ED ( );(2)∵∠2 =∠ (已知), ∴AC ∥ED ( ); (3)∵∠A +∠ = 180°(已知), ∴AB ∥FD ( ); (4)∵∠2 +∠ = 180°(已知),∴AC ∥ED ( ); 二、解答下列各题11.如图9,∠D =∠A ,∠B =∠FCB ,求证:ED ∥CF .A CB 4 1 2 3 5 图4 a b c d 1 2 3 图3 A BC ED 1 2 3 图1 图2 4 3 2 1 5 a b 1 2 3 AF CD B E图8 E B AF D C 图9 A D C B O 图5 图6 5 1 2 4 3 l 1 l 2 图7 5 4 3 2 1 A D C B12.如图10,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由.13.如图11,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME 。
2、平行线的判定和性质练习题
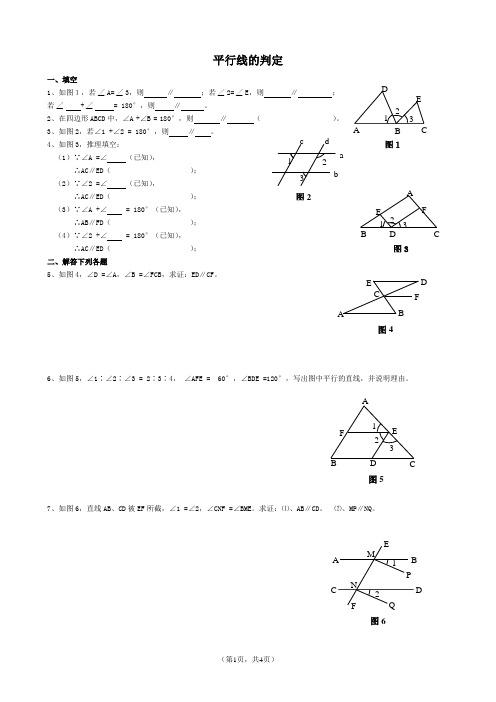
一、填空1、如图1,若∠A=∠3,则 ∥ ;若∠2=∠E ,则 ∥ ;若∠ +∠ = 180°,则 ∥ 。
2、在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( )。
3、如图2,若∠1 +∠2 = 180°,则 ∥ 。
4、如图3,推理填空:(1)∵∠A =∠ (已知),∴AC∥ED( ); (2)∵∠2 =∠ (已知),∴AC∥ED( ); (3)∵∠A +∠ = 180°(已知), ∴AB∥FD( ); (4)∵∠2 +∠ = 180°(已知), ∴AC∥ED( ); 二、解答下列各题5、如图4,∠D =∠A,∠B =∠FCB,求证:ED∥CF。
6、如图5,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由。
7、如图6,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:⑴、AB∥CD。
⑵、MP∥NQ。
a bc d 1 23 图2AB CED12 3 图11 2 3 AF CDB E图3E BAFD C图41 32 A E CD BF 图5F2A B CDQE1 P MN 图6一、填空1、如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = 。
2、如图2,直线AB 、CD 被EF 所截,若∠1 =∠2,则∠AEF +∠CFE = 。
3、如图3所示:⑴、若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( )。
⑵、若∠2 =∠ ,则AE∥BF。
⑶、若∠A +∠ = 180°,则AE∥BF。
4、如图4,AB∥CD,∠2 = 2∠1,则∠2 = 。
5、如图5,AB∥CD,EG⊥AB 于G ,∠1 = 50°,则∠E = 。
6、如图6,AB∥CD,AC⊥BC,图中与∠CAB 互余的角有 。
平行线的性质和判定的综合应用

学习目标:1 、掌握平行线的性质和判断.2、分清平行线的性质和判断,已知平行用性质,要证平行用判断.3、可以综合运用平行线性质和判断解题 .学习要点:平行线性质和判断综合应用学习难点:平行线性质和判断灵巧运用教课过程一、复习回首1、判断两直线平行的方法有(1)定义法 :在同一平面内不订交的两条直线是平行线。
(2)传达法 :条直线都和第三条直线平行 ,这两条直线也平行。
(3)同一平面内,垂直于同一条直线的两条直线平行。
(4)三种角判断 (3 种方法 ): 同位角相等 ,两直线平行。
bCaE内错角相等 ,两直线平行。
同旁内角互补,两直线平行。
A3 41B在这六种方法中,定义一般不常用。
回答,另一世增补,教师最后重申2C DF(一生)2、平行线的性质有:两直线平行,同位角相等 两直线平行,内错角相等 两直线平行,同旁内角互补下边同学们把两类定理作一比较:判断定理性质定理条件结论条件结论同位角相等 两直线平行 两直线平行 同位角相等内错角相等 两直线平行 两直线平行 内错角相等同旁内角互补两直线平行两直线平行同旁内角互补二、基础应用 :A1、填空:F (1)、∵∠ 4E 5∠ A=____, ( 已知)判断∴ AC ∥ ED ( 同位角相等,两直4 2 3线平行。
)1(2)、 ∵ AB ∥ DFBDC∴ ∠2=∠ 4 ( 两直线平行 , 内错角相等。
) 性质(3)、 ∵ AB ∥ DE (已知)∴ ∠ 3= ∠ B ( 两直线平行 ,同位角相等 .)性质(第一题综合应用判断和性质,同学们回答的特别好,接着看 2 、 3 题)2.如下图以下推理正确的选项是( C )A .∵∠ 1= ∠ 4,∴ BC ∥ ADB .∵∠ 2= ∠ 3,∴ AB ∥ CDC .∵ AD ∥ BC ,∴∠ BCD +∠ ADC=180 ° D .∵∠ 1+∠ 2+∠ C=180 °,∴ BC ∥ ADBA1 243CD3.如图,已知 AB ∥CD ,四种说法此中正确的个数是( B)①∠ A +∠ B=180 °;②∠ B +∠ C=180 °; ③∠ C +∠ D=180 °;④∠ D +∠ A=180 ° A . 1个C . 3个B . 2个D . 4个DCAB(经过上边的练习,老师发现同学们关于判断和性质掌握的特别好,我们持续利用判断和性质来解决下边的问题)三、师生互动 (教师指引学生剖析例1,并出示完好的解题过程)例1:如图,点 E为 DF 上的点,点 B为 AC 上的点,∠1= ∠ 2,∠C= ∠ D,求证: DF ∥ AC解: ∵∠1=∠2 (已知)∠1=∠ 3 ( 对顶角相等 )∴ ∠2=∠3(等量代换)∴ BD∥CE(同位角相等,两直线平行)D E F 231A B C∴ ∠C=∠ABD(两直线平行 , 同位角相等)又∵∠ C=∠ D ( 已知 )∴ ∠D=∠ABD (等量代换)∴ DF∥AC(内错角相等,两直线平行)(下面同学们,以小组为单位,研究变式 1 和变式 2 , 2 分钟时间,2分钟后各小组排代表率先到黑板上解说,看哪一组表现得好)变式 1:如图,点 B、 E分别在 AC、DF上, BD、 CE 均与 AF订交,∠ 1=∠ 2,∠ C=∠ D,试问:∠ A与∠ F相等吗?请说出你的原因。
平行线的判定与性质综合

)
) )
(2)已知: CD∥EF, ∠AGD= ∠ACB. 求证: ∠1= ∠2
(3)已知:∠AGD= ∠ACB
∠1= ∠2.
求证: CD∥EF.
解: ∠A与∠F 理由如下: ∵∠1=∠2 (已知) ∠1=∠3 (对顶角相等) ∴ ∠2=∠3(等量代换)
如图,已知,分别和直线,交于点,,分别和直线,交于点,, 点在上(点与,,三点不重合). 如果点在,两点之间运动时,,,之间有何数量关系请说 明理由; 如果点在,两点外侧运动时,,,有何数量关系(只须写出 结论).
思考5: 已知,如图,BE平分∠ABD,DE平分 ∠1+∠2 =90° ∠BDC,DG平分∠CDF, 求证:1)AB CD 2)BE DG C 3)ED GD A G E 4 3 6 5 2 1 B D F
平行线的判定与性质的 综合运用
判定两直线平行的方法有三种:
(1)定义法;在同一平面内不相交的两条直线是平行线。 (2)平行公理推论(平行的传递性):两条直线都和第三条直 线平行,这两条直线也平行。 b C (3)在同一平面内:因为a⊥c,a⊥b;
所以b//c (4)三种角判定(3种方法): 同位角相等,两直线平行。 内错角相等,两直线平行。 同旁内角互补,两直线平行。 在这六种方法中,定义一般不常用。 A C E
训练二
如图,AB∥CD,AD∥BC,试探求∠B与∠D, ∠A与∠C的关系? D
C
A
B
(变式)如果 AB ∥ CD ,且 ∠ B= ∠ D ,你能推 理得出AD∥BC吗?
题组训练(1)
1.如图,已知∠1=∠2,∠A=76°,求∠ABC的度数。 D
平行线的判定和性质(综合篇)

平行线的判定和性质(综合篇)一、重点和难点:重点:平行线的判定性质。
难点:①平行线的性质与平行线的判定的区分②把握推理论证的格式。
二、例题:这部份内容所涉及的题目主若是从已知图形中识别出对顶角、同位角、内错角或同旁内角。
解答这种题目的前提是熟练地把握这些角的概念,关键是把握住这些角的大体图形特点,有时还需添加必要的辅助线,用以突出大体图形的特点。
上述类型题目大致可分为两大类。
一类题目是判定两个角相等或互补及与之有关的一些角的运算问题。
其方式是“由线定角”,即运用平行线的性质来推出两个角相等或互补。
另一类题目主若是“由角定线”,也确实是依照某些角的相等或互补关系来判定两直线平行,解此类题目必需要把握好平行线的判定方式。
例1.如图,已知直线a,b,c被直线d所截,假设∠1=∠2,∠2+∠3=180°,求证:∠1=∠7分析:运用综合法,证明此题的思路是由已知角的关系推证出两直线平行,然后再由两直线平行解决其它角的关系。
∠1与∠7是直线a和c被d所截得的同位角。
须证a//c。
法(一)证明:∵d是直线(已知)∴∠1+∠4=180°(平角概念)∵∠2+∠3=180°,∠1=∠2(已知)∴∠3=∠4(等角的补角相等)∴a//c(同位角相等,两直线平行)∴∠1=∠7(两直线平行,同位角相等)法(二)证明:∵∠2+∠3=180°,∠1=∠2(已知)∴∠1+∠3=180°(等量代换)∵∠5=∠1,∠6=∠3(对顶角相等)∴∠5+∠6=180°(等量代换)∴a//c (同旁内角互补,两直线平行)∴∠1=∠7(两直线平行,同位角相等)。
例2.已知如图,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证:BC平分∠DBE。
分析:只要求得∠EBC=∠CBD,由∠1+∠2=180°推出∠1=∠BDC,从而推出AE//FC,从而推出∠C=∠EBC而∠C=∠A于是可得∠A=∠EBC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学设计——平行线的判定与性质的综合运用
三台外国语学校刘发冬
一、教材分析
(一)本课的地位和作用
本节教材是在学生学习了平行线的有关概念及性质和判定后,对其进行一个综合的有效运用,是技能的培养。
本课时在中考当中存在着很重要的地位,它不仅是学习初中几何阶段的基础,同时也是中考高频的考点。
更是对学生数学思想以及逻辑推理的引领。
(二)教学目标
根据上述教材结构与内容分析,考虑到学生已有的认知结构和心理特征,我制定如下教学目标
1、知识目标:
(1)、复习平行线的判定和性质定理,旧知再认。
(2)、学会对知识进行分类整理,掌握推理(证明)的书写方法。
(3)、掌握本节常见常见辅助线作法。
2、能力目标:
通过计算,提高综合运用知识分析问题和解决问题的能力。
通过作图形的辅助线,体会辅助线在几何解题中的妙用。
同时培养学生自主探索的能力和合作交流的能力;
3、情感与价值目标:
通过旧知的复习,让学生学会温故知新。
通过一题多解让学生学会从不同的角度去思考问题。
通过同桌的讨论、交流和解决问题的过程,让学生更多的展示自己,建立自信,树立正确的价值观。
(三)教学重点、难点
我从新课程标准出发,在吃透教材基础上,确立了如下的教学重点、难点
重点:熟练运用平行线的性质和判定解决相关问题
难点:(1)能正确的书写简单的推理(证明)过程。
(2)掌握本课时的常用辅助线作法。
二、教法设想
在本节课教学中,我从学生思维的起点出发,突出教师为主导、学生为主体的教学原则,在组织教学中,我主要采用了多媒体教学和自主探究
法,让学生在老师的引导下提出问题,自主探索、合作交流,收获新知;通过尝试应用,巩固实践,来深化新知,感受收获的喜悦。
实行合作交流、点对点的辅导,采用兵教兵的策略,让大家获得更多的学习兴趣。
本堂课中,我安排了几次同桌交流、小组讨论的活动,让学生自主学习,然后相互讨论,分享方法。
还有能够在推理、思考的过程中学会交流,进行体验。
三、学法研究
教学中重视指导学生掌握一些最基本的学习方法和数学思想。
通过本节课的教学,让学生学会观察分析、自主探索、总结归纳的学习方法,掌握巧作平行线,培养学生的空间想象能力,充分调动学生自己动手、动脑,引导他们自己分析、讨论、得出结论,鼓励他们尝试自己完成解题过程,大胆展示自我。
四、教学设计
本节课的设计是以教学大纲和教材为依据,遵循因材施教的原则,坚持以学生为主体,充分发挥学生的主观能动性。
在教学过程中,我采用自主探究、多媒体辅助教学的模式,我在其中只起穿针引线的作用,注重对学生的启发和引导,鼓励学生们大胆的猜想推导和应用,最后引导学生用学到的新知识解决一些实际问题。
其基本过程如下:
五、教学过程教
学环节教学过程学生
活动
设计理念
设置问题情境
1、平行线的判定与性质
判定定理性质定理
条件结论条件结论
同位角两直线平行同位角相
内错角两直线平行两直线平
行
内错角
同旁内角两直线同旁内角
2、如果两条直线都与第三条直线,那么这
两条直线也互相平行.
3、同一平面内,垂直于
的两条直线平行.
4、如图(1),直线AB、CD与
直线EF相交于点M、N。
(1)∵∠1=∠2
∴
(2)∵∠3=∠2
∴
(3)∵∠3+∠4=180°
∴
(4)∵AB∥CD,
∴、、
自主
复习
填空、
小组
交流、
共同
展示
让学生通过填空,引导他们
对所学的平行线性质和
判定的复习。
然后再小组
交流相互补充,最后统一
展示订正。
目的在于引发
学生的思考与分析,激励
学生大胆说出来。
新知识的探索与交流
如图(2),已知AB∥CD,直线EF交AB于点G,
交CD于点H,∠MGB=∠NHD.
求证:GM∥HN
1、学生自主完成
2、同桌相互交流
3、小组统一订正
4、学生展示思路
5、学生展示解题过程
同桌
讨论
交流,
完成
问题
的解
答
在这一环节,我设计了1
练习题
通过练习让学生初步
结实和学习性质和概念的
综合运用
拓展延伸如图(4),如图,若直线MN⊥AB于点D,∠ABC=130°,∠FCB=40°,
试判断直线MN与EF的位置关系,
并说明理由.
变式练习
如图(5),已知AB∥CD,
∠1=20°,∠2=40°,则∠3
等于()
A. 100°
B. 60°
C.30°
D.20°
[设计意图] 使学生明确探索一个新的知识要从学
过的知识入手,找寻它们的联系,探究规律,得出结论。
这
里关键如何巧妙的作出辅助线,利用平行线的判定和性质求
解。
例题的设计,让学生通过作不同的辅助线都可以解决此
题,教会学生学会一题多解。
并总结归纳出:
(1)判定:利用角相等、或角互补等推出直线平行。
(2)性质:利用平行得到角相等或互补;
(3)巧作辅助线构造三线八角“≠”证平行
探究问题二:关于拐
点问题的探究。
我首先引
领学生分析问题,引导大
家找到题的切入点,然后
让孩子自行解决。
然后展
示过程,最后探讨其他方
法和方法的归类和总结。
巩固实践
课堂测评一、选择题(每小题15分,共45分)
1.如图1-1,直线a⊥c,b⊥c,若∠1=70°,则∠2=( )
A.70°B.80°C.90°D.110°
2.如图1-2,若∠1=∠2=∠3=55°,则∠4的度数是( )
A.110°B.115°C.120°
D.125°
3.如图1-3,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
A.55°
B.45°
C.35°
D.25°
二、填空题(每小题15分,共30分)
1、如图1-5,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠
2= .
让学
生充
分的
进行
思考,
完成
这4
道巩
固实
践题
通过测评了解学生的
掌握情况,走近学生邻批
作业。
给予学生鼓励和帮
助。
发现共同的问题并进
行讲解。
2、如图1-6,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1=_ _ _.
解答题(10+15)分
1. 如图1-4已知AB∥DE,∠ABC=70°,∠CDE=140°,求∠BCD的度数。
2.已知,如图1-10,B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,
求证:DE//BC.
通过检测,让学生在课堂上完成相关练习,老师邻批学生作业发现学生掌握情况和解决存在问题。
小组交流,组员提出质疑,组内合作交流求解。
然后对于个别问题组长或组员之间相互解决,促进学生掌握相应知识。
六设计说明
板书设计
这样设计便于突出知识目标。
七、教学反思
1、教学理念
本节课在“以学生发展为核心”的理念下,最大限度地实现学生的主体地位。
从学生的实际出发,创设有助于学生自主学习的问题情境,在师生之间、生生之间的互动中,使数学教学成为一种“过程教学”,让学生在“数学活动”中获得数学的“思想、方法、能力、素质”,同时获得对
数学的情感;教师是学习活动的设计者、组织者、参与者,力求为学生的发展创设一个和谐与开放的思考、讨论、探究的氛围,激发学生的学习兴趣,使学生在平等、尊重、信任、理解和宽容中受到鼓励和鼓舞,从而实现传授知识和培养能力的融合。
2、教学设计的优势
在本节教学中我结合学生的实际要求,用生活中的实际问题引入新课,调动了学生的兴趣;同时,教学过程中注意因材施教,根据学生的基础,创设多姿多彩的问题情境,为每一个学生创造发挥自己才能的空间,让学生体验解决问题策略的多样性,发展学生的实践能力,合作探究能力,自主学习能力与创新精神。
本节课,通过学生自主探究来获取知识,合作交流来解决实际问题,从而体验成功的喜悦,达到资源与信息的共享,实现课堂教学的交互性,有效的提高了课堂的教学效率。
此外,在教学中,加强数学教学与信息技术教育的整合,利用计算机、实物投影等多媒体教学手段,向学生展示丰富多彩的数学世界,有利于激发学习数学的兴趣,加之与探究性教学的结合,也有利于调动学生学习数学的积极性。
3、存在问题
本课是一节习题课,在教学中不能把知识的结果强加于学生,虽然应用直观形象的手段,让学生经历了知识的生成过程,但因学生水平的差异,接收起可能有所差异。
同时针对本课设计了相应例题和练习。
经过教师的指导,学生的分组讨论,都得到了圆满的解决。
解题时,不能写出完整的解题过程,还有待于进一步加强练习。
