人教版 七年级数学下册 5.3 平行线的性质(二) 精品课时作业习题(含解析)
人教版七年级数学下册5.3《平行线的性质》课时练习(简单答案)
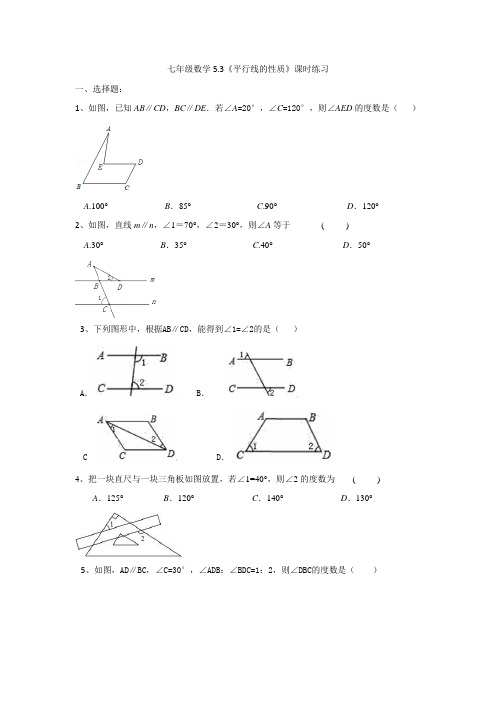
七年级数学5.3《平行线的性质》课时练习一、选择题:1、如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是()A.100°B.85°C.90°D.120°2、如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )A.30°B.35°C.40°D.50°3、下列图形中,根据A B∥CD,能得到∠1=∠2 的是()A.B.C D.4、把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )A.125°B.120°C.140°D.130°5、如图,AD∥B C,∠C=30°,∠AD B:∠BDC=1:2,则∠DBC 的度数是()A.30° B.36° C.45° D.50°6、如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,则∠BFD的度数是()A.20°B.30°C.40°D.45°7、将一副直角三角板ABC和DEF如图放置(其中∠A=60︒,∠F=45︒),使点E落在AC边上,且ED∥BC,则∠CEF的度数为()A.15°B.35°C.20°D.22.5°8、如图,把一块三角板的直角顶点放在一直尺的一边上,若∠1=50°,则∠2 的度数为()A.55° B.50° C.45° D.40°二、填空题:9、如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,那么∠ACD的度数为。
DCBA10、如图,AB∥CD,点E在CB的延长线上,若∠ABE=60º,则∠ECD的度数为。
人教版初中七年级数学下册第五章《相交线与平行线》经典习题(含答案解析)(2)

一、选择题1.如图,//AB CD ,EC 分别交,AB CD 于点,F C ,链接DF ,点G 是线段CD 上的点,连接FG ,若13∠=∠,24∠∠=,则结论① C D ∠=∠,②FG CD ⊥,③EC FD ⊥,正确的是( )A .①②B .②③C .①③D .①②③B解析:B【分析】 由平行线的性质和垂直的定义,逐个判断得结论.【详解】∵∠1=∠3,∠2=∠4,又∵∠1+∠2+∠3+∠4=180°,∴∠1+∠2=∠3+∠4=∠1+∠4=90°,∴∠EFD=∠1+∠2=90°,∴EC ⊥FD ,故③正确;∵AB ∥CD ,∴∠1=∠C ,∴∠FGD=∠4+∠C=∠4+∠1=90°,∴FG ⊥CD ,故②正确;∵∠1不一定等于∠2,∴∠C≠∠D ,故①不正确.故选:B .【点睛】本题考查了平行线的性质,三角形的外角性质及垂直的定义,由相等的角和平角的定义得到互余的角是解决本题的关键.2.下列命题中是真命题的有( )①两个角的和等于平角时,这两个角互为邻补角;②过一点有且只有一条直线与已知直线平行;③两条平行线被第三条直线所截,所得的一对内错角的角平分线互相平行;④图形B由图形A平移得到,则图形B与图形A中的对应点所连线段平行(或在同一条直线上)且相等;A.1个B.2个C.3个D.4个B解析:B【分析】根据补角和邻补角的定义可判断①,根据平行公理可判断②,根据平行线的性质和判定可判断③,根据平移的性质可判断④,进而可得答案.【详解】解:两个角的和等于平角时,这两个角互为补角,故命题①是假命题;过直线外一点有且只有一条直线与已知直线平行,故命题②是假命题;两条平行线被第三条直线所截,所得的一对内错角的角平分线互相平行,故命题③是真命题;图形B由图形A平移得到,则图形B与图形A中的对应点所连线段平行(或在同一条直线上)且相等,故命题④是真命题.综上,真命题有2个.故选:B.【点睛】本题考查了真假命题、平行线的判定和性质以及平移的性质等知识,属于基础题型,熟练掌握上述知识是解题的关键.3.下列说法正确的是()A.命题一定是正确的B.定理都是真命题C.不正确的判断就不是命题D.基本事实不一定是真命题B解析:B【分析】根据命题的定义、真命题与假命题的定义逐项判断即可得.【详解】A、命题有真命题和假命题,此项说法错误;B、定理都是经过推论、论证的真命题,此项说法正确;C、不正确的判断是假命题,此项说法错误;D、基本事实是真命题,此项说法错误;故选:B.【点睛】本题考查了命题、真命题与假命题,熟练掌握理解各概念是解题关键.4.下列所示的四个图形中,∠1和∠2是同位角的是()A .②③B .①②③C .①②④D .①④C解析:C【分析】 根据同位角的定义逐一判断即得答案.【详解】图①中的∠1与∠2是同位角,图②中的∠1与∠2是同位角,图③中的∠1与∠2不是同位角,图④中的∠1与∠2是同位角,所以在如图所示的四个图形中,图①②④中的∠1和∠2是同位角.故选:C .【点睛】本题考查了同位角的定义,属于基础概念题型,熟知概念是关键.5.如图,A 是直线l 外一点,过点A 作AB l ⊥于点B ,在直线l 上取一点C ,连接AC ,使2AC AB =,P 在线段BC 上,连接AP .若3AB =,则线段AP 的长不可能是( )A .4B .5C .2D .5.5C解析:C【分析】 根据题意计算出AC 的长度,由垂线段最短得出AP 的范围,选出AP 的长度不可能的选项即可.【详解】3AB =,26AC AB cm ∴==,结合垂线段最短,得:36AP ≤≤.故选:C .【点睛】本题主要考查直线外一点与直线上各点连接的所有线段中,垂线段最短,熟记概念并求出对应线段的范围是解题关键.6.下面命题中是真命题的有()①相等的角是对顶角②直角三角形两锐角互余③三角形内角和等于180°④两直线平行内错角相等A.1个B.2个C.3个D.4个C解析:C【分析】利用平行线的性质、三角形的内角和、直角三角形的性质、对顶角的性质分别判断后即可确定正确的选项.【详解】解:①相等的角不一定是对顶角,故不符合题意;②直角三角形两锐角互余,故符合题意;③三角形内角和等于180°,故符合题意;④两直线平行内错角相等,故符合题意;故选:C.【点睛】此题考查了命题与定理,解题的关键是了解平行线的性质、对顶角的定义、直角三角形的性质及三角形的内角和等知识,难度不大.7.如图,直线a∥b,则∠A的度数是()A.28°B.31°C.39°D.42°C解析:C【解析】试题分析:根据平行线的性质可得∠1=70°,再根据三角形的一个外角等于和它不相邻的两个内角的和可得∠A=70°-31°=39°.故选C.考点:平行线的性质8.如图是郝老师的某次行车路线,总共拐了三次弯,最后行车路线与开始的路线是平行的,已知第一次转过的角度120︒,第三次转过的角度135︒,则第二次拐弯的角度是()A .75︒B .120︒C .135︒D .无法确定A解析:A【解析】 分析:根据两直线平行,内错角相等,得到∠BFD 的度数,进而得出∠CFD 的度数,再由三角形外角的性质即可得到结论.详解:如图,延长ED 交BC 于F .∵DE ∥AB ,∴∠DFB =∠ABF =120°,∴∠CFD =60°.∵∠CDE =∠C +∠CFD ,∴∠C =∠CDE -∠CFD =135°-60°=75°.故选A .点睛:本题考查了平行线的性质及三角形外角的性质.解题的关键是理解题意,灵活应用平行线的性质解决问题,属于中考常考题型.9.如图,一副直角三角板图示放置,点C 在DF 的延长线上,点A 在边EF 上,//AB CD ,90ACB EDF ∠=∠=︒,则CAF ∠=( )A .10︒B .15︒C .20︒D .25︒B解析:B【分析】 根据平行线的性质可知,BAF=EFD=45∠∠ ,由BAC=30∠ 即可得出答案。
【人教版】七年级数学下册《5.3.1 平行线的性质》习题课件(附答案)

(2)拓展: ①如图②,若∠A=20°,∠C=50°,则∠APC 30 °; =________ ②猜想图③中∠A,∠C,∠APC三者之间的关系 ∠APC=∠A-∠C . 为____________________
∵EF⊥AB,∴∠BOF=90°,
∵FH∥AB,∴∠HFO=∠BOF=90°, ∵AB∥CD,∴FH∥CD,∴∠FGC+∠GFH=180°, ∵∠FGC=125°,∴∠GFH=55°, ∴∠EFG=∠GFH+∠HFO=55°+90°=CD于点M,如图②.
∵EF⊥AB,∴∠BOF=90°,
∴∠1=∠2,
即AD是∠BAC的平分线.
14.如图:已知AB∥CD,EF⊥AB于点O,∠FGC= 125°,求∠EFG的度数. 下面提供三种思路: (1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K. 请你利用三个思路中的两个思路,将图形补充完整, 求∠EFG的度数.
解:(一)利用思路(1). 过点F作FH∥AB,如图①.
∴∠AED=180°-∠AEC=138°.
∵EF平分∠AED, 1 ∴∠DEF= ∠AED=69°. 2 又∵AB∥CD,∴∠AFE=∠DEF=69°.
13.如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3.
AD是∠BAC的平分线吗?若是,请说明理由. AD是∠BAC的平分线.理由如下: 解: ∵AD⊥BC,EG⊥BC,∴EG∥AD. ∴∠3=∠1,∠E=∠2. 又∵∠E=∠3,
70 =________ °;
②如图①,若∠A=40°,∠C=60°,则∠APC
100 °; =________
③猜想图①中∠A,∠C,∠APC三者之间有怎样的等量关
系?并说明理由. 解:③∠APC=∠A+∠C.理由如下: 过P点向左侧作PE∥AB,则∠APE=∠A, ∵AB∥CD,∴PE∥CD, ∴∠CPE=∠C. 又∵∠APC=∠APE+∠CPE, ∴∠APC=∠A+∠C.
人教版七年级下《5.3平行线的性质》课后练习含答案(2份)5.3.1 平行线的性质课后练习

5.3.1 平行线的性质班级:___________ 姓名:___________ 得分:___________一、填空题(每小题6分,共30分)1.如图,已知a∥b,∠1=55°,则∠2的度数是( )A.35°B.45°C.55°D.125°第1题图第2题图第3题图2.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为()A.10°B.15°C.2021D.25°3.如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数是( )A.70°B.65°C.60°D.50°4.如图,若AB//CD,∠BEF=70°,则∠ABE+∠EFC+∠FCD的度数是( )A.215°B.250°C.32021D.无法知道第4题图第5题图5.如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.其中正确的个数为( )A.1个B.2个C.3个D.4个二、填空题(每小题6分,共30分)6.如图,已知∠1=∠2,∠3=73°,则∠4的度数为.CBA D第6题图第7题图第8题图7.如图,点D、E分别在AB、BC上,DE∥AC,AF∥BC,∠1=70°,则∠2=.8.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC=_______9.如图,BC⊥AE,垂足为C,过C作CD∥AB.若∠ECD=48°,则∠B=.第9题图第10题图10.如图,直线a∥b,AB⊥BC,如果∠1=60°,那么∠2=.三、解答题(每小题2021共40分)11.如图,AB∥CD,直线EF交AB、CD于点G、H.如果GM平分∠BGF,HN平分∠CHE,那么,GM与HN平行吗?为什么?12.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.3.B【解析】∵AB∥CD,∴∠1+∠BEF=180°,∵∠1=50°,∴∠BEF=130°,∵EG平分∠BEF,∴∠BEG=∠BEF=65°,∴∠2=∠BEG=65°.故选:B.4.B【解析】分别过点E、F作EG∥AB,HF∥CD,再根据平行线的性质即可得出结论.解:分别过点E、F作EG∥AB,HF∥CD,则AB∥EG∥HF∥CD,∵AB∥EG,∴∠ABE=∠BEG,又∵EG∥HF,∴∠EFH=∠GEF,∴∠ABE+∠EFH=∠BEG+∠GEF=∠BEF=70°,∵∠HFC+∠FCD=180°,∠EFH+∠HFC=∠EFC,∴∠ABE+∠EFC+∠FCD=180°+70°=250°.故选B.5.C【解析】根据平行线的性质、角平分线的定义、余角的定义作答.解:①∵BC⊥BD,∴∠DBE+∠CBE=90°,∠ABC+∠DBF=90°,又∵BD平分∠EBF,∴∠DBE=∠DBF,∴∠ABC=∠CBE,即BC平分∠ABE,正确;②由AB∥CE,BC平分∠ABE、∠ACE易证∠ACB=∠CBE,∴AC∥BE正确;③∵BC⊥AD,∴∠BCD+∠D=90°正确;④无法证明∠DBF=60°,故错误.故选C.6.107°【解析】根据已知一对同位角相等,利用同位角相等两直线平行得到a与b平行,利用两直线平行同旁内角互补得到一对角互补,再利用对顶角相等即可确定出∠4的度数.解:∵∠1=∠2,∴a∥b,∴∠5+∠3=180°,∵∠4=∠5,∠3=73°,∴∠4+∠3=180°,则∠4=107°.故答案为:107°7.70°【解析】根据两直线平行,同位角相等可得∠C=∠1,再根据两直线平行,内错角相等可得∠2=∠C.解:∵DE∥AC,∴∠C=∠1=70°,∵AF∥BC,∴∠2=∠C=70°.故答案为:70°.8.400【解析】由AD∥BC,∠D=100°,根据两直线平行,同旁内角互补,可以得到∠DCB=80°,再由CA平分∠BCD,得到∠BCA=40°,从而由两直线平行,内错角相等,可得∠DAC=40°.9.42°【解析】先根据两直线平行,同位角相等求出∠A,再根据直角三角形两锐角互余即可求出.解:∵CD∥AB,∠ECD=48°,∴∠A=∠ECD=48°,∵BC⊥AE,∴∠B=90°-∠A=42°.10.30°【解析】∵AB⊥BC,∴∠1+∠3=∠ABC=90°,∴∠3=∠ABC-∠1=90°-60°=30°,∵a//b,∴∠2=∠3=30°.11.GM∥HN【解析】首先根据平行线的性质可得∠BGF=∠CHE,再根据角平分线的性质可以证明∠NHG=∠MGH,然后根据内错角相等,两直线平行得证结果.答:GM∥HN理由如下:∵AB∥CD∴∠BGF=∠GHC又∵GM平分∠BGF∴∠HGM=12∠BGF又∵HN平分∠CHG。
人教版七年级下册数学作业课件 第五章 第2课时 平行线的性质和判定的综合运用 (2)

A 分点训练•打好基础 B 综合运用•提升能力 C 思维拓展•冲刺满分
知识点 平行线的性质和判定的综合运用 1.如图,∠A=∠D,如果∠B=35°,那么∠C 的 大小为( C ) A.55° B.45° C.35° D.25°
2.如图,若∠A+∠ABC=180°,则下列结论一定 正确的是( D ) A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
3.如图,若∠1=∠3,∠2=60°,则∠4 的度数为 (C) A.60° B.100° C.120° D.130°
【变式题】图变本质不变:先判定两直线平行,再 利用平行线的性质求角度 (1)(2020·岳阳中考)如图,DA⊥AB,CD⊥DA,∠B =56°,则∠C 的度数是( D ) A.154° B.144° C.134° D.124°
12.如图,∠1+∠2=180°,∠3=100°,OK 平分 ∠DOH,则∠KOH 的度数为 40° . 解析:∵∠1+∠2=180°,∴AB∥CD. ∴∠GOD=∠3=100°.∴∠DOH=180° -∠GOD=180°-100°=80°.∵OK 平分 ∠DOH,∴∠KOH=12∠DOH=12×80°=40°.
(2) 如 图 ∠1 + ∠2 = 180°, ∠4 = 35°, 则 ∠3 = 35 °.
4.如图,在点 A 测点 B 的方向是 南偏东 60° .
5.如图,四边形 ABCD 中,AB∥CD,∠B=60°. 当∠D= 60 °时,AD∥BC.
6.将一长方形纸条按如图所示方式折叠.若∠1= 40°,则∠2= 110 °.
13.(2020·孝南区期末)如图,已知∠1=∠BDC, ∠2+∠3=180°. (1)试说明:AD∥CE; 解:∵∠1=∠BDC, ∴AB∥CD.∴∠2=∠ADC. ∵∠2+∠3=180°, ∴∠ADC+∠3=180°.∴AD∥CE.
七年级数学下册53平行线的性质教材习题解析素材(新版)新人教版.docx

平行线的性质教材习题解析习题5・3(P22)1.解析:本题考查平行线的性质2.解答木题的关键是,要理解“两次转弯后,和原来的方向相同“的意义,即两次转弯前后的公路所在的直线平行,根据“两直线平行,内错角相等”得,第二次的拐角ZB应等于135*.2.解析:本题考查平行线的性质3.已知AD〃BC,厶・fiT,根据“两直线平行,同旁内角互补”可得,^B-I8(r-Z4-12T;不用度量方法,仅根据平行线的性质,不能求得ZD的度数.因为ZD 与ZA是同旁内角,而直线AB与CD是否平行不得而知,因此不能用平行线的性质來求解.3.解析:本题考查了平行线的三个性质.解题时要弄清楚直线和角的位置关系.(1)由4・1师,根据平行线的性质2 “两直线平行,内错角相等”得,乂2・11叭(2)由zi・mr,根据平行线的性质1 “两直线平行,同位角相等”得,(3)由,根据平行线的性质3“两直线平行,同旁内角互补”得,z<-i8(r-ii(r-7r■4.解析:本题考查平行线的性质2,性质3及性质1(或邻补角定义).由性质2可求得Z2,由性质3可求得Z3,由性质1(或邻补角定义)可求得Z4.因为。
〃内,根据“两直线平行,内错角相等”,可得因为根据“两直线平行,同旁内角互补”,可得Z3=i8(r-Z5=iior;因为Z4与Z5互为邻补角,所以&・wr-z5・iir (或根据“两直线平行,同位角相等”,可得Z4-Z3-UF).5.解析:本题考查平行线的性质3的应用.木题求解时,可以把公路两侧的管道看成平行线,对接的管道看作截线,应用“两直线平行,同旁内角互补”可得,另一侧应以iar-iar=«r 的角铺设.6.解析:本题考查平行线的性质和判定的综合应用,以及分析推理能力.解题时,应对照图形区分每一步推理是使用平行线的判定,还是使用平行线的性质,然后再填写理由.答案依次是:内错角相等,两直线平行;两直线平行,内错角相等.7.解析:本题考查平行线的性质2和性质3•第(1)题关键是寻找其中的同位角或内错角.注意到AB〃CD, AC是截线,因此只有Z1和Z4是内错角,它们相等;其他角中没有同位角,不存在相等的关系;第(2)题屮ZACE被CD分为ZACD和ZECD两个角,运用平行线的性质3,由AB〃CD 得到ZBAC+ZACD--W,由CD〃EF 得到ZECD+ZCEF-IW ,所以ZBAC+ ZACE+ ZCEF= ZBAC+ ZACD+ ZECD+ ZCEF-3HT ,本题答案应为(1) C;(2) C.8.解析:本题考查平行线的性质1和性质3的实际运用.解答本题的关键是已知光线平行,同吋水面与水底面也是平行的,然后根据平行线的性质可以求出各角.由“两直线平行,同位角相等”得,Z4-Z2-m.由“两直线平行,同旁内角互补”得,心・1抄-/4・瑚,Z7-18T -Zl-137 , ZB-I80T -0・BT9.解析:本题考查文字语言与符号语言的互相转化,及平行线的判定与性质.用式子表示一些三段论推理的句子,一方面可以培养学生儿何不同语言相互转化的能力,另一方面, 通过用符号表示一些简单的推理过程,为后面学习证明做准备.(1) VZ1=Z2(已知),・・・AB〃EF(内错角相等,两直线平行);(2)・・・DE〃BC(已知),AZ1=ZB, Z3=ZC(两直线平行,同位角相等).10.解析:本题考查平行线、垂线在生活中的运用,涉及如何画平行线、垂线的问题.答案略.11.解析:本题考查相交线、垂线、平行线在生活中的应用.画好一个篮球场地,需要用到许多垂线、平行线的知识,通过解决这样一个问题,让学生感受到平行线知识在实际生活中的应用.第(1)题答案不唯一,比如操场上的单杠与立柱垂直,双杠中的两根杠子平行等等;第(2)题在纸上画篮球场地,可以用直角三角板或平行线的性质来保证垂直.画平行线可以用推三角尺的方法或用平行线的判定方法来操作.画图略.12.解析:本题考查真、假命题的概念和判断,以及如何说明一个命题是假命题,体会反例的作用.(1)假命题,比如:冊和70•都是锐角,但它们的和1处不是锐角;(2)真命题;(3)假命题,只要作出一对不互补的同旁内角即可,例如一个三角形中,任意两个内角都可以看作是同旁内角,但它们不互补.13.解析:本题考查分析推理能力和对证明过程的理解,主要是填写证明过程川的关键步骤和理由,涉及平行线的性质、角平分线的定义、等量代换等知识.答案依次是:(1)ZC;两直线平行,内错角相等;两直线平行,同旁内角互补.(2)2 ;角平分线的定义;等量代换(或等式的性质).14.解析:本题考查平行线的性质、平角的定义等.本题是证明三角形内角和定理的另一种方法.(1)ZDAB二44°,因为DE〃BC,根据“两直线平行,内错角相等”可得,ZDAB=ZB=44°;(2)ZEAC=57°,因为DE〃BC,根据“两直线平行,内错角相等”可得,ZEAC=ZC=57°;(3)ZBAC=79°,因为ZDAE 是平角,所以ZBAC=180° -ZDAB-ZEAC=180° -44° -57° =79°・由以上结论可得:ZB+ZC+ZBAC二180°,这实际上说明了三角形三个内角和为180° .15.解析:本题考查平角的定义、平行线的性质和判定的综合应用等•解答时关键要认识到两面镜子是平行的,从而Z2与Z3是一对内错角,所以它们相等.本题要求说明两条光线平行,需要分析这两条光线是被哪一条直线所截,形成了哪些角?这些角有什么数量关系,进而发现形成的Z5与Z6是一对内错角,只要Z5与Z6相等,就能说明这两条光线平行.因为两而镜子是平行放置的,根据“两直线平行,内错角相等”可得,由平角等于1ST 可得,Z5-IW-Z1-Z2 , ZB-l8(r-z3-Z4 .因为Z1-Z2,厶所以又由“内错角相等,两直线平行”可以判断,进入潜望镜的光线与离开潜望镜的光线是平行的.。
七年级数学下册第五章相交线与平行线5.3平行线的性质5.3.2命题、定理、证明课时练习(pdf,含解析人教版

初中数学·人教版·七年级下册——第五章相交线与平行线5.3.2命题、定理、证明测试时间:30分钟一、选择题1.下列说法正确的是()A.“作线段CD=AB”是一个命题B.过一点作已知直线的平行线有且只有一条C.命题“若x=1,则x2=1”是真命题D.“具有相同字母的项称为同类项”是同类项的定义2.下列命题中,是真命题的是()A.两条直线被第三条直线所截,内错角相等B.邻补角互补C.相等的角是对顶角D.两个锐角的和是钝角3.如图,下列命题错误的是()A.如果AB∥CD,那么∠1=∠4B.如果AB∥CD,那么∠1=∠3C.如果AD∥BC,那么∠3=∠4D.如果AD∥BC,那么∠3+∠2=180°4.下列命题中,是真命题的有()①两条直线被第三条直线所截,同位角的平分线平行;②垂直于同一条直线的两条直线互相平行;③过一点有且只有一条直线与已知直线平行;④对顶角相等,邻补角互补.A.1个B.2个C.3个D.4个5.把命题“同角的余角相等”改写成“如果……那么……”的形式,正确的是()A.如果是同角,那么余角相等B.如果两个角相等,那么这两个角是同一个角的余角C.如果是同角的余角,那么相等D.如果两个角是同一个角的余角,那么这两个角相等6.下列命题的逆命题是真命题的是()A.若a>0,b>0,则a+b>0B.直角都相等C.同位角相等,两直线平行D.若a=b,则|a|=|b|7.下列命题中,是假命题的是()A.对顶角相等B.两条直线被第三条直线所截,同旁内角互补C.在同一平面内,垂直于同一条直线的两条直线互相平行D.若一个角的两边分别与另一个角的两边平行,那么这两个角相等或互补二、填空题8.“直角都相等”的题设是,结论是.9.命题“互补的两个角不能都是锐角”是命题(填“真”或“假”).10.把“垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式是.11.命题“若a>b,则|a|>|b|”是假命题,请举出一个反例加以说明:.12.“若实数a,b,c满足a<b<c,则a+b<c”,能够说明该命题是假命题的一组a,b,c的值可以依次为.13.如图,请在AB∥CD,∠A=30°,∠CDA=30°三项中选择两个作为条件,一个作为结论,写一个真命题:如果且,那么.三、解答题14.把下列命题写成“如果……那么……”的形式,并判断其真假.(1)等角的补角相等;(2)不相等的角不是对顶角;(3)相等的角是内错角.15.(1)完成下面的推理说明:已知:如图,BE∥CF,BE、CF分别平分∠ABC、∠BCD.求证:AB∥CD.证明:∵BE、CF分别平分∠ABC、∠BCD(已知),∴∠1=12∠,∠2=12∠().∵BE∥CF(),∴∠1=∠2().∴12∠ABC=12∠BCD().∴∠ABC=∠BCD().∴AB∥CD().(2)说出(1)的推理中运用了哪两个互逆的真命题.一、选择题1.答案C“作线段CD=AB”不是判断事情的语句,故A错误;过直线外一点作已知直线的平行线有且只有一条,故B错误;命题“若x=1,则x2=1”是真命题,故C正确;具有相同字母且相同字母的指数也相同的项称为同类项,故D错误.2.答案B两条平行直线被第三条直线所截,内错角相等,故A选项错误,是假命题;邻补角互补,故B选项正确,是真命题;相等的角不一定是对顶角,故C选项错误,是假命题;两个锐角的和不一定是钝角,故D选项错误,是假命题,故选B.3.答案B如果AB∥CD,那么∠1=∠4,故A选项正确;由AB∥CD,不能得出∠1=∠3,故B选项错误;如果AD∥BC,那么∠3=∠4,故C选项正确;如果AD∥BC,那么∠3+∠2=180°,故D选项正确.故选B.4.答案A两条平行线被第三条直线所截,同位角的平分线平行,故①是假命题;在同一平面内,垂直于同一条直线的两条直线互相平行,故②是假命题;过直线外一点有且只有一条直线与已知直线平行,故③是假命题;对顶角相等,邻补角互补,故④是真命题.故选A.5.答案D命题“同角的余角相等”改写成“如果……那么……”的形式为“如果两个角是同一个角的余角,那么这两个角相等”.故选D.6.答案C A.若a>0,b>0,则a+b>0的逆命题为若a+b>0,则a>0,b>0,逆命题错误,为假命题;B.直角都相等的逆命题为相等的角都是直角,逆命题错误,为假命题;C.同位角相等,两直线平行的逆命题为两直线平行,同位角相等,逆命题正确,为真命题;D.若a=b,则|a|=|b|的逆命题为若|a|=|b|,则a=b,逆命题错误,为假命题,故选C.7.答案B对顶角相等,故A选项中是真命题;两条平行直线被第三条直线所截,同旁内角互补,故B选项中是假命题;在同一平面内,垂直于同一条直线的两条直线互相平行,故C选项中是真命题;若一个角的两边分别与另一个角的两边平行,那么这两个角相等或互补,故D选项中是真命题,故选B.二、填空题8.答案n个角是直角;这n个角相等9.答案真解析根据锐角的定义得出,互补的两个角不能都是锐角,此命题是真命题.10.答案如果两条直线垂直于同一条直线,那么这两条直线平行11.答案a=1,b=-2(答案不唯一)解析当a=1,b=-2时,满足a>b,但不满足|a|>|b|(答案不唯一).12.答案1,2,3(答案不唯一)解析当a=1,b=2,c=3时,满足a<b<c,不满足a+b<c(答案不唯一),所以能够说明原命题是假命题的一组a,b,c的值可以依次为1,2,3.13.答案AB∥CD;∠A=30°;∠CDA=30°(答案不唯一)解析根据两直线平行,内错角相等可直接写出一个真命题.三、解答题14.解析(1)如果两个角分别是两个相等的角的补角,那么这两个角相等.是真命题.(2)如果两个角不相等,那么这两个角不是对顶角.是真命题.(3)如果两个角相等,那么这两个角是内错角.是假命题.15.解析(1)∵BE、CF分别平分∠ABC、∠BCD(已知),∴∠1=12∠ABC,∠2=12∠BCD(角平分线的定义).∵BE∥CF(已知),∴∠1=∠2(两直线平行,内错角相等).∴12∠ABC=12∠BCD(等量代换).∴∠ABC=∠BCD(等式的性质).∴AB∥CD(内错角相等,两直线平行).(2)①两直线平行,内错角相等;②内错角相等,两直线平行.。
5.3.1 平行线的性质(第2课时)平行线的性质和判定的综合运七年级数学下册同步备课系列(人教版)

又∵∠A=100°,∠C=110°(已知),
∴∠ 1 = 80 °,∠ 2 = 70 °(等量代换).
∴∠AEC=∠1+∠2= 80 °+ 70 ° = 150 °.
当堂巩固
1. 填空:如图,
A
(1)∠1=∠2 时,AB∥CD.
1
(2)∠3= ∠5 或∠4 时,AD∥BC. B
D
5 2
3 C
4 F
解:过点C作CF∥AB,
A
则 _∠__B_=_∠__1( 两直线平行,内错角相等 )
C
又∵AB∥DE,AB∥CF,
D
∴___C_F__∥__D_E___(平行于同一直线的两条直线互相平行 )
∴∠E=∠__2__( 两直线平行,内错角相等 )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
B 1F 2
感受中考
2.(3分)(2021•包头8/26)如图,直线l1∥l2,直线l3交l1于点A,交l2于点B, 过点B的直线l4交l1于点C.若∠3=50°,∠1+∠2+∠3=240°,则∠4等于( )
A.80°
B.70°
C.60°
D.50°
【 分 析 】 由 题 意 得 , ∠ 2=60° , 由 平 角 的 定 义 可 得 ∠5=70°,再根据平行线的性质即可求解.
c 图1
b
c
a 图2
3. 运用平行线的性质填一填
图形
同a 位 角b
1 2 c
内 错 角
a 3
b
2
c
同 旁
a
内 角
b
42 c
已知 a//b
结果 ∠1 = ∠2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业8 §5.3 平行线的性质(二)
典型例题
【例1】如图5-103,已知直线l3、l4分别交直线l1、l2于点A、B和C、D,且l1∥l2 l3⊥l1,则下列说法中正确的是( )
A.线段AB是直线l1、l2间的距离
B.线段CD是直线l1,l2间的距离
C.线段AB的长度是直线l1、l2间的距离
D.线段CD的长度是直线l1,l2间的距离
图5-103
【解析】只有同时满足下列两个条件才是平行线间的距离:①夹在两平行线之间的线段同时垂直于这两条平行线;②夹在两条平行线之间的线段的长度.本题中,因为l1⊥l3,所以∠BAC=90°.又因为l1∥l2,所以∠BAC+∠ABD=180°,所以∠ABD=90°.即l3⊥l2.故同时垂直于两条平行线l1,l2并且夹在这两条平行线间的线段AB的长度,叫做这两条平行线l1、l2的距离.
【答案】 A
【例2】如图5-104,AB∥CD,EPF为折线.
(1)试探究∠P与∠α、∠β的关系,并给了证明;
(2)若交换(1)中的条件与结论,是否还成立,请说明理由.
图5-104
【解析】(1)由测量可得∠P=∠α+∠β.证明∠P=∠α+∠β的方法很多,可利用平行线的性质,或利用三角形相关知识求证;(2)交换(1)中的条件与结论,仍成立,可综合运用平行线的性质与平行线的条件进行证明.
【答案】(1)探究∠P=∠α+∠β.证明如下:
证法一过点P作直线PQ∥AB,如图5-105.
图5-105
因为AB∥CD,所以PQ∥CD.即AB∥PQ∥CD.
根据平行线的性质“两直线平行,内错角相等”,可得∠1=∠α,∠2=∠β
所以∠1+∠2=∠α+∠β
即∠P=∠α+∠β
证法二 延长FP 交AB 于Q ,如图15-106.
图5-106
因为AB ∥CD ,根据平行线的性质“两直线平行,内错角相等”可得∠1=∠β 因为三角形的内角和为180°,所以∠α+∠1+∠EPQ=180°.
所以∠α+∠β+∠EPQ=180° 又∠EPF 与∠EPQ 互为邻补角,所以∠EPF+∠EPQ=180°. 所以∠EPF=∠α+∠β.
证法三 过P 作MN ⊥AB 于M 、N ,N 如图15-107.
图15-107
因为AB//CD ,所以MN ⊥CD
由平角的定义,有∠EPF=180°-(∠1+∠2)=(90°-∠1)+(90°-∠2)=∠α+∠β
【例3】 已知,如图5-108,DB ∥FG ∥EC ,∠ABD=70°,∠ACF=34°,AP 平分∠BAC ,求∠PAG 的度数.
图5-108
【解析】 题目中已知角与待求角较分散,可利用平行线的性质将已知角与待求角联系在一起.然后结合角平分线的性质求解.
【答案】 因为DB ∥EC ,根据“两直线平行,同旁内角互补”可得∠BAC=∠DBA+∠ACE. 因为∠DBA=70°,∠ACE=34°,所以∠BAC=70°+34°=104°. 因为PA 平分∠BAC ,所以∠CAP=
2
1
2∠BAC=52°. 又因为GF ∥CE ,根据两直线平行,内错角相等. 可得∠GAC=∠ACE=34°.
因此∠PAG=∠CAP-∠GAC=52°-34°=18°
总分100分 时间40分钟 成绩评定____________ 一、填空题(每题5分,共50分) 课前热身
1.如图5-109,直线c 与a 、b 相交,且a ∥b ,若∠1=40°,则∠2=____________. 答案:40°
2.如图5-110,直线AB 、CD 被直线EF 所截,若∠1=∠2,则∠AEF+∠CFE=__________度.
图5-109 图5-110
答案:180
3.如图5-111,OE是∠AOB的平分线,CD∥OB交OA于C、交OE于D,∠ACD=50°,则∠COE的度数是____________.
答案:25°
4.已知,如图5-112,AB∥CD,EF⊥AB,EH>EF,则AB与CD间的距离是____________.
图5-111 图5-112
答案:线段EF的长度
5.如图5-113,D、E、F和点A、B、C,各自在一条直线上,若∠1=∠2,∠C=∠D,则∠A=____________,∠C=____________.
答案:∠F;∠D(或∠CEF)
6.如图5-114,AB∥CD,MP∥AB,MN平分∠AMD,∠A=40°,∠D=30°,则∠NMP=____________.
图5-113 图5-114
答案:5°
课下作业
7.如图5-115,l1∥l2,∠1是∠2的2倍,则∠3=____________.
图5-115 图5-116
答案:60°
8.如图5-116,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,∠1=40°,则∠2的度数是___________.
答案:100°
9.一个人从A点出发沿北偏东60°方向走了2 m到了B点,再沿南偏西15°方向走了3m到C点,则∠ABC___________.
答案:45°
10.如图5-117,AB ∥CD ,△ADC 的面积为9,AB=
3
2
CD ,则△ABC 的面积为_____________.
图5-117
答案:6
二、选择题(每题5分,共10分) 模拟在线
11.(2010,四川)如图5-118所示,l 1∥l 2,∠1=120°,∠2=100°,则∠3=( ) A.20° B.40° C.50° D.60
图5-118 图5-119
答案:B
12.(2010江苏)已知:如图5-119,∠AOB 的两边OA 、OB 均为平面反光镜,∠AOB=40°.在OB 上有一点P ,从P 点射出一束光线经OA 上的Q 点反射后,反射光线QR 恰好与OB 平行,则∠QPB 的度数是( ) A.60° B.80° C.100° D.120° 答案:B
三、解答题(每题20分,共40分)
13.如图5-120,已知直线m ∥n ,A 、B 为直线n 上两点,C 、D 为直线m 上两点 (1)请写出图中面积相等的三角形;
(2)如果A 、B 、C 为三个定点,点D 在m 上移动,那么,无论D 点移动到任何位置,总有___________与△ABC 的面积相等,理由是:________________________.
图5-120
答案:(1)S △ABC =S △ABD ,S △ACD =S △CDB ,S △ACO =S △BDO (2)△ABD ;平行线间的距离处处相等
14.如图5-121,已知AD ⊥BC 于D ,EG ⊥BC 于G ,∠E=∠3,AD 平分∠BAC 吗?若平分,请写出推理过程;若不平分,试说明理由.
图5-121答案:AD平分∠BAC.证明如下:
∵AD⊥BC,EG⊥BC(已知),
∴AD∥EG.∴∠2=∠3(两直线平行,内错角相等).
∴∠l=∠E(两直线平行,同位角相等).又∵∠E=∠3
(已知),∴∠1=∠2(等量代换).即AD平分∠BAC.。
