第十二章练习题答案
12第十二章习题参考答案

5、3、 4、 A.数量 B.质量 C.违约责任 D.解决争议的方法根据合同法有关规定,承担违约责任的方式有以下几种(A.继续履行B.采取补救措施 违约责任的免责条件主要有( ABCDA.不可抗力B.货物本身的自然性质ABCD ) D.违约金我国合同法上的支付损失赔偿金的构成要件有(C.赔偿损失)C.货物的合理损耗D.债权人的过错ABCD )第十二章练习题参考答案一、单项选择1、 合同法中最重要的基本原则是(A. 平等原则B. 自愿原则 2、 下列哪一情况不属于要约的失效( A. 拒绝要约的通知到达要约人B )C.公平原则B )B .受要约人依法撤销要约C. 承诺期限届满,受要约人未作出承诺D. 受要约人对要约的内容作出实质性变更3、 依据《中华人民共和国担保法》的规定,定金的数额可以由当事人约定,但不得超过主合 同标的额的( D )A.5%B.10%C.15%D.20%4、 下列哪一项不是承担违约责任的方式(D )A.赔偿损失B.采取补救措施C.违约金D.终止履行5、 根据《合同法》第 91 条规定,下列哪一项不属于合同的权利义务可以终止的法定原因( D )A.债务相互抵消B.债权人免除债务C.债权债务同归于一人D.合同履行6、 《合同法》施行的起始日期是(C )A.1999年1月1日B.1999年5月1日C.1999 年 10 月 1 日D.1999 年 12 月 1 7、 合同的书面形式内容不包括(D ) A.合同书 B.信件 C.数据电文8、 下列哪一项不是解决合同争议的途径( A.协商B.投诉C.调解9、 下列哪一项不属于违约责任的分类( A.过错责任与无过错责任 B.单独责任与共同责任 C.单方责任与混合责任D.违约责任与无违约责任10、 合同 ( A ),是指合同成立以后,尚未履行完毕之前由合同当事人双方依法对原合同的 内容进行的修改。
A .变更B .转让C .解除D .终止11、 合同 ( D ),是指合同当事人依法将合同的全部或者部分权利义务转让给其他人的合法 行为。
第十二章化学动力学基础(二)练习题及答案

第十二章 化学动力学基础(二)练习题一、 选择题1.以下有关催化剂不正确的说法,是催化剂(A )改变反应物的平衡转化率 (B )改变反应途径(C )改变频率因子 (D )降低活化能 2.催化剂加快反应速率,是由于它能使(A )指前因子增大 (B )几率因子增大 (C )碰撞频率增加 (D )活化分子数增加 3.反应本性、温度、反应途径、浓度与活化能关系正确的是(A )反应途径与活化能无关 (B )反应物浓度与活化能有关(C )反应温度与活化能无关 (D )反应本性与活化能有关 4.气固相催化反应Pt<700K 2CO(g) + O 2(g)2CO 2(g)的速率方程是: r = k p (o 2)/p (co), 其反应级数应为:(A) 一级反应 (B) 二级反应 (C) 对 O 2是一级,对 CO 是负一级 (D) 级数不能确定 5.某反应速率常数与各基元反应速率常数的关系为 12124()2k k k k , 则该反应的表观活化能E a 与各基元反应活化能的关系为:(A) E a =E 2 +12E 1 - E 4 (B) E a = E 2+12(E 1- E 4)(B) E a = E 2+ (E 1- 2E 4)1/2 (D) E a = E 2+ E 1- E 46.在平行反应中要提高活化能较低的反应的产率,应采取的措施为: (A) 升高反应温度 (B) 降低反应温度 (C) 反应温度不变(D) 不能用改变温度的方法。
7.化学反应速率常数的 Arrhenius 关系式能成立的范围是:(A) 对任何反应在任何温度范围内 (B) 对某些反应在任何温度范围内 (C) 对任何反应在一定温度范围内 (D) 对某些反应在一定温度范围内8.一个基元反应,正反应的活化能是逆反应活化能的2倍,反应时吸热120 kJ·mol-1,则正反应的活化能是(kJ·mol-1):(A) 120 (B) 240 (C) 360 (D) 609.物质A 发生两个一级平行反应A B,A C,设两反应的指前因子相近且与温度无关,若E1> E2,则有:(A) k1> k2 (B) k2 > k1 (C) k2= k1 (D) 无法比较k1, k2 的大小10.催化剂能极大地改变反应速率,以下说法不正确的是:(A) 催化剂改变了反应历程(B) 催化剂降低了反应的活化能(C) 催化剂改变了反应的平衡,以致使转化率大大地提高了(D) 催化剂能同时加快正向和逆向反应速率11.下面四种说法中不正确的是:(A)在具有速控步的反应历程中,达到稳态后,速控步后的各个步骤的反应速率都等于速控步的反应速率,速控步前的各步骤均处于平衡状态(B) 根据微观可逆性原理,在反应历程中不可能出现2A → C + 3D 这样的基元反应(C) 在光化学反应中,体系的Gibbs自由能总是在不断地降低(D) 在采用温度跃变的驰豫法来研究溶液中的快速反应时,该反应必须是放热或吸热反应12.除多光子吸收外,一般引起化学反应的光谱,其波长范围应是:(A) 可见光(400 - 800 nm) 及紫外光(150 - 400 nm)(B) X射线(5 - 10-4 nm)(C) 远红外射线(D) 微波及无线电波13.在光的作用下,O2可转变为O3,当1 mol O3生成时,吸收了3.01×1023个光子,则该反应之总量子效率Φ为:(A) Φ=1 (B) Φ=1.5(C) Φ=2 (D) Φ=314.根据微观可逆性原理,反应物分子能量消耗的选择性和产物能量分配的特殊性 有对应关系,因此对正向反应产物主要是平动激发,则对逆向反应更有利于促进反 应进行的能量形式应为:(A)振动能 (B)转动能(C)平动能 (D)能量形式不限,只要足够高 15.对Einstain 光化当量定律的认识下述说法正确的是:(A) 对初级,次级过程均适用 (B) 对任何光源均适用 (C) 对激光光源及长寿命激发态不适用 (D) 对大、小分子都适用 16.在简单碰撞理论中,有效碰撞的定义是:(A) 互撞分子的总动能超过E c (B) 互撞分子的相对总动能超过E c (C)互撞分子联心线上的相对平动能超过E c (D)互撞分子的内部动能超过E c 17.在碰撞理论中校正因子P 小于1的主要因素是:(A) 反应体系是非理想的 (B) 空间的位阻效应 (C) 分子碰撞的激烈程度不够 (D) 分子间的作用力 18.Lindemann 单分子反应机理是假定多原子分子被振动激发后 (A) 立即分解 (B) 有一时滞 (C) 发出辐射 (D) 引发链反应19.同一个反应在相同反应条件下未加催化剂时平衡常数及活化能为k 及E a ,加入正催化剂后则为k '、E a ',则存在下述关系: (A) k '=k , E a =E a ' (B) k '≠k , E a ≠E a ' (C) k '=k , E a >E a ' (D) k '<k , E a '<E a20.过渡态理论的速率常数的公式为()()()k k T h q q q E RT =≠-B AB//exp /∆0,下述说法正确的是(A) q ≠不是过渡态的全配分函数 (B) q A , q B 是任意体积中分子的配分函数 (C) q A , q B , q ≠均是分子在基态时的配分函数(D) ()k T h B /是过渡态M≠中任一个振动自由度配分函数二、 判断题1.关于催化剂特征的不正确描述是在反应前后催化剂的物理性质和化学性质全不改变。
大学生安全知识教育-第12章习题答案

第十二章预防犯罪思考与练习一、简答题1. 导致大学生犯罪的原因有哪些?答:(一)主观原因1. 缺乏正确的人生观和价值观2. 法制观念淡薄3. 义气交友,容易冲动4. 心理扭曲(二)家庭原因1. 环境因素2. 心理因素3. 结构因素4. 功能因素(三)社会原因1. 政治因素2. 经济因素3. 教育因素2. 如何预防大学生犯罪?答:(一)自身预防首先,应加强对大学生政治素质的教育培养,增强其公德意识,引导大学生正确认识社会,树立正确的人生观、价值观。
其次,在生活中,学会理财,杜绝浪费与攀比。
最后,对待人际交往要慎重,杜绝与社会不良人员的接触。
(二)家庭预防家庭是社会的细胞,遏制大学生犯罪,首先应从家庭抓起。
一是提高父母自身素质,优化家庭环境。
二是注意家教方法。
过分溺爱和纵容,这对孩子的心理健康和正确行为的培养是极其有害的。
三是善于发现孩子犯罪的早期征兆。
(三)学校预防加强和改进高校的学生管理,建立健全管理约束机制。
(四)社会预防营造一种和谐的良好社会氛围,贯彻落实“教育、感化、挽救”方针。
3. 正当防卫的要件有哪些?答:(1)存在现实的不法侵害。
(2)不法侵害正在进行。
(3)具有防卫意识。
(4)针对不法侵害本人进行防卫。
(5)没有明显超过必要限度造成重大损害。
4. 如何避免大学生沾染黄、赌、毒?答:(1)优化家庭环境。
(2)创造良好学校环境,充分发挥学校对大学生教育担任的主导作用。
(3)建立和谐社会环境,确保大学生健康学习生活。
(4)大学生自身树立健康的人生观、价值观和世界观。
无机及分析化学第十二章沉淀滴定和重量滴定课后练习与答案

第十二章沉淀溶解平衡与沉淀滴定法一、选择题1.下列说法违反无定形沉淀条件的是()A. 在浓溶液中进行B. 在不断搅拌下进行C. 陈化D. 在热溶液中进行2.下列不属于沉淀重量法对沉淀形式要求的是()A.沉淀的溶解度小B.沉淀纯净C.沉淀颗粒易于过滤和洗涤 D.沉淀的摩尔质量大3.指出下列哪一条不是晶形沉淀所要求的沉淀条件()A.沉淀作用宜在较稀溶液中进行 B.应在不断地搅拌作用下加入沉淀剂C.沉淀应陈化 D.沉淀宜在冷溶液中进行4.在重量法测定硫酸根实验中,硫酸钡沉淀是()A.非晶形沉淀B.晶形沉淀C.胶体D.无定形沉淀5.晶形沉淀的沉淀条件是()A.浓、冷、慢、搅、陈 B.稀、热、快、搅、陈C.稀、热、慢、搅、陈 D.稀、冷、慢、搅、陈6.用 SO42-沉淀 Ba2+时,加入过量的 SO42-可使 Ba2+沉淀更加完全,这是利用()A.络合效应B.同离子效应 C.盐效应D.酸效应7.在重量分析中,待测物质中含的杂质与待测物的离子半径相近,在沉淀过程中往往形成()A.后沉淀 B.吸留 C.包藏 D.混晶8. 为了获得纯净而易过滤、洗涤的晶形沉淀,要求()A.沉淀时的聚集速度小而定向速度大B.沉淀时的聚集速度大而定向速度小C.溶液的过饱和程度要大D.沉淀的溶解度要小9.下列哪些要求不是重量分析对称量形式的要求()A.要稳定B.颗粒要粗大C.相对分子质量要大D.组成要与化学式完全符合10. 恒重是指样品经连续两次干燥或灼烧称得的重量之差小于()。
A. 0.1mgB. 0.1gC. 0.3mgD. 0.3g11. 有利于减少吸附和吸留的杂质,使晶形沉淀更纯净的选项是()A.沉淀时温度应稍高B. 沉淀完全后进行一定时间的陈化C.沉淀时加入适量电解质D. 沉淀时在较浓的溶液中进行12.重量分析中,依据沉淀性质,由()计算试样的称样量。
A.沉淀的质量B.沉淀的重量C.沉淀灼烧后的质量D.沉淀剂的用量13.在重量分析中能使沉淀溶解度减小的因素是()。
七年级数学下册《第十二章全等三角形-角的平分线的性质》练习题
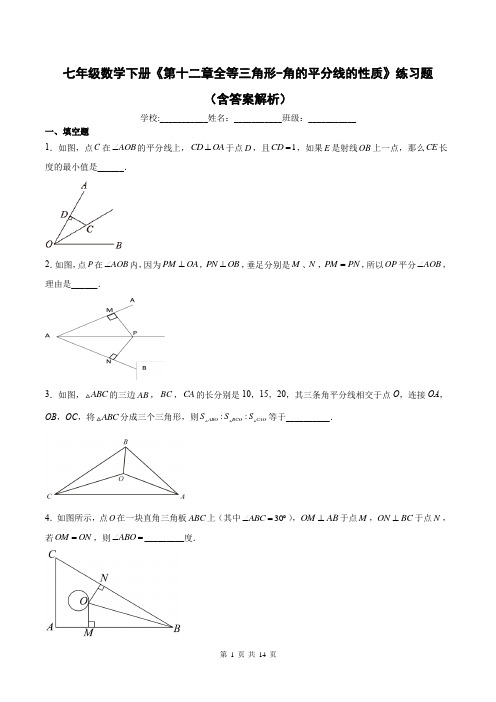
七年级数学下册《第十二章全等三角形-角的平分线的性质》练习题(含答案解析)学校:___________姓名:___________班级:___________一、填空题1.如图,点C 在AOB ∠的平分线上,CD OA ⊥于点D ,且1CD =,如果E 是射线OB 上一点,那么CE 长度的最小值是______.2.如图,点P 在AOB ∠内,因为PM OA ⊥,PN OB ⊥,垂足分别是M 、N ,PM PN =,所以OP 平分AOB ∠,理由是______.3.如图,ABC 的三边AB ,BC ,CA 的长分别是10,15,20,其三条角平分线相交于点O ,连接OA ,OB ,OC ,将ABC 分成三个三角形,则::ABO BCO CAO S S S 等于__________.4.如图所示,点O 在一块直角三角板ABC 上(其中30ABC ∠=︒),OM AB ⊥于点M ,ON BC ⊥于点N ,若OM ON =,则ABO ∠=_________度.5.如图,BE、CF都是ABC的角平分线,且110∠=︒,则ABDC∠=___________.二、单选题6.如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF若添加下列条件中的某一个.就能使DOE≅FOE,你认为要添加的那个条件是()A.OD=OE B.OE=OF C.∠ODE =∠OED D.∠ODE=∠OFE<,将ABC以点A为中心逆时针旋转得到ADE,点D在BC边上,DE交7.如图,在ABC∆中,AB AC∠=∠,其中所有正确结论的AC于点F.下列结论:∠AFE DFC△△;∠DA平分BDE∠;∠CDF BAD序号是()A.∠∠B.∠∠C.∠∠D.∠∠∠8.如图,三条公路两两相交,现计划在∠ABC中内部修建一个探照灯,要求探照灯的位置到这三条公路的距离都相等,则探照灯位置是∠ABC()的交点.A.三条角平分线B.三条中线C .三条高的交点D .三条垂直平分线9.如图,Rt∠ABC 中,∠C =90°,AD 平分∠BAC ,交BC 于点D ,AB =10,S △ABD =15,则CD 的长为( )A .2B .3C .4D .5三、解答题10.已知40AOB ∠=︒.(1)用直尺和圆规作出AOB ∠的平分线OD (不写作法,但保留作图痕迹,写出结论);(2)已知AOB ∠与BOC ∠互为补角,画出符合条件的所有可能的图形,并求出COD ∠的度数.11.如图,在由边长为1的小正方形组成的正方形网格中,一段圆弧经过网格的格点A 、B 、C .(1)请完成如下操作:∠以点O 为原点,竖直和水平方向所在的直线为坐标轴,小正方形的边长为单位长,建立平面直角坐标系; ∠用直尺和圆规画出该圆弧所在圆的圆心D 的位置,不写作法,保留作图痕迹,并连接AD 、CD .(2)请在(1)的基础上,解答下列问题:∠写出点的坐标:C ______、D ______;∠D 的半径为______(结果保留根号);∠若扇形DAC 是一个圆锥的侧面展开图,则该圆锥的底面积为______(结果保留π);∠若点E 的坐标为()7,0,试判断直线EC 与D 的位置关系,并说明理由.12.如图,已知AOC BOC ∠=∠,点P 在OC 上,PD OA ⊥,PE OB ⊥,垂足分别为D ,E .求证:OPD OPE ≌.13.如图,∠ABC 中,∠ACB =90°,AB =10,BC =6,若点P 从点A 出发,以每秒1个单位长度的速度沿折线A -C -B -A 运动,设运动时间为t 秒(t >0).(1)若点P 在AC 上,且满足P A =PB 时,求此时t 的值;(2)若点P 恰好在∠BAC 的平分线上,求t 的值.14.如图,在∠ABC 中,AD 是它的角平分线,且BD =CD ,DE ∠AB ,DF ∠AC ,垂足分别为E 、F ,求证:AB =AC参考答案:1.1【分析】过点C 作CE ∠OB 于点E ,根据角平分线的性质解答即可.【详解】解:过点C 作CE ∠OB 于点E ,∠点C 在∠AOB 的平分线上,CD ∠OA 于点D ,且CD =1,∠CE =CD =1,即CE 长度的最小值是1,故答案为:1.【点睛】本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.2.角的内部到角两边距离相等的点在角的角平分线上【分析】根据角平分线判定定理即可得到结果.【详解】解:∠PM∠OA ,PN∠OB ,PM=PN∠OP 平分∠AOB (在角的内部,到角的两边距离相等的点在这个角的平分线上)故答案为:角的内部到角两边距离相等的点在角的角平分线上.【点睛】本题考查角平分线判定定理,掌握角平分线判定定理的内容是解题的关键.3.2:3:4【分析】过点O 分别向三边作垂线段,通过角平分线的性质得到三条垂线段长度相等,再通过面积比等于底边长度之比得到答案.【详解】解:过点O 分别向BC 、BA 、AC 作垂线段交于D 、E 、F 三点.∠CO 、BO 、AO 分别平分、、ACB CBA BAC ∠∠∠∠OD OE OF == ∠12ABO SAB OE =,12△BCO S BC OD =,12△CAO S AC OF = ∠::::10:15:202:3:4ABO BCO CAO S S S AB BC AC ===故答案为:2:3:4【点睛】本题考查了角平分线的性质,往三角形的三边作垂线段并得到面积之比等于底之比是解题关键.4.15【分析】根据ON BC ⊥,OM AB ⊥,OM ON =判断OB 是ABC ∠的角平分线,即可求解.【详解】解:由题意,ON BC ⊥,OM AB ⊥,OM ON =,即点O 到BC 、AB 的距离相等,∠ OB 是ABC ∠的角平分线,∠ 30ABC ∠=︒, ∠1152ABO ABC ∠=∠=︒. 故答案为:15.【点睛】本题考查角平分线的定义及判定,熟练掌握“到一个角的两边距离相等的点在这个角的平分线上”是解题的关键.5.40°##40度【分析】根据三角形的内角和定理以及角平分线的定义,列出算式计算即可.【详解】解:∠BE 、CF 都是∠ABC 的角平分线,∠∠A =180°−(∠ABC +∠ACB ),=180°−2(∠DBC +∠BCD )∠∠BDC =180°−(∠DBC +∠BCD ),∠∠A =180°−2(180°−∠BDC )∠∠BDC =90°+12∠A ,∠∠A =2(110°−90°)=40°.【点睛】本题考查的是三角形内角和定理和角平分线的定义,用已知角表示出所求的角是解题的关键.6.D【分析】根据OB 平分∠AOC 得∠AOB =∠BOC ,又因为OE 是公共边,根据全等三角形的判断即可得出结果.【详解】解:∠OB 平分∠AOC∠∠AOB =∠BOC当∠DOE ∠∠FOE 时,可得以下结论:OD =OF ,DE =EF ,∠ODE =∠OFE ,∠OED =∠OEF .A 答案中OD 与OE 不是∠DOE ∠∠FOE 的对应边,A 不正确;B 答案中OE 与OF 不是∠DOE ∠∠FOE 的对应边,B 不正确;C 答案中,∠ODE 与∠OED 不是∠DOE ∠∠FOE 的对应角,C 不正确;D 答案中,若∠ODE =∠OFE ,在∠DOE 和∠FOE 中,DOE FOE OE OEODE OFE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∠∠DOE ∠∠FOE (AAS )∠D 答案正确.故选:D .【点睛】本题考查三角形全等的判断,理解全等图形中边和角的对应关系是解题的关键.7.D【分析】根据旋转的性质可得对应角相等,对应边相等,进而逐项分析判断即可求解.【详解】解:∠将ABC 以点A 为中心逆时针旋转得到ADE ,∠ADE ABC ≌,E C ∴∠=∠,AFE DFC ∠=∠,∴AFE DFC △△,故∠正确;ADE ABC ≌,AB AD ∴=,ABD ADB ∴∠=∠,ADE ABC ∠=∠,ADB ADE ∴∠=∠,∴DA 平分BDE ∠,故∠正确;ADE ABC ≌,BAC DAE ∴∠=∠,BAD CAE ∴∠=∠,AFE DFC△△,CAE CDF∴∠=∠,CDF BAD∠=∠∴,故∠正确故选D【点睛】本题考查了性质的性质,等边对等角,相似三角形的性质判定与性质,全等三角形的性质,掌握以上知识是解题的关键.8.A【分析】根据角平分线的性质即可得到探照灯的位置在角平分线的交点处,即可得到结论.【详解】解:∠探照灯的位置到这三条公路的距离都相等,∠探照灯位置是∠ABC的三条角平分线上,故选:A.【点睛】此题考查了角平分线的性质,数据角平分线的性质定理是解题的关键.9.B【分析】过点D作DE∠AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用∠ABD 的面积列式计算即可得解.【详解】解:如图,过点D作DE∠AB于E,∠∠C=90°,AD平分∠BAC,∠DE=CD,∠S△ABD=12AB•DE=12×10•DE=15,解得:DE=3,∠CD=3.故选:B.【点睛】本题考查了三角形的面积和角平分线的性质,能熟记角平分线上的点到角两边的距离相等是解此题的关键.10.(1)见解析(2)图见解析,60°或120°【分析】(1 )根据角平分线的定义作出图形即可;(2)分两种情形,分别画出图形求解即可.(1)解:如图,射线OD即为所求.(2)解:如图,∠BOC与∠AOB、∠BOC'与∠AOB都互为补角,∠∠AOB=40°,且OD平分∠AOB,∠∠BOC=140°,∠BOC'=140°,∠AOD=∠BOD=12∠AOB=20°,当射线OA在∠BOC的外侧时,∠COD=∠BOC+∠BOD=140°+20°=160°;当射线OA在∠BOC'内部时,∠C'OD=∠BOC'-∠BOD=140°-20°=120°.综上,∠COD的度数为60°或120°.【点睛】本题考查作图 复杂作图,角平分线的定义,补角的定义等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.11.(1)答案见详解(2)∠62(,);20(,);∠∠54π;∠相切,理由见详解 【分析】(1)∠根据叙述,利用正方形的网格即可作出坐标轴;∠利用过三点的圆可得圆心为圆上任意两条弦的垂直平分线的交点,即可得到D .(2)∠利用(1)中所作的坐标系,即可表示出点的坐标;∠在Rt OAD 中,利用勾股定理即可求得半径长;∠理由直角三角形全等可证得∠ADC =90°,则可求得AC 的长度,AC 的长就是圆锥的底面圆的周长,在利用圆的周长公式即可求得答案;∠利用勾股定理逆定理证明DCE 为直角三角形即可证得DC CE ⊥,从而即可得出结论.(1)∠如图,建立平面直角坐标系;∠利用过三点的圆可得圆心为圆上任意两条弦的垂直平分线的交点,即可得到D ,如图所示:(2)∠根据平面直角坐标系可得C (6,2);D (2,0);故答案为:C (6,2);D (2,0);∠在Rt AOD △中,90AOD ∠=︒,4AO =,2OD =,AD =故答案为:∠由∠得AD =在Rt DCF △中,90DFC ∠=︒,4DF =,2CF =,DC ∴在Rt AOD △和Rt DFC 中,AD DC OA DF=⎧⎨=⎩, ()Rt AOD Rt DFC HL ≅,DAO CDF ∴∠=∠,90DAO ADO ∠+∠=︒,90CDF ADO ∴∠+∠=︒,18090ADC ADO CDF ∴∠=︒-∠-∠=︒,AC ∴==,由2r π=,解得r =2254S r πππ∴===⎝⎭, ∴该圆锥的底面积为54π, 故答案为:54π. ∠直线EC 与D 相切,由图可知,在Rt CEF 中,90CFE ∠=︒,1EF =,2CF =,22222125CE EF CF ∴=+=+=,又由∠得DC =2220DC ==,2220525DC CE +=+=,22525DE ==,222DC CE DE ∴+=,∴DCE 为直角三角形,90DCE ∠=︒,DC CE ∴⊥,∴直线EC 与D 相切.【点睛】本题考查了不共线的三点确定圆心的方法、直线与圆相切的判定、根据平面直角坐标系写出点的坐标、勾股定理和圆锥的侧面展开图的弧长即为圆锥的底面圆的周长,垂径定理,圆锥的计算,正确求出弧长是难点.12.见解析【分析】根据角平分线的性质得PD PE =,再用HL 证明OPD OPE ≌.【详解】证明:∠AOC BOC ∠=∠,∠OC 为AOB ∠的角平分线,又∠点P 在OC 上,PD OA ⊥,PE OB ⊥,∠PD PE =,90PDO PEO ∠=∠=︒,又∠PO PO =(公共边),∠()HL OPD OPE ≌.【点睛】本题考查角平分线的性质,全等三角形的判定,利用合适的条件证明三角形全等是本题的关键. 13.(1)254 (2)323【分析】(1)连接PB ,在Rt ∠ABC 中,根据勾股定理得AC =6,由于AP =PB =t ,则PC =8-t ,在Rt ∠PCB 中,根据勾股定理得222PC BC PB +=,进行计算即可得;(2)由题意得,PC =t -8 , PB =14-t ,过点P 作PE ∠AB ,由于AP 平分∠BAC ,且∠ACB =90°得PC =PE ,根据HL 得Rt ∠ACP ∠Rt ∠AEP ,即可得AC =AE =8, BE =2,在 Rt ∠PEB 中,根据勾股定理得222PE BE PB +=,进行计算即可得.(1)解:如图所示,连接PB ,∠在Rt ∠ABC 中,AB =10,BC =6,∠8AC =由于AP =PB =t ,则PC =8-t ,在Rt ∠PCB 中,根据勾股定理得:222PC BC PB +=222(8)6t t -+= 解得254t =, 即此时t 的值为254. (2)解:由题意得,PC =t -8 , PB =14-t ,如图所示,过点P 作PE ∠AB ,由于AP 平分∠BAC ,且∠ACB =90°,∠ PC =PE ,在Rt ∠ACP 与Rt ∠AEP 中,PC PE AP AP =⎧⎨=⎩∠Rt ∠ACP ∠Rt ∠AEP (HL ),∠AC =AE =8, BE =2,在 Rt ∠PEB 中,根据勾股定理得,222PE BE PB +=,222(8)2(14)t t -+=- 解得:323t =, ∠当点P 在∠BAC 的平分线上时,t 的值为323. 【点睛】本题考查了勾股定理,角平分线的性质,全等三角形的判定和性质,解题的关键是掌握这些知识点.14.证明见解析【分析】根据角平分线的性质得到DE=DF,证明Rt∠BDE≅Rt∠CDF(HL),根据全等三角形的性质得到结论.【详解】证明:∠AD是∠ABC的角平分线又∠DE∠AB于E,DF∠AC于F∠DE=DF,∠BED=∠CFD=90°又∠BD=CD∠Rt∠BED∠Rt∠CFD(HL)∠∠B=∠C∠AB=AC.【点睛】本题考查全等三角形的性质和判定,角平分线的性质,解题的关键是掌握这些性质定理进行证明.。
2023-2024学年人教版八年级数学上册《第十二章 三角形全等的判定》同步练习题附带答案

2023-2024学年人教版八年级数学上册《第十二章三角形全等的判定》同步练习题附带答案学校:___________班级:___________姓名:___________考号:___________一、选择题1.如图,在△ACD与△ABD中∠C=∠B,再添加下列哪个条件,能判定△ADC≌△ADB()A.AC=AB B.AC⊥CD C.DA平分∠BDC D.CD=BD2.如图,一块玻璃碎成三片,小智只带了第③块去玻璃店,就能配一块一模一样的玻璃,你能用三角形的知识解释,这是为什么?()A.ASA B.AAS C.SAS D.SSSBC若ΔABC的面积3.如图,AE垂直于∠ABC的平分线于点D,交BC于点E,CE=13为12,则ΔCDE的面积是()A.2B.3C.4D.64.工人常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分別与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≅△MOC,共依据是()A.SSS B.SAS C.ASA D.AAS5.如图,在△ABC中∠C=90°,D是AC上一点,DE⊥AB于点E,BE=BC连接BD,若AC=8cm,则AD+DE等于()A.6cm B.7cm C.8cm D.10cm6.如图,为了测出池塘两端A,B间的距离,小铱在地面上取一个可以直接到达A点和B点的点O,连接AO并延长到C,使OC=OA;连接BO并延长到D,使OD=OB,连接CD并和测量出它的长度,小铱认为CD的长度就是A,B间的距离,她是根据△OAB≌△OCD来判断的AB=CD,那么判定这两个三角形全等的依据是().A.SSS B.SAS C.ASA D.AAS7.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知∠B=∠E,AB=DE,BF=EC,△ABC的周长为24cm,FC=3cm制作该风筝框架需用材料的总长度至少为()A.44cm B.45cm C.46cm D.48cm8.如图,AB⊥BC,EC⊥BC,AD⊥DE,AD=DE,AB=3,BC=8,则CE长为()A.4 B.5 C.8 D.10二、填空题9.如下图,已知AC=AB,要使△ABE≌△ACD.则需添加一个条件.10.数学实践活动课中,老师布置了“测量小口圆柱形瓶底部内径”的探究任务,某学习小组设计了如下方案:如图,用螺丝钉将两根小棒AC,BD的中点O固定,现测得C,D之间的距离为75mm,那么小口圆柱形瓶底部的内径AB=mm.11.如图,在Rt△ABC中∠BAC=90°,AB=AC分别过点B、C作经过点A的直线的垂线段BD、CE,若BD=5厘米,CE=8厘米,则DE的长为.12.如图,△ABC中,AD是中线AC=3,AB=5则AD的取值范围是.13.如图,在四边形ABEF中,AB=4,EF=6,点C是BE上一点,连接AC、CF,若AC=CF,∠B=∠E=∠ACF,则BE的长为.三、解答题14.图1是郝老师制作的风筝,图2是风筝骨架的示意图,其中AB=AC,BD=CD,∠C=23°.求∠B的度数.15.如图,已知在△ABC中,D、E是BC上两点,且∠ADE=∠AED,∠BAD=∠EAC,求证:AB=AC.16.如图,C是AB上一点,点D,E分别在AB两侧AD∥BE,且AD=BC,BE=AC求证:CD=EC.17.如图所示,点O在一块直角三角板ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,求∠ABO度数.18.课间,小明拿着老师的直角三角尺玩,不小心掉到两堆砖块之间,如图所示,已知∠ACB= 90°,AC=BC,AD⊥DE,BE⊥DE.(1)试说明:△ADC≌△CEB;(2)已知DE=35cm,请你帮小明求出砖块的厚度a(每块砖的厚度相同)参考答案1.C2.A3.A4.A5.C6.B7.B8.B9.∠C=∠B (答案不唯一)10.7511.13厘米12.1<AD <413.1014.解:在△ABD 和△ACD 中{AB =AC AD =AD BD =CD ∴△ABD ≌△ACD(SSS) ∴∠B =∠C ∵∠C =23° ∴∠B =23°.15.证明:∵∠ADE =∠AED∴AD =AE ,∠ADB =∠AEC在△ABD 与△ACE 中{∠BAD =∠EAC AD =AE ∠ADB =∠AEC∴△ABD ≌△ACE(ASA)∴AB =AC16.证明:∵AD ∥BE∴∠A =∠B在△ADC 和△BCE 中{AD =BC∠A =∠B AC =BE∴△DAC ≌△CBE∴CD =CE ;17.解:∵OM ⊥AB ,ON ⊥BC ∴∠OMB =∠ONB =90°在Rt △OMB 和Rt △ONB 中{OM =ON OB =OB∴Rt △OMB ≌Rt △ONB(HL)∴∠OBM =∠OBN∵∠ABC =30°∴∠ABO =15°.18.(1)解:∵∠ACB =90°∴∠ACD +∠BCE =90°∵AD ⊥DE∴∠ACD +∠DAC =90°∴∠BCE =∠DAC在△ADC 与△CEB 中{∠ADC =∠BEC =90°∠BCE =∠DACAC =BC∴△ADC ≌△CEB(AAS);(2)解:∵△ADC ≌△CEB∴DC =BE ,AD =CE∴DE =DC +CE =BE +AD =35cm ∵一共有7块砖∴每块砖块的厚度a 为:35÷7=5cm .。
(完整版)宏观经济学第12章练习题及答案
第十二章练习题及答案一、判断题1.国民收入核算体系将GNP作为核算国民经济活动的核心指标。
()2.GDP被定义为在某一既定时期一国之内所生产的全部产品的市场价值总和。
()3.用货币去度量性质不同的各种产品,才能使各种产品能够进行加总,得出一国产出的总价值。
()4.如果农民种植的粮食用于自己消费,则这种粮食的价值就无法计入GDP之内。
()5.家庭成员提供的家务劳动要计入GDP之内。
()6.本年生产但未销售出去的最终产品价值不应计入本年的GDP之内。
()7.最终产品只包括消费品,不包括投资品。
()8.最终产品是按照产品的物质属性来划分的。
()9.某种物品是中间产品还是最终产品取决于它本身的性质,例如,汽车一定是最终产品,煤只能是中间产品。
()10.国内生产总值中的最终产品只是指有形的物质产品。
()11.用价值增值法计算一国产出的总价值,可以避免重复计算的问题。
()12.国民生产总值等于各种最终产品和中间产品的价值总和。
()13.对于整个经济来说,所有的价值增值之和必定等于所有的最终产品的总价值。
()14.若某企业年生产20万元的产品,只销售掉10万元的产品,则当年该企业所创造的GDP 为10万元。
()15.以前所生产而在当年售出的存货,应当是当年GDP的一部分。
()16.某公司生产的汽车多卖掉一些比少卖掉一些时,GDP增加要多一些。
()17.某人2000年用10万元购买了一辆产于1998年的小汽车,这10万元应该计入2000年的GDP。
()18.一栋旧建筑物的销售额应加到国民生产总值中去。
()19.销售一栋建筑物的房地产经纪商的佣金应加到国民生产总值中去。
()20.一个在日本工作的美国公民的收入是美国GDP的一部分,也是日本GNP的一部分。
()21.国内生产总值是重要的流量变量。
()22.计算国内生产总值有三种方法,当计算结果出现差异时,以收入法的结果为主。
()23.国民收入的核算中使用的生产法、收入法和支出法其内在逻辑是不一致的,因而它们最后所计算出来的国民生产总值数量也可能是不一致的。
基础护理学第12章练习题与答案
第十二章【习题】一、选择题(-)A1 型题1.执行给药原则中 ,下列首要的是A.遵医嘱给药B.给药途径要准确C.给药时间要准确D. 注意用药不良反应E.给药过程中要观察疗效2.剧毒药及麻醉药的最主要保管原则是A.与内服药分别放置B.放阴凉处C.装密封瓶中保存D. 应加锁并专人保管,认真交班E.应有明显标签3. 剧毒药瓶上的标签颜色是A.蓝色B.红色C.黑色D.绿色E.黄色4.应放在 4℃冰箱内保存的药物是A.氨茶喊B.苯巴比妥钠C.泼尼松(强的松 )D. 胎盘球蛋白E.青霉素5.发挥药效最快的给药途径是A. 口服B.外敷 C 吸入D. 皮下注射E.静脉注射6.股静脉的穿刺部位为A.股动脉内侧0.5cmB.股动脉外侧 0.5cmC.股神经内侧0.5cmD.股神经外侧 0.5cmE.股神经和股动脉之间7.在超声波雾化器工作原理中 ,将电能转换为超声波声能的装置是A.超声波发生器B.雾化罐透声膜 C 雾化罐过滤器1D. 晶体换能器E.电子管8.超声波雾化器在使用过程中,水槽内的水温超过多少时应及时调换冷蒸馏水A.30℃B.40℃C.50℃D.60℃E.0℃9.肌内注射时,选用联线法进行体表定位,其注射区域正确的是A.髂嵴和尾骨联线的外上1/3 处B.髂嵴和尾骨联线的中1/3 处C.髂前上棘和尾骨联线的外上1/3 处D. 髂前上棘和尾骨联线的中1/3 处E.髂前上棘和尾骨联线的后1/3 处10.肌肉小剂量注射选用上臂三角肌时,其注射区是A.三角肌下缘2~3 横指处 B.三角肌上缘2-3 横指处C.上臂内侧,肩峰下 2 ~3 横指处D.上臂外侧 ,肩峰下 2-3 横指处E.肱二头肌下缘2~3 横指处11.静脉注射过程中,发现患者局部肿胀、疼痛、试抽有回血,可能的原因是A.静脉痉挛B.针头刺人过深,穿破对侧血管壁C.针头斜面一半在血管外D.针头斜面紧贴血管内壁E.针头刺入皮下12.氧气雾化吸入时,氧流量应调至A.0.5L/minB.1-2L/minC.2-4L/minD.6-8L/minE.8~10L/min13.臀大肌注射时,应避免损伤A.臀部动脉B. 臀部静脉C.坐骨神经D.臀部淋巴E.骨膜14.小儿头皮静脉注射 ,应除外的是A.贵要静脉B.耳后静脉C.额静脉D.枕静脉E.颞浅静脉15.抢救青霉素过敏性休克的苜选药物是A.盐酸异丙嗪B.去氧肾上腺素 C 盐酸肾上腺素D. 异丙肾上腺素E.去甲肾上腺素16. 青霉素皮内注射的剂量是、20~50UA.10UB.40UC.80UD.1OOUE.150U17.链霉素皮内注射的剂量是A.0.25UB. 2.5UC. 25UD. 250UE.2500U18.接受破伤风抗毒素脱敏注射的患者出现轻微反应时,护士应采取的正确措施是A.立即停止注射,迅速给予抢救处理B.立即报告医生C.重新开始脱敏注射D.停止注射,待反应消退后,减少剂量增加次数注射E.注射苯海拉明抗过敏19.过敏性休克出现中枢神经系统症状,其原因是A.肺水肿B.有效循环血量锐减C.脑组织缺氧D. 肾衰竭E.毛细血管扩张 ,通透性增加20.破伤风抗毒素试验液的剂量是每毫升含A. 15UB. 20UC. 150UD. 200UD.200UE. 2500U(二) A2 型题21.患者张某 ,需要口服磺胺类药 ,护士嘱咐其服药期间需多喝水的目的是A.减轻胃肠道刺激B.增强药物疗效C.维持血液 pHD. 避免损害造血系统E.增加药物溶解度,避免结晶析出22.患者李某 ,因患呼吸系统疾病 ,需同时服用下列几种药物 ,安排在最后服用的药物是A.维生素 CB.维生素 B1C.氨茶碱D. 复方甘草片E.蛇胆川贝液23.患者刘某 ,因慢性充血性心力衰竭住院 ,医嘱 : 地高辛 0. 25mg,po,qd, 护士发药时应特别注意A.嘱患者服药后多喝水B.待患者服下后再离开C.给药前应测量脉率D. 服药后不宜多喝水E.应将药研碎再喂服24.患者郭某 ,病情危重 ,需进行股静脉注射 ,下列正确的叙述是A.选择股动脉外侧0.5cm 处进针B.右手持注射器 ,针头于皮肤呈20°角进针C.患者取仰卧位 ,下肢伸直 ,略内收D. 患者有出血倾向时,不宜采用股静脉注射E.注射完毕 ,无菌棉签按压3~5min25 .患者李某, 66 岁,因老年慢性支气管炎,痰液黏稠不易咳出,为帮助患者祛痰,给予氧气雾化吸人 ,下列操作中错误的一项是A.吸入前嘱患者先漱口 B. 用蒸馏水稀释药液在15ml 以内C.氧气流量为6~8L/minD. 雾化吸入器进气口接氧气,湿化瓶中加人蒸馏水E.嘱患者呼气时 ,移开出气口26.患者陈某 ,因结核性脑膜炎需注射链霉素 ,患者侧卧 ,正确的体位是A.下腿伸直,上腿稍弯曲B.上腿伸直,下腿稍弯曲C.双膝向腹部弯曲D. 两腿弯曲E.两腿伸直27. 患儿 1 岁零 8 个月,因支气管炎需肌内注射靑霉素,其注射部位最好选用A.臀大肌B.臀中肌、臀小肌C.上臂三角肌D. 前臂外侧肌E.股外侧肌28. 患者张某,静脉注射25% 葡萄糖,患者述说疼痛,推注稍有阻力,局部无肿胀,抽无回血,应考虑是A.静脉痉挛B.针刺入过深,穿破对侧血管壁C.针头斜面一半在血管外D.针头斜面紧贴血管内壁E.针头刺人过浅,药物注人皮下29.李某,患急性肺炎,注射青霉素数秒后,出现胸闷气促、面色苍白、脉细弱、出冷汗,血压:65/45mmHg, 此时首先应采取的急救措施是A.立即通知医生B.静脉注射 0.1% 盐酸肾上腺素C.立即停药、平卧,报告医生 ,就地抢救,皮下注射0.1% 盐酸肾上腺素1mlD. 立即吸氧 ,行胸外心脏按压E.即刻注射强心剂30.郭某,因肺结核注射链霉素,出现了发热、皮疹、荨麻疹.医嘱静脉注射葡萄糖酸钙,其目的是A.收缩血管,增加外周阻力B.松弛支气管平滑肌C.减轻毒性症状D. 降低体温E.缓解皮肤瘙痒( 三) A3/A4 型题( 31-32 题共用题干)患者李阿姨 ,63 岁,因支气管扩张合并肺部感染、左心力衰竭入院治疗。
宏观经济学第12章练习题及答案范文
第十二章练习题及答案一、判断题1.国民收入核算体系将GNP作为核算国民经济活动的核心指标。
()2.GDP被定义为在某一既定时期一国之内所生产的全部产品的市场价值总和。
()3.用货币去度量性质不同的各种产品,才能使各种产品能够进行加总,得出一国产出的总价值。
()4.如果农民种植的粮食用于自己消费,则这种粮食的价值就无法计入GDP之内。
()5.家庭成员提供的家务劳动要计入GDP之内。
()6.本年生产但未销售出去的最终产品价值不应计入本年的GDP之内。
()7.最终产品只包括消费品,不包括投资品。
()8.最终产品是按照产品的物质属性来划分的。
()9.某种物品是中间产品还是最终产品取决于它本身的性质,例如,汽车一定是最终产品,煤只能是中间产品。
()10.国内生产总值中的最终产品只是指有形的物质产品。
()11.用价值增值法计算一国产出的总价值,可以避免重复计算的问题。
()12.国民生产总值等于各种最终产品和中间产品的价值总和。
()13.对于整个经济来说,所有的价值增值之和必定等于所有的最终产品的总价值。
()14.若某企业年生产20万元的产品,只销售掉10万元的产品,则当年该企业所创造的GDP 为10万元。
()15.以前所生产而在当年售出的存货,应当是当年GDP的一部分。
()16.某公司生产的汽车多卖掉一些比少卖掉一些时,GDP增加要多一些。
()17.某人2000年用10万元购买了一辆产于1998年的小汽车,这10万元应该计入2000年的GDP。
()18.一栋旧建筑物的销售额应加到国民生产总值中去。
()19.销售一栋建筑物的房地产经纪商的佣金应加到国民生产总值中去。
()20.一个在日本工作的美国公民的收入是美国GDP的一部分,也是日本GNP的一部分。
()21.国内生产总值是重要的流量变量。
()22.计算国内生产总值有三种方法,当计算结果出现差异时,以收入法的结果为主。
()23.国民收入的核算中使用的生产法、收入法和支出法其内在逻辑是不一致的,因而它们最后所计算出来的国民生产总值数量也可能是不一致的。
基础护理学第十二章习题(含答案)
一、选择题(一)单项选择1.在下列给药途径中,发挥药效最快的给药途径是A.口服B.皮下注射C.吸入疗法D.肌内注射E.静脉注射2.皮内注射进行药物皮肤试验时,选择前臂掌侧下段是因为该处A.皮肤较薄、肤色较淡B.无大血管C.离大神经远D.皮下脂肪薄E.操作较方便3.服磺胺药物需多饮水的目的是A.避免结晶析出堵塞肾小管B.避免损害造血系统C.减轻服药引起的恶心D.避免影响血液酸碱度E.增加药物疗效4.无痛注射方法中,哪项是不正确的A.解除病人思想顾虑,分散注意力B.进针要快C.拔针要快D.推药液慢E.先注射刺激性强的药液,再注射刺激性弱的药液5.两岁以下婴幼儿肌内注射时最好选用A.臀大肌B.前臂外侧C.股外侧肌D.上臂三角肌E.臀中肌、臀小肌6.皮内试验过程中,下列哪项是错误的A.无菌操作B.针尖与皮肤呈5°角刺入C.严格核对D.拔针后用无菌棉签按压针眼E.用70%乙醇消毒皮肤7.以联线法取肌内注射部位的定位法是A.髂嵴与脊柱联线外1/3处B.髂嵴与尾骨联线外1/3处C.髂前上棘与脊柱联线外1/3处D.髂前上棘外侧三横指处E.髂前上棘和尾骨联线外上1/3处8.灭菌注射器及针头哪部份手可接触A.针尖B.针梗C.活塞D.针栓E.乳头9.皮下注射时,针头与皮肤的角度为A.15°~20°B.50°~60°C.20°~25°D.90°E.30°~40°10.肌内注射时,为使臀部肌肉放松,应采取的姿势为A.侧卧位,下腿伸直,上腿稍弯曲B.俯卧位,足尖相对,足跟分开C.俯卧位,足尖分开,足跟相对D.坐位,腰背前倾E.站立位,身体需挺直11.青霉素过敏性休克抢救时,首选药物是A.盐酸肾上腺素B.盐酸异丙嗪C.去甲肾上腺素D.异丙肾上腺素E.盐酸麻黄素12.表示饭后的外文缩写的正确写法是A.hsB.acC.pcD.sosE.Co13.同时服用下列药物,最后服用的是A.维生素B1B.复方阿司匹林C.麦迪霉素D.硫酸亚铁片E.止咳糖浆14.下列哪种病人给药时须将药研碎溶解后用A.鼻饲病人B.发热病人C.禁食病人D.腹泻病人E.呕吐病人15.药物保管原则中,下列哪一项不妥A.药柜宜放在光线充足处B.由专人保管,定期检查C.内服药与外用药应分别保管D.麻醉药应加锁E.瓶签模糊的药物应认真核对16.不妥的药瓶标签是A. 内服药用蓝色边B.外用药用红色边C. 剧毒药用黑色边D. 瓶签—药名应用中文,不可用外文E.瓶签上可涂蜡保护17. 剧毒药品必须A. 放在柜子里B. 与普通药统一领取C. 专柜加锁,专人保管D. 随便放置E. 医生保管18.王先生,因外伤需注射破伤风抗毒素,皮试结果局部皮丘红肿,硬结1.7cm,痒感。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2
=
∞ n=0
(−1)n
2 n +1
2 2 (2n +1)
=
1∞
(−1)n
∞
,所以
(−1)n
=
2 n=0 2n (2n +1)
n=0 2n (2n +1)
2 arctan 1 . 2
∑ 7.
将函数
f
(x) = ln x 展开成 x − 2 的幂级数,并运用结果求常数项级数
∞ n=1
1 n ⋅ 2n
(−1)n 的和.
n=0 2n (2n +1)
∑ ∑ 解:记
S(x)
=
∞ n=0
(−1)n x2n+1 2n +1
,则
S (0)
=
0 , S′(x)
=
∞ n=0
(−1)n
x2n
=
1 1+ x2
,
∫ 所以 S(x) − S(0) =
x1 0 1+t2
dt
=
arctan
x
,即
S(x)
=
arctan
x
;
∑ ∑ ∑ 因为 arctan
a2
+
b2
≥
2
ab
),
∑ ∑ ∑ ∑ ∞
又 an2
n=1
∞
收敛,
1
n2
n=1
收敛,所以
∞ n=1
1 2
(an
2
+
1 n2
)
也收敛,所以
∞ n=1
an n
绝对收敛.ຫໍສະໝຸດ 4. 求下列幂级数的收敛域
∑ ∑ ∑ ∞
(1)
xn ;[−1,1) .(2) ∞ (x −1)n ;[−2, 4) (3) ∞ (x −1)2n . (1− 3,1+ 3)
∞ (−1)2n−1 n=1 n2n
=
ln
2
−
∞ n=0
1 n2n
∞
,所以
n=1
1 n ⋅ 2n
= ln 2 .
8.
将函数
f (x) =
x2
1
展开成 x + 4 的幂级数.
+ 3x + 2
解:
f
(x)
=
x2
+
1 3x
+
2
=
−
x
1 +
2
+
1 x +1
=
1 2 − (x
+
4)
−
1 3−(x +
4)
∑ ∑ 1
∞
比较判别法的极限形式,与
1
n2
n=1
比较
∑ ∑ (4)
∞ n=1
n 3n
;收敛.比值判别法(5)
∞ n=1
( 2n +1)n 3n − 2
;收敛.根式判别法
∑ ∫ ∞
(6)
1
+∞
.发散,与反常积分
1
dx 比较
n=2 n ln n
2 x ln x
2. 判别下列级数是绝对收敛,条件收敛,还是发散?
∑ ∑ ∑ ∞
第十二章 无穷级数练习题
A
1. 判别下列级数的敛散性
∑ (1) ∞ 3n + 4n ;收敛. 运用收敛级数的性质及等比级数的特征 5n n=1
∑ ∑ ∞
(2)
n2 +1 ;发散.比较判别法的极限形式,与 ∞ 1 比较
n=1 n3 + 3n − 2
n=1 n
∑ ∑ (3)
∞ n=1
sin
1 n2
;收敛.
1− cos bn 2
bn
1−
an cos
bn
=
1 lim
an
2 n→∞ 1− cos an
+ an
=
1 2
lim
n→∞
1
−
an cos an
= +1
1, 2
an
∑ 所以级数 ∞ an 收敛.(比较判别法的极限形式)
b n=1 n
∑ 2.
− an
=
cos bn
,所以 −an
=
cos bn
− cos an
<
0
所以
0
<
an
<
bn
(余弦函数在区间
(0,
π) 2
内单调递减),
∞
∑ 因为
bn
n=1
收敛,所以
lim
n→∞
bn
=
0
,由夹逼原理知
lim
n→∞
an
=
0;
an
(2)因为 lim bn b n→∞
n
=
lim
n→∞
an bn 2
=
lim
n→∞
=
∞ n=1
xn
=
x 1− x
,
∑ 所以 S1(x)
= ( x )′ = 1− x
1 (1− x)2
,所以 S (x)
=
xS1 ( x)
=
x (1− x)2
;
∞ n=1
n 2n
=
S(1) 2
=
2.
∑ ∑ 6. 求幂级数 ∞ (−1)n x2n+1
n=0 2n +1
在区间 (−1,1)
∞
内的和函数,并运用结果求数项级数
n=0
(x + 4)n 3n+1
, x ∈ (−7, −1) ,
3
∑ ∑ ∑ 所以
∞
f (x) = (−1)n
n=0
(x + 4)n 2n+1
∞
− (−1)n
n=0
(x + 4)n 3n+1
=
∞ n=0
(−1)n
(
1 2n+1
−
1 3n+1
)(
x
+
4)
n
,
x
∈
(−6,
−2)
.
9. 设 f (x) = x (0 ≤ x ≤ π ), 将 f (x) 展开成以 2π 为周期的正弦级数.
2 − (x + 4)
=
1⋅ 2 1−
1 x+4
=
1 2
∞
(−1)n
n=0
(x + 4)n 2n
=
∞
(−1)n
n=0
(x + 4)n 2n+1
, x ∈ (−6, −2) ,
2
∑ ∑ 1
3 − (x + 4)
=
1⋅ 3 1−
1 x+4
=
1 ∞ (−1)n 3 n=0
(x + 4)n 3n
=
∞
(−1)n
n=0 2n +1
n=0 n ⋅ 3n
3n
n=0
∑ ∑ ∞
5. 求幂级数 nxn
n=1
在区间 (−1,1)
∞
内的和函数,并运用结果求数项级数
n 的和.
2n
n=1
∑ ∑ ∑ ∫ ∑ ∞
∞
∞
解:记 S (x) = nxn = x nxn−1 , S1(x) = nxn−1 ,则
n=1
n =1
n=1
x
0 S1(t)dt
(1)
(−1)n−1 ;条件收敛(2) ∞
(−1)n−1 ;条件收敛 (3)
∞ n2 cos n .绝对收敛
n=1 2n −1
n=1 n2 + 1
3n
n=1
∑ ∑ ∞
3. 已知 an2
n=1
收敛,求证: ∞ an 绝对收敛. n=1 n
证明:因为
an n
≤
1 2
(an2
+
1 n2
)
(注:运用重要的不等式
解:将函数 f (x) = x (0 ≤ x ≤ π ) 先做奇延拓,再做周奇延拓,化为以 2π 为周期的奇函数,
∫ ∫ 所以 bn
=
2 π
π f (x) sin nxdx = 2
0
π
π x sin nxdx = 2 (−1)n+1 ,
0
n
∑ 所以
∞
f (x) = 2
(−1)n+1 sin nx , 0 ≤ x < π ) .
n=1 n
B
∑ 1.
设数列{an}、{bn}满足 0 < an
<π 2
, 0 < bn
<
π 2
, cos an
− an
= cos bn ,且级数
∞
bn
n=1
收敛,
∑ 求证:(1)
lim
n→∞
an
= 0 ,(2)级数
∞ n=1
an bn
收敛;
证明:因为 0
<
an
<
π 2
,0
<
bn
<
π 2
, cos an
的和.
∑ 解:因为 ln(1+ x) = ∞ (−1)n−1 xn , x ∈ (−1,1] ,
n=` n
∑ 所以 ln
x
=
ln[2 + (x −
2)]
=
ln 2 + ln(1+
