梁在简单载荷作用下变形的
各种梁的弯矩剪力计算(大全)表

表1 简单载荷下基本梁的剪力图与弯矩图注:外伸梁= 悬臂梁+ 端部作用集中力偶的简支梁表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件常用截面几何与力学特征表表2-5 .......资料.注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EI w 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
各类梁的弯矩剪力计算汇总表

表1 简单载荷下基本梁的剪力图与弯矩图表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
2)三跨等跨梁的内力和挠度系数 表2-12注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
建筑力学专业习题集

东北农业大学网络教育学院建筑力学作业题(一)一、单项选择题(将正确答案字母序号填入括号里,每小题1分,共5分)1、平面力系向点1简化时,主矢F R =0,主矩M 1≠0,如将该力系向另一点2简化,则( )。
A :F R ≠0,M 2≠0;B :F R =0,M 2≠M 1;C :F R =0,M 2=M 1;D :F R ≠0,M 2=M 1。
2. 大小相等的四个力,作用在同一平面上且力的作用线交于一点C ,试比较四个力对平面上点O 的力矩,哪个力对O 点之矩最大( )A .力P 1B .力P 2C .力P 3D .力P 4 3. 两端铰支的等直压杆,其横截面如图所示。
试问压杆失稳时,压杆将绕横截面上哪一根轴转动?( ) Py 1Z 1yZA. Z 轴B. Y 轴C. Z 1轴D. Y 1轴4. 如图所示矩形截面,判断与形心轴z 平行的各轴中,截面对哪根轴的惯性距最小以下结论哪个正确?( )A. 截面对Z 1 轴的惯性矩最小B. 截面对Z 2 轴的惯性矩最小C. 截面对与Z 轴距离最远的轴之惯性矩最小D. 截面对Z 轴惯性矩最小5. 指出以下应力分布图中哪些是正确的( )• ·C P 1 P 2 P 3A. 图(a)(b) 正确B. 图(b)(c) 正确C. 图(c)(d) 正确D. 图(b) (d) 正确二、判断题(每小题1分,共5分)1. 作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,此力系必然平衡。
( )2. 一空间力系,若各力作用线平行某一固定平面,则其独立的平衡方程只有3个。
( )3. 压缩与弯曲的组合变形,在进行强度计算时,如考虑附加弯矩的影响,结果是偏于安全的。
( )4. 下图为几何不变体系且无多余约束。
( )5. 矩形截面梁受横向力作用而弯曲时,其横截面上最大剪应力的大小是平均剪应力的3倍。
( )三、填空题(每空1分;共15分。
)1. 横截面面积A=10cm 2的拉杆,P=40KN ,当α=60°斜面上的σ = ,σα= ,τα= 。
§8-6 提高梁的刚度的措施

§8-6 提高梁的刚度的措施
影响梁弯曲变形的因素不仅与梁的支承和载荷情况有关,而且还与梁 的材料、截面尺寸、形状和梁的跨度有关。所以,要想提高弯曲刚度,就应 从上述各种因素入手: 一、调整加载方式 二、减小跨度或增加支座 三、选择合理截面 四、合理选用材料
§8-6 提高梁的刚度的措施 一、合理安排梁的约束与加载方式
矩形木梁的合理高宽比 ( h/b= ) 1.5
b
英(T.Young)于1807年著«自然哲学与机械技术讲义 »一书中指出: 矩形木梁的合理高宽比 为
h 2 时,强 度 最 大; h 3 时,刚 度 最 大.
b
b
§8-6 提高梁的刚度的措施
三、选择合理截面
bh2 Wz 6
h2 d 2 b2
Wz
机械加工,镗孔,尾架,减少挠度。
§8-6 提高梁的刚度的措施
跨度为l 的简支梁,承受均布载荷q作用,如果将梁两端的铰支座各向 内移动 l/4,最大挠度将仅为前者的8.75%。
§8-6 提高梁的刚度的措施 三、选择合理截面
§8-6 提高梁的刚度的措施 三、选择合理截面
矩形木梁的合理高宽比
h 北宋李诫于1100年著«营造法式 »一书中指出:
b 6
(d 2
b2 )
d 2b b3 6
ቤተ መጻሕፍቲ ባይዱ
dW 0 db
d 2 3b2 0
b d 3
h d 2 b2 d 2 d 2 2d 33
h b
2d
3 d
23 2
3
h
b
§8-6 提高梁的刚度的措施 四、合理选用材料
各种材料的弹性模量E差别不大。 选用高强度材料,只能提高许用应力 同类的材料,“E”值相差不多,故换用同类材料只能提高强度,不能提高 刚度。
梁的变形与刚度计算
查表,得
y
C
y
4
Cq
y
Cm
l
q
A
2 5ql ml 384EI 16 EI
()
Bq
θA θAq θAm
3 ml ql 24 EI 3EI
Aq
m
A
C y cq
(
)
Bm
Am
C ycm
θB θBq θBm
3 ml ql 24 EI 6 EI
(
2
3
ml 16 EI
ml 3EI ml 3EI 一、梁的刚度条件
w
max
L
w L
max
1 1 w (对土建工程: ( ~ )) 250 1000 L
其中[]称为许用转角;[w/L]称为许用挠跨比。通常依此 条件进行如下三种刚度计算: 、校核刚度:
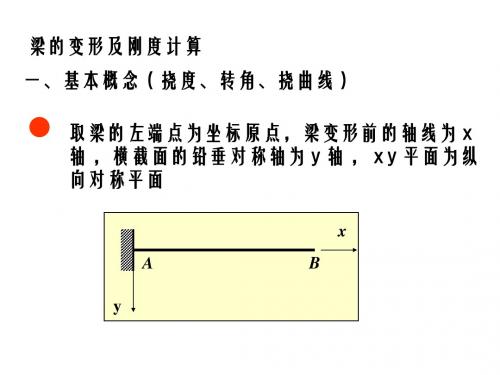
梁的变形及刚度计算 一、基本概念(挠度、转角、挠曲线) 取梁的左端点为坐标原点,梁变形前的轴线为 x 轴 ,横截面的铅垂对称轴为 y 轴 , x y 平面为纵 向对称平面
x
A
y
B
一、基本概念(挠度、转角、挠曲线)
度量梁变形后横截面位移的两个基本量 1、挠度( y): 横截面形心 C (即轴线上的点)在垂直于 x
例题求图示梁截面B的挠度
q A EIz
a C
B
L
解法1:为了利用附录IV表中的结果,可将原荷载视 为图(1)和图(2)两种情况的叠加
q A EIz
a C
B
L L c q (2) B
q A c L (1) B A
a
q
梁的变形与刚度计算

(e) 结果(转角和挠度方程)。 AC段
ቤተ መጻሕፍቲ ባይዱ
Pb 2 2 EIv1 ' EI 1 (l b 2 3x1 ) 6l (0 x1 a) EIv Pb (l 2 b 2 x 2 ) 1 1 6l
CB段
Pb 2 2 3l 2 2 EIv2 ' EI 2 6l l b 3x b x 2 a (a x 2 l ) EIv Pb l 2 b 2 x 2 x l x a 3 2 2 2 6l b
例9-4。图示杆系中,AB和CD梁的抗弯为EI,BD杆的拉压刚度是EA,不计剪切变形的影响,求BD
杆的内力。
A
B l/2
解(a) 确定静不定梁的基本结构 取D为多余约束
A
R'D
B
C
l
D
D (1)
RD
C
(2)
D
(b) 求变形几何关系
vD1 vD2
(c) 求物理关系
l 3 RD l 2 R l l D 3EI EA 3EI 2 EA R' D l 3 ql 4 8 EI 3EI
第 9 章
梁的变形与刚度设计
DESIGN OF BEAMS FOR BENDING DEFLECTIONS
一。 弯曲变形概念
y
θ
P
受载荷作用后,梁的轴线将弯曲成为一条光滑的连续曲线 在平面弯曲的情况下,这是一条位于载荷所在平面内的平 面曲线。梁弯曲后的轴线称为挠曲线。
x
O
v
梁截面有沿垂直方向的线位移v,称为挠度;相对于原截面转过的角位移θ,称为转角 挠曲线是一条连续光滑平面曲线,其方程是
建筑力学13-梁的变形

再积分一次,可以得到挠曲线方程
y 1 EI z [ ( M ( x ) dx ) dx Cx D )
【例 10.1】简支梁受均布荷载q作用,如图10.3所示,EI为常数。 试求此梁的转角和挠曲线方程,以及此梁的最大挠度ymax(通常用 符号f表示)和两端截面的转角θA和θB。 【解】(1) 列出挠曲线的近似微分方程 RA=RB= ql/2 M(x)= qlx/2 - qx2/2 EId2y/dx2 =-M(x)=- qlx/2 +qx2/2 (2) 积分 将上式连续积分两次,可以得到 EI dy/dx =EIθ=- qlx2/4 + qx3/6 +C EIy=- qlx3/12 + qx4/24 +Cx+D
(3) 确定积分常数 为了确定积分出现的四个积分常数,除了要利用边界条件外, 还要利用相邻两段梁在交接外变形的连续条件。 边界条件: x1=0,y1=0 x2=l,y2=0 连续条件: x1=x2=a,θ1=θ2y1=y2 将以上条件代入式(a)、(b)、(c)、(d),联立求解,可得积分 常数 D1=D2=0C1=C2= Pb/6l (l2-b2)
【例11.5】一简支梁由18号工字钢制成,受均布荷载q的作用,如 图10.7所示。已知材料的E=210GPa,[σ]=150MPa,[f/l] =1/400。试校核梁的强度和刚度。 【解】(1) 由型钢表查得18号工字钢 Wz=185cm3=185×103mm3 Iz=1660cm4=1660×104mm4 (2) 强度校核 Mmax= ql2/8 = 24×32/8kN· m=27kN· m σmax= Mmax/Wz = 27×106/185×103MPa=146MPa<[σ]
理论力学11梁的位移计算

dvM dxEI ( z x)
θ ( x) = = ∫
⎛ M ( x) ⎞ v( x) = ∫ dxEI ⎜∫ z
dx + C
dx ⎟dx + Cx + D C,D 为积分常数,由梁的位移约束条件确定。 ⎝ EI z⎠ 挠曲线近似微分方程通解的积分常数确定以后,就得 到了挠曲线方程和转角方程,这种求梁变形的方法称为积 分法。
本章小结
挠曲线、挠度、转角、挠曲线方程、转角方程
v = f ( x)
θ = θ ( x)
挠曲线微分方程
dv θ ≈ tgθ = dx
dv ±
2
2
dx dv 2 ⎤⎡ 1+ ( ) ⎥⎢ dx ⎦⎣
将b处约束去掉基本静定系静定基相当系统加上q及约束力变形协调条件marblqlvbeirb39梁的位移计算本章小结挠曲线挠度转角挠曲线方程转角方程dx挠曲线微分方程dxdv40梁的位移计算积分法求梁的位移边界条件和连续条件dvmdxdx叠加法求梁的位移梁的刚度条件4041梁的位移计算提高梁的刚度的主要措施增大截面惯性矩
23
梁的位移计算
24
梁的位移计算
25
梁的位移计算
思考:
应用叠加法求梁的位移,必须满足的条件是什么? 答:小变形,材料符合胡克定律。
26
梁的位移计算
4 3
已知图1B点的挠度和转角分别为 ql / 8 EI , ql / 6 EI , 图2C截面的转角为多少?
q
A
l
B
ql / 8 EI
3
q
A B
3
16
例
3
求简支梁最大挠度,F已知,EI为常数。
解
1、建立挠曲线微分方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程中虽然经常是限制弯曲变形,但在另 一些情况下,常常又利用弯曲变形达到某 种要求。例如,叠板弹簧应有较大的变形, 才可以更好地起缓冲减振作用。弹簧扳手 要有明显的弯曲变形,才可以使测得的力 矩更为准确。 弯曲变形计算除用于解决弯曲刚度问题外, 还用于求解静不定系统和振动计算。所以 弯曲变形的研究是非常的重要的。
悬臂梁受集中力的情况
悬臂梁受集中力偶的情况
悬臂梁受分布力的情况
绞支梁受集中力的情况
绞支梁受集中力偶的情况
绞支梁受分布力的情况
四、用叠加法求弯曲变形:
1. 叠加法原理(力的独立性原理): 在小变形前提下,当构件或结构同时作用几 个载荷时,如果各载荷与其产生的效果(支 反力,内力,应力和位移、变形等)成线性 关系(互不影响,各自独立),则它们同时作 用所产生的总效果等于各载荷单独作用时 所产生的效果之和(代数和、矢量和):
2. 求梁的弯曲变形的叠加法是:
分别求出各载荷单独作用时的变形(位移),然 后把各载荷在同一处引起的位移进行叠加 (代数叠加)。
谢谢观赏!
梁在简单载荷作用下变形学在学习工程中的查询。
工程中对某些受弯杆件除强度要求外,往往还有 刚度要求,即要求它变形不能过大。以机床主轴 为例,若其变形过大,将影响齿轮的啮合和轴承 的配合,造成磨损不匀,产生噪音,降低寿命, 还会影响加工精度;以吊车梁为例,当变形过大 时,将使梁上小车行走困难,出现爬坡现象,还 会引起较严重的振动;再以化工厂的管道为例, 弯曲变形如果超过容许数值,就会造成物料的淤 积,影响输送;较长的回转滚筒,弯曲变形过大, 就会引起脆性材料的开裂;电机转子的轴变形过 大,可能导致与定子相碰。所以,若变形超过允 许数值,即使仍然是弹性的,也被以为是一种失 效。
