正切函数的主要性质
正弦、余弦、正切函数图象及其性质
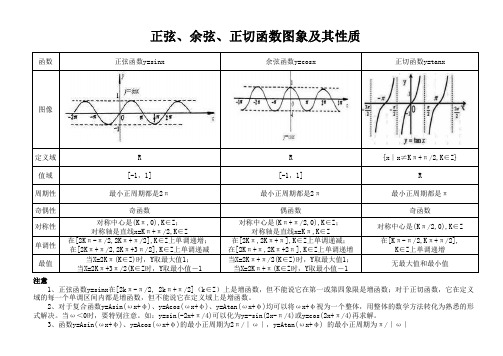
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1,1][-1,1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z;对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时,Y取最大值1;当X=2Kπ+3π/2(K∈Z时,Y取最小值-1当X=2Kπ+π/2(K∈Z)时,Y取最大值1;当X=2Kπ+π(K∈Z时,Y取最小值-1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2](k∈Z)上是增函数,但不能说它在第一或第四象限是增函数;对于正切函数,它在定义域的每一个单调区间内都是增函数,但不能说它在定义域上是增函数。
2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体,用整体的数学方法转化为熟悉的形式解决。
当ω<0时,要特别注意。
如:y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。
3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣,y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。
正切函数的图像和性质
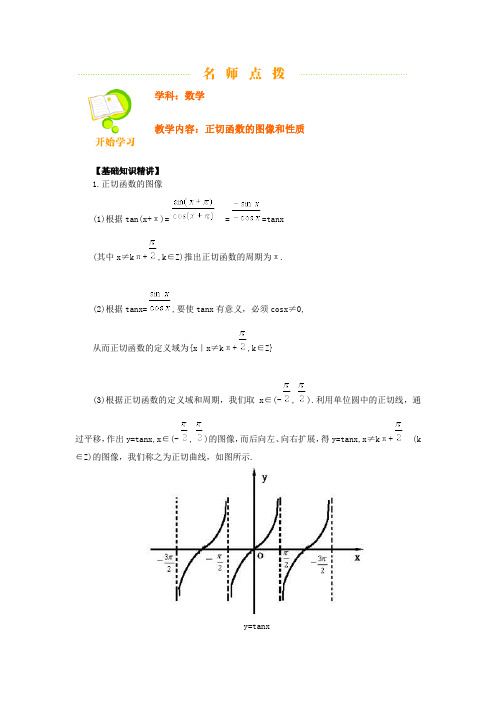
学科:数学教学内容:正切函数的图像和性质【基础知识精讲】1.正切函数的图像(1)根据tan(x+π)= ==tanx(其中x≠kπ+,k∈Z)推出正切函数的周期为π.(2)根据tanx=,要使tanx有意义,必须cosx≠0,从而正切函数的定义域为{x|x≠kπ+,k∈Z}(3)根据正切函数的定义域和周期,我们取x∈(-,).利用单位圆中的正切线,通过平移,作出y=tanx,x∈(-,)的图像,而后向左、向右扩展,得y=tanx,x≠kπ+ (k ∈Z)的图像,我们称之为正切曲线,如图所示.y=tanx2.余切函数的图像如下:y=cotx3.正切函数、余切函数的性质:{x|x∈R且x≠kπ+,k∈Z}{xR R每个区间(kπ-,kπ+) 上递增(k∈Z) 每个区间递减注:正切函数在每一个开区间(kπ-,kπ+)(k∈Z)内是增函数,但不能说成在整个定义域内是增函数,类似地,余切函数也是如此.【重点难点解析】本节重点是正切函数图像的画法及性质的运用.正切函数的图像一般用单位圆中的正切线作.因y=tanx定义域是{x|x∈R,x≠kπ+,k∈Z},所以它的图像被平行线x=kπ+ (k ∈Z)隔开而在相邻两平行线之间的图像是连续变化的.1.正切函数应注意以下几点:(1)正切函数y=tanx的定义域是{x|x≠kπ+,k∈Z},而不是R,这点要特别注意:(2)正切函数的图像是间断的,不是连续的,但在区间(kπ-,kπ+)(k∈Z)上是连续的;(3)在每一个区间(kπ-,kπ+)(k∈Z)上都是增函数,但不能说正切函数是增函数.2.解正切不等式一般有以下两种方法:图像法和三角函数线法.图像法即先画出正切函数的图像,找到符合条件的边界角,再写出所有符合条件的角的集合.三角函数线法则先在单位圆中作出角的边界值时的正切线,得到边界角的终边,在单位圆中划出符合条件的区域(这里特别要注意函数的定义域),再用不等式正确表示区域.例1作出函数y=|tanx|的图像,并根据图像求其单调区间.分析:要作出函数y=|tanx|的图像,可先作出y=tanx的图像,然后将它在x轴上方的图像保留,而将其在x轴下方的图像向上翻(即作出关于x轴对称图像),就可得到y=|tanx|的图像.所以其图像如图所示,单调增区间为[kπ,kπ+(k∈Z);单调减区间为kπ-,kπ](k∈Z).说明:根据图像我们还可以发现:函数y=|tanx|的最小正周期为π.一般地,y=A|tan(ωx+φ)|的最小正周期与y=Atan(ωx+φ)的最小正周期相同,均为.例2求函数y=lg(tanx-)+的定义域.解:欲使函数有意义,必须由此不等式组作图∴函数的定义域为(kπ+,kπ+).评析:解正切不等式一般有两种方法:图像法和三角函数线法.图像法即先画出函数图像,找出符合条件的边界角,再写出符合条件的角的集合.三角函数线法则是先在单位圆中作出角的边界值时的正切线,得到边界角的终边,在单位圆中画出符合条件的区域.要特别注意函数的定义域.例3求函数y=tan(2x-)的单调区间.解:y=tanx,x∈(-+kπ, +kπ)(k∈Z)是增函数.∴-+kπ<2x-<+kπ,(k∈Z).即-+<x<+,(k∈Z)函数y=tan(2x-)的单调递增区间是(-+,+ ).(k∈Z)例4求函数f(x)=tan(2x+)的周期.解:因为tan(2x+ +π)=tan(2x+)即tan[2(x+)+]=tan(2x+)∴tan(2x+)的周期是.例5求函数y=3tan(2x+)的对称中心的坐标.分析:y=tanx是奇函数,它的对称中心有无穷多个,即(,0)(k∈Z).函数y=Atan(ωx+φ)的图像可由y=tanx经过变换图像而得到,它也有无穷多个对称中心,这些对称中心恰好为图像与x轴交点.解:由2x+= ,(k∈Z)得x=- (k∈Z)∴对称中心坐标为(-,0)(k∈Z)注意:函数y=Atan(ωx+φ)(A>0,ω>0)的图像及性质可与函数y=Asin(ωx+φ)(A>0,ω>0)的图像及性质加以比较研究.【难题巧解点拔】例判断函数f(x)=tan(x-)+tan(x+)的奇偶性,并求此函数的周期及单调区间.分析:奇偶性的判断必须考虑①定义域是否关于原点对称.②是否对任意x有f(-x)=-f(x)或f(-x)=f(x)成立;关于周期和单调性必须将函数化为一个三角函数的形式方可求.解:此函数的定义域为{x|x∈R且x≠kπ+,k∈Z}它是关于原点对称.又f(-x) =tan(-x+)+tan(-x-)=-tan(x-)-tan(x+)=-f(x)故此函数是奇函数.y=tan(x-)+tan(x+)=tan[(x-)+(x+)][(1-tan(x-)tan(x+)∵sin(-a)=cosacos(-a)=sina∴tan(-a)=cotacot(-a)=tana故tan[-(x+)]=cot(x+)即-tan(x-)=cot(x+)∴y=tan2x[1+cot(x+)tan(x+)]=2tan2x故此函数周期为当kπ-<2x<kπ+-<x<+ (k∈Z)即x∈(-,+ )时,原函数是增函数.评析:此题的难点在于通过三角恒等化简,将函数化为一个三角函数.同时要求同学们必须熟悉正切函数的性质.y=Atan(ωx+φ)(A≠0)的周期为T=.例2已知≤1,求函数y=cot2x-2cotx+5的值域.分析:从已知条件的不等式中解出cotx的范围,然后在此条件下求被求函数的值域.解:由已知条件,可得0≤lg[-9cos(x+)]≤1.得-≤cos(x+)≤∴kπ+≤x+≤kπ+,(k∈Z).∴kπ+≤x≤kπ+,(k∈Z).∴0≤cotx≤ y=cot2x-2cotx+5=(cotx-1)2+4∴当x=kπ+,(k∈Z)时,y取最小值4.当x=kπ+,(k∈Z)时,y取最大值5.从而函数y=cot2x-2cotx+5的值域是[4,5].【课本难题解答】课本第72页第5题:(1){x|-+kπ≤x< +kπ,k∈Z}(2){x|+kπ≤x<+kπ,k∈Z}第6题:(1)D (2)C (3)C (4)B【命题趋势分析】从历届高考试题可以看到,本节内容主要考查函数的定义域,周期性,图像及单调性等知识,一般以选择题,填空题题型出现,属基本题.【典型热点考题】例1满足tanα≥cotα的角的一个取值区间是( )A.(0,)B.[0,]C.[,]D.(,)分析:本考查正切函数单调性,应化同名函数,再化角为同一单调区间内.解:由选择项,可以考虑α∈(0,)的情况.∵tanα≥tan(-α),且α, -α∈(0, )∴α≥-α,∴≤α<.故选C.例2函数y=的最小正周期是( )A. B. C.π D.2π解法1:将四个选项分别代入函数式验算,可知B正确.∴应选B.解法2:y==cos4x∴T==∴应选B.例3函数y=+的定义域是 .由①②得0<x≤4 ⑤∴0<x<或π≤x≤4.∴应填(0,)∪[π,4]例4如果α、β∈(,π),且tanα<cotβ,那么必有( )A.α<βB.β<αC.α+β<D.α+β>解:∵tanα<cotβ<0,∴tanαtanβ>1.有tan(α+β)=>0有α+β∈(π,)∴α+β<.∴应选C.说明:本题也可采取化为同名函数的方法,或都取特殊值比如取α=β=,可排除A、B、D.。
正切函数的性质与图象

π π 例4、若x , ,求函数 3 4 1 y 2 tan x 1的最值及相应的x的值. 2 cos x
由于tan[ ( x 2) ] tan( x ) tan( x ) 2 3 2 3 2 3
所以,原函数的定义域是 {x | x 1 2k , k Z }. 3 所以原函数的周期是2.
2 2 3 2 解得 5 2k x 1 2k , k Z 因此,函数的增区间 3 3 ( 5 2k , 1 2k ), k Z 3 3
y tan x T π
例4 求下列函数的周期:
解 : f ( x) 3 tan(2 x ) 4
(1) y 3 tan(2 x ) ); 2 4
f (x ) 2 周期T 2
3 tan[2( x ) ] 2 4
值的范围.
(1) tan x 0, (2) tan x 0, (3) tan x 0
y
解:
3 2
2
0
2
3 2
x
(1).x (k
2
, k ), (k Z )
(k Z )
(2).x k ,
(3).x (k , k ), (k Z ) 2
解: (1) 90 167 173 180 ) y tan x, 在 (90 0 ,270 0 上是增函数
又
又
tan167 0 tan173 0 11 3 (2) tan( ) tan( ) 4 4 13 3 tan( ) tan( ) 5 5 是增函数 3 3 且 y tan x, x ( , ) , 2 4 5 2 2 2
正切函数的图象及性质

11 6
●
2
●
2
0
6
3
2
2 3
5 6
● ● ● ● ●
x
3 2
-1
现在利用正切线画出函 数y tan x, x (
y
, )的图象 2 2
1
o1
2
4
0
1
4
2
x
利用正切函数的周期性,把图象向左,右扩展,得到正切函数 y tan x, x R且x k , (k Z )的图象 , 并把它 叫做正切曲线. 2 y
(2) y tan x 性质: 定义域
值 周 奇 域 期 偶 性 奇 R 函 数
单调增区间
对 称 中心
渐近线 方程
x x k ,k Z 2
k, x k 0 k ,k 2 2 2 k Z k Z k Z
2
正切函数的主要性质如下:
定义域 值 域 周期性 奇偶性 单调性
xx
2 k , k Z
实数集
T
奇函数(正切曲线关于原点对称)
在(
k, k),k Z内为增函数 2 2
例1.求函数 y tan x )的定义域 , 周期和单调区间。 ( 4
解:令 z x
y
解:
3 2
2
0
2
3 2
x
(1). x (k
2
, k ), (k Z )
正切函数的性质及其应用

正切函数的性质及其应用正切函数是三角函数中的一种,表示一个角的正切值。
在数学和物理学中,正切函数具有一些重要的性质,并且在各种应用中扮演着关键角色。
本文将探讨正切函数的性质以及一些常见的应用。
一、正切函数的定义和图像特点正切函数的定义公式为:tan(x) = sin(x) / cos(x),其中x为角度或弧度。
根据定义,我们可以得出正切函数的几个图像特点。
1. 定义域和值域:正切函数的定义域是所有实数除去所有使得cos(x) = 0的点,通常写作D: x ≠ (2n + 1) * π / 2,其中n为整数。
值域是整个实数集,记作R。
2. 周期性:正切函数的图像在一个周期内呈周期性变化。
周期为π,即tan(x) = tan(x + kπ),其中k为整数。
3. 奇函数性质:正切函数具有奇函数性质,即满足tan(-x) = -tan(x),这是由于sin(-x) = -sin(x),cos(-x) = cos(x)。
4. 渐近线:正切函数在x = (n + 1/2) * π,其中n为整数时,有垂直渐近线。
在x = n * π,其中n为整数时,有水平渐近线。
基于这些性质,我们可以画出正切函数的图像。
图像在每个周期内呈现周期性的上升与下降,同时存在垂直和水平渐近线。
二、正切函数的应用正切函数在各个领域有着广泛的应用。
以下是一些常见的应用示例:1. 三角测量:正切函数在三角测量中扮演着重要的角色。
例如,在测量一个目标物体的高度时,可以利用正切函数来计算角度并得到正确的高度值。
2. 电工学:在电路分析中,正切函数可以用来计算交流电路中电压和电流的相位差。
相位差是指两个波形之间的时间延迟,正切函数可以帮助我们解决相关的计算问题。
3. 工程学:在工程学中,正切函数经常用于解决角度和距离的计算问题。
例如,在建筑工程中,可以利用正切函数来计算楼梯的坡度和斜面的角度。
4. 自然科学:正切函数在自然科学中也有着广泛的应用。
正切函数的图像和性质

例1.观察图象,写出满足下列条件的x值的范围:
( 1 ) t a n x 0 ; ( 2 ) t a n x 0 ; ( 3 ) t a n x 0
解:
(1)x(k,k) kZ
2
(2)xk k Z
y ytanx
(3)x( k,k)
kZ
2
2
2
o 2
x 2
特征
1.有无穷多支曲线组成,由直线 xk,kZ隔开
f(x ) sin x ,x R为奇函数 f(x ) c o sx ,x R为偶函数
f(x)=tanx呢?
利用正切线作正切函数的图像
2
4
3
8
8
3 84 8 2
图象
y
3 2
2
3
x
2
2
特征
其中x的取值集合,即定义域为
{x|xR且 xk ,kz}
又由图像可知正切函数2的值域是实数集R
在(在kR上,没有k单)调上 性 单调增
22
没有最值
例6
▪ (1)定义域
y
tan
x
2 3
解:原函数要有意义,自变量x应满足
即
x
1 3
2k,
k
Z
2x32k,kZ
所以,原函数的定义域是{x| x132k,kZ}.
例6
y
tan
x
2 3
▪ (2)周期性
由于 ta n [ 2 (x 2 ) 3 ] ta n ( 2 x 3 ) ta n ( 2 x 3 )
对称中心:(2 k,0) k Z
三角函数
1.4.3正切函数的性质与图象
正切函数和正切线
三角函数正切函数的性质与图像

正切函数的图像向右平移π个单位,可以得 到余弦函数的图像。
左右翻转
正切函数的图像关于$y$轴对称,即$tan( - x) = tan(x)$。 正切函数的图像向左翻转后,可以得到正切函数的图像。
03
正切函数的图像绘制
利用Python绘制正切函数图像
导入matplotlib库
定义正切函数
首先需要导入matplotlib库,该库是 Python中用于绘图的常用库之一。
使用xlabel和ylabel参数可以添加x轴和y轴的标签,例如x轴 标签为“$x$”,y轴标签为“$y$”。
显示网格线
使用grid参数可以显示网格线,以便更好地观察图像的细节 。
04
三角函数的实际应用
物理中的三角函数
简谐振动
简谐振动的位移与时间的关系可以表示为正弦或余弦函数,利用三角函数性 质可以更深入地理解简谐振动的特征。
正切函数的对称性
正切函数图像无对称轴,但在$x = \frac{\pi}{2} + k\pi$ 处,函数图像呈现对称性。
正切函数的奇偶性
$tan( - x) = - tan(x)$,因此正切函数为奇函数。
正切函数的应用
正切函数在解直角三角形、求三角形的面积、研究三角恒 等式等方面具有广泛应用。
对未来研究正切函数的展望
三角函数正切函数的性质与图像
xx年xx月xx日
contents
目录
• 正切函数概述 • 正切函数的性质 • 正切函数的图像绘制 • 三角函数的实际应用 • 总结与展望
01
正切函数概述
正切函数的定义
正切函数:tan(x) = sin(x) / cos(x) 值域:(-∞,∞)
定义域:{x | x ≠ π/2 + kπ,k ∈ Z} 周期:π
正切函数的特征和实际意义

正切函数的特征和实际意义正切函数是数学中的一种基本三角函数,其特征和实际意义在数学和物理问题中都有重要的应用。
本文将探讨正切函数的特征以及其在实际中的意义。
一、正切函数的特征正切函数的特征主要表现在以下几个方面:1. 定义域和值域:正切函数的定义域为所有实数除以π的倍数(nπ,其中n为整数),值域为整个实数集。
也就是说,正切函数可以取任意实数值。
2. 周期性:正切函数以π为一个周期,即tan(x + π) = tan(x)。
在一个周期内,正切函数的值在正无穷和负无穷之间变化。
3. 对称性:正切函数关于原点对称,即tan(-x) = -tan(x)。
这意味着正切函数的图像关于原点对称。
4. 奇函数性质:正切函数是一个奇函数,即tan(-x) = -tan(x)。
这意味着正切函数的图像关于原点对称且关于y轴对称。
二、正切函数的实际意义正切函数在实际中有广泛的应用,主要包括以下几个方面:1. 几何应用:正切函数可以用于解决几何问题,特别是在三角形和圆形问题中。
例如,通过正切函数可以计算三角形的边长和角度等相关信息。
2. 物理应用:正切函数在物理学中有广泛应用。
例如,在力学中,正切函数可以解决斜面上物体的运动问题,帮助计算物体的位移、速度和加速度等相关参数。
此外,在波动学和电路中,正切函数也有重要的应用。
3. 信号处理:正切函数在信号处理中有重要的应用,特别是在调制和解调过程中。
通过正切函数,可以将模拟信号转换为数字信号,或者将数字信号转换为模拟信号。
4. 经济学和金融学:在经济学和金融学中,正切函数可以用于解决复杂的经济和金融问题。
例如,在计算投资回报率和利息问题时,正切函数可以提供准确的结果。
5. 工程应用:工程学中的许多问题可以使用正切函数来解决。
例如,在建筑和土木工程中,正切函数可以用于计算斜坡的倾斜度和坡度,以及求解其他相关问题。
总结:正切函数作为数学中的基本三角函数,在解决几何、物理、信号处理、经济学和工程等实际问题中发挥着重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
