2013年1月自考高数(一)试题及详解
2013-数一真题大全及答案

2013年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)已知极限0arctan limkx x xc x →−=,其中,c k 为常数,且0c ≠,则( )(A )12,2k c ==−(B )12,2k c ==(C )13,3k c ==−(D )13,3k c ==(2)曲面2cos()0x xy yz x +++=在点(0,1,1)−处的切平面方程为( ) (A )2x y z −+=− (B )2x y z ++= (C )23x y z −+=− (D )0x y z −−=(3)设1()2f x x =−,102()sin (1,2,...)n b f x n xdx n π==⎰,令1()sin n n S x b n x π∞==∑,则9()4S −=( )(A )34 (B )14(C )14−(D )34−(4)设222222221234:1,:2,:22,:22,l x y l x y l x y l x y +=+=+=+=为四条逆时针的平面曲线,记33()(2)(1,2,3,4)63ii l y x I y dx x dy i =++−=⎰,则()i MAX I =( )(A )1I (B )2I (C )3I (D )3I(5)设矩阵A,B,C 均为n 阶矩阵,若,B AB C =则可逆,则 (A )矩阵C 的行向量组与矩阵A 的行向量组等价 (B )矩阵C 的列向量组与矩阵A 的列向量组等价 (C )矩阵C 的行向量组与矩阵B 的行向量组等价 (D )矩阵C 的行向量组与矩阵B 的列向量组等价(6)矩阵1111a a b a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭与2000b 0000⎛⎫ ⎪⎪ ⎪⎝⎭相似的充分必要条件为(A )a 0,b 2== (B )为任意常数b a ,0= (C )0,2==b a(D )为任意常数b a ,2=(7)设123X X X ,,是随机变量,且22123~N(0,1)~N(~(5,3)X N ,X 0,2),X ,{22}(1,2,3),j j P P X j =−≤≤=则( )(A )123P P P >> (B )213P P P >> (C )312P P P >> (D )132P P P >>(8)设随机变量~(),~(1,),X t n Y F n 给定(00.5),a a <<常数c 满足{}P X c a >=,则2{}P Y c >=( ) (A )α (B )1α−(C )2α (D )12α−二、填空题:9−14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9)设函数()f x 由方程(1)x y y x e−−=确定,则1lim (()1)n n f n→∞−= .(10)已知321xxy e xe =−,22xxy e xe =−,23xy xe =−是某二阶常系数非齐次线性微分方程的3个解,该方程的通解为y = .(11)设sin sin cos x t y t t t=⎧⎨=+⎩(t 为参数),则224t d y dx π== .(12)21ln (1)xdx x +∞=+⎰.(13)设ij A (a )=是三阶非零矩阵,|A |为A 的行列式,ij A 为ij a 的代数余子式,若ij ij a A 0(i,j 1,2,3),____A +===则(14)设随机变量Y 服从参数为1的指数分布,a 为常数且大于零,则{1|}P Y a Y a ≤+>=________。
2013年高数1(上)考题及答案
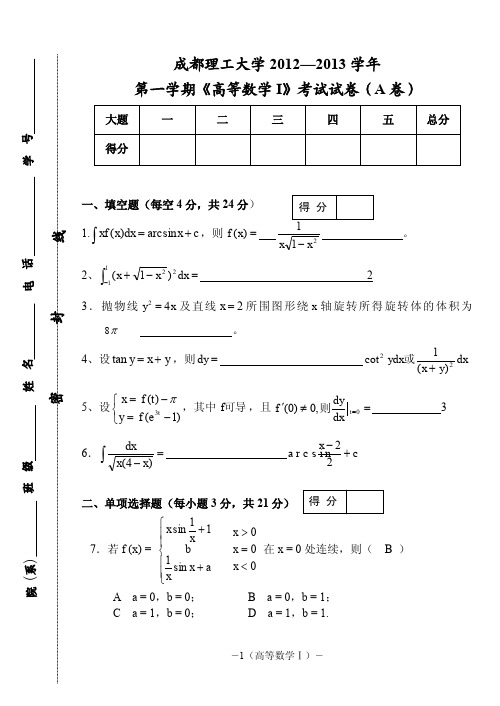
D. y C1 (e x x) C 2 (e x x) x 得 分
-2(高等数学Ⅰ)-
ቤተ መጻሕፍቲ ባይዱ
14、. 求极限 lim (sin x) x
x 0
解: (sin x) x e x ln sin x ,
lim x ln sin x lim
f ( x) 。
x ( x t ) f (t )dt 解: f ( x) e x 0
令y f ( x )
x x f (t )dt xf ( x) xf ( x) e x 0 f (t )dt 则 y' c x 0
y ' ' e x f ( x)
得 分
1 x 1 x2
。
2
3 . 抛 物 线 y2 4x 及 直 线 x 2 所 围 图 形 绕 x 轴 旋 转 所 得 旋 转 体 的 体 积 为
8
。
cot 2 ydx或 1 dx ( x y) 2
4、设 tan y x y ,则 dy
x f (t ) dy 5、设 ,其中 f可导 ,且 f (0) 0, 则 3t dx y f (e 1)
x0 x 0 在 x = 0 处连续,则( B ) x0
B a = 0,b = 1; D a = 1,b = 1.
-1(高等数学Ⅰ)-
8、当 x 0 时,下列各式中不成立的是( (A) sin x 2 ~ x 2 ; (C) e 2 x 1 ~2 x ; 9、曲线 y xe (D )
(A)没有渐近线 (C)仅有斜渐近线
11、设 f ( x)具有二阶连续导数,且 f (1) 0, lim A. f (1)是f ( x)的极大值
自考高等数学000202013年1月真题答案详解1

绝密★ 考试完毕前全国2013年1月高等教化自学考试高等数学(一)试题课程代码:00020试卷总体分析:试卷详Array解:请考生按规定用笔将全部试题的答案涂、写在答题纸上。
选择题局部留意事项:1.答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题 纸”的相应代码涂黑。
错涂、多涂或未涂均无分。
1.设函数()21f x x x +=+,贝f(x)=A. x (x+1) B .x (x-1) C. (x+1) (x-2) D .(x-1) (x+2) 答案:B学问点:复合函数2.若x →0时函数f (x )为x 2的高阶无穷小量,则20()lim x f x x→= A .0 B .12C .1D .∞答案:A学问点:无穷小量的比拟解:依据高阶无穷小量的定义20()lim x f x x→=0. 3.设函数()()2931f x x x x =++,则高阶导数()(12)f x = A .12! B .11! C .10! D .0 答案:D学问点:高阶导数 4.曲线23xy x=+ A .仅有铅直渐近线 B .仅有程度渐近线 C .既有程度渐近线又有铅直渐近线 D .无渐近线答案:B学问点:曲线的渐近线5.设函数f (x )连续,()()d ax x tf t t Φ=⎰,则()x 'Φ=A . x f (x )B .a f (x )C .-x f (x )D .-a f (x ) 答案:C学问点:变限积分的导数 解:()()'()()d 'ax x tf t txf x Φ==-⎰非选择题局部留意事项:用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2013年10月全国自考《高等数学(一)》试题和答案

绝密★考试结束前全国2013年10月高等教育自学考试高等数学(一)试题课程代码:00020请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分注意事项:1. 答题前,考生务必将自己的考试课程名称、姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2. 每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试题卷上。
一、单项选择题(本大题共10小题,每小题3分,共30分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题纸”的相应代码涂黑。
错涂、多涂或未涂均无分。
1.下列等式成立的是【B】A.(e x)2=2x e B.(e x)2=e2xC.e2x D.e x2.下列函数为偶函数的是【A】A.y=x sin x B.y=x cos xC.y=sin x+cos x D.y=x(sinx+cos x)3.极限22x3x9limx2x3→---=【C】A.0 B.2 3C.32D.924.函数f(x)=1xe x 1-的所有间断点是【D 】A .x=0B .x=1C .X=0,x=-1D .x=0,x=15.设函数f(x)=arctan(x 2),则导数f (1)'=【C 】 A .-1 B .0 C .1D .26.某产品产量为q 时总成本C(q)=1100+2q 1200,则q=1200时的边际成本为【D 】A .0B .12C .1D .27.已知函数f(x)=ax 2-4x+1在x=2处取得极值,则常数a=【B 】 A .0 B .1 C .2 D .38.极限2x 0x ln(x 1)lim x→-+=【C 】A .-12B .0C .12D .19.若f(x)是g(x)的一个原函数,则下列选项正确的是【B 】 A .f (x)dx ⎰=g(x)+c B .g(x)dx ⎰=f(x)+c C .f (x)dx ⎰=g(x)D .g(x)dx ⎰=f(x)10.设函数z=ln(x 2+y 2),则z zx y∂∂+∂∂=【A 】 A .222(x y)x y ++ B .222(x y)x y -+ C .22x y x y++D .22x y x y-+非选择题部分注意事项:用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2013~2014年全国自考概率论与数理统计试题及答案要点

全国2013年1月高等教育自学考试概率论与数理统计(经管类)试题一、单项选择题(本大题共10小题,每小题2分,共20分)二、填空题(本大题共15小题,每小题2分,共30分)三、计算题(本大题共2小题,每小题8分,共16分)四、综合题(本大题共2小题,每小题12分,共24分)五、应用题(10分)全国2013年1月高等教育自学考试 概率论与数理统计(经管类)答案1、本题考查的是和事件的概率公式,答案为C.2、解:()()(|)1()()P B AB P AB P B AB P AB P AB ⋂===()()()0.50.15(|)0.5()()1()0.7P BA P B P AB P B A P B P A P A --=====- ()()0.15(|)0.3()()()0.5P B AB P AB P AB B P A P B P B ⋂=====()()(|)1()()P A AB P AB P A AB P AB P AB ⋂=== ,故选B.3、解:本题考查的是分布函数的性质。
由()1F +∞=可知,A 、B 不能作为分布函数。
再由分布函数的单调不减性,可知D 不是分布函数。
所以答案为C 。
4、解:选A 。
{||2}{2}{2}1{2}{2}1(2)(2)1(2)1(2)22(2)P X P X P X P X P X >=>+<-=-≤+<-=-Φ+Φ-=-Φ+-Φ=-Φ 5、解:因为(2)0.20.16P Y c ===+,所以0.04c =又(2)10.80.20.02P X c d ==-==++,所以10.020.040.14d =--= ,故选D 。
6、解:若~()X P λ,则()()E X D X λ==,故 D 。
7、解:由方差的性质和二项分布的期望和方差:1512(1)()()3695276633D X Y D X D Y -+=+=⨯⨯+⨯⨯=+= ,选A8、解:由切比雪夫不等式2(){|()|}1D X P X E X εε-<>-,可得21600{78008200}{|8000|200}10.96200P X P X <<=-<>-= ,选C 。
13年专升本高数真题答案

共 7 页,第 1 页2013年河南省普通高等学校选拔优秀专科毕业生进入本科阶段学习考试高等数学 答案及解析一、选择题(每小题2分,共60分)1.答案:C【解析】:易知,需满足,即,故应选C.⎩⎨⎧>-≤≤-0111x x 21≤<x 2.答案:D【解析】:因为,则,,故应选D.1()1f x x =-()[]x x x x f f 11111-=--={}[()]f f f x =()[]x xx x f f =--=1113.答案:B【解析】:因为为奇函数,则也为奇函数,应选B.()x x -+21ln )y x =-∞<<+∞4.答案:B 【解析】:因为,故是的可去间断点,应选B.22lim 2sin lim 00==→→xxx x x x 0x =()f x 5.答案:A【解析】:当时,,则与是等价无穷小0x →()1112lim 11lim00=-++=--+→→x x x xxx x x x x x --+11x 量,应选A.6.答案:C【解析】:因,应选C.0()()lim x f x g x x →--=()()()()()()()()b a x x g g x f x f x x g g f x f x x x +=--+-=--+-→→→0lim 0lim 00lim 0007.答案:B【解析】:因为曲线,则,故对应点处的法线cos (0,0)sin x a t a b y b t=⎧>>⎨=⎩t a b t a t b dt dx dt dy dx dy cot sin cos //-=-==4π=t 斜率为,应选B.ba8.答案:D【解析】: 因为,则,应选D.()()f x g x '=2d (sin )f x =()()xdx x g xdx x x f 2sin sin cos sin 2sin 22='9.答案:A【解析】:设函数具有任意阶导数,且,则;()f x 2()[()]f x f x '=()()()()[]322x f x f x f x f ='='';()()[]()()[]42!332x f x f x f x f ='⨯='''()()()[]()()[]534!4432x f x f x f x f ='⨯⨯=()()n f x =1![()]n n f x +10.答案:A【解析】:方程两边对求导,其中看作的函数,,所以x yxy e+=y x y ()1+'⋅=+'+x ex y x yx ,应选A.()()11--=--=--=='++x y y x y xy xy x y e e x dy dx x y x y x 11.答案:B【解析】:因为,则在上单调增加,应选B.()0(0)f x x a ''><<()f x '[0,]a 12.答案:A【解析】:点是曲线的拐点,则,故,应选A.(0,1)32y x bx c =++()()00,10=''=y y 0,1b c ==13.答案:A【解析】:因为,则2216x y x x +=+--()()3221-+++=x x x ;;()()543221lim 621lim 222=⎪⎪⎭⎫ ⎝⎛-+++=⎪⎭⎫ ⎝⎛--++-→-→x x x x x x x x ()()∞=⎪⎪⎭⎫ ⎝⎛-+++=⎪⎭⎫ ⎝⎛--++→→3221lim 621lim 323x x x x x x x x 故是曲线的垂直渐近线,应选A.3=x 14.答案:B【解析】: 因为,则,故应选B.()xxf x e e -=-()()C e e dx e ex F x x x x++=-=--⎰15.答案:D【解析】: 根据不定积分的相关性质,易知,正确,应选D.22d ()d ()d f x x f x x =⎰16.答案:D【解析】:因为为奇函数,故,应选D.x x sin 20sin 2=⎰-dx x x ππ17.答案:A 【解析】:方程两边对求导,得,则,故221()d x x f t t xe ++=⎰x ()x x xe e x f +++=+222()()x x e x e x f 2-+=,应选A.()f x '=x xe 18.答案:C【解析】:由P 无穷广义积分的结论可知,应选C.19.答案:B【解析】:微分方程的阶数是指微分方程中最高导数的阶数,应选B.20.答案:B【解析】:对方程分离变量,得,两边积分,得,代入,2d 2d 0y xy x -=xdx y dy 22=C x y+=-21(1)1y =-,故方程的特解是,应选B.0=C 21y x -=21.答案:C【解析】:向量的方向角需满足,应选C.1cos cos cos 222=++γβα22.答案:B【解析】:直线的方向向量与平面法向量平行,故与垂直相交,应选B.L π23.答案:D【解析】:缺少变量的二次曲面方程为柱面,应选D.共 7 页,第 3 页24.答案:C 【解析】:,应选C.0x y →→=()()41421lim 42lim 0000-=++-=++-→→→→xy xy xy xy y x y x 25.答案:B【解析】:因为,则22(,23)z fx y x y =-+zy∂=∂1223yf f ''-+26.答案:A 【解析】:因为为X 型积分,则交换积分次序后,Y 型积分的2 22 00 2d (, )d (, )d x I x f x y y x f x y y =+⎰⎰⎰积分区域为:,故可以化为,应选A.(){}282,20,y x y y y x -≤≤≤≤I 2d (, )d y f x y x ⎰⎰27.答案:C 【解析】: 积分,应选C. 122 01d d x x y y =⎰⎰21213121210321102=⋅=⋅⎰⎰x x ydy dx x 28. 答案:D【解析】:参数方程,则,应L ()10,2≤≤⎩⎨⎧==y yy y x 22d d Lxy x x y +=⎰[]1522105141042===+⋅⋅⎰⎰y dy y dy y ydy y y 选D.29.答案:C 【解析】:因为,则收敛半径,收敛区间为,应选C.121lim lim 1=++=∞→+∞→n n u u n n n n 1=R (1,1)-30.答案:A【解析】:A 为交错级数,且单调递减,,故收敛;B 、C 中,11+n 011lim=+∞→n n 111sinlim ,1111ln lim ==⎪⎭⎫ ⎝⎛+∞→∞→nn n n n n 且发散,故B 、C 均发散;D 中,故D 发散;应选A.∑∞=11n n∞=∞→!lim n n nn 二、填空题(每小题2分,共20分)31.答案:既不充分也不必要【解析】:函数在点有定义与极限存在没有关系,故为既不充分也不必要()f x 0x 0lim ()x x f x →条件.32.答案:32【解析】:因为,故.2331lim --∞→==⎪⎭⎫⎝⎛-e e x p pxx p =3233.答案:21【解析】:因为函数为连续函数,则,得,故.()()a x x a a a e x axx =+-=-+-→→2cos lim ,1lim 0a a =-121=a 34.答案:32x -【解析】:因为,则,故.421f x x ⎛⎫=⎪⎝⎭()21x x f =()32x x f -='35.答案:C x x ++sin 2ln 【解析】:2cos d 2sin x x x x +=+⎰()Cx x x x x x d ++=++⎰sin 2ln sin 2sin 236.答案:π32【解析】:,则.21221,cos -=⋅-=⋅⋅>=<→→→→→→ba ba b a 32,π>=<→→b a 37.答案:1-+=-xCex y 【解析】:由一阶线性微分方程的通解公式得,.()1-+=+=⎪⎭⎫ ⎝⎛+⎰⎰=---⎰⎰xxxdx dx Cex C dx xe e C dx xe e y 38.答案:-5【解析】:令,则,将代入方程,则,()xyz z y x y x F 22,-++=xy F yz F z x 21,21-='-='1,0==y x 2-=z 故.52121101010-=---=''-=∂∂======y x y x z x y x xyyz F F xz39.答案:542=-+z y x 【解析】:令,故点处的切平面法向量,故切()1,2,2,,,22-='='='-+=z y x F y F x F z y x z y x F ()5,2,1{}1,4,2-平面方程为,即.()()()052412=---+-z y x 542=-+z y x 40.答案:()()nn n n x 44101-⋅-∑∞=+【解析】:.()()()()∑∑∞=+∞=--=⎪⎭⎫ ⎝⎛--=-+⋅=-+==010441441414411414411n nn n nn n x x x x x x f 三、计算题(每小题5分,共50分)41..011lim ln(1)x x x →⎡⎤-⎢⎥+⎣⎦共 7 页,第 5 页【解析】:原式=.()()()()21211lim 2111lim 1ln lim 1ln 1ln lim 200200-=+-=-+=-+=+-+→→→→x x x x x x x x x x x x x x42.已知函数由方程所确定,求.()x x y =arctanyx=d d x y 【解析】:方程两边同时对求导,可知,,即y 2222222222111yx y x x yx x x y x xy ++'⋅+='-⋅+,故.2222y x y x x y x x y x ++'=+'-d d xy yx yx y x x y x x +-=+'-='=2243.求不定积分.x ⎰【解析】:.Cx x x x C t t t t dt tt t t dtt t t t tdt dx x tx tdt dx ++-=++-⋅=+-+-⋅=+-⋅==⎰⎰⎰⎰==arctan arctan arctan arctan 111arctan 1arctan arctan arctan 22222222244.设,求.21,0(),0x x x f x e x ⎧+≤⎪=⎨>⎪⎩31(2)d f x x -⎰【解析】:.()()()e e t t dt e dt t dt tf dx x f ttt x +=+⎪⎪⎭⎫ ⎝⎛+=++==----=-⎰⎰⎰⎰313121013100121131245.求微分方程的通解.23xy y y e '''+-=【解析】:原方程对应的齐次方程为,则特征方程为,特征根为,02=-'+''y y y 0122=-+r r 21,121=-=r r 故原方程对应的齐次方程的通解为.又知不是特征根,则原方程的()为任意常数2121211,,C C e C eC y x x+=-1=λ特解可设为,代入原方程可得,即,故原方程的通解为xAe y =*xxxxe Ae Ae Ae 32=-+23=A .x x xe eC e C y 232121++=-46.设,求全微分.2+sin2+xyu x y e =d u 【解析】:方法一:由题意可知,所以,2cos 2,2xy xy xe y yu ye x x u +=∂∂+=∂∂.()()dy xe y dx ye x dy yudx x u du xy xy +++=∂∂+∂∂=2cos 22方法二:对等式两边同时求微分,可知.()()()()dyxe y dx ye x ydx xdy e ydy xdx xy d e ydy xdx de y d dx du xy xy xy xy xy +++=+⋅++=++=++=2cos 222cos 222cos 222sin 247.一平面过点且平行于向量和,求此平面方程.(1,0,1)-{2,1,1}a =-{1,1,2}b =- 【解析】:由题意可知,所求平面平行于向量和,则所求平面的法向量,即{2,1,1}a =-{1,1,2}b =- →→→⨯=b a n ,又知平面过点,由平面的点法式方程可知,平面方{}3,5,135211112--=--=--=⨯=→→→→→→→→→k j i kj ib a n (1,0,1)-程为,即.()()01351=+---z y x 435=--z y x 48.计算,其中是由所围成的闭区域.d d xyDex y ⎰⎰D 1,,2,0y y x y x ====【解析】:由题意可知,如图所示,该区域为Y 型区域,则.d d x yDe x y ⎰⎰()()()1232112122121021-=-=-=⎪⎪⎭⎫ ⎝⎛==⎰⎰⎰⎰e y e dy e y dy ye dx e dy y y x yyx 49.计算积分,其中为曲线上从点到点2222(210)d (215)d Lx xy y x x xy y y +-++--+⎰L cos y x =π,02A ⎛⎫ ⎪⎝⎭一段弧.π,02B ⎛⎫- ⎪⎝⎭【解析】:由题意可知,,则()()152,,102,2222+--=+-+=y xy x y x Q y xy x y x P ,即,说明该曲线积分与积分路径无关,选取直线路径y x x Q y x y P 22,22-=∂∂-=∂∂xQy P ∂∂=∂∂,故⎪⎭⎫ ⎝⎛-→=22:,0ππx y .2222(210)d (215)d Lxxy y x x xy y y +-++--+⎰()ππππππ1012103103222232--=⎪⎪⎭⎫ ⎝⎛+=+=⎰--x x dx x 50.求幂级数的收敛域.0(1)2(1)nn n x n ∞=-+∑【解析】:该幂级数的为非标准不缺项的类型,令,则原幂级数可变形为,因为t x =-1()∑∞=+012n n nn t ,则幂级数的收敛半径为,故幂级数的收敛区间()()2221121lim lim11=++=+∞←+∞←n n u u n n n n nn ()∑∞=+012n nn n t 2=R ()∑∞=+012n n n n t 为;()2,2-当时,级数收敛;当时,级数收敛发散;2-=t ()()∑∞=+-011n n n 2=t ()∑∞=+011n n共 7 页,第 7 页则幂级数的收敛域为,故原幂级数的收敛域为.()∑∞=+012n n n n t [)2,2-0(1)2(1)nn n x n ∞=-+∑[)3,1-四、应用题(每小题6分,共12分)51.某房地产公司有50套公寓要出租,当月租金定为2000元时,公寓会全部租出去,当月租金每增加100元时,就会多一套公寓租不出去,而租出去的公寓每月需花费200元的维修费,试问租金定为多少可获得最大收入?最大收入是多少?【解析】:设租金定位元时,收入为,则,即x ()x S ()()200100200050-⎪⎭⎫⎝⎛--=x x x S ,令,得唯一的驻点,又知()()2000,14000721002≥-+-=x x x x S ()07250=+-='x x S 3600=x ,则为的极小值点,结合实际情况,也就是对应的最大值,所以当租金定位3600()0501<-=''x S 3600=x ()x S 元时,有最大收入,最大收入为115600元.52.曲线,直线以及轴围成一平面图形,试求平面图形绕轴旋转一周所得旋转体3(0)y x x =≥2x y +=y D D y 的体积.【解析】:由题意可知,如图所示,该区域为X 型区域,则体积=.()()ππππ151453222221053214213=⎪⎪⎭⎫ ⎝⎛--=--=--⎰⎰x x x dx x x x dx x x x 五、证明题(8分)53.设在区间上连续,且,证明:方程在区间(0,1)内有且仅有一个实根.()f x [0,1]()1f x <02()d 1xx f t t -=⎰【证明】:存在性:令,因为在区间上连续,则在区间上()()[]1,0,120∈--=⎰x dt t f x x F x()f x [0,1]()x F [0,1]也连续,而且,由零点定理可知,在区间(0,1)内至少存在一点()()()()()1,011,1010<>-=-=⎰x f dt t f F F ξ,使得;()0=ξF 唯一性:因为,则在区间(0,1)内单调递增,故方程在()()()()1,02<>-='x f x f x F ()x F 02()d 1xx f t t -=⎰区间(0,1)内至多有一实根;综上所述,方程在区间(0,1)内有且仅有一个实根.2()d 1xx f t t -=⎰。
(2008—2013)自考全国卷高等数学(一)试题及部分答案大全(1)

全国2008年1月高等教育自学考试高等数学(一)试题课程代码:00020一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列区间中,函数f (x)= ln (5x+1)为有界的区间是( C )A.(-1,51)B.(-51,5)C.(0,51) D.(51,+∞) 2.设函数g (x)在x = a 连续而f (x) = (x-a)g(x),则'f (a) =( D ) A.0 B.g '(a) C.f (a)D.g (a)3.设函数f (x)定义在开区间I上,∈0x I ,且点(x 0, f (x 0) )是曲线y= f (x)的拐点,则必有( B ) A.在点(x 0,f (x 0))两侧,曲线y=f (x)均为凹弧或均为凸弧. B.当x<x 0时,曲线y=f (x)是凹弧(或凸弧), 则x>x 0时,曲线y=f (x)是凸弧(或凹弧). C.x<x 0时,f (x)<f(x 0) 而x>x 0时,f(x)>f(x 0). D.x<x 0时,f (x)>f(x 0) 而x>x 0时,f(x)<f(x 0).4.设某商品的需求函数为D(P)=475-10P-P 2,则当P = 5时的需求价格弹性为( A ) A. B. C.100 D.-1005.无穷限积分⎰+∞xe -x dx =( B )21 D.21 二、填空题(本大题共10小题,每小题3分,共30分) 请在每小题的空格中填上正确答案。
错填、不填均无分。
y =x1x1-+的定义域是___________. 0lim→h h3x )h x (33-+=___________. 0x lim →2xx2cos 1-=___________. 9.已知某商品的成本函数为C(q )=20 -10q+q 2(万元),则q =15 时的边际成本为___________.10.抛物线y = x 2上点(2,4)处的切线方程是___________.⎰=+)x 1(x dx___________.331xx dx +⎰=___________.xydx+2x 1-dy = 0的通解是___________. 14.设z = arctan (xy),则xz∂∂=___________. 15.dx⎰1⎰+122x xxydy=___________.三、计算题(一)(本大题共5小题,每小题5分,共25分) 16.设y = xarctanx-ln 2x 1+,求y ''(1) 17.求极限x cos 1120x )x 1(lim -→+⎰dx xx ln19.计算定积分I=⎰π20( sin x -sin 3x )dx20.设z = z (x,y)是由方程x 2-z 2+lnzy=0确定的函数,求dz 四、计算题(二)(本大题共3小题,每小题7分,共21分) y = x 2x ,求y '' I=dx x21x21210⎰+- 23.计算二重积分I =⎰⎰σD22d y x ,其中D 是由直线x = 2,y = x 和双曲线xy = 1围城的区域 . 五、应用题(本大题共9分)24.求内接于半径为R 的半圆而周长最大的矩形的各边边长. 六、证明题(本大题共5分)25.证明:当函数y = f (x)在点 x 0 可微,则f ( x )一定在点x 0可导.全国2008年7月高等教育自学考试高等数学(一)试题课程代码:00020一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
2013数学一真题及答案

2013硕士研究生入学考试数学一真题及答案解析来源:文都教育1. 已知极限0arctan lim kx x xc x→-=,其中k ,c 为常数,且0c ≠,则()4.设221:1L x y +=,222:2L x y +=,223:22L x y +=,224:22L x y +=为四条逆时针方向的平面曲线,记33()(2)(1,2,3,4)63ii L yxI y dx x dy i =++-=⎰ ,则{}1234ma x ,,,I I I I =A. 1IB. 2IC. 3I D 4I答案:D解析:由格林公式,22(1)2iiD yI xdxdy=--⎰⎰ 14D D ⊂,在4D 内22102yx-->,因此14I I <2222222(1)(1)(1)yyyI x dxdy x dxdy x dxdy=--=--+--⎰⎰⎰⎰⎰⎰∴Ab i =C i .即C 的列向量可由A 的列表示. ∵AB=C ∴A=CB -1=CP .同理:A 的列可由C 的列向量表示.6.矩阵1111a ab a a⎛⎫⎪ ⎪ ⎪⎝⎭与2000000b ⎛⎫⎪⎪ ⎪⎝⎭相似的充分必要条件为( ) A. 0,2a b == B. 0,a b = 为任意常数{}2P Y c>=( )答案:A 解:~(1)~()Y F n t n ∴,2()).p Y c p c α>=>=9.设函数y=f(x)由方程y-x=e x(1-y) 确定,则01lim [()1]n n f n→-= 。
答案:1 解:令X =0,得y =1.12.21(1)dx x =+⎰。
答案: ln2解:2111ln ln (1)1(1)x x dx dx x xx x+∞+∞+∞=-++++⎰⎰=0+1ln1x x+∞+=0-ln1ln 2.2=13.设A=(a ij )是3阶非零矩阵,A 为A 的行列式,A ij 为a ij 的代数余子式.若a ij +A ij =0(i ,j=1,2,3),则|A |= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问如何使用两种原料方可使电能消耗达到最低,并求此时的最低能耗. 解: N = x + 2 xy + 2 y − 4 x − 6 y + 105 ,分别取
2 2
∂N = 2x + 2 y − 4 = 0 , ∂x
∂N ∂2 N ∂2 N = 2 x + 4 y − 6 = 0 ,得 x = 1 , y = 1 . A = 2 = 2 > 0 , B = = 2, ∂y ∂x ∂x∂y
tf (t )dt ,则 Φ′( x) =
C. − xf ( x ) D. − af ( x )
பைடு நூலகம்
B. af ( x )
∫
a x
tf (t )dt ,则 Φ′( x) = − xf ( x ) . 选(C).
非选择题部分
注意事项: 用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上. 二、填空题(本大题共 10 小题,每小题 3 分,共 30 分) 6.设函数 f ( x ) = lg
孙久厚教授
全国高等教育自学考试高等数学(一)试题及解答
sunjh@
11.极限 lim
sin x = _______. x → 0 (1 + x) ln( 1 + x)
解: lim
x →0
sin x sin x = lim = 1. x → 0 (1 + x) x (1 + x) ln(1 + x)
x3 1 x4 2 = ,则 f (0) = 0 , f ′( x) = − 1 + x , 3 1 + x2 1 + x2
当 x > 0 时, f ′( x) > 0 ,函数单调增加,则当 x > 0 时, f ( x) > f (0) = 0 ,即
arctan x > x −
x3 . 3
-5-
1
x →0
1 x →0
解: lim f ( x) = lim− (1 + 3 x) x = lim− [(1 + 3 x) 3 x ]3 = e3 , −
x →0
x →0
lim+ f ( x) = lim+ e3 cos 2 x = e3 , f (0) = e3 ,则函数 f ( x ) 在 x = 0 处连续.
解: f ( x ) = x , f ′( x ) = 2 x ,由 f ′(ξ ) =
2
1 f (1) − f (0) = 1 ,得 ξ = . 1− 0 2
10.函数 f ( x ) = x 4 − 解: f ( x ) = x 4 −
4 3 x + 1 在区间 [−1, 1] 上的最小值为_______. 3
x →0
x →0
1 . e2
2
8.某商品需求量 Q 与价格 P 的函数关系为 Q = 150 − 2 P ,则 P = 6 时的边际需求为 _______. 解: Q ( P ) = 150 − 2 P , Q′( P) = −4 P ,则 P = 6 时的边际需求为 Q′(6) = −24 .
2
2 9.函数 f ( x ) = x 在区间 [0, 1] 上满足拉格朗日中值定理的中值 ξ = _______.
4 3 x + 1 , f ′( x) = 4 x 3 − 4 x 2 ,令 f ′( x) = 0 ,得 x = 0 或 x = 1 . 3 10 2 2 f ( −1) = , f (0) = 1 , f (1) = ,函数在区间 [−1, 1] 上的最小值为 f (1) = . 3 3 3
-2-
= 2 (1 + x) 2 3
3 0 −1
+ arctan x 1 0 =
2 π + . 3 4
20. 计算二重积分 I =
∫∫ xdxdy ,其中区域 D 是由曲线
D
1 y = , y = x 2 及直线 x = 2 围成. x 1 2 解:联立解 y = x 与 y = ,得交点 (1, 1) ,则 x
18.求不定积分 xe 解: xe
∫
−2 x
∫
−2 x
dx = −
1 1 1 1 xde−2 x = − [ xe − 2 x − ∫ e − 2 x dx ] = − ( x + )e − 2 x + C . ∫ 2 2 2 2
⎧ 1 , x≥0 1 ⎪ 2 ,计算定积分 I = ∫ f ( x )dx . 19.设函数 f ( x) = ⎨1 + x −1 ⎪ 1+ x, x < 0 ⎩ ⎧ 1 , x≥0 1 0 1 1 ⎪ 2 ,则 I = ∫ f ( x )dx = ∫ 解: f ( x ) = ⎨1 + x 1 + x dx + ∫ dx −1 −1 0 1 + x2 ⎪ 1+ x, x < 0 ⎩
解: f ( x + 1) = x 2 + x = x( x + 1) = ( x + 1 − 1)( x + 1) ,则 f ( x ) = x( x − 1) . 选(B). 2.若 x → 0 时函数 f ( x ) 为 x 的高阶无穷小量,则 lim
2
x →0
f ( x) = x2
D. ∞
A. 0
2x
= y′(0) = 2 .
22.求曲线 y = xe 的凹凸区间及拐点. 解: y = xe ,得 y′ = e (1 + 2 x) , y′′ = 4e (1 + x) . 令 y′′ = 0 , 得 x = −1 , 则y=−
2x 2x 2x
1 . e2
y′′ < 0 ,得 x < −1 ,即 x ∈ (−∞, − 1) 时,曲线凸;
12. 定积分
∫
1
−1
xcosxdx = _______.
1
解: x cos x 为奇函数,则
∫
−1
xcosxdx = 0 .
13.微分方程 xy′ = y 的通解为_______. 解: xy′ = y 即 x
dy dy dx = y ,则 , ln y = ln x + ln C ,得通解 y = Cx . = dx y x
解: f ( x ) = x 2 ( x 9 + x 3 + 1) = x11 + x 5 + x 2 ,则 f (12 ) ( x ) = 0 . 选(D). 4. 曲线 y =
x 3 + x2
B.仅有水平渐近线
A.仅有铅直渐近线
-1-
孙久厚教授
全国高等教育自学考试高等数学(一)试题及解答
sunjh@
2x + 1 ,则 f ( x ) 的定义域为_______. 7 2x + 1 1 解: f ( x ) = lg ,则 f ( x ) 的定义域为 2 x + 1 > 0 ,得 x > − . 7 2
1 2 x2
7. 极限 lim(1 − 2 x )
x →0
1
2
= _______.
1
2
解: lim(1 − 2 x 2 ) x = lim[(1 − 2 x 2 ) − 2 x ]− 2 = e − 2 =
x
14.若
∫
f ( x)dx = 3e 3 + C ,则 f ( x) = _______.
x x x
解:
∫
f ( x)dx = 3e 3 + C ,则 f ( x) = (3e 3 + C )′ = e 3 .
y
15. 设函数 z = e sin( x − y ) ,则 解: z = e sin( x − y ) ,则
dy 1+ x 1 − arctanx 2 ,求 dx 1− x 2
x =0
.
1 − x 1 ⋅ (1 − x) − (1 + x)(−1) 2x 1+ x 1 , − ⋅ − arctanx 2 ,则 y′ = 2 1+ x (1 − x) 2(1 + x 4 ) 1− x 2
x =0
dy 2 x ,则 − 2 4 1− x 1+ x dx
B.
1 2
2
C. 1
解:当 x → 0 时函数 f ( x ) 为 x 的高阶无穷小量,则 lim
x→0
f ( x) = 0 . 选(A). x2
3.设函数 f ( x ) = x 2 ( x 9 + x 3 + 1) ,则高阶导数 f (12 ) ( x ) = A. 12! B. 11! C. 10! D. 0
-4-
孙久厚教授
全国高等教育自学考试高等数学(一)试题及解答
sunjh@
y′′ > 0 ,得 x > −1 ,即 x ∈ (−1, + ∞) 时,曲线凹. 拐点为 (−1, −
23.计算定积分 I =
1 2 0
1 ). e2
∫
1 2 0
x 1 − x2
dx .
1 0 2
解: I =
∫
1 12 1 dx = − ∫ d(1 − x 2 ) = − 1 − x 2 2 2 0 2 1− x 1− x x
=1−
2 . 2
五、应用题(本题 9 分) 24. 设某企业生产一定量的某产品时可用两种原料, 第一种为 x (千吨), 第二种为 y (千吨), 其电能消耗量 N (万度)与两种原料使用量的关系为 N = x + 2 xy + 2 y − 4 x − 6 y + 105 ,
