实验六--自相关模型的检验和处理-学生实验报告
自相关实验报告

自相关实验报告摘要本实验旨在探究自相关的概念及其在信号处理和时间序列分析中的应用。
通过使用不同的信号样本进行自相关分析,我们可以了解信号之间的相关性以及信号的周期性特征。
本实验使用了Python编程语言进行实现,并使用Markdown文本格式进行输出。
引言自相关是信号处理和时间序列分析中常用的一种方法,用于描述信号的相关性和周期性。
自相关分析可以帮助我们了解信号在不同时间点之间的相关程度,以及寻找信号的周期性特征。
在信号处理领域,自相关常常用于信号的匹配和识别。
在时间序列分析中,自相关可以帮助我们了解时间序列数据的趋势和周期性变化。
因此,掌握自相关分析方法对于理解和应用信号处理和时间序列分析领域的研究具有重要意义。
实验步骤1. 生成信号样本首先,我们需要生成用于自相关分析的信号样本。
在本实验中,我们使用Python的NumPy库生成包含不同频率和振幅的信号样本。
import numpy as np# 生成信号样本def generate_signal(frequency, amplitude, duration, sampling_rate):time = np.arange(0, duration, 1 / sampling_rate) signal = amplitude * np.sin(2 * np.pi * frequency * time)return signal# 设置信号参数frequency = 10 # 频率为10Hzamplitude = 1 # 振幅为1duration = 5 # 信号时长为5秒sampling_rate = 1000 # 采样频率为1000Hz# 生成信号样本signal = generate_signal(frequency, amplitude, duratio n, sampling_rate)2. 计算自相关计算信号样本的自相关函数可以帮助我们分析信号的周期性,并找到信号中的重复模式。
实验六 自相关

实验六自相关6.1 实验目的掌握自相关问题出现的来源、后果、检验及修正的原理,以及相关的EViews 软件操作方法。
6.2 实验内容以实验五已克服异方差的中国的消费函数模型(见输出结果图 5.4)为例,练习检查和克服模型的自相关的操作方法。
由图5.4得到的回归式为:Lny t = -0.0486+ 0.9561 Lnx t . (6.1) (-0.05) (68.7) R2 = 0.997, DW=0.55 F = 47216.3 实验步骤6.3.1 检验模型是否存在自相关(1)观察残差图,如图6.1,可初步判断残差项存在一定程度的正自相关。
(2)用DW检验判断是否存在自相关由EViews输出结果(图5.4)知DW = 0.55,若给定α = 0.05,查附表,d L= 1.08,d U= 1.36。
因为DW = 0.55< 1.26, 依据判别规则,认为误差项u t存在严重的正自相关。
图6.1(3)用LM检验判断是否存在自相关在估计窗口选择View/Residual Tests/Serial Correalation LM Test(见图6.2)。
图6.2点击后会自动弹出一个设定滞后期(Lag Specification)对话框。
输入1,点击OK键,得到LM检验结果,见图6.3。
图6.3根据p-值判断拒绝原假设,所以BG(LM)检验结果也说明(6.1)式存在自相关。
(4)用回归检验法判断自相关① 将估计结果(6.1)式得到的残差定义为u t ,首先做一阶自回归,得到估计结果见图6.4。
② 对该估计式采用LM 检验法检验其自相关性,如图6.5。
可以判断出仍然存在自相关。
③ 用残差的二阶自回归形式重新建立模型,见图6.6。
④ 再次用LM 检验法判断其自相关性,如图6.7。
从图6.7可以看出,此时p -值已经达到0.3,落在接受域,即认为误差项不存在自相关。
对图6.6的输出结果进行整理,可以得到残差的二阶回归式为t uˆ= 1.3436 1ˆ-t u - 0.81752ˆ-t u + v t (6.2)(5.18) (-3.03) R 2 = 0.71, s.e. = 0.02, TR 2 = 1.1图6.4图6.5图6.6图6.7 6.4.2 克服自相关图6.8图6.9用广义最小二乘法估计回归参数。
自相关性实验报告心得

自相关性实验报告心得
在时间序列分析中,自相关性是一项非常重要的概念,用于判断时间序列中数据点之间的相关性程度。
自相关性实验能够帮助我们更好地掌握时间序列数据的本质和规律,从而更好地进行预测和分析。
实验中,通过使用自相关性函数ACF和偏自相关性函数PACF图表,可以很清晰地看到时间序列数据中自相关性的程度,并进一步分析数据的周期性、趋势和季节性等规律。
在进行实验时,需要注意数据量的选择和数据处理的方法,以免影响实验结果。
此外,还需要注意选择适当的自相关性和偏自相关性函数,才能更准确地分析时间序列数据的相关性。
通过自相关性实验,我深刻地认识到,时间序列分析是一项非常重要的工具,掌握它可以有效地预测未来趋势,帮助我们更好地做出决策和规划。
因此,我将继续学习和探索时间序列分析中的相关知识,不断提升自己的能力和水平。
自相关实训报告

一、实训目的本次实训旨在通过学习自相关分析的方法,掌握时间序列数据的自相关性,了解自相关分析在时间序列预测和数据分析中的应用,提高对时间序列数据的分析和处理能力。
二、实训内容1. 自相关函数(ACF)和偏自相关函数(PACF)的计算(1)选择合适的时间序列数据,例如某城市过去一年的日平均气温数据。
(2)使用统计软件(如R、Python等)计算ACF和PACF。
(3)绘制ACF和PACF图,观察其特征。
2. 自相关分析在时间序列预测中的应用(1)选取合适的时间序列预测模型,如ARIMA模型。
(2)根据ACF和PACF图,确定模型的阶数。
(3)使用统计软件对时间序列数据进行建模和预测。
(4)比较预测结果与实际数据的差异,评估模型的准确性。
3. 自相关分析在数据分析中的应用(1)选取一组相关的时间序列数据,如不同城市的日平均气温。
(2)计算各时间序列的ACF和PACF。
(3)分析各时间序列之间的自相关性,探讨其可能的影响因素。
(4)根据自相关性,提出改进措施或解决方案。
三、实训过程1. 数据准备(1)收集所需的时间序列数据,如某城市过去一年的日平均气温数据。
(2)将数据导入统计软件,进行数据清洗和预处理。
2. 自相关函数计算(1)使用统计软件计算ACF和PACF。
(2)观察ACF和PACF图,确定时间序列数据的自相关性特征。
3. 时间序列预测(1)根据ACF和PACF图,选择合适的ARIMA模型。
(2)使用统计软件对时间序列数据进行建模和预测。
(3)评估模型的准确性,并进行必要的调整。
4. 数据分析(1)计算不同时间序列的ACF和PACF。
(2)分析各时间序列之间的自相关性,探讨影响因素。
(3)根据自相关性,提出改进措施或解决方案。
四、实训结果与分析1. 自相关函数计算结果通过计算ACF和PACF,发现所选时间序列数据的自相关性较强,且具有明显的周期性特征。
2. 时间序列预测结果使用ARIMA模型进行预测,预测结果与实际数据的差异较小,模型的准确性较高。
自相关的检验与修正

实验2自相关的检验与修正、实验目的:掌握自相关模型的检验方法与处理方法.。
、实验内容及要求:表1列出了1985—2007年中国农村居民人均纯收入与人均消费性支出的统计数据。
(1)利用OLS法建立中国农村居民人均消费性支出与人均纯收入的线性模型。
(2)检验模型是否存在自相关。
(3)如果存在自相关,试采用适当的方法加以消除。
表1 1985 —2007年中国农村居民人均纯收入与人均消费性支出(单位:元)年份全年人均纯收入(现价)全年人均消费性支出(现价)消费价格指数(1985=100)1985397.6317.42100 1986423.8357106.1 1987462.6398.3112.7 1988544.9476.7132.4 1989601.5535.4157.9 1990686.3584.63165.1 1991708.6619.8168.9 1992784659.8176.8 1993921.6769.7201 199412211016.81248 19951577.71310.36291.4 19961923.11572.1314.4 19972090.11617.15322.3 199821621590.33319.1 19992214.31577.42314.3 20002253.41670314 20012366.41741316.5 20022475.61834315.2 20032622.241943.3320.2 20042936.42185335.6 20053254.932555343 200635872829348.1实验如下:首先对数据进行调整,将全年人均纯收入和全年人均消费性支出相应调整为全年实际人均纯收入和全年实际人均消费性支出。
LIL I. .一.... U h ―................ H全年人沟地收入全年人均泊箜低立出J泊费桥特描旷全年人均实际地收/全年人枸实加寸抵性女出tMM1昭W7…6J17.4Z m35^.60 31X42恤(山妙1441斯石Mid JMJ m.T41M7ma«44J J-L7JJ2.44IL5636*05MU UU期M45W.A8州IMJ nus ltf.1Uf矽»ill14^1TlV.b他E I4B.9m到W:71417*4⑷話珊肿1W3Kl.«THL73D1 4SU1M1M喻i*ii toirn3JS49*14』I・M157TJ IJ1IU4^1.4:出紺阳阳J157!4314J«1.«750•巧2000J3t:J 5OL75[潮2U3159U331S,1491^8L9M2114J isn«314J■04J1S0LJB32WI22S3J L6TO314 71T..U531.852«1UWJ P4I JMJ卿AS1W2倔ud)m31SJ■SS.I1繩US:621.21ifl-jjj irsij UU4乂MU wn困口6.4sits»71.97izM.yj皿會埠HLN T I4.W 加?n«HU 1W負建tUMSW741 4055T43M 8iraj^171711用OLS 估计法估计参数<-□ Group; UN1TTUD Wcrldilft UNTTTLED;;UMtided\[UMr][fi&£|[Oto[jKt |ftjrtt£narrtfeJprMafe]匚][Sart|Eart£pflgj&]旦fc#^[Sapli4j 』T 程]色3y?.弓13S$ [1936 VT1937 1920 193919^?19931934 1935 1936 1037 1939 2»J0 2001 20 J 2 205J 20342035G3E?017397 5000 317.42M1399 43DO 330,«Q0 410 47DO 353.420C 411 56D0 36D.050C SSOEWDO333.0 30C416.690041^ 54J0443 44DU 375 190C 45S5100 382.340C 492.34 DO 410.0000 541 4200 443.680C 611.6700 501030C 648 50 DO 50L75M 677 53DO 4DL3SO0 704 52 DO 501 aaoo J17MOO 531 B500 747 68DO 550.080C 75541D0 M1.350C G10 94DO GO5.930C C74 97D0 esijD7oo 阳⑹0 71J.030C 1033.4S0 81Z7DOO 112R170 Q7B 71 nr也 E\ie\;&zi e Edit Object View Proc Qui:k Options Window Heipdaw Uy ciO Eq uatio n: U NTTTLED Worlcflvc UMTTTLEI>:U 般―、3. frx| JDEU |f i rure I UEUE ihstma 世 心已工竄 '曲ts KKdtCoefficientSU Error t SkteticProa.G 50.21B7S 14 548SB 3.E642100.(]0Q9KC 6969260.02134231 99373 C 0000R-gquan&10S7QQ34dep^nd&ntvarjqu Q013-etiusted R-squar?d C.978947&D, ciependeTitvar15E.3tZ3 3.El ofreer&ssion 22.97705 4<aike info cnteilori 9.1B9B13 Sun squared resic 1105B.87 Sshwa-irz. cnUnon9.2ft Log hka || hood -1026826 Hannar^Oiilrin cfit&r. 9214646 h-S^tlStlC1023.933 □urciin Batson sealU4 码rroa(r-statistic) 0.000030-i e Edit Otwect Viav Proc Quick Options 州nticm 卜口 dacg iy图2DeDerKfentA ;an3ti«: T LlEtnnd: LEastSqijarss Dats: 04/24^5 Tria: 12:32 fianph 1Q95200?ricuaec ooser/atcns 、u图4从图4中可以看出,中国农村居民人均消费性支出与人均纯收入存在着显著的正相关关系。
《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤:(只需关键步骤)
1、分析→回归→线性→保存→残差
2、转换→计算变量;分析→回归→线性。
3、转换→计算变量;分析→回归→线性
三、实验结果分析:(提供关键结果截图和分析)
1.用普通最小二乘法建立y与x1和x2的回归方程,用残差图和DW检验诊断序列的自相关性;
由图可知y与x1和x2的回归方程为:
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283,查DW表,n=23,k=2,显著性水平由DW<1.26,也说明残差序列存在正的自相关。
自相关系数,也说明误差存在高度的自相关。
分析:从输出结果中可以看到DW=0.745,查DW表,n=52,k=3,显著性水平 =0.05,dL=1.47,dU=1.64.由DW<1.47,也说明残差序列存在正的自相关。
α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。
2.用迭代法处理序列相关,并建立回归方程;
回归方程为:y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716,
查DW 表,n=52,k=3,显著性水平0.5 由此可知DW 落入无自相关性区
域,说明残差序列无自相关
3.用一阶差分法处理序列相关,并建立回归方程;
从结果中看到回归残差的DW=2.042,根据P 104表4-4的DW 的取值范围来诊断 ,误差项。
计量经济学实验报告自相关
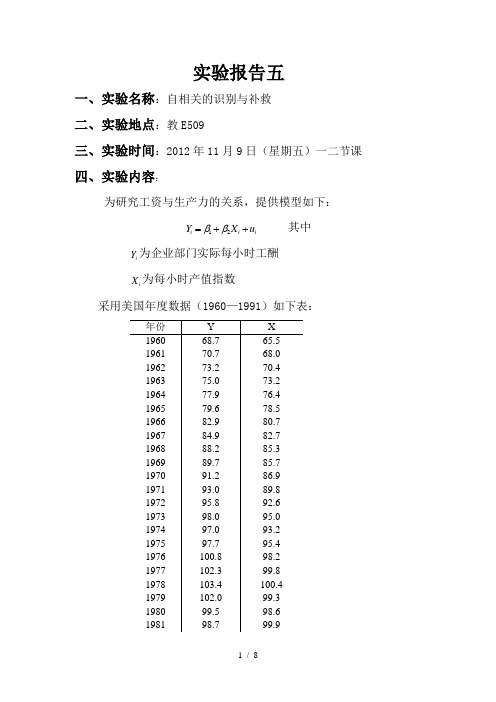
实验报告五一、实验名称:自相关的识别与补救 二、实验地点:教E509三、实验时间:2012年11月9日(星期五)一二节课 四、实验内容:为研究工资与生产力的关系,提供模型如下:12i i i Y X u ββ=++ 其中i Y 为企业部门实际每小时工酬 i X 为每小时产值指数采用美国年度数据(1960—1991)如下表:根据所给的模型与数据,利用计量经济学软件对模型参数进行估计,分析回归结果并完成以下问题:(1) 根据DW 值判断是否存在自相关,并根据上述回归残差,画出残差与时间的关系图进行验证; (2) 画出t e 与1t e -的散点图,判断自相关类型(3) 分别用d 统计量、Cochrane-Orcutt 法与Durbin 两步法估计ρ,并对回归进行修正, 比较修正结果,说明哪一种估计ρ的方法好。
五、实验目的:1. 掌握自相关的识别方法2. 能针对具体问题提出解决自相关问题的措施3. 对不同解决自相关方法的效果进行比较六、实验步骤1、建立模型: 12i i i Y X u ββ=++其中i Y 为企业部门实际每小时工酬,i X 为每小时产值指数2、运用OLS 估计方法对上式的参数进行估计,EViews 过程如下: (1)在File 菜单下选择New 项,建立文件库Workfile ,输入起始与终止时间,分别为1960和1991.(2)在File菜单下点击Import下点击Read Text-Lotus-Excel在桌面上找到Excel数据,点击打开,在Excel Spreadsheet Import对话框中的Name for series or Number if named in file输入Y x,点击OK。
(3)点击Quick菜单下的Estimate Equation,在新对话框中输入Y C x,点击确定。
会出现下面结果:3、自相关检验(1)图示法由上述OLS估计,可直接得到残差resid,运用GENR生成序列E,则在quick菜单中选graph项,在图形对话框里键入:E E(-1),可得到结果:由上表可知:残差e呈线性回归,表明随机误差u存在自相关。
实验六自相关模型地检验和处理-学生实验报告材料

廣柬財建大孕辜商李幌HUASHANG COLLEGEGUANGDONG UNIVERSITY OF FINANCE & ECONOMICS实验报告课程名称:____________ 计量经济学______________实验项目:实验六自相关模型的检验和处理实验类型:综合件口设计性口验证性专业班别:_____________________________________姓名:________________________________________ 学号:________________________________________实验课室:指导教师:石立实验日期:2014年6月13日广东商学院华商学院教务处制、实验项目训练方案实验训练内容(包括实验原理和操作步骤):【实验原理】自相关的检验:图形法检验、D-W 检验 自相关的处理:广义差分变换、迭代法【实验步骤】本实验中考虑以下模型:【模型1】财政收入CS 对收入法GDPS 的回归模型 【模型2】财政支出CZ 对财政收入CS 的回归模型 【模型3】消费品零售额SLC 对收入法GDPS 的回归模型 【模型4】财政收入的对数log (cs )对时间T 的回归模型【模型5】收入法GDPS 的对数log ( GDPS )对时间T 的回归模型 数据见“附表:广东省宏观经济数据(部分)-第六章”(一)自相关的检验1•图形法检验使用图形检验法分别检验上述 【模型1-4】是否存在自相关问题。
分别作这四个 模型的残差散点图(即残差后一项对前一项的散点图:e t 对e-)和残差趋势图(即 残差e t 对时间t 的线图),并判断模型是否存在自相关以及是正的自相关还是负的自 相关。
结论:从图上看,CS 对GDPS 回归的残差有一定的自相关。
【模型1】残差散点图残差趋势图RESID(-I)------ Residual ------------- Actual ----------- Fitted【模型2】 残差散点图 残差趋势图1500050-100 •-150-150-100 -50 0 50 100 150RESID(-I)Residual Actual Fitted结论:从图上看,CZ 对CS 回归的残差应【模型3】 残差散点图DL bE K+400-2000 200400RESID(-I)400 . 200 -0_ -200 _ -400 - -600 r------ Residual Actual --------- Fitted结论:从图上看,SLC 对GDPS 回归的残差有很强的自相关结论:从图上看,log(CS)对T 回归的残差也有很强的自相关【模型4】残差散点图DISERG-54-3. ^1-0. 10^3—.OU .2.6RESID(-1)(请对得到的图表进行处理,以上在一页内)2. D-W检验分别计算上述【模型1-3】和【模型5】的D-W统计量的值,判断模型是否存在自相关冋题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.811131
0.0000
AR(2)
-0.613537
0.174363
-3.518737
0.0019
R-squared
0.998601
Mean dependent var
7.869818
Adjusted R-squared
0.998410
S.D. dependent var
1.458838
Coefficient
Std. Error
t-Statistic
Prob.
GDPS
0.227124
0.042324
5.366357
0.0000
C
-863.1769
929.2543
-0.928892
0.3630
AR(1)
1.536140
0.186539
8.234941
0.0000
AR(2)
-0.503590
0.199972
-2.518301
0.0196
R-squared
0.999440
Mean dependent var
2323.710
Adjusted R-squared
0.999364
S.D. dependent var
2354.344
S.E. of regression
59.39227
Akaike info criterion
【模型1】残差散点图 残差趋势图
结论:从图上看,CS对GDPS回归的残差有一定的自相关。
【模型2】残差散点图 残差趋势图
结论:从图上看,CZ对CS回归的残差应
【模型3】残差散点图 残差趋势图
结论:从图上看,SLC对GDPS回归的残差有很强的自相关
【模型4】残差散点图 残差趋势图
结论:从图上看,log(CS)对T回归的残差也有很强的自相关
Dependent Variable: SLC
Method: Least Squares
Date:06/13/14Time: 11:25
Sample (adjusted): 1980 2005
Included observations: 26 after adjustments
Convergence achieved after 14 iterations
Convergence achieved after 3 iterations
Coefficient
Std. Error
t-Statistic
Prob.
T
0.183936
0.011690
15.73461
0.0000
C
5.020003
0.214241
23.43160
0.0000
AR(1)
1.470687
Prob(F-statistic)
0.000000
Inverted AR Roots
1.06
.47
Estimated AR process is nonstationary
DW检验值达到了1.717996,消除了自相关。 没有消除和消除了自相关的回归方程为: SLC=0.370241380274GDPS+148.696223954 SLC=0.227124192654GDPS-863.176882154+(AR(1)=1.5361,AR(2)=-0.5036
实验报告
课程名称:计量经济学
实验项目:实验六 自相关模型的
检验和处理
实验类型:综合性□ 设计性□ 验证性
专业班别:
姓名:
学号:
实验课室:
指导教师:石立
实验日期:2014年6月13日
广东商学院华商学院教务处 制
一、实验项目训练方案
小组合作:是□否
小组成员:无
实验目的:
掌握自相关模型的检验和处理方法
实验场地及仪器、设备和材料
实验室:普通配置的计算机,Eviews软件及常用办公软件。
实验训练内容(包括实验原理和操作步骤):
【实验原理】
自相关的检验:图形法检验、D-W检验
自相关的处理:广义差分变换、迭代法
【实验步骤】
本实验中考虑以下模型:
【模型1】财政收入CS对收入法GDPS的回归模型
【模型2】财政支出CZ对财政收入CS的回归模型
(请对得到的图表进行处理,以上在一页内)
2.D-W检验
分别计算上述【模型1-3】和【模型5】的D-W统计量的值,判断模型是否存在自相关问题。
【模型1】
CS=12.50360 +0.080296GDPS
(15.58605) (0.001891)
(0.802615) (42.45297)
R^2=0.985232 SE=61.92234 DW=0.942712 F=1802.255
11.14684
Sum squared resid
77603.71
Schwarz criterion
11.34040
Log likelihood
-140.9090
Hannan-Quinn criter.
11.20258
F-statistic
13087.46
Durbin-Watson stat
1.717996
结论:DW值偏近0,存在自相关
【模型2】
DW=1.561721
结论:DW值接近2,不存在自相关
【模型3】
DW=0.293156
结论:DW值接近0,存在很强的自相关
【模型5】
DW=0.198218
结论:DW值偏近0,存在严重的自相关
(请对得到的图表进行处理,以上在一页内)
(二)自相关的处理
1.【模型3】SLC对GDPS回归自相关的处理
S.E. of reriterion
-2.710105
Sum squared resid
【模型3】消费品零售额SLC对收入法GDPS的回归模型
【模型4】财政收入的对数log(cs)对时间T的回归模型
【模型5】收入法GDPS的对数log(GDPS)对时间T的回归模型
数据见“附表:广东省宏观经济数据(部分)-第六章”
(一)自相关的检验
1.图形法检验
使用图形检验法分别检验上述【模型1-4】是否存在自相关问题。分别作这四个模型的残差散点图(即残差后一项对前一项的散点图: 对 )和残差趋势图(即残差 对时间 的线图),并判断模型是否存在自相关以及是正的自相关还是负的自相关。
2.【模型5】LOG(GDPS)对T回归自相关的处理
Dependent Variable: LOG(GDPS)
Method: Least Squares
Date:06/13/14Time:11:26
Sample (adjusted): 1980 2005
Included observations: 26 after adjustments
