高中数学必修二《空间几何体的表面积和体积》基础练习题
高中数学(必修二)专题复习二---空间几何体的表面积与体积

65CDC'AB'A'D'高中数学(必修二)专题复习二---空间几何体的表面积与体积★热点考点题型探析【例1】有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为( )A.24πcm 2,12πcm 3B.15πcm 2,12πcm3C.24πcm 2,36πcm3D.以上都不正确侧视图变式:已知一个空间几何体的三视图如图所示,根据图中标出 的尺寸(单位:cm),可得这个几何体的体积为________cm 3.【例2】长方体的一个顶点上三条棱的长分别是3、4、5,且它的八个顶点都在同一个球面上,这个球的表面积是( )A. 202πB. 252πC. 50πD. 200π变式:某正方体的各顶点均在同一球的球面上,若该球的体积为π34,则该正方体的表面积为 .【例3】有一根长为π3cm ,底面半径为2 cm 的圆柱形铁管,用一段铁丝在铁管上缠绕1圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 厘米.变式1:有一根长为π5cm ,底面直径为3cm 的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 厘米.变式2:如图是长宽高分别为3、2、1的长方体,有一蜘蛛潜伏在A 处,C 1处有一小虫被蜘蛛网粘住,则蜘蛛沿正方体表面从A 点爬到C 1点 的最短距离为( )A 、31+B 、102+C 、23D 、32★抢分练习1.制作一个圆柱形无盖水桶,计算用多少铁皮,是求( );计算存放这只水桶用多少空间,是求( ). A. 圆柱的侧面积 B. 圆柱的底面积 C. 圆柱的表面积D. 圆柱的体积(容积)E. 圆柱的侧面积+1个圆柱的底面积 2.一个圆柱体的高不变,底面半径扩大3倍,它的体积( ). A. 扩大3倍B. 扩大6倍C. 扩大9倍D. 扩大27倍3.一个直角三角形,两条直角边分别长3厘米和5厘米,如果分别以这两条直角边为轴所在直线旋转一周后可以得到两个圆锥,这两个圆锥的体积( )A. 以3厘米直角边为轴得到的圆锥体积大B. 一样大C. 以5厘米直角边为轴得到的圆锥体积大D. 无法比较4.柱体和一个圆锥体的底面半径和高都相等,如果圆柱体体积是30立方厘米,圆锥体体积是( )立方厘米;如果圆锥体体积是30立方厘米,圆柱体体积是( )立方厘米. A. 10B. 15C. 30D. 60E. 905.如果两个球的体积之比为8:27,那么两个球的表面积之比为( ) A.8:27 B. 2:3 C.4:9 D. 2:96. 棱长都是1的三棱锥的表面积为( ) A.3 B. 32 C. 33 D. 347.正方体的内切球和外接球的半径之比为( )A B 2 C .23 8.正四棱锥的高为6,侧棱长为8,则棱锥的底面边长为( )A. B. D.9.已知圆锥的表面积为a ,且它的侧面展开图是圆心角为32π的扇形,则圆锥的底面半径为( ) A.2aπ B.ππ2a C. ππa D. ππa 10.若一个球的半径扩大2倍时,则球的表面积扩大______倍,体积扩大_____倍.11.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_______厘米.12.若一个六棱锥的高为10cm,底面是边长为6cm 的正六边形,则这个六棱锥的体积为 . 13.圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成︒60角,则圆台的侧面积为_______.14.四边形ABCD 中,)0,0(A ,)0,1(B ,)1,2(C ,)3,0(D ,绕y 轴旋转一周,则所得旋转体的体积为_______.★能力提高1.(1)若一个长方体的共顶点的三个面的面积分别为3,5,15,则它的体积为________;(2)若一个长方体的共顶点的三个面的面积分别是2、3、6,这个长方体的对角线长是______.2.将一圆形纸片沿半径剪开为两个扇形,其圆心角之比为3∶4. 再将它们卷成两个圆锥侧面,则两圆锥的高之比为( )A .3∶4B .9∶16C .27∶64D .都不对3.已知三棱锥S —ABC 的三条侧棱两两垂直,SA =5,SB =4,SC =3,D 为AB 中点,E 为AC 中点,则四棱锥S —BCED 的体积为_______.4.三棱柱111C B A ABC 的侧棱垂直于地面,其高为cm 6,底面三角形的边长分别为cm cm cm 5,4,3,以上,下底面的内切圆为底面,挖去一个圆柱,求剩余部分形成的几何体的体积.5.如图,在底半径为2,母线长为4的圆柱,求圆柱的表面积.6.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12m ,高4m ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4m (高不变);二是高度增加4m (底面直径不变).(1) 分别计算按这两种方案所建的仓库的体积; (2) 分别计算按这两种方案所建的仓库的表面积; (3) 哪个方案更经济些?33 2正视图 侧视图俯视图链接高考1.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h= cm.第1题 第2题 第3题2.已知,某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的侧面积是( )3π B.3π C.23π5π 3.如图是某几何体的三视图,则该几何体的体积为( )A. 942π+B. 3618π+C. 9122π+ D. 9182π+4.某几何体的三视图如图所示,其中正视图,侧视图均为矩形,俯视图为等腰直角三角形,则该几何体的侧面积为 .第4题 第5题 第6题 第7题5.一个正三棱柱的侧棱长和底面边长相等,体积为23它的三视图中的俯视图如图所示.左视图是一个矩形.则这个矩形的面积是( )A .4 B. 2336.圆柱形容器内盛有高度为3cm 的水,若放入三个相同的珠(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是____cm.7.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为 .22 (正视图)22(俯视图)2⋅(侧视图)。
精品解析-2018-2019学年人教版高二数学必修2第1章第3节空间几何体的表面积与体积单元测试

绝密★启用前2018-2019学年人教版高二数学必修2第1章第3节空间几何体的表面积与体积单元测试考试时间:100分钟;满分:120分学校:___________姓名:___________班级:___________考号:___________分卷I一、选择题(共12小题,每小题4.0分,共48分)1.某个几何体的三视图如图所示(其中正视图中的圆弧是半径为2的半圆),则该几何体的体积为( )A. 80+5πB. 80+10πC. 92+14πD. 120+10π【答案】B【解析】由三视图知,几何体是半圆柱与长方体的组合体,下面长方体的长、宽、高分别是4、5、4,体积为4×5×4=80,上面半圆柱的半径为2,高为5,体积为1·π·4·5=10π,∴几何体的体积V=V半圆柱+V长方体=80+10π,故选B.2.若圆锥的高等于底面直径,则它的底面积与侧面积之比为( )A.1∶B.1∶C.∶D.1∶5【答案】D【解析】若圆锥的高等于底面直径,则h=2r,则母线l==5r,而圆锥的底面面积为πr2,圆锥的侧面积为πrl=5πr2,故圆锥的底面积与侧面积之比为1∶5.3.《算数书》竹简于上世纪八十年代在湖北省张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“禾盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈1L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈ 4L 2h 相当于将圆锥体积公式中的圆周率π近似取为( )A .15 50 B . 5 C . D .【答案】D【解析】设圆锥的底面半径为r ,则圆锥的底面周长L =2πr ,∴r =,∴V =1πr 2h =1.令1=4L 2h ,提π=,故选D.4.如图,在梯形ABCD 中,∠ABC =,AD ∥BC ,BC =2AD =2AB =2,将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A .π B .4 π C .5 π D . π 【答案】C【解析】由题意,旋转而成的几何体是圆柱,挖去一个圆锥(如图),该几何体的体积为π×12× -1×π×12=5π.5.现有一个底面直径为20 cm 的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6 cm ,高为20 cm 的圆锥形铅锤,铅锤完全浸没在水中.当铅锤从水中取出后,杯里的水将下降( ) A . 0.6 cm B . 0.15 cm C . 1.2 cmD. 0.3 cm【答案】A【解析】设杯里的水下降h cm,由题意知π( 0)2h=1× 0×π× 2,解得h=0.6 cm.6.已知一个铜质的五棱柱的底面积为16 cm2,高为4 cm,现将它熔化后铸成一个正方体的铜块(不计损耗),那么铸成的铜块的棱长是( )A. 2 cmB. 3 cmC. 4 cmD. 8 cm【答案】C【解析】∵铜质的五棱柱的底面积为16 cm2,高为4 cm,∴铜质的五棱柱的体积V=1 ×4=64(cm3),设熔化后铸成一个正方体的铜块的棱长为a cm,则a3=64,解得a=4 cm,故选C.7.一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,如果正四棱柱的底面边长为2 cm,那么该棱柱的表面积为( )A. (2+4) cm2B. (4+8) cm2C. (8+16) cm2D. (16+32) cm2【答案】C【解析】∵一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,正四棱柱的底面边长为2 cm,球的直径为正四棱柱的体对角线,∴正四棱柱的体对角线为4,正四棱柱的底面对角线长为2,∴正四棱柱的高为 1 =2,∴该棱柱的表面积为 × 2+4× × =8+16,故选C.8.一个直角三角形的直角边分别为3与4,以其直角边为旋转轴,旋转而成的圆锥的侧面积为( ) A.15πB. 0πC. 1 πD.15π或 0π【答案】D【解析】以直角三角形的直角边为旋转轴,旋转而成的圆锥,有以下两种情况:根据圆锥的侧面积计算公式S侧面积=πr×l母线长.①以直角边3为旋转轴时,旋转而成的圆锥的侧面积S=4π×5=20π;②以直角边4为旋转轴时,旋转而成的圆锥的侧面积S=3π×5=15π.故选D.9.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A. 0πB. 4πC. πD. π【答案】C【解析】由三视图可知,组合体的底面圆的面积和周长均为4π,圆锥的母线长l==4,所以圆锥的侧面积为S锥侧=1×4π×4=8π,圆柱的侧面积S柱侧=4π×4=16π,所以组合体的表面积S=8π+16π+4π=28π,故选C.10.圆柱的轴截面是正方形,且轴截面面积是S,则它的侧面积是( )A.B.πSC. πSD. 4πS【答案】B【解析】∵圆柱的轴截面是正方形,且轴截面面积是S,∴圆柱的母线长为,底面圆的直径为,∴圆柱的侧面积S=π××=πS.故选B.11.已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为V1;直径为2的球的体积为V2,则V1∶V2等于( )A.1∶1B.1∶C.1∶D.1∶4【答案】B【解析】由三视图知,该几何体是圆柱挖去一个同底等高的圆锥,圆柱与圆锥的底面半径为1,高都为1,∴几何体的体积V1=π×12×1-1×π×12×1=π;直径为2的球的体积V2=4π×13=4π,∴V1∶V2=1∶ .故选B.12.如图,一个正三棱柱的正视图是边长为的正方形,则它的外接球的体积等于( )A. πB.1 5π54C.9πD.π【答案】B【解析】因为正三棱柱ABC-DEF的正视图是边长为的正方形,所以正三棱柱的高是,底面正三角形的高也是.设它的外接球的球心为O,半径为R,底面△ABC的中心为G,所以△OGA是直角三角形,OG是高的一半,所以OG=,GA是正三角形ABC的高的,所以GA=.在△OAG中由勾股定理得R2=OG2+GA2.解得R2= 5.1.所以球的体积为V=4×π×3=1 5π54故选B.分卷II二、填空题(共4小题,每小题4.0分,共16分)13.一块正方形薄铁皮的边长为4,以它的一个顶点为圆心,剪下一个最大的扇形,用这块扇形铁皮围成一个圆锥,则这个圆锥的容积等于________.(铁皮厚度忽略不计)【答案】15【解析】如图所示,剪下最大的扇形的半径即圆锥的母线长l等于正方形的边长4,扇形的弧长=1×( π×4)=2π,即为圆锥的底面周长,设圆锥的底面半径为r,高为h,则2πr=2π,所以r=1,4所以h==15,所以圆锥的容积为1πr2h=15 .14.一个体积为12的正三棱柱(底面为正三角形,且侧棱垂直于底面)的三视图如图所示,则侧视图的面积为________.【答案】6【解析】由三视图可知底面正三角形的高为2,则底面边长为4,所以底面面积为4,因此该三棱柱的高为12÷4=3,故侧视图的面积为2× =6.,则油桶直立15.一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的14时,油的高度与桶的高度的比值是________.【答案】1-14【解析】设圆柱桶的底面半径为R,高为h,油桶直立时油面的高度为x,由题意知,油部分所在圆弧对应的扇形的圆心角为,则(141)h=πR2x,所以=14-1.16.(1)表面积相等的正方体和球中,体积较大的几何体是________;(2)体积相等的正方体和球中,表面积较小的几何体是________.【答案】(1)球(2)球【解析】设正方体的棱长为a,球的半径为r.(1)当6a2=4πr2时,V球=4πr3=πa3>a3=V正方体.(2)当a3=4πr3时,S球=4πr2=6πa2<6a2=S正方体.三、解答题(共7小题,每小题8.0分,共56分)17.直角三角形的两条直角边长分别为15和20,以它的斜边为轴旋转生成的旋转体,求旋转体的表面积.【答案】设此直角三角形为ABC,AC=20,BC=15,AC⊥BC,则AB=25.过C作CO⊥AB于点O,直角三角形绕AB所在直线旋转生成的旋转体,它的上部是圆锥(1),它的下部是圆锥(2),两圆锥底面圆相同,其半径是OC,且OC= 0155=12,圆锥(1)的侧面积S1=π×1 × 0=240π,圆锥(2)的侧面积S2=π×1 ×15=180π.旋转体的表面积应为两个圆锥侧面积之和,即S=S1+S2=420π.【解析】18.已知正三棱锥V-ABC的正视图、俯视图如图所示,其中VA=4,AC=2,求该三棱锥的表面积.【答案】由正视图与俯视图可得正三棱锥的直观图,如图所示,且VA=VB=VC=4,AB=BC=AC=2,取BC的中点D,连接VD,则VD⊥BC,所以VD==4= 1 ,则S△VBC=1VD·BC=1× 1 × = 9,S△ABC=1×( )2×=3,所以三棱锥V-ABC的表面积为3S△VBC+S△ABC=3 9+3=3( 9+).【解析】19.如图,圆柱的底面直径与高都等于球的直径.求证:(1)球的体积等于圆柱体积的;(2)球的表面积等于圆柱的侧面积.【答案】(1)设球的半径为R,则圆柱的底面半径为R,高为2R.因为V球=4πR3,V圆柱=πR2· R=2πR3,所以V球=V圆柱.(2)因为S球=4πR2,S圆柱侧=2πR· R=4πR2,所以S球=S圆柱侧.【解析】20.设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为r的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?【答案】如图.在容器内注入水,并放入一个半径为r的铁球,这时水面记为AB,将球从圆锥内取出后,这时水面记为EF.三角形PAB为轴截面,是正三角形,三角形PEF也是正三角形,圆O是正三角形PAB的内切圆.由题意可知,DO=CO=r,AO=2r=OP,AC=r,∴V球=4πr3,V圆锥=1π(r)2· r= πr3.又设HP=h,则EH=h,.∴V水=1π(h)2h=π9∵V水+V球=V圆锥,h3+4πr3= πr3,即π9∴h=15r,即圆锥内的水深是15r.【解析】21.如图几何体上半部分是母线长为5,底面圆半径为3的圆锥,下半部分是下底面圆半径为2,母线长为2的圆台,计算该几何体的表面积和体积.【答案】几何体的表面积S=S圆锥侧+S圆台侧+S圆台底= π×5+π( + )× +π× 2=15π+10π+4π= 9π;圆锥的高h=5=4,圆台的高H=1=,所以几何体的体积V=V圆锥+V圆台=1×π× 2×4+π×( 2+22+ × )×=1 π+19π.【解析】22.已知直角三角形ABC,其中∠ABC= 0°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.【答案】如图以斜边AB为轴旋转一周,得旋转体是以AB边的高CO为底面半径的两个圆锥组成的组合体.∵AB=2,CB=1,∠B= 0°,∴CB=sin 0°·AB=1,CA=cos 0°·AB=,CO==,故此旋转体的表面积S=π×OC×AC+π×OC×BC=π××(+1)=π.故此旋转体的体积V=1·πr2·h=1·π·CO2·AB=1×π××4=π.【解析】23.在长方体ABCD-A1B1C1D1中,截下一个棱锥C-A1DD1,求棱锥C-A1DD1的体积与剩余部分的体积之比.【答案】已知长方体是直四棱柱,设它的底面ADD1A1的面积为S,高为h,则它的体积为V=Sh.而棱锥C-A1DD1的底面积为1S,高为h,故三棱锥C-A1DD1的体积-11=1×1Sh=1Sh,余下部分体积为Sh-1Sh=5Sh.∴棱锥C-A1DD1的体积与剩余部分的体积之比为1∶5.【解析】。
人教A高中数学必修二课时分层训练:第一章 空间几何体 2 含解析

第一章1.3空间几何体的表面积与体积1.3.2球的体积和表面积课时分层训练‖层级一‖……………………|学业水平达标|1.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为()A.8π3 B.32π3C.8π D.82π3解析:选C设球的半径为R,则截面圆的半径为R2-1,∴截面圆的面积为S=π(R2-1)2=(R2-1)π=π,∴R2=2,∴球的表面积S=4πR2=8π.2.已知各顶点都在一个球面上的正四棱锥的高为3,体积为6,则这个球的表面积为()A.16π B.20πC.24π D.32π解析:选A设正四棱锥的高为h,底面边长为a,由V=13a2h=a2=6,得a= 6.由题意,知球心在正四棱锥的高上,设球的半径为r,则(3-r)2+(3)2=r2,解得r=2,则S球=4πr2=16π.故选A.3.某几何体的三视图如图所示,它的体积为()A.72π B.48πC.30π D.24π解析:选C 由三视图可知几何体由一个半球和倒立的圆锥组成的组合体.V =13π×32×4+12×43π×33=30π.4.等体积的球和正方体的表面积S 球与S 正方体的大小关系是( )A .S 正方体>S 球B .S 正方体<S 球C .S 正方体=S 球D .无法确定解析:选A 设正方体的棱长为a ,球的半径为R ,由题意,得V =43πR 3=a 3,∴a =3V ,R =33V 4π,∴S 正方体=6a 2=63V 2=3216V 2,S 球=4πR 2=336πV 2 < 3216V 2.5.球的表面积S 1与它的内接正方体的表面积S 2的比值是( )A.π3B.π4C.π2 D .π解析:选C 设球的内接正方体的棱长为a ,球的半径为R ,则3a 2=4R 2,所以a 2=43R 2,球的表面积S 1=4πR 2,正方体的表面积S 2=6a 2=6×43R 2=8R 2,所以S 1S 2=π2. 6.已知正方体的棱长为2,则与正方体的各棱都相切的球的表面积是________.解析:过正方体的对角面作截面如图.故球的半径r =2,∴其表面积S =4π×(2)2=8π.答案:8π7.球内切于正方体的六个面,正方体的棱长为a ,则球的表面积为________. 解析:正方体的内切球球心是正方体的中心,切点是六个面(正方形)的中心,经过四个切点及球心作截面,如图,所以有2r 1=a ,r 1=a 2,所以球的表面积S 1=4πr 21=πa 2.答案:πa 28.圆柱形容器的内壁底半径是10 cm ,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了53cm ,则这个铁球的表面积为________cm 2. 解析:设该铁球的半径为r ,则由题意得43πr 3=π×102×53,解得r 3=53,∴r=5,∴这个铁球的表面积S =4π×52=100π(cm 2).答案:100π9.若三个球的表面积之比为1∶4∶9,求这三个球的体积之比.解:设三个球的半径分别为R 1,R 2,R 3,∵三个球的表面积之比为1∶4∶9,∴4πR 21∶4πR 22∶4πR 23=1∶4∶9,即R 21∶R 22∶R 23=1∶4∶9,∴R 1∶R 2∶R 3=1∶2∶3,得R 31∶R 32∶R 33=1∶8∶27,∴V 1∶V 2∶V 3=43πR 31∶43πR 32∶43πR 33=R 31∶R 32∶R 33=1∶8∶27.10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r =1,l =3,试求该组合体的表面积和体积.解:该组合体的表面积S =4πr 2+2πrl =4π×12+2π×1×3=10π,该组合体的体积V =43πr 3+πr 2l =43π×13+π×12×3=13π3.‖层级二‖………………|应试能力达标|1.(2019·吉林白城四中二模)如图是一个空间几何体的三视图,则该几何体的外接球的表面积是( )A.24π B.36πC.48π D.60π解析:选C由三视图可知:该几何体为直三棱柱,并且为棱长是4的正方体的一半.可得该几何体的外接球的半径r=23,其外接球的表面积S=4π×()232=48π,故选C.2.一平面截一球得到直径是6 cm的圆面,球心到这个圆面的距离是4 cm,则该球的体积是()A.100π3cm3 B.208π3cm3C.500π3cm3 D.41613π3cm3解析:选C根据球的截面的性质,得球的半径R=32+42=5(cm),所以V球=43πR3=500π3(cm3).3.一个几何体的三视图如图所示,则此几何体的表面积S=()A.32+π B.32+2πC.28+2π D.28+π解析:选A由三视图可知此几何体的上半部分为半个球,下半部分是一个长方体,故其表面积S=4π×12+4×2×3+2×2+2×2-π=32+π.4.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r =()A.1 B.2C.4 D.8解析:选B如图,该几何体是一个半球与一个半圆柱的组合体,球的半径为r,圆柱的底面半径为r,高为2r,则表面积S=12×4πr2+πr2+4r2+πr·2r=(5π+4)r2.又S=16+20π,∴(5π+4)r2=16+20π,∴r2=4,r=2,故选B.5.已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图、侧视图、俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是________.解析:依题意得,该几何体是球的一个内接正方体,且该正方体的棱长为2.设该球的直径为2R,则2R=22+22+22=23,所以该几何体的表面积为4πR2=4π(3)2=12π.答案:12π6.已知一个球与一个正三棱柱的三个侧面和两个底面都相切,且这个球的体积是323π,那么这个三棱柱的体积是________. 解析:设球的半径为r ,则43πr 3=323π,得r =2,三棱柱的高为2r =4.又正三棱柱的底面三角形的内切圆半径与球的半径相等,所以底面正三角形的边长为43,所以正三棱柱的体积V =34×(43)2×4=48 3.答案:48 37.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________ cm.解析:设球的半径为r ,则圆柱形容器的高为6r ,容积为πr 2×6r=6πr 3,高度为8 cm 的水的体积为8πr 2,3个球的体积和为3×43πr 3=4πr 3,由题意得6πr 3-8πr 2=4πr 3,解得r =4(cm).答案:48.轴截面是正三角形的圆锥内有一个内切球,若圆锥的底面半径为1 cm ,求球的体积.解:如图所示,作出轴截面,O 是球心,与边BC ,AC相切于点D ,E .连接AD ,OE ,∵△ABC 是正三角形,∴CD=12AC .∵Rt △AOE ∽Rt △ACD ,∴OE AO =CD AC .∵CD =1 cm ,∴AC =2 cm ,AD = 3 cm ,设OE =r ,则AO =(3-r ),∴r 3-r=12,∴r =33 cm ,V球=43π⎝⎛⎭⎪⎫333=4327π(cm3),即球的体积等于4327π cm3.。
《作业推荐》高中数学人教A版(2019) 必修(第二册)同步练习:8.3空间几何体的表面积与体积

《作业推荐》—8.3空间几何体的表面积与体积一、单选题(共45 分)1.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为()A.22B.20C.10D.11【答案】A【解析】【分析】根据长方体的表面积公式计算即可.【详解】所求长方体的表面积S=2×(1×2)+2×(1×3)+2×(2×3)=22.故选:A.【点睛】本题主要考查了长方体的表面积公式,属于基础题型.2.圆柱的底面半径为1,母线长为2,则它的侧面积为( (A.2πB.3πC.πD.4π【答案】D【解析】【分析】根据圆柱的侧面积公式,计算即可.【详解】圆柱的底面半径为r=1,母线长为l(2(则它的侧面积为S侧(2πrl(2π×1×2(4π(故选D(【点睛】本题考查了圆柱的侧面积公式应用问题,是基础题.3.在三棱锥P−ABC中,PA⊥平面ABC,且ΔABC为等边三角形,AP=AB=2,则三棱锥P−ABC的外接球的表面积为()A.272π B.283π C.263π D.252π【答案】B 【解析】计算出ΔABC 的外接圆半径r ,利用公式R =√r 2+(PA 2)2可得出外接球的半径,进而可得出三棱锥P −ABC 的外接球的表面积. 【详解】ΔABC 的外接圆半径为r =AB 2sinπ3=2√33,∵PA ⊥底面ABC ,所以,三棱锥P −ABC 的外接球半径为R =√r 2+(PA 2)2=√(2√33)2+12=√213, 因此,三棱锥P −ABC 的外接球的表面积为4πR 2=4π×(√213)2=28π3.故选:B. 【点睛】本题考查三棱锥外接球表面积的计算,解题时要分析几何体的结构,选择合适的公式计算外接球的半径,考查计算能力,属于中等题.4.把球的体积扩大到原来的2倍,那么表面积扩大到原来的( ) A.2倍 B.√43倍C.√34倍D.√23倍【答案】B 【解析】 【分析】根据球的体积公式,分别求得原来球的体积和变大后的球的体积,进而得到变化前后半径之间的关系,再由球的表面积公式即可求解. 【详解】设变化前后球的半径分别为r,r 1,表面积分別为S,S 1.由条件可知43πr 13=43πr 3⋅2,∴r 1=√23r ,因此扩大后球的表面积S 1=4πr 12=4π(√23r)2=√43S .故选:B 【点睛】本题主要考查了球的体积和表面积的计算与应用,其中解答中熟记球的体积公式、表面积公式,准确运算是解答的关键,着重考查了运算与求解能力,属于基础题.5.若一个圆锥的表面积为3π,侧面展开图是半圆,则此圆锥的高为( ) A.1 B.√2C.√3D.2【答案】C 【解析】结合表面积,侧面为半圆,建立等式,即可.【详解】设圆锥的母线长为l,底面半径为r,高为ℎ,则πr2+πrl=3π,2πrl=π,所以l=2,r=1,ℎ=√3.【点睛】本道题考查了立体几何表面积计算公式,结合题意,建立方程,计算结果,即可,属于基础题.6.在三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC,且AB=2.若三棱锥P−ABC的外接球体积为36π,则当该三棱锥的体积最大时,其表面积为( )A.6+6√3B.8+6√3C.8+8√5D.6+8√5【答案】C【解析】【分析】第一步确定球心位置在PC的中点,求出半径得到各棱长,再计算各面面积可解.【详解】因为PA⊥平面ABC,所以PA⊥BC,又因为AB⊥BC,所以BC⊥平面PAB,所以BC⊥PB,设PC的中点为O,则O到P−ABC的四个顶点的距离都相等,所以点O是三棱锥外接球球心,又由外接球的体积为43πR3=36π,得外接球半径R=3,所以PC=6.设PA=a,BC=b,则PA2+AB2+BC2=PC2,得a2+b2=32,所以V P−ABC=13×12×2b×a=13ab⩽13×a2+b22=163,当且仅当a=b=4时,V P−ABC取得最大值163.此时PB=AC=√42+22=2√5,所以,三棱锥的表面积S=2×12×2×4+2×12×4×2√5=8+8√5.故选:C.【点睛】本题考查与球有关外接问题及求锥体的表面积.其解题规律:(1)直棱柱外接球的球心到直棱柱底面的距离恰为棱柱高的12.(2)正方体外接球的直径为正方体的体对角线的长.此结论也适合长方体,或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥.(3)求多面体外接球半径的关键是找到由球的半径构成的三角形,解三角形即可.7.如果一个球的外切圆锥的高是这个球的半径的3倍,则圆锥的侧面积S1和球的表面积S2之比为()A.4 : 3B.3 : 1C.3 : 2D.9 : 4【答案】C【解析】【分析】画出轴截面如图所示,设球的半径为r,将圆锥的侧面积、球的表面积分别用r表示,即可得答案.【详解】画出轴截面如图所示,设球的半径为r,则OD=r,PO=2r,∠PDO=90°,∴∠CPB=30°.又∠PCB=90°,PC=√3r,PB=2√3r,∴CB=√33∴圆锥的侧面积S1=π×√3r×2√3r=6πr2,球的表面积S2=4πr2,∴S1:S2=3:2.故选:C.【点睛】本题考查圆锥的侧面积、球的表面积求解,考查函数与方程思想、转化与化归思想,考查空间想象能力和运算求解能力.8.等体积的球和正方体的表面积S1,S2的大小关系是()A.S1>S2B.S1<S2C.S1=S2D.无法确定【答案】A【解析】【分析】根据体积相等得出正方体棱长和球的半径的大小关系,求出表面积即可得解.【详解】设正方体的棱长为a ,球的半径为R ,由题意得V =43πR 3=a 3,所以a =√V 3,R =√3V4π3.所以S 1=6a 2=6√V 23=√216V 23, S 2=4πR 2=√36πV 23, 所以S 1>S 2. 故选:A 【点睛】此题考查正方体和球体的体积表面积计算,根据体积相等得出等量关系,关键在于对代数式的准确化简.9.南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面α所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为V 1,V 2,被平行于这两个平面的任意平面截得的两个截面面积分别为S 1,S 2,则( )A.如果S 1,S 2总相等,则V 1=V 2B.如果S 1=S 2总相等,则V 1与V 2不一定相等C.如果V 1=V 2 ,则S 1,S 2总相等D.存在这样一个平面α使S 1=S 2相等,则V 1=V 2 【答案】A 【解析】 【分析】由祖暅原理的含义直接判断即可得出答案. 【详解】 如图所示:由祖暅原理的含义可得当平面α∥β,并且和α平行的平面截得两个几何体的所得的截面面积S 1=S 2时,V 1=V 2,则A 选项正确. 故选:A. 【点睛】本题考查了祖暅原理的理解和应用,属于基础题. 二、填空题(共 25 分)10.若正方形ABCD 的边长为1,利用斜二测画法得到直观图A ′B ′C ′D ′,则直观图A ′B ′C ′D ′的周长等于_____. 【答案】3 【解析】 【分析】根据斜二测画法的规则,结合“一变两不变”的原则,即可求解,得到答案. 【详解】根据斜二测画法画出图形后求出周长,如图,因为正方形ABCD 的边长为1, 则由斜二测画法可得A ′D ′=1,B ′C ′=1,A ′B ′=12,D ′C ′=12,所以四边形A ′B ′C ′D ′的周长为1+1+12+12=3.【点睛】本题主要考查了平面图形的直观图的画法以及应用,其中解答中熟记斜二测画法的规则,画出平面图形的直观图是解答的关键,着重考查了数形结合思想,以及推理与运算能力,属于基础题.11.《九章算术》中,将四个面都为直角三角形的四面体称为鱉臑.如图,四面体P −ABC 为鱉臑,PA ⊥平面ABC ,∠ABC 为直角,且PA =AB =BC =2,则P −ABC 的体积为________.【答案】43【解析】【分析】计算出△ABC的面积,然后利用锥体的体积公式可求得三棱锥P−ABC的体积.【详解】由题意知PA⊥平面ABC,∠ABC=π2,PA=AB=BC=2,所以△ABC的面积为S△ABC=12AB⋅BC=2,因此,V P−ABC=13S△ABC⋅PA=13×2×2=43.故答案为:43.【点睛】本题考查三棱锥体积的计算,考查锥体体积公式的应用,考查计算能力,属于基础题.12.在ΔABC中,AB=AC=6,BC=4,AD是BC边上的中线,将ΔABD沿AD折起,使二面角C−AD−B等于120∘,则四面体ABCD外接球的体积为______.【答案】32√3π【解析】【分析】由题意可知折起的三棱锥是一条侧棱垂直于底面的棱锥,由题意求出高AD及底面外接圆的半径r,利用公式R=√r2+(AD2)2求出外接球的半径R,进而求出外接球的体积.【详解】因为AB=AC,D为BC的中点,所以AD⊥BC,在折起的过程中,AD⊥BD,AD⊥CD,BD∩CD=D,所以AD⊥平面BCD,因为二面角C−AD−B等于120∘,所以∠BDC=120∘,且BD=CD=2,AD=√AB2−BD2=4√2,在ΔBCD中,∠CBD=∠BCD=30∘,ΔBCD外接圆半径为r=BD2sin30∘=2,设外接球的半径为R,则R=√r2+(AD2)2=√22+(2√2)2=2√3,因此,所以外接球的体积为V=43πR3=43π×(2√3)3=32√3π.故答案为:32√3π.【点睛】本题考查一条侧棱垂直于底面的三棱锥的外接球半径与三棱锥棱长的关系及球的体积公式,考查计算能力,属于中档题.13.如图所示,在上、下底面对应边的比为1:2的三棱台中,过上底面一边A1B1作一个平行于棱C1C的平面A1B1EF,记平面分三棱台两部分的体积为V1(三棱柱A1B1C1−FEC),V2两部分,那么V1:V2=______.【答案】3:4【解析】【分析】设三棱台的高为ℎ,上底面的面积是S,则下底面的面积是4S,计算体积得到答案.【详解】设三棱台的高为ℎ,上底面的面积是S,则下底面的面积是4S,∴V台=13ℎ(S+4S+2S)=73Sℎ,∴V1=Sℎ,∴V1V2=Sℎ73Sℎ−Sℎ=34.故答案为:3:4.【点睛】本题考查了三棱台的体积问题,意在考查学生的计算能力.14.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也,又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L 与高h 计算其体积V 的近似公式V ≈136L 2ℎ.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈7264L 2ℎ相当于将圆锥体积公式中的圆周率π近似取为____. 【答案】227【解析】 【分析】由题意,讲圆锥体积公式V=13Sℎ代入到近似公式中,即可求解圆周率π的近似值.【详解】设圆锥底面圆的半径为r ,则圆锥底面圆周长L =2πr ,∴r =L 2π,∴V =13πr 2ℎ=L 2ℎ12π,令L 2ℎ12π=7264L 2ℎ,得π=227.故答案为:227【点睛】本题考查中国传统文化,利用圆锥体积公式,近似计算圆周率,是基础题. 三、解答题(共 30 分)15.如图四棱锥P −ABCD 中,底面ABCD 正方形,E 为PD 中点.(1)求证:PB ∥平面ACE ;(2)已知PA ⊥平面ABCD 且PA =AB =2,求三棱锥D −ACE 体积.【答案】(1)证明见解析;(2)23【解析】 【分析】(1)连接BD 交AC 与O ,连接OE ,根据中位线定理即可证明OE ∥PB ,从而证明PB ∥平面ACE ; (2)根据V D−ACE =V E−ACD =12V P−ACD ,由三棱锥体积公式即可求解.【详解】(1)连接BD交AC与O,连接OE则OE∥PB,又OE⊆平面AEC,且PB⊄平面AEC 所以PB∥平面ACE(2)取AD的中点F,连接EF,则PA∥EF∵PA⊥平面ABCD∴V D−ACE=V E−ACD=12V P−ACD.=12[13×(12AD×CD)×PA]=12×[13×(12×2×2)×2]=23【点睛】本题考查了直线与平面的平行判定,三棱锥体积的求法,属于基础题.16.如图是一个烟筒的直观图(图中数据的单位为厘米),它的下部是个正四棱台形物体,上部是一个正四棱柱形物体(底面与四棱台形物体的上底面重合).为防止雨水的侵蚀,同时使烟筒更美观,现要在烟筒外部粘贴瓷砖,请你计算需要多少平方厘米的瓷砖?(结果精确到1cm2,可用计算工具)【答案】14359(cm2)【解析】【分析】上部四棱柱的侧面积容易求出;要计算四棱台侧面积需先计算出斜高,再计算侧面积,两者相加即为需要瓷砖面积.【详解】解;由题意,需贴瓷砖的部分为四棱柱与四棱台的侧面积.S四棱柱侧=4×40×80=12800(cm2),四棱台的斜高ℎ′=√102−(50−402)2=5√3(cm),S四棱台侧=4×40+502×5√3≈1559(cm2)故需要瓷砖的面积为12800+1559=14359(cm2).【点睛】本题考查几何体的侧面积求解,关键是得出所需要的数据,准确利用公式,属于基础题.17.在平面几何中可利用等积变换求三角形的面积,通常有两种方案:一是同一三角形选不同的边作为底边所得面积相等;二是不同的三角形利用“等底同高”或“等高同底”得到三角形面积相等.在空间图形中能否借鉴平面几何的“等积变换”求三棱锥的体积?如图所示,正方体ABCD−A1B1C1D1,的棱长为1,E为线段B1C上的一点,在求三棱锥A−DED1的体积时,随着E点的变化,底面ΔDED1的面积在变化,点A到底面的距离也在变化,导致体积难求.(1)能否利用“等体积转换法”求解三棱锥A−DED1的体积?(2)求三棱锥E−ADD1的体积关键是求高,即求E点到平面AA1D1D的距离,如何求出E点到平面AA1D1D的距离?(3)求出三棱锥A−DED1的体积.【答案】(1)能;(2)见解析;(3)16【解析】【分析】(1)选ΔADD1为底面,底面积不变,点E到面ADD1的距离不变即可判断.(2)由于正方体的侧面AA1D1D与侧面BB1C1C平行,故E点到平面AA1D1D的距离等于C点到平面AA1D1D的距离.(3)利用(1)(2)借助三棱锥的体积公式即可求解.【详解】(1)选ΔADD1为底面,则底面积不变,利用同一几何体的等积变换得,三棱锥A−DED1的体积等于三棱锥E−ADD1的体积.(2)由于正方体的侧面AA1D1D与侧面BB1C1C平行,因此E点到平面AA1D1D的距离等于C点到平面AA1D1D的距离,利用“等底同高”体积相等得,三棱锥E−ADD1的体积等于三棱锥C−ADD1的体积.(3)由问题1、2得,V A−DED1=V E−ADD1=V C−ADD1=13×12×1×1×1=16.【点睛】本题考查了等体法求三棱锥的体积、三棱锥的体积公式,属于基础题.。
空间几何体的表面积和体积经典例题(教师讲义打印一份)
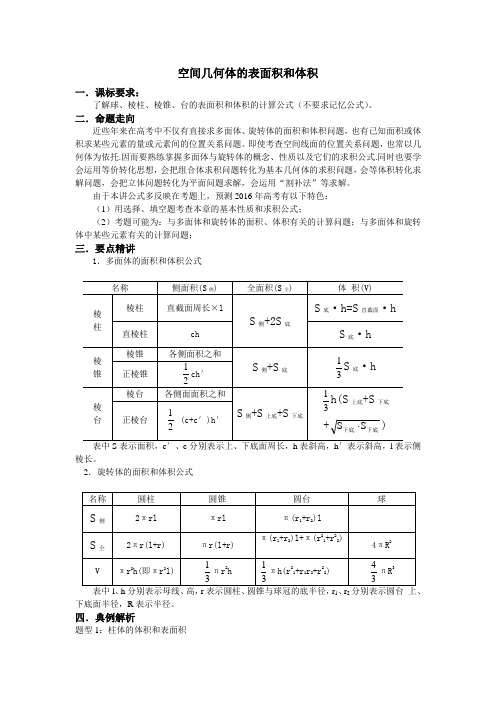
空间几何体的表面积和体积一.课标要求:了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
二.命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测2016年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;三.要点精讲1.多面体的面积和体积公式表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
2.旋转体的面积和体积公式表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台上、下底面半径,R表示半径。
四.典例解析题型1:柱体的体积和表面积例1.一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长. 解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由(2)2得:x 2+y 2+z 2+2xy+2yz+2xz=36(3)由(3)-(1)得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。
点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察。
我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系。
例2.如图1所示,在平行六面体ABCD —A 1B 1C 1D 1中,已知AB=5,AD=4,AA 1=3,AB ⊥AD ,∠A 1AB=∠A 1AD=3π。
高中数学必修2 空间几何体的表面积与体积最全试题及答案

空间几何体的表面积与体积一.相关知识点1.几何体的表面积(1)棱柱、棱锥、棱台的表面积就是各个面的面积的和。
(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环。
(3)若圆柱、圆锥的底面半径为r,母线长l,则其表面积为S柱=2πr2+2πrl,S锥=πr2+πrl。
(4)若圆台的上下底面半径为r1,r2,母线长为l,则圆台的表面积为S=π(r21+r22)+π(r1+r2)l。
(5)球的表面积为4πR2(球半径是R)。
2.几何体的体积(1)V柱体=Sh。
(2)V锥体=13Sh。
(3)V台体V圆台=13π(r21+r1r2+r22)h,V球=43πR3(球半径是R)。
一、细品教材1.(必修2P28A组T3改编)如图,将一个长方体用过相邻三条棱的中点的平面截出一个棱锥,则该棱锥的体积与剩下的几何体体积的比为________。
2.(必修2P36A组T10改编)一直角三角形的三边长分别为6 cm,8 cm,10 cm,绕斜边旋转一周所得几何体的表面积为________。
细品教材答案:1.1∶47; 2.3365π cm2二、基础自测1.(2016·全国卷Ⅱ)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20π B.24πC.28π D.32π2.已知正四棱锥的侧棱与底面的边长都为32,则这个四棱锥的外接球的表面积为()A.12π B.36πC.72π D.108π3.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为__________。
4.(2016·北京高考)某四棱柱的三视图如图所示,则该四棱柱的体积为________。
5.(2016·赤峰模拟)已知三棱柱ABC-A1B1C1的侧棱和底面垂直,且所有棱长都相等,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为7π,则此三棱柱的体积为________。
基础自测答案1.C;2.B;3.2;4.32;5.94三.直击考点考点一空间几何体的表面积【典例1】(1)某几何体的三视图如图所示,则该几何体的表面积等于()A.8+22B.11+22C.14+2 2 D.15(2)(2016·全国卷Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径。
高中数学必修二同步练习题库:空间几何体的表面积和体积(填空题:较易)

空间几何体的表面积和体积(填空题:较易)1、过长方体的一个顶点的三条棱长分别是1、2、2,且它的八个顶点都在同一球面上,则这个球的表面积是__________.2、有一个几何体的三视图及其尺寸如下(单位:),则该几何体的表面积为.3、已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为_________ .4、在平行四边形中,,,若将其沿折成直二面角,则三棱锥的外接球的表面积为.5、半径为的球内接正方形的表面积为 __________;体积为__________ .6、已知正方体棱长为,则正方体外接球的体积为__________.7、已知球的大圆周长为,则球的表面积为__________.8、已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为,则这个球的表面积为________.9、已知圆柱的侧面展开圆矩形面积为,底面周长为,它的体积是__________.10、在矩形ABCD中,AC=2,现将△ABC沿对角线AC折起,使点B到达点B'的位置,得到三棱锥B'-ACD,则三棱锥B'-ACD的外接球的表面积是_________11、如图所示的多面体,它的正视图是斜边长为的直角三角形,左视图为边长是的正方形,俯视图为有一个内角为的直角梯形,则该多面体的体积为__________.12、中,,,,将三角形绕直角边旋转一周所成的几何体的表面积为__________.13、如果棱长为的正方体的八个顶角都在同一个球面上,那么球的表面积是__________.14、一个正方体的顶点都在球面上,若正方体的棱长为,则球的表面积是__________.15、底面直径是,高是的圆柱的侧面积为__________.16、已知两个球的表面积之比为,则这两个球的半径之比为__________.17、正方体的表面积与其外接球表面积的比为______.18、正四棱锥底面边长为4,高为1,则其侧面积为_________.19、将边长为2的正方形绕其一边旋转一周,所得几何体的体积为__________.20、母线长为的圆锥体,其侧面展开图的面积为,则该圆锥的体积为________________.21、—个几何体的主视图、左视图、俯视图都是以为半径的圆,则该几何体的体积是__________.22、如图所示,从棱长为6 的正方体铁皮箱中分离出来由三个正方形面板组成的几何图形.如果用图示中这样一个装置来盛水,那么最多能盛的水的体积为________.23、一个几何体的三视图如图所示,则该几何体的体积为____.24、一个四棱锥的三视图和直观图如图所示,其中分别是的中点,是上的一点,平面,则三棱锥的体积为__________.25、若正四棱柱的底面边长为与底面所成的角为,则三棱锥的表面积为__________.26、《九章算术》卷《商功》记载一个问题“今有圆堡壔(),周四丈八尺,高一丈一尺.问积几何?”意思是:今有圆柱形土筑小城堡,底面周长为丈尺,高丈尺,则它的体积是__________立方尺.(取,丈尺)27、长、宽、高分别为2,1,2的长方体的每个顶点都在同一个球面上,则该球的表面积为__________.28、已知正六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,当球的体积最小时,正六棱柱底面边长为_________.29、某几何体的三视图如图所示,则该几何体的体积为__________.30、长方体的长、宽、高分别为,其顶点都在球的球面上,则球的表面积为__________.31、一个多面体从前面、后面、左侧、右侧、上方看到的图形分别如图所示(其中每个正方形边长都为1),则几何体的表面积为__________.32、某四棱锥的三视图如图所示(单位:),则该几何体的体积是_________ ,侧面积是_________ .33、某三棱锥的三视图如图所示,则该三棱锥的4个面中,直角三角形的个数是__________个,它的表面积是__________.34、半径为的球的体积与一个长、宽分别为6、4的长方体的体积相等,则长方体的表面积为_____.35、已知圆锥的母线长是10,侧面展开图是半圆,则该圆锥的侧面积为36、一个圆台上、下底面的半径分别为和,若两底面圆心的连线长为,则这个圆台的表面积为__________.37、半径为的半圆卷成一个圆锥,则圆锥的体积为_______.38、某三棱锥的三视图如图所示,则该三棱锥的体积是______39、已知正方体的棱长为1,则正方体的外接球的体积为.40、正方体的全面积是,它的顶点都在一个球面上,则这个球的表面积是_________。
2023年新高考数学一轮复习8-2 空间几何体的表面积和体积(真题测试)解析版

专题8.2 空间几何体的表面积和体积(真题测试)一、单选题1.(2020·天津·高考真题)若棱长为 ) A .12π B .24π C .36π D .144π【答案】C【解析】【分析】求出正方体的体对角线的一半,即为球的半径,利用球的表面积公式,即可得解.【详解】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R =,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C.2.(2020·北京·高考真题)某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为(). A .63+ B .623+ C .123+ D .1223+【答案】D【解析】【分析】首先确定几何体的结构特征,然后求解其表面积即可.【详解】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+ ⎪⎝⎭故选:D.【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.3.(2022·浙江·高考真题)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是( )A .22πB .8πC .22π3D .16π3【答案】C【解析】【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可根据球,圆柱,圆台的体积公式求出.【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的底面半径,圆台的上底面半径都为1cm ,圆台的下底面半径为2cm ,所以该几何体的体积(322214122ππ1π122π2π12333V =⨯⨯+⨯⨯+⨯⨯⨯+⨯=3cm .故选:C .4.(2022·全国·高考真题)已知正三棱台的高为1,上、下底面边长分别为面上,则该球的表面积为( )A .100πB .128πC .144πD .192π【答案】A【解析】【分析】根据题意可求出正三棱台上下底面所在圆面的半径12,r r ,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积.【详解】设正三棱台上下底面所在圆面的半径12,r r ,所以123432,260sin 60r r ==,即123,4r r ==,设球心到上下底面的距离分别为12,d d ,球的半径为R ,所以1d =2d =121d d -=或121d d +=,即1=1,解得225R =符合题意,所以球的表面积为24π100πS R ==. 故选:A .5.(2021·浙江·高考真题)某几何体的三视图如图所示,则该几何体的体积是( )A .32B .3C .2D .【答案】A【解析】【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【详解】几何体为如图所示的四棱柱1111ABCD A B C D -,其高为1,底面为等腰梯形ABCD ,1=故1111131222ABCD A B C D V -=⨯⨯=, 故选:A. 6.(2021·全国·高考真题(理))已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为( )A B C D A 【解析】【分析】由题可得ABC 为等腰直角三角形,得出ABC 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.【详解】,1AC BC AC BC ⊥==,ABC ∴为等腰直角三角形,AB ∴=,则ABC 1, 设O 到平面ABC 的距离为d ,则2d =所以11111332O ABC ABC V S d -=⋅=⨯⨯⨯= 故选:A.7.(2022·全国·高考真题(文))已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为( )A .13B .12CD 【答案】C【解析】【分析】先证明当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD ,四边形ABCD 所在小圆半径为r ,设四边形ABCD 对角线夹角为α, 则2111sin 222222ABCD S AC BD AC BD r r r α=⋅⋅⋅≤⋅⋅≤⋅⋅= (当且仅当四边形ABCD 为正方形时等号成立)即当四棱锥的顶点O 到底面ABCD 所在小圆距离一定时,底面ABCD 面积最大值为22r又22r h 1+=则2123O ABCDV r h -=⋅⋅=当且仅当222r h =即h 时等号成立,故选:C8.(2022·全国·高考真题)已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3l ≤≤ ) A .8118,4⎡⎤⎢⎥⎣⎦ B .2781,44⎡⎤⎢⎥⎣⎦ C .2764,43⎡⎤⎢⎥⎣⎦ D .[18,27]【答案】C【解析】【分析】设正四棱锥的高为h ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围.【详解】∵ 球的体积为36π,所以球的半径3R =,设正四棱锥的底面边长为2a ,高为h ,则2222l a h =+,22232(3)a h =+-,所以26h l =,2222a l h =- 所以正四棱锥的体积42622411214()=333366936l l l V Sh a h l l ⎛⎫==⨯⨯=⨯-⨯- ⎪⎝⎭, 所以5233112449696l l V l l ⎛⎫⎛⎫-'=-= ⎪ ⎪⎝⎭⎝⎭,当3l ≤≤0V '>,当l ≤0V '<,所以当l =V 取最大值,最大值为643,又3l =时,274V =,l =814V =, 所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是276443⎡⎤⎢⎥⎣⎦,. 故选:C.二、多选题9.(2022·广东茂名·二模)某一时段内,从天空降落到地面上的液态或固态的水,未经蒸发,而在水平面上积聚的深度称为这段时间的降雨量.24h 降雨量的等级划分如下:在一次暴雨降雨过程中,小明用一个大容量烧杯(如图,瓶身直径大于瓶口直径,瓶身高度为50cm ,瓶口高度为3cm )收集雨水,容器内雨水的高度可能是( )A .20cmB .22cmC .25cmD .29cm【答案】CD【解析】【分析】设降雨量为x ,容器内雨水高度为h,根据雨水的体积相等关系可得到h,x 之间的关系49h x =,结合题意可得4200400[,)999x ∈,由此判断出答案. 【详解】设降雨量为x ,容器内雨水高度为h,根据体积相等关系可得:22π100π150x h ⨯=⨯,解得49h x = , 由于[50,100)x ∈ ,故4200400[,)999x ∈, 故20040020040020,22[,),25,29[,)9999∉∈故选:CD .10.(2023·湖北·高三阶段练习)折扇是我国古老文化的延续,在我国已有四千年左右的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1).图2是一个圆台的侧面展开图(扇形的一部分),若两个圆弧,DE AC 所在圆的半径分别是3和9,且120ABC ∠=,则该圆台的( )A .高为42B .体积为5023π C .表面积为34πD .上底面积、下底面积和侧面积之比为1:9:22【答案】AC【解析】 【分析】设圆台的上底面半径为r ,下底面半径为R ,求出1,3r R ==,即可判断选项A 正确;利用公式计算即可判断选项BCD 的真假得解.【详解】解:设圆台的上底面半径为r ,下底面半径为R ,则11223,22933r R ππππ=⨯⨯=⨯⨯,解得1,3r R ==.圆台的母线长6l =,圆台的高为h ==,则选项A 正确;圆台的体积()22133113π=⨯+⨯+=,则选项B 错误; 圆台的上底面积为π,下底面积为9π,侧面积为()13624ππ+⨯=,则圆台的表面积为92434ππππ++=,则C 正确;由前面可知上底面积、下底面积和侧面积之比为1:9:24,则选项D 错误.故选:AC .11.(2022·湖南·长沙一中模拟预测)传说古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.“圆柱容球”是阿基米德最为得意的发现;如图是一个圆柱容球,12O O ,为圆柱上下底面的圆心,O 为球心,EF 为底面圆1O 的一条直径,若球的半径2r =,则( )A .球与圆柱的表面积之比为12:B .平面DEF 截得球的截面面积最小值为165π C .四面体CDEF 的体积的取值范围为3203⎛⎤ ⎥⎝⎦,D .若P 为球面和圆柱侧面的交线上一点,则PE PF +的取值范围为2⎡+⎣【答案】BCD【解析】【分析】利用球的表面积公式及圆柱的表面积公式可判断A ,由题可得O 到平面DEF 的距离为1d 平面DEF 截得球的截面面积最小值可判断B ,由题可得四面体CDEF 的体积等于12E DCO V -可判断C ,设P 在底面的射影为P ',设2t P E '=,PE PF +PE PF +的取值范围可判断D.【详解】由球的半径为r ,可知圆柱的底面半径为r ,圆柱的高为2r ,则球表面积为24r π,圆柱的表面积222226r r r r πππ+⋅=, 所以球与圆柱的表面积之比为23,故A 错误;过O 作1OG DO ⊥于G ,则由题可得12OG == 设O 到平面DEF 的距离为1d ,平面DEF 截得球的截面圆的半径为1r ,则1d OG ≤,22221114164455r r d d =-=-≥-=, 所以平面DEF 截得球的截面面积最小值为165π,故B 正确; 由题可知四面体CDEF 的体积等于12E DCO V -,点E 到平面1DCO 的距离(0,4]d ∈, 又114482DCO S =⨯⨯=,所以123228(0,]33E DCO V d -=⨯∈,故C 正确; 由题可知点P 在过球心与圆柱的底面平行的截面圆上,设P 在底面的射影为P ', 则2222222,2,2,16PP PE P E PF P F P E P F '''''==+=++=,设2t P E '=,则20,4t ⎡⎤∈⎣⎦,PE PF +所以()2224PE PF +==+2424⎡⎤=++⎣⎦,所以2PE PF ⎡+∈+⎣,故D 正确.故选:BCD.12.(2022·全国·高考真题)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,,2FB ED AB ED FB ==∥,记三棱锥E ACD -,F ABC -,F ACE -的体积分别为123,,V V V ,则( )A .322V V =B .31V V =C .312V V V =+D .3123V V =【答案】CD【解析】【分析】直接由体积公式计算12,V V ,连接BD 交AC 于点M ,连接,EM FM ,由3A EFM C EFM V V V --=+计算出3V ,依次判断选项即可.【详解】设22AB ED FB a ===,因为ED ⊥平面ABCD ,FB ED ,则()2311114223323ACD V ED S a a a =⋅⋅=⋅⋅⋅=, ()232111223323ABC V FB S a a a =⋅⋅=⋅⋅⋅=,连接BD 交AC 于点M ,连接,EM FM ,易得BD AC ⊥, 又ED ⊥平面ABCD ,AC ⊂平面ABCD ,则ED AC ⊥,又ED BD D =,,ED BD ⊂平面BDEF ,则AC ⊥平面BDEF ,又12BM DM BD ==,过F 作FG DE ⊥于G ,易得四边形BDGF 为矩形,则,FG BD EG a ===,则,EM FM ===,3EF a =,222EM FM EF +=,则EM FM ⊥,212EFM SEM FM =⋅=,AC =, 则33123A EFM C EFM EFM V V V AC S a --=+=⋅=,则3123V V =,323V V =,312V V V =+,故A 、B 错误;C 、D 正确.故选:CD.三、填空题 13.(2021·全国·高考真题(文))已知一个圆锥的底面半径为6,其体积为30π则该圆锥的侧面积为________.【答案】39π【解析】【分析】利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.【详解】∵216303V h ππ=⋅=∴52h =∴132l =∴136392S rl πππ==⨯⨯=侧. 故答案为:39π.14.(2020·江苏·高考真题)如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半径为0.5 cm ,则此六角螺帽毛坯的体积是 ____ cm 3. 【答案】1232π-【解析】【分析】先求正六棱柱体积,再求圆柱体积,相减得结果.【详解】正六棱柱体积为262⨯ 圆柱体积为21()222ππ⋅=所求几何体体积为2π故答案为: 2π15.(2019·天津·高考真题(文)若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________. 【答案】4π. 【解析】【分析】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.【详解】借助勾股定理,2=,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,圆柱的底面半径为12,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,故圆柱的体积为21124ππ⎛⎫⨯⨯= ⎪⎝⎭. 16.(2022·吉林·长春市第二实验中学高三阶段练习)在三棱锥P ABC -中,点P 在底面的射影是ABC 的外心,2,3BAC BC PA π∠===___________. 【答案】12548π 【解析】【分析】先由正弦定理得,ABC 外接圆的半径,再由勾股定理,即可求出半径,从而可得外接球体积.【详解】解:设ABC 的外心为1O ,连接1PO ,则球心O 在1PO 上,连接1O A ,则1O A 为ABC 外接圆的半径r ,连接OA ,设外接球的半径为R ,则OA OP R ==,在ABC 中,由正弦定理得2,BC r sin BAC ==∠解得1r =,即11O A =, 在1Rt PAO 中,12,PO =在1Rt AOO ,中22211OO AO AO +=,即()22221R R -+=,解得:54R =, 所以外接球的体积为:3344125334854R V πππ⎛⎫⋅ ⎪⎝⎭===, 故答案为:12548π 四、解答题17.(2022·安徽芜湖·高一期末)如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终不离开桌面,设直径AB 所在直线与桌面所成的角为α.要使倾斜后容器内的溶液不会溢出,求α的最大值. 【答案】4π【解析】【分析】当水杯倾斜过程中,溶液恰好不溢出时,此时α最大;在这个临界条件下,结合溶液的体积不变,可以得到关于α的一个不等式,即可求出α的取值范围,得到最大值.【详解】如图所示,在Rt △CDE 中20tan DE α=,()2221020tan 103020tan 10202παπαπ⨯⨯⨯⨯-+≥⨯⨯解得tan 1α≤,即α的最大值4π. 18.(2022·全国·南宁二中高三期末(文))图1是由矩形ABGF ,Rt ADE △和菱形ABCD 组成的一个平面图形,其中2AB =,1==AE AF ,60BAD ∠=︒,将该图形沿AB ,AD 折起使得AE 与AF 重合,连接CG ,如图2.(1)证明:图2中的C ,D ,E ,G 四点共面;(2)求图2中三棱锥C BDG -的体积.【答案】(1)证明见解析【解析】【分析】(1)依题意可得//AB FG ,//AB CD ,即可得到//AB GE ,从而得到//CD EG ,即可得证;(2)依题意可得AE AD ⊥、AE AB ⊥,即可得到AE ⊥平面ABCD 从而得到BG ⊥平面ABCD ,再根据13C BDG G BCD BCD V V BG S --==⋅计算可得;(1)证明:在矩形ABGF 和菱形ABCD 中,//AB FG ,//AB CD ,所以//AB GE ,所以//CD EG ,所以C 、D 、E 、G 四点共面;(2)解:在Rt ADE △中AE AD ⊥,矩形ABGE 中AE AB ⊥,AD AB A ⋂=,,AD AB ⊂平面ABCD ,所以AE ⊥平面ABCD ,又//BG EA ,所以BG ⊥平面ABCD ,又11sin 2222BCD S BC CD BCD =⋅⋅∠=⨯⨯=所以11133C BDG G BCD BCD V V BG S --==⋅=⨯ 19.(2022·山西吕梁·高一期末)如图是某种水箱用的“浮球”,它是由两个半球和一个圆柱筒组成.已知球的半径是2cm ,圆柱筒的高是2cm .(1)求这种“浮球”的体积;(2)要在100个这种“浮球”的表面涂一层防水漆,每平方厘米需要防水漆0.5g ,共需多少防水漆?【答案】(1)356(cm)3π (2)1200g π【解析】【分析】(1)由球的体积公式和圆柱的体积公式求解即可;(2)由球的表面积公式和圆柱的侧面积公式求解即可.(1)因为该“浮球”的圆柱筒底面半径和半球的半径2cm r =,圆柱筒的高为2cm ,所以两个半球的体积之和为331432(cm)33V r ππ==, 圆柱的体积2328(cm)V r h ππ==,∴该“浮球”的体积是31256(cm)3V V V π=+=; (2)根据题意,上下两个半球的表面积是221416(cm)S r ππ==,而“浮球”的圆柱筒侧面积为2228(cm)S rh ππ==,∴“浮球”的表面积为21224(cm)S S S π=+=;所以给100个这种浮球的表面涂一层防水漆需要100240.51200g ππ⨯⨯=.20.(2022·全国·高三专题练习)如图1,在直角梯形ABCD 中,//AD BC ,∠BAD =90°,12AB BC AD a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图2中1A BE 的位置,使平面1A BE ⊥平面BCDE ,得到四棱锥1A BCDE -.当四棱锥1A BCDE -的体积为a 的值.【答案】6a =.【解析】【分析】在直角梯形ABCD 中,证明BE AC ⊥,在四棱锥1A BCDE -中,由面面垂直的性质证得1A O ⊥平面BCDE ,再利用锥体体积公式计算作答.【详解】如图,在直角梯形ABCD 中,连接CE ,因E 是AD 的中点,12BC AD a ,有//,AE BC AE BC =,则四边形ABCE 是平行四边形,又,90BAD AB BC ∠==,于是得ABCE 是正方形,BE AC ⊥,在四棱锥1A BCDE -中,1BE AO ⊥,因平面1A BE ⊥平面BCDE ,且平面1A BE 平面BCDE BE =,1A O ⊂平面1A BE ,因此1A O ⊥平面BCDE ,即1A O 是四棱锥1A BCDE -的高,显然112AO AO CO AC ====,平行四边形BCDE 的面积2S CO BE a =⋅==,因此,四棱锥1A BCDE -的体积为2311133V S AO a =⋅===6a =, 所以a 的值是6.21.(2022·北京·高一期末)《九章算术》中对一些特殊的几何体有特定的称谓,例如:将底面为直角三角形的直三棱柱称为堑堵,将一堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥)和一个鳖臑 (四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中,已知3AB =,4BC =,5AC =.当阳马111C ABB A -体积等于24时, 求:(1)堑堵111ABC A B C -的侧棱长;(2)鳖臑1C ABC -的体积;(3)阳马111C ABB A -的表面积.【答案】(1)6(2)12 (3)51313【解析】【分析】(1)设堑堵111ABC A B C -的侧棱长为x ,根据阳马111C ABB A -体积等于24求解即可;(2)根据棱锥的体积计算即可;(3)分别计算111C ABB A -的侧面积与底面积即可(1)因为3AB =,4BC =,5AC =,所以222AB BC AC +=.所以△ABC 为直角三角形.设堑堵111ABC A B C -的侧棱长为x ,则113A ABB S x 矩形,则111143243AA BB V x C , 所以6x =,所以堑堵111ABC A B C -的侧棱长为6.(2)因为13462ABC S =⨯⨯=△, 所以1111661233ABC ABC V S CC C . 所以鳖臑1C ABC -的体积为12.(3) 因为11113462A B C S,11164122BB C S , 11165152AA C S ,1132133132ABC S , 113618A ABB S 矩形,所以阳马111C ABB A -的表面积的表面积为612151831351313. 22.(2022·重庆市巫山大昌中学校高一期末)如图,AB 是圆柱OO '的一条母线,BC 过底面圆心O ,D 是圆O 上一点.已知5,3AB BC CD ===,(1)求该圆柱的表面积;(2)将四面体ABCD 绕母线AB 所在的直线旋转一周,求ACD △的三边在旋转过程中所围成的几何体的体积.【答案】(1)75π2(2)15π【解析】【分析】(1)由题意求出柱的底面圆的半径即可求解;(2)ACD △绕AB 旋转一周而成的封闭几何体的体积为两个圆锥的体积之差,结合圆锥体积公式求解即可(1)由题意知AB 是圆柱OO '的一条母线,BC 过底面圆心O ,且5AB BC ==, 可得圆柱的底面圆的半径为52R =, 则圆柱的底面积为221525πππ24S R ⎛⎫==⨯= ⎪⎝⎭, 圆柱的侧面积为252π2π525π2S Rl ==⨯⨯= 所以圆柱的表面积为12257522π25ππ42S S S =+=⨯+=. (2) 由线段AC 绕AB 旋转一周所得几何体为以BC 为底面半径,以AB 为高的圆锥,线段AD 绕AB 旋转一周所得的几何体为BD 为底面半径,以AB 为高的圆锥,所以以ACD △绕AB 旋转一周而成的封闭几何体的体积为:22221111πππ55π4515π3333V BC AB BD AB =⋅⋅-⋅⋅=⋅⋅-⋅⋅=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修二《空间几何体的表面积和体积》基础练习题1. 已知圆锥的表面积为6,且它的侧面展开图是一个半圆,则这个圆锥的底面半径为( )A.√2πB.√1πC.√2πD.√π2. 长方体的长,宽,高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为( ) A.12π B.13π C.14π D.15π3. 已知三边长分别为4、5、6的△ABC 的外接圆恰好是球O 的一个大圆,P 为球面上一点,若点P 到△ABC 的三个顶点的距离相等,则三棱锥P −ABC 的体积为:( ) A.8 B.10 C.20 D.304. 中心角为135∘的扇形,其面积为S 1,其围成的圆锥的表面积为S 2,则S1S 2=( )A.118B.138C.811D.8135. 已知一个正四棱锥的底面边长为2,高为√3,则该正四棱锥的全面积为( ) A.8 B.12 C.16 D.206. 在三棱柱ABC −A 1B 1C 1中,若AB =4,BC =3,AA 1=12,且AB ⊥BC ,AA 1⊥底面ABC ,E 为AA 1的中点,从E 拉一条绳子绕过侧棱CC 1到达B 点的最短绳长为( )A.2√2B.2√3C.8D.10 7. 圆锥的底面积为4π,其轴截面是正三角形,则其侧面积是( ) A.2π B.4π C.8π D.16π8. 已知三棱锥A −BCD 中,AB =AC =BD =CD =2,BC =2AD ,直线AD 与底面BCD 所成角为π3,则此时三棱锥外接球的体积为( ) A.8πB.√2π3C.4√2π3D.8√23π9. 某几何体的三视图如图,它的侧视图与正视图相同,则它的体积为( )10. 设地球半径为R ,在北纬45∘圈上有甲、乙两地,它们的经度差为90∘,则甲、乙两地间的最短纬线之长为________,甲、乙两地的球面距离为________.11. 一个几何体的三视图如图所示(单位:m ),则该几何体的体积为________m 3. 12. 设地球的半径为R ,赤道上东经40∘的点A 与北纬45∘、东经130∘的点B 的球面距离是________.13. 一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为________.A.2+4√2π3B.4+8√2π3C.2+8√2π3D.4+4√2π314. 圆锥的底面半径为3,高是4,在这个圆锥内部有一个内切球,则此内切球的半径为________.15. 一圆锥的内切球的表面积与圆锥的侧面积之比为2:3,则该圆锥母线与底面的夹角为________.16. 若某多面体的三视图如图所示,则此多面体的体积为________,外接球的表面积为________.17. 在三棱锥P−ABC中,AP,AB,AC两两垂直,且AP=AB=AC=√3,则三棱锥P−ABC的内切球的表面积为________.18. 如图是某几何体的三视图,则它的体积为________.19. 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为________.参考答案一、选择题1.A解:设圆锥的底面半径为r,母线长为l,∵圆锥的侧面展开图是一个半圆,∴2πr=πl,∴l=2r,∵圆锥的表面积为πr2+πrl=πr2+2πr2=6,∴r2=2π,即r=√2π.故选A.2.C解:设该球的半径为R,则该球的半径等于长方体体对角线的一半,即R=√32+22+122=√142,所以该球的表面积=4πR2=14π.故选C.3.B解:P在面ABC上的射影为O,则OA=OB=OC=OP=R,∴S△ABC=12absinC=abc4R∴V P−ABC=13S ABC R=abc12=10,故选B 4.C解:设扇形半径为1,则扇形弧长为1×3π4=3π4,设围成圆锥的底面半径为r,则2πr=3π4,r=38,扇形的面积S1=12×1×3π4=3π8,圆锥的表面积S2=S1+πr2=3π8+9π64=33π64,∴S1S2=811.故选C.5.B如图,四棱锥P−ABCD为正四棱锥,高OP=√3,底面边长AB=2.过O作OG⊥BC,垂足为G,连接PG,则斜高PG=√1+3=2.∴正四棱锥的全面积是S=2×2+4×1×2×2=12.26.D解:如图,把三棱柱ABC−A1B1C1展成平面图得到矩形ABB1A1,E为AA1的中点,连接EB,则从E拉一条绳子绕过侧棱CC1到达B点的最短绳长为EB,因为三棱柱ABC−A1B1C1的底边AB=4,BC=3,AC=5,所以展开图中AB=8,则侧棱长为12,E为AA1的中点,可得AE=6,所以从E拉一条绳子绕过侧棱CC1到达B点的最短绳长为EB=√AE2+AB2=10,故选D.7.C解:如图:根据题意,设圆锥的底面半径为r,母线长为l,高等于ℎ.∵底面积为4π,∴πr2=4π,解得r=2.又∵圆锥的轴截面是正三角形,∴l=2r=4,ℎ=√3r=2√3,可得圆锥的侧面积是S=πrl=π×2×4=8π.故选C.8.D解:如图所示,取BC的中点O,连接OA,OD.∵AB=AC=BD=CD=2,∴OD⊥BC,OA⊥BC,OA∩OD=O,∴BC⊥平面OAD,BC⊂平面BCD,∴平面OAD⊥平面BCD,平面OAD∩平面BCD=OD,∴AD在平面BCD是射影是OD,∴∠ADO=π3.又OA=OD,∴△OAD是等边三角形,设AD=x,则OD=OC=OB=x,∴2x2=4,∴x=√2,∴点O是三棱锥A−BCD的外接球的球心,因此外接球的半径R=√2.∴外接球的体积V=43πR3=8√2π3.故选D.9.D由三视图知:几何体是长方体与半球体的组合体,长方体的底面是的对称线长为2√2正方形,高为1,球的半径为√2,故体积为12×2√2×2√2×1+12×43π×(√2)3=4+4√23π,二、填空题10. √24πR,π3R解:设甲、乙两地分别对应球面上A、B两点,由题意得:北纬45∘圈小圆Q的半径为r=Rcos45∘=√22R,∴甲、乙两地间的最短纬线之长为π2×√22R=√24πR.∵甲、乙两地的经度差为140∘−50∘=90∘,∴Rt△AQB中,AB=R,∴△AOB是边长为R的等边三角形,可得甲、乙两地的球心角∠AOB=60∘,π故答案为:√24πR,π3R.11. 8π3解:根据几何体的三视图,得;该几何体是底面相同的圆柱与两个圆锥的组合体,且圆柱底面圆的半径为1,高为2,圆锥底面圆的半径为1,高为1;∴该几何体的体积为V几何体=2×13π⋅12×1+π⋅12⋅2=83π.故答案为:83π.12. π2R解:如图,C是赤道面内,B在上的射影,由题意∠BOC=90∘,∠AOC=45∘,所以有三面角公式可得:cos∠AOB=cos90∘cos45∘=0,所以∠AOB=π2;A、B两点的球面距离是:R(π2).故答案为:π2R.13. 2+2√6解:根据几何体的三视图得,该几何体是底面为等腰三角形,高为2的三棱锥,如图所示,S△PAC=12×2×2=2,S△PAB=12×2×√22+12=√5△PBC中,PC=2√2,PB=3,BC=√5,∴cos∠BPC=(2√2)2+32−(√5)22×2√2×3=√22,∴∠BPC=π4,∴S△PBC=12×3×2√2×sinπ4=3,∴该三棱锥的侧面积是S侧=2+√5+3=5+√5故答案为:5+√5.14. 32解:如图所示,作出轴截面,∵CD=3,AD=4,∴AC=5,∵∴OEAO =CDAC.Rt△AOE∼Rt△ACD,设OE=R,则AO=4−R,∴R4−R =35,∴R=32.故答案为:32.15. 60∘解:设内切球的半径为r,圆锥的底面半径为R,母线长为l,由S△=12lr+12lr+12×2R×l=12×2R×√l2−R2得r=R√l2−R2l+R,由4πr2πRl =23得lR=2,所以夹角为60∘.故答案为:60∘.16. 13,3π解:由三视图可知:该几何体是正方体的内接正四面体(红颜色),∴多面体的体积为1−4×13×12×1×1×1=13.此多面体外接球的直径是此正方体的对角线√3.因此其球的表面积是4π⋅(√32)2=3π.故答案为:13;3π.17.(4−2√3)π解:三棱锥体积为S P−ABC=13×12×(√3)3=√32,其图像如图所示,设内接球的半径为r,且S△ABP=S△ACP=S△ABC,∴3⋅13r⋅S△PAB+13r⋅S△BCP=√32,解得r =√3−12,∴ 三棱锥P −ABC 的内切球表面积为4π(√3−12)2=(4−2√3)π,故答案为:(4−2√3)π. 18. 203或163解:由题意三视图对应的几何体如图1所示,所以几何体的体积为正方体的体积减去一个三棱锥的体积,即:23−13×12×2×2×2=203.或者,三视图对应的几何体如图2所示, 则它的体积为203−43=163.故答案为:203或163. 19.50π。
