2016-2017学年宁夏石嘴山市平罗中学高三(上)期中数学试卷和答案(文科)
数学---宁夏石嘴山市第三中学2017届高三上学期期中考试(文)
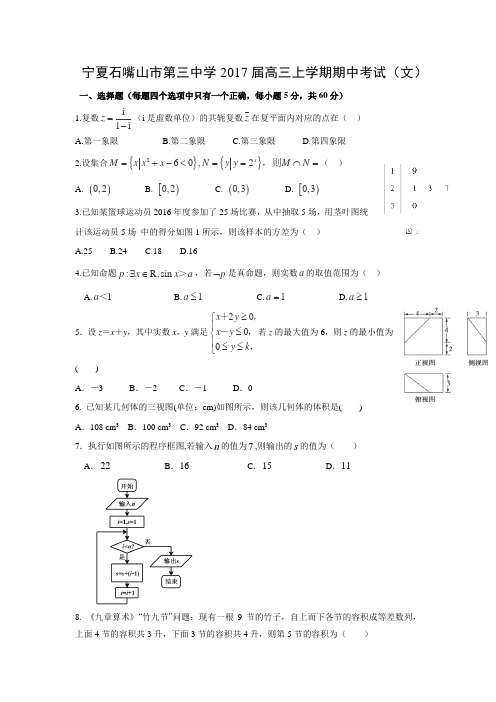
宁夏石嘴山市第三中学2017届高三上学期期中考试(文)一、选择题(每题四个选项中只有一个正确,每小题5分,共60分) 1.复数i1iz =-(i 是虚数单位)的共轭复数z 在复平面内对应的点在( ) A.第一象限B.第二象限C.第三象限D.第四象限2.设集合{}{}260,2x M x x x N y y M N =+-<==⋂=,则( ) A. ()0,2B. [)0,2C. ()0,3D. [)0,33.已知某篮球运动员2016年度参加了25场比赛,从中抽取5场,用茎叶图统计该运动员5场 中的得分如图1所示,则该样本的方差为( ) A.25B.24C.18D.164.已知命题:R,sin p x x a ∃∈>,若p ⌝是真命题,则实数a 的取值范围为( ) A.1<a B.1≤a C.1=a D.1≥a5.设z =x +y ,其中实数x ,y 满足20 00x y x y y k ≥⎧⎪≤⎨⎪≤≤⎩+,-,,若z 的最大值为6,则z 的最小值为( )A .-3B .-2C .-1D .06. 已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( ) A .108 cm 3 B .100 cm 3 C .92 cm 3 D .84 cm 37.执行如图所示的程序框图,若输入n 的值为7,则输出的s 的值为( ) A .22 B .16 C .15 D .118. 《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为( )A.1升B.升C.升D.升9.直线()0,0022>>=+-b a by ax ,被圆014222=+-++y x y x 截得的弦长为4,则ba 11+的最小值为( ) A .41 B .2 C .21D .410.已知点,,在圆上运动,且,若点的坐标为,则的最大值为( )A.6B.7C.8D.911.双曲线C 的左右焦点分别为12,F F ,且2F 恰为抛物线24y x =的焦点,设双曲线C 与该抛物线的一个交点为A ,若12AF F ∆是以1AF 为底边的等腰三角形,则双曲线C 的离心率为( )B.1C.1D.2+12. 函数(){}2,min-=x x x f ,其中,若动直线与函数的图像有三个不同的交点,它们的横坐标分别为、、,则的取值范围是 ( )A .()32,B .()43,C .()54,D .()65,二、填空题:(每题5分,共20分)13.已知,lg ,24a x a==则x =________.14.等比数列的各项均为正数,且,则________.15.抛物线C :y 2=2px (p >0)的焦点为F ,M 是抛物线C 上的点,若△OFM 的外接圆与抛 物线C 的准线相切,且该圆面积为36π,则p = .16.在四面体S ﹣ABC 中,SA ⊥平面ABC ,∠BAC =120°,SA =AC =2,AB =1,则该四面体的外 接球的表面积为 . 三、解答题:(共6道题,满分70分)A B C 221x y +=AB BC ⊥P (2,0)PA PB PC ++{}n a 154a a =2122232425log +log +log +log +log =a a a a a17.(本小题满分12分)如图△ABC 中,已知点D 在BC 边上,且(1)求AD 的长, (2)求cos C .18.如图,四面体中,、分别的中点,,.(1)求证:平面; (2)求点到平面的距离.19.为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:0,sin 3AD AC BAC ⋅=∠=AB BD ==ABCD O E BD BC 2CA BC CD BD ====AB AD ==AO ⊥BCD E ACD(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;(2)用简单随机抽样方法从这条道路中抽取条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过的概率.20.如图,DP⊥x轴,点M在DP的延长线上,且|DM|=2|DP|.当点P在圆x2+y2=1上运动时.(1)求点M的轨迹C的方程;(2)过点T(0,t)作圆x2+y2=1的切线交曲线C于A,B两点,求△AOB面积S的最大值和相应的点T的坐标.21.(本小题满分12分)已知函数2()ln(1)1f x p x p x=+-+.625.0(1)讨论函数的单调性;(2)当时,()f x kx ≤恒成立,求实数的取值范围;(3111请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一部分,做答时请写清题号.22.如图,已知AD ,BE ,CF 分别是△ABC 三边的高,H 是垂心,AD 的延长线交△ABC 的外接圆于点G .求证:DH =DG .23.在直角坐标系中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C :ρsin 2θ=2cos θ,过点P (-2,-4)的直线l :⎩⎨⎧x =-2+22ty =-4+22t(t 为参数)与曲线C 相交于M ,N两点.(1)求曲线C 的直角坐标方程和直线l 的普通方程; (2)证明|PM |,|MN |,|PN |成等比数列.选修4—5:不等式选讲24、设函数1()11()2f x x x x R =++-∈的最小值为a . (1)求a ;(2)已知两个正数,m n 满足22,m n a +=求11m n+的最小值. 参考答案一、选择题二、填空题 13.1014.5 15.8 16.三、解答题 17.(1)3(2)36 18.(1)证明:连结.∵,,∴. ∵,,∴.在中,由已知可得,,而,∴,∴,即.,∴平面.(2)解:设点到平面的距离为. ∵,∴, 在△ACD 中,CA =CD =2,AD =,∴, 而,,∴,∴点E 到平面ACD 的距离为.19.解:(1)6条道路的平均得分为∴该市的总体交通状况等级为合格.(2)设表示事件“样本平均数与总体平均数之差的绝对值不超过”OC BO DO =AB AD =AO BD ⊥BO DO =BC CD=CO BD ⊥AOC ∆1AO=CO =2AC =222AO CO AC +=90AOC ∠=AO OC ⊥BD OC O = AO ⊥BCD E ACD h A ACD A CDE V V --=1133ACD CDES h S AO ∆∆⋅=⋅212ACDS ∆==1AO =2122CDE S ∆==17CDE ACDAO S h S ∆∆⋅===7215.7)1098765(61=+++++A 5.0从条道路中抽取条的得分组成的所有基本事件为:,,,,,,,,,,,,,,共个基本事件事件包括,,,,,,共个基本事件.…10分 ∴. 答:该样本平均数与总体平均数之差的绝对值不超过的概率为. 20.解:(1)设点M 的坐标为(x ,y ),点P 的坐标为(x 0,y 0), 则x =x 0,y =2y 0,所以x 0=x ,y 0=,①因为P (x 0,y 0)在圆x 2+y 2=1上,所以x 02+y 02=1②,将①代入②,得点M 的轨迹方程C 的方程为x 2+=1;…(2)由题意知,|t |≥1,设切线l 的方程为y =kx +t ,k ∈R ,由,得(4+k 2)x 2+2ktx +t 2﹣4=0③,设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2), 由③得:x 1+x 2=﹣,x 1x 2=,又直线l 与圆x 2+y 2=1相切,得=1,即t 2=k 2+1,∴|AB |===,又|AB |==≤2,且当t =±时,|AB |=2,综上,|AB |的最大值为2,62)6,5()7,5()8,5()9,5()10,5()7,6()8,6()9,6()10,6()8,7()9,7()10,7()9,8()10,8()10,9(15A )9,5()10,5()8,6()9,6()10,6()8,7()9,7(7157)(A P 5.0157依题意,圆心O到直线AB的距离为圆x2+y2=1的半径,∴△AOB面积S=|AB|×1≤1,当且仅当t=±时,△AOB面积S的最大值为1,相应的T的坐标为(0,﹣)或(0,).21.(本小题满分12分)解:(1)的定义域为(0,+∞),p 时,>0,故在(0,+∞)单调递增;当1当时,<0,故在(0,+∞)单调递减;当0<<1时,令=0,解得.则当时,>0;时,<0.故在单调递增,在单调递减(2)因为,所以p=时,恒成立当1令,则,因为,由得,且当时,;当时,.所以在上递增,在上递减.所以,故(3)由(2)知当时,有,当时,即,令,则,即所以,,…,,相加得而所以,22、解:连结CG ,∵AD ⊥BC ,∴∠ABC +∠GAB =90°同理可得∠ABC +∠FCB =90°,从而得到∠GAB =∠FCB =90°﹣∠ABC 又∵∠GAB 与∠GCB 同对弧BG , ∴∠GAB =∠GCB ,可得∠GCB =∠FCB , ∵CD ⊥GH ,即CD 是△GCH 的高线∴△CHG 是以HG 为底边的等腰三角形,可得DH =DG .23.解:(1)把⎩⎪⎨⎪⎧x =ρcos θy =ρsin θ代入ρsin 2θ=2cos θ,得y 2=2x由⎩⎨⎧x =-2+22ty =-4+22t(t 为参数),消去t 得x -y -2=0∴曲线C 的直角坐标方程和直线l 的普通方程分别是y 2=2x ,x -y -2=0.(2)证明将⎩⎨⎧x =-2+22ty =-4+22t (t 为参数)代入y 2=2x ,整理得t 2-102t +40=0. 设t 1,t 2是该方程的两根,则t1+t2=102,t1·t2=40,∵|MN|2=(t1-t2)2=(t1+t2)2-4t1·t2=40 |PM|·|PN|= t1·t2=40,∴|MN|2==PM|·|PN| ∴|PM|,|MN|,|PN|成等比数列……10分24、解:(1)函数3-,2211()11=2,21 223,12x xf x x x x xx x⎧≤-⎪⎪⎪=++--+-<<⎨⎪⎪≥⎪⎩,当x∈(﹣∞,1]时,f(x)单调递减当x∈[1,+∞)时,f(x)单调递增,所以当x=1时,f(x)的最小值a=32.(2)由(1)知m2+n2=32,由m2+n2≥2mn,得mn≤34,∴≥43故有+≥2≥43,当且仅当m=n=3时取等号.所以+的最小值为43.。
宁夏平罗中学2017届高三第一次模拟考试数学(文)试题含答案

——————————装——————————订——————————线————————————平罗中学2017届高三第一次模拟考试能力测试文科数学第I卷(选择题)一、选择题:本大题12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1,0,1M=-,{}(2)(1)0N x x x=+-<,则M N=A。
{}1,0M=- B.{}0,1M=C。
{}0M= D.{}1M=-2.已知),(211Rbaiaibi∈+=+-,其中i为虚数单位,则=+baA.4-B.4C.10-D.103.下列命题中正确的是A.若p q∨为真命题,则p q∧为真命题B.“5x=”是“2450x x--=”的充分不必要条件C.命题“若1x<-,则2230x x-->”的否命题为:“若1x<-,则2230x x--≤”D.已知命题p:x R∃∈,210x x+-<,则p⌝:x R∃∈,210x x+-≥4.在公差不为零的等差数列{}na中,731,,aaa依次成等比数列,前7项和为35,则数列{}na 的通项等于A .nB .1+n C. 12-n D .12+n5.若4sin 3cos 0αα-=,则21cos 2sin 2αα+的值为A .2516B .1C 。
2548D .25646.执行下图的程序框图,如果输入的46a b ==,,那么 输出的n =A 3B . 4C 。
5D 6 7.设直线1+=x y 与纵轴及直线2=y 所围成的封闭图形为区域D ,不等式组⎩⎨⎧≤≤≤≤-2011y x 所确定的区域为E,在区 域E 内随机取一点,该点恰好在区域D 的概率为A.41 B 。
81 C.21 D. 以上答案均不正确8。
函数()ln f x x x =-212的递减区间为 A. (),-∞1 B 。
(),01 C 。
(),+∞1 D 。
(),+∞09. 某几何体的三视图如图所示,则该几何体的体积为A. 2 B 。
宁夏平罗中学高三数学上学期第二次(10月)月考试题 文(无答案)

班级_________ 姓名____________ 学号_____________ 考场号_____________ 座位号_________——————————装——————————订——————————线————————————平罗中学2016—2017学年度第一学期第二次月考试卷高三数学(文)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}2|280,3,1,1,3,5A x x x B =-->=--,则A B =I ( )A .{}1,1,3-B .{}3,1,1--C .{}3,5-D .{}3,52.=ο300sin ( )A .23-B .21- C .21D .233.已知命题:R p x ∀∈, sin 1x ≤,则 ( ) A .:R p x ⌝∃∈,sin 1x ≥ B .:R p x ⌝∀∈,sin 1x ≥ C .:R p x ⌝∃∈,sin 1x > D .:R p x ⌝∀∈,sin 1x > 4.下列函数中,在其定义域内既是奇函数又是减函数的是( )A. 3x y -= B. x y 21log = C. x y = D. x y )21(=5.三个数60.70.70.76log 6,,的大小关系为 ( ) A 60.70.70.7log 66<< B 60.70.70.76log 6<<C 0.760.7log 660.7<< D 60.70.7log 60.76<<6. 已知ABC ∆中,6,30,120AB A B ===o o,则ABC ∆的面积为( )A .9B .18C .93D .183 7.若()13124sin ,53sin ,,43,=⎪⎭⎫ ⎝⎛--=+⎪⎭⎫⎝⎛∈πββαππβα,则=⎪⎭⎫ ⎝⎛+4cos πα( )A.6556 B. 6516- C. 6556- D.6556或6516- 8.为了得到函数sin 23y x π⎛⎫=+⎪⎝⎭的图像,只需将函数sin y x =的图象上所有的点( )A .横坐标伸长到原来的2倍,再向左平行移动3π个单位长度 B .横坐标缩短到原来的12倍,再向左平行移动3π个单位长度C .横坐标缩短到原来的12倍,再向左平行移动6π个单位长度D .横坐标缩短到原来的12倍,再向右平行移动6π个单位长度9.函数sin()(0,0,0)y A x A ϖϕϖϕπ=+>><<在一个周期内的图象如下,此函数的解析式为( )A .22sin(2)3y x π=+B .2sin(2)3y x π=+ C .2sin()23x y π=-D .2sin(2)3y x π=- 10.已知函数221,1(x),1xx f x ax x ⎧+<⎪=⎨+≥⎪⎩,若[]2(0)4f f a =+,则实数a =( )A .0B .2C .2-D .0或2 11.若 是三角形的最小内角,则函数的最小值是( ) A.B.C. D.12.已知函数()()sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭,其图象相邻两条对称轴之间的距离为2π,且函数12f x π⎛⎫+⎪⎝⎭是偶函数.下列判断正确的是( )A .函数()f x 的最小正周期为2πB .函数()f x 的图象关于点7,012π⎛⎫⎪⎝⎭对称C .函数()f x 的图象关于712x π=-对称 D .函数()f x 在3,4ππ⎡⎤⎢⎥⎣⎦上单调递增二、填空题:本大题共4小题,每小题5分. 13.函数3)4lg(--=x x y 的定义域是14.函数()ln (0)f x x x x =>的单调递增区间是____.15 在ABC ∆中,135sin 3a b A ===,,,则sin B = 16.若sin α+cos αsin α-cos α=3,tan(α-β)=2,则tan(β-2α)=____三、解答题:解答应写出文字说明.证明过程或演算步骤 17.(本小题满分10分)(1)化简f(a)=3sin()cos()cos()2cos(3)sin(3)ππαπααπαπα-++-+;(2)求f (623π-)的值;18.(本小题满分12分)已知c bx ax x f ++=24)( 图象经过点(0,1),且在1x =处的切线方程是2y x =- (1)求)(x f y =的解析式; (2)求)(x f y =的单调递增区间。
2019-2020学年宁夏石嘴山市平罗中学高三(上)期中数学试卷试题及答案(文科)(PDF版 含答案)

D. 5 2
D. b a c
4.“ 2k (k Z ) ”是“ cos 2 ”的 (
)
4
2
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
5.已知角 的顶点为坐标原点,始边与 x 轴的非负半轴重合,且 tan 2 .若角 的终边 3
-2-
题,每个试题考生都必须作答.第 22、23 题为选考题,考生根据要求作答.(一)必考题: 共 60 分) 17.已知角 的顶点与原点 O 重合,始边与 x 轴的非负半轴重合,它的终边过点 P(3 , 4) .
55 (Ⅰ)求 sin( ) 的值; (Ⅱ)若角 满足 sin( ) 5 ,求 cos 的值.
(Leabharlann )A.2B. 3 2
C.1
D. 1 2
7.已知数列{an} 满足
a1
2, an1
an an 1
,则
an
(
)
A. 2 n
B.
2 2n
1
C. 2n 1 2
D.
2 2n
1
8.函数 f (x) x2ln | x | 的图象大致是 ( )
A.
B.
-1-
C.
D.
9.已知
|
a
|
13.曲线 y 2x x3 在点 (1, 1) 处的切线方程为
.
14.已知 sin
3cos
,则 cos 2 1 sin 2
.
15.已知向量
a
(1,
2),
b
2016年宁夏石嘴山市平罗中学高考数学三模试卷(文科) 含解析

2016年宁夏石嘴山市平罗中学高考数学三模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|2x≥1,x∈R},集合N={x||x﹣2|≥3,x∈R},则M∩N=()A.(﹣∞,﹣1]B.[﹣1,0]C.[5,+∞)D.∅2.已知向量=(0,4),=(2,2),则下列结论中正确的是()A.B.C.D.3.在复平面内,复数g(x)满足,则z的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限4.根据如图所示的程序,当输入a,b分别为2,3时,最后输出的m的值是( )A.0 B.2 C.3 D.15.设函数f(x)=,则f[f(﹣1)]=()A.﹣1 B.1 C.﹣2 D.26.如图为某几何体的三视图,则该几何体的表面积为()A.20+2π B.20+3π C.24+2π D.24+3π7.在等比数列{a n}中,a3,a15是方程x2﹣6x+8=0的根,则的值为()A.B.4 C.D.±48.设x,y满足,则z=x+y()A.有最小值2,最大值3 B.有最小值2,无最大值C.有最大值3,无最小值D.既无最小值,也无最大值9.过双曲线=1(a>0,b>0)的焦点且垂直于实轴的直线交双曲线的渐近线于A,B两点,已知|AB|等于虚轴长的两倍,则该双曲线的离心率为( )A.B.C.D.210.在区间[0,1]上随机取两个实数a、b,则函数在区间[0,1]上有且只有一个零点的概率是()A.B.C.D.11.已知抛物线C:y2=16x,焦点为F,直线l:x=﹣1,点A∈l,线段AF与抛物线C的交点为B,若|FA|=5|FB|,则|FA|=( )A.B.35 C.D.4012.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当﹣6,若在区间(﹣2,6]内关于x的f(x)﹣log a(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是()A.(1,2) B.(2,+∞)C.D.二、填空题:本大题共4小题,每小题5分.13.已知||=2,||=2,与的夹角为45°,且λ﹣与垂直,则实数λ=.14.设等差数列{a n}的前n项和为S n,若a2=﹣11,a5+a9=﹣2,则当S n取最小值时,n等于.15.下列命题:。
宁夏石嘴山市高三上学期数学期中考试试卷

宁夏石嘴山市高三上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分) (2018高一上·温州期中) 已知集合A={1,2},集合B满足A∪B={1,2,3},则集合A的子集个数有________个;这样的集合B有________个.2. (1分) (2018高一上·武邑月考) 设,则 ________.3. (1分) (2016高一下·华亭期中) 若角α的终边经过点P(1,﹣2),则tan2α的值为________.4. (1分) (2018高二上·福州期末) 在正方体ABCD-A1B1C1D1中,下列给出四个命题:⑴四边形ABC1D1的面积为⑵ 的夹角为60°;⑶⑷则正确命题的序号是________.(填出所有正确命题的序号)5. (1分)(2019·青浦模拟) 不等式的解集是________6. (1分) (2018高三上·北京期中) 已知向量,则a与b夹角的大小为________.7. (1分) (2019高二下·深圳月考) 曲线在点处的切线的倾斜角为________8. (1分)(2018高二上·深圳期中) 已知变量满足约束条件若目标函数的最小值为2,则的最小值为________.9. (1分) (2017高二上·武清期中) 过点P(3,1)作直线l将圆C:x2+y2﹣4x﹣5=0分成两部分,当这两部分面积之差最小时,直线l的方程是________.10. (1分)计算:cos42°sin18°+sin42°cos18°=________11. (1分) (2016高一上·绵阳期末) 雾霾是人体健康的隐形杀手,爱护环境,人人有责.某环保实验室在雾霾天采用清洁剂处理教室空气质量.实验发现,当在教室释放清洁剂的过程中,空气中清洁剂的含剂浓度y(mg/m3)与时间t(h)成正比;释放完毕后,y与t的函数关系为y=()t﹣a(a为常数),如图,已知当教室的空气中含剂浓度在0.25mg/m3以上时,教室最适合人体活动.根据图中信息,从一次释放清洁剂开始,这间教室有________ h最适合人体活动.12. (1分)已知与的夹角为120°,若(+)⊥(﹣),且||=2,则在方向上的正射影的数量为________13. (1分) (2018高二上·南京月考) 抛物线与过焦点的直线交于两点,为原点,则________.14. (1分)在△ABC中,已知AB=8,AC=5,△ABC的面积是12,则cos(2B+2C)的值为________.二、解答题 (共6题;共15分)15. (2分) (2019高一下·湖州月考) 已知向量 , , .(1)求的坐标表示;(2)若与的夹角为 ,求 ;(3)若 ,求的值.16. (2分) (2019高二上·林芝期中) 解下列不等式:(1);(2)17. (2分)过点(0,4),斜率为﹣1的直线与抛物线y2=2px(p>0)交于两点A、B,且弦|AB|的长度为4.(1)求p的值;(2)求证:OA⊥OB(O为原点).18. (3分) (2017高二上·莆田月考) 已知椭圆的右焦点为,且点在椭圆上.(1)求椭圆的标准方程;(2)过椭圆上异于其顶点的任意一点作圆的两条切线,切点分别为(不在坐标轴上),若直线在轴,轴上的截距分别为,证明:为定值.19. (3分) (2018高三上·大连期末) 已知函数 .(1)时,求在上的单调区间;(2)且,均恒成立,求实数的取值范围.20. (3分) (2018高二下·遵化期中) 设函数(Ⅰ)讨论的单调性;(Ⅱ)若 a = 1 ,证明:当 x >0 时, f (x ) <e x − 1 .参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共15分)15-1、15-2、15-3、16-1、16-2、17-1、18-1、18-2、19-1、19-2、20-1、。
宁夏石嘴山市平罗中学2016届高三上学期期末数学试卷(文科)Word版含解析

2014-2015学年宁夏石嘴山市平罗中学高三(上)期末数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题所给的四个答案中有且只有一个答案是正确的.把正确选项涂在答题卡的相应位置上.)1.已知集合M={0,1,2,3},N={x|x 2﹣3x <0},则M∩N=( )A .{0}B .{x|x <0}C .{x|0<x <3}D .{1,2}2.复数z=(i 是虚数单位)在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.已知α为锐角,cos α=,则tan (+2α)=( )A .B .C .﹣3D .﹣24.已知向量,若向量与垂直,则k 的值为( )A .B .7C .D .5.连续抛掷两枚正方体骰子(它们的六个面分别标有1,2,3,4,5,6),记所得朝上的面的点数分别为x ,y ,过坐标原点和点P (x ,y )的直线的倾斜角为θ,则θ>60°的概率为( )A .B .C .D .6.已知三条不重合的直线m 、n 、l 与两个不重合的平面α、β,有下列命题:①若m∥n,n ⊂α,则m∥α;②若l⊥α,m⊥β,且l∥m,则α∥β;③若m ⊂α,n ⊂α,m∥β,n∥β,则α∥β; ④若α⊥β,α∩β=m ,n ⊂β,n⊥m,则n⊥α.其中正确的命题个数是( )A .1B .2C .3D .47.设x,y满足约束条件,则z=2x﹣y的最大值为()A.10 B.8 C.3 D.28.如图是一个空间几何体的三视图,则该几何体的侧面积为()A.B.C.8 D.129.已知p:A={x||x﹣a|<4},q:B={x|(x﹣2)(3﹣x)>0},若¬p是¬q的充分条件,则实数a的取值范围为()A.﹣1<a<6 B.a≤﹣1或a≥6C.a<﹣1或a>6 D.﹣1≤a≤610.已知函数:y=a n x2(a n≠0,n∈N*)的图象在x=1处的切线斜率为2a n﹣1+1(n≥2,n∈N*),且当n=1时其图象过点(2,8),则a7的值为()A.B.7 C.5 D.611.已知抛物线y2=2px(p>0)与双曲线的一条渐近线交于一点M(1,m),点 M 到抛物线焦点的距离为 3,则双曲线的离心率等于()A.3 B.4 C.D.12.定义在(0,)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则()A . f ()>f ()B .f (1)<2f ()sin1 C . f()>f () D . f ()<f ()二.填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上.)13.对某学校400名学生的体重进行统计,得到的频率分布直方图如图所示,则体重在75kg 以上的同学的人数为 .14.如果执行如图程序框图(判断条件k≤20?),那么输出的S= .15.在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,若b 2+c 2=a 2+bc ,且=4,则△ABC 的面积等于 . 16.下面给出的四个命题中:①以抛物线y 2=4x 的焦点为圆心,且过坐标原点的圆的方程为(x ﹣2)2+y 2=4;②若m=﹣2,则直线(m+2)x+my+1=0与直线(m ﹣2)x+(m+2)y ﹣3=0相互垂直;③命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”;④将函数y=sin2x的图象向右平移个单位,得到函数y=sin(2x﹣)的图象.其中是真命题的有(将你认为正确命题的序号都填上).三、解答题(共70分,解答应写出文字说明、证明过程或演算过程.)17.已知数列{a n}的前n项和S n=n2(n∈N*),数列{b n}为等比数列,且满足b1=a1,2b3=b4(1)求数列{a n},{b n}的通项公式;(2)求数列{a n b n}的前n项和.18.某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组.(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由.19.如图,在四棱锥P﹣ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.(I)若F为PE的中点,求证BF∥平面ACE;(Ⅱ)求三棱锥P﹣ACE的体积.20.过椭圆Γ: +=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为.(Ⅰ)求椭圆Γ的方程;(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且⊥?若存在,求出该圆的方程;若不存在,请说明理由.21.已知函数f(x)=lnx﹣kx+1.(1)求函数f(x)的单调区间;(2)若f(x)≤0恒成立,试确定实数k的取值范围;(3)证明:ln2≤n(n+1)(n∈N,n>1)请考生在第22,23,24题中选一题作答,并将答题卡上相应的题号涂黑.如果多做,则按所做第一题记分.22.如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B 作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.(Ⅰ)求证:AD∥EC;(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.23.,过点P(﹣2,﹣4)的直线l的参数方程为(t为参数),直线l与曲线C分别交于M、N两点.(1)写出曲线C和直线l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.24.=|x+a|+|x﹣2|.(1)当a=﹣3时,求不等式f(x)≥3的解集;(2)设集合A={x|f(x)≤|x﹣4|},集合B={x|1≤x≤2},且B⊆A,求a的取值范围.2014-2015学年宁夏石嘴山市平罗中学高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题所给的四个答案中有且只有一个答案是正确的.把正确选项涂在答题卡的相应位置上.)1.已知集合M={0,1,2,3},N={x|x2﹣3x<0},则M∩N=()A.{0} B.{x|x<0} C.{x|0<x<3} D.{1,2}【分析】求出N中不等式的解集确定出N,再找出两集合的交集即可.【解答】解:由N中的不等式变形得:x(x﹣3)<0,解得:0<x<3,即N=(0,3),∵M={0,1,2,3},∴M∩N=.故选:D【点评】本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.10.已知函数:y=a n x2(a n≠0,n∈N*)的图象在x=1处的切线斜率为2a n﹣1+1(n≥2,n∈N*),且当n=1时其图象过点(2,8),则a7的值为()A.B.7 C.5 D.6【分析】求导函数,利用y=a n x2(a n≠0,n∈N*)的图象在x=1处的切线斜率为2a n﹣1+1,可得数列相邻项的关系,进而利用等差数列的通项公式可求a7的值.【解答】解:求导函数,可得y′=2a n x,∵函数:y=a n x2(a n≠0,n∈N*)的图象在x=1处的切线斜率为2a n﹣1+1(n≥2,n∈N*),∴2a n=2a n﹣1+1(n≥2,n∈N*),∴a n﹣a n﹣1=(n≥2,n∈N*),∵当n=1时其图象过点(2,8),∴8=4a1,∴a1=2∴数列{a n}是以2为首项,为公差的等差数列∴a7=a1+6×=5故选C.【点评】本题考查导数知识的运用,考查等差数列,解题的关键是确定数列为等差数列.11.已知抛物线y2=2px(p>0)与双曲线的一条渐近线交于一点M(1,m),点 M 到抛物线焦点的距离为 3,则双曲线的离心率等于()A.3 B.4 C.D.【分析】利用抛物线的定义可得p的值,把点M(1,m)代入抛物线方程可得m,代入双曲线的一条渐近线方程可得,再利用双曲线的离心率e=即可得出.【解答】解:由题意,抛物线上的点M(1,m),点 M 到抛物线焦点的距离为 3,∴,解得p=4.∴知抛物线的方程为y2=8x,把点M(1,m)代入得m2=8,解得,取点.把点代入双曲线的一条渐近线方程得.∴双曲线的离心率e===3.故选A.【点评】熟练掌握圆锥曲线的定义和性质及其双曲线的离心率e=是解题的关键.12.定义在(0,)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则()A. f()>f()B.f(1)<2f()sin1 C. f()>f()D. f()<f()【分析】把给出的等式变形得到f′(x)sinx﹣f(x)cosx>0,由此联想构造辅助函数g(x)=,由其导函数的符号得到其在(0,)上为增函数,则,整理后即可得到答案.【解答】解:因为x∈(0,),所以sinx>0,cosx>0.由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx.即f′(x)sinx﹣f(x)cosx>0.令g(x)=x∈(0,),则.所以函数g(x)=在x∈(0,)上为增函数,则,即,所以,即.故选D.【点评】本题考查了导数的运算法则,考查了利用函数导函数的符号判断函数的单调性,考查了函数构造法,属中档题型.二.填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置上.)13.对某学校400名学生的体重进行统计,得到的频率分布直方图如图所示,则体重在75kg以上的同学的人数为64 .【分析】由频率分布直方图计算出体重在75kg以上的学生的频率,再乘以400即可.【解答】解:体重在75kg以上的学生的频率为:0.032×5=0.16所以体重在75kg以上的同学的人数为:400×0.16=64故答案为:64【点评】本题考查频率分布直方图,是基础知识、基本运算的考查,较简单.14.如果执行如图程序框图(判断条件k≤20?),那么输出的S= 420 .【分析】执行程序框图,分析程序框图的功能和意义,计算并输出S=2×(1+2+…+20)的值,不难计算为420.【解答】解:执行程序框图,有k=1S=0满足条件k≤20,第1次执行循环体,有S=2,k=2满足条件k≤20,第2次执行循环体,有S=2+4,k=3满足条件k≤20,第3次执行循环体,有S=2+4+6,k=4…满足条件k≤20,第19次执行循环体,有S=2+4+..+38,k=20满足条件k≤20,第20次执行循环体,有S=2+4+…+40,k=21不满足条件k≤20,退出执行循环体,输出S的值根据程序框图的意义和功能,得S=2×(1+2+…+20)=420故答案为:420.【点评】本题主要考察程序框图和算法,属于基础题.15.在△ABC中,角A,B,C所对的边分别是a,b,c,若b2+c2=a2+bc,且=4,则△ABC的面积等于2.【分析】利用已知表达式,通过余弦定理求出cosA,求出sinA,通过向量的数量积求出bc 的值,然后求出三角形的面积.【解答】解:因为b2+c2=a2+bc,所以cosA==,∴sinA=.因为,所以,bccosA=4,∴bc=8,△ABC的面积:S===2.故答案为:2.【点评】本题考查余弦定理的应用,向量的数量积的应用,三角形面积的求法,考查计算能力,注意整体思想的应用.16.下面给出的四个命题中:①以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的方程为(x﹣2)2+y2=4;②若m=﹣2,则直线(m+2)x+my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互垂直;③命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”;④将函数y=sin2x的图象向右平移个单位,得到函数y=sin(2x﹣)的图象.其中是真命题的有②③(将你认为正确命题的序号都填上).【分析】①求出抛物线的焦点,结合圆的方程进行求解.②根据直线垂直的关系进行判断.③根据含有量词的命题的否定进行判断.④根据三角函数的图象关系进行判断.【解答】解:①∵抛物线y2=4x的焦点(1,0)∴所求圆的圆心为(1,0)又∵所求圆过坐标原点,∴所求圆的半径R=1∴所求圆的方程为(x﹣1)2+y2=1,故①错误,②若m=﹣2,则两条直线方程为﹣2y+1=0与﹣4x﹣3=0,满足相互垂直;故②正确,③命题“∃x∈R,使得x2+3x+4=0”的否定是“∀x∈R,都有x2+3x+4≠0”;正确,故③正确,④将函数y=sin2x的图象向右平移个单位,得到函数y=sin2(x﹣)的图象.故④错误,故答案为:②③【点评】本题主要考查命题的真假判断,涉及知识点较多,综合性较强,但难度不大.三、解答题(共70分,解答应写出文字说明、证明过程或演算过程.)17.已知数列{a n}的前n项和S n=n2(n∈N*),数列{b n}为等比数列,且满足b1=a1,2b3=b4(1)求数列{a n},{b n}的通项公式;(2)求数列{a n b n}的前n项和.【分析】(1)利用数列的前n项和的公式,先求得a1,后看≥2时,a n=S n﹣S n﹣1,求得数列的通项公式,设出等比数列{b n}的公比,利用2b3=b4求得q,利用b1=a1求得首项,则等比数列的通项公式可求.(2)数列{a n b n}的前n项和为T n,然后利用错位相减法求得T n.【解答】解:(1)由已知S n=n2,得a1=S1=1当n≥2时,a n=S n﹣S n﹣1=n2﹣(n﹣1)2=2n﹣1所以a n=2n﹣1(n∈N*)由已知,b1=a1=1设等比数列{b n}的公比为q,由2b3=b4得2q2=q3,所以q=2所以b n=2n﹣1(2)设数列{a n b n}的前n项和为T n,则T n=1×1+3×2+5×22++(2n﹣1)2n﹣1,2T n=1×2+3×22+5×23++(2n﹣1)2n,两式相减得﹣T n=1×1+2×2+2×22++2×2n﹣1﹣(2n﹣1)2n(10分)=1+2(2+22++2n﹣1)﹣(2n ﹣1)2n=1+4(2n﹣1﹣1)﹣(2n﹣1)2n(11分)=﹣(2n﹣3)2n﹣3所以T n=(2n﹣3)2n+3【点评】本题主要考查了等差数列的性质和等比数列的性质.当数列是由等差数列和等比数列的积构成时,可求得利用错位相减法求和.18.某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组.(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由.【分析】(1)直接利用条件求出某职员被抽到的概率,然后求解科研攻关小组中男、女职员的人数;(2)列出基本事件的所有情况,求出选出的两名职员中恰有一名女职员的数目,即可求解概率;(3)实验结束后,第一次做实验的职员得到的实验数据为68,70,71,72,74,第二次做实验的职员得到的实验数据为69,70,70,72,74,求出两组数据的均值与方差,即可判断.【解答】解:(1)即:某职员被抽到的概率为.…(2分)设有x名男职员,则∴x=3即:男、女职员的人数分别是3,1.…(4分)(2)把3名男职员和1名女职员记为a1,a2,a3,b,则选取两名职员的基本事件有(a1,a2),(a1,a3),(a1,b),(a2,a1),(a2,a3),(a2,b),(a3,a1),(a3,a2),(a3,b),(b,a1),(b,a2),(b,a3),共12种,其中有一名女职员的有6种,所以,选出的两名职员中恰有一名女职员的概率为…(8分)(3),∴即第二次做实验的职员做的实验更稳定….(12分)【点评】本题考查古典概型的概率的求法,均值与方差的应用,基本知识的考查.19.如图,在四棱锥P﹣ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.(I)若F为PE的中点,求证BF∥平面ACE;(Ⅱ)求三棱锥P﹣ACE的体积.【分析】(I)由题意可得E、F都是线段PD的三等分点.设AC与BD的交点为O,则OE是△BDF 的中位线,故有BF∥OE,再根据直线和平面平行的判定定理证得BF∥平面ACE.(II )由条件证明CD⊥平面PAE ,再根据三棱锥P ﹣ACE 的体积V P ﹣ACE =V C ﹣PAE =S △PAE CD=(PAPD )AB=PAPDAB ,运算求得结果.【解答】解:(I )若F 为PE 的中点,由于底面ABCD 为矩形,E 为PD 上一点,AD=2AB=2AP=2,PE=2DE ,故E 、F 都是线段PD 的三等分点.设AC 与BD 的交点为O ,则OE 是△BDF 的中位线,故有BF∥OE,而OE 在平面ACE 内,BF 不在平面ACE 内,故BF∥平面ACE .(II )由于侧棱PA 丄底面ABCD ,且ABCD 为矩形,故有CD⊥PA,CD⊥AD,故CD⊥平面PAE ,.三棱锥P ﹣ACE 的体积V P ﹣ACE =V C ﹣PAE =S △PAE CD=(S △PAD )AB=(PAPD )AB=PAPDAB=121=.【点评】本题主要考查直线和平面垂直的判定定理的应用,用等体积法求棱锥的体积,属于中档题.20.过椭圆Γ:+=1(a >b >0)右焦点F 2的直线交椭圆于A ,B 两点,F 1为其左焦点,已知△AF 1B 的周长为8,椭圆的离心率为.(Ⅰ)求椭圆Γ的方程;(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P ,Q ,且⊥?若存在,求出该圆的方程;若不存在,请说明理由.【分析】(Ⅰ)由题意列关于a ,c 的方程组,求解方程组的a ,c 的值,由b 2=a 2﹣c 2求得b 的值,则椭圆方程可求;(Ⅱ)假设满足条件的圆存在,设出圆的方程,分直线PQ 的斜率存在和不存在讨论,当直线PQ 的斜率存在时,设其方程为y=kx+t ,和椭圆方程联立后化为关于x 的一元二次方程,利用根与系数关系求出P ,Q 两点横纵坐标的积,由⊥得其数量积等于0,代入坐标的乘积得到k 和t 的关系,再由圆心到直线的距离等于半径求出圆的半径,然后验证直线斜率不存在时成立.从而得到满足条件的圆存在.【解答】解:(Ⅰ)由已知,得,解得:,∴b2=a2﹣c2=4﹣3=1.故椭圆Γ的方程为;(Ⅱ)假设满足条件的圆存在,其方程为x2+y2=r2(0<r<1).当直线PQ的斜率存在时,设其方程为y=kx+t,由,得(1+4k2)x2+8ktx+4t2﹣4=0.设P(x1,y1),Q(x2,y2),则,①∵,∴x1x2+y1y2=0,又y1=kx1+t,y2=kx2+t,∴x1x2+(kx1+t)(kx2+t)=0,即(1+k2)x1x2+kt(x1+x2)+t2=0.②将①代入②,得,即t2=(1+k2).∵直线PQ与圆x2+y2=r2相切,∴r==∈(0,1),∴存在圆x2+y2=满足条件.当直线PQ的斜率不存在时,易得=,代入椭圆Γ的方程,得=,满足.综上所述,存在圆心在原点的圆x2+y2=满足条件.【点评】本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,体现了分类讨论的数学思想方法,涉及直线和圆锥曲线的关系问题,常采用把直线和圆锥曲线联立,利用根与系数的关系求解,考查了计算能力,属高考试卷中的压轴题.21.已知函数f(x)=lnx﹣kx+1.(1)求函数f(x)的单调区间;(2)若f(x)≤0恒成立,试确定实数k的取值范围;(3)证明:ln2≤n(n+1)(n∈N,n>1)【分析】(1)由函数f(x)的定义域为(0,+∞),而f′(x)=﹣k.能求出函数f(x)的单调区间.(2)由(1)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(),由此能确定实数k的取值范围;(3)根据lnx≤x﹣1,得到ln2+ln3+ln4+…+ln(n+1)≤1+2+3+…+n,整理即可.【解答】解:(1)函数f(x)的定义域为(0,+∞),f′(x)=﹣k.当k≤0时,f′(x)=﹣k>0,f(x)在(0,+∞)上是增函数;当k>0时,若x∈(0,)时,有f′(x)>0,若x∈(,+∞)时,有f′(x)<0,则f(x)在(0,)上是增函数,在(,+∞)上是减函数.(2)由(1)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(),要使f(x)≤0恒成立,则f()≤0即可,即﹣lnk≤0,得k≥1;(3)由(2)得:k=1时,lnx≤x﹣1,令x=2,3,4,…,n+1,则ln2<2﹣1=1,ln3<3﹣1=2,ln4<4﹣1=3,…,ln(n+1)<(n+1)﹣1=n,左右两边分别相加得:ln2+ln3+ln4+…+ln(n+1)≤1+2+3+…+n,∴ln(234…(n+1))≤,∴ln2≤n(n+1)(n∈N,n>1).【点评】本题考查函数单调区间的求法,确定实数的取值范围,渗透了分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.请考生在第22,23,24题中选一题作答,并将答题卡上相应的题号涂黑.如果多做,则按所做第一题记分.22.如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B 作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.(Ⅰ)求证:AD∥EC;(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.【分析】(I)连接AB,根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D,又根据同弧所对的圆周角相等得到∠BAC=∠E,等量代换得到∠D=∠E,根据内错角相等得到两直线平行即可;(II)根据切割线定理得到PA2=PBPD,求出PB的长,然后再根据相交弦定理得PAPC=BPPE,求出PE,再根据切割线定理得AD2=DBDE=DB(PB+PE),代入求出即可.【解答】解:(I)证明:连接AB,∵AC是⊙O1的切线,∴∠BAC=∠D,又∵∠BAC=∠E,∴∠D=∠E,∴AD∥EC.(II)∵PA是⊙O1的切线,PD是⊙O1的割线,∴PA2=PBPD,∴62=PB(PB+9)∴PB=3,在⊙O2中由相交弦定理,得PAPC=BPPE,∴PE=4,∵AD是⊙O2的切线,DE是⊙O2的割线,∴AD2=DBDE=9×16,∴AD=12【点评】此题是一道综合题,要求学生灵活运用直线与圆相切和相交时的性质解决实际问题.本题的突破点是辅助线的连接.23.,过点P(﹣2,﹣4)的直线l的参数方程为(t为参数),直线l与曲线C分别交于M、N两点.(1)写出曲线C和直线l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.【分析】(1)直接利用关系式把极坐标方程转化成直角坐标方程.(2)利用参数方程和抛物线方程建立成关于t的一元二次方程组,利用根和系数的关系求出两根和与两根积,进一步利用等比数列进一步求出a的值.【解答】解:(1)曲线C:ρsin2θ=2acosθ(a>0),转化成直角坐标方程为:y2=2ax线l的参数方程为(t为参数),转化成直角坐标方程为:x﹣y﹣2=0.(2)将直线的参数方程(t为参数),代入y2=2ax得到:,所以:,t1t2=32+8a,①则:|PM|=t1,|PN|=t2,|MN|=|t1﹣t2||PM|,|MN|,|PN|成等比数列,所以:,②由①②得:a=1.【点评】本题考查的知识要点:极坐标方程与直角坐标方程的互化,参数方程与直角坐标方程的互化,利用根和系数的关系建立方程组求解,等比数列的应用.24.=|x+a|+|x﹣2|.(1)当a=﹣3时,求不等式f(x)≥3的解集;(2)设集合A={x|f(x)≤|x﹣4|},集合B={x|1≤x≤2},且B⊆A,求a的取值范围.【分析】(1)将a=﹣3代入f(x),通过讨论x的范围,得到各个区间上不等式的解集,取并集即可;(2)根据绝对值的几何意义求出集合A,结合B={x|1≤x≤2},且B⊆A,得到关于a的不等式组,解出即可.【解答】解:(1)a=﹣3时,f(x)=|x﹣3|+|x﹣2|≥3,x≥3时,x﹣3+x﹣2≥3,解得:x≥4,2<x<3时,3﹣x+x﹣2=1<3,不成立,x≤2时,3﹣x+2﹣x≥3,解得:x≤1,故不等式的解集是{x|x≥4或x≤1};(2)由f(x)≤|x﹣4|,得:|x+a|≤|x﹣4|﹣|x﹣2|≤|x﹣4﹣x+2|=2,解得:﹣2﹣a≤x≤2﹣a,∴A=,而B={x|1≤x≤2},且B⊆A,∴,解得:﹣3≤a≤0.【点评】本题考查了解绝对值不等式问题考查分类讨论思想,是一道中档题.。
2016-2017学年宁夏石嘴山三中高三(上)期末数学试卷(文科)(解析版)

2016-2017学年宁夏石嘴山三中高三(上)期末数学试卷(文科)一、选择题:本大题共12小题.每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的.1.(5分)若复数(m2﹣3m)+(m2﹣5m+6)i(m∈R))是纯虚数,则m的值为()A.0B.2C.0或3D.2或32.(5分)设全集I是实数集R,M={x|x≥3}与N={x|(x﹣3)(x﹣1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为()A.{x|1<x<3}B.{x|1≤x<3}C.{x|1<x≤3}D.{x|1≤x≤3}3.(5分)命题p:方程表示焦点在y轴上的椭圆,则使命题p成立的充分不必要条件是()A.3<m<5B.4<m<5C.1<m<5D.m>14.(5分)某程序框图如图所示,若该程序运行后输出的值是,则a的值为()A.13B.12C.11D.105.(5分)设S n是等差数列{a n}的前n项和,若,则=()A.1B.2C.3D.46.(5分)《算法统宗》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有()盏灯.A.14B.12C.8D.107.(5分)设函数f(x)=2sin(2x+),将f(x)图象上每个点的横坐标缩短为原来的一半之后成为函数y=g(x),则g(x)的图象的一条对称轴方程为()A.x=B.x=C.x=D.x=8.(5分)已知变量x,y满足约束条件,则的取值范围是()A.[2,5]B.(﹣∞,2]∪[5,+∞)C.(﹣∞,3]∪[5,+∞)D.[3,5]9.(5分)如图所示,在正方体ABCD﹣A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为()A.30°B.45°C.60°D.90°10.(5分)函数f(x)=的图象大致是()A.B.C.D.11.(5分)已知双曲线C1:﹣=1(a>0,b>0)经过抛物线C2:y2=2px(p>0)的焦点,且双曲线的渐近线与抛物线的准线围成一个等边三角形,则双曲线C1的离心率是()A.2B.C.D.12.(5分)已知函数f(x)是定义在R上的可导函数,其导函数记为f′(x),若对于任意实数x,有f(x)>f′(x),且y=f(x)﹣1为奇函数,则不等式f(x)<e x的解集为()A.(﹣∞,0)B.(0,+∞)C.(﹣∞,e4)D.(e4,+∞)二.填空题:共4小题,每小题5分.13.(5分)已知函数f(x)=,则f[f()]=.14.(5分)观察下列不等式:①1+<;②1++<;③1+++<;…照此规律,第五个不等式为.15.(5分)直四棱柱ABCD﹣A1B1C1D1的底面边长AB=BC=CD=2,AD=4,高为4,则它的外接球的表面积为.16.(5分)已知函数f(x)=,当x∈(﹣∞,m]时,f(x)的取值范围为[﹣16,+∞),则实数m的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数的最小正周期为π.(Ⅰ)求f(x)的单调递增区间;(Ⅱ)若a,b,c分别为△ABC的三内角A,B,C的对边,角A是锐角,f(A)=0,a =1,b+c=2,求△ABC的面积.18.(12分)国家实行二孩生育政策后,为研究家庭经济状况对生二胎的影响,某机构在本地区符合二孩生育政策的家庭中,随机抽样进行了调查,得到如下的列联表:(1)请完成上面的列联表,并判断能否在犯错误的概率不超过1%的前提下认为家庭经济状况与生育二胎有关?(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.附:19.(12分)如图,在四棱锥S﹣ABCD中,平面SAD⊥底面ABCD,,在AD 边上取一点E,使得BCDE为矩形,SA=2AE=DE=2.(1)证明:BC⊥平面SBE;(2)若(λ∈R),且SA∥平面BEF,求λ的值.20.(12分)已知椭圆C:+=1(a>b>0)的离心率为,以M(1,0)为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+﹣1=0相切.(1)求椭圆C的标准方程;(2)已知点N(3,2),和平面内一点P(m,n)(m≠3),过点M任作直线l与椭圆C 相交于A,B两点,设直线AN,NP,BN的斜率分别为k1,k2,k3,k1+k3=3k2,试求m,n满足的关系式.21.(12分)已知函数.(1)当a=1时,求函数f(x)在[1,e]上的最小值和最大值;(2)当a≤0时,讨论函数f(x)的单调性;(3)是否存在实数a,对任意的x1,x2∈(0,+∞),且x1≠x2,都有恒成立,若存在,求出a的取值范围;若不存在,说明理由.[选修题]:[选修4-4:坐标系与参数方程]:请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.(10分)在直角坐标系xOy中,曲线C1的参数方程为:(θ为参数),以直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ﹣sinθ)=6.(Ⅰ)试写出直线l的直角坐标方程和曲线C1的普通方程;(Ⅱ)在曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.[选修4-5:不等式选讲]23.已知函数f(x)=|x+a|+|2x﹣1|(a∈R).(Ⅰ)当a=1时,求不等式f(x)≥2的解集;(Ⅱ)若f(x)≤2x的解集包含[],求a的取值范围.2016-2017学年宁夏石嘴山三中高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题.每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的.1.【解答】解:∵复数(m2﹣3m)+(m2﹣5m+6)i(m∈R))是纯虚数,则m2﹣3m=0,m2﹣5m+6≠0,解得m=0.故选:A.2.【解答】解:由题意M={x|x≥3}与N={x|(x﹣3)(x﹣1)≤0}={x|1≤x≤3}由图知阴影部分所表示的集合为N∩(∁I M)∴N∩(∁I M)={x|1≤x<3}故选:B.3.【解答】解:命题p:方程表示焦点在y轴上的椭圆⇔0<5﹣m<m﹣1,解得3<m<5.则使命题p成立的充分不必要条件是4<m<5.故选:B.4.【解答】解:模拟执行程序框图,可得S=1,k=1不满足条件k>a,S=1+=2,k=2不满足条件k>a,S=1++=2,k=3不满足条件k>a,S=1++=2,k=4不满足条件k>a,S=1+++=2﹣,k=5不满足条件k>a,S=1++++=2,k=6不满足条件k>a,S=1+++++=2﹣,k=7…最后一次循环,不满足条件k>a,S=2﹣=,k=x+1满足条件k>a,退出循环,输出S的值为.可解得:x=12,即由题意可得a的值为11.故选:C.5.【解答】解:∵,∴===×=××=3,故选:C.6.【解答】解:设第一层有a盏灯,则由题意知第一层至第七层的灯的盏数构成一个以a1为首项,以为公比的等比数列,∴=381,解得a1=192,∴a5=a1×()4=192×=12,故选:B.7.【解答】解:函数f(x)=2sin(2x+),将f(x)图象上每个点的横坐标缩短为原来的一半之后成为函数y=g(x)=2sin(4x+).令4x+=kπ+,k∈Z,可解得函数对称轴方程为:x=kπ+,k∈Z,当k=0时,x=是函数的一条对称轴.故选:D.8.【解答】解作出不等式组对应的平面区域如图,则的几何意义是区域内的点到原点的斜率,由图象知OC的斜率最小,OA的斜率最大,由得,即A(1,5),此时OA的斜率k=5,由得,即C(2,4),此时OC的斜率k==2,即2≤≤5,则的取值范围是[2,5],故选:A.9.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为2,则E(2,0,1),F(2,1,0),A1(2,0,2),G(0,2,1),=(0,1,﹣1),=(﹣2,2,﹣1),设EF与A1G所成的角为θ,则cosθ===,∴θ=45°.∴EF与A1G所成的角为45°.故选:B.10.【解答】解:因为f(0)==1,说明函数的图象过(0,1),排除D;因为当x>2时,2﹣x<0,2e﹣x>0,所以f(x)=<0恒成立,即当x>2时,函数图象在x轴下方,排除A.因为当x<0时,2﹣x>0,2e﹣x>0,所以f(x)=>0恒成立,即当x<0时,函数图象在x轴上方,排除C.故选:B.11.【解答】解:抛物线C2:y2=2px(p>0)的焦点为(,0),由题意可得a=,双曲线C1:﹣=1的渐近线方程为y=±x,抛物线的准线方程为x=﹣,代入渐近线方程可得交点为(﹣a,b),(﹣a,﹣b),由双曲线的渐近线与抛物线的准线围成一个等边三角形,可得边长为2b,高为a,即有a=b,c==a,即有e==.故选:D.12.【解答】解:令g(x)=,则=,∵f(x)>f′(x),∴g′(x)<0,即g(x)为减函数,∵y=f(x)﹣1为奇函数,∴f(0)﹣1=0,即f(0)=1,g(0)=1,则不等式f(x)<e x等价为=g(0),即g(x)<g(0),解得x>0,∴不等式的解集为(0,+∞),故选:B.二.填空题:共4小题,每小题5分.13.【解答】解:由分段函数可知,f()=,f(﹣1)=,故答案为:.14.【解答】解:由已知中的不等式1+,1++,…得出左边式子是连续正整数平方的倒数和,最后一个数的分母是不等式序号n+1的平方右边分式中的分子与不等式序号n的关系是2n+1,分母是不等式的序号n+1,故可以归纳出第n个不等式是1+…+<,(n≥2),所以第五个不等式为1+++++<故答案为:1+++++<15.【解答】解:将直四棱柱补成正六棱柱,由此求得其外接球的半径为=2,故它的外接球的表面积为=32π.故答案为32π.16.【解答】解:x≤0时,f(x=12x﹣x3,∴f′(x)=﹣3(x+2)(x﹣2),∴x<﹣2时,函数单调递减,﹣2<x≤0时,函数单调递增,∴当x=﹣2时,图象在y轴左侧的函数取到极小值﹣16,∵当x=8时,y=﹣2x=﹣16,∴当x∈(﹣∞,m]时,f(x)的取值范围为[﹣16,+∞),则实数m的取值范围是[﹣2,8].故答案为:[﹣2,8].三、解答题:解答应写出文字说明,证明过程或演算步骤.17.【解答】(本题满分为12分)解:(Ⅰ)=,…(2分)∴T==π,从而可求ω=1,…(3分)∴f(x)=sin(2x+)…(4分)由2kπ﹣≤2x+≤2kπ+,(k∈Z),可得:,所以f(x)的单调递增区间为:.…(6分)(Ⅱ)∵f(A)=0,∴,又角A是锐角,∴,∴,即.…(8分)又a=1,b+c=2,所以a2=b2+c2﹣2bc•cos A=(b+c)2﹣3bc,∴1=4﹣3bc,∴bc=1.…(10分)∴.…(12分)18.【解答】解:(1)2×2列联表:K2=≈0.2386<3.841,故不能在犯错误的概率不超过1%的前提下认为家庭经济状况与生育二胎有关;(2)采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取2个;(3)在(2)的条件下,从中随机抽取2个家庭,2个家庭都是经济状况好的概率是=.19.【解答】(1)证明:因为SA=2,AE=1,∠SAD=60°,所以SE=,所以SE⊥AD又平面SAD⊥平面ABCD,且平面SAD∩平面ABCD=AD,所以SE⊥平面ABCD,所以SE⊥CB,又BE⊥CB,且SE∩BE=E.所以CB⊥平面SBE.(2)解:连接AC交BE于点M,连接FM,因为SA∥平面BEF,平面SAC∩平面BEF=FM,所以FM∥AS.因为EM∥CD,所以=,因为FM∥AS,所以=,所以.20.【解答】解:(1)由椭圆C:+=1(a>b>0),焦点在x轴上,则M(1,0)到直线x﹣y+﹣1=0的距离d==1,∴b=d=1,离心率e===,解得:a=,∴椭圆C的标准方程;(2)①当直线斜率不存在时,由,解得x=1,,不妨设,,∵k1+k3=2,∴,∴m,n的关系式为3n=2m.②当直线的斜率存在时,设点A(x1,y1),B(x2,y2),直线l:y=k(x﹣1),联立椭圆整理得:(3k2+1)x2﹣6k2x+3k2﹣3=0,由韦达定理可知:x1+x2=,x1•x2=,∴,=,=.∴,∴m,n的关系式为3n=2m.21.【解答】(1)当a=1时,.则,x∈[1,e]∴当x∈(1,2)时,f′(x)<0,当x∈(2,e)时,f′(x)>0,∴f(x)在(1,2)上是减函数,在(2,e)上是增函数.∴当x=2时,f(x)取得最小值,其最小值为f(2)=﹣2ln2.又,.,∴f(e)<f (1)∴.(2)f(x)的定义域为(0,+∞),,①当﹣2<a≤0时,f(x)在(0,﹣a)上是增函数,在(﹣a,2)上是减函数,在(2,+∞)上是增函数.②当a=﹣2时,在(0,+∞)上是增函数.③当a<﹣2时,则f(x)在(0,2)上是增函数,在(2,﹣a)上是减函数,在(﹣a,+∞)上是增函数.(3)假设存在实数a,对任意的x1,x2∈(0,+∞),且x1≠x2,都有恒成立,不妨设0<x1<x2,若,即f(x2)﹣ax2>f(x1)﹣ax1,令只要g(x)在(0,+∞)为增函数要使g′(x)≥0在(0,+∞)恒成立,只需﹣1﹣2a≥0,,故存在满足题意.[选修题]:[选修4-4:坐标系与参数方程]:请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.【解答】解:(Ⅰ)直线l的方程为:ρ(2cosθ﹣sinθ)=6,即2x﹣y﹣6=0.曲线C1的参数方程为:(θ为参数),普通方程为;(Ⅱ)设点P(cosθ,2sinθ),则点P到直线l的距离为d==,故当sin(﹣θ)=﹣1时,d取得最大值为2.[选修4-5:不等式选讲]23.【解答】解:(1)当a=1时,不等式f(x)≥2可化为|x+1|+|2x﹣1|≥2,①当时,不等式为3x≥2,解得x,故此时不等式f(x)≥2的解集为x;②当﹣1≤x<时,不等式为2﹣x≥2,解得x≤0,故此时不等式f(x)≥2的解集为﹣1≤x<0;③当x<﹣1时,不等式为﹣3x≥2,解得,故x<﹣1;综上原不等式的解集为{x|x≤0或x};(2)因为f(x)≤2x的解集包含[],不等式可化为|x+a|+2x﹣1≤2x,即|x+a|≤1,解得﹣a﹣1≤x≤﹣a+1,由已知得,解得所以a的取值范围是.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年宁夏石嘴山市平罗中学高三(上)期中数学试卷(文科)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合M={1,2,3},N={2,3,4},则()A.M⊆N B.N⊆M C.M∩N={2,3}D.M∪N={1,4}2.(5分)“”是“sin2α=1”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件3.(5分)等差数列{a n}的前n项和为S n,且S3=6,a1=4,则公差d等于()A.1 B.C.﹣2 D.34.(5分)下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.B.y=e﹣x C.y=lg|x|D.y=﹣x2+15.(5分)函数f(x)=x3+x在点x=1处的切线方程为()A.4x﹣y+2=0 B.4x﹣y﹣2=0 C.4x+y+2=0 D.4x+y﹣2=06.(5分)在等差数列{a n}中,已知a5=15,则a2+a4+a6+a8的值为()A.30 B.45 C.60 D.1207.(5分)在△ABC中,三边a,b,c所对的角分别为A,B,C,若a2+b2=ab+c2,则角C为()A.30°B.45°C.150° D.135°8.(5分)已知||=1,||=2,<,>=60°,则|2﹣|=()A.2 B.4 C.D.89.(5分)已知向量=(cosα,﹣2),=(sinα,1),且∥,则tan(α﹣)等于()A.3 B.﹣3 C.D.10.(5分)已知{a n}是等比数列,且a n>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于()A.5 B.10 C.15 D.2011.(5分)||=1,||=,•=0,点C在∠AOB内,且∠AOC=30°,设=m+n(m、n∈R),则等于()A.B.3 C.D.12.(5分)函数f(x)=x3+x,x∈R,当时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是()A.(0,1) B.(﹣∞,0)C.D.(﹣∞,1)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.(5分)设=(1,2),=(﹣1,x),若⊥,则x=.14.(5分)已知复数z满足(z﹣2)i=1+i(i是虚数单位),则|z|=.15.(5分)已知函数f(x)=,则f[f()]的值是.16.(5分)已知数列{a n}的前n项和S n=n2﹣9n,则其通项a n=.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=﹣2sin2x+2sinxcosx+1.(1)求f(x)的最小正周期及对称中心;(2)若x∈[﹣,],求f(x)的最大值和最小值.18.(12分)已知数列{a n}是等差数列,a2=6,a5=18;数列{b n}的前n项和是T n,且T n+b n=1.(1)求数列{a n}的通项公式;(2)求证:数列{b n}是等比数列.19.(12分)△ABC的内角A,B,C所对的边分别为a,b,c.向量=(a,b)与=(cosA,sinB)平行.(Ⅰ)求A;(Ⅱ)若a=,b=2,求△ABC的面积.20.(12分)已知正项等比数列{a n}满足:a3=4,a4+a5=24.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若b n=,求数列{b n}的前n项和S n.21.(12分)已知函数f(x)=xlnx.(Ⅰ)求f(x)的最小值;(Ⅱ)若对所有x≥1都有f(x)≥ax﹣1,求实数a的取值范围.[选修4-4:坐标系与参数方程](共1小题,满分10分)22.(10分)以平面直角坐标系的原点为极点,正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点A的极坐标为(2,),直线l过点A 且与极轴成角为,圆C的极坐标方程为ρ=cos(θ﹣).(Ⅰ)写出直线l参数方程,并把圆C的方程化为直角坐标方程;(Ⅱ)设直线l与曲线圆C交于B、C两点,求|AB|•|AC|的值.[选修4-5:不等式选讲](共1小题,满分0分)23.已知函数f(x)=|x﹣1|+|x﹣a|.(I)若a=﹣1,解不等式f(x)≥3;(II)如果∀x∈R,f(x)≥2,求a的取值范围.2016-2017学年宁夏石嘴山市平罗中学高三(上)期中数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合M={1,2,3},N={2,3,4},则()A.M⊆N B.N⊆M C.M∩N={2,3}D.M∪N={1,4}【解答】解:M∩N={1,2,3}∩{2,3,4}={2,3}故选:C.2.(5分)“”是“sin2α=1”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件【解答】解:当时,sin2α=1成立,当sin2α=1时,α=不一定成立,例如故”是“sin2α=1”充分不必要条件故选:A.3.(5分)等差数列{a n}的前n项和为S n,且S3=6,a1=4,则公差d等于()A.1 B.C.﹣2 D.3【解答】解:∵S3=6=(a1+a3),且a3=a1+2d,a1=4,∴d=﹣2,故选:C.4.(5分)下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是()A.B.y=e﹣x C.y=lg|x|D.y=﹣x2+1【解答】解:A中,y=为奇函数,故排除A;B中,y=e﹣x为非奇非偶函数,故排除B;C中,y=lg|x|为偶函数,在x∈(0,1)时,单调递减,在x∈(1,+∞)时,单调递增,所以y=lg|x|在(0,+∞)上不单调,故排除C;D中,y=﹣x2+1的图象关于y轴对称,故为偶函数,且在(0,+∞)上单调递减,故选:D.5.(5分)函数f(x)=x3+x在点x=1处的切线方程为()A.4x﹣y+2=0 B.4x﹣y﹣2=0 C.4x+y+2=0 D.4x+y﹣2=0【解答】解:∵f(x)=x3+x∴f′(x)=3x2+1∴容易求出切线的斜率为4当x=1时,f(x)=2利用点斜式,求出切线方程为4x﹣y﹣2=0故选:B.6.(5分)在等差数列{a n}中,已知a5=15,则a2+a4+a6+a8的值为()A.30 B.45 C.60 D.120【解答】解:在等差数列{a n}中,若m+n=p+q,则a m+a n=a p+a q,∴a2+a4+a6+a8=(a2+a8)+(a4+a6)=2a5+2a5=4a5=4×15=60.故选:C.7.(5分)在△ABC中,三边a,b,c所对的角分别为A,B,C,若a2+b2=ab+c2,则角C为()A.30°B.45°C.150° D.135°【解答】解:∵在△ABC中,由余弦定理a2+b2=c2+2abcosC,又a2+b2=ab+c2,∴cosC=,∴C=45°故选:B.8.(5分)已知||=1,||=2,<,>=60°,则|2﹣|=()A.2 B.4 C.D.8【解答】解:∵,∴==1×2×=1,因此=4||2﹣4+||2=4×12﹣4×1+22=4,∴==2(舍负).故选:A.9.(5分)已知向量=(cosα,﹣2),=(sinα,1),且∥,则tan(α﹣)等于()A.3 B.﹣3 C.D.【解答】解:∵,∴cosα+2sinα=0,∴tanα=,∴tan()==﹣3,故选:B.10.(5分)已知{a n}是等比数列,且a n>0,a2a4+2a3a5+a4a6=25,那么a3+a5的值等于()A.5 B.10 C.15 D.20【解答】解:由等比数列的性质得:a2•a4=a32,a4•a6=a52∴a2a4+2a3a5+a4a6=25可化为(a3+a5)2=25又∵a n>0∴a3+a5=5故选:A.11.(5分)||=1,||=,•=0,点C在∠AOB内,且∠AOC=30°,设=m+n(m、n∈R),则等于()A.B.3 C.D.【解答】解:法一:如图所示:=+,设=x,则=.=∴==3.法二:如图所示,建立直角坐标系.则=(1,0),=(0,),∴=m+n=(m,n),∴tan30°==,∴=3.故选:B.12.(5分)函数f(x)=x3+x,x∈R,当时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是()A.(0,1) B.(﹣∞,0)C.D.(﹣∞,1)【解答】解:由f(x)=x3+x,∴f(x)为奇函数,增函数,∴f(msinθ)+f(1﹣m)>0恒成立,即f(msinθ)>f(m﹣1),∴msinθ>m﹣1,当时,sinθ∈[0,1],∴,解得m<1,故实数m的取值范围是(﹣∞,1),故选:D.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.13.(5分)设=(1,2),=(﹣1,x),若⊥,则x=.【解答】解:∵=(1,2),=(﹣1,x),且⊥,∴•=1×(﹣1)+2x=0,解得x=故答案为:14.(5分)已知复数z满足(z﹣2)i=1+i(i是虚数单位),则|z|=.【解答】解:(z﹣2)i=1+i,∴z﹣2=,z=2+=2+1﹣i=3﹣i,|z|==;故答案为:.15.(5分)已知函数f(x)=,则f[f()]的值是.【解答】解:,故答案为:16.(5分)已知数列{a n}的前n项和S n=n2﹣9n,则其通项a n=2n﹣10.【解答】解:∵S n=n2﹣9n,∴a1=S1=﹣8n≥2时,a n=S n﹣S n﹣1=n2﹣9n﹣(n﹣1)2+9(n﹣1)=2n﹣10n=1,a1=8适合上式故答案为:2n﹣10三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=﹣2sin2x+2sinxcosx+1.(1)求f(x)的最小正周期及对称中心;(2)若x∈[﹣,],求f(x)的最大值和最小值.【解答】解:(1)∴f(x)的最小正周期为,令,则,∴f(x)的对称中心为;(2)∵∴∴∴﹣1≤f(x)≤2∴当时,f(x)的最小值为﹣1;当时,f(x)的最大值为2.18.(12分)已知数列{a n}是等差数列,a2=6,a5=18;数列{b n}的前n项和是T n,且T n+b n=1.(1)求数列{a n}的通项公式;(2)求证:数列{b n}是等比数列.【解答】(1)解:设{a n}的公差为d,∵a2=6,a5=18;则,解得∴a n=2+4(n﹣1)=4n﹣2.(2)证明:当n=1时,b1=T1,由,得;当n≥2时,∵,,∴.∴.化为.∴数列{b n}是以为首项,为公比的等比数列.19.(12分)△ABC的内角A,B,C所对的边分别为a,b,c.向量=(a,b)与=(cosA,sinB)平行.(Ⅰ)求A;(Ⅱ)若a=,b=2,求△ABC的面积.【解答】解:(Ⅰ)因为向量=(a,b)与=(cosA,sinB)平行,所以asinB﹣=0,由正弦定理可知:sinAsinB﹣sinBcosA=0,因为sinB ≠0,所以tanA=,可得A=;(Ⅱ)a=,b=2,由余弦定理可得:a2=b2+c2﹣2bccosA,可得7=4+c2﹣2c,解得c=3,△ABC的面积为:=.20.(12分)已知正项等比数列{a n}满足:a3=4,a4+a5=24.(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若b n=,求数列{b n}的前n项和S n.【解答】解:(Ⅰ)设正项等比数列{a n}的首项为a1,公比为q,则由a 3=4,a4+a5=24得,由于a n>0,q>0解得,所以a n=.(Ⅱ)由a n=.得.∴∴.21.(12分)已知函数f(x)=xlnx.(Ⅰ)求f(x)的最小值;(Ⅱ)若对所有x≥1都有f(x)≥ax﹣1,求实数a的取值范围.【解答】解:(Ⅰ)f(x)的定义域为(0,+∞),f(x)的导数f'(x)=1+lnx.令f'(x)>0,解得;令f'(x)<0,解得.从而f(x)在单调递减,在单调递增.所以,当时,f(x)取得最小值.(Ⅱ)依题意,得f(x)≥ax﹣1在[1,+∞)上恒成立,即不等式对于x∈[1,+∞)恒成立.令,则.当x>1时,因为,故g(x)是[1,+∞)上的增函数,所以g(x)的最小值是g(1)=1,从而a的取值范围是(﹣∞,1].[选修4-4:坐标系与参数方程](共1小题,满分10分)22.(10分)以平面直角坐标系的原点为极点,正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,设点A的极坐标为(2,),直线l过点A 且与极轴成角为,圆C的极坐标方程为ρ=cos(θ﹣).(Ⅰ)写出直线l参数方程,并把圆C的方程化为直角坐标方程;(Ⅱ)设直线l与曲线圆C交于B、C两点,求|AB|•|AC|的值.【解答】解:(Ⅰ)由题知点A的极坐标为(2,),的直角坐标为A(),所以直线L过A点倾斜角为的参数方程为,t为参数.因为圆C的极坐标方程为ρ=cos(θ﹣).所以ρ=cosθ+sinθ,所以圆C的直角坐标方程为x2+y2﹣x﹣y=0.(Ⅱ)将直线的参数方程代到圆C的直角坐标方程中整理得:t2+()t+3﹣=0设B,C对应的参数分别为t1,t2∴|AB|•|AC|=|t1t2|=.[选修4-5:不等式选讲](共1小题,满分0分)23.已知函数f(x)=|x﹣1|+|x﹣a|.(I)若a=﹣1,解不等式f(x)≥3;(II)如果∀x∈R,f(x)≥2,求a的取值范围.【解答】解:(Ⅰ)当a=﹣1时,f(x)=|x+1|+|x﹣1|,由f(x)≥3即|x+1|+|x﹣1|≥3当x≤﹣1时,不等式可化为﹣x﹣1+1﹣x≥3,解得x≤﹣;当﹣1<x<1时,不等式化为x+1+1﹣x≥3,不可能成立,即x∈∅;当x≥1时,不等式化为x+1+x﹣1≥3,解得x≥.综上所述,f(x)≥3的解集为(﹣∞,﹣]∪[,+∞);(Ⅱ)由于|x﹣1|+|x﹣a|≥|(x﹣1)﹣(x﹣a)|=|a﹣1|,则f(x)的最小值为|a﹣1|.要使∀x∈R,f(x)≥2成立,则|a﹣1|≥2,解得a≥3或a≤﹣1,即a的取值范围是(﹣∞,﹣1]∪[3,+∞).。
