热学第五章
合集下载
第五章 热力循环——热力学第二定律

dSsys
QR
T
由于传热δQR而引 起体系熵的变化
我们称
QR
T
为随
QR热流产生的熵流。
熵流定义:dS f δQR /T
功源熵变为零,因此功的传递不会引起熵的流动。
(2) 熵产dSg
dSsys≥δQ/T
Δ等S式g>0dS,sys 不 可QT R 逆 dS过g 积程分
Ssys
Q 0
Q
T
S g
dS g ——熵产生Δ,Sg由=0于,过可程的逆不过可程逆性引起的熵变。
普:对物质没限制,适用于任一物质
5.4 水蒸气动力循环
1. 卡诺循环
T (R)
WS (R) QH
QH QL QH
1 QL QH
以水蒸气为工质的卡诺循环示意图:
2
T
1 TL TH
QH 锅
透 WS ,Tur
TH 1
2
平
炉
W S ,Pump
3
冷凝器 QL
TL
4
3
1 水泵
4
6
5S
图1 卡简诺单的循蒸环汽动各力步装骤置的能量图平2 衡T—和S图熵上平的卡衡诺式循环
过程的不可逆程度越大,熵产生量也越大;熵产生永远
不会小于零。 ΔSg<0,不可能过程
5.2 熵
2. 熵平衡式
熵流 S f (Q T )
物流入
mi si
i
in
敞开体系
S g SA
物流出
m jsj
j
out
W
敞开系统熵平衡示意图
熵平衡的一般关系式:熵流+熵入+熵产-熵出=熵积累
dSopsys dt
传热学-第五章 对流换热(Convection Heat Transfer)

根据傅里叶定律:
[ ] qw,x
=
−λ⎜⎜⎝⎛
∂t ∂y
⎟⎟⎠⎞w , x
W m2
注意和第三类边 界条件的区别
根据牛顿冷却公式
[ ] qw,x = hx (tw -t∞ ) W m2
根据能量守恒
对流换热过程 微分方程式
[ ] hx
=
−
tw
λ
− t∞
⎜⎜⎝⎛
∂t ∂y
⎟朝下
自然对流
(5) 流体的热物理性质
热导率 λ [w/(m℃)]
比热容 c [J/(kg℃)]
密 度 ρ [kg/m3]
动力粘度 η [Ns/m2] 运动粘度 ν =η/ρ [m2/s] 体积胀系数 α [1/K]
α
=
1 ⎜⎛ v⎝
∂v ∂T
⎟⎞ ⎠p
=
−
1
ρ
⎜⎛ ⎝
∂ρ
∂T
⎟⎞ ⎠p
λ↑ ⇒ h↑流体内部和流体与壁面间导热热阻小
第五章 对流换热(Convection Heat Transfer)
§5-1 对流换热概说
1. 对流换热的定义和性质
定义:对流换热是指 流体流经固体时流体 与固体表面之间的 热量传递现象。
对流换热与热对流不同,既有热对流,也有导热;不是 基本传热方式 对流换热实例:(1) 暖气管道; (2) 电子器件冷却;(3) 换热器
ρ、c↑ ⇒ h↑单位体积流体能携带更多能量
η ↑ ⇒ h↓有碍流体流动、不利于热对流 α ↑ ⇒ h↑自然对流换热增强
综上所述,表面传热系数是众多因素的函数:
h = f (u, tw , tf , λ, cp , ρ, α ,η, l )
对流换热分类小结
[ ] qw,x
=
−λ⎜⎜⎝⎛
∂t ∂y
⎟⎟⎠⎞w , x
W m2
注意和第三类边 界条件的区别
根据牛顿冷却公式
[ ] qw,x = hx (tw -t∞ ) W m2
根据能量守恒
对流换热过程 微分方程式
[ ] hx
=
−
tw
λ
− t∞
⎜⎜⎝⎛
∂t ∂y
⎟朝下
自然对流
(5) 流体的热物理性质
热导率 λ [w/(m℃)]
比热容 c [J/(kg℃)]
密 度 ρ [kg/m3]
动力粘度 η [Ns/m2] 运动粘度 ν =η/ρ [m2/s] 体积胀系数 α [1/K]
α
=
1 ⎜⎛ v⎝
∂v ∂T
⎟⎞ ⎠p
=
−
1
ρ
⎜⎛ ⎝
∂ρ
∂T
⎟⎞ ⎠p
λ↑ ⇒ h↑流体内部和流体与壁面间导热热阻小
第五章 对流换热(Convection Heat Transfer)
§5-1 对流换热概说
1. 对流换热的定义和性质
定义:对流换热是指 流体流经固体时流体 与固体表面之间的 热量传递现象。
对流换热与热对流不同,既有热对流,也有导热;不是 基本传热方式 对流换热实例:(1) 暖气管道; (2) 电子器件冷却;(3) 换热器
ρ、c↑ ⇒ h↑单位体积流体能携带更多能量
η ↑ ⇒ h↓有碍流体流动、不利于热对流 α ↑ ⇒ h↑自然对流换热增强
综上所述,表面传热系数是众多因素的函数:
h = f (u, tw , tf , λ, cp , ρ, α ,η, l )
对流换热分类小结
第五章(热力学第二定律和第三定律)

13 结束选择
理学院 物理系 陈强
请在放映状态下点击你认为是对的答案
判断下列说法中哪一种是不正确的 (1)可逆过程一定是准静过程;
(2)准静过程一定是可逆过程;
(3)不可逆过程一定找不到另一个过 程使系统和外界完全复原; (4)非准静过程一定是不可逆过程。
14 结束选择
理学院 物理系 陈强
请在放映状态下点击你认为是对的答案
刹车摩擦生热。
烘烤车轮,车不开。
热
9
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
(3) 热传导不可逆 热量不能自动从低温高温
(4) 扩散不可逆 自由膨胀,不可自动收缩
10
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
• 功向热转化的过程
是不可逆的。
• 一切自发过程都是
单方向进行的不可 逆过程。
烧后放出的热量
热源
单热源热机(第二类永动机)是不可能的。
18
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
一. 自然过程的方向性
1. 功热转换(机械能热能)
孤立系统中发生功热转换时, 机械能可以全部转 变为热能, 但反方向的过程不会发生.
例如:
v0
v=0
功热
热 功的转换过程必伴随有其它变化: • 热机:总有部分热量从高温低温热源 • 等温膨胀:热全部转换为功, 但同时体积变大.
熵增加原理 §5-4. 熵及热力学第二定律的统计意义 §5-5. 热力学第二定律的应用举例 §5-6. 自由能与吉布斯函数 §5-7. 热力学第三定律
7
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
§5-1. 可逆与不可逆过程
理学院 物理系 陈强
请在放映状态下点击你认为是对的答案
判断下列说法中哪一种是不正确的 (1)可逆过程一定是准静过程;
(2)准静过程一定是可逆过程;
(3)不可逆过程一定找不到另一个过 程使系统和外界完全复原; (4)非准静过程一定是不可逆过程。
14 结束选择
理学院 物理系 陈强
请在放映状态下点击你认为是对的答案
刹车摩擦生热。
烘烤车轮,车不开。
热
9
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
(3) 热传导不可逆 热量不能自动从低温高温
(4) 扩散不可逆 自由膨胀,不可自动收缩
10
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
• 功向热转化的过程
是不可逆的。
• 一切自发过程都是
单方向进行的不可 逆过程。
烧后放出的热量
热源
单热源热机(第二类永动机)是不可能的。
18
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
一. 自然过程的方向性
1. 功热转换(机械能热能)
孤立系统中发生功热转换时, 机械能可以全部转 变为热能, 但反方向的过程不会发生.
例如:
v0
v=0
功热
热 功的转换过程必伴随有其它变化: • 热机:总有部分热量从高温低温热源 • 等温膨胀:热全部转换为功, 但同时体积变大.
熵增加原理 §5-4. 熵及热力学第二定律的统计意义 §5-5. 热力学第二定律的应用举例 §5-6. 自由能与吉布斯函数 §5-7. 热力学第三定律
7
理学院 物理系 陈强
第五章 热力学第二定律和第三定律
§5-1. 可逆与不可逆过程
热力学-5.热力学第一定律

§4 热容 焓
一、 热容
热容 比热容
摩尔热容
热容是过程量,式中的下标 x 表示具体的过程。
二、 焓
对于某封闭系统在非体积功为零的条件下热力学第一 定律可写成:
dU Q pedV
对于定容过程,体积功为零,上式可写成:
Q dU
或
QV U (W,=0,恒容)
式中QV为定容过程的热效应。
c
E 可
Zn 逆 电 池
CuSO4
ZnSO4
4、功的一般表达式
dWi Yidxi
• x是广义坐标,它是广延量,广延量的特征是:若系 统在相同情况下质量扩大一倍,则广延量也扩大一 倍。
• Y是广义力,它是强度量,强度量的特征是:当系统 在相同情况下质量扩大一倍时,强度量不变。
不同形式功的计算表达式小结:
V2 V1
系
V2 RT dV nRT ln V2
V V1
V1
6
24 V∕m3
W e,膨=33.27 (atm ·m3) W e,压=-33.27 (atm ·m3)
W e,总=0 (atm ·m3)
完成次数 一次完成
W e,膨 (atm · m3)
18
W e,压
W e,总
(atm ·m3) (atm ·m3)
(3)按过程中经历的各个状态的性质分类:
准静态过程:初态、每个中间态、终态都可近 似地看成是平衡态的过程。
非静态过程:只要有一个状态不是平衡态,整 个过程就是非静态过程。
理想气体自由膨胀过程是一个非静态过程。
气体自由膨胀过程
初态
真空
末 态
膨胀
实际过程是非准静态过程,但只要过程进行的 时间远大于系统的弛豫时间,均可看作准静态过程。 如:实际汽缸的压缩过程可看作准静态过程。
第5章 热力学第一定律

功与过程(路径)有关,它是过程量,不是状态量。
[例题] 在定压下,气体体积从V1 变被压缩到V2 (1)设过程为 准静态过程,试计算外界对系统所做的功。(2)若为非静态过
程结果如何?
[解]
(1)
A
V2 V1
pdV
p
V2 dV
V1
p(V2
V1 )
A 外界对系统做正功
(2)
A V2 pdV V1
在一定的过程中,系统改变单位温度时吸收或放出的热量叫做 系统的热容。
质量为m的系统,热容的定义
Q C lim
T 0 T
•常用的也是基本的有体积不变的等体过程和压强不变的等压过程
等容(定容)热容
等容过程,外界对系统所做的功为零。由热力学第一定律可知
(Q)V U U U (T ,V )
CV
lim (Q)V T 0 T
S1
V1
p1
p1 T1
l1
S1
p1
S2 p2
V2 p2 T2
l2
S2 p2
做功 吸热
A AL AR p1S1l1 p2S2l2 p1V1 p2V2
Q0
U 2 U1 p1V1 p2V2 即: U1 p1V1 U 2 p2V2
即H1 H 2
绝热节流过程前后的焓不变
引入焦汤系数描述
U U (T )
CV
(
U T
)V
dU dT
dU CV dT
CV CV ,m ,
CV ,m
dU m dT
U U0
T T0
CV
dT
dU CV ,mdT
T
U U0 T0 CV ,mdT
H U pV U (T ) vRT
[例题] 在定压下,气体体积从V1 变被压缩到V2 (1)设过程为 准静态过程,试计算外界对系统所做的功。(2)若为非静态过
程结果如何?
[解]
(1)
A
V2 V1
pdV
p
V2 dV
V1
p(V2
V1 )
A 外界对系统做正功
(2)
A V2 pdV V1
在一定的过程中,系统改变单位温度时吸收或放出的热量叫做 系统的热容。
质量为m的系统,热容的定义
Q C lim
T 0 T
•常用的也是基本的有体积不变的等体过程和压强不变的等压过程
等容(定容)热容
等容过程,外界对系统所做的功为零。由热力学第一定律可知
(Q)V U U U (T ,V )
CV
lim (Q)V T 0 T
S1
V1
p1
p1 T1
l1
S1
p1
S2 p2
V2 p2 T2
l2
S2 p2
做功 吸热
A AL AR p1S1l1 p2S2l2 p1V1 p2V2
Q0
U 2 U1 p1V1 p2V2 即: U1 p1V1 U 2 p2V2
即H1 H 2
绝热节流过程前后的焓不变
引入焦汤系数描述
U U (T )
CV
(
U T
)V
dU dT
dU CV dT
CV CV ,m ,
CV ,m
dU m dT
U U0
T T0
CV
dT
dU CV ,mdT
T
U U0 T0 CV ,mdT
H U pV U (T ) vRT
第五章 热力学第一定律

Cp,mCV,mR
摩尔定容热容
CV ,m
i 2
R
摩尔定压热容
Cp,m
i
2R 2
比热容比γ
Cp,m i 2
CV,m
i
§7. 热力学第一定律对理想气体的应用 A、Q、U 的计算
待求量
方法
A
Q
ΔU
间接法 UAQ UAQ UAQ
直接法
A V2 pdV V1
QC m(T2T1)
U2i R(T2T1)
(2)外界对系统传递热量
机理:传递热量是通过系统与外界边界处分子之间 的碰撞来完成的,是系统外物体分子无规则热运动 与系统内分子无规则热运动之间交换能量的过程。
2、热力学第一定律的数学表述
U2U 1QA
对于无限小过程
dUdQ dA
热力学第一定律是反映热现象中能量转化与守恒的定律
三、热力学第一定律的讨论
由于在热传导过程中,固体温度处 处不同,它不满足热学平衡条件 , 经过的每一个中间状态都不是平 衡态,该过程不是准静态过程。
温度T1固体 T2温度恒温热源
➢ 要使物体温度从T1变为 T2 的过程是准静态的,应要求任一 瞬时,物体中各部分间温度差ΔT 均在非常小范围之内。
➢ 例如可采用一系列温度彼此相差ΔT 的恒温热源,这些热源 的温度从T1逐步增加到T2 ,使物体依次与一系列热源接触。
§6. 气体的内能 焦耳-汤姆孙实验 一、焦耳实验
绝热自由膨胀过程 (A=0,Q=0)
U 1(T 1,V 1)U 2(T 2,V 2)常量
理想气体内能仅是温度的函数,与体积无关。 ——焦耳定律(Joule law)
理想气体宏观特性: 1)满足pV=νRT关系; 2)满足道耳顿分压定律; 3)满足阿伏加德罗定律; 4)满足焦耳定律U=U(T)。
第5章热力学循环热力学第二定律

• S = klnΩ • 式中k为玻耳兹曼常数,Ω为热力学几率。
• 由于熵与体系内部分子运动混乱程度有关,因此熵 值较小的状态对应于比较有序的状态,熵值较大的 状态对应于比较无序的状态。
• 另一种解释是针对随机事件而言的,按现代信息 论的方法,把熵视为信息缺失的量度。
• ΔSsys +Δssur ≥ 0物理意义是:孤立体系的熵只能 增加永不减少,这就是熵增原理。
dSf QR
T
• dSf表示由于传热δQR而引起体系熵的变化。 体系与外界传递的热量可正(吸热)、可负(放热)、 可零(绝热),因此熵流dSt亦可正、可负、可零。
• 要注意,功的传递不会引起熵的流动,这从 熵的定义便可知道。前已论及,功源里没有熵 变。但这样说并不意味着每当有功输入或输出 体系时,体系均无熵变,而只是说,这种熵变 并不是功传递的直接结果。
概述
• 一、热力学分析——以热力学第一和第二定律为基础,导 出各种关系式,从而对化工过程进行分析与评价,以求实 现合理利用能源。
• 二、相平衡关系计算。这对于传质没备的设计和操作是必 不可少的。
• 三、化学平衡状态计算。它是研究化学反应动力学以及设 计反应器和操作分析计算的前提。
5.1.热力学第二定律
或者到达极限时保持恒定。其数学表达式为
•
ΔSt ≥ 0
• 式中ΔSt为孤立体系的总熵变。为孤立体系热力学第二定
律的数学表达式。对于不可逆过程用不等号;可逆过程用
等号。孤立体系的总熵变为封闭体系的熵变与外界环境熵
变和
•即 ΔSt = ΔSsys +Δssur
( ΔSsys +Δssur ≥ 0 ) 热力学第二定律各种表述方式都内含共同的实质,即 有关热现象的各种实际宏观过程都是不可逆的。克劳修斯 的说法指出了热传导过程的不可逆性,开尔文的说法则指 出了功转化为功这一过程的不可逆性。
• 由于熵与体系内部分子运动混乱程度有关,因此熵 值较小的状态对应于比较有序的状态,熵值较大的 状态对应于比较无序的状态。
• 另一种解释是针对随机事件而言的,按现代信息 论的方法,把熵视为信息缺失的量度。
• ΔSsys +Δssur ≥ 0物理意义是:孤立体系的熵只能 增加永不减少,这就是熵增原理。
dSf QR
T
• dSf表示由于传热δQR而引起体系熵的变化。 体系与外界传递的热量可正(吸热)、可负(放热)、 可零(绝热),因此熵流dSt亦可正、可负、可零。
• 要注意,功的传递不会引起熵的流动,这从 熵的定义便可知道。前已论及,功源里没有熵 变。但这样说并不意味着每当有功输入或输出 体系时,体系均无熵变,而只是说,这种熵变 并不是功传递的直接结果。
概述
• 一、热力学分析——以热力学第一和第二定律为基础,导 出各种关系式,从而对化工过程进行分析与评价,以求实 现合理利用能源。
• 二、相平衡关系计算。这对于传质没备的设计和操作是必 不可少的。
• 三、化学平衡状态计算。它是研究化学反应动力学以及设 计反应器和操作分析计算的前提。
5.1.热力学第二定律
或者到达极限时保持恒定。其数学表达式为
•
ΔSt ≥ 0
• 式中ΔSt为孤立体系的总熵变。为孤立体系热力学第二定
律的数学表达式。对于不可逆过程用不等号;可逆过程用
等号。孤立体系的总熵变为封闭体系的熵变与外界环境熵
变和
•即 ΔSt = ΔSsys +Δssur
( ΔSsys +Δssur ≥ 0 ) 热力学第二定律各种表述方式都内含共同的实质,即 有关热现象的各种实际宏观过程都是不可逆的。克劳修斯 的说法指出了热传导过程的不可逆性,开尔文的说法则指 出了功转化为功这一过程的不可逆性。
第五章-传热学
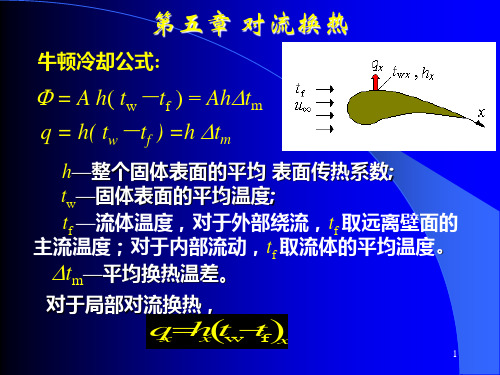
h
' h,x
' h,y
cpuxtvytdxdy
8
单位时间内微元体热力学能的增加为
dU
d
cp
t
dxdy
于是根据微元体的能量守恒
h
dU
d
可得
2t x2
2t y2
dxdy
cpuxtvytdxdy
cp
t
dxdy
cptux tvy ttu xv y
2t x2
2t y2
2
20
cp
uxt
v t y
=
2t x2
2t y2
1
11 1
1
2
1 1
1
2
对流换热微分方程组简化为
h t tw tf y w
u v 0 x y
简化方程组只有4个方
程,但仍含有h、u、v、 p、t 等5个未知量,方
程组不封闭。如何求解?
uuxvuy1ddpxy2u2
u t x
v t y
26
第六节 相似理论基础
相似原理指导下的实验研究仍然是解决复杂对流换 热问题的可靠方法。
相似原理回答三个问题: (1)如何安排实验? (2)如何整理实验数据? (3)如何推广应用实验研究结果?
一、 相似原理的主要内容
1.物理现象相似的定义 2.物理现象相似的性质 3.相似特征数之间的关系 4.物理现象相似的条件
三、解的函数形式——特征数关联式
特征数是由一些物理量组成的无量纲数,例如毕 渥数Bi和付里叶数Fo。对流换热的解也可以表示成 特征数函数的形式,称为特征数关联式。
通过对流换热微分方程的无量纲化可以导出与对 流换热有关的特征数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29
第五章 热力学第二定律与熵
二、卡诺定理的应用
利用卡诺定理求出物质某些平衡 性质之间的关系,是应用第二定 律解决实际问题的一方面,具体 看两个例子。
p
(p)V
A
T
F
B
1. 证明 ( U )T T ( p )V p V T
D T T E C
(V )T
o
H
G
V
如图物质经历一个微小可逆卡诺循环,循环足够小,ABCD 可近似视为平行四边形,对外做的功为: △W=ABEF的面积= 中体积的改变。
如热传递现象:对两个高低温物体,若借助热机则可对 外做部分有用功,但若直接接触,结果就是最终无非使它 们的温度相同,使可用能量变成不可用能量,而浪费掉。
22
第五章 热力学第二定律与熵
3.与第零定律的比较 第零定律:指出温度相同是达到热平衡的诸物 体所具有的共同性质。 第二定律却从热量自发流动的方向判别出物体 温度的高低。
28
第五章 热力学第二定律与熵
全部传到高温热源 Q1 Q1 热量 Q2 Q2
显然违反克氏表述,故 a b 的假设是错误的, 正确的表述只能是b热机效率不能大于a机的效率。
b a
即证明了卡诺定理的第二条。若b机也是可逆机, 同样可以证明有: a b 最终只有一个可能,即 a b ,这就证明了卡 诺定理的第一条。上述证明没有涉及到工作物质, 所以效率与工作物质无关。
14
第五章 热力学第二定律与熵
高温热库T1 Q1 W= Q1 Q2 低温热库T2 Q2
Q1 Q2 Q2
15
第五章 热力学第二定律与熵
高温热库T1 Q2 Q1 W
Q2 Q2 低温热库T2 W= Q1 Q2
Q1 Q2
16
第五章 热力学第二定律与熵
二、利用两种表述判断可逆与不可逆 1.自由膨胀是不可逆的
高温热源 T1
Q1
卡诺致冷机
虽然卡诺致冷机能把热量从 低温物体移至高温物体,但需 外界作功且使环境发生变化。
W
Q2
低温热源 T2
13
第五章 热力学第二定律与熵
T1 Q1
Q2
T1
Q2
Q1 –Q2
A
W=Q1 T2 Q2
B A’
B’
Q1 –Q2 =W T2 Q2 (b)
(a)
3.两种表述的等效性
反证法:假设开氏(或克氏)正确,则克氏(或开氏)就正 确。若开氏(或克氏)不真,则克氏(或开氏)就不真。
类似于前面的微小卡诺循环图,外界对表面系统 所做的功 W A
W A
4
第五章 热力学第二定律与熵
一、热力学第二定律的两种表述及其等效性 第二定律的提出 功热转换的条件第一定律无法说明。
重物下落,水温升高; 水温下降,重物升高? 只要重物位能增加小于等于水降 内能减少,不违反第一定律。 电流通过电阻,产生热量 对电阻加热,电阻内产生反向 电流? 只要电能不大于加入热能,不 违反第一定律。
假设气体向真空中自由膨胀是可逆过 程,从气体充满容器开始,先让气体自 动回到容器左边,再经等温膨胀过程, 让气体充满容器,构成一个循环。
真空
该循环唯一的效果是从单一热源吸收热量使之全部转化为 功,显然违背开尔文表述。说明自动返回左边的过程不可能 ,即自由膨胀是不可逆过程。
2.扩散是不可逆的 3.大多数的化学反应是不可逆的
诺定理及其应用,热力学温标的建
立。
24
第五章 热力学第二定律与熵
一、卡诺定理
1.卡诺定理 针对卡诺循环,卡诺提出了卡诺定 理,其表述为: (1)在相同的高温热源和相同的低温 卡诺 热源间工作的一切可逆热机其效率都 T2 相等,而与工作物质无关。 1 T1 (2)在相同高温热源与相同低温热源 间工作的一切热机中,不可逆热机的 T2 1 T1 效率都不可能大于可逆热机的效率。
注意
(1)热力学第二定律是大量实验和经验的总结。 (2)热力学第二定律开尔文说法与克劳修斯说法具有等 效性。 (3)热力学第二定律可有多种说法,每一种说法都反映 了自然界过程进行的方向性 。
23
第五章 热力学第二定律与熵
§5.2 卡诺定理
本节主要内容 本节主要讨论建立热力学第二定律 的数学表达式所必须的基础,即卡
8
第五章 热力学第二定律与熵
永 动 机 的 设 想 图
9
第五章 热力学第二定律与熵
10
第五章 热力学第二定律与熵
11
第五章 热力学第二定律与熵
12
第五章 热力学第二定律与熵
2.第二定律的克劳修斯表述
热传导过程的不可逆性:
第二定律的克劳修斯表述: 不可能把热量从低温物体传到高 温物体而不引起其他影响。也可 以表述为:热量不能自发地从低 温物体传到高温物体。 克 劳 修 斯
30
(p)V (V )T
(p)V , (V )T 分别表示体积不变时压强的改变和等温过程AB
第五章 热力学第二定律与熵
由第一定律,在AB过程中吸收热量为:
Q1 =ABGH的面积+ (U )T
(U )T 表示在等温过程中系统内能的改变。设A点的压强
为p,在等温过程AB中压强的变化为 (p)T ,则B点的压强 就是 p (p)T ,则
7
第五章 热力学第二定律与熵
第二定律的开尔文表述:不可能从单一 热源吸收热量,使之完全变为有用功而不产 生其他影响。
说明:
单一热源:指温度处处相同且恒定不变的 热源。 开尔文 其他影响:指除了由单一热源吸收热量全部转化为功以外 的任何其他变化。 理想气体等温膨胀并不违背开尔文表述。在这一过程中除 了气体从单一热源吸热完全变为功外,还引起了其它变化, 即过程结束时,气体的体积增大了。 第二类永动机不可能制造成。
第五章 热力学第二定律与熵
第五章
热力学第二定律与熵
1
第五章 热力学第二定律与熵
热力学第二定律是在研究如何提高热机效率的 推动下被发现的,并用于解决与热现象有关过程进 行的方向问题,与第一定律一起构成了热力学的主 要理论基础。 第一节 第二节 热力学第二定律的表述及其实质 卡诺定理
第三节
熵与熵增加原理
5
第五章 热力学第二定律与熵
热传导的方向性、气体自由膨胀的不可逆性问题 第一定律无法说明。 一切实际的宏观热力学过程都是不可逆的 耗散过程是不可逆的 非静态过程是不可逆的 归纳:1)自发过程有方向性; 2)自发过程的反方向过程并非不可进行,而是 要有附加条件; 3)并非所有不违反第一定律的过程均可进行。
19
第五章 热力学第二定律与熵
四、热力学第二定律的实质 1.第二定律的实质 自然界中的不可逆过程多种多样,其特点是: 自然界一切与热现象有关的 实际宏观过程都是不可逆的。 在一切与热相联系的自然现象中它们自 发地实现的过程都是不可逆的,这就是热 力学第二定律的实质。
20
第五章 热力学第二定律与熵
17
第五章 热力学第二定律与熵
4.由两种表述判别过程可逆或不可逆的方法 由自由膨胀过程的不可逆性可以看出:判别过 程可逆或不可逆,方法是需设想某种方法把这一 过程与开氏或克氏表述联系起来,使系统回到初 态,若因此违背第二定律,则过程是不可逆的, 否则是可逆的。
第二定律可以有其他各种表述,但都是相互等 价的,可以由一种表述导出另一种表述。 三、利用四种不可逆因素判断可逆与不可逆 可逆过程:准静态无摩擦(无耗散)过程为可逆 过程。
6
第五章 热力学第二定律与熵
1.第二定律的开尔文表述
以热机为例,效 率总是小于1的, 当热机效率达到1 时,热机在低温 热源不再放出热 量,即从高温热 源吸收的热量全 部对外做功。
p
A
T1 T2
T1
D
高温热源 T1
Q1 W
卡诺热机
W
B
o
T2
C
Q2
低温热源T2
V
第二类永动机:从单一热源吸取热量全部转化为功。 开尔文勋爵(即汤姆孙)总结这一类现象提出了 第二定律的表述。
热功转换
功
有序
完全 不完全 自发 自发传热 非自发传热
热
无序 低温物体
热传导
高温物体
非均匀、非平衡
自发
均匀、平衡
21
第五章 热力学第二定律与熵
2.与第一定律的比较 第一定律主要从数量上说明功和热量的等价性。 第二定律却从转换能量的质的方面来说明功与热 量的本质区别,从而揭示自然界中普遍存在的一 类不可逆过程。 任何不可逆过程的出现,总伴随有“可用(做有 用功的)能量”被贬值为“不可用能量”的现象 发生。
2
第五章 热力学第二定律与熵
本章教学目标 要清楚不可逆过程的特征以及自然现象不可 逆性的实质
掌握热力学第二定律的不同表述
掌握卡诺定理内容 掌握熵的增加原理和不可逆过程熵的计算
3
第五章 热力学第二定律与熵
§5.1 热力学第二定律的表述及其实质
本节主要内容 本节主要讨论热力学第二定律的两种表 述及其等效性、利用两种表述判断可逆 与不可逆、利用四种不可逆因素判断可 逆与不可逆、热力学第二定律的实质以 及与第一、第零定律的比较。
p 1 梯形ABGH的面积= [ p (p)T ]( V )T 2
1 Q1 [ p (p)T ]( V )T (U )T 2
A
(p)V
T
F
B
由可逆卡诺循环的效率
D T T E C
(V )T
W T1 T2 Q1 T1
o
H
G
31
V
第五章 热力学第二定律与熵
18
第五章 热力学第二定律与熵
准静态过程:只有始终同时满足力学、热学、化 学平衡条件的过程才是准静态过程。 由此可见:任何一个不可逆过程中必包含有四种 不可逆因素中的某一种或某几种。
第五章 热力学第二定律与熵
二、卡诺定理的应用
利用卡诺定理求出物质某些平衡 性质之间的关系,是应用第二定 律解决实际问题的一方面,具体 看两个例子。
p
(p)V
A
T
F
B
1. 证明 ( U )T T ( p )V p V T
D T T E C
(V )T
o
H
G
V
如图物质经历一个微小可逆卡诺循环,循环足够小,ABCD 可近似视为平行四边形,对外做的功为: △W=ABEF的面积= 中体积的改变。
如热传递现象:对两个高低温物体,若借助热机则可对 外做部分有用功,但若直接接触,结果就是最终无非使它 们的温度相同,使可用能量变成不可用能量,而浪费掉。
22
第五章 热力学第二定律与熵
3.与第零定律的比较 第零定律:指出温度相同是达到热平衡的诸物 体所具有的共同性质。 第二定律却从热量自发流动的方向判别出物体 温度的高低。
28
第五章 热力学第二定律与熵
全部传到高温热源 Q1 Q1 热量 Q2 Q2
显然违反克氏表述,故 a b 的假设是错误的, 正确的表述只能是b热机效率不能大于a机的效率。
b a
即证明了卡诺定理的第二条。若b机也是可逆机, 同样可以证明有: a b 最终只有一个可能,即 a b ,这就证明了卡 诺定理的第一条。上述证明没有涉及到工作物质, 所以效率与工作物质无关。
14
第五章 热力学第二定律与熵
高温热库T1 Q1 W= Q1 Q2 低温热库T2 Q2
Q1 Q2 Q2
15
第五章 热力学第二定律与熵
高温热库T1 Q2 Q1 W
Q2 Q2 低温热库T2 W= Q1 Q2
Q1 Q2
16
第五章 热力学第二定律与熵
二、利用两种表述判断可逆与不可逆 1.自由膨胀是不可逆的
高温热源 T1
Q1
卡诺致冷机
虽然卡诺致冷机能把热量从 低温物体移至高温物体,但需 外界作功且使环境发生变化。
W
Q2
低温热源 T2
13
第五章 热力学第二定律与熵
T1 Q1
Q2
T1
Q2
Q1 –Q2
A
W=Q1 T2 Q2
B A’
B’
Q1 –Q2 =W T2 Q2 (b)
(a)
3.两种表述的等效性
反证法:假设开氏(或克氏)正确,则克氏(或开氏)就正 确。若开氏(或克氏)不真,则克氏(或开氏)就不真。
类似于前面的微小卡诺循环图,外界对表面系统 所做的功 W A
W A
4
第五章 热力学第二定律与熵
一、热力学第二定律的两种表述及其等效性 第二定律的提出 功热转换的条件第一定律无法说明。
重物下落,水温升高; 水温下降,重物升高? 只要重物位能增加小于等于水降 内能减少,不违反第一定律。 电流通过电阻,产生热量 对电阻加热,电阻内产生反向 电流? 只要电能不大于加入热能,不 违反第一定律。
假设气体向真空中自由膨胀是可逆过 程,从气体充满容器开始,先让气体自 动回到容器左边,再经等温膨胀过程, 让气体充满容器,构成一个循环。
真空
该循环唯一的效果是从单一热源吸收热量使之全部转化为 功,显然违背开尔文表述。说明自动返回左边的过程不可能 ,即自由膨胀是不可逆过程。
2.扩散是不可逆的 3.大多数的化学反应是不可逆的
诺定理及其应用,热力学温标的建
立。
24
第五章 热力学第二定律与熵
一、卡诺定理
1.卡诺定理 针对卡诺循环,卡诺提出了卡诺定 理,其表述为: (1)在相同的高温热源和相同的低温 卡诺 热源间工作的一切可逆热机其效率都 T2 相等,而与工作物质无关。 1 T1 (2)在相同高温热源与相同低温热源 间工作的一切热机中,不可逆热机的 T2 1 T1 效率都不可能大于可逆热机的效率。
注意
(1)热力学第二定律是大量实验和经验的总结。 (2)热力学第二定律开尔文说法与克劳修斯说法具有等 效性。 (3)热力学第二定律可有多种说法,每一种说法都反映 了自然界过程进行的方向性 。
23
第五章 热力学第二定律与熵
§5.2 卡诺定理
本节主要内容 本节主要讨论建立热力学第二定律 的数学表达式所必须的基础,即卡
8
第五章 热力学第二定律与熵
永 动 机 的 设 想 图
9
第五章 热力学第二定律与熵
10
第五章 热力学第二定律与熵
11
第五章 热力学第二定律与熵
12
第五章 热力学第二定律与熵
2.第二定律的克劳修斯表述
热传导过程的不可逆性:
第二定律的克劳修斯表述: 不可能把热量从低温物体传到高 温物体而不引起其他影响。也可 以表述为:热量不能自发地从低 温物体传到高温物体。 克 劳 修 斯
30
(p)V (V )T
(p)V , (V )T 分别表示体积不变时压强的改变和等温过程AB
第五章 热力学第二定律与熵
由第一定律,在AB过程中吸收热量为:
Q1 =ABGH的面积+ (U )T
(U )T 表示在等温过程中系统内能的改变。设A点的压强
为p,在等温过程AB中压强的变化为 (p)T ,则B点的压强 就是 p (p)T ,则
7
第五章 热力学第二定律与熵
第二定律的开尔文表述:不可能从单一 热源吸收热量,使之完全变为有用功而不产 生其他影响。
说明:
单一热源:指温度处处相同且恒定不变的 热源。 开尔文 其他影响:指除了由单一热源吸收热量全部转化为功以外 的任何其他变化。 理想气体等温膨胀并不违背开尔文表述。在这一过程中除 了气体从单一热源吸热完全变为功外,还引起了其它变化, 即过程结束时,气体的体积增大了。 第二类永动机不可能制造成。
第五章 热力学第二定律与熵
第五章
热力学第二定律与熵
1
第五章 热力学第二定律与熵
热力学第二定律是在研究如何提高热机效率的 推动下被发现的,并用于解决与热现象有关过程进 行的方向问题,与第一定律一起构成了热力学的主 要理论基础。 第一节 第二节 热力学第二定律的表述及其实质 卡诺定理
第三节
熵与熵增加原理
5
第五章 热力学第二定律与熵
热传导的方向性、气体自由膨胀的不可逆性问题 第一定律无法说明。 一切实际的宏观热力学过程都是不可逆的 耗散过程是不可逆的 非静态过程是不可逆的 归纳:1)自发过程有方向性; 2)自发过程的反方向过程并非不可进行,而是 要有附加条件; 3)并非所有不违反第一定律的过程均可进行。
19
第五章 热力学第二定律与熵
四、热力学第二定律的实质 1.第二定律的实质 自然界中的不可逆过程多种多样,其特点是: 自然界一切与热现象有关的 实际宏观过程都是不可逆的。 在一切与热相联系的自然现象中它们自 发地实现的过程都是不可逆的,这就是热 力学第二定律的实质。
20
第五章 热力学第二定律与熵
17
第五章 热力学第二定律与熵
4.由两种表述判别过程可逆或不可逆的方法 由自由膨胀过程的不可逆性可以看出:判别过 程可逆或不可逆,方法是需设想某种方法把这一 过程与开氏或克氏表述联系起来,使系统回到初 态,若因此违背第二定律,则过程是不可逆的, 否则是可逆的。
第二定律可以有其他各种表述,但都是相互等 价的,可以由一种表述导出另一种表述。 三、利用四种不可逆因素判断可逆与不可逆 可逆过程:准静态无摩擦(无耗散)过程为可逆 过程。
6
第五章 热力学第二定律与熵
1.第二定律的开尔文表述
以热机为例,效 率总是小于1的, 当热机效率达到1 时,热机在低温 热源不再放出热 量,即从高温热 源吸收的热量全 部对外做功。
p
A
T1 T2
T1
D
高温热源 T1
Q1 W
卡诺热机
W
B
o
T2
C
Q2
低温热源T2
V
第二类永动机:从单一热源吸取热量全部转化为功。 开尔文勋爵(即汤姆孙)总结这一类现象提出了 第二定律的表述。
热功转换
功
有序
完全 不完全 自发 自发传热 非自发传热
热
无序 低温物体
热传导
高温物体
非均匀、非平衡
自发
均匀、平衡
21
第五章 热力学第二定律与熵
2.与第一定律的比较 第一定律主要从数量上说明功和热量的等价性。 第二定律却从转换能量的质的方面来说明功与热 量的本质区别,从而揭示自然界中普遍存在的一 类不可逆过程。 任何不可逆过程的出现,总伴随有“可用(做有 用功的)能量”被贬值为“不可用能量”的现象 发生。
2
第五章 热力学第二定律与熵
本章教学目标 要清楚不可逆过程的特征以及自然现象不可 逆性的实质
掌握热力学第二定律的不同表述
掌握卡诺定理内容 掌握熵的增加原理和不可逆过程熵的计算
3
第五章 热力学第二定律与熵
§5.1 热力学第二定律的表述及其实质
本节主要内容 本节主要讨论热力学第二定律的两种表 述及其等效性、利用两种表述判断可逆 与不可逆、利用四种不可逆因素判断可 逆与不可逆、热力学第二定律的实质以 及与第一、第零定律的比较。
p 1 梯形ABGH的面积= [ p (p)T ]( V )T 2
1 Q1 [ p (p)T ]( V )T (U )T 2
A
(p)V
T
F
B
由可逆卡诺循环的效率
D T T E C
(V )T
W T1 T2 Q1 T1
o
H
G
31
V
第五章 热力学第二定律与熵
18
第五章 热力学第二定律与熵
准静态过程:只有始终同时满足力学、热学、化 学平衡条件的过程才是准静态过程。 由此可见:任何一个不可逆过程中必包含有四种 不可逆因素中的某一种或某几种。
