2015级入学考试(数学)
2015级(初二上)10月考试数学 试题

第8题图D B A 2015级(初二上)10月考试数学 试题(考试时间120分钟,满分150分)A 卷(共100分)一、选择题(每小题3分,共30分)1、若4-40=m ,则估计m 的值所在范围是( )A 、21<<mB 、32<<m C 、43<<m D 、54<<m 2、适合下列条件的ABC ∆中,是直角三角形的个数有( )①15,12,9===c b a ②045,=∠=A b a ③17,15,8===c b a ④0062,28=∠=∠B A ⑤5.2,2,5.1===c b aA 、2个B 、3个C 、4个D 、5个 3、已知0)2(32=-+-y x x ,则y x +的平方根是( )A 、3B 、3±C 、9D 、9± 4、下列各组数中,互为相反数的是( )A 、23-3-)(和 B 、31-3-2和)( C 、327-3-和 D 、3-273和 5、在二次根式5.1,131,21231453-b a ,,,,中,是最简二次根式的有( ) A 、2个 B 、3个 C 、4个 D 、5个 6、在1315,==∆AC AB ABC ,中,高12=AD ,则ABC ∆的周长是( )A 、42B 、32C 、42或32D 、30或357、小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现绳子刚好接触地面,则旗杆的高度是( )A 、8米B 、10米C 、12米D 、14米8、如图所示,在ABC Rt ∆中,BD A ,090=∠平分ABC ∠,交AC 于点D ,且54==BD AB ,,则点D 到BC 的距离是( )A 、3B 、4C 、5D 、6第13题图1C9、已知等边三角形的边长为a ,则它边上的高、面积分别是( )A 、4,22a aB 、4,232a aC 、43,232a aD 、43,432a a 10、已知m 是13的整数部分,n 是13的小数部分,则nm nm +-的值是( ) A 、1313-6 B 、1313-136 C 、3133-13+ D 、13-6二、填空题(每小题4分,共16分)11、设3,2==b a ,用含b a ,的式子表示54= 12、在关系式3-2x x y -=中,自变量x 的取值范围是 13、实数在数轴上的位置如图所示,则化简22)11()4-+-a a (=14、如图所示,已知长方体木箱长cm BB cm AB cm BC 168,121===,高宽其中点E 是线段11C B 的一个三等分点,在长方体木箱的下底面A 处有一只蚂蚁,想沿着表面爬到上表面E 处吃食物,则蚂蚁爬行的最短路程....是 三、计算或解方程(共18分)15、计算下列各题(每小题3分,共12分) (1) 2)63(1226---+- (2)3643632932-+-++(3)22)3223()3223(+-- (4)0)2(231121-++++π第17题图CBA(1)09)142=--x ( (2)0125)127-3=-+x (四、解答题(每小题8分,共16分)17、在ABC ∆中,已知211710===BC AC AB ,,,求ABC S ∆18、已知43=a ,0312=-++-c c b ,求33c b a ++的立方根?H G F ED 第20题图CB A19、(每小题5分,共10分) (1)先化简,再求值:21122-++m mm ,其中61=m(2)已知y x ,满足条件421025+=---y x x ,求y x -的算术平方根?20、(本题10分)如图,在ABC Rt ∆中,F E AC BE D AB CD ABC ,,450于,于⊥⊥=∠是BC 的中点,CBE ABE ∠=∠DC DF BE ,与分别交于H G ,.(1)猜想线段AC BH 与的数量关系。
2015年新初一高端班补录考试-数学部分 解析A4

本题评析:本题考查学生对繁分数的熟练掌握
17、 答案:100.48 dm3 知识点:立体几何 详解:设圆的直径为 x,列方程: d 16.56 d 解得 d 4 , 所以 v
1 2 1 d 2d 3.14 16 8 100.48dm3 4 4
难度星级:★★★
本题评析:本题是一道余数问题,要求学生对商和余数的关系有深入的理解。
二试
六、计算题(每题 2 分,共 12 分)
23、 答案: 16 知识点:有理数加减混合运算。 详解: 23 11 28 46 23 11 28 46 16 难度星级:★
难度星级:★★
本题评析: 本题里面涉及到了一个乘方的概念,三次方即立方也就是三个相同的数相 乘,二次方及平方也就是两个相同的数相乘,相信孩子们小学也接触过,另一个值得 注意负数的 n 次方和一个数的 n 次方的相反数。相对而言还属于中档题。
27、答案: 2a b 知识点:合并同类项 详解: 3a 2b 5a b 3a 5a 2b b 2a b 难度星级:★★★
难度星级:★★
本题评析:观察该题,发点:有理数的混合运算
15 ,因此先提取公因子即可,考查了孩 29
3 3 3 3 8 3 2 2 8 详解: 32 2 9 2 2 1 2 2 2 3 2 3 3 27
10、 答案:A 知识点:位值原理 详解: 设原两位数为 10a+b, 则交换个位与十位以后, 新两位数为 10b+a, 两者之差为 (10a+b) -(10b+a)=9(a-b)=27,即 a-b=3,a、b 为一位自然数,即 96,85,74,63,52,41 满足条 件,共计 6 个 难度星级:★★★
2015级九(上)数学中期考试卷

24、 (10 分) 如图, 已知 PA、 PB 切⊙O 于 A、 B 两点, 连 AB, 且 PA, PB 的长是方程 x 2m x 3 0
2
的两根,AB = m. 试求: (1)⊙O 的半径; ⌒ 围成图形(即阴影部分)的面积. (2)由 PA,PB,AB
25、 (9 分)如图 24-3-6(1)、24-3-6(2)、24-3-6(3)、…、24-3-6(n),M、N 分别是⊙O 的内接正 23、 (8 分)如图,已知四边形 ABCD 内接于⊙O,∠BOD= 80 ,求∠BAD 和∠BCD 的度数。
1 圆周的一个扇形,将留下的扇形围成一个 3
-1-
18. (7 分)如图,在 Rt△OAB 中,∠OAB=90°,且点 B 的坐标为(4,2) .画出△OAB 绕 点 O 逆时针旋转 90°后的△OA1B1,并求点 A 旋转到点 A1 所经过的路线长.
20、 (7 分)在正方形 ABCD 中,E 是 AD 的中点,F 是 BA 延长线上一点,AF= (1)说明线段 BE 与 DF 之间的关系. (2) 可以通过平行移动、 翻折、 旋转中的哪一种方法,•使△ABE 移到△ADF 的位置?
图①
图②
图③
-2-
22、 (8 分)已知抛物线 y=-x2+bx+c 与 x 轴的两个交点分别为 A(m, 0), B(n, 0), 且mn 4,
m 1 n 3
(1)求此抛物线的解析式; (2)设此抛物线与 y 轴的交点为 C,过 C 作一条平行 x 轴的直线交抛物线于另一点 P, 求△ACP 的面积.
21、 (8 分)某商场销售一批名牌衬衫,平均每天可售出 20 件,每件盈利 45 元,为了扩大销 售、增加盈利,尽快减少库存 ,商场决定采取适当的降价措施,经调查发现,如果每件衬衫 ...... 每降价 1 元,商场平均每天可多售出 4 件,若商场平均每天盈利 2 100 元,每件衬衫应降价多 少元?
湖北省宜昌市长阳县第一高级中学2014-2015学年高一上学期入学考试数学试题(无答案)Word版

注意事项:1. 本试卷分为试题卷和答题卷两部分,考试时间120分钟,满分120分。
2. 所有答案均须做在答题卷相应区域,做在其它区域内无效。
一、选择题(下列各小题中,只有一个选项是符合题目要求的,请在答题卡上指定的位置填写符合要求求的求的选项代号。
本大题共15小题,每小题3分,计45分) 1. 13-的倒数是( ) A. 3- B. 3 C. 13-D. 132.根据《国家中长期教育改革和发展规划纲要》,教育经费投入应占当年GDP 的4%.若设2014年GDP 的总值为n 亿元,则2014年教育经费投入可表示为( )亿元. A .4%n B .(1+4%)n C .(1﹣4%)n D .4%+n3.在以下永洁环保、绿色食品、节能、绿色环保四个标志中,是轴对称图形的是( )A .B .C .D .4.要调查城区九年级8000名学生了解禁毒知识的情况,下列调查方式最合适的是( ).A .在某校九年级选取50名女生B .在某校九年级选取50名男生C .在某校九年级选取50名学生D .在城区8000名九年级学生中随机选取50名学生 5.合作交流是学习教学的重要方式之一,某校九年级每个班合作学习小组的个数分别是:8,7.实数a ,b 在数轴上的位置如图所示,以下说法正确的是( )9.我市大约有34万中小学生参加了“廉政文化进校园”教育活动,将数据34万用科学记(A)(B)(C)(D)第8题数法表示,正确的是( ).A .0.34×105B .3.4×105C .34×105D .340×10510.若式子在实数范围内有意义,则x 的取值范围是( )11.如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC 平移到△DEF 的位置,下面正确的平移步骤是( )A .先把△ABC 向左平移5个单位,再向下平移2个单位B .先把△ABC 向右平移5个单位,再向下平移2个单位 C .先把△ABC 向左平移5个单位,再向上平移2个单位D .先把△ABC 向右平移5个单位,再向上平移2个单位12.如图,在梯形ABCD 中,AB ∥CD ,AD =BC ,点E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点, 则下列结论一定正确的是( ).A .∠HGF =∠GHEB .∠GHE =∠HEFC . ∠HEF =∠EFGD .∠HGF =∠HEF14. 2012﹣2013NBA 整个常规赛季中,科比罚球投篮的命中率大约是83.3%,下列说法错15.已知抛物线y=ax 2﹣2x+1与x 轴没有交点,那么该抛物线的顶点所在的象限是( )A .第四象限B .第三象限C .第二象限D .第一象限二、解答题(将解答过程写在答题卡上指定的位置,本大题共9小题,计75分) 16.(6分)计算:(﹣20)×(﹣)+.第12题B G17.(6分)解方程组⎩⎨⎧=+=-221y x y x18.(6分)先将下列代数式化简,再求值:(a+b )(a ﹣b )+b (b ﹣2),其中,b=1. 19.(8分)某市实施“限塑令”后,2008年大约减少塑料消 耗约4万吨.调查结果分析显示,从2008年开始,五年内该 市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间 x(年)逐年成直线上升,y 与x 之间的关系如图所示. (1)求y 与x 之间的关系式;(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少?20.(8分)如图,点E ,F 分别是锐角∠A 两边上的点,AE=AF ,分别以点E ,F 为圆心,以AE 的长为半径画弧,两弧相交于点D ,连接DE ,DF . (1)请你判断所画四边形的性状,并说明理由; (2)连接EF ,若AE=8厘米,∠A=60°,求线段EF 的长. 21.(8分)读书决定一个人的修养和品位,在“文明湖北,美丽宜昌”读书活动中,某学习小组开展综合实践活动,随机调查了该校部分学生的课外阅读情况,绘制了平均每人每天课外阅读时间统计图.(1)补全扇形统计图中缺失的数据;(2)被调查学生中,每天课外阅读时间为60分钟左右的有20人,求被调查的学生总人数; (3)请你通过计算估计该校学生平均每人每天课外阅读的时间.22. (11分)如图,△ABC 和△ABD 都是⊙O 的内接三角形,圆心O 在边上,边AD 分别与BC ,OC 交于E ,F 两点,点C 为弧AD 的中点.(1)求证:OF ∥BD ; (2)若FE 1ED 2=,且⊙O 的半径R=6cm . ①求证:点F 为线段OC 的中点;y (万吨)②求图中阴影部分(弓形)的面积.23.(11分)半径为2cm 的⊙O 与边长为2cm 的正方形ABCD 在水平直线l 的同侧,⊙O 与l 相切于点F ,DC 在l 上.(1)过点B 作圆的一条切线BE ,E 为切点.①如图1,当点A 在⊙O 上时,求∠EBA 的度数; ②如图2,当E ,A ,D 三点在同一直线上时,求线段OA 的长;(2)以正方形ABCD 的边AD 与OF 重合的位置为初始位置,向左移动正方形(图3),至边BC 与OF 重合时结束移动,M ,N 分别是边BC ,AD 与⊙O 的公共点,求扇形MON 的面积的范围.24.(11分) 已知抛物线y =ax 2+bx +c 与直线y =mx +n 相交于两点,这两点的坐标分别是(0,21)和(m -b ,m 2-mb +n ),其中a ,b ,c ,m ,n 为实数,且a ,m 不为0. (1)求c 的值;(2)设抛物线y =ax 2+bx +c 与x 轴的两个交点是(x 1,0)和(x 2,0),求x 1x 2的值; (3)当-1≤x ≤1时,设抛物线y =ax 2+bx +c 上与x 轴距离最大的点为P (x,y 求这时|y o |的最小值。
2015年考研数学试题详解及评分参考

2sin 2q
故选 (B) .
æ1 1 1 ö
æ1 ö
(5) 设矩阵 A = çççè11
2 4
a a2
÷ ÷÷ø
,
b
=
ç ç çè
d d
2
÷ ÷ ÷ø
,若集合
W
=
{1,
2} ,则线性方程组
Ax
=
b
有无穷
多解的充分必要条件为
(A) a Ï W, d Ï W (B) a Ï W, d Î W (C) a Î W, d Ï W (D) a Î W, d Î W
【答】 应填 -dx .
【解】 令 F (x, y, z) = ez + xyz + x + cos x - 2 ,有
Fx¢(x, y, z) = yz +1- sin x, Fy¢ = xz, Fz¢(x, y, z) = ez + xy
又当 x = 0, y = 1 时,有 ez = 1 ,即 z = 0 .
【答】 应选 (D) .
【解】 因 Ax = b 有无穷多解的充分必要条件为 r( A) = r( A, b) < 3 ,而
æ1 1 1 1 ö æ1 1
1
1ö
(A,b) = çç1 2 a
d
÷ ÷
®
ç ç
0
1
a -1
d -1
÷ ÷
çè1 4 a2 d 2 ÷ø çè 0 0 (a -1)(a - 2) (d -1)(d - 2) ÷ø ,
【解法二】 因在正交变换为 x = P y 下,有 f = xT Ax = yT (PT AP) y = 2 y12 + y22 - y32 .
2015年合肥某38中招生入学数学真卷(二)

2015年合肥某38中招生入学数学真卷(二)(时间:60分钟满分100分)―、选择题。
(每题3分,共15分)1.一个比的前项是8,如果前项增加16,要使比值不变,后项应该()。
A.增加16B.乘2C.除以13D.乘132. 某校合唱队共有100名学生,他们参加活动的次数统计如图所示,则合唱团学生参加活动的人均次数()。
A.2.4B.2.3C.2.2D.2.13. P种长方形卡片长25厘米,宽15厘米,用这样的卡片拼成个正方形最少需要()块。
A.15B.12C.8D.14. 甲、乙两包糖的重量比是4:1,如果从甲包取出10克放入乙包后,甲、乙两包糖的重量比变为7:8,那么两包糖重量的总和是()克。
A.30B.40C.50D.205. 一堆西瓜第一次卖出总个数的14又6个,第二次卖出余下的13又4个,第三次又卖出余下的12又3个,正好卖完,这堆西瓜原有()个。
A.27B.28C.29D.30二、填空题。
(每小题3分,共21分)1. 六年级四班的男、女生人数比为3:2,后来又转来5名女生,全班共45人。
求现在班上男、女生人数比。
2. 三块重量相等的锡铁合金第一块合金中锡与铁的比是1:5,第二块合金中锡与铁的比是2:7,第三块合金中锡与铁的比是3:4,如果把三块合金熔成一块,那么新熔成的合金中锡与铁的比是。
3. —个四位数添上一个小数点后变成的数比原数小2059.2,则这个四位数是。
4. —瓶饮料3.5元。
某商场规定5个空瓶可换1瓶饮料,某人用28元买饮料喝,最多能换到瓶饮料。
5. 请把65626795286572680539,,,,这4个数按从小到大排列。
6. 小明做了一份数学试卷共25道题,规定答对一道题得2分,答错一题扣一分,未答题不得分。
小明共得了34分,且知未答的题目数是奇数,则他答错道题。
7. 在齿轮箱里有3个齿轮相互衔接,第一个齿轮有28个齿,第二个齿轮有42个齿,第三个齿轮有108个齿,现在在3个齿轮相互咬合处作上标记,到下一次这3个齿轮再次在标记处相互咬合时,第2个齿轮需转圈。
2015年秋—中国地质大学(北京)继续教育学院入学考试高等数学模拟试卷及答案
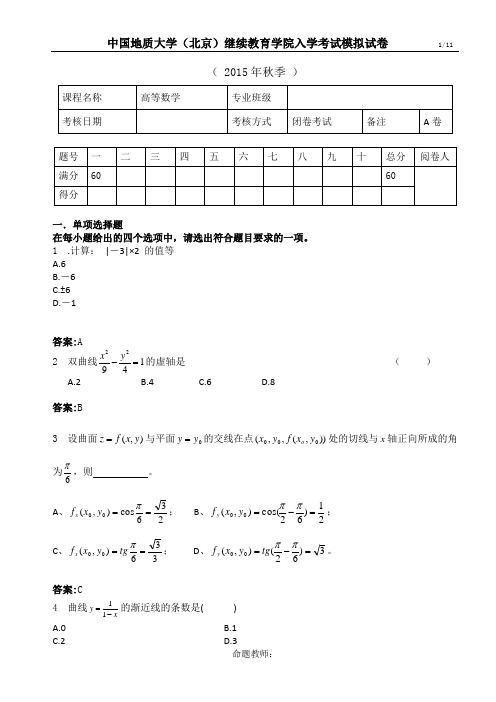
( 2015年秋季 )一.单项选择题在每小题给出的四个选项中,请选出符合题目要求的一项。
1 .计算: |-3|×2 的值等 A.6 B.-6 C.±6 D.-1答案:A2 双曲线14922=-y x 的虚轴是 ( ) A.2 B.4 C.6 D.8答案:B3 设曲面),(y x f z =与平面0y y =的交线在点)),(,,(000y x f y x o 处的切线与x 轴正向所成的角为6π,则 。
A 、236cos),(00==πy x f x ; B 、21)62cos(),(00=-=ππy x f y ;C 、336),(00==πtg y x f x ; D 、3)62(),(00=-=ππtg y x f y 。
答案:C 4 曲线xy -=11的渐近线的条数是( )A.0B.1C.2D.3答案:C5 假设检验时,当样本容量一定时,缩小犯第Ⅱ类错误的概率,则犯第Ⅰ类错误的概率( )A .必然变小B .必然变大C .不确定D .肯定不变答案:B 6 设2a 0π<<,则=→x x sin lim a x ( )A.0B.1C.不存在D.aasin答案:D7 =→xsin x 1sinx lim20x ( )A .1B .∞C .不存在D .0答案:D17 下列级数中条件收敛的是( )A .∑∞=--11)32()1(n n n B .∑∞=--11)1(n n nC .∑∞=--11)31()1(n nn D .∑∞=-+-1212)1(n n n n答案:B 8 幂级数 ∑∞=---1n n1n n)1x ()1( 的收敛区间是( ) A.(]2,0 B.(]1,1- C.[]0,2-D.()+∞-∞,答案:A 9 =+→)2x (x x2sin lim 0x ( )A.1B.0C.∞D.2答案:A10 已知方程y-ln x z=0确定函数z=z(x,y),则y x z ∂∂∂2=( )A .0B .xC .e yD .xe y答案:C11 设=0,,则下列结论必定正确的是( )A .为f(x)的极大值点 B. 为f(x)的极小值点C .不为f(x)的极值点 D.可能不为f(x)的极值点答案:A12 下列运算中正确的有( )A. =1B. =1C. =1D.=1答案:C13 设f(0)=0,且存在,则等于( )A .B.C. f(0)D.答案:B14 极限等于( )A.B. eC.D. 1答案:C15等于( )A .2 B.1 C.1/2 D.0答案:D16 曲线y=x 2+x -2在点(47,23)处的切线方程为( ) A.16x -4y -17=0B.16x+4y -31=0C.2x-8y+11=0D.2x+8y -17=0答案:A17 抛物线y=x 2在哪一点处切线的倾角为45°( ) A.(0,0) B.(21,41) C.(41,2) D.(1,1)答案:B18 反比例函数的图象经过点P (2-,1),则这个函数的图象位于A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限答案:C19 设',)(',)()(y x f e e f y x f x 则存在且==( )A .)()()()('x f x x f x e e f e e f +B .)(')(')(x f e e f x f x ⋅C .)(')()(')()(x f e e f e e f x f x x f x x ⋅++D .)()('x f x e e f答案:C20 设)(x f 在1=x 处可导,且21)1()21(lim0=--→h f h f h ,则=)1('f ( )A . 21B . 21-C . 41D .41-答案:D21 设)(x f 在2=x 处可导,且2)2('=f ,则=--+→hh f h f h )2()2(lim0( ) A .4 B .0 C .2 D .3答案:A22 若e cos x y x =,则'(0)y =( )A .0B .1C .1-D .2答案:C23 当0>x 时, xx y 1sin =( )A .有且仅有水平渐近线B .有且仅有铅直渐近线C .既有水平渐近线,也有铅直渐近线D .既无水平渐近线,也无铅直渐近线答案:A24 设总体X 在区间〔-1,1〕上均匀分布, X 1,X 2,…,X n 为其样本,则样本均值 X =n1∑=ni 1X i 的方差为() A .0 B .31 C .3D .n 31答案:D25 假设检验时,犯第二类错误的概率应为( ) A .P{接受H 0 | H 0 为真} B .P{拒绝H 0 | H 0 为真} C .P{接受H 0 | H 1 为真} D .P{拒绝H 0 | H 1 为真}答案:C26 设ζ为随机变量,E ζ=2,D ζ=4,则E ζ2=( )A .1B .2C .4D .8答案:D27 5个人排成一行,则甲排在正中间的概率是 ( )A .21 B. 52 C. 51 D.101答案:C28 在一次选举活动中, 要从 7名男同学,5名女同学中任意选取一名主席,那么不同的选法有( )(A )5种. (B )7种. (C )12种. (D )35种.答案:D29 某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 ( ) A .12512 B .12516 C .12548 D .12596答案:C30 某企业有职工150人,其中高级职称15人,中级职称45人,一般职员90人,现抽取30人进行分层抽样,则各职称人数分别为 ( ) A .5,10,15 B .3,9,18 C .3,10,17 D .5,9,16答案:B31 设函数y x e z +-=,则全微分=)1,1(dz ( ) A .dy dx -- B .dy dx + C .dy dx - D .dy dx +-答案:D32 若βα,是两个不重合的平面,m l ,是两条不重合的直线,现给出下列四个命题: ①若βαα⊥,//l ,则β⊥l ;②若βα⊥⊥⊥m l m l ,,,则βα⊥; ③若βα⊥⊥l l ,,则βα//;④若αα⊄⊥⊥m l m l ,,,则α//m其中正确的命题是 ( ) A. ①② B. ②④ C. ③④ D. ②③④答案:D 33 两直线13411+=-=-z y x 和1222-=-+=zy x 的夹角为( ) A.2π B. 3πC.4πD. 6π答案:C34 四个命题:①过平面外一点有无数条直线和这个平面垂直; ②过平面外一点只有一条直线和这个平面平行; ③过平面外一点有无数个平面和这个平面垂直; ④过平面外一点有无数个平面和这个平面平行;其中正确的命题是 ( ) A.① B.② C.③ D.④答案:C35 在空间直角坐标系中,点A (-1,2,4)关于xy 面的对称点A 1的坐标是( ) A.(1,-2,4) B.(1,-2,-4) C.(-1,2,-4) D.(1,2,4)答案:C36 若从一批有8件正品,2件次品组成的产品中接连抽取2件产品(第一次抽出的产品不放回去),则第一次取得次品且第二次取得正品的概率是( )A .91B .92C .458D .4516答案:C37 设f(x,y)=⎪⎩⎪⎨⎧=≠++),0,0()y ,x (,0);0,0()y ,x (,yx y 2x 22;则f x (0,0)=( ) A.0 B.1 C.2 D.不存在答案:B38 设f(x)在(-∞,+∞)内连续,则⎰2x 0)t (f 1dx d dt=( )A.f(x 2)B.2xf(x 2)C.f′(x 2)D.2xf′(x 2)答案:B39 设f(x)=⎪⎩⎪⎨⎧<>,0x ,x 1sin x ;0x ,x 1sin 那末lim 0x → f(x)不存在的原因是( )A.f(0)无定义B.lim 0x -→ f(x)不存在C.lim 0x +→ f(x)不存在 D.lim 0x -→f(x)与lim 0x +→f(x)都存在但不等答案:C40 =⎰→2x sin limx tdt x( ) A .∞ B .0 C .21D .1答案:C41 0lim =∞→n n u 是级数∑∞=0n n u 发散的 。
2015年考研数学三真题与答案详细讲解

2015年全国硕士研究生入学统一考试数学(三)试题解析一、选择题:1:8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸...指定位置上. (1)设{}n x 是数列,下列命题中不正确的是 ( ) (A) 若lim →∞=n n x a ,则 221lim lim +→∞→∞==n n n n x x a(B) 若221lim lim +→∞→∞==n n n n x x a , 则lim →∞=n n x a(C) 若lim →∞=n n x a ,则 331lim lim +→∞→∞==n n n n x x a(D) 若331lim lim +→∞→∞==n n n n x x a ,则lim →∞=n n x a【答案】(D)【解析】答案为D, 本题考查数列极限与子列极限的关系.数列()n x a n →→∞⇔对任意的子列{}k n x 均有()k n x a k →→∞,所以A 、B 、C 正确; D 错(D 选项缺少32n x +的敛散性),故选D(2) 设函数()f x 在(),-∞+∞连续,其2阶导函数()f x ''的图形如右图所示,则曲线()=y f x 的拐点个数为 ( )(A) 0 (B) 1 (C) 2 (D) 3 【答案】(C)【解析】根据拐点的必要条件,拐点可能是()f x ''不存在的点或()0f x ''=的点处产生.所以()y f x =有三个点可能是拐点,根据拐点的定义,即凹凸性改变的点;二阶导函数()f x ''符号发生改变的点即为拐点.所以从图可知,拐点个数为2,故选C.(3) 设 (){}2222,2,2=+≤+≤D x y xy x x y y ,函数(),f x y 在D 上连续,则( )【答案】(B)【解析】根据图可得,在极坐标系下该二重积分要分成两个积分区域所以故选B.(4) 下列级数中发散的是( )(A)(B)(D) 【答案】(C)【解析】ABCD为正项C.(5)穷多解的充分必要条件为( )【答案】(D)故选(D)(6) 设二次型( )【答案】(A)选(A ) (7) ,则: ( )【答案】(C)(C) .(8)值,( )【答案】(B)(B) .二、填空题:小题,每小题4分,共24分.请将答案写在答题纸...指定位置上.(10)(11)(12)3,则(13)设3E为3阶单位矩阵,则【答案】(14)【答案】指定位置上.解答应写出文字三、解答题:15~23小题,共94分.请将解答写在答题纸...说明、证明过程或演算步骤.(15)(本题满分10 分).【答案】【解析】法一:则有,法二:由已知可得得c;求进一步,b值代入原式(16)(本题满分10 分)【答案】(17)(本题满分10分)MC(I)(II)试由(I )中的定价模型确定此商品的价格.【答案】(I)略【解析】(I). (II)(I)中的定价模(18)(本题满分10 分)4,表达式.此为可分离变量的微分方程,(19)(本题满分10分)(I(II求导公式.【解析】(I(II)由题意得(20) (本题满分11分)(I)(II)3【解析】(II)由题意知(21) (本题满分11 分)(I)(II.【解析】A(22) (本题满分11 分),直到第2个大于3(I)(II)【答案】;【解析】(I)3(II) 法一:分解法:,.注:Ge表示几何分布)法二:直接计算(23) (本题满分11 分).(I) (II).【答案】;【解析】(I);(II).文档容由金程考研网整理发布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本溪县高中2015级入学考试数学试卷考试时间:120分 满分:150分一、选择题(共10小题,每小题3分,满分30分)1.已知边长为a 的正方形的面积为8,则下列说法中,错误的是( )A . a 是无理数B . a 是方程x 2﹣8=0的一个解 C . a 是8的算术平方根D . a 满足不等式组2.已知a ,b ,c 是ΔABC 的三边长,那么方程cx 2+(a +b )x +4c =0的根的情况是 ( )(A )没有实数根 (B )有两个不相等的实数根 (C )有两个相等的实数根 (D )有两个异号实数根3. 有3 cm ,3 cm ,6 cm ,6 cm ,12 cm ,12 cm 的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为( ) A .1B .2C .3D .44.若-1<a <0,则31,a a a一定是 ( )(A)a 1最小,3a 最大 (B) 3a 最小,a 最大 (C) a 1最小,a 最大 (D) a1最小, 3a 最大5.盒子里有完全相同的三个小球,球上分别标有数字-2,1,4.随机摸出一个小球,其数字为p (放回),再随机摸出一个小球,其数字记为q ,则满足关于x 的方程x 2+px +q=0有实数根的概率是( ) A.19 B.13 C.23 D.896. 如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x 表示时间,y 表示小明离家的距离,小明家、食堂、图书馆在同一直线上. 根据图中提供的信息,有下列说法: (1)食堂离小明家0.4 km ;(2)小明从食堂到图书馆用了3 min ; (3)图书馆在小明家和食堂之间;(4)小明从图书馆回家的平均速度是0.04km/min其中正确的有( ) A .4个B .3个C .2个D .1个7.如图,对折矩形纸片ABCD ,使BC 与AD 重合,折痕为EF ,把纸片展平;再一次折叠纸片,使BC 与EF 重合, 折痕为GH ,把纸片展平;再一次折叠纸片,使点A 落在GH 上的点N 处,并使折痕经过点B ,折痕BM 交GH 于点 I .若AB =4 cm ,则GI 的长为( )A .410cm B .43cm C .54cm D .515cm 8.若},,,max{21n s s s 表示实数n s s s ,,,21 中的最大者.设),,(321a a a A =,⎪⎪⎪⎭⎫ ⎝⎛=321b b b B ,记}.,,max{332211b a b a b a B A =⊗设,1(-=x A )1,1+x ,⎪⎪⎪⎭⎫ ⎝⎛--=|1|21x x B ,若1-=⊗x B A ,则x 的取值范围为( )A .9.如图,已知抛物线x x y l 221:21-=与x 轴分别交于O 、A 两点,它的对称轴为直线x=a ,将(第7题)IABCDE FG H MN(第6题)y /min抛物线1l 向上平移4个单位长度得到抛物线2l ,则图中两条抛物线、对称轴与y 轴所围成的图形(图中阴影部分)的面积为( )A .4B .6C .8D .1610.如图,△ABC 中,D 、E 两点分别在BC 、AD 上,且AD 为∠BAC 的角平分线.若∠ABE=∠C,AE :ED=2:1,则△BDE 与△ABC 的面积比为何?( ) A . 1:6B . 1:9C . 2:13D . 2:15第9题二、填空题(共8小题,每小题3分,满分24分)11.若m 是方程210x x +-= 的一个根,则代数式3222013m m ++的值= .12. 在很小的时候,我们就用手指练习过数数. 一个小朋友按如下图(1)的规则练习数数,数到2016时对应的指头是 __________ (填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).第12题 图(1) 第13题 图(2) 第14题 图(3)13.如左下图(2),在△ABC 中,AB=BC ,∠ABC=90°,E 是AB 上一点,BE=2,AE=3BE ,P 是AC上一动点,则PB+PE 的最小值是 .14.如左下图(3)所示,直线2+-=x y 分别与x 轴、y 轴交于点A 、 B ,点P 为函数x y 2=(x >0)图象上的一点,过点P 分别作x 轴、y 轴的垂线段PE 、PF,当PE 、PF 分别与线段AB 交于点C、D 时,则AD ·BC 的值为.15.观察下列不等式:21241324613524681357......>⋅>⋅⋅>⋅⋅⋅>照此规律,由此猜测第n 个不等式为:*()n N ∈16.若对于多项式x 2+2x+3,当x 取x 1、x 2(x 1≠x 2)时,多项式的值相等;当x 取x 3、x 4(x 3≠x 4)时,多项式的值相等;当x 取x 5、x 6(x 5≠x 6)时,多项式的值相等;…;当x 取x 2013、x 2014(x 2013≠x 2014)时,多项式的值相等;则当x= 时,(x- x 1)2+(x- x 2)2+(x- x 3)2+(x- x 4)2…+(x - x 2013)2+ (x- x 2014)2的值最小.17.设,C ,C ,C 321… … 为一群圆, 其作法如下:1C 是半径为a 的圆, 在1C 的圆内作四个相等的圆2C (如图), 每个圆2C 和圆1C 都内切, 且相邻的两个圆2C 均外切, 再在每一个圆2C 中, 用同样的方法作四个相等的圆3C , 依此类推作出,C ,C ,C 654…… , 则第10题第17题第18题(1) 圆2C 的半径长等于(用a 表示);(2) 圆k C 的半径为 ( k 为正整数,用a 表示,18.如图,平行四边形ABCD 中,AE 平分∠BAD 交BC 边于E ,EF⊥AE 交CD 边于F ,延长BA 到点G ,使AG=CF ,连接GF .若BC=7,DF=3,tan∠AEB=3,则GF 的长为 . 三、解答题(共2小题,共22分)19.(10分)如图a ,,,AB BD CD BD ^^垂足分别为B 、D ,AD 和BC 相交于E ,EF BD ^于F ,我们可以证明111AB CD EF+=成立(不要求考生证明).若将图a 中的垂直改为斜交,如图b ,//,AB CD AD BC 、相交于E ,EF//AB 交BD 于F ,则:(1)111AB CD EF+=还成立吗?如果成立,请给出证明;如果不成立,请说明理由; (2) 请找出,ABD BCD S S V V 和EBD S V 之间的关系,并给出证明.20.(12分)定义符号{}mi n a b ,的含义为:当a b ≥时, {}min a b b =,;当a b <时,{}min a b a =,.如:{}min 122-=-,,{}min 121-=-,.(1)求{}2min x -1,-2;(2)已知2min{2,3}3x x k -+-=-, 求实数k 的取值范围;(3) 当23x -≤≤时,22min{215,(1)}215x x m x x x --+=--.直接写出实数m 的取值范围.四、解答题(共6小题,满分74分) 21.(12分)如图1,已知双曲线ky x=(k>0)与直线y= k′x 交于A,B 两点,点A 在第一象限,试解答下列问题(1)若点A 的坐标为(4,2),则点B 的坐标为 ;若点A 的横坐标为m ,则点B 的坐标可表示为 ;(2)如图2,过原点O 作另一条直线l ,交双曲线ky x= (k >0)于P ,Q 两点,点P 在第一象限.①证明四边形APBQ 一定是平行四边形;②设点A ,P 的横坐标分别为m ,n ,四边形APBQ 可能是矩形吗?可能是正方形吗?若可能,直接写出m ,n 应满足的条件;若不可能,请说明理由.22.(12分)有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x 的值。
放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y 的值,两次结果记为(x ,y )。
(1)用树状图或列表法表示(x ,y )所有可能出现的结果;(2)求使分式有意义的(x ,y )出现的概率;(3)化简分式;并求使分式的值为整数的(x ,y )出现的概率。
23.(12分)(1)操作发现:如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,且点G 在矩形ABCD 内部.小明将BG 延长交DC 于点F ,认为GF=DF ,你同意吗?说明理由. (2)问题解决:保持(1)中的条件不变,若DC=2DF ,求AB AD值. (3)类比探究: 保持(1)中的条件不变,若DC=nDF ,求ABAD的值(直接写出答案)24.(12分)一个批发与零售兼营的文具店规定:凡一次购买铅笔301支以上(包括301支),可以按批发价付款;购买300支以下(包括300支)只能按零售价付款. 现有小王购买铅笔,如果给初三年级学生每人买1支,只能按零售价付款,需用(m²-1)元,(m 为正整数,且m²-1>100);如果多买60支,则可按批发价付款,同样需用(m²-1)元 (1)设初三年级共有X 名学生,则 ①X 的取值范围是 ;②铅笔的零售价每支 元,批发价每支应为 元;(用含x 、m 的代数式表示) (2)若按批发价每购15支与按零售价每购15支少一元,试求初三年级共有多少学生?并确定m 的值25.(12分)如图,在长方形ABCD 中,AB=5cm,BC=7cm,点P 从A 开始沿线段AB 向点B 以1cm/s 的速度移动,点Q 从点B 开始沿线段BC 向点C 以2cm/s 的速度移动,点P 、Q 分别从A ,B 两点同时出发了t 秒钟,直至两动点中某一点到达端点后停止(即0<t <3.5) (1)经过几秒钟后,PQ 的长度等于5cm . (2)经过几秒钟后,△BPQ 的面积等于4cm .(3)经过几秒钟后,△DPQ 是等腰三角形?(第25题)26.(14分)如图,抛物线y =ax 2+bx+c 的开口向上,顶点M 在第三象限,抛物线与x 轴交于A 、B 两点,与y 轴负半轴交于点C ,点A 坐标为(-3,0),点B 坐标为(1,0).(1)试用含a 的式子表示b ,c ;(2)连接AM 、CM 、CB ,试说明△OCB 与四边形AMCO 的面积之比是一个定值,并求出这个定值;(3)连接AC ,若∠AC M =90°,解决下列问题:①求抛物线解析式并证明∠MAO =∠ACB ;②线段AM 上是否存在点D ,使以点A 、O 、D 为顶点的三角形与△ACB 相似?若存在,求出点D 坐标;若不存在,说明理由.FA ED B C(第26题)c。
