高中数学必修一基本初等函数知识点+练习题含答案解析(非常详细)

第一部分基本初等函数知识点整理第二章 基本初等函数一、指数函数 （一）指数1、 指数与指数幂的运算：复习初中整数指数幂的运算性质： a m *a n =a m+n(a m )n=a mn(a*b)n =a n b n2、根式的概念：一般地，若a x n =，那么x 叫做a 的n 次方根，其中n >1，且n ∈N *．当n 是奇数时，正数的n 次方根是一个正数，负数的n 次方根是一个负数。

此时，a 的n 次方根用符号 表示。

当n 为偶数时，正数的n 次方根有两个，这两个数互为相反数。

此时正数a 的正的n 次方根用符号 表示，负的n 的次方根用符号 表示。

正的n 次方根与负的n 次方根可以合并成 （a>0）。

注意：负数没有偶次方根；0的任何次方根都是0，记作00=n。

当n 是奇数时，a a n n =，当n 是偶数时，⎩⎨⎧<≥-==)0()0(||a a a a a a nn 式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数。

3、 分数指数幂正数的分数指数幂的)1,,,0(*>∈>=n N n m a a an m nm ，)1,,,0(11*>∈>==-n N n m a a aanmnm nm0的正分数指数幂等于0，0的负分数指数幂没有意义4、 有理数指数米的运算性质（1）r a ·s r ra a+=),,0(R s r a ∈>； （2）rss r a a =)( ),,0(R s r a ∈>；（3）s r r a a ab =)(),,0(R s r a ∈>．5、无理数指数幂一般的，无理数指数幂a a（a>0,a 是无理数）是一个确定的实数。

有理数指数幂的运算性质同样使用于无理数指数幂。

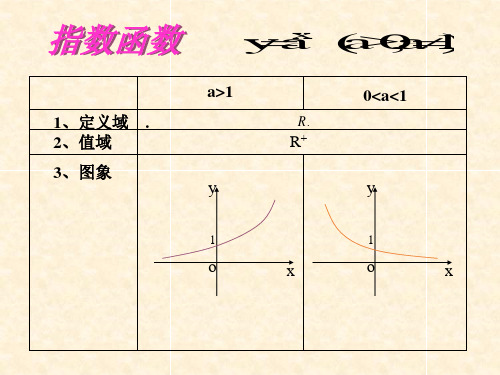
（二）、指数函数的性质及其特点1、指数函数的概念：一般地，函数)1,0(≠>=a a a y x 且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：指数函数的底数的取值范围，底数不能是负数、零和1．为什么？（1）在[a ，b]上，值域是)]b (f ),a (f [或)]a (f ),b (f [；（2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈； （3）对于指数函数)1a 0a (a )x (f x ≠>=且，总有a )1(f =； （4）当a>1时，若X 1<X 2 ,则有f(X 1)<f(X 2)。

二、对数函数 （一）对数1．对数的概念：一般地，如果N a x =)1,0(≠>a a ，那么数x 叫做以．a 为底．．N 的对数，记作：N x a log =（a — 底数，N— 真数，N a log — 对数式）说明：○1 注意底数的限制0>a ，且1≠a ； ○2 x N N a a x =⇔=log ； ○3 注意对数的书写格式： 两个重要对数：○1 常用对数：以10为底的对数N lg ； ○2 自然对数：以无理数 71828.2=e 为底的对数的对数N ln ．（二）对数的运算性质如果0>a ，且1≠a ，0>M ，0>N ，那么： ○1 M a (log ·=)N M a log ＋N a log ； ○2 =NM a log M a log －N a log ； ○3 n a M log n =M a log )(R n ∈． 注意：换底公式abb c c a log log log =（0>a ，且1≠a ；0>c ，且1≠c ；0>b ）． 利用换底公式推导下面的结论 （1）b mnba nam log log =；（2）a b b a log 1log =．（二）对数函数1、对数函数的概念：函数0(log >=a x y a ，且)1≠a 叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）．注意：○1 对数函数的定义与指数函数类似，都是形式定义，注意辨别。

如：x y 2log 2=，5log 5x y = 都不是对数函数，而只能称其为对数型函数．○2 对数函数对底数的限制：0(>a ，且)1≠a ．N a log三、幂函数 1、幂函数定义：一般地，形如αx y =)(R a ∈的函数称为幂函数，其中α为常数． 2、幂函数性质归纳． （1）所有的幂函数在（0，+∞）都有定义并且图象都过点（1，1）；（2）0>α时，幂函数的图象通过原点，并且在区间),0[+∞上是增函数．特别地，当1>α时，幂函数的图象下凸；当10<<α时，幂函数的图象上凸；（3）0<α时，幂函数的图象在区间),0(+∞上是减函数．在第一象限内，当x 从右边趋向原点时，图象在y 轴右方无限地逼近y 轴正半轴，当x 趋于∞+时，图象在x 轴上方无限地逼近x 轴正半轴．第二部分练习题含答案解析第二章 基本处等函数一、选择题(每小题5分，共60分)1．计算log 225·log 322·log 59的结果为( ) A ．3 B ．4 C ．5D ．6解析：原式＝lg25lg2·lg22lg3·lg9lg5＝2lg5lg2·32lg2lg3·2lg3lg5＝6. 答案：D2．设f (x )＝⎩⎨⎧2e x －1，x <2，log 3(x 2－1)，x ≥2，则f (f (2))的值为( )A ．0B ．1C ．2D ．3解析：f (2)＝log 3(22－1)＝1，f (f (2))＝2e 1－1＝2e 0＝2. 答案：C3．如果log 12x >0成立，则x 应满足的条件是( )A ．x >12 B.12<x <1 C ．x <1D ．0<x <1解析：由对数函数的图象可得． 答案：D4．函数f (x )＝log 3(2－x )在定义域区间上是( ) A ．增函数B ．减函数C ．有时是增函数有时是减函数D ．无法确定其单调解析：由复合函数的单调性可以判断，内外两层单调性相同则为增函数，内外两层的单调性相反则为减函数．答案：B5．某种放射性元素，100年后只剩原来的一半，现有这种元素1克，3年后剩下( )A ．0.015克B ．(1－0.5%)3克C ．0.925克D.1000.125克解析：设该放射性元素满足y ＝a x (a >0且a ≠1)，则有12＝a 100得a ＝(12)1100.可得放射性元素满足y ＝[(12)1100]x ＝(12)x 100.当x ＝3时，y ＝(12)3100＝100(12)3＝1000.125.答案：D6．函数y ＝log 2x 与y ＝log 12x 的图象( ) A ．关于原点对称 B ．关于x 轴对称 C ．关于y 轴对称D ．关于y ＝x 对称解析：据图象和代入式判定都可以做出判断，故选B. 答案：B7．函数y ＝lg(21－x －1)的图象关于( )A ．x 轴对称B ．y 轴对称C ．原点对称D ．y ＝x 对称解析：f (x )＝lg(21－x －1)＝lg 1＋x 1－x ，f (－x )＝lg 1－x 1＋x ＝－f (x )，所以y ＝lg(21－x－1)关于原点对称，故选C.答案：C8．设a >b >c >1，则下列不等式中不正确的是( ) A ．a c >b c B ．log a b >log a c C ．c a >c bD ．log b c <log a c解析：y ＝x c 在(0，＋∞)上递增，因为a >b ，则a c >b c ；y ＝log a x 在(0，＋∞)上递增，因为b >c ，则log a b >log a c ；y ＝c x 在(－∞，＋∞)上递增，因为a >b ，则c a >c b .故选D.答案：D9．已知f (x )＝log a (x ＋1)(a >0且a ≠1)，若当x ∈(－1,0)时，f (x )<0，则f (x )是( )A．增函数B．减函数C．常数函数D．不单调的函数解析：由于x∈(－1,0)，则x＋1∈(0,1)，所以a>1.因而f(x)在(－1，＋∞)上是增函数．答案：A10．设a＝424，b＝312，c＝6，则a，b，c的大小关系是()A．a>b>c B．b<c<a C．b>c>a D．a<b<c解析：a＝424＝12243，b＝12124，c＝6＝1266.∵243<124<66，∴12243<12124<1266，即a<b<c.答案：D11．若方程a x＝x＋a有两解，则a的取值范围为()A．(1，＋∞) B．(0,1)C．(0，＋∞) D．Ø解析：分别作出当a>1与0<a<1时的图象．(1)当a>1时，图象如下图1，满足题意．图1图2(2)当0<a<1时，图象如上图2，不满足题意．答案：A12．已知f(x)是偶函数，它在(0，＋∞)上是减函数，若f(lg x)>f(1)，则x的取值范围是()A ．(110，1)B ．(0，110)∪(1，＋∞) C ．(110，10)D ．(0,1)∪(0，＋∞)解析：由于f (x )是偶函数且在(0，＋∞)上是减函数，所以f (－1)＝f (1)，且f (x )在(－∞，0)上是增函数，应有⎩⎨⎧x >0，－1<lg x <1，解得110<x <10. 答案：C第Ⅱ卷(非选择题，共90分) 二、填空题(每小题5分，共20分)13．若函数f (x )＝a x (a >0，且a ≠1)的反函数的图象过点(2，－1)，则a ＝________.解析：由互为反函数关系知，f (x )过点(－1,2)，代入得a －1＝2⇒a ＝12. 答案：1214．方程log 2(x －1)＝2－log 2(x ＋1)的解为________． 解析：log 2(x －1)＝2－log 2(x ＋1)⇔log 2(x －1)＝log 24x ＋1，即x －1＝4x ＋1，解得x ＝±5(负值舍去)，∴x ＝ 5.答案： 515．设函数f 1(x )＝x 12，f 2(x )＝x －1，f 3(x )＝x 2，则f 1(f 2(f 3(2007)))＝________.解析：f 1(f 2(f 3(2007)))＝f 1(f 2(20072))＝f 1((20072)－1)＝[(20072)－1]12＝2007－1.答案：1200716．设0≤x ≤2，则函数y ＝4x －12－3·2x ＋5的最大值是________，最小值是________．解析：设2x ＝t (1≤t ≤4)，则y ＝12·4x －3·2x ＋5＝12t 2－3t ＋5＝12(t －3)2＋12. 当t ＝3时，y min ＝12；当t ＝1时，y max ＝12×4＋12＝52. 答案：52 12三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分) 17．(10分)已知a ＝(2＋3)－1，b ＝(2－3)－1，求(a ＋1)－2＋(b ＋1)－2的值． 解：(a ＋1)－2＋(b ＋1)－2＝(12＋3＋1)－2＋(12－3＋1)－2＝(3＋32＋3)－2＋(3－32－3)－2＝16(7＋432＋3＋7－432－3)＝16[(7＋43)(2－3)＋(7－43)(2＋3)]＝16×4＝23.18．(12分)已知关于x 的方程4x ·a －(8＋2)·2x ＋42＝0有一个根为2，求a 的值和方程其余的根．解：将x ＝2代入方程中，得42·a －(8＋2)·22＋42＝0，解得a ＝2. 当a ＝2时，原方程为 4x ·2－(8＋2)2x ＋42＝0，将此方程变形化为2·(2x )2－(8＋2)·2x ＋42＝0. 令2x ＝y ，得2y 2－(8＋2)y ＋42＝0. 解得y ＝4或y ＝22.当y ＝4时，即2x ＝4，解得x ＝2； 当y ＝22时，2x ＝22，解得x ＝－12. 综上，a ＝2，方程其余的根为－12.19．(12分)已知f (x )＝2x －12x ＋1，证明：f (x )在区间(－∞，＋∞)上是增函数．证明：设任意x 1，x 2∈(－∞，＋∞)且x 1<x 2，则f (x 1)－f (x 2)＝2x 1－12x 1＋1－2x 2－12x 2＋1＝(2x 1－1)(2x 2＋1)－(2x 2－1)(2x 1＋1)(2x 1＋1)(2x 2＋1)＝2x 1－2x 2－(2x 2－2x 1)(2x 1＋1)(2x 2＋1)＝2(2x 1－2x 2)(2x 1＋1)(2x 2＋1).∵x 1<x 2，∴2x 1<2x 2，即2x 1－2x 2<0.∴f (x 1)<f (x 2)．∴f (x )在区间(－∞，＋∞)上是增函数．20．(12分)已知偶函数f (x )在x ∈[0，＋∞)上是增函数，且f (12)＝0，求不等式f (log a x )>0(a >0，且a ≠1)的解集．解：f (x )是偶函数，且f (x )在[0，＋∞)上递增，f (12)＝0，∴f (x )在(－∞，0)上递减，f (－12)＝0，则有log a x >12，或log a x <－12. (1)当a >1时，log a x >12，或log a x <－12，可得x >a ，或0<x <aa ； (2)当0<a <1时，log a x >12，或log a x <－12，可得0<x <a ，或x >aa . 综上可知，当a >1时，f (log a x )>0的解集为(0，aa )∪(a ，＋∞)； 当0<a <1时，f (log a x )>0的解集为(0，a )∪(aa ，＋∞)．21．(12分)已知函数f (x )对一切实数x ，y 都满足f (x ＋y )＝f (y )＋(x ＋2y ＋1)x ，且f (1)＝0，(1)求f (0)的值； (2)求f (x )的解析式；(3)当x ∈[0，12]时，f (x )＋3<2x ＋a 恒成立，求a 的范围．解：(1)令x ＝1，y ＝0，则f (1)＝f (0)＋(1＋1)×1，∴f (0)＝f (1)－2＝－2. (2)令y ＝0，则f (x )＝f (0)＋(x ＋1)x ，∴f (x )＝x 2＋x －2.(3)由f (x )＋3<2x ＋a ，得a >x 2－x ＋1.设y ＝x 2－x ＋1，则y ＝x 2－x ＋1在(－∞，12]上是减函数，所以y ＝x 2－x ＋1在[0，12]上的范围为34≤y ≤1，从而可得a >1.22．(12分)设函数f (x )＝log a (1－a x )，其中0<a <1.(1)求证：f (x )是(a ，＋∞)上的减函数；(2)解不等式f (x )>1.解：(1)证明：设任意x 1，x 2∈(a ，＋∞)且x 1<x 2，则f (x 1)－f (x 2)＝log a (1－a x 1)－log a (1－a x 2)＝log a 1－a x 11－a x 2＝log a 1－a x 2＋a x 2－a x 11－a x 2＝log a ⎣⎢⎡⎦⎥⎤1＋a x 2－a x 11－a x 2＝log a (1＋ax 1－ax 2x 1x 2－ax 1)＝log a [1＋a (x 1－x 2)x 1(x 2－a )]．∵x 1，x 2∈(a ，＋∞)且x 1<x 2，∴x 1－x 2<0,0<a <x 1<x 2，x 2－a >0.∴a (x 1－x 2)x 1(x 2－a )<0，∴1＋a (x 1－x 2)x 1(x 2－a )<1，又∵0<a <1，∴log a [1＋a (x 1－x 2)x 1(x 2－a )]>0，∴f (x 1)>f (x 2)，所以f (x )＝log a (1－a x )在(a ，＋∞)上为减函数．(2)因为0<a <1，所以f (x )>1⇔log a (1－a x )>log a a ⇔⎩⎪⎨⎪⎧ 1－a x >0，①1－a x <a .②解不等式①，得x >a 或x <0.解不等式②，得0<x <a 1－a .因为0<a <1，故x <a 1－a ，所以原不等式的解集为{x |a <x <a 1－a}．。