第10章-组合变形
第10章 组合变形

10.1 组合变形的概念 工程中大多数的杆件在荷载作用下,往往同时发生两种或两种以上的变形。
在小变形的前提下,一般采用叠加原理计算组合变形的强度问题。即当杆件 承受复杂荷载作用而同时产生几种变形时,只要将荷载进行适当地分解,使 杆在各分荷载的作用下发生基本变形,再分别计算各基本变形所引起的应力, 然后将计算结果叠加,就可得到总的应力。实践证明:在线弹性、小变形的 情况下,用叠加原理所得到的结果与实际情况是相当符合的。
第10章 组合变形
【本章教学要点】 知识模块 组合变形的概念 叠加原理 掌握程度 掌握 掌握 掌握 理解 斜弯曲构件 重点掌握 偏心受压(受拉)构 件 截面核心的概念 理解 重点掌握 了解 知识要点 基本变形、组合变形 适用条件:小变形、线弹性 叠加法求解组合变形的步骤 斜弯曲概念 危险截面、危险点的确定;应力公式;强度条 件 偏心受压(受拉)概念
危险截面、危险点的确定;应力公式;强度条 件
截面核心
【本章技能要点】
技能要点
掌握程度
应用方向
斜弯曲构件计算
偏心受压(受拉)构件 计算 截面核心
掌握
掌握 了解
危险截面、危险点的判别;强度校核、截面设 计、许可荷载确定
危险截面、危险点的判别;强度校核、截面设 计、许可荷载确定 截面核心的确定
【导入案例】 工程结构的变形:单一或多样?
例10-5 试求图10.16所示偏心受拉杆的最大正应力。
7.5 I I 50
K z y I-I 截面 (b) 图 10.16
P 2kN
20
10 40 15 (a)
10.4 截面核心 10.4.1 截面核心的概念 人为地将偏心压力的作用点限制在截面形心周围的一个区域,则杆件整 个横截面上就只产生压应力而不出现拉应力,这个荷载作用的区域就称 为截面核心。 10.4.2 截面核心的确定
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算

解:危险截面在 A 处,其上之内力分量为: 弯矩: M y = FP1 a , M z = FP2 H 扭矩: M x = FP2 a 轴力: FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心, 面边界交于 a、b 两点,这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用,最 大压应力值大于最大拉应力值,故 b 点为危险点,其应力状态如图所示。 10-7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解: (a)为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10-9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10-9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试:
1.假定骨骼为实心圆截面,确定横截面 B-B 上的应力分布; 2.假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成,忽略海绵状承受 应力的能力,确定横截面 B-B 上的应力分布;
工程力学之组 合 变 形

工程力学第10章组合变形学习目标(1)了解组合变形的概念及其强度问题的分析方法;(2)掌握斜弯曲、拉伸(压缩)与弯曲和偏心压缩的应力及强度计算。
10.1 组合变形的概念例如,烟囱的变形,除自重W引起的轴向压缩外,还有水平风力引起的弯曲变形,同时产生两种基本变形,如图10-1(a)所示。
又如图10-1(b)所示,设有吊车的厂房柱子,作用在柱子牛腿上的荷载F,它们合力的作用线偏离柱子轴线,平移到轴线后同时附加力偶。
此时,柱子既产生压缩变形又产生弯曲变形。
再如图10-1(c)所示的曲拐轴,在力F作用下,AB 段同时产生弯曲变形和扭转变形。
10.1 组合变形的概念图10-110.1 组合变形的概念上述这些构件的变形,都是两种或两种以上的基本变形的组合,称为组合变形。
研究组合变形问题依据的是叠加原理,进行强度计算的步骤如下:(1)将所作用的荷载分解或简化为几个只引起一种基本变形的荷载分量。
(2)分别计算各个荷载分量所引起的应力。
(3)根据叠加原理,将所求得的应力相应叠加,即得到原来荷载共同作用下构件所产生的应力。
(4)判断危险点的位置,建立强度条件。
10.2例如图10-2(a)所示的横截面为矩形的悬臂梁,外力F作用在梁的对称平面内,此类弯曲称为平面弯曲。
斜弯曲与平面弯曲不同,如图10-2(b)所示同样的矩形截面梁,外力F的作用线通过横截面的形心而不与截面的对称轴重合,此梁弯曲后的挠曲线不再位于梁的纵向对称面内,这类弯曲称为斜弯曲。
斜弯曲是两个平面弯曲的组合,本节将讨论斜弯曲时的正应力及其强度计算。
10.2图10-210.210.2.1 正应力计算斜弯曲时,梁的横截面上同时存在正应力和切应力,但因切应力值很小,一般不予考虑。
下面结合图10-3(a)所示的矩形截面梁说明斜弯曲时正应力的计算方法。
图10-310.2.1 正应力计算10.2.1.1 外力的分解由图10-3(a)可知:10.2.1.2 内力的计算如图10-3(b)所示,距右端为a 的横截面上由F y 、F z 引起的弯曲矩分别是:10.2 10.2.1 正应力计算10.2.1.3 应力的计算由M z 和M y (即F y 和F z )在该截面引起K 点的正应力分别为:F y 和F z 共同作用下K 点的正应力为:10.210-110.210.2.1 正应力计算10.2.1.3 应力的计算通过以上分析过程,我们可以将组合变形问题计算的思路归纳为“先分后合”,具体如下:10.210.2.2 正应力强度条件同平面弯曲一样,斜弯曲梁的正应力强度条件仍为:10-2即危险截面上危险点的最大正应力不能超过材料的许用应力[σ]。
组合变形

M y 187 N m
T 1020 N m
合弯矩:
2 M M y M z2 4402 187 2
478N m
第四强度理论:
W
r4
1 W
M 2 0.75T 2
603 109
32
21.2110 6 m3
危险截面: B 截面
T 21.7 N m M 26.7 N m
第三强度理论:
r3
W
1 W
M 2 T 2
T图
21.7 N m
353 109
32
2
4.2110 6 m3
2
r3
8.18MPa
26.7 21.7 4.21106
第四强度理论:
式中: T
r4
危险截面上的扭矩 危险截面上的合弯矩
M
M
实心轴 W
2 2 My Mz
D3
32 D3 空心轴 W 1 4 32
,
例题 8-5 45钢的传动轴AB的直径为35mm,许用应力为 85MPa。电动机功率P = 2.2kW,由带轮C 传入。带轮C转速为 966r/min,带轮的直径为 D = 132mm,带拉力为F+F’ = 600N。齿轮E的 d 节圆直径为: 1 50mm 。
Fz Fz F sin 240 F sin 300 257 N
二、作出轴的弯矩图 和扭矩图
T图
21.7 N m
My 图
7.43N m 20.4 N m 11.4 N m 24.1N m
Mz 图
材料力学第10章 组合变形

因此,截面O为危险截面。
危险截面上,由轴力引起的正应力均匀分布,其值
为
,由弯矩引起的正应力线性分布,其值为
。利用叠加原理,将拉伸及弯曲正应力叠加
后,危险截面上正应力沿截面高度的变化情况如图10.5
(e)所示,仍为线性分布。而且可以看出,最大拉应
力和最大压应力分别发生在O截面上、下边缘各点,其
值为
(10.4)
图10.5
依据上述分析,弯拉(压)组合变形时危险点处于单向应力状态,所以可将 截面上的σmax与材料的许用应力相比较建立其强度条件。对于拉压强度相等 的材料,强度条件为
对于抗拉与抗压性能不同的材料,强度条件为
下面举例说明弯拉(压)组合变形的强度计算。 例10.2如图10.6(a)所示的钢支架,已知载荷F=45 kN,尺寸如图。 (1)如材料为钢材,许用应力[σ]=160 MPa,试选择AC杆的工字钢型号。 (2)如材料为铸铁,许用拉应力[σt]=30 MPa,许用压应力[σc]=160 MPa,且AC杆截面形式和尺寸如图10.6(e)所示,A=15×10-3 m2,z0=75mm ,Iy=5.31×10-5 m4。试校核AC杆的强度。
其力矩矢量分别与y轴和z轴的正向一致(见图10.2(b))。 为了确定横截面上最大正应力点的位置,先求截面中性轴位置。记中性轴上 任一点的坐标为(y0,z0),由于中性轴上各点处的正应力均为零,所以由式 可得中性轴方程为
(10.2) 可见,中性轴是一条通过横截面形心的直线(见图10.2(c)),其与y轴的 夹角θ为
图10.3 例10.1如图10.4(a)所示,20a号工字钢悬臂梁承受均布载荷q和集中力
。已知钢的许用弯曲正应力[σ]=160 MPa,a=1 m。试求梁的许可 载荷集度[q]。 解由于梁所受到的横向力不在梁的两个纵向对称面内,此时可以将横向力向 两个纵向对称面分解(向y和z轴分解),从而将其看成是梁在其两个相互垂
材料力学(单辉祖)第十章组合变形

弯压组合
可见,危险截面为C截面 其轴力和弯矩分别为
FNC 3 kN M c M max 4 2 8kN m
A
FAy
10kN m a x
g g f
C m
FBy
B
危险点 截面C上的最低点f 和最高点g
FN M c s A W
f
18
弯压组合
A I
4
10kN
解 首先计算折杆的支座反力 由平衡方程可得 FAx A
FAx 0, FAy 5kN, FBy 5kN
FAy
m
10kN
C 1.2m B 1.6m FBy
a x 1.6m
m
由于折杆左右对称,所以只需分析一半即可。 折杆AC部分任一截面上的内力
FN FAy sin 3 kN FS FAy cos 4 kN M xFAy cos
杆件变形分析步骤 首先, 在杆件原始尺寸上分别计算由横向力和 轴向力引起变形、应力 然后, 利用叠加原理,合成在横向力和轴向力 共同作用下杆件变形、应变和应力等物理量 若杆件抗弯刚度EI较大,轴力引起杆件的弯曲 变形较小,可以忽略
10
弯拉组合
细长杆件强度问题, 受力如图,抗弯刚度 EI,截面抗弯模量W , 横截面面积A。
n
e n
P
z b h y
30
偏心拉伸(压缩)
解: 1. 力系简化 力P对竖直杆作用等效于作 用在杆轴线上一对轴力P和 一对作用在竖直平面内力 偶mz=Pe
FN P 2000 N, M z mz Pe 120 N m
mz P
n
e n
P
mz P
可见,竖直杆发生弯拉组合变形
第十章 应力状态,强度理论与组合变形1

2 2
s
2 3
2(s1s 2
s 2s 3
s 3s1 )]
(10 11)
用主应力表示的体积改变比能为:
uV
= 1 2
6E
(s1 s 2
s 3 )2
用主应力表示的形状改变比能为:
usd
=
u
uv
=
1
6E
s 1
s2 2
s 2
s3
2
s 3
s
1
2
(10-13)
14
强度理论
问题:
复杂应力状态下 的强度?
屈服判据 s1-s3= sys Tresca条件, 1864, 法
实验验证: 很好地预测了塑性材料屈服。
设计:
强度条件: s1-s3[s]=sys/n
19
10.2.2 延性材料的屈服强度理论
四、形状改变比能理论(第四强度理论)
? ? 思考: Tresca条件与s2无关
滑移改变形状 能量
假说: 延性材料屈服取决于其形状改变比能 ud。
1 2
(s 1 s 2 )2 (s 2 s 3 )2 (s 3 s 1 )2 [s ] = s ys / n
21
强度理论汇总:
强度条件的一般形式: 工作应力许用应力
相当应力
破 s1 理论 坏
e1 理论
sr [s]
sr1 = s1 常用
脆性破坏 [s]=sb/n 塑性屈服 [s]=sys /n
5
注意到txy=tyx,解得:
sa=sxcos2a+s ysin2a-2t xy sinacosa t a=(s x-s y)sinacosa+txy(cos2a -sin2a)
材料力学第六版答案第10章
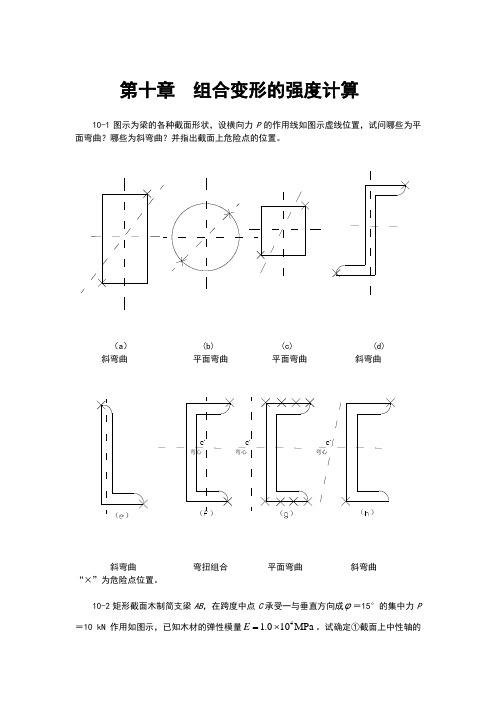
第十章 组合变形的强度计算10-1图示为梁的各种截面形状,设横向力P 的作用线如图示虚线位置,试问哪些为平面弯曲?哪些为斜弯曲?并指出截面上危险点的位置。
(a ) (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心()()弯心弯心()()斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ,在跨度中点C 承受一与垂直方向成ϕ=15°的集中力P =10 kN 作用如图示,已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置;②危险截面上的最大正应力;③C 点的总挠度的大小和方向。
解:66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴:οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴:ο47.25=α10-3 矩形截面木材悬臂梁受力如图示,P 1=800 N ,P 2=1600 N 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力状态-单向+纯剪切 强度条件(塑性材料)
2 r3 M N 4 T [ ] 2 2 r4 M N 3 T [ ] 2
单辉祖:材料力学教程
15
例 题
例10-3 图示钢质传动轴,Fy = 3.64 kN, Fz= 10 kN, F’z =1.82 kN, F’y = 5 kN, D1 = 0.2 m, D2 = 0.4 m, [] = 100 MPa, 轴径 d=52 mm, 试按第四强度理论校核轴的强度
③ 将所得结果叠加,即得杆件组合变形时的应力。
单辉祖:材料力学教程 5
§2 弯拉(压)组合 §3 偏心压缩
弯拉(压)组合 例题
偏心压缩
单辉祖:材料力学教程
6
弯拉(压)组合
产生弯曲与轴向拉压的组合变形的情况:
杆上除作用有横向力外,同时还作用有轴向力; 外力作用线虽然平行于杆轴,但不通过截面形心。
max
8.66 103 N 8.27 103 N m 111.5MPa [ ] 3 2 5 3 1.8110 m 7.75 10 m
9
单辉祖:材料力学教程
例10-2 图中所示结构,承受载荷F=12kN作用。横梁AC用 No14工字钢制成,许用应力[σ]=160MPa,试校核其强度。
2 2 M T r3 [ ] W
2 2 r4 M 3 T [ ]
2 2 M 0 . 75 T r4 [ ] W 单辉祖:材料力学教程
14
弯拉(压)扭组合强度计算
弯拉扭组合 危险截面-截面A 危 险 点- a
a M N M
单辉祖:材料力学教程
解:1. 外力分析
F' y D2 Fz D1 M1 M2 1 kN m 2 2
16
2. 内力分析 M1 , M2 T 图 Fy , F’y Mz 图
Fz , F’z My 图
2 M My M z2
max M
W
BC段 M 图- 凹曲线
max, B
FNB A M B Wz
M B Wz
21.8kN 9.82kN m 106.4MPa [ ] 3 2 5 3 2.15 10 mm 1.02 10 mm
max, B
12kN m 117.6MPa [ ] 5 3 1.02 10 mm
解:1、横梁的外力与内力分析:
T 30.9kN, FAx 21.8kN, FAy 9.82kN
M e (30.9kN) cos 45(100mm) 2180 N m
梁处于轴向载荷和弯矩的共同作用 下,绘制弯矩图与轴力图。
单辉祖:材料力学教程
10
2、横梁的应力与强度校核 AB段受弯拉组合共同作用;BC段受弯曲作用,B截 面为危险截面:
Fx F cos 30 8.66 103 N
Fy F sin 30 5.00 103 N
M e Fx e 1.732 103 N m
梁处于轴向载荷和弯矩 的共同作用下,绘制弯 矩图与轴力图。
单辉祖:材料力学教程 8
2、梁的截面设计
max
强度条件:
Fx M A A Wz
(1.6kN )(0.100m) F 1135 N (0.150m) sin 70
由此得
Fy F cos 70 388N
Fz F sin 70 1067 N
19
单辉祖:材料力学教程
2、内力分析 M1 , M2 T 图 Fy Mz 图
Fz , Fp My 图
2 M My M z2
Fx M A [ ] A Wz
考虑到最大弯曲正应力一般大于轴向拉伸应力,故依照 弯曲强度选择工字型钢
M A 8.27 103 N m 5 3 Wz 5 . 17 10 m 6 [ ] 160 10 Pa
由型钢表中查得,若选取No12.6工字钢,则满足上述条 件,此时截面A的最大正应力为
max M
W
BC段 M 图- 凹曲线
单辉祖:材料力学教程 20
3. 强度校核 弯扭组合 危险截面-截面C+
M C 214 N m
TC 160 N Байду номын сангаас m
r4
2 2 MC 0 . 75 T C
D
3
d 1 32 D
4
弯扭组合强度计算 弯拉(压)扭组合强度计算 例题
单辉祖:材料力学教程
13
弯扭组合强度计算
弯扭组合 危险截面: 截面A 危险点: a 与 b
W a T T T Wp 2W
a M M
应力状态-单向+纯剪切 强度条件(塑性材料, 圆截面)
2 2 r3 M 4 T [ ]
单辉祖:材料力学教程
3
组合变形的实例
单辉祖:材料力学教程
4
组合变形问题的求解思路
杆件在组合变形时的应力,可采用叠加原理进行计算: ① 将组合变形分解为若干基本变形的组合; ② 计算杆件相应于每种基本变形的应力;
FN A
T Ip
My Iz
Fs S z ( w) I zb
281MPa [ ]
单辉祖:材料力学教程
21
例 10-5 圆弧形圆截面杆,许用应力为[] ,试按第三强 度理论确定杆径
解:
M1 FRsin
M 2 F BC FR(1 cos )
M M1 FRsin T M 2 FR(1 cos )
M 2 T 2 r3 W 32FR 2(1 cos ) r3 πd 3 90 时, r3 最大
单辉祖:材料力学教程
r3,max
32 2FR [ ] 3 πd
3
d
32 2FR π[ ]
22
§5 矩形截面杆组合变形一般情况
内力分析 应力分析
N M
FN Fez z Fey y A Iy Iz
当偏心距足够小,以致最大弯曲拉应力σM,max>|σN| ,横截 面上各点处均受压;反之,如果偏心距足够大,以致最大 弯曲拉应力σM,max<|σN|,则横截面上部分区域受拉,部分 区域受压。
单辉祖:材料力学教程 12
§4 弯扭与弯拉(压)扭组合
危险点 a, b, c
S一般可
单辉祖:材料力学教程
忽略不计
25
强度条件
a点处
b点处
c点处
单辉祖:材料力学教程
26
本章结束!
单辉祖:材料力学教程
27
第 10 章 组合变形
本章主要研究:
弯扭组合强度计算 弯拉(压)扭组合强度计算 矩形截面杆组合变形
单辉祖:材料力学教程
1
§1 §2 §3 §4 §5
引言 弯拉(压)组合 偏心压缩 弯扭组合与弯拉(压)扭组合 矩形截面杆组合变形一般情况
单辉祖:材料力学教程
2
§1 引 言
组合变形的实例 组合变形问题的求解思路
18
例10-4 图示圆截面轴,在载荷FP与F作用下处于平衡状态。 已知载荷FP=1.6kN,轴的外径D=30mm,内径d=27mm,摇臂 尺寸R1=100mm,R2=150mm,许用应力[σ]=300MPa,试按第 四强度理论校核轴的强度。
解:1、外力分析
M
x
0, FP R1 F sin 70R2 0
单辉祖:材料力学教程 17
3. 强度校核 弯扭组合 危险截面-截面B
M B 1.064 kN m TB 1.0 kN m
2 MB 0.75TB2 r4 W
r4
单辉祖:材料力学教程
2 2 32 M B 0.75TB 99.4 MPa [ ] 3 πd
最大正应力发生在横截面B+,且小于许用应力,故横梁 符合强度要求。
单辉祖:材料力学教程
11
偏心压缩
杆在作用线平行但偏离杆轴的外力作用下的变形或受力形 式,称为偏心拉伸或偏心压缩。 将偏心压力F平移到形心处, 得附加力偶矩。
M y Fez , M z Fey
在截面上任一点(y,z)处的正应力为:
强度条件
单辉祖:材料力学教程
23
内力分析
图示钢质曲柄,试分析截面 B 的强度
FSy Fy M z Fy l T Fy a
FN Fx M y Fx a
单辉祖:材料力学教程
24
应力分析
M y , M z , FN
T , FSy
a 点- 最大
b 点- 最大 c 点- 相当大
N M
FN M ( x) y A Iz
单辉祖:材料力学教程
7
例
题
例10-1 图中所示梁,承受载荷F作用。已知载荷F=10kN ,方位角α =30º,梁长l=2m,载荷作用点与梁轴的距离 e=l/10,许用应力[σ ]=160MPa。试选择工字钢型号。 解:1、梁的内力分析:
