回归分析1
第一章 回归分析概述

4 随机误差
由人们无法控制且难以解释的干 扰所导致的误差作为随机误差归入随 机误差项.
线性回归模型的一般形式为
y 0 1x1 2 x2 L p xp
其中0,1,2,L
,
为未知参数(称为回归参数)
p
如果(xi1,xi2,L ,xip;yi),i=1,2,L ,n是变量
(x1,x2,L ,xp;y)的一组观测值,则线性回归模型的 数据形式可表示为
数据整理不仅要把一些数据进行换 算,差分,甚至将数据标准化,有时也要 剔除一些“异常值”或利用插值的方法补 齐空缺的数据。
(三)确定理论回归模型 的数学形式
要确定回归模型的数学形式,我们首
先 应 将 收 集 的 样 本 数 据 绘 制 关 于 yi 与 xi (i 1, 2,L , n) 的样本散点图。根据散点
yi 0 1xi1 2 xi2 L p xip i , i 1, 2,L , n
为了估计模型参数的需要,一般线 性回归模型应满足以下几个基本假设:
1
解释变量 x1, x2,L
,
x
是非随机变量;
p
2 高斯-马尔可夫条件(简称G-M条件)
E(i)=0,i=1,2,L ,n
Cov(
i
,j
)=
民的收入 x 与消费支出 y 就呈现出某种不确
定性。
我们将上海市城镇居民可支配收入与支 出的数据(1985 年~2001 年)用散点图表示,
可以发现居民的收入 x 与消费支出 y 基本上
呈现线性关系,但并不完全在一条直线上。 附数据与图形。
年份
1985 1986 1987 1988 1989 1990 1991 1992 1993
第一章 回归分析概述
第5章多元线性回归分析1

样本,可表示为
Y 1 1 2 X 2 1 3 X 3 1 ... k X k 1 u 1
Y 2 1 2 X 2 2 3 X 3 2 ... k X k 2 u 2
Y n 1 2 X 2 n 3 X 3 n ... k X k n u n
相关系数,即全部自变量参与回归的总体相
关系数,Rmxi 为去掉xi 的复相关系数。可见
部分相关系数的平方是在总体拟合效果中扣 除了其他变量综合拟合效果之后剩余部分。
15
16
多元线性回归模型
●多元线性回归模型及古典假定 ●多元线性回归模型的估计 ●多元线性回归模型的检验
17
§5.1多元线性回归模型及古典假定
j 个解释变量的单位变动对应变量平均值的影响。
20
多元线性回归
指对各个回归系数而言是“线性”的,对变量则 可是线性的,也可是非线性的 例如:生产函数
YALKu
取自然对数
l n Y ln A l n L l n K l n u
21
多元总体回归函数
Y 的总体条件均值表示为多个解释变量的函数
因为 Xe=0 ,则正规方程为:
XXβˆ =XY
32
OLS估计式
由正规方程 多元回归中 二元回归中
XXβˆ =XY ( X X ) k k 是 满 秩 矩 阵 ,其 逆 存 在
βˆ=(XX)-1XY
ˆ1Y-β ˆ2X2-β ˆ3X3
ˆ2(
yix2 i)( x3 2 i)-( yix3 i)( x2 ix3 i) ( x2 2 i)( x3 2 i)-( x2 ix3 i)2
现代统计方法--回归分析1

现代统计方法的种类
三、相关分析方法 1、定性资料分析 2、回归分析 3、典型相关分析 4、主成分分析 5、因子分析 6、对应分析
现代统计方法的种类
四、预测决策方法: 1、回归分析 2、判别分析 3、定性资料分析 4、聚类分析
统计分析方法应用流程
现实经济问题
提炼具体问题 确定欲达目标
分类研究
结构简化 研究
ˆ 1 、 1
1回归分析2判别分析3定性资料分析4聚类分析统计分析方法应用流程现实经济问题提炼具体问题确定欲达目标根据定性理论设计指标变量搜集整理统计数据选择统计方法构造理论模型进行统计计算估计模型参数修改yes应用分类研究结构简化研究相关分析研究预测决策研究教材统计软件简介eview关于spssspssstatisticalpackagesocialscience即社会科学统计软件包是世界著名的统计分析软件
一元线性回归分析
1、一元线性回归模型 2、回归模型的参数估计 3、OLSE估计的性质 4、回归方程的显著性检验 5、回归方程的拟合优度 6、残差分析 7、回归系数的区间估计
一元线性回归分析模型
1、回归模型建模的实践背景 2、一元线性回归模型的数学形式: 1)、理论模型: y 0 1 x
ξ♐♣☯♧
现代统计方法
前言
统计学的几个问题
1、自1969年设立诺贝尔经济学奖以来,已有 42名学者获奖,而其中有2/3的人是统计学家、 计量经济学家、数学家。 2、目前的研究趋势是:从一般的逻辑推理发展 到重视实证研究;从理论论述发展到数量研 究。 3、硕士和博士的学位论文,如果没有数量模型 和分析,其文章的水平会有问题。
关于S-PLUS
另外Auckland大学的Robert Gentleman 和 Ross Ihaka 及其他志愿人员开发了一个R系 统,其语法形式与S语言基本相同,但实现 不同,两种语言的程序有一定的兼容性。R 是一个GPL自由软件,现在的版本是1.00版, 它比S-PLUS 还少许多功能,但已经具有了 很强的实用性
回归分析实验案例数据1

实验课程案例数据1香烟消费数据:一个国家保险组织想要研究在美国所有50个州和哥伦比亚特区的香烟消费模式,表1给出了研究中所选的变量,表2给出了1970年的数据。
讨论下列问题:表1. 香烟消费数据的变量表2. 香烟消费数据(1970年)州年龄HS 收入黑人比例女性比例价格销量AL2741.3294826.251.742.789.8AK22.966.74644345.741.8121.3AZ26.358.13665350.838.5115.2AR29.139.9287818.351.538.8100.3CA28.162.64493750.839.7123CO26.263.93855350.731.1124.8CT29.1564917651.545.5120DE26.854.6452414.351.341.3155DC28.455.2507971.153.532.6200.4FL32.352.6373815.351.843.8123.6GA25.940.6335425.951.435.8109.9HI2561.9462314836.782.1ID26.459.532900.350.133.6102.4IL28.652.6450712.851.541.4124.8IN27.252.93772 6.951.332.2134.6IO28.8593751 1.251.438.5108.5KA28.759.93853 4.85138.9114KY27.538.531127.250.930.1155.8LA24.842.2309029.851.439.3115.9ME2854.733020.351.338.8128.5MD27.152.3430917.851.134.2123.5MA2958.54340 3.152.241124.3MI26.352.8418011.25139.2128.6MN26.857.638590.95140.1104.3MS25.141262636.851.637.593.4MO29.448.8378110.351.836.8121.3MT27.159.235000.35034.7111.2NB28.659.33789 2.751.234.7108.1NV27.865.24563 5.749.344189.5NH2857.637370.351.134.1265.7NJ30.152.5470110.851.641.7120.7NM23.955.23077 1.950.741.790NY30.352.7471211.952.241.7119NC26.538.5325222.25129.4172.4ND26.450.330860.449.538.993.8OH27.753.240209.151.538.1121.6OK29.451.63387 6.751.339.8108.4OR29603719 1.35129157PA30.750.2397185244.7107.3RI29.246.43959 2.750.940.2123.9SC24.837.8299030.550.934.3103.6SD27.453.331230.350.338.592.7TN28.141.8311915.851.641.699.8TX26.447.4360612.55142106.4UT23.167.332270.650.636.665.5VT26.857.134680.251.139.5122.6V A26.847.8371218.550.630.2124.3WA27.563.54053 2.150.340.396.7WV3041.63061 3.951.641.6114.5WI27.254.53812 2.950.940.2106.4WY27.262.938150.85034.4132.2(1)在销量关于6个自变量的回归模型中,检验假设“不需要女性比例这一变量”;(2)在上面的模型中,检验假设“不需要女性比例和HS这两个变量”;(3)计算收入变量回归系数的95%的置信区间;(4)去掉收入这个变量后拟合回归方程,其他变量对于销量的解释比例是多少?(5)用价格、年龄和收入作自变量拟合模型,它们对销量的解释比例是多少?(6)仅用收入作自变量拟合模型,它们对销量的解释比例是多少?(7)(8)【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】(9)(10)。
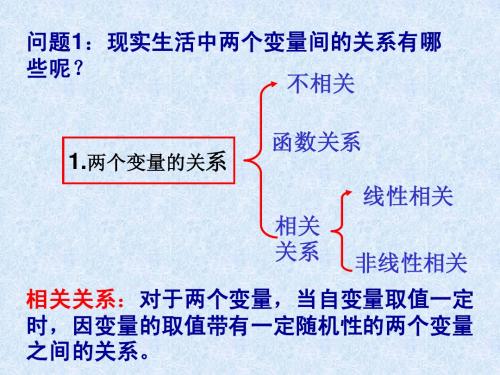
3.2回归分析(1)
1035 1107
1177 1246
解:作出11个点(x,y)构成的散点图, 由图可知,这些 点在一条直线附 近,可以用线性 回归模型
y a bx
来表示它们之间的关系. 根据公式(1)可得
y 因此线性回归方程为 527.591 14.453x
b 14.453, 这里 a, b 分别为a,b的估计值, a 527.591.
(i 1, 2,3,, n) ,
根据线性回归模型,对于每一个 对应的随机误差项
xi ,
i2
i 1 n
i yi (a bxi ) ,
Q( , ) ( yi xi ) 2
i 1 n
我们希望总误差越小越好,即要使 越小越好.故只要求出使
b 取得最小值时的 , 的值作为 a ,
例1.下表给出我国从1949至1999年人口数 据资料,试根据表中数据估计我国2004年 的人口数。
年份 人口 数/ 百万 49 542 54 603 59 672 64 705 69 807 74 909 79 975 84 89 94 99 1035 1107 1177 1246
分析:先画图
年份 人口 数/ 百万 0 542 5 603 10 672 15 705 20 807 25 909 30 975 35 40 45 50
解决这个问题的方法是:先作散点图,如下图所示: 从散点图中可以看出,样 本点呈直线趋势,时间x与 位置观测值y之间有着较好 的线性关系.因此可以用 线性回归方程来刻画它们 之间的关系.
根据线性回归的 系数公式:
n xi yi nx y ˆ n b i 1 b xi2 n( x ) 2 i 1 a y bx ˆ a
高中数学选修1-2-回归分析第一节.ppt

,a^ = y -b^ x ,
n
xi- x 2
n
x2i -n x 2
i=1
i=1
其中 x =1ni=n1xi, y =1ni=n1yi,( x , y )称为样本点的中心.
课前探究学习
课堂讲练互动
(3)解释变量和预报变量 线性回归模型与一次函数模型的不同之处是增加了随机误差项e, 因变量y由 自变量x 和 随机误差e 共同确定,即自变量x只解 释部分y的变化,在统计中,我们也把自变量x称为解释变量,因变 量y称为预报变量.
课前探究学习
课堂讲练互动
【变式1】 以下是某地搜集到的新房屋的销售价格y和房屋的面积x 的数据:
房屋面积/m2 115 110 80 135 105 销售价格/万元 24.8 21.6 18.4 29.2 22
(1)画出数据对应的散点图; (2)求线性回归方程,并在散点图中加上回归直线; (3)据(2)的结果估计当房屋面积为150 m2时的销售价格.
1.1 回归分析的基本思想及其初步应用
课前探究学习
课堂讲练互动
【课标要求】 1.了解随机误差、残差、残差分析的概念; 2.会用残差分析判断线性回归模型的拟合效果; 3.掌握建立回归模型的步骤; 4.通过对典型案例的探究,了解回归分析的基本思想方法
和初步应用.
课前探究学习
课堂讲练互动
【核心扫描】 1.利用散点图分析两个变量是否存在相关关系,求线性回归方
6
所以
(yi-y^ i)2≈0.013
6
18,
(yi- y )2=14.678 4.
i=1
i=1
所以,R2=1-01.40.16378184≈0.999 1, 回归模型的拟合效果较好.
SPSS统计分析_第六章_回归分析1

进行共线性论断常用的参数有
(l)容许度(Tolerance) 在只有两个自变量的情况下,自变量X1与X2之间共 线性体现在两变量间相关系数r12上。精确共线性时
对应r122=1,当它们之间不存在共线性时r122=0。
r122越接近于1,共线性越强。 多于两个自变量的情况, Xi与其他自变量X之间的复
线形趋势:自变量与因变量的关系是线形的,如果不 是,则不能采用线性回归来分析。 独立性:可表述为因变量y的取值相互独立,它们之 间没有联系。反映到模型中,实际上就是要求残差间 相互独立,不存在自相关。 正态性:自变量x的任何一个线形组合,因变量y均服 从正态分布,反映到模型中,实际上就是要求随机误 差项εi服从正态分布。 方差齐性:自变量的任何一个线形组合,因变量y的 方差均齐性,实质就是要求残差的方差齐。
2、一元线性回归方程的检验
检验的假设是总体回归系数为0。另外要检验回归方 程对因变量的预测效果如何。 (1)回归系数的显著性检验
对斜率的检验,假设是:总体回归系数为0。检验该
假设的t值计算公式是;t=b/SEb,其中SEb是回归系 数的标准误。
对截距的检验,假设是:总体回归方程截距a=0。检
2.多元线性回归分析中的参数
(l)复相关系数 R 复相关系数表示因变量 xi 与他的自变量y之间
线性相关密切程度的指标,复相关系数使用
字母R表示。 复相关系数的取值范围在0-1之间。其值越 接近1表示其线性关系越强,越接近0表示线 性关系越差。
(2)R2判定系数与经调整的判定系数
与一元回归方程相同,在多元回归中也使用判定系数
验该假设的t值计算公式是: t=a/SEa,其中SEa是截 距的标准误。
(2) R2判定系数
第九章 回归分析(一元线性回归)(1)

将表中各对数据描在坐标平面上得图
数 据 和 拟 合 直 线
这样的图称为观测数据的散点图。 从图上可以看出,随着温度x的升高, 某化学过程的生产量y的平均值也在增加, 它们大致成一直线关系,但各点不完全在一 条直线上,这是由于y还受到其它一些随机 因素的影响。
温度 xi
为了研究某一化学反应过程中温度 x 对产
品得率 Y 的影响. 测得数据如下:
C 100 110 120 130 140 150 160 170 180 190
45 51 54 61 66 70 74 78 85 89
得率 yi %
为了研究这些数据所蕴藏的规律性, 将温度 x i 作 为横坐标,得率 y i 作为纵坐标, 在 xoy 坐标系中作 散点图 从图易见, 虽然这些点是散乱的, 但大体上散布在 某条直线附近, 即该化学反应过程中温度与产品
回归分析正是研究预报变量之变动对响 应变量之变动的影响程度,其目的在于根据 已知预报变量的变化来估计或预测响应变量 的变化情况。
“回归(regression)”名称的由
来:
回归名称的由来要归功于英国统计学F.高尔顿 (F.Galton:1822~1911),他把这种统计分析方法 应用于研究生物学的遗传问题,指出生物后代有回 复或回归到其上代原有特性的倾向。高尔顿和他的 学生、现代统计学的奠基者之一K.皮尔逊 (K.Pearson:1856~1936)在研究父母身高与其 子女身高的遗传问题时,在观察了1078对夫妇后, 以每对夫妇的平均身高作为x,取他们的一个成年儿 子的身高为y,将结果绘成散点图后发现成一条直线。 计算出回归方程为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 原因 ⑴消费除受收入影响外,还受其他因素的影响; ⑵线性关系只是一个近似描述; ⑶收入变量观测值的近似性:收入数据本身并不绝 对准确地反映收入水平。
★★矩阵形式
Y 1 1 Y 2 1 1 Y n
令 Y 1 Y Y 2 Y n 1 1 X 1
X X
11 12
X X
21 22
u1 u2 U un
n X 1i X X X ki
X X
1i 2 1i
X X X
2i
1i
X 1i X ki
X 2i X ki
• 因此,一个更符合实际的数学描述为: C = + Y+ (2.2.2) 其中: 是一个随机误差项,是其他影响因素的 “综合体”。 • 线性回归模型的特征:
⑴ 通过引入随机误差项,将变量之间的关系用一 个线性随机方程来描述,并用随机数学的方法来 估计方程中的参数;
⑵ 在线性回归模型中,被解释变量的特征由解释 变量与随机误差项共同决定。
线性回归模型在上述意义上的基本假设
对单方程线性回归模型的一般形式为:
Yi 0 1 X 1i 2 X 2i k X ki i
„
(1)解释变量X1,X2,…,Xk 是确定性变 量,不是随机变量;解释变量之间互不相关。 (2)随机误差项具有0均值和同方差。即 E(i)=0 i=1,2, …,n Var (i)=2 i=1,2, …,n
X
1n
X
2n
X k1 0 u1 X k 2 1 u 2 2 X kn u n k
0 1 B 2 k u1 U u2 un
(3)随机误差项在不同样本点之间是独立的 ,不存在序列相关。即 Cov(i, j)=0 i≠j i,j= 1,2, …,n (4)随机误差项与解释变量之间不相关。即 Cov(Xji, i)=0 j=1,2, …,k i=1,2, …,n
(5)随机误差项服从0均值、同方差的正态 分布。即 i~N(0, 2 ) i=1,2, …,n
2.将非线性模型转化为线性模型的数学 处理方法
⑴变量置换 例如,描述税收与税率关系的拉弗曲线:抛物线 s = a + b r + c r2 c<0 s:税收; r:税率
设X1 = r,X2 = r2, 则原方程变换为
s = a + b X1 + c X2 c<0 • 变量置换仅用于变量非线性的情况。
线性回归模型
• • • • • •
§1 §2 §3 §4 §5 §6
回归分析概述 线性回归模型的参数估计 线性回归模型的统计检验 回归预测 极大似然估计 有约束回归
§1
回归分析概述
一、线性回归模型的特征
二、线性回归模型的普遍性
三、线性回归模型的基本假设
一、线性回归模型的特征
1、线性回归模型的特征
1 2
Z 0 1 X 1 2 X 2 3 X 3
结论:
• 实际中的许多问题,都可以最终化为线性问题, 所以,线性回归模型有其普遍意义。
• 即使对于无法采取任何变换方法使之变成线性 的非线性模型,目前使用得较多的参数估计方 法——非线性最小二乘法,其原理仍然是以线性 估计方法为基础。
⑵ 函数变换 例如,Cobb-Dauglas生产函数:幂函数 Q = AKL Q:产出量,K:投入的资本;L:投入的劳动 方程两边取对数: ln Q = ln A + ln K + ln L
(3)级数展开
例如,不变替代弹性CES生产函数:
Q A(1 K
2 L )
1
• 线性模型理论方法在计量经济学模型理论方法的 基础。
Back :
三、线性回归模型的基本假设
• 对于线性回归模型,模型估计的任务是用回归 分析的方法估计模型的参数。最常用的估计方 法是普通最小二乘法。为保证参数估计量具有 良好的性质,通常对模型提出若干基本假设。 如果实际模型满足这些基本假设,普通最小二 乘法就是一种适用的估计方法;如果实际模型 不满足这些基本假设,普通最小二乘法就不再 适用,而要发展其它方法来估计模型。
2
ˆ0 ˆ1 X 1i ˆ k X ki Yi
i 1
2
minQ
Q 0 ˆ 0 Q ˆ 0 1 Q ˆ 0 2 Q 0 ˆ k
得到下列方程组 0 ˆ ˆ ˆ X X 1i ki Y i 1 k 0 ˆ ˆ X 1i ˆ X ki X 1i 0 Y i X 1i 1 k 0 ˆ ˆ ˆ 0 X X 1i ki X 2 i Y i X 2i 1 k 0 ˆ ˆ ˆ 0 Y i xki X X 1i ki X ki 1 k 0
求参数估计值的实质是求一个k+1元方程组
正规方程
变成矩阵形式
ˆ ˆ X ˆ X ˆ X Y n i 0 1 1i 2 2i k ki ˆ X ˆ X2 ˆ X X ˆ X X X Y 1i i 0 1i 1 1i 2 2 i 1i k ki 1i ˆ 2 ˆ ˆ ˆ X X X X X X k ki X kiYi 0 ki 1 1i ki 2 2i ki
4. 单方程线性回归模型的一般形式
单方程线性回归模型的一般形式为:
Yi 0 1 X 1i 2 X 2i „ k X ki i
i=1,2,„n (2.1.3)
X X , X , 1 2 其中,Y 称被解释变量, „ k 称解释变量,k 为解
释变量的数目,μ 为随机误差项,i 为观测值下标,n 为样本 容量, Байду номын сангаас0 , 1 , 2 , „k 为待估参数。
ˆ ˆ X ˆ X ˆ X e Yi 0 1 1i 2 2i k ki i ˆ ˆ ˆ ˆ ˆ Yi 0 1 X 1i 2 X 2i k X ki
ˆ ei Yi Y i
Q ei Y i Y ˆi
2 i 1 i 1 n n n
2、模型的理论方程中为什么必须包含随机 误差项?
从数学角度看,引入随机误差项,将变量 之间的关系用一个线性随机方程来描述, 才能 用随机数学的方法来估计方程中的参数。 从经济学角度看, 客观经济现象是十分复 杂的,是很难用有限个变量、某一种确定的形 式来描述的,这就是设置随机误差项的原因。
3、随机误差项主要包括哪些因素的影响? •(1)在解释变量中被忽略的因素的影响; •(2)变量观测值的观测误差的影响; •(3)模型关系的设定误差的影响; •(4)其它随机因素的影响。
X X
11 12
X X
21 22
X X
X
1n
X
2n
k2 X kn
k1
Y XB U
§2
线性回归模型的参数估计
• 1. 普通最小二乘法(OLS) • 最小二乘 法(OLS)的原理是通过求残差 (误差项的估计值)平方和最小确定回 归参数估计值。这是求极值问题。用Q 表示残差平方和,求其最小值条件下的 回归参数的估计值。
重要提示
• 几乎没有哪个实际问题能够同时满足所有基本假设; • 通过模型理论方法的发展,可以克服违背基本假设 带来的问题; • 违背基本假设问题的处理构成了单方程线性模型的 理论方法的主要内容: 异方差问题(违背同方差假设) 序列相关问题(违背序列不相关假设) 共线性问题(违背解释变量不相关假设) 随机解释变量(违背解释变量确定性假设)
n X 1i X ki
X X
1i 2
1i
X X X
2i 2i
1i
X 1i X ki
X 2i X ki
ˆ 0 X Yi ki ˆ 1 X Y X X ki 1i ˆ 1i i 2 2 X ki X kiYi ˆ k
1
方程两边取对数后,得到:
LnQ LnA Ln(1 K
2 L )
Ln(1 K 2 L ) 对 在ρ =0处展开台劳级数,取关于ρ 的线性项,即 得到一个线性近似式。
K 2 ln Y ln A 1m ln K 2 m ln L m12 (ln( )) L 变量置换得到
二、线性回归模型的普遍性
线性回归模型是计量经济学模型的主要形 式,许多实际经济活动中经济变量间的复杂 关系都可以通过一些简单的数学处理,使之 化为数学上的线性关系。
1.线性的含义
对变量而言 对参数而言
Yi 0 1 X 1i 2 X 2i
2 Yi 0 1 X1i 2 X 2 i
当给定一个容量为 n的样本, 样本观测值为 (Yi , X 1i , X 2i ,, X ki ) i 1,2,, n 得: Yi 0 1 X 1i 2 X 2i k X ki ui
