2.医学统计学 变异度和正态分布
正态分布在医学研究中的应用

正态分布在医学研究中的应用在医学研究中,正态分布是一种非常重要的统计分布,经常被用来分析各种医学数据。
正态分布又被称为高斯分布,它的特点是数据呈现出一个钟形曲线,并且均值、中位数和众数相等,标准差决定了曲线的宽度。
在医学研究中,正态分布可以被应用于很多不同的领域,以下将详细介绍几个典型的应用:首先,正态分布在流行病学研究中扮演着重要的角色。
流行病学是研究疾病在人群中传播和发生规律的学科。
在流行病学研究中,研究者经常收集大量的数据,比如说疾病的发病率、死亡率等,这些数据往往符合正态分布。
通过对这些数据的分析,我们可以了解疾病的传播规律、风险因素等重要信息,为疾病的预防和控制提供科学依据。
其次,正态分布在临床试验设计和分析中也得到广泛应用。
临床试验是评价药物疗效和安全性的金标准,而正态分布则是评价临床试验数据是否具有统计学意义的基础。
在临床试验设计时,研究者通常会采用双盲、随机、安慰剂对照等方法,确保研究结果的科学性和客观性。
而在数据分析阶段,正态分布可以帮助我们判断药物的疗效是否显著,是否达到临床可接受的水平。
此外,正态分布也在医学统计学研究中扮演着重要的角色。
医学统计学是将统计学理论和方法应用于医学领域的学科,其研究内容涉及数据采集、统计分析、假设检验等多个方面。
而统计分布作为医学统计学的基础,正态分布的特性被广泛应用于医学数据的处理和解读中,有助于科学地评估和推断医学实践中的现象和结论。
总之,正态分布在医学研究中的应用是多方面的,它不仅有助于我们理解医学数据的特性和规律,还提供了重要的工具和方法,为医学研究和临床实践提供了科学支持。
因此,深入理解和应用正态分布对于医学领域的研究人员和从业者来说是非常重要的。
医学统计学重点总结

n Yˆi -Yi 2 i 1
s Y X 意义
的意义
SS总 SS回 SS剩
总 回 剩
决定系数
r 2 SS回 归 SS总
SS回归
F MS回归 =
回归
MS剩余 SS剩余
剩余
tr tb F
直线回归与直线相关的区别与联系
联系
均表示线性关系;
四分位间距:两个特定的百分位数,常用于描 述不对称资料的特征;
方差和标准差:常用来描述正态分布的资料; 变异系数:
常用于比较度量衡单位不同的两组或多组资料 的变异度; 比较均数相差悬殊的两组或多组资料的变异度。
7
正态分布
Normal distribution 德国数学家Gauss发现 最早用于物理学、天文学 Gaussian distribution
都表示变异的大小;
SX S / n
样本含量一定时,标准差越大,标准误越大。
标准误与标准差(2)
标准差 含义:
一组变量值离散程度; 标准差越小,均数的代表性越好;
应用: 估计参考值范围; 与n的关系:样本含量越大,标准差越稳定,n 很大
时,标准差趋向于总体标准差。
① 各观察单位间或者相同,或者存在质的 差别;
② 有质的差别者之间无连续性。
三类资料
(3) 等级资料(ranked data,ordinal data) 以等级表达每个观察单位的某项观察指标,如 疗效分级、心功能分级等。 特点:
① 各观察单位间或者相同,或者存在质的差别; ② 各等级间只有顺序,而无数值大小,故等级之
相关系数的性质
-1 ≤ r ≤ 1 r>0为正相关 r<0为负相关 r=0为零相关或无相关 相关系数绝对值越大,两变量间相关程度越密切; 相关系数越接近于0,表示相关越不密切。
2.医学统计学 变异度和正态分布

-3.0
-2.5 -2.0
0.0013 0.0013 0.0012 0.0011 0.0010
0.0062 0.0059 0.0055 0.0052 0.0049 0.0228 0.0217 0.0207 0.0197 0.0188
-1.9
-1.6 -1.0
0.0287 0.0274 0.0262 0.0250 0.0239
医学统计学
—Medical Statistics
彭志行
Department of Epidemiology & Biostatistics
School of Public Health Nanjing Medical University
Review:
□统计学和医学统计学的基本概念 □建立医学统计思维 □医学统计学的内容
查标准正态分布表: (-1.78)=0.0375 结果:身高在132cm以下男童的比例为3.75%.
质量控制
质量控制的意义
监控日常工作、科研过程、生产过程中误差的变 化,分析变化的趋势是否出现异常,从而引起警 觉和注意,以便分析原因,并及时采取措施。
质量控制图(quality control chart)
总结
□每个观察指标均有其特定的变异规律; □描述变异:
图形描述 统计量描述 平均数:均数、几何均数、中位数 变异度:标准差、四分位数间距、变异系数、极差
□不同分布的指标,用不同的统计量描述; □用平均数与变异度共同描述。
第三章
正态分布及其应用
─Normal distribution and its applications
□频数分布
□描述集中位置的指标
因为变异,世界才变得如此丰富多彩!
医学统计学课后习题答案解析

医学统计学第一章 绪论答案名词解释:(1) 同质与变异:同质指被研究指标的影响因素相同,变异指在同质的基础上各观察单位(或个体)之间的差异。
(2) 总体和样本:总体是根据研究目的确定的同质观察单位的全体。
样本是从总体中随机抽取的部分观察单位。
(3) 参数和统计量:根据总体个体值统计算出来的描述总体的特征量,称为总体参数,根据样本个体值统计计算出来的描述样本的特征量称为样本统计量。
(4) 抽样误差:由抽样造成的样本统计量和总体参数的差别称为抽样误差。
(5) 概率:是描述随机事件发生的可能性大小的数值,用p 表示(6) 计量资料:由一群个体的变量值构成的资料称为计量资料。
(7) 计数资料:由一群个体按定性因数或类别清点每类有多少个个体,称为计数资料。
(8) 等级资料:由一群个体按等级因数的级别清点每类有多少个体,称为等级资料。
是非题:1. ×2. ×3. ×4. ×5. √6. √7. ×单选题:1. C2. E3. D4. C5. D6. B第二章 计量资料统计描述及正态分布答案名词解释:1. 平均数 是描述数据分布集中趋势(中心位置)和平均水平的指标2. 标准差 是描述数据分布离散程度(或变量变化的变异程度)的指标3. 标准正态分布 以μ服从均数为0、标准差为1的正态分布,这种正态分布称为标准状态分布。
4. 参考值范围 参考值范围也称正常值范围,医学上常把把绝大多数的某指标范围称为指标的正常值范围。
填空题:1. 计量,计数,等级2. 设计,收集资料,分析资料,整理资料。
3. σμχ-=u (变量变换)标准正态分布、0、1 4. σ± σ96.1± σ58.2± 68.27% 95% 99%5. 47.5%6.均数、标准差7. 全距、方差、标准差、变异系数8. σμ96.1± σμ58.2±9. 全距 R10. 检验水准、显著性水准、0.05、 0.01 (0.1)11. 80% 90% 95% 99% 95%12. 95% 99%13. 集中趋势、离散趋势14. 中位数15. 同质基础,合理分组16. 均数,均数,μ,σ,规律性17. 标准差18. 单位不同,均数相差较大是非题:1. ×2. √3. ×4. ×5. ×6. √7. √8. √9. √ 10. √11. √ 12. √ 13. × 14. √ 15. √ 16. × 17. × 18. × 19. √ 20. √21. √单选题:1. B2. D3. C4. A5. C6. D7. E8. A9. C 10. D11. B 12. C 13. C 14. C 15. A 16. C 17. E 18. C 19. D 20. C21. B 22. B 23. E 24. C 25. A 26. C 27. B 28. D 29. D 30. D31. A 32. E 33. D 34. A 35. D 36. D 37. C 38. E 39. D 40. B41. C 42. B 43. D 44. C 45. B问答题:1.均数﹑几何均数和中位数的适用范围有何异同?答:相同点,均表示计量资料集中趋势的指标。
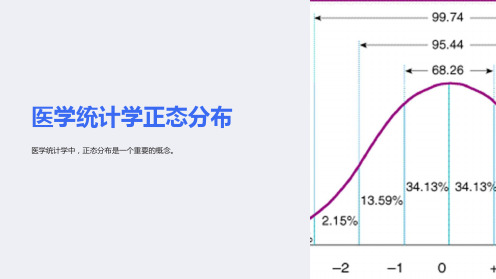
医学统计学正态分布
正态分布的假设检验
假设检验是医学统计学中常用的方法之一。
通过检验数据是否服从正态分布,可以判断相关统计推断的适用性。
正态分布的可视化方法
图表是可视化呈现正态分布的重要工具。
直方图、箱线图和概率图等方法可以帮助理解数据的分布特征。
医学统计学正态分布
医学统计学中,正态分布是一个重分布,又称为高斯分布,是一种以钟形曲线为特征的概率分布。
它具有对称性、单峰性和中心极限定理等重要特点。
正态分布的公式和参数
正态分布的概率密度函数可以使用以下公式表示:
()=1/(√(2)) * e^(-((−)²/2²))
其中,表示均值,表示标准差。
正态分布的应用领域
正态分布在医学统计学中广泛应用。
它可以用来描述人口生理指标、药物浓度、医学测试结果等。
正态分布与医学统计学的关系
医学统计学研究中常常假设数据服从正态分布。
正态分布的假设可以帮助进行参数估计和假设检验等统计推断。
正态分布的重要性
正态分布的重要性在于它在自然界和人类行为中的广泛应用。
医学统计学之正态分布

第23页
举例 说明 通 过正 态分 布 求随 机 变量的
频数分布范围。
例:某地 13 岁女孩 118 人的身高(cm)
资料,估计该地 13 岁正常女孩身高在 135
厘米以下及 155 厘米以上者各占正常女孩
N(μ1 ,σ2)、N(μ2 ,σ2)
N(μ,0.52)、N(μ,12)、N(μ,22)
max
σ=0.5
f(x)
f(x)
σ=1 σ=2
0 医学统计学之正态分布
µ1
µ2
0
µ
第13页
➢ 正态曲线下面积分布有一定规律性。
✓ 对于服从正态分布随机变量(X),随机变量值出现在某 一区区间间所(围成x1,区x2)域概面率积与大正小态相分对布应概(率相密等度)曲。线与横轴在该
医学统计学之正态分布
第26页
✓ 制定医学参考值范围时,应从正常人群中抽样,且样本含量应 较大(n>100),根据资料的分布类型采用正态分布法或百分位 数法。 正态分布法: 适用于资料服从正态分布或近似正态分布时。 公式;
双侧 1-α参考值范围: X U 2 S
单侧 1-α参考值范围: X U S或 X U S
式中σ为总体标准差;μ为总体均数;π
为圆周率,即3.14159···;e为自然对数底,
即2.71828···。
医学统计学之正态分布
第9页
✓ 若某一随机变量概率密度函数(频率曲线方程) 为上式,则称该变量X服从参数为μ和σ正态分布, 记为:X~N(μ,σ2)。
✓ 函数方程中μ为位置参数,σ为形状参数。
本资料起源
医学统计知识点整理

医学统计学知识点整理第一节统计学中基本概念一、同质与变异同质:统计研究中,给观察单位规定一些相同的因素情况。
如儿童的生长发育,规定同性别、同年龄、健康的儿童即为同质的儿童。
变异:同质的基础上个体间的差异。
“同质”是相对的,是客观事物在特定条件下的相对一致性,而“变异”则是绝对的μ.δ.πX.S.p1.2.变量:确定总体之后,研究者应对每个观察单位的某项特征进行观察或测量,这种特征能表现观察单位的变异性,称为变量。
一、数值变量资料又称为计量资料、定量资料:观测每个观察单位某项指标的大小而获得的资料。
表现为数值大小,带有度、量、衡单位。
如身高(cm)、体重(kg)、血红蛋白(g)等。
二、无序分类变量资料又称为定性资料或计数资料:将观察对象按观察对象的某种类别或属性进行分组计数,分组汇总各组观察单位后得到的资料。
分类:二分类:+ -;有效,无效;多分类:ABO血型系统特点:没有度量衡单位,多为间断性资料【例题单选】某地A、B、O、AB血型人数分布的数据资料是( )A.定量资料B.计量资料C.计数资料D.等级资料分组统计描述:是利用统计指标、统计表和统计图相结合来描述样本资料的数量特征及分布规律。
统计推断:是使用样本信息来推断总体特征。
统计推断包括区间估计和假设检验。
第四节统计表与统计图★一、统计表统计表的基本结构与要求标题:高度概括表的主要内容,时间、地点、研究内容,位于表的上方,居中摆放,左侧加表的序号。
标目:横标目和纵标目。
线条:通常采用三线表和四线表的形式。
没有竖线或斜线。
数字:表内数字一律用阿拉伯数字。
同一指标,小数位数应一致,位次对齐。
无数字用“—”表示。
暂缺用“…”表示。
“0”为确切值。
备注:位于表的下面,通常是对表内数字的注解和说明,必要时可以用“*”等标出。
一张统计表的备注不宜太多。
二、制表原则1.(7理分布。
【例题填空】描述某地十年间结核病死亡率的变化趋势宜绘制_________图。
医学统计学(第2章)正态分布

dx
(2-18) )
F(X)
p(a〈x〈b)
0 12.00 14.50 17.00 19.50 22.00 24.50 27.00 29.50 32.00
正态分布曲线下面积的含义
1.表示变量值(x)在a-b区间变量值所占 1.表示变量值 表示变量值( 全部(总体)变量值的比例或概率 比例或概率(p)。 全部(总体)变量值的比例或概率(p)。 2变量值在整个曲线下的面积为100%,或 变量值在整个曲线下的面积为100%,或 出现的概率为1 出现的概率为1。
第五节 医学参考值范围的制定
一、概念 医学参考值是指包括绝大多数“ 医学参考值是指包括绝大多数“正 常人” 的各种生理及生化指标常数, 常人 ” 的各种生理及生化指标常数 , 也 称正常值。 称正常值。 正常值是指在一定范围内波动的值, 正常值是指在一定范围内波动的值, 医学上常用95% 医学上常用95%的范围作为判定正常或 异常的参考标准。 异常的参考标准。
二、 标准正态分布
1.标准正态分布及标准化变量值(u) 标准正态分布及标准化变量值( ) 标准正态分布及标准化变量值 任何正态分布的X值通过 值转换后,称为标 任何正态分布的 值通过u值转换后 称为标 准化的正态分布, 准化的正态分布,即u ~N( µ=0 , σ2=1) ( ) 概率密度函数为: 。概率密度函数为: 2
Φ(−u) 表示从-∞到- u值对应曲线范围 表示从- 值分布比例。 内X值分布比例。
例1: :
Φ(u = −1) = 0.1587 Φ(µ =1) =1− Φ(u = −1)
=1− 0.1587 = 0.8413
例2:标准正态变量值u=(-1,1)和u= 标准正态变量值u=( 1.96,1.96)区间内面积各为多少? ( -1.96,1.96)区间内面积各为多少?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
丙
乙
甲均数30kg 乙均数30kg 丙均数30kg
甲
24 26 28 30 32 34 36
图2.2 三组儿童体重的离散程度
2.3 描述离散程度的指标
极差(Range)
四分位数间距(interquartile range)
正确应用(1)
算术均数:适用于单峰对称分布资料; 几何均数:适合于作对数变换后单峰对称分布资料; 中位数和百分位数:适用于任何分布的资料; 中位数和百分位数在样本含量较少时不稳定,越靠两 端越不稳定; 中位数在抗极端值的影响方面,比均数具有较好的稳 定性,但不如均数精确。
因此,当资料适合计算均数或几何均数时,不宜用中 位数表示其平均水平。
3
1
2
均数相等、方差不等的正态分布图示
2
3 1 2
1
3
正态分布的特征
□正态分布有两个参数(parameter),即位 置参数(均数)和变异度参数(标准差)。
□高峰在均数处; □均数两侧完全对称; □正态分布有两个拐点; □正态曲线下的面积分布有一定的规律。
正态曲线下的面积规律
总结
□每个观察指标均有其特定的变异规律; □描述变异:
图形描述 统计量描述 平均数:均数、几何均数、中位数 变异度:标准差、四分位数间距、变异系数、极差
□不同分布的指标,用不同的统计量描述; □用平均数与变异度共同描述。
第三章
正态分布及其应用
─Normal distribution and its applications
查标准正态分布表: (-1.78)=0.0375 结果:身高在132cm以下男童的比例为3.75%.
质量控制
质量控制的意义
监控日常工作、科研过程、生产过程中误差的变 化,分析变化的趋势是否出现异常,从而引起警 觉和注意,以便分析原因,并及时采取措施。
质量控制图(quality control chart)
□小于-3的面积为 0.13%;
□小于-2的面积为 2.28%; □小于- 的面积为15.87%。
3.2 标准正态分布
□标准正态分布(standard normal distribution)是 均数为0,标准差为1的正态分布。 □记为N(0,1)。 □标准正态分布是一条曲线。 □概率密度函数:
-3.0
-2.5 -2.0
0.0013 0.0013 0.0012 0.0011 0.0010
0.0062 0.0059 0.0055 0.0052 0.0049 0.0228 0.0217 0.0207 0.0197 0.0188
-1.9
-1.6 -1.0
0.0287 0.0274 0.0262 0.0250 0.0239
正态曲线下的面积规律
95%
2.5%
2.5%
-1.96
+1.96
正态曲线下的面积规律
90%
5%
5%
-1.64
+1.64
正态曲线下的面积规律
99%
0.53;2.58
正态曲线下的面积规律
□正态曲线下面积总和为1; □正态曲线关于均数对称;对称的区域内面积相等; □对任意正态曲线,按标准差为单位,对应的面积相等; □ -1.64~ +1.64内面积为90%; □ -1.96~ +1.96内面积为95%; □ -2.58~ +2.58内面积为99%。
不同质的资料应考虑分别计算平均数。
正确应用(2)
标准差的基本内容是离均差,它显示一组变量值 与其均数的间距,故标准差直接地、总结地、平均地 描述了变量值的离散程度。 在同质的前提下,标准差大表示变量值的离散程
度大,即变量值的分布分散、不整齐、波动较大;反
之,标准差小表示变量值的离散程度小,即变量值的
□X轴与正态曲线所夹面积恒等于1 。 □对称区域面积相等。
S(-,-X)
S(X,)=S(-,-X)
正态曲线下的面积规律
• 对称区域面积相等。
S(-x1, -x2)
S(-x1,-x2)=S(x2,x1)
-x1 -x2
x2 x1
正态曲线下的面积规律
S(-, )=0.5 S(-, -1)=0.1587 S(-, -2)=0.0228 S(-, -3)=0.0013 S(-, )=1 S(-, +1)=0.8413 S(-, +2)=0.9772 S(-, +3)=0.9987
S(-1,
)=0.3413
-3
-2 -
+ +2 +3
-4
-3
-2
-1
0
1
2
3
4
正态曲线下的面积规律
S(-, -3)=0.0013
S(-, -2)=0.0228
S(-, -1)=0.1587
S(-3, -2)=0.0215
S(-2, -1)=0.1359
(u)
1 2 e
u
2
2
(-∞< u <+∞)
正态分布转换为标准正态分布
若 X~N(,2),作变换:
u X
则u服从标准正态分布。 u称为标准正态离差(standard normal deviation)
标准正态分布曲线下面积(u)
u 0.00 -0.02 -0.04 -0.06 -0.08
离散趋势的描述—方差
□方差(variance)
2
X
n
2
s
2
X
X
2
n 1
离散趋势的描述—标准差
□标准差(standard deviation, sd)
s
X
X
2
n1
n-1: 自由度(degree of freedom)
□甲组 26 28 30 32 34
0.0548 0.0526 0.0505 0.0485 0.0465 0.1587 0.1539 0.1492 0.1446 0.1401
-0.5
0
0.3085 0.3015 0.2946 0.2877 0.2810
0.5000 0.4920 0.4840 0.4761 0.4681
u 0
总结
□正态分布是描述个体变异的重要分布之一, 也是统计学理论中的重要分布之一; □正态分布是一簇分布,由两个参数决定: 均数和标准差; □正态分布曲线下的面积是有规律的,且与 标准正态分布曲线下的面积对应(以标准正 态离差为单位)。
-3
-2 -
+ +2 +3
-4
-3
-2
-1
0
1
2
3
4
正态曲线下的面积规律
1-S(- , +)=0.3174 1-S(-2 , +2)=0.0456 1-S(-3 , +3)=0.0026
-3
-2 -
+ +2 +3
-4
-3
-2
分布集中、整齐、波动较小。
变异系数派生于标准差,其应用价值在于排除了 平均水平的影响,并消除了单位。
平均数与变异度
□均数±标准差(min,max)
□中位数±四分位数间距 (min,max)
□变异度小,则均数代表性好!
□变异度大,数据分散,则均数代表性差!
□平均数所表示的集中性与变异度所表示的离散 性,从两个不同的角度阐明计量资料的特征!
□频数分布
□描述集中位置的指标
因为变异,世界才变得如此丰富多彩!
人类基因组计划(1990-)
Human Genome Project
黑猩猩与人染色体差异
1.23%(Science, 2002)
There are 1.23% different chromosomes between human and jocko. (Science,2002)
同种动物之间的染色体差异
双胞胎之间的染色体差异
个体变异是统计学应用的前提
个体变异 抽样误差
统计推断
平均数应用的注意事项
同质的资料计算平均数才有意义。
均数适用于:单峰对称分布的资料 几何均数适用于:对数变换后单峰对称的资料 中位数适用于:任何分布资料,有不确定值的资料
例5 只用平均数描述资料的弊病
变异度
方差(Variance)
标准差(Standard Deviation)
变异系数( coefficient of variation )
离散趋势的描述—极差、四分位数间距
□全距(range),极差
R = max-min
□四分位数间距(inter-quartile range)
QU - QL = P75 - P 25
□乙组 24 27 30 33 36
□丙组 26 29 30 31 34
极差 方差 □甲组 8 10.00 □乙组 12 22.50 □丙组 8 8.50
标准差 3.16 4.74 2.92
离散趋势的描述—变异系数
□变异系数(coefficient of variation, CV)
排除了平均水平的影响,并取消了单位。因此 变异系数常用于:
3.3 正态分布的应用
□估计频数分布 □质量控制 □参考值范围的建立
估计频数分布
Example6:某市120名12岁男童身高均数142.67cm,标 准差为s=6.00cm。设该资料服从正态分布,试求该 地12岁男童身高在132cm以下者占该地12岁男童总数 的比例。
