探索与表达规律
北师大版七年级数学上册探索与表达规律课件

1
2
3
4
5
6
7
8
9 10 11 12
13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
规律: “M”形中 七数之和=7×中间数
北师大版七年级《数学》上册 3.5.1 探索与表达规律
北师大版七年级《数学》上册
第三章 整式及其加减
3.5.1 探索与表达规律
北师大版七年级《数学》上册 3.5.1 探索与表达规律
学情分析
本节内容是在学生学习了“用字母表示数”、“ 列代数式”、“去括号”、“合并同类项”等知识的基 础上进行的,它既是对前面所学知识的综合应用, 也是对这些知识的拓展与延伸,对学生体会数学建 模具有重要的作用。
拓展训练
1. 用火柴棒按下图中的方式搭图形。
①
②
(1) 按图示规律填空:
图形符号 ①
②
③
火柴棒根数 4
6
8
③
④
⑤
10
12
(2)按照这种方式搭下去,搭第n个图形需要多少根火柴?
2n+2或2(n+1)
北师大版七年级《数学》上册 3.5.1 探索与表达规律
考考你 视察图1至图5中小黑点的摆放规律,并按照这样的规 律继续摆放.记第n个图中小黑点的个数为y.解答下列 问题:
作业:
习题3.8第1、2题
随堂练习
1.照这样的规律摆下去,摆第7、8个正方形
需要多少颗棋子? 2.探究:摆第n个正方形
需要多少颗棋子?
北师大版七年级《数学》上册 3.5.1 探索与表达规律
北师大版数学七年级上册3.5《探索与表达规律》(第1课时)教学设计

北师大版数学七年级上册3.5《探索与表达规律》(第1课时)教学设计一. 教材分析《探索与表达规律》是北师大版数学七年级上册3.5的内容,本节课主要让学生通过观察、实验、猜测、推理等方法,探索并表达一些简单的数学规律。
教材内容由浅入深,环环相扣,符合学生的认知规律。
教学内容主要包括:探索数列的规律、探索图形的规律、探索事件的规律等。
二. 学情分析学生在之前的学习中已经接触过一些规律性的知识,如数的规律、图形的规律等,具备一定的观察、实验、推理能力。
但七年级学生思维仍以形象思维为主,对于一些抽象的规律还需要通过具体的实例来理解。
此外,学生的学习习惯、学习兴趣等方面也需要考虑到。
三. 教学目标1.理解探索与表达规律的意义,掌握探索简单数学规律的方法。
2.能通过观察、实验、猜测、推理等方法,探索并表达一些简单的数学规律。
3.培养学生的观察能力、实验能力、推理能力,提高学生解决实际问题的能力。
4.激发学生学习数学的兴趣,培养学生的合作意识。
四. 教学重难点1.探索简单数学规律的方法。
2.如何将探索得到的规律进行表达。
五. 教学方法1.情境教学法:通过设置具体的情境,让学生在实际问题中感受到规律的存在。
2.探究式教学法:引导学生通过观察、实验、猜测、推理等方法,主动探索数学规律。
3.小组合作教学法:鼓励学生分组讨论,培养学生的合作意识。
4.反馈评价教学法:及时给予学生反馈,提高学生的学习效果。
六. 教学准备1.教学课件:制作课件,展示探索与表达规律的过程。
2.教学素材:准备一些具体的实例,用于引导学生探索规律。
3.学生活动材料:为学生提供一些实验器材,如卡片、小球等。
4.教学评价工具:设计相关的问题,用于检验学生对知识掌握的程度。
七. 教学过程1.导入(5分钟)利用课件展示一些生活中的规律现象,如日历中的星期循环、四季更替等,引导学生对规律产生好奇。
2.呈现(10分钟)呈现教材中的例1,让学生观察并尝试找出数列的规律。
中考数学复习 查补重难点 整式相关运算与探索表达规律(解析版)
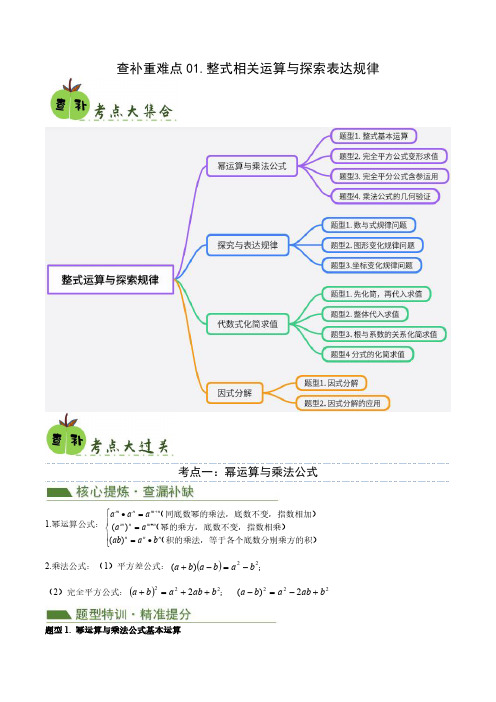
查补重难点01.整式相关运算与探索表达规律考点一:幂运算与乘法公式1.幂运算公式:⎪⎩⎪⎨⎧∙===∙∙+底数分别乘方的积)(积的乘法,等于各个,指数相乘)(幂的乘方,底数不变数不变,指数相加)(同底数幂的乘法,底n n n n m n m n m n m b a ab a a a a a )()(2.乘法公式:(1)平方差公式:();22)(b a b a b a -=-+(2)完全平方公式:()2222222)(2b ab a b a b ab a b a +-=-++=+;题型1.幂运算与乘法公式基本运算1)符号处理不当:在幂的运算中,很多同学计算时符号容易出错。
计算时,可以先确定计算符号,负数进行运算时,看次方,负数的奇次幂结果为负,偶次幂结果为正。
2)忽视指数为“1”的幂:在幂的运算中,有些同学会忽视指数为“1”的幂,从而导致计算的错误。
指数为“1”时通常省略不写,但是计算时不能漏加。
3)忽视0指数幂、负指数幂成立的条件:在计算零指数幂或负指数幂时,要注意,底数不能等于0.4)运用完全平方公式时,①丢掉系数的平分;②丢掉中间乘积项或漏了系数的“2倍”;③不能正确区分中间项符号特征。
5)运用平方差公式时,没找准“a ”与“b ”。
例1.(2023·江苏镇江·中考真题)下列运算中,结果正确的是()A .22423m m m +=B .243·m m m =C .422m m m ÷=D .246()m m =【答案】C【分析】根据合并同类项、同底数幂的乘法运算和除法运算、幂的乘方运算逐项分析,即可求解.【详解】解:22223m m m +=,故A 选项错误;24246m m m m +⋅==,故B 选项错误;42422m m m m -÷==,故C 选项正确;()42248m m m ⨯==,故D 选项错误.故选:C .【点睛】本题考查了合并同类项、同底数幂的乘法运算和除法运算、幂的乘方运算,掌握以上运算法则是解题的关键.变式1.(2023年江苏省镇江市中考数学真题)如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出2x 个球放入乙袋,再从乙袋中取出(22)x y +个球放入丙袋,最后从丙袋中取出2y 个球放入甲袋,此时三只袋中球的个数相同,则+2x y 的值等于()A .128B .64C .32D .16【答案】A 【分析】先表示每个袋子中球的个数,再根据总数可知每个袋子中球的个数,进而求出2x ,2y ,最后逆用同底数幂相乘法则求出答案.【详解】调整后,甲袋中有29-22)x y +(个球,29222292x x y y +--=-,乙袋中有(292)y -个球,52+2252x y y x +-=+,丙袋中有(52)x +个球.∵一共有29+29+5=63(个)球,且调整后三只袋中球的个数相同,∴调整后每只袋中有633=21÷(个)球,∴52=21x +,292=21y -,∴216x =,28y =,∴222168128x y x y +=⋅=⨯=.故选:A .【点睛】本题考查了幂的混合运算,找准数量关系,合理利用整体思想是解答本题的关键.变式2.(2023·四川成都·统考中考真题)下列计算正确的是()A .22(3)9x x -=-B .27512x x x +=C .22(3)69x x x -=-+D .22(2)(2)4x y x y x y -+=+【答案】C【分析】分别根据积的乘方、合并同类项、乘法公式逐项求解判断即可.【详解】解:A 、22(3)9x x -=,故原计算错误,不符合题意;B 、7512x x x +=,故原计算错误,不符合题意;C 、22(3)69x x x -=-+,故原计算正确,符合题意;D 、22(2)(2)4x y x y x y -+=-,故原计算错误,不符合题意,故选:C .【点睛】本题考查积的乘方、合并同类项、乘法公式,熟记完全平方公式和平方差公式,正确判断是解答的关键.题型2.完全平方公式变形求值(知二求二)乘法公式求值类的题目,关键在于恒等变形,反复利用平方差公式和完全平方公式,结合公式中各项的情况,做出相应的变形。
北师大版七年级数学上册探索与表达规律课件

a-8 a-7 a-6
a-1
a a+1
a+6 a+7 a+8
用式子表示九个数的关系: (a-8)+ (a-7) + (a-6) + (a-1) + a +
(a+1) + (a+6) + (a+7) + (a+8)= 9a.
规律六: 方框中九个数的和是正中间这个数的九倍.
创设情境,探索规律
尝试解决:
九数之和=9×中间数
创设情境,探索规律
九数之和=9×中间数 这个关系在任何一个月的日历中也成立吗? 如果用a表示中间数,请按前面找出的关系填出 框中另外8个数.
a
视察日历方框中九个数,四人小组讨论并用计算 器计算验证自己的结论,四人小组再任选一方框用计 算器验证结论是否成立.
创设情境,探索规律
用代数式填写,得到:
让老师来猜一猜!
创设情境,探索规律
游戏规则:你在心里想好一个两位数,将十
位数字乘2,然后加上3,再乘5,然后再加上个位 数字.把你的结果告知我,我就知道你心里想的两 位数.
(1)如果本来的两位数是12,则最后得到的 两位数是多少?如果最后得到的两位数是93 ,你 能求出本来的两位数吗?
27, 78.
规律四:
1 2 3 4 5 下一个比上一
6 7 8 9 10 11 12 个多6.
13 14 15 16 17 18 19
a
20 21 22 23 24 25 26
a+6
27 28 29 30 31
a+12
创设情境,探索规律
尝试解决: (1)一个数列上三个数之间有什么相等关系? (2)你能用数学符号表示出这个规律吗?
探索与表达规律总结(一)

探索与表达规律总结(一)前言在创作的过程中,我们不仅需要积极探索新的领域和知识,同时也需要将自己的想法和创意表达出来。
通过探索与表达的规律总结,我们可以更好地提升创作的效果和质量。
本文将从以下几个方面进行总结:正文1. 持续探索•在创作之前,要对相关领域进行深入的研究和了解,积累大量的知识储备。
•通过阅读、学习以及参与相关活动,不断拓宽自己的视野和思维方式。
•坚持持续学习和探索,不断更新知识,紧跟时代的发展。
2. 深入思考•在创作过程中,要具备深入思考的能力,对问题进行全面、细致的分析。
•对于复杂的问题,可以采用分解、分类、归纳等方法,将问题分解为更小的部分进行思考。
•注重细节,并思考其中的内在规律和联系,以获得更深层次的理解。
3. 寻找灵感•灵感是创作的源泉,而寻找灵感则是一个创作者必不可少的能力。
•多与他人交流,倾听他人的想法和见解,从中获得启发和灵感。
•深入生活,关注身边的人、事、物,发现其中的美和价值,并通过创作表达出来。
4. 有效表达•在创作之前,要明确自己的创作目的和受众群体,以便有针对性地进行表达。
•选择合适的表达方式和工具,如文字、音乐、绘画等,以最佳方式将创意传达给读者、听众或观众。
•注重表达效果和表达方式的多样性,以吸引读者的注意力和共鸣。
结尾通过持续探索与深入思考,我们可以在创作中找到更多的灵感,并找到最适合我们表达的方式和工具。
同时,不断总结、提炼和实践探索与表达的规律,能够帮助我们在创作中更加高效地发挥我们的创造力和才华。
让我们一起积极探索,不断挖掘内心的创作潜力吧!。
七年级探索与表达规律教案

七年级探索与表达规律教案一、课题探索与表达规律二、教学目标1. 知识与技能目标让学生学会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
使学生能够分析简单问题的数量关系,并用代数式表示数量关系。
2. 情感与态度目标培养学生的观察能力、动手能力和创新意识,激发学生学习数学的兴趣。
让学生在探索规律的过程中,体会数学的趣味性和实用性,增强学生学好数学的信心。
三、教学重点&难点1. 教学重点探索实际问题中的数量关系,并用代数式表示规律。
会验证所探索的规律。
2. 教学难点从具体情境中抽象出数量关系和规律,并正确地用代数式表示。
四、教学方法1. 讲授法讲解规律探索的基本方法和思路,让学生有一个整体的认识。
2. 探究法给出一些实例,让学生通过自主探究、小组合作等方式去发现规律,提高学生的探究能力。
3. 讨论法在探究过程中,组织学生进行讨论,分享各自的发现和想法,促进学生之间的交流和思维碰撞。
五、教材分析1. 本课题所在教材的地位在七年级数学教材中,探索与表达规律是代数部分的重要内容。
它是在学生学习了用字母表示数、代数式等知识的基础上进行的,为后续学习方程、函数等知识奠定了基础。
2. 教材内容的特点教材通过生活中的实例,如日历中的数字规律等,引导学生观察、分析、归纳,体现了数学来源于生活又应用于生活的特点。
同时,教材注重培养学生的思维能力和创新意识,通过探究活动让学生经历从特殊到一般的思维过程。
六、教学过程1. 导入(趣味引入)同学们,今天老师给大家带来一个小魔术。
我这里有一个日历(拿出日历展示),我随便圈出一个九宫格,你们能快速算出这九个数字的和吗?(让学生尝试回答)其实这里面是有规律的哦。
你们看,这日历上的数字排列看似杂乱无章,但实际上隐藏着很多数学规律呢。
咱们今天就一起来探索这些规律。
2. 规律探索一:日历中的规律老师把日历画在黑板上(简单画出日历的一部分),咱们一起来观察。
北师大版数学七年级上册3.5《探索与表达规律》(第1课时)教案

北师大版数学七年级上册3.5《探索与表达规律》(第1课时)教案一. 教材分析《探索与表达规律》是北师大版数学七年级上册3.5的内容,本节课主要让学生通过观察、分析、归纳等方法探索数学规律,进一步培养学生的逻辑思维能力和抽象概括能力。
教材内容主要包括探索数字变化的规律、图形的规律和字母表示的规律等,通过这些探索活动,让学生体会数学的趣味性和魅力。
二. 学情分析七年级的学生已经具备了一定的数学基础,对于简单的规律探索和归纳总结已经有了一定的能力。
但学生在探索复杂规律时,可能还会存在一定的困难,需要教师在教学中给予引导和帮助。
此外,学生可能对数学规律的探究兴趣不够浓厚,教师需要通过设计有趣的教学活动,激发学生的学习兴趣。
三. 教学目标1.知识与技能目标:让学生通过观察、分析、归纳等方法探索数学规律,提高学生的逻辑思维能力和抽象概括能力。
2.过程与方法目标:培养学生独立思考、合作交流的能力,提高学生的解决问题的能力。
3.情感态度与价值观目标:让学生体验数学的趣味性,培养学生的学习兴趣,增强学生对数学的热爱。
四. 教学重难点1.教学重点:让学生掌握探索数学规律的方法,提高学生的逻辑思维能力和抽象概括能力。
2.教学难点:如何引导学生发现并表达复杂的数学规律,以及如何运用规律解决实际问题。
五. 教学方法1.引导发现法:教师通过提出问题,引导学生观察、分析、归纳,发现数学规律。
2.合作交流法:学生分组讨论,分享各自的发现和思考,共同探索数学规律。
3.实践操作法:学生通过动手操作,验证规律的正确性,加深对规律的理解。
六. 教学准备1.教师准备:教师需要准备相关的教学素材,如数字变化规律的图片、图形变化规律的例子等。
2.学生准备:学生需要提前预习本节课的内容,了解探索数学规律的基本方法。
七. 教学过程1.导入(5分钟)教师通过提出一个简单的数字变化规律问题,激发学生的学习兴趣,引导学生进入本节课的主题。
2.呈现(15分钟)教师展示相关的数字变化规律的图片和图形变化规律的例子,让学生观察、分析,尝试归纳出规律。
北师大版数学七年级上册3.5《探索与表达规律》(第2课时)说课稿

北师大版数学七年级上册3.5《探索与表达规律》(第2课时)说课稿一. 教材分析北师大版数学七年级上册3.5《探索与表达规律》(第2课时)是本册教材中的一个重要内容。
这部分内容主要让学生掌握探索与表达规律的方法,培养学生观察、思考、归纳的能力。
教材通过具体的例子引导学生发现规律,并用代数式表示出来。
本节课的内容与实际生活紧密相连,有利于激发学生的学习兴趣,提高学生运用数学知识解决实际问题的能力。
二. 学情分析面对七年级的学生,他们在之前的学习中已经初步接触了代数知识,对于如何用字母表示数,以及简单的代数式运算已经有了一定的了解。
但是,如何通过观察找到规律,并用代数式表示出来,对于一部分学生来说还是一个新的挑战。
因此,在教学过程中,我需要关注这部分学生的学习需求,通过引导他们积极参与课堂活动,提高他们的学习兴趣和自信心。
三. 说教学目标根据教材内容和学情分析,我制定了以下教学目标:1.让学生掌握探索与表达规律的方法,培养观察、思考、归纳的能力。
2.让学生能够通过具体的例子发现规律,并用代数式表示出来。
3.提高学生运用数学知识解决实际问题的能力。
4.激发学生的学习兴趣,增强学生对数学学科的认同感。
四. 说教学重难点1.教学重点:让学生掌握探索与表达规律的方法,能够发现规律并用代数式表示出来。
2.教学难点:如何引导学生发现规律,并用代数式准确地表示出来。
五. 说教学方法与手段为了实现教学目标,突破教学重难点,我采用了以下教学方法与手段:1.引导发现法:通过具体的例子引导学生观察、思考,发现规律。
2.小组合作学习:让学生在小组内共同探讨,互相启发,共同提高。
3.激励评价法:在教学过程中,对学生的每一次进步都给予积极的评价,提高学生的自信心。
六. 说教学过程1.导入新课:通过一个具体的生活例子,引导学生发现其中的规律,激发学生的学习兴趣。
2.探索规律:让学生通过小组合作学习,共同探讨如何发现规律,并用代数式表示出来。
