苏教版初二下数学压轴题
苏科版八年级下册数学期中复习易错压轴题(无答案)

1.把一副三角尺如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角尺DCE绕着点C按顺时针方向旋转15°得到△D1CE1(如图②),此时AB与CD1交于点O,则线段AD1的长为()2.如图,将△ABC的边AB绕着点A顺时针旋转a(0°<a<90°)得到AB',边AC绕着点A逆时针旋转β(0°<β<90°)得到AC',连接B'C'.当a+β=90°时,我们称△AB'C'是△ABC的“双旋三角形”如果等边三角形ABC的边长为a.那么它的“双旋三角形”的面积是_.(用含a的代数式表示)3.如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为_.4.如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,O是坐标原点,点A,C分别在x轴、y轴正半轴上,P为边OA上任意-点(与点O,A不重合),连接CP,过点P作PM⊥CP 交AB于点D,且PM=CP,过点M作MN//OA,交BO于点N,连接ND,BM,设OP=t.(1)求点M的坐标;(用含t的代数式表示)(2)试判断线段MN的长度是否随点P的位置的变化而改变,并说明理由.5.如图,在周长为12的菱形ABCD中,AE=1,AF=2.若P为对角线BD上一动点,则PE+PF的最小值为()A.1B.2C.3D.46.如图,在矩形ABCD中,点E,F分别在边AB.BC上,且AE=1AB,将矩形沿直线3EF折叠,点B恰好落在边AD.上的点P处,连接BP交EF于点Q.有下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()A.①②.B.②③C.①③D.①④7.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点若OCEF的周长为18,则OF的长为8.如图,菱形ABCD的面积为120c㎡.正方形AECF的面积为50c㎡,则菱形的边长为cm.9.如图,在△ABO中,AB⊥OB,AB=△√3,0B=1,把ABO绕点O旋转120°后,得到△A1B1O,则点A的对应点A1的坐标为.10.如图,在正方形ABCD中,AB=8,AC与BD交于点O,N为AO的中点,点M在边BC.上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为.11.如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=1S矩形ABCD,则点P到A,B两3点距离之和PA+PB的最小值为()A.√29B.√34C.5√2D.√4112.如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12,点P在正方形ABCD的边,上,则满足PE+PF=9的点P的个数是()A.0B.4C.6D.813.阅读下列材料:如图①,在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.(1)写出图①所示筝形的两个性质(定义除外).①;②(2)如图②,在平行四边形ABCD中,点E,F分别在边BC,CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形;(3)如图③,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.14.问题情境(1)如图①,在正方形ABCD中,E为边BC上一点(不与点B,C重合),垂直于AE的一条直线MN分别交AB,AE,CD于点M,P.N.判断线段DN,MB,EC之间的数量关系,并说明理由;问题探究(2)在(1)的基础上,解答下列问题:①如图②,若垂足P恰好为AE的中点,连接BD,交MN于点Q.连接EQ,并延长交边AD于点F,求∠AEF的度数;15.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M,N分别是DC,DF的中点,连接MN.若AB=7,BE=5,则MN=.16.如图,正方形ABCD的顶点A在y轴的正半轴上,顶点B在x轴的正半轴上,顶点C的坐标为(3,2),M,N分别为AB,AD的中点,则MN的长为.17.如图,正方形ABCD的两条对角线相交于点O.E为OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形ABCD的边长为4√2,则DF=.18.如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长度的速度沿射线BC方向匀速运动.设运动时间为t s.(1)当t=时,以OB,OP为邻边的平行四边形是菱形;(2)当点P在(B的垂直平分线上时,求t的值;(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.19.如图①,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使点B落在边AD上的E处,折痕为PQ.过点E作EF//AB交PQ于点F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在边AD上移动时,折痕的端点P,Q也随之移动.①当点Q与点C重合时(如图②),求菱形BFEP的边长;②若限定点P,Q分别在边BA,BC上移动,求出点E在边AD上移动的最大距离.。
苏教版八年级下册数学压轴题(非常好的题目)之欧阳育创编

压轴题精选时间:2021.02.04创作:欧阳育1、如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.⑴求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似?2、“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AO B 置于直角坐标系中,边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ,以P 为圆心、以2OP 为半径作弧交图象于点R .分别过点P 和R 作x 轴和y 轴的平行线,两直线相交于点M ,连接OM 得到∠MOB,则∠MOB=31∠AOB.要明白帕普斯的方法,请研究以下问题:(1)设)1,(a a P 、)1,(b b R ,求直线OM 对应的函数表达式(用含b a ,的代数式表示).(2)分别过点P 和R 作y 轴和x 轴的平行线,两直线相交于点Q .请说明Q 点在直线OM 上,并据此证明∠MOB=31∠AOB.3、(14分)如图,在平面直角坐标系xOy 中,矩形OEFG 的顶点E 坐标为(4,0),顶点G 坐标为(0,2).将矩形OEFG 绕点O 逆时针旋转,使y x OP Q A B点F 落在轴的点N 处,得到矩形OMNP ,OM 与GF 交于点A .(1)判断△OGA 和△OMN 是否相似,并说明理由;(2)求过点A 的反比例函数解析式;(3)设(2)中的反比例函数图象交EF 于点B ,求直线AB 的解析式;(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG 的对称中心,并说明理由.4、如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象经过点()0,2B ,且与x轴的正半轴相交于点A ,点P 、点Q 在线段AB 上,点M 、N 在线段AO 上,且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形,90OPM MQN ∠=∠=。
江苏八年级下期末真题精选(压轴60题19个考点专练)~【满分全攻略】2022~2023

江苏八年级下期末真题精选(压轴A.6B.3(2020•重庆)4.如图,在平面直角坐标系中,是x轴上一点,连接AE.若ADA.6B.12(2022春•泰州期末)5.如图,A(a,b)、B(-a,-b A、B作y轴的平行线,与反比例函数(2022春•高邮市期末)8.如图,在平面直角坐标系中,的图像经过OA 的中点C 和点9.如图,在平面直角坐标系中,边,在第一象限内作矩形点O 重合,折痕为MN ,点()0ky k =≠的图像恰好过A.27 4五.反比例函数与一次函数的交点问题(共(2021•武威二模)11.已知反比例函数y(1)求这两个函数的关系式;a___________(1)直接写出=(2)结合图象直接写出关于x的不等式C n在反比例函数y(3)点(),2(2022春•安居区期末)(1)求该反比例函数和一次函数的表达式;的面积;(2)连接AO,求AOB(3)直接写出关于x的不等式mx (2014•巴中)15.如图,在平面直角坐标系(1)求反比例函数和直线EF(2)求△OEF的面积;(3)请结合图象直接写出不等式(2018春•秦淮区期末)16.如图,在直角坐标系中,函数(1)点A 、B 的坐标分别是 、 ;(2)在同一平面直角坐标系中,画出函数34y x=-的图象;(3)垂直于y 轴的直线l 与函数1y 、2y 、3y 的图象分别交于点3(N x ,3)y ,若123x x x <<,结合函数的图象,直接写出六.反比例函数的应用(共5小题)(2022•青秀区校级一模)17.学校的自动饮水机,开机加热时每分钟上升10开始下降,此时水温y ℃与通电时间x (min )成反比例关系.当水温降至机再自动加热,若水温在20︒时接通电源,水温y 则下列说法中正确的是( )A .水温从20︒升高到100B .水温下降过程中,y 与C .早晨8点接通电源从20D .在单次加热—降温的过程中,水温不低于100℃,停止加热,水温开始下降,此时水温()℃与开机后用时()min 成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温()y ℃和时间()min 的关系如图,为了在上午第一节下课时()8:45能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )A .7:20B .7:30C .7:45D .8:00(2022春•海州区校级期末)19.某车队要把4000吨货物运到灾区,已知每天的运输量不变.(1)从运输开始,每天运输的货物吨数n (吨)与运输时间t (天)之间有怎样的函数表达式?(2)因灾区道路受阻,实际每天比原计划少运20%,推迟2天完成任务,求原计划完成任务的天数.(2021•蒸湘区校级一模)20.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量y (微克)与时间x (分钟)的函数关系如图,并发现衰退时y 与x 成反比例函数关系.(1)=a _____________;(2)当5100≤≤x 时,y 与x 之间的函数关系式为_____________;当100x >时,y 与x 之间的函数关系式为_____________;(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多(1)求k的值;(2)恒温系统在一天内保持大棚内温度不低于七.三角形中位线定理(共(2019•铁西区二模)22.如图,△ABC中,∠A=60° ,AC(2015•呼伦贝尔)26.如图,在平行四边形ABCD (1)求证:△ADE≌△CBF;(2)若∠ADB是直角,则四边形一十.平行四边形的判定与性质(共2022春•南京期末).在ABCD 中,6cm AB =(2011•北京)30.在▱ABCD 中,∠一十一.菱形的性质(共(2021春•滨湖区期末)32.如图,已知菱形ABCD=,连接动点,且PC CQA.45B.(2022•新市区校级三模)33.已知如图,在菱形ABCD(1)求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形一十二.菱形的判定与性质(共(2023•郧西县模拟)34.在Rt△ABC中,∠BAC=90°,A .逐渐增大C .不变(2022春•靖江市校级期末)36.如图,线段AB 的长为10,点(2018•邵阳模拟)38.如图,矩形ABCD 中,点边于点,E F AF AE =、.(1)求证:四边形AFCE 是菱形;(2)若8,6BC AB ==,求EF 的长.(2021春•淮安区期末)39.如图所示,在矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交BC ,AD 于点E ,F ,垂足为O ,连接AE ,CF .(1)求证:四边形AFCE 为菱形;(2)求AF 的长.(2019•无锡模拟)40.已知:如图,在平行四边形ABCD 和矩形ABEF 中,AC 与DF 相交于点G .(1) 试说明DF =CE ;(2) 若AC =BF =DF ,求∠ACE 的度数.(2011•福州)41.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,ab ≠0),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.(2022春•工业园区期末)42.已知,如图,在长方形ABCD 中,46AB AD ==,.延长BC 到点E ,使3CE =,连接DE .(1)动点P 从点B 出发,以每秒1个单位的速度沿BC CD DA --向终点A 运动,设点P 运动的时间为t 秒,求当t 为何值时,ABP 和DCE △全等?(2)若动点P 从点B 出发,以每秒1个单位的速度仅沿着BE 向终点E 运动,连接DP .设点P 运动的时间为t 秒,是否存在t ,使PDE △为等腰三角形?若存在,请求出t 的值;否则,说明理由.(2012•云南)43.如图,在矩形ABCD 中,对角线BD 的垂直平分线MN 与AD 相交于点M ,与BD 相交于点O ,与BC 相交于点N ,连接BM 、DN .(1)求证:四边形BMDN 是菱形;(2)若4AB =,8AD =,求MD 的长.一十四.正方形的性质(共5小题)(2012•黔东南州)44.点P 是正方形ABCD 边AB 上一点(不与A 、B 重合),连接PD 并将线段PD 绕点P 顺时针旋转90°,得线段PE,连接BE,则∠CBE 等于( )(2022春•仪征市期末)46.在正方形ABCD中,点(1)当α=20°时,求∠DAE的度数;(2)判断△AEG的形状,并说明理由;(3)当GF=1时,求CE的长.一十五.正方形的判定(共(2022春•隆安县期末)(1)求证:BC=BE;(2)连接CF,若∠ADF=∠BCF(1)证明四边形EGFH是平行四边形;形EGFH是正方形.一十六.正方形的判定与性质(共(2022春•仪征市期末)51.我们知道菱形与正方形的形状有差异,“接近度”.A .424-(2022•南京模拟)53.在矩形ABCD 中,点A 顺时针旋转90°得到A .25B .(2022•常熟市模拟)54.如图,在Rt ABC △中,动点,A B C ABC ''△△≌,将(2022•平邑县一模)56.在正方形ABCD 中,点E 在射线BC 上(不与点B 、C 重合),连接DB ,DE ,将DE 绕点E 逆时针旋转90 得到EF ,连接BF .(1)如图1,点E 在BC 边上.①依题意补全图1;②若=6AB ,=2EC 求BF 的长;(2)如图2,点E 在BC 边的延长线上,用等式表示线段BD ,BE ,BF 之间的数量关系.(2016春•工业园区期末)57.如图,在△ABC 中,∠BAC =50°,将△ABC 绕点A 按逆时针方向旋转后得△AB 1C 1.当B 1B ∥AC 时,求∠BAC 1的度数.(2021•厦门二模)58.在正方形ABCD 中,将边AD 绕点A 逆时针旋转()090a a ︒<<︒得到线段AE ,AE 与CD 延长线相交于点F ,过B 作//BG AF 交CF 于点G ,连接BE .(1)如图1,求证:2BGC AEB ∠=∠;(2)当(4590a ︒<<︒)时,依题意补全图2,用等式表示线段AH EF DG ,,之间的数量关系,并证明.一十八.作图-旋转变换(共1小题)(2022春•盱眙县期末)59.如图,在平面直角坐标系中,已知ABC 的三个顶点的坐标分别为()()()5,1,2,2,1,4A B C ---,请按下列要求画图:(1)将ABC 先向右平移4个单位长度、再向下平移1个单位长度,得到111A B C △,画出111A B C △;(2)222A B C △与ABC 关于原点O 成中心对称,画出222A B C △.一十九.条形统计图(共1小题)(2022春•盱眙县期末)60.我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A (体操)、B (乒乓球)、C (毽球)、D (跳绳)四项活动.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图.请根据统计图回答下列问题:(1)这次被调查的学生共有_____人;(2)请将统计图2补充完整;(3)统计图1中B项目对应的扇形的圆心角是_____度;(4)已知该校共有学生1000人,根据调查结果估计该校喜欢体操的学生有_____人.∵△AOB 和△ACD 均为正三角形,∴60AOB CAD ∠=∠=︒,∴AD ∥OB ,∴ABP AOP S S = ,∵四边形ABCD为矩形,O为对角线,∴AO=OD,∴∠ODA=∠OAD,又∵AD为∠DAE的平分线,∴∠OAD=∠EAD,∴∠EAD=∠ODA,∵AD AC =,∴,ABD ABC EAD EACS S S S == ∴23BED BEC S S ∆∆==∵AB AC AD AC ==,,∴AD AB =,∵AB y ∥轴,∴AD x ⊥轴.∵反比例函数()0k y x x=<∴设k B x x ⎛⎫ ⎪⎝⎭,,令0x =,则077y =-=-,()0,7H ∴- 直线AB 的解析式为y x =-∴设直线CG 的表达式为y =将点()3,2C -代入y x t =+;(3)解:由图象可知,若123x x x <<,垂直于y 轴的直线l 在x 轴与直线=2y -之间,∴饮水机的一个循环周期为1003分钟,每一个循环内,在水温不超过50℃.∵7:20至8:45之间有85分钟,100 85-段内,A选项不符合题意;100设AD 的解析式为:y mx n =+,把()0,10D 、()2,20A 代入y mx =∵在▱ABCD中,AE=4,∴22=-= EC AC AE∵在▱ABCD中,AE=4,AB=∴222016=-=-EC AC AE∴BC=BE-EC=3-2=1,的周长=2(AB+BC∴ABCD故答案为:20或12.考点:平行四边形的性质;坐标与图形性质.26.(1)证明见解析;(2)若。
苏教版八年级下册数学压轴题非常好的题目精修订

苏教版八年级下册数学压轴题非常好的题目 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-压轴题精选1、如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.⑴求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似?2、“三等分角”是数学史上一个着名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB 置于直角坐标系中,边OB 在x 轴上、边OA 与函数xy 1的图象交于点P ,以P 为圆心、以2OP 为半径作弧交图象于点R .分别过点P 和R 作x 轴和y 轴的平行线,两直线相交于点M ,连接OM 得到∠MOB ,则∠MOB=31∠AOB .要明白帕普斯的方法,请研究以下问题:(1)设)1,(a a P 、)1,(bb R ,求直线OM 对应的函数表达式(用含b a ,的代数式表示).(2)分别过点P 和R 作y 轴和x 轴的平行线,两直线相交于点Q .请说明Q 点在直线OM 上,并据此证明∠MOB=31∠AOB .3、(14分)如图,在平面直角坐标系xOy 中,矩形OEFG 的顶点E 坐标为(4,0),顶点G 坐标为(0,2).将矩形OEFG 绕点O 逆时针旋转,使点F 落在轴的点N 处,得到矩形OMNP ,OM 与GF 交于点A .(1)判断△OGA 和△OMN 是否相似,并说明理由;yxOPQAB(2)求过点A 的反比例函数解析式; (3)设(2)中的反比例函数图象交EF于点B ,求直线AB 的解析式;(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG 的对称中心,并说明理由.4、如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象经过点()0,2B ,且与x轴的正半轴相交于点A ,点P 、点Q 在线段AB 上,点M 、N 在线段AO 上,且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形,90OPM MQN ∠=∠=。
苏教版八年级下册数学压轴题(非常好的题目)之欧阳与创编

压轴题精选时间:2021.03.08创作:欧阳与1、如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t秒.⑴求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似?2、“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB 置于直角坐标系中,边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ,以P 为圆心、以2OP 为半径作弧交图象于点R .分别过点P 和R 作x 轴和y 轴的平行线,两直线相交于点M ,连接OM 得到∠MOB ,则∠MOB=31∠AOB .要明白帕普斯的方法,请研究以下问题:(1)设)1,(a a P 、)1,(b b R ,求直线OM 对应的函数表达式(用含b a ,的代数式表示).(2)分别过点P 和R 作y 轴和x 轴的平行线,两y O P Q A B直线相交于点Q.请说明Q点在直线OM上,并据此1∠AOB.证明∠MOB=33、(14分)如图,在平面直角坐标系xOy中,矩形OEFG的顶点E坐标为(4,0),顶点G坐标为(0,2).将矩形OEFG绕点O逆时针旋转,使点F落在轴的点N处,得到矩形OMNP,OM与GF交于点A.(1)判断△OGA和△OMN是否相似,并说明理由;(2)求过点A的反比例函数解析式;(3)设(2)中的反比例函数图象交EF于点B,求直线AB的解析式;(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG的对称中心,并说明理由.4、如图,在平面直角坐标系xOy中,一次函数y kx b=+的图象经过点()0,2B,且与x轴的正半轴相交于点A,点P、点Q在线段AB上,点M、N在线段AO上,且OPM与QMN是相似比为3∶1的两个等腰直角三角形,90∠=∠=。
苏教版初二下数学压轴题
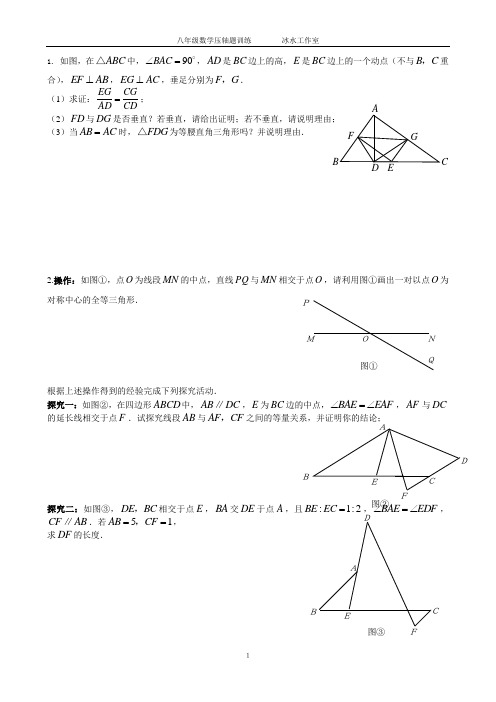
11. 如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,E 是BC 边上的一个动点(不与B C ,重合),EF AB ⊥,EG AC ⊥,垂足分别为F G ,.(1)求证:EG CGAD CD=; (2)FD 与DG 是否垂直?若垂直,请给出证明;若不垂直,请说明理由; (3)当AB AC =时,FDG △为等腰直角三角形吗?并说明理由.2.操作:如图①,点O 为线段MN 的中点,直线PQ 与MN 相交于点O ,请利用图①画出一对以点O 为对称中心的全等三角形.根据上述操作得到的经验完成下列探究活动.探究一:如图②,在四边形ABCD 中,AB DC ∥,E 为BC 边的中点,BAE EAF ∠=∠,AF 与DC 的延长线相交于点F .试探究线段AB 与AF CF ,之间的等量关系,并证明你的结论;探究二:如图③,DE BC ,相交于点E ,BA 交DE 于点A ,且:1:2BE EC =,BAE EDF ∠=∠,CF AB ∥.若51AB CF ==,,求DF 的长度.FAGCEBP O M N Q图① A B EFC D图②D AB EFC 图③23.如图,在平面直角坐标系中,O 是坐标原点,点A 的坐标为()40-,,点B 的坐标为()()00.b b >,P 是直线AB 上的一个动点,作PC x ⊥轴,垂足为.C 记点P 关于y 轴的对称点P ′(点P ′不在y 轴上),连结PP P A P C ''′,,.设点P 的横坐标为.a (1)当3b =时,①求直线AB 的解析式;②若点P ′的坐标是()1m -,,求m 的值; (2)若点P 在第一象限,记直线AB 与P C ′的交点为.D 当13P D DC =′∶∶时,求a 的值; (3)是否同时存在a b ,,使P CA △′为等腰直角三角形?若存在,请求出所有满足要求的a b ,的值;若不存在,请说明理由.4.如图,在等腰梯形ABCD 中,AD BC ∥,5AB DC ==,6AD =,12BC =.动点P 从D 点出发沿DC 以每秒1个单位的速度向终点C 运动,动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动.两点同时出发,当P 点到达C 点时,Q 点随之停止运动. (1)梯形ABCD 的面积等于 ;(2)当PQ AB ∥时,P 点离开D 点的时间等于 秒; (3)当P Q C ,,三点构成直角三角形时,P 点离开D 点多少时间?C B35、 如图1,在平面直角坐标系中,等腰Rt △AOB 的斜边OB 在x 轴上,直线y=3x- 4经过等腰Rt △AOB 的直角顶点A ,交y 轴于C 点,双曲线ky x=也经过A 点。
苏教版八年级下册数学压轴题(非常好的题目)之欧阳家百创编
压轴题精选欧阳家百(2021.03.07)1、如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒. ⑴求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似? 2、“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB 置于直角坐标系中,边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ,以P 为圆心、以2OP 为半径作弧交图象于点R .分别过点P 和R 作x 轴和y 轴的平行线,两直线相交于点M ,连接OM 得到∠MOB ,则∠MOB=31∠AOB .要明白帕普斯的方法,请研究以下问题:(1)设)1,(a a P 、)1,(b b R ,求直线OM 对应的函数表达式(用含b a ,的代数式表示).(2)分别过点P 和R 作y 轴和x 轴的平行线,两直线相交于点Q .请说明Q 点在直线OM 上,并据此证明∠MOB=31∠AOB .3、(14分)如图,在平面直角坐标系xOy 中,矩形OEFG 的顶点E坐标为(4,0),顶点G 坐标为(0,2).将矩形OEFG 绕点O 逆时针旋转,使点F 落在轴的点N 处,得y xO PQA B到矩形OMNP ,OM 与GF 交于点A .(1)判断△OGA 和△OMN 是否相似,并说明理由;(2)求过点A 的反比例函数解析式;(3)设(2)中的反比例函数图象交EF 于点B ,求直线AB 的解析式;(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG 的对称中心,并说明理由.4、如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象经过点()0,2B ,且与x轴的正半轴相交于点A ,点P 、点Q 在线段AB 上,点M 、N 在线段AO 上,且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形,90OPM MQN ∠=∠=。
苏教版八年级数学下册《反比例函数》压轴题专题训练(含解析)
《反比例函数》压轴题专题训练一.选择题(共10小题)1.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=()A.B.C.D.12第1题第2题第3题2.如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为()A.12B.10C.8D.63.如图,平行四边形ABCO的顶点B在双曲线y=上,顶点C在双曲线y=上,BC中点P恰好落在y轴上,已知S▱OABC=10,则k的值为()A.﹣8B.﹣6C.﹣4D.﹣24.如图,平行四边形ABCD的顶点A的坐标为(﹣,0),顶点D在双曲线y=(x>0)上,AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为()A.4B.6C.7D.8第4题第5题第6题5.如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,4),反比例函数y=的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是()A.B.C.﹣12D.6.如图,A、C两点在反比例函数y=的图象上,B、D两点在反比例函数y=的图象上,AB⊥x轴于点E,CD⊥x轴于点F,AB=3,CD=2,EF=,则k1﹣k2的值为()A.﹣3B.﹣2C.D.﹣17.如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,),过点E作直线l∥BD交y轴于点F,则点F的坐标是()A.(0,﹣)B.(0,﹣)C.(0,﹣3)D.(0,﹣)第7题第8题8.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为()A.(,0)B.(2,0)C.(,0)D.(3,0)9.如图,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2,△ADC与△ABC关于AC所在的直线对称.若点A和点D在同一个反比例函数y=的图象上,则OB的长是()A.2B.3C.2D.310.如图,点A是射线y═(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=交CD边于点E,则的值为()A.B.C.D.1二.填空题(共13小题)11.如图,直线y=﹣2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.则k=.12.如图,直线y=﹣x+b与双曲线y=(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,AC⊥x轴于点C,BD⊥y轴于点D,当b=时,△ACE、△BDF与△ABO面积的和等于△EFO面积的.13.如图,两个反比例函数y=和y=在第一象限的图象如图所示,当P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B,则四边形P AOB的面积为.14.y=kx﹣6的图象与x,y轴交于B、A两点,与的图象交于C点,CD⊥x轴于D点,如果△CDB的面积:△AOB的面积=1:9,则k=.15.如图,A、B是第二象限内双曲线y=上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为.16.如图,点A、B在反比例函数y=(k≠0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C.若OM=MN=NC,△AOC的面积为9,则k 的值为.17.如图,A,B是反比例函数y=(x>0)图象上的两点,过点A作AP∥y轴,过点B 作BP∥x轴,交点为P连接OA,OP,若△AOP的面积为2,则△ABP的面积为.18.如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,反比例函数y=(x>0)与AB相交于点D,与BC 相交于点E,若BE=3CE,四边形ODBE的面积是9,则k=.19.如图,已知点A是一次函数y=x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=(x>0)的图象过点B,C,若△OAB的面积为8,则△ABC的面积是.20.如图在平面直角坐标系中,周长为12的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上.点B,在反比例函数y=位于第一象限的图象上.则k的值为.21.如图,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(k>0,x>0)的图象上,点D的坐标为(4,3).则k的值为.22.如图,已知反比例函数y=在第一象限内的图象上一点A,且OA=4,AB⊥x轴,垂足为B,线段OA的垂直平分线交x轴于点C(点C在点B的左侧),则△ABC的周长等于.23.如图,正方形ABCD位于第一象限,边长为3,横坐标为1的点A在直线y=x上,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD公共点,则k的取值范围是.三.解答题(共11小题)24.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC=6.对角线AC,BD相交于点E,反比例函数(x>0)的图象经过点E,分别与AB,CD交于点F,G.(1)若OC=8,求k的值;(2)连接EG,若BF﹣BE=2,求△CEG的面积.25.如图,四边形ABCD是菱形,对角线AC⊥x轴,垂足为A.反比例函数y=的图象经过点B,交AC于点E.已知菱形的边长为,AC=4.(1)若OA=4,求k的值;(2)连接OD,若AE=AB,求OD的长.26.如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=(k>0)的图象经过BC边的中点D(3,1).(1)求这个反比例函数的表达式;(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.求OF的长.27.如图,反比例函数y=(x>0,k是常数)的图象经过A(1,3),B(m,n),其中m>1.过点B作y轴的垂线,垂足为C.连接AB,AC,△ABC的面积为.(1)求k的值和直线AB的函数表达式:(2)过线段AB上的一点P作PD⊥x轴于点D,与反比例函数y=(x>0,k是常数)的图象交于点E,连接OP,OE,若△POE的面积为1,求点P的坐标.28.如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).(1)求点C的坐标;(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.29.如图,△AOB的边OB在x轴上,且∠ABO=90°反比例函数的图象与边AO、AB分别相交于点C、D,连接BC.已知OC=BC,△BOC的面积为12.(1)求k的值;(2)若AD=6,求直线OA的函数表达式.30.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线y=在第一象限内交于点C(1,m).(1)求m和n的值;(2)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y=交于点P、Q,且PQ=2QD,求△APQ的面积.31.如图,函数y=x与函数y=(x>0)的图象相交于点A(n,4).点B在函数y=(x>0)的图象上,过点B作BC∥x轴,BC与y轴相交于点C,且AB=AC.(1)求m、n的值;(2)求直线AB的函数表达式.32.如图,反比例函数y=的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.33.如图,在平面直角坐标系xOy中,正比例函数y=10x与反比例函数y=交于点A,点A的横坐标为,反比例函数y=图象上有一点B,过点B作BC∥x轴,过点A作AC⊥BC,垂足为点C.(1)求k的值;(2)已知点B在AC的右侧,若△ABC的面积为4,求直线AB的解析式.34.已知点P(m,n)是反比例函数y=(x>0)的图象上的一动点,P A∥x轴,PB∥y 轴,分别交反比例函数y=(x>0)的图象于点A,B,点C是直线y=2x上的一点.(1)点A的坐标为(,),点B的坐标为(,);(用含m的代数式表示)(2)在点P运动的过程中,连接AB,证明:△P AB的面积是一个定值,并求出这个定值;(3)在点P运动的过程中,以点P,A,B,C为顶点的四边形能否为平行四边形?若能,求出此时m的值;若不能,请说明理由.答案与解析一.选择题(共10小题)1.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=()A.B.C.D.12【分析】所给的三角形面积等于长方形面积减去三个直角三角形的面积,然后即可求出B 的横纵坐标的积即是反比例函数的比例系数.【解答】解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b),∵点D,E在反比例函数的图象上,∴=k,∴E(a,),∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣﹣k﹣•(b﹣)=9,∴k=,故选:C.【点评】此题考查了反比例函数的综合知识,利用了:①过某个点,这个点的坐标应适合这个函数解析式;②所给的面积应整理为和反比例函数上的点的坐标有关的形式.2.如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数y=在第二象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为()A.12B.10C.8D.6【分析】设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(b﹣a,a+b),再根据反比例函数图象上点的坐标特征得(a+b)•(b﹣a)=8,因为S正方形AOBC=a2,S正方=b2,从而求得正方形AOBC和正方形CDEF的面积之差为8.形CDEF【解答】解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(b﹣a,a+b),∴(a+b)•(b﹣a)=﹣8,整理为a2﹣b2=8,∵S正方形AOBC=a2,S正方形CDEF=b2,∴S正方形AOBC﹣S正方形CDEF=8,故选:C.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k ≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=|k|;也考查了正方形的性质.3.如图,平行四边形ABCO的顶点B在双曲线y=上,顶点C在双曲线y=上,BC中点P恰好落在y轴上,已知S▱OABC=10,则k的值为()A.﹣8B.﹣6C.﹣4D.﹣2【分析】连接BO,过B点和C点分别作y轴的垂线段BE和CD,证明△BEP≌△CDP (AAS),则△BEP面积=△CDP面积;易知△BOE面积=×6=3,△COD面积=|k|.由此可得△BOC面积=△BPO面积+△CPD面积+△COD面积=3+|k|=10,解k 即可,注意k<0.【解答】解:连接BO,过B点和C点分别作y轴的垂线段BE和CD,∴∠BEP=∠CDP,又∠BPE=∠CPD,BP=CP,∴△BEP≌△CDP(AAS).∴△BEP面积=△CDP面积.∵点B在B在双曲线y=上,所以△BOE面积=×6=3.∵点C在双曲线y=上,且从图象得出k<0,∴△COD面积=|k|.∴△BOC面积=△BPO面积+△CPD面积+△COD面积=3+|k|.∵四边形ABCO是平行四边形,∴平行四边形ABCO面积=2×△BOC面积=2(3+|k|),∴2(3+|k|)=10,解得k=±4,因为k<0,所以k=﹣4.故选:C.【点评】本题主要考查了反比例函数k的几何意义、平行四边形的面积,解决这类问题,要熟知反比例函数图象上点到y轴的垂线段与此点与原点的连线组成的三角形面积是k.4.如图,平行四边形ABCD的顶点A的坐标为(﹣,0),顶点D在双曲线y=(x>0)上,AD交y轴于点E(0,2),且四边形BCDE的面积是△ABE面积的3倍,则k的值为()A.4B.6C.7D.8【分析】连结BD,由四边形EBCD的面积是△ABE面积的3倍得平行四边形ABCD的面积是△ABE面积的4倍,根据平行四边形的性质得S△ABD=2S△ABE,则AD=2AE,即点E为AD的中点,E点坐标为(0,2),A点坐标为(﹣,0),利用线段中点坐标公式得D点坐标为,再利用反比例函数图象上点的坐标特征得k的值.【解答】解:如图,连结BD,∵四边形EBCD的面积是△ABE面积的3倍,∴平行四边形ABCD的面积是△ABE面积的4倍,∴S△ABD=2S△ABE,∴AD=2AE,即点E为AD的中点,∵E点坐标为(0,2),A点坐标为(﹣,0),∴D点坐标为(,4),∵顶点D在双曲线y=(x>0)上,∴k=×4=6,故选:B.【点评】本题考查了反比例函数图象上点的坐标特点,以及平行四边形的性质,关键是正确分析出S△ABD=2S△ABE.5.如图,在平面直角坐标系xOy中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣3,4),反比例函数y=的图象与菱形对角线AO交于D 点,连接BD,当BD⊥x轴时,k的值是()A.B.C.﹣12D.【分析】先利用勾股定理计算出OC=5,再利用菱形的性质得到AC=OB=OC=5,AC ∥OB,则B(﹣5,0),A(﹣8,4),接着利用待定系数法确定直线OA的解析式为y=﹣x,则可确定D(﹣5,),然后把D点坐标代入y=中可得到k的值.【解答】解:∵C(﹣3,4),∴OC==5,∵四边形OBAC为菱形,∴AC=OB=OC=5,AC∥OB,∴B(﹣5,0),A(﹣8,4),设直线OA的解析式为y=mx,把A(﹣8,4)代入得﹣8m=4,解得m=﹣,∴直线OA的解析式为y=﹣x,当x=﹣5时,y=﹣x=,则D(﹣5,),把D(﹣5,)代入y=,∴k=﹣5×=﹣.故选:B.【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了菱形的性质.6.如图,A、C两点在反比例函数y=的图象上,B、D两点在反比例函数y=的图象上,AB⊥x轴于点E,CD⊥x轴于点F,AB=3,CD=2,EF=,则k1﹣k2的值为()A.﹣3B.﹣2C.D.﹣1【分析】直接利用反比例函数的性质和k的意义分析得出答案.【解答】解:过点A作AM⊥y轴,BN⊥y轴,DQ⊥y轴,CN⊥y轴垂足分别为M,N,Q,R,由题意可得:S矩形AMEQ=S矩形FCRO=﹣k1,S矩形EBNO=S矩形QDFO=k2,则S矩形AMEQ+S矩形EBNO=S矩形FCRO+S矩形QDFO=﹣k1+k2,∵AB=3,CD=2,∴设EO=2x,则FO=3x,∵EF=,∴EO=1,FO=1.5,∴S矩形ABNM=1×3=3,则﹣k1+k2=3,故k1﹣k2=﹣3.故选:A.【点评】此题主要考查了反比例函数图象上点的坐标性质,正确得出EO,FO的长是解题关键.7.如图,正方形ABCD的顶点B、C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过点A(m,2)和CD边上的点E(n,),过点E作直线l∥BD交y轴于点F,则点F的坐标是()A.(0,﹣)B.(0,﹣)C.(0,﹣3)D.(0,﹣)【分析】由A(m,2)得到正方形的边长为2,则BC=2,所以n=2+m,根据反比例函数图象上点的坐标特征得到k=2•m=(2+m),解得m=1,则A(1,2),B(1,0),D(3,2),E(3,),然后利用待定系数法确定直线BD的解析式,再根据平行线的性质和E的坐标求得直线l的解析式,求x=0时对应函数的值,从而得到点F的坐标.【解答】解:∵正方形的顶点A(m,2),∴正方形的边长为2,∴BC=2,而点E(n,),∴n=2+m,即E点坐标为(2+m,),∴k=2•m=(2+m),解得m=1,∴A(1,2),E(3,),∴B(1,0),D(3,2),设直线BD的解析式为y=ax+b,把B(1,0),D(3,2)代入得,解得,∵过点E作直线l∥BD交y轴于点F,∴设直线l的解析式为y=x+q,把E(3,)代入得3+q=,解得q=﹣,∴直线l的解析式为y=x﹣当x=0时,y=﹣,∴点F的坐标为(0,﹣),故选:A.【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式.8.在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为()A.(,0)B.(2,0)C.(,0)D.(3,0)【分析】过点B作BD⊥x轴于点D,易证△ACO≌△BCD(AAS),从而可求出B的坐标,进而可求出反比例函数的解析式,根据解析式与A的坐标即可得知平移的单位长度,从而求出C的对应点.【解答】解:过点B作BD⊥x轴于点D,∵∠ACO+∠BCD=90°,∠OAC+∠ACO=90°,∴∠OAC=∠BCD,在△ACO与△BCD中,∴△ACO≌△BCD(AAS)∴OC=BD,OA=CD,∵A(0,2),C(1,0)∴OD=3,BD=1,∴B(3,1),∴设反比例函数的解析式为y=,将B(3,1)代入y=,∴k=3,∴y=,∴把y=2代入,∴x=,当顶点A恰好落在该双曲线上时,此时点A移动了个单位长度,∴C也移动了个单位长度,此时点C的对应点C′的坐标为(,0)故选:A.【点评】本题考查反比例函数的综合问题,涉及全等三角形的性质与判定,反比例函数的解析式,平移的性质等知识,综合程度较高,属于中等题型.9.如图,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2,△ADC与△ABC关于AC所在的直线对称.若点A和点D在同一个反比例函数y=的图象上,则OB的长是()A.2B.3C.2D.3【分析】作DE⊥x轴于E,根据三角函数值求得∠ACD=∠ACB=60°,即可求得∠DCE =60°,根据轴对称的性质得出CD=BC=2,解直角三角形求得CE=1,DE=,设A(m,2),则D(m+3,),根据系数k的几何意义得出k=2m=(m+3),求得m=3,即可得到结论.【解答】解:作DE⊥x轴于E,∵Rt△ABC中,∠ABC=90°,BC=2,AB=2,∴=,∴∠ACB=60°,∴∠ACD=∠ACB=60°,∴∠DCE=180°﹣60°﹣60°=60°,∵CD=BC=2,∴CE=CD=1,DE=CD=,设A(m,2),则D(m+3,),∵k=2m=(m+3),解得m=3,∴OB=3,故选:B.10.如图,点A是射线y═(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=交CD边于点E,则的值为()A.B.C.D.1【分析】设点A的横坐标为m(m>0),则点B的坐标为(m,0),把x=m代入y=x得到点A的坐标,结合正方形的性质,得到点C,点D和点E的横坐标,把点A的坐标代入反比例函数y=,得到关于m的k的值,把点E的横坐标代入反比例函数的解析式,得到点E的纵坐标,求出线段DE和线段EC的长度,即可得到答案.【解答】解:设点A的横坐标为m(m>0),则点B的坐标为(m,0),把x=m代入y=x得:y=m,则点A的坐标为:(m,m),线段AB的长度为m,点D的纵坐标为m,∵点A在反比例函数y=上,∴k=m2,即反比例函数的解析式为:y=,∵四边形ABCD为正方形,∴四边形的边长为m,点C,点D和点E的横坐标为m+m=m,把x=m代入y=得:y=m,即点E的纵坐标为m,则EC=m,DE=m﹣m=m,=,故选:A.【点评】本题考查了反比例函数图象上的点的坐标特征和正方形的性质,正确掌握代入法和正方形的性质是解题的关键.二.填空题(共13小题)11.如图,直线y=﹣2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=在第一象限经过点D.则k=3.【分析】作DE⊥x轴,垂足为E,连OD.证出△BOA≌△AED,得到AE=BO,AO=DE,从而求出S△DOE,根据反比例函数k的几何意义,求出k的值.【解答】解:作DE⊥x轴,垂足为E,连OD.∵∠DAE+∠BAO=90°,∠OBA+∠BAO=90°,∴∠DAE=∠OBA,又∵∠BOA=∠AED,AB=DA,∴△BOA≌△AED(HL),∴OA=DE.∵y=﹣2x+2,可知B(0,2),A(1,0),∴OA=DE=1,∴OE=OA+AE=1+2=3,∴S△DOE=•OE•DE=×3×1=,∴k=×2=3.故答案为:3.【点评】本题主要考查了反比例函数k的几何意义,构造△BOA≌△AED是解题的关键.12.如图,直线y=﹣x+b与双曲线y=(x>0)交于A、B两点,与x轴、y轴分别交于E、F两点,AC⊥x轴于点C,BD⊥y轴于点D,当b=2时,△ACE、△BDF与△ABO面积的和等于△EFO面积的.【分析】△ACE、△BDF与△ABO面积的和等于△EFO面积的,即S△OBD+S△AOC=S,根据反比例函数的解析式与三角形的面积的关系即可求解.△EOF【解答】解:直线y=﹣x+b中,令x=0,解得:y=b,则OF=b;令y=0,解得:x=b,则OE=b.则S△EOF=OE•OF=b2.∵S△OBD=S△AOC=,又∵△ACE、△BDF与△ABO面积的和等于△EFO面积的,∴S△OBD+S△AOC=S△EOF,即:×b2=1,解得:b=±2(﹣2舍去),∴b=2.故答案是:2.【点评】本题主要考查了反比例函数中k的几何意义,正确理解△ACE、△BDF与△ABO 面积的和等于△EFO面积的,即S△OBD+S△AOC=S△EOF是解题的关键.13.如图,两个反比例函数y=和y=在第一象限的图象如图所示,当P在y=的图象上,PC⊥x轴于点C,交y=的图象于点A,PD⊥y轴于点D,交y=的图象于点B,则四边形P AOB的面积为1.【分析】此题所求的四边形P AOB的面积可由分割法,S四边形P AOB=S□PCOD﹣S△DBO﹣S△ACO.【解答】解:由于P点在y=上,则S□PCOD=2,A、B两点在y=上,则S△DBO=S△ACO=×1=.∴S四边形P AOB=S□PCOD﹣S△DBO﹣S△ACO=2﹣﹣=1.∴四边形P AOB的面积为1.故答案为:1.【点评】本题考查了反比例函数k的几何意义,|k|可以表示为图象上一点到两坐标轴作垂线所围成的矩形的面积.14.y=kx﹣6的图象与x,y轴交于B、A两点,与的图象交于C点,CD⊥x轴于D点,如果△CDB的面积:△AOB的面积=1:9,则k=4.【分析】由于△CDB的面积:△AOB的面积=1:9,且两三角形相似,则=,C(,2)代入直线y=kx﹣6求得k值.【解答】解:由题意得:△CDB的面积:△AOB的面积=1:9,且两三角形相似,则=,又A(0,﹣6),则C(,2),代入直线y=kx﹣6,可得:k=4.故答案为:4.【点评】本题考查了反比例函数系数k的几何意义,这里相似三角形的相似比是解决问题的突破口.15.如图,A、B是第二象限内双曲线y=上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为﹣4.【分析】分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x 轴于点E,由于反比例函数的图象在第二象限,所以k<0,由点A是反比例函数图象上的点可知,S△AOD=S△AOF=,再由A、B两点的横坐标分别是a、2a可知AD=2BE,故点B是AC的二等分点,故DE=a,CE=a,所以S△AOC=S梯形ACOF﹣S△AOF=6,故可得出k的值.【解答】解:分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,∵反比例函数y=的图象在第二象限,∴k<0,∵点A是反比例函数图象上的点,∴S△AOD=S△AOF=,∵A、B两点的横坐标分别是a、2a,∴AD=2BE,∴点B是AC的二等分点,∴DE=a,CE=a,∴S△AOC=S梯形ACOF﹣S△AOF=(OE+CE+AF)×OF﹣=×4a×﹣=6,解得k=﹣4,故答案为:﹣4.【点评】本题考查的是反比例函数系数k的几何意义,根据题意得出辅助线得出S△AOC =S梯形ACOF﹣S△AOF=6是解答此题的关键.16.如图,点A、B在反比例函数y=(k≠0)的图象上,过点A、B作x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C.若OM=MN=NC,△AOC的面积为9,则k 的值为6.【分析】根据三角形面积公式得到S△AOM=S△AOC=3,再根据反比例函数的比例系数k 的几何意义得到S△AOM=|k|=3,然后利用k>0去绝对值求解.【解答】解:∵OM=MN=NC,∴S△AOM=S△AOC=×9=3,∴S△AOM=|k|=3,而k>0,∴k=6.故答案为6.【点评】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.17.如图,A,B是反比例函数y=(x>0)图象上的两点,过点A作AP∥y轴,过点B 作BP∥x轴,交点为P连接OA,OP,若△AOP的面积为2,则△ABP的面积为4.【分析】根据反比例函数特征,设A(m,),B(n,),根据题意可得AP=﹣,且A点到y轴的距离为m,依据已知△AOP的面积为2,得到m和n的关系式n=3m,计算△ABP面积=AP×BP,即可得到结果.【解答】解:设A(m,),B(n,),根据题意可得AP=﹣,且A点到y轴的距离为m,则AP×m=(﹣)×m=2,整理得,所以n=3m,B点坐标可以表示为(3m,)△ABP面积=AP×BP=(﹣)×(3m﹣m)=4.故答案为4.【点评】本题主要考查了反比例函数图象上点的坐标特征,解决此类型问题,一般设某个点坐标为(x,),而后用横纵坐标的绝对值表示线段的长度.18.如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B在第一象限,四边形OABC是矩形,反比例函数y=(x>0)与AB相交于点D,与BC 相交于点E,若BE=3CE,四边形ODBE的面积是9,则k=3.【分析】把所给的四边形面积分割为长方形面积减去两个直角三角形的面积,然后即可求出B的横纵坐标的积即是反比例函数的比例系数.【解答】解:设B点的坐标为(a,b),∵BE=3CE,∴E的坐标为(,b),又∵E在反比例函数y=的图象上,∴k=,∵S四边形ODBE=9,∴S矩形ABCD﹣S△OCE﹣S△OAD=9,即ab﹣﹣=9,∴ab=12,∴k==3.故答案为:3.【点评】此题考查了反比例函数的综合知识,利用了:①过某个点,这个点的坐标应适合这个函数解析式;②所给的面积应整理为和反比例函数上的点的坐标有关的形式.19.如图,已知点A是一次函数y=x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=(x>0)的图象过点B,C,若△OAB的面积为8,则△ABC的面积是.【分析】过C作CD⊥y轴于D,交AB于E,设AB=2a,根据直角三角形斜边中线是斜边一半得:BE=AE=CE=a,设A(x,x),则B(x,x+2a),C(x+a,x+a),因为B、C都在反比例函数的图象上,列方程可得结论.【解答】解:如图,过C作CD⊥y轴于D,交AB于E.∵AB⊥x轴,∴CD⊥AB,∵△ABC是等腰直角三角形,∴BE=AE=CE,设AB=2a,则BE=AE=CE=a,设A(x,x),则B(x,x+2a),C(x+a,x+a),∵B,C在反比例函数的图象上,∴x(x+2a)=(x+a)(x+a),解得x=a,∵S△OAB=AB•DE=•2a•x=8,∴ax=8,∴a2=8,∴a2=,∵S△ABC=AB•CE=•2a•a=a2=.故答案为:.【点评】本题考查了反比例函数图象上点的坐标特征、等腰直角三角形的性质、三角形面积,熟练掌握反比例函数上的点符合反比例函数的关系式是关键.20.如图在平面直角坐标系中,周长为12的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上.点B,在反比例函数y=位于第一象限的图象上.则k的值为k=.【分析】分析题意,要求k的值,结合图形只需求出点B的坐标即可;设y轴与BC的交点为M,连接OB,根据周长为12的正六边形ABCDEF的对称中心与原点O重合可知OB=2,BM=1,OM⊥BC;接着,利用直角三角形勾股定理求出OM的值,结合点B在反比例函数位于第一象限的图象上,可以得到点B的坐标;【解答】解:如图,连接OB∵周长为12的正六边形ABCDEF的对称中心与原点O重合,∴正六边形ABCDEF的边长为2,∴OB=2,BM=1,∵OM⊥BC,∴OM===•点B在反比例函数y=位于第一象限的图象上,点B的坐标为(1,).将点(1,)代入y=中,得k=.故故答案为k=【点评】本题考查了正多边形性质,锐角三角函数,反比例函数的性质,等边三角形的性质和判定的应用,关键是求出B的坐标.21.如图,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=(k>0,x>0)的图象上,点D的坐标为(4,3).则k的值为32.【分析】根据题意可以求得菱形的边长,从而可以求得点A的坐标,进而求得k的值.【解答】解:由题意可得,点D的坐标为(4,3),∴CD=5,∵四边形ABCD是菱形,∴AD=CD=5,∴点A的坐标为(4,8),∵点A在反比例函数y=(k>0,x>0)的图象上,∴8=,得k=32,故答案为:32.【点评】本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用反比例函数的性质解答.22.如图,已知反比例函数y=在第一象限内的图象上一点A,且OA=4,AB⊥x轴,垂足为B,线段OA的垂直平分线交x轴于点C(点C在点B的左侧),则△ABC的周长等于2.【分析】根据线段垂直平分线的性质可知AC=OC,由此推出△ABC的周长=OB+AB,设OB=a,AB=b,根据勾股定理和函数解析式即可得到关于a、b的方程组,解之即可求出△ABC的周长.【解答】解:∵OA的垂直平分线交OB于C,∴AC=OC,∴△ABC的周长=OB+AB,设OB=a,AB=b,则:,解得a+b=2,即△ABC的周长=OB+AB=2.故答案是:2.【点评】本题考查反比例函数图象性质和线段中垂线性质,以及勾股定理的综合应用,关键是一个转换思想,即把求△ABC的周长转换成求OB+AB即可解决问题.23.如图,正方形ABCD位于第一象限,边长为3,横坐标为1的点A在直线y=x上,正方形ABCD的边分别平行于x轴、y轴.若双曲线y=与正方形ABCD公共点,则k的取值范围是1≤k≤16.【分析】根据题意求出点A的坐标,根据正方形的性质求出点C的坐标,根据反比例函数图象上点的坐标特征解答即可.【解答】解:∵点A在直线y=x上,横坐标为1,∴点A的坐标为(1,1),∵正方形ABCD的边长为3,∴点C的坐标为(4,4),当双曲线y=经过点A时,k=1×1=1,当双曲线y=经过点C时,k=4×4=16,∴双曲线y=与正方形ABCD公共点,则k的取值范围是1≤k≤16,故答案为:1≤k≤16.【点评】本题考查的是反比例函数与一次函数的交点问题以及正方形的性质,掌握反比例函数图象上点的坐标特征、以及正方形的性质是解题的关键.三.解答题(共21小题)24.如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴的正半轴上,AB=8,BC =6.对角线AC,BD相交于点E,反比例函数(x>0)的图象经过点E,分别与AB,CD交于点F,G.(1)若OC=8,求k的值;(2)连接EG,若BF﹣BE=2,求△CEG的面积.【分析】(1)先利用矩形的性质和线段中点坐标公式得到E(5,4),然后把E点坐标代入y=可求得k的值;(2)利用勾股定理计算出AC=10,则BE=EC=5,所以BF=7,设OB=t,则F(t,7),E(t+3,4),利用反比例函数图象上点的坐标得到7t=4(t+3),解得t=4,从而得到反比例函数解析式为y=,然后确定G点坐标,最后利用三角形面积公式计算△CEG的面积.【解答】解:(1)∵在矩形ABCD的顶点B,AB=8,BC=6,而OC=8,∴B(2,0),A(2,8),C(8,0),∵对角线AC,BD相交于点E,∴点E为AC的中点,∴E(5,4),把E(5,4)代入y=得k=5×4=20;(2)∵AC==10,∴BE=EC=5,∵BF﹣BE=2,∴BF=7,设OB=t,则F(t,7),E(t+3,4),∵反比例函数(x>0)的图象经过点E、F,∴7t=4(t+3),解得t=4,。
苏教版八年级下册数学压轴题(非常好的题目)之欧阳育创编
压轴题精选时间:2021.02.04创作:欧阳育1、如图,在平面直角坐标系内,已知点A (0,6)、点B (8,0),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动,同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动,设点P 、Q 移动的时间为t 秒.⑴求直线AB 的解析式;⑵当t 为何值时,△APQ 与△AOB 相似? 2、“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB 置于直角坐标系中,边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ,以P 为圆心、以2OP 为半径作弧交图象于点R .分别过点P 和R 作x 轴和y 轴的平行线,两直线相交于点M ,连接OM 得到∠MOB ,则∠MOB=31∠AOB .要明白帕普斯的方法,请研究以下问题:(1)设)1,(a a P 、)1,(b b R ,求直线OM 对应的函数表达式(用含b a ,的代数式表示).(2)分别过点P 和R 作y 轴和x 轴的平行线,两直线相交于点Q .请说明Q 点在直线OM 上,并据此证明∠MOB=31∠AOB .3、(14分)如图,在平面直角坐标系xOy 中,矩形OEFG 的顶点E坐标为(4,0),顶点G 坐标为(0,2).将矩形OEFG 绕点O 逆时针旋y xO P QA B转,使点F 落在轴的点N 处,得到矩形OMNP ,OM 与GF 交于点A .(1)判断△OGA 和△OMN 是否相似,并说明理由;(2)求过点A 的反比例函数解析式;(3)设(2)中的反比例函数图象交EF 于点B ,求直线AB 的解析式;(4)请探索:求出的反比例函数的图象,是否经过矩形OEFG 的对称中心,并说明理由.4、如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象经过点()0,2B ,且与x轴的正半轴相交于点A ,点P 、点Q 在线段AB 上,点M 、N 在线段AO 上,且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形,90OPM MQN ∠=∠=。
2019-2020学年苏科版八年级下册期末数学压轴题考前精练1(含解析)
2020年八年级期末数学压轴题考前精练1一、选择题(共6题) 1.下列说法:①一组对边平行,另一组对边相等的四边形是平行四边形; ②两条对角线相等且互相平分的四边形是矩形;③在反比例函数y=中,如果自变量x <2时,那么函数值y >2. 其中正确的有( )A .0个B .1个C .2个D .3个2.如图,平行四边形ABCD 的顶点A 的坐标为(-,0),顶点D 在双曲线y=(x >0)上,AD 交y 轴于点E (0,2),且四边形BCDE 的面积是△ABE 面积的3倍,则k 的值为( )A .4B .6C .7D .83.如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH 是菱形,则四边形ABCD 只需要满足一个条件,是( )A .四边形ABCD 是梯形B .四边形ABCD 是菱形C .对角线AC=BDD .AD=BC第3题 第4题4.如图,将矩形ABCO 放在直角坐标系中,其中顶点B 的坐标为(10, 8),E 是BC 边上一点将△ABE 沿AE 折叠,点B 刚好与OC 边上点D 重合,过点E 的反比例函数y=k x的图象与边AB 交于点F , 则线段AF的长为 ( ) A .154B. 2 C .158D .325.在平面直角坐标系中,分别过点A (m ,0),B (m +2,0)作垂直于x 轴的直线l 1和l 2,探究直线 l 1、l 2与函数y=x3的图像(双曲线)之间的关系,下列结论错误的是( ) A.两条直线中总有一条与双曲线相交B.当 m =1 时,两条直线与双曲线的交点到原点的距离相等C.当 m <0 时,两条直线与双曲线的交点都在 y 轴左侧D.当 m >0 时,两条直线与双曲线的交点都在 y 轴右侧6.如图,正方形ABCD 的边长为3,E 、F 是对角线BD 上的两个动点,且EF =2,连接AE 、AF ,则 AE+AF 的最小值为 ( )A .52B .32 C.29 D.522二、填空题(共6题)1.如图,在Rt △ABC 中,∠ABC=90°,AB=BC=,将△ABC 绕点C 逆时针旋转60°,得到△MNC ,连接BM ,则BM 的长是______.第3题 第4题2.如图,E ,F 是正方形ABCD 的边AD 上两个动点,满足AE=DF .连接CF 交BD 于点G ,连接BE 交AG 于点H .若正方形的边长为2,则线段DH 长度的最小值是______.3.如图,正方形ABCD 的边长为2,顶点A 在x 轴上,顶点B 在y 轴上,则OD 的最大值是第3题 第4题4.如图,在菱形ABCD 中,∠ABC =120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B 、D 重合),折痕为EF ,若BC =4,BG =3,则GE 的长为 .5.如图,点A 、B 都在反比例函数y=xk(x >0)的图像上,过点B 作BC ∥x 轴交y 轴于点C ,连接AC 并延长交x 轴于点D ,连接BD ,DA =3DC ,S △ABD =6.则k 的值为.6.如图,矩形ABCD 中,点 E 、F 分别在AB 、CD 上,EF ∥BC ,EF 交BD 于点G .若EG =5,DF =2,则图中两块阴影部分的面积之和为.第5题第6题三、解答题(共6题)1.“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:(1)A型自行车去年每辆售价多少元?(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?2.实践操作在矩形ABCD 中,AB =4,AD =3,现将纸片折叠,点D 的对应点记为点P ,折痕为EF (点E 、F 是折痕与矩形的边的交点),再将纸片还原. 初步思考(1)若点P 落在矩形ABCD 的边AB 上(如图①)① 当点P 与点A 重合时,∠DEF = ▲ °;当点E 与点A 重合时,∠DEF = ▲ °; ② 当点E 在AB 上,点F 在DC 上时(如图②), 求证:四边形DEPF 为菱形,并直接写出....当AP =3.5时的菱形EPFD 的边长.深入探究 (2)若点P 落在矩形ABCD 的内部(如图③),且点E 、F 分别在AD 、DC 边上,请直接写出AP 的最小值 .拓展延伸(3)若点F 与点C 重合,点E 在AD 上,线段BA 与线段FP 交于点M (如图④).在各种不同的折叠位置中,是否存在某一情况,使得线段AM 与线段DE 的长度相等?若存在,请直接写出线段AE 的长度;若不存在,请说明理3.如图,正方形 ABCD 中,AB =4,点 E 为边AD 上一动点,连接 CE ,以 CE 为边,作正方形CEFG (点D 、F 在CE 所在直线的同侧),H 为CD 中点,连接 FH .(1)如图 1,连接BE ,BH ,若四边形 BEFH 为平行四边形,求四边形 BEFH 的周长; (2)如图 2,连接 EH ,若 AE =1,求△EHF 的面积; (3)直接写出点E 在运动过程中,HF 的最小值.A PB FECD(第6题①) P A BF E C D(第6题③) (第6题②)A PB FE CD(第6题④) M EC (F ) DA PB4.如图,直线1y k x =(x ≥0)与双曲线2k y x=(x >0)相交于点P (2,4).已知点A (4,0),B (0,3),连接AB ,将Rt △AOB 沿OP 方向平移,使点O 移动到点P ,得到△A 'PB '.过点A '作A 'C ∥y 轴交双曲线于点C .(1)求k1和k2的值(2)求直线PC 的表达式;(3)直接写出线段AB 扫过的面积.5.某服装店进货一批甲、乙两种款型的时尚T 恤衫,甲种款型共花了 10400 元,乙种款型共花了6400元,甲种款型的进货件数是乙种款型进货件数的2倍,甲种款型每件的进货价比乙种款型每件的进货价少30元.商店将这两种T 恤衫分别按进货价提高60%后进行标价销售,销售一段时间后,甲种款型全部售完,乙种款型剩余一半.商店对剩下的乙种款型T 恤衫按标价的五折进行降价销售,很快全部售完. (1)甲、乙两种款型的T 恤衫各进货多少件?(2)求该商店售完这批T 恤衫共获利多少元?(获利=销售收入-进货成本)6.如图,在平面直角坐标系xoy 中,矩形OABC 的顶点B 坐标为)5,12(,点D 在CB 边上从点C 运动到点B ,以AD 为边作正方形ADEF ,连BF BE 、,在点D 运动过程中,请探究以下问题: (1)ABF △的面积是否改变,如果不变,求出该定值;如果改变,请说明理由; (2)若BEF △为等腰三角形,求此时正方形ADEF 的边长;(3)设),(y x E ,直接写出y 关于x 的函数关系式及自变量x 的取值范围.【答案与解析】一、选择题1. 解:①一组对边平行,另一组对边相等的四边形是可能是等腰梯形,故错误;②两条对角线相等且互相平分的四边形是矩形,正确;③在反比例函数y=中,如果自变量x<2时,那么函数值y>2或y<0,故错误,正确的有1个,故选:B.2.3.4.5.6.二、填空题1.2.3.4.5.6.三、解答题1、(1)设去年A型车每辆售价x元,则今年售价每辆为(x-200)元,由题意,得80000x=80000×(1−10%)x−200解得:x=2000,经检验,x=2000是原方程的根,答:去年A型车每辆售价2000元;(2)设今年新进A型车a辆,则B型车(60-a)辆,获利y元,由题意,得y=(2000-200-1500)a+(2400-1800)(60-a)=-300a+36000.∵B型车的进货数量不超过A型车数量的两倍,∴60-a≤2a,∴a≥20.∵y=-300a+36000,∴k=-300<0,∴y随a的增大而减小,∴a=20时,y最大=30000元,∴B型车的数量为:60-20=40(辆).答:当新进A型车20辆,B型车40辆时,这批车获利最大.2.⑴①90;45②由折叠可知,DE=DF ,PE=PF ,∠EDP=∠FDP ∵DF∥EP∴∠FDP=∠EPD ∴∠EDP=∠EPD ∴DE=PE∴DE=DF=PE=PF ∴DEPF 为菱形AP=3.5 时,设 AE=x ,则 PE=DE= 3.5 x则 2223+ 3.5-=x x (),8528x 解得 ,所以菱形边长为 85283.4.(2)最小值为1易知 AP + PF + FC ≥ AC ,当且仅当 A 、P 、F 、C 共线时取等号,由折叠,FP=FD ,所以 PF+FC=FD+FC=CD∴AP ≥ AC - CD = 1 ,即最小值为 1 (3)连接 EM ∵DE=EP=AM△EAM≌△MPE(HL )易证设 AE=x ,则 AM=DE= 3- x , 则 BM=x +1∵MP=EA=x,CP=CD=4 ∴MC= 4— x222(1)3(4)x x ++=-35x =解得5.6.6. 解:(1)作FH⊥AB交AB延长线于H∵正方形ADEF中,AD=AF,∠DAF=90°………1分∴∠DAH+∠F AH=90°∵∠H=90°∴∠F AH+∠AFH=90°∴∠DAH=∠AFH ………………………2分∵矩形OABC中,AB=5,∠ABD=90°∴∠ABD =∠H∴△ABD≌△FHA ………………3分∴FH=AB=5∴112555222AEFS AB FH=⨯=⨯⨯=…………4分(2)①当EB=EF时,作EG⊥CB∵正方形ADEF中,ED=EF∴ED=EB∴DB=2DG同(1)理得△ABD≌△GDE……………………5分GCABD Fx Oy E∴DG =AB =5 ∴ DB =10 ∴2255AD BD AB =+=…………………6分②当EB =BF 时,∠BEF =∠BFE∵正方形ADEF 中,ED =AF ,∠DEF =∠AFE =90° ∴∠BED =∠BF A ∴△ABF ≌△DBE ………………7分 ∴BD =AB =5 ∵矩形OABC 中,∠ABD =90° ∴ 2252AD BD AB =+=…………………8分③当FB =FE 时,作FQ ⊥AB 同理得BQ =AQ=52, BD =AQ=52,…………………9分 ∴22552AD BD AB =+=…………………10分 (3)22(517)y x x =-+≤≤……………………12分C AB DF xOyEOQ C AB DF xyE。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
1. 如图,在ABC △中,90BAC ∠=
,AD 是BC 边上的高,E 是BC 边上的一个动点(不与B C ,重
合),EF AB ⊥,EG AC ⊥,垂足分别为F G ,.
(1)求证:
EG CG
AD CD
=; (2)FD 与DG 是否垂直?若垂直,请给出证明;若不垂直,请说明理由; (3)当AB AC =时,FDG △为等腰直角三角形吗?并说明理由.
2.操作:如图①,点O 为线段MN 的中点,直线PQ 与MN 相交于点O ,请利用图①画出一对以点O 为对称中心的全等三角形.
根据上述操作得到的经验完成下列探究活动.
探究一:如图②,在四边形ABCD 中,AB DC ∥,E 为BC 边的中点,BAE EAF ∠=∠,AF 与DC 的延长线相交于点F .试探究线段AB 与AF CF ,之间的等量关系,并证明你的结论;
探究二:如图③,DE BC ,相交于点E ,BA 交DE 于点A ,且:1:2BE EC =,BAE EDF ∠=∠,
CF AB ∥.若51AB CF ==,,
求DF 的长度.
F
A
G
C
E
B
P O M N Q
图① A B E
F
C D
图②
D A
B E
F
C 图③
2
3.如图,在平面直角坐标系中,O 是坐标原点,点A 的坐标为()40-,,
点B 的坐标为()()00.b b >,P 是直线AB 上的一个动点,作PC x ⊥轴,垂足为.C 记点P 关于y 轴的对称点P ′(点P ′不在y 轴上),连结
PP P A P C ''′,,.设点P 的横坐标为.a (1)当3b =时,
①求直线AB 的解析式;
②若点P ′的坐标是
()1m -,,
求m 的值; (2)若点P 在第一象限,记直线AB 与P C ′
的交点为.D 当13P D DC =′∶∶时,求a 的值; (3)是否同时存在a b ,,使P CA △′为等腰直角三角形?若存在,请求出所有满足要求的a b ,的值;若不存在,请说明理由.
4.如图,在等腰梯形ABCD 中,AD BC ∥,5AB DC ==,6AD =,12BC =.动点P 从D 点出发
沿DC 以每秒1个单位的速度向终点C 运动,动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动.两点同时出发,当P 点到达C 点时,Q 点随之停止运动. (1)梯形ABCD 的面积等于 ;
(2)当PQ AB ∥时,P 点离开D 点的时间等于 秒; (3)当P Q C ,,三点构成直角三角形时,P 点离开D 点多少时间?
C B
3
5、 如图1,在平面直角坐标系中,等腰Rt △AOB 的斜边OB 在x 轴上,直线y=3x- 4经过等腰Rt △AOB 的直角顶点A ,交y 轴于C 点,双曲线k
y x
=也经过A 点。
(1)求点A 坐标; (2)求k 的值;
(3)若点P 为x 正半轴上一动点,在点A 的右侧的双曲线上是否存在一点M ,使得△PAM 是以点A 为直角顶点的等腰直角三角形。
若存在,求出点M 的坐标,若不存在,请说明理由。
(4)若点P 为x 负半轴上一动点,在点A 的左侧的双曲线上是否存在一点N ,使得△PAN 是以点A 为直角顶点的等腰直角三角形。
若存在,求出点N 的坐标,若不存在,请说明理由。
6、如图,在平面直角坐标系中,已知OA=12cm ,OB=6cm ,点P 从点O 开始沿OA 边向点A 以1厘米/
秒的速度移动,点Q 从点B 开始沿BO 边向点O 以1厘米/秒的速度移动,如果P 、Q 同时出发,用t 秒表示移动的时间(06t ≤≤),那么
(1)设△POQ 的面积为y (厘米2),求y 关于t(秒)的函数解析式;
(2)当t=3时,将△POQ 沿直线PQ 翻折后得到△PCQ ,试判断点C 是否落在直线AB 上,并说明理
由;
(3)当t 为何值时,以O 、P 、Q 为顶点的三角形与△AOB 相似?
备用图
4
7、阅读:如图1把两块全等的含45°的直角三角板ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,把三角板ABC 固定不动,让三角板DEF 绕点D 旋转,两边分别与线段AB 、BC 相交于点P 、Q,易说明△APD ∽△CDQ .
猜想(1):如图2,将含30°的三角板DEF (其中∠EDF=30°)的锐角顶点D 与等腰三角形ABC (其
中∠ABC = 120°)的底边中点O 重合,两边分别与线段AB 、BC 相交于点P 、Q .写出图中的相似三角形 (直接填在横线上); 验证(2):其它条件不变,将三角板DEF 旋转至两边分别与线段AB 的延长线、边BC 相交于点P 、Q .上述结论还成立吗?请你在图3上补全图形,并说明理由.
连结PQ ,△APD 与△DPQ 是否相似?为什么? 探究(3):根据(1)(2)的解答过程,你能将两三角板改为一个更为一般的条件,使得(1)
8、等腰△ABC ,AB=AC ,∠BAC=120°,P 为BC 的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P ,三角板绕P 点旋转.
(1)如图a ,当三角板的两边分别交AB 、AC 于点E 、F 时.求证:△BP E ~△CFP ;
(2)操作:将三角板绕点P 旋转到图b 情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F .
① 探究1:△BP E 与△CFP 还相似吗?(只需写出结论)
② 探究2:连结EF ,△BP E 与△PFE 是否相似?请说明理由;
E 图1
图2 D(O) B C
F
E P
Q
A 图3
A
C
B B
P
B
9、已知,如图,直线
39
22
y x
=+与x轴、y轴分别相交于A、B两点,与双曲线
k
y
x
=在第一象限内交于点C,
S△AOC=9。
(1)求S△AOB (2)求k的值
(3)D是双曲线
k
y
x
=上一点, DE垂直x轴于E,若以O、D、E为顶点的三角形与△AOB相似,试
求点D的坐标。
10.已知反比例函数
k
y
x
=与直线y=
1
4
x相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是
k
y
x
=
上的动点,过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交
k
y
x
=于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.(直接写出结
果).
5。
