用转化的策略解决问题练习题
用转化的策略解决问题
一、说教材
本单元是在学生已经学习了用画图和列表，以及列举、倒推、替换和假设等策略基础上进行教学的。本节课主要是让学生学会用转化的策略解决问题。转化是一种常见的、极其重要的解决问题的策略。通过转化能把较复杂的问题变成较简单的问题，把新问题变成旧问题。
二、说教学目标
本节课的教学目标拟定为：
四、说教学过程
分析本节课，纵观全程，既把平移，旋转运用到图形等积变化的问题中，又蕴涵探索图形面积公式的转化，还有计算小数乘法和分数除法时的转化，还有数量关系之间的转化等。通过回忆和交流，意识到转化是经常使用的策略，从而主动应用转化的策略解决问题。基于此，我采用以下步骤解决。
一、故事引入,感知策略。
数学是和生活密切联系的，课的开始，我先跟学生讲了一个爱迪生和他的助手测量灯泡体积的故事。助手花了几个小时的时间来计算灯泡的体积，也没有算出来，爱迪生能很快的算出来，让学生猜一猜爱迪生是用的什么方法？在本册书第28页的思考题中也有过把圆钢的体积转化成水的体积的经验，因而学生很容易接受，根据学生的回答，我适时小结：把灯泡的体积转化成水的体积，就是一种非常重要的解决问题的策略，叫做“转化”。通过有趣的故事引入教学，使学生感受策略的价值，激发学生的求知欲，并初步体会“转化”的策略。
四、回顾知识，体验转化。
为了进一步丰富学生对转化策略的认识，帮助学生进一步体会知识之间的联系。我让学生回忆以前学过的知识中，在哪些地方都运用到了转化的策略？我先给学生一个交流的机会，让他们把回忆的内容给小组成员说说，然后全班交流汇报。通过讨论交流学生会联想到圆柱的体积转化成长方体来计算，三角形转化成平行四边形计算面积，推导圆面积时，把圆面积转化成长方形等等……让学生具体说一说推导过程。边演示边叙述，比如……课件演示一句话概括。引导学生认识到在运用转化的策略解决问题的共同点：把新问题转化成熟悉的或者已经解决过的问题。这一环节的设计，有效地建立新旧知识之间联系，大量的学习材料，让学生感受到了转化的应用价值。
用转化的策略解决问题前置性学习单
《用转化的策略解决问题》前置性学习单班级小组姓名时间学习内容：书P71-72的例1、“试一试”和“练一练”、练习十四的第1 — 3题。
学习目标：1.通过阅读故事，能初步感受到使用转化的策略解决实际问题，并能运用这样的策略猜字谜。
2.通过学习例题，能感受到比较图形的大小，也可以运用转化的策略进行比较。
3.在理解转化策略的基础上，能够回顾以前在哪些数学知识中运用过这一策略。
学习重点：感受并理解转化的策略，初步掌握转化的方法和技巧。
学习难点：合理应用转化的策略解决问题上课时间：5月6日学习过程：一、阅读故事：阿普顿是美国普林斯顿大学数学系毕业的高材生，对没有大学文凭的爱迪生有点瞧不起。
有一次，爱迪生让他测算一只梨形灯泡的容积。
于是，他拿起灯泡，测出了他的直径高度，然后加以计算。
但是灯泡不具有规则形状：它像球形，又不像球形；像圆柱体，又不像圆柱体。
计算很复杂。
即使是近似处理也很繁琐。
他画了草图，在好几张白纸上写满了密密麻麻的数据算式，也没有算出来。
爱迪生等了很长时间，也不见阿普顿报告结果。
他走过来一看，便忍不住笑出了声，“你还是换种方法吧！”只见爱迪生取来一杯水。
轻轻地往阿普顿刚才反复测算的灯泡里倒满了水，然后把水倒进量筒，几秒种就测出了水的体积，当然也就算出了灯泡的容积。
这时羞红了脸的阿普顿傻呆呆地站在一旁，恨不得找条地缝钻下去。
这个故事让你想到了什么？二、猜字谜(根据谜面，各打一字)。
(1) 72 小时 (2) 15 天 (3) 100 厘米三、自主尝试：2.回顾：我们曾用转化的策略解决过哪些问题三、我的疑问： _____________________________________________________________课堂展示提升1. 交流阅读故事后的联想到什么？ 预设：（1）爱迪生是用转化的策略把不规则的灯泡转化成水的体积来计算的；（2）转化的策略非常神奇（3）像这样的用转化的策略解决问题还有“曹冲称象”、“阿基米德测皇冠”等。
五年级数学《用转化的策略解决问题》练习题(分课时)
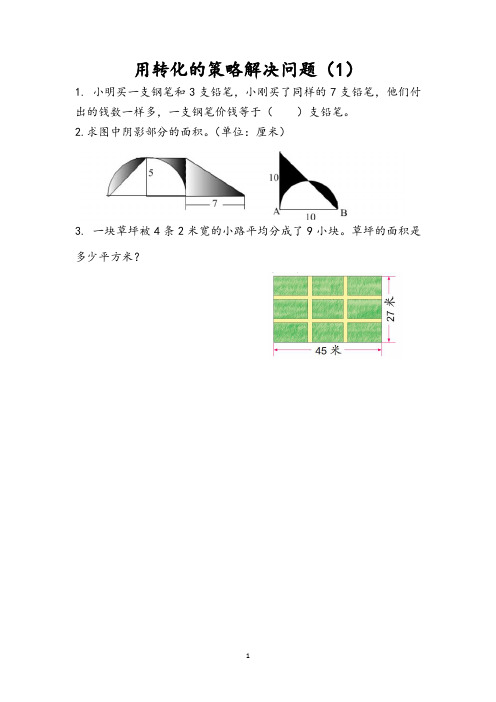
用转化的策略解决问题（1）1. 小明买一支钢笔和3支铅笔，小刚买了同样的7支铅笔，他们付出的钱数一样多，一支钢笔价钱等于（）支铅笔。
2.求图中阴影部分的面积。
（单位：厘米）3. 一块草坪被4条2米宽的小路平均分成了9小块。
草坪的面积是多少平方米？参考答案1. 42. 5×7=35（平方厘米） 10×（10÷2）÷2=25（平方厘米）3. 2×2=4（米）（45-4）×（27-4）=41×23=943（平方米）答：草坪的面积是943平方米。
用转化的策略解决问题（2）1.2.求图中阴影部分的面积。
（单位：厘米）3. 4个圆的直径都是2厘米，阴影部分的面积是多少平方厘米？1281641321161814121++++++参考答案1.2.5×（5×2）=50（平方厘米）3.14×62 ÷2=56.52 （平方厘米）3. 4×4+3.14×（4÷2）2×3=53.68（平方厘米） 答：阴影部分的面积是53.68平方厘米。
1281641321161814121++++++12812712811=-=练习十六1. 9998+998+98+8=2.求图中阴影部分的面积。
（单位：厘米）3.如图，平行四边形ABCD的底BC长是12厘米，线段FE长是4厘米，那么平行四边形中的阴影部分面积是多少平方厘米？参考答案1. 9998+998+98+8=10000+1000+100+10-2×4=111022.5×8=40（平方厘米）3. 12×4÷2×2=48（平方厘米）答：平行四边形中的阴影部分面积是48平方厘米。
用“转化”的策略解决问题
用“转化”的策略解决问题引言在人生和工作中，我们常常会遇到各种问题和挑战。
解决这些问题的关键在于找到合适的策略和方法。
其中，一种被广泛应用的策略是“转化”策略。
本文将介绍什么是“转化”，以及如何利用它来解决问题。
什么是“转化”“转化”是一种心理策略，指的是改变对问题或挑战的看法和态度，从而达到解决问题的目的。
当我们用“转化”策略来解决问题时，我们不再将问题视为难题或障碍，而是将其视为一个机会或挑战。
这种转变的心态能够帮助我们更加积极主动地面对问题，并找到更好的解决方案。
如何使用“转化”策略解决问题以下是一些使用“转化”策略解决问题的实践方法：1. 重新定义问题当我们面临一个问题时，我们可以尝试重新定义这个问题。
我们可以从不同的角度思考问题，并找到不同的解决方法。
例如，如果我们遇到了一个复杂的技术问题，我们可以尝试将其视为一个学习机会，通过解决这个问题来提升自己的技术能力。
2. 寻找机会即使在困难和挑战之中，我们也可以找到一些机会。
通过用“转化”策略来看待问题，我们可以发现问题背后隐藏着的机会。
例如，如果我们在工作中遇到了一个团队合作的问题，我们可以将其视为一个机会，来提升团队协作和沟通能力。
3. 探索不同的解决方案当我们改变对问题的看法后，我们也应该尝试探索不同的解决方案。
这可以帮助我们发现新的思路和方法。
例如，如果我们在项目管理中遇到了一个进度延迟的问题，我们可以尝试采用不同的方法来组织和管理项目，以提高效率和准确性。
4. 鼓励创新在问题解决过程中，我们应该鼓励创新和尝试新的方法。
有时候，传统的解决方法可能不再适用，我们需要有勇气尝试一些新的想法和策略。
例如，如果我们在市场营销中遇到了一个销售下滑的问题，我们可以尝试使用新的营销手段和渠道，来吸引更多的客户。
结论“转化”策略是一种重要的解决问题的方法。
通过改变对问题的看法和态度，我们可以更加积极主动地面对问题，并找到更好的解决方案。
尝试用“转化”策略来解决问题，你将会发现它的积极影响。
新苏教版六年级下册第三单元解决问题的策略练习【精品】
知识梳理模块一转化法解决问题的策略一、用转化的策略解决问题分数与比、除法有着密切的关系，在解决实际问题的过程中，可根据实际情况把分数问题转化为较为熟悉的知识解题，使计算更加得心应手。
二、用假设法解决实际问题1、先假设只有一种数量，再观察假设后原数量的变化关系，从而求出另一种量；2、用假设法解决问题就是通过对假设后数量关系变化情况的分析解决问题。
三、拓展提升1、根据两个量的关系推导出其他相关量的关系；2、已知两个量的差倍关系的实际问题；3、鸡兔同笼题型中的得失问题。
5例1 修路队修一条路，已经修了全长的6，还剩160 米没修。
已经修了多少米？2例2 已知甲校学生人数是乙校人数的53，甲校的女生人数是甲校学生人数的10，乙校的男生人数是乙校学生人数的21。
求两校女生人数占两校学生总人数的百分之几？50例3 甲、乙两袋糖的质量比是4:3，从甲袋中取出26 千克糖放入乙袋，这时两袋糖的质量比是5:7。
这两袋糖共有多少千克？变式1 爸爸将整理书籍的任务按5:3 的分配给了兄弟两人，结果哥哥整理了1440 本书，超额完成了20%，剩下的是由弟弟整理的。
弟弟整理了多少本书？模块二 假设法变式 2 妈妈买了一台电视机和一台冰箱，共花了 5400 元，冰箱的单价是电视机的 80%，电视机和冰箱的单价各是多少？变式 3 A 、B 两城相距 600 千米。
甲、乙两车分别从 A 、B 两城同时出发，相向而行，甲车的速度是乙车 3 的 。
相遇时甲、乙两车各行驶了多少千米？ 7例 4 小阳有 1 角、5 角的硬币共 5 枚，一共一元 7 角。
那么 1 角、5 角的硬币各有多少枚？例 5 一名篮球运动员在一场比赛中一共投中 12 个球，有 2 分球，也有 3 分球。
已知这名运动员一共得分 33 分，他投中 2 分球和 3 分球各有多少个？例 6 六年级有 8 名学生进行乒乓球比赛，如果每两名学生之间都进行一场比赛，那么一共要比赛多少场？变式 4 一次抢答竞赛中共 10 道题，答对一道题加 10 分，答错扣 5 分。
【题型突破】六年级上册数学第四单元题型专项训练-应用题(解题策略+专项秀场) 苏教版(含答案)
苏教版数学六班级上册题型专练第四单元解决问题的策略应用题专项训练解题策略数学应用题：学校数学中把含有数量关系的实际问题用语言或文字叙述出来，这样所形成的题目叫做应用题。
任何一道应用题都由两部分构成。
第一部分是已知条件（简称条件），其次部分是所求问题（简称问题）。
应用题的条件和问题，组成了应用题的结构。
一、转化法。
解题时，假如用一般方法临时解答不出来，就可以变换一种方式去思考，或转变思考的角度，或转化为另外一种问题。
这就是转化思路。
运用转化思路解题就叫转化法。
【例1】（2021·江苏六班级期末）星光学校组织数学竞赛，共有20道竞赛题，规定做对一道题得5分，做错或不做一道题倒扣3分，结果小强得了60分。
小强做对了几道题？分析：依据“做对一道题得5分，做错或不做一道题倒扣3分”可知：做错或不做一题比做对一题少得3+5＝8分；全部做对20道题共得20×5＝100（分）；假设小华全部做对得分是100分，比60分多得100-60＝40（分），那么他做错了：40÷8＝5（道）；所以小华做对：20-5＝15道题；据此解答。
（20×5-60）÷（3+5）＝40÷8＝5（道）20-5＝15（道）答：小强做对了15道题。
二、方程法。
方程法就是在解决问题时，让未知量与已知量处于同样的地位，即把未知量当作一个已知量看待，然后依据题中已知量和未知量之间存在的等量关系，列出相应的方程，最终求未知量是多少。
【例1】（2021·南京六班级）丁晓原有书的本数是王阳的5倍，若两人同时各借出5本给其他同学，则丁晓书的本数是王阳的10倍，两人原来各有书多少本？分析：设王阳原来有x本，依据（王阳本数－5）×10＝丁晓本数－5，列出方程求出x的值是王阳原来本数，王阳原来本数×5＝丁晓原来本数。
解：设王阳原来有x本。
（x-5）×10＝5x-510x-50＝5x-55x＝45x＝99×5＝45（本）答：丁晓原来有45本，王阳原来有9本。
【典型例题系列】六年级数学下册典型例题系列之第三单元解决问题的策略(原卷版)苏教版
2021-2022学年六年级数学下册典型例题系列之第三单元解决问题的策略（原卷版）编者的话：《2021-2022学年六年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。
专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。
本专题是第三单元解决问题的策略。
本部分内容主要介绍五种常见的解决问题的策略，即线段法、列表法、转化法、假设法、方程法等，考点和题型综合性较强，建议作为本章重点内容进行讲解，一共划分为五个考点，欢迎使用。
【考点一】策略一：线段法解题。
【方法点拨】稍复杂的分数应用题，为了使量率看起来更直观，往往采用画线段图的方式解决问题。
【典型例题】李伯伯家的苹果园今年收苹果3000千克，今年比去年少收14，去年收苹果多少千克？（画出线段图再列式解答）【对应练习1】李叔叔饲养白兔和黑兔一共400只，白兔只数是黑兔只数的35。
李叔叔饲养白兔和黑兔各多少只？（先将下面的线段图补充完整，再列式解答。
）黑兔：白兔：【对应练习2】松树棵数是柏树棵数的60%，松树比柏树少48棵。
松树和柏树各有多少棵？（补全下面的图形，并填空）松树有（）棵，柏树有（）棵。
【对应练习3】学校图书馆里科技书比故事书少200册，已知科技书的册数是故事书的35，图书馆里科技书有多少册【对应练习4】聪聪读一本童话故事书，上午读了72页，下午读的页数是上午的89，聪聪这一天共读了多少页？【对应练习5】某车间有工人150名，已知这些工人人数的45，恰好是全厂人数的112，全厂共有工人多少名？【考点二】策略二：列表法解题。
【方法点拨】在解决“鸡兔同笼”问题时，可以使用列表的方式，通过假设各种情况，再列表一一找出符号题目的情况。
【典型例题】一名篮球运动员在一场比赛中一共投中11个球，有2分球，也有3分球。
用转化的策略解决实际问题
例2 学校美术组有35人，其中
男生人数是女生的
2 3
。女生
有多少人？
例2 学校美术组有35人，其中
男生人数是女生的
2 3
。女生
有多少人？ χ人
解：设女生有χ人。
χ+ 23χ=35 53χ χ==3251
答：女生有21人。
例2 学校美术组有35人，其中
男生人数是女生的
2 3
用转化的策略解决实际问题2
红彩带比绿彩带长 ( 2 )。 这三堆棋子一共有白子多少枚？若每堆有60枚呢？每堆有240枚呢？ ( 5 ) 用转化的策略解决实际问题2
7 只数是白兔的 ,黑兔有多少只?
例2 学校美术组有35人，女生
5
只数是白兔的 ,黑兔有多少只?
χ=35
人数是美术组总人数的 。
5.看图填空。
车的速度是每小时多少千米？
5.看图填空。 人数是美术组总人数的 。
35× =21（人） 4、有三堆围棋子，每堆9枚。
（1） 答：小明已经看了36页。
男生人数是女生的 。 男生人数是女生的 。
5
女生人数是美术组总人数的 合唱组人数是美术组人数的
7
35× =21（人）
χ+ χ=35
2 答：学校合唱组有56人。 绿彩带比红彩带短 ， 例2 学校美术组有35人，其中 7 学校美术组有35人，是合唱组人数的 。
))。
40×
3 8
=15（只）
答：黑兔有15只。
小明已经看了多少页？
已经看的页数是没有看的页数
的
( (
3 4
) )
。
48×
3 4
=36（页）
小学数学解决问题的六大基本策略,附例题及分析!
数学一直都是很多学生最怕的一门学科，不少家长都反映，学习数学太难了。
小学数学的学习决定着孩子将来的学习生涯，所以作为家长我们需要还孩子提供最适合的学习方法，帮助他们提高学习成绩。
今天给大家分享一下数学学习方法，希望对大家有帮助。
1小学数学学习内容一年级：数字的认识、钟表的认识、图形的认识、简单的加减法。
二年级：简单的乘除法、长度单位的认识、位置和方向的辨别、角的认识。
三年级：四则运算的综合应用、质量单位的认识、矩形的认识和计算、分数的初步认识。
四年级：平行和相交、统计的基础学习、不规则图形的认识和运算、倍数和因数的学习。
五年级：认识负数和小数、小数的基本运算、方程的认识、分数的加减法运算。
六年级：分数的四则运算、认识比、圆柱和圆锥的学习、正比例和反比例。
以上就是小学数学的全部内容，完全按照孩子的认识规律，从简到难，逐层深入，几何和代数穿插学习，同步进行。
2小学数学六大基本策略随着孩子学习的深入，接触到的数学解决问题策略也会越来越多。
掌握各种解决问题的策略，对孩子的数学学习真的很重要，可以让孩子随时保持清晰的思维。
小学数学解决问题中的六大基本策略分别是：画图策略、转化策略、列表策略、枚举策略、替换策略、逆推策略。
画图策略在解题过程中，运用画图的方法，画出与题意相关的示意图，借助示意图来帮助推理、思考，这是小学数学解决问题中最常用的一种策略。
常见的画图方式有：线段图、集合图等。
将疑难问题的文字“翻译成图”，能够立竿见影地理清思路，找到解题策略。
例：某班有45位同学，其中有30人没有参加数学小组，有20人参加航模小组，有8小组都参加了。
问：只参加一个小组的学生有多少人？分析：画出集合图。
方框表示全班所有人。
区域①表示只参加数学小组的同学。
区域②表示只参加航模小组的人。
区域③表示同时参加数学、航模两个小组的人。
区域④表示两个小组都没有参加的人。
图片、图形转达信息的效率要远远高于文字和语言。
利用集合图将复杂的文字概念关系转化为直观的图，可以帮助孩子快速理清各种量之间的逻辑关系，提高解题效率。
2021春苏教版 五年级数学下册 第7单元 解决问题的策略 授课+习题课件(付,109页)
形的（1- 16 ）。
原来的加法算式可 以转化成……
计算 1 ＋ 1 ＋ 1 ＋ 1 2 4 8 16
把正方形看作单位“1”，把算式中的加数填入下图。
1
用转化后的算式算一算，看看与原
4
来的计算结果是否相同？
1
2
1
1 16
8
回顾解决问题的过程，你有什么体会？
有些复杂的算式可以 转化成简单的算式。
(14＋23)×10÷2＝185(根) 答：钢管的根数是185根。 结合上面的计算想一想，下面10个自然数的和，怎样 计算比较简便？ 19＋20＋21＋22＋23＋24＋25＋26＋27＋28 ＝(19＋28)×10÷2 ＝235
3．99999＋9999＋999＋99＋9可以转化成怎样的算式来计 算？先想一想，再算出结果。
有时画图可以帮 助我们找到转化 的方法。
1.计算
2.下图是一个装满了铅笔的铅笔架。你能联系梯形面积 公式，计算出铅笔的支数吗？
结合上面的计算想一想，下面10个连 续自然数的和，怎样计算比较简便？
15＋16＋17＋18＋19＋20＋21＋22＋23＋24 ＝（15＋24）×10÷2 ＝ 390÷2 ＝ 195
提升点 用数形结合法转化计算题
4．(1)观察下面每个图形中小正方形的排列规律，并填空。
4
5
(2)根据上面的规律用简便方法计算。 2＋4＋6＋8＋10＋12＋14＋16＋18＋20
＝10×11 ＝110
5．如下图，涂色部分是正方形，请你求出图中最大的长方 形的周长。 (34＋25)×2＝118(cm) 答：最大的长方形的周长是118 cm。
6
7
知识点 用直接转化的策略解决问题
用转化的策略解决问题练习题
练一练练一练练一练222用分数表示各图中的涂色部分用分数表示各图中的涂色部分用分数表示各图中的涂色部分练一练练一练练一练3?挑战挑战挑战11161616支足球队参加比赛比赛以单场淘汰制即每场比赛支足球队参加比赛比赛以单场淘汰制即每场比赛支足球队参加比赛比赛以单场淘汰制即每场比赛淘汰一支球队进行
用转化的策略解决问题练习题
练一练1、每个小方格的边长是1厘米，下边图形的周长是多少厘米？
练一练2、用分数表示各图中的涂色部分
练一练3
挑战1、有16支足球队参加比赛，比赛以单场淘汰制（即每场比赛淘汰一支球队）进行。一共要进行多少场比赛后才能产生冠军？
挑战2、有三堆有白子多少枚？
小学数学解题策略----转化策略
数学解题策略转化策略【趣味故事】爱迪生是个大创造家，电灯，是他奉献给人类的创造之一。
他一辈子有过上千种创造，顶峰期几乎三天二日就有一次创造。
有一次，他想要测定灯泡的体积。
他将这个问题交给了数学系毕业的助手去解决。
助手是数学系毕业的，他分别测量灯泡的球径，圆柱的半径和高度，然后计算球的体积和圆柱的体积。
这类计算要用到很复杂的数学知识，但结果也是近似的。
过了几天，爱迪生催问助手。
助手说，计算太烦琐，他还没有计算好呢。
爱迪生大吃了一惊，问：“这么简单的问题怎么还出不来？〞助手说：“这个灯泡不是一个规则的形状，所以量起来很麻烦。
〞爱迪生一言不发，拿起一个空灯泡，往水里一浸，咕嘟咕嘟地灌满了水，然后将灯泡的外壁擦干，将水往量杯里一倒，指着量筒上的刻度说：这不就是答案吗？只见助手目瞪口呆，好半天才喃喃的说：“是的先生，确实很简单。
〞从这个例子可看出，解决问题的方法总是有许多个，一个行不通，就用另一个试试。
直接的行不通，可以绕一个弯，引进中介，运用间接的方法，可以将难的问题转换成比拟方便的问题。
【介绍】转化策略是一种最常用的策略，是指把一个数学问题变更为一类已经解决或比拟容易解决的问题，从而使原问题得以解决的一种策略。
转化的手段和具体方法是多样而灵活的。
课堂教学中遇到有些应用题，数量关系较为复杂，求解时有一定的难度，可考虑运用转化的策略方法进行解答。
【例1】一个两位小数，去掉小数点后比原来的数大53.46。
这个两位小数是多少？【分析与解】题中“两位小数去掉小数点〞是什么意思呢？把它换句话说就是“把这个两位小数扩大100倍，得到一个新数〔整数〕〞。
新数比原来的数大多少呢？原数是1倍数，新数是100倍数，新数比原数大100倍-1倍=99倍，这样，题中“去掉小数点后比原来的数大53.46〞这个条件换句话说就是“原数的99倍等于53.46〞。
现在，题中的数量关系就明朗了，原来的问题也就转化成一个我们早已会解的、比拟简单的新问题了：“一个数的99倍是53.46，求这个数。
六年级数学下册《解决问题的策略》练习题
六年级数学下册解决问题的策略练习题模块一 用转化策略解决问题例1、星河小学美术组男生人数占总人数的52;已知女生有21人,男生有多少人 例2、六年级一班学生人数在40~50人之间,男生人数是女生人数的87;六年级一班男、女生人数各有多少人 例3、甲、乙、丙三人合修一条路,甲修的长度是乙、丙修的长度和的31,乙修的长度是甲、丙修的长度和的21,丙修了100米;这条路长多少米1、修一条长30千米的路,已经修的是剩下的32;已经修了多少千米 2、甲、乙、丙三人一共储蓄35万元,甲的钱数是乙的43,乙的钱数是丙的76;三人各储蓄多少元 3、一个工程队修一条公路,第一天修了它的72,第二天修了60千米;这时剩下的长度是已修的52;这条公路全长多少千米 模块二 用假设再调整策略解决问题例1、全班42人去划船,租10只船整好坐满;每只大船坐5人,每只小船坐3人;租的大船、小船各有多少只 例2、在一个停车场,摩托车和小轿车共有12辆,共有40个轮子;这个停车场的摩托车和小轿车各有多少辆 例3、长江小学举办环保知识竞赛,一共有20道题,答对一题得5分,不答不扣分,答错一题倒扣3分;赵斌回答完所有的题目,结果得了84分;他答对了多少道题1、小红买6角和8角的邮票一共13枚;用去8元4角钱,这两种邮票各买了多少枚2、龟、鹤共有10个头、32只脚;龟、鹤各有多少只3、学校有象棋、跳棋共26副,恰好可供120个学生同时进行活动;2人下一副象棋,6人下一副跳棋;象棋和跳棋各有多少副1. 山岩有120只,比绵羊少61;绵羊有多少只 2. 一根铁丝用去的长度是剩下的53,用去的比剩下的少16米;这根铁丝长多少米 课后作业巩固练习经典例题巩固练习经典例题3. 鸡、兔共有80只,兔的腿比鸡的腿一共多50只;鸡、兔各多少只4. 小华解答数学判断题,答对一题得4分,答错一题倒扣4分;他答了20道题目,结果只得了56分;小华答对了多少题。
(完整版)解决问题的策略
解决问题的策略（1）知识点：1.用倒过来推想的策略解决问题2.用替换的策略解决问题3.用假设的策略解决问题4.用转化的策略解决问题一．用倒过来推想的策略解决问题在解决实际问题的过程中，学会用倒过来推想的策略寻求解决问题的思路，并能根据具体的问题确定合理的解题步骤，从而有效的解决问题。
2.提高解决特定问题的价值，进一步发展分析，综合和简单推理能力。
例1：40个同学分成了两组做游戏，如果从第一组调4人到第二组，那么两组的人数就相等了。
原来的两组各有多少人？根据题意，解决这个问题的关键有两点：1，是根据给出的条件计算出现在两组各有多少人；二是从现在两组各有的人数，倒过来推算出原来两组各有多少人？【完全解答】40=÷（个）22020+4=24（个）ΛΛ第一组20-4=16（个）ΛΛ第二组答：原来的第一组有24人，第二组有16人。
举一反三：1：小红和小明共有16张邮票，如果小红给小明2张，那么两人的邮票同样多，原来两人各有多少张？2：甲乙丙三堆黄沙共72吨，如果甲堆，乙堆各给6吨给丙堆，三堆就同样重了，原来的甲乙丙各有黄沙多少吨？例2：车上原来有一些乘客，到和平桥站下去了12人，到十字街站又上来了17人，现在车上共有52人，车上原来有多少人？思路：现在车上共有52人--->十字街站没有上来17人—>和平桥站没有下去12人——>原来有多少人？【完全解答】52-17+12=47人。
答：车上原有47人。
举一反三：1.三（7）班图书角有一些书，先被同学们借出了8本，后来又被借出了26本，这时还剩24本，图书角原来多少本书？2.商场有一些电视机，上午售出总数的一半多10台，还剩200台，商场原有电视机多少台？二．用替换的策略解决问题1,学会用替换的策略理解题意，分析数量关系，并能根据问题的特点确定合理的解题步骤。
知识点1：两个量是倍数关系的替换例1：买1张桌子和4把椅子共用去120元，已知一把椅子的价钱是1，求每把桌子和每把椅子各多少元？一张桌子的21，可以把1张桌子的价方法一：根据1把椅子的价钱是一张桌子的2钱替换成2把椅子的价钱，如果120元全部买椅子，可以买（2+4）把椅子，每把椅子的价钱是120÷6=20（元），每张桌子的价钱是20⨯2=40（元）1，可以把4把椅子的钱方法二：根据1把椅子的价钱是1张桌子的2替换成2把桌子的价钱，如果120元全部买桌子，可以买（1+2）把，每张椅子的价钱是120÷3=40（元），每把椅子的价钱是402÷=20（元）思路：根据一把椅子和一把桌子的价钱关系进行替换，两个量是倍数关系的替换，总量没有变。
解决问题的策略之转化
解决问题的策略——转化赵丹丹教学内容：教科书第71—72页的例1、“试一试”和“练一练”，练习十四的第1—3题。
教学目标：1、使学生初步学会运用转化的策略分析问题，灵活确定解决问题的思路，并能根据问题的特点确定具体的转化方法，从而有效地解决问题。
2、使学生通过回顾曾经运用转化策略解决问题的过程，从策略的角度进一步体会知识之间的联系，感受转化策略的应用价值。
3、使学生进一步积累运用转化策略解决问题的经验，增强解决问题的策略意识，主动克服在解决问题中遇到的困难，获得成功的体验。
框架：一、教学例题（揭示转化）二、回顾举例（揭示复杂转化简单）华罗庚的话三、图形题、试一试（变个形、画个图、从反面思考路莎彼得的话）四、课堂练习。
五、全课小结。
六、文化渗透（曹冲称象、爱迪生巧测灯泡容积的故事）教学过程：一、教学例题，揭示转化。
1．请同学们看屏幕，老师这儿有两个平面图形，请你仔细观察，它们的面积相等吗？（停顿3秒，给学生思考的时间）2．你能一下子就看出来吗？哦，有的同学看出来了，有的同学还在思考，确实不容易看出来。
没关系，同学们之间可以交流交流，相互启发一下。
3. 讨论好了吗？哪位同学来说说你的想法？（电脑演示的问题）生：把左边图形上面的半圆往下移，拼成（变成）一个长方形。
（师电脑演示：先分割出半圆。
怎么移？（学生回答后再演示：向下平移）平移了几格？师：对，把这个半圆向下平移5格，就把这个图形变成了长方形。
）右边图形的左右两个半圆往上移，也拼成（变成）一个长方形。
（师电脑演示：先分割出两个半圆）怎么移的？（学生回答后再演示：旋转）师：对，把两个半圆分别旋转180度，也把这个图形变成了长方形。
（注意听学生发言，怎么移的？）4．现在你能判断这两个图形的面积相等吗？生：相等5．对，这两个图形的面积相等。
下面，我们来回顾一下这个问题的解决过程，为什么刚开始看不出两个图形的面积相等，后来一下子就看出来呢？（多请几位同学）生：把不规则的图形变成规则图形，面积就容易比较了。
《用“转化”的策略解决问题》教案
引导：看图想一想，可以把这一算式转化成怎样的算式计算？
延伸：如果老师在算式的后面再添上一个加数 ，和是多少？再加一个 呢？这样一直加下去，加到 ，和是多少？
小结：在解决问题时，要善于从不同的角度灵活地分析问题，这样有利于我们想到合理的转化方法。
爱迪生等了很长时间，也不见阿普顿报告结果。他走过来一看，便忍不住笑出了声，“你还是换种方法吧！”只见爱迪生取来一杯水。轻轻地往阿普顿刚才反复测算的灯泡里倒满了水，然后把水倒进量筒，几秒种就测出了水的体积，当然也就算出了灯泡的容积。这时羞红了脸的阿普顿傻呆呆地站在一旁，恨不得找条地缝钻下去。
这个故事让你联想到什么？将不规则物体转化成求水的体积，用到了一个重要的策略——转化。（板书：转化）
第六单元解决问题的策略第（1）课时
课题
用“转化”的策略解决问题
பைடு நூலகம்教材简析
教科书第71～72页例1、“试一试”、“练一练”和练习十四的1～3题
学情分析
通过前面的学习，学生有了零星的解决问题的经验，具备了策略教学的基础。但是学生对于“策略”一词会感到抽象，难懂。同时，运用策略解决问题对于学生来说，也具有一定的困难。所以。教学中，教学中为学生提供自主探索的平台，进一步感知转化的策略在生活中的应用。
第二个图形是怎样转化成长方形的？你是怎样想到把左右两个半圆进行旋转的？左右两个半圆分别旋转了多少度？
现在你怎样看出这两个图形的面积相等吗？比较面积是否相等什么可以变什么不能变？
小结：刚才我们在解决这个问题时，为什么要把原来的图形转化成长方形？（原来的复杂，转化后简单便于比较）板书：不规则规则
用转化的策略解决问题
用“转化”的策略解决问题课题名称解决问题的策略设计思路苏教版国标本六年级数学下册“解决问题的策略”这一章节是让学生在解决实际问题的过程中,学会用转化的策略寻求解决问题的思路,并根据具体的问题确定合理的解题方法,从而有效地解决问题.通过把转化策略与以前学过的相关的解决问题的方法进行比较,体会转化策略的内在价值,进一步增强解决问题的策略意识,提高学生从不同角度分析问题的能力,获得解决问题的成功体验,提高学好数学的自信心.教学内容教科书第71～72页的例1、“试一试”和“练一练”,练习十四的第1～3题.教学目标1、使学生初步学会运用转化的策略分析问题,灵活确定解决问题的思路,并能根据问题的特点确定具体的转化方法,从而有效地解决问题.2、使学生通过回顾曾经运用转化策略解决问题的过程,从策略的角度进一步体会知识之间的联系,感受转化策略的应用价值.3、使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难.教学过程一、交流问题,确定转化1、出示例1,让学生仔细观察教材提供的两个图形,明白要我们做什么,然后独立思考可以怎样比较这两个图形的面积.2、让学生在小组里交流自己是怎样想的.学生可能有两种想法.一种想法是用数方格的方法计算每个图形的面积后再比较.在学生提出在这种想法后,教师可让学生具体说说数方格的过程,注意提醒学生先把方格线补画完整,这样方格才方便.另一种想法是联系以有的知识经验,将这两个图形转化成长方形,再比较它们的面积.如果没有学生提出这样的想法,教师可提示学生进一步观察两个图形并思考：如果将图形中凸出的部分分割下来,并移到凹进去的部分,会使原来的图形转化成什么形状3、相机揭示课题：用“转化”的策略解决问题﹝通过利用学生平时已积累的经验,利用分割图形使复杂的内在关系变为浅显、易懂的、有条理的展现在学生面前,这样学生做得就轻松了.﹞二、探索方法,解决问题.1、提问：怎样把这两个图形分别转化成长方形呢自己在方格纸上画一画.教师可在课前将例题中的图复印下来,发给学生,以便操作学生尝试将两个图形转化成长方形.2、交流1第一个图形是怎样转化成长方形的你是怎么想到把上面的半圆进行平移的上面的半圆向什么方向平移了几格2第二个图形是怎样转化成长方形的你是怎样想到把左右两个半圆进行旋转的左右两个半圆分别按什么方向旋转了多少度3现在能看出这两个图形的面积相等吗3、小结：`刚才我们在解决问题时为什么要把原来的图形转化成长方形原来的图形相对复杂,不便于直接比较面积.转化成长方形后就容易看出每个图形的面积,也便于比较了﹝转化策略的运用“给学生一个平台,他们将撑起一片蓝天；给学生一个支点,他们有可能撬起怎个地球”确实孩子学习的潜力,我们不能低估,多给他们学习的机会他们会创造出更多意想不到的成果.﹞三、回顾、运用1、引导：在以往的学习中,我们曾经运用转化的策略解决过那些问题要让学生充分发表自己的想法,教师可有选择地板书.2、提问：这些运用转化策略解决问题的过程有什么共同点都是把新的问题转化成熟悉的或已经解决过的问题3、小结：转化是一种常用的、也是重要的解决问题的策略.在我们以往的学习中,早就运用这一策略分析并解决问题了.以后再遇到一个陌生的问题时,你会怎么想呢四、尝试策略1、教学“试一试”1出示“试一试”中的算式,提问：这道题可以怎样计算2出示题目右边的正方形图,提出要求：你能说说图中哪一部分表示这几个数的和吗3引导：看图想一想,可以把这一算式转化成怎样的算式计算如果学生有困难,可提示：空白部分上大正方形的几分之几能不能根据空白部分求出涂色部分4小结：在解决问题时我们要善于从不同的角度灵活地分析问题,这样有利于我们想到合理的转化方法.2、指导完成“练一练”.1出示方格纸上的两个图形,让学生思考怎样计算右边图形的周长.2提问：如果每个小方格的边长是1厘米,右边图形的周长是多少厘米学生计算后,再让学生说说解决这个问题的策略是什么把稍复杂的图形转化成简单的图形五、拓展巩固1、做练习十四第一题1出示问题,指导学生理解图意.明确图中每一排的点分别表示每一轮参加比赛的球队,把两个点合成一个点的过程表示进行了一场比赛.单场淘汰制就是每场比赛都要淘汰1支球队.2让学生数一数,一共要进行多少场比赛后才能产生冠军明确数的时候可以根据示意图一层一层地数.3启发：如果不画图,有更简单的计算方法吗如果学生有困难,可以提示：产生冠军,一共要淘汰多少支球队4进一步提出问题：如果有64支球队,产生冠军一共要比赛多少场2、做练习十四第2题.让学生各自看图填空.学生解决问题后,要让他们说说是怎样想到转化的方法的,以及分别是怎样转化的.六、课堂作业做练习十四第3题先让学生独立解答,再通过交流和评点进一步指出转化策略在解题过程中的作用.七、全课小结今天我们学习了运用转化的策略解决问题,你对转化的策略又有了哪些新的认识你们有何感想呢教学随笔本次设计针对学生的实际学习情况采用定性描述和定量评价相结合的方式进行,重在关注学生解决问题的过程,特别要肯定学生在解决问题过程中所作出的努力,以帮助学生进一步树立学好数学的自信心.我从以下几个方面入手：1、从知识与技能方面根据解决问题的需要,恰当运用转化的策略进行思考；根据具体问题灵活确定解题思路,合理选择解题方法,并有效地解决问题2、从数学思考与解决问题方面：在运用策略解决问题的过程中进行合理灵活的思考,并清楚表述自己的想法；具有主动运用策略解决问题的意识体验解决问题的策略的多样性初步形成评价与反思的意识,并在此过程中逐步提升对转化策略价值的认识.。
用“转化”的策略解决问题-教案
用“转化”的策略解决问题（第1课时）教学内容：五年级下册第105～108页例1、“练一练”和练习十六第1-3题。
教学目标：1. 使学生初步学会运用转化的策略分析问题，并能根据问题的特点确定具体的转化方法，从而有效地解决问题。
2. 学生通过回顾曾经运用转化策略解决问题的过程，从策略的角度进一步体会知识之间的联系，感受转化策略的应用价值。
3. 使学生进一步积累运用转化的策略解决问题的经验，增强解决问题的策略意识，主动克服在解决问题中遇到的困难，获得成功的体验。
教学准备：多媒体课件一套，学生作业纸一张。
教学过程：一、引入师：（出示七巧板）同学们玩过七巧板吗？七巧板可以拼出很多图案。
今天老师给大家也带来了一些由七巧板拼成的图案，一起来欣赏，你知道是什么吗？你能想办法知道这些图案的面积吗？（这些图案的面积哪一个大一些？）生可能：算出每一个基本图形的面积再相加；还原成正方形，再求正方形的面积有没有更方便的方法？哪种方法更简便？师：同学们都善于动脑筋。
怎样求简便？为什么可以这样求？二、新授师：刚才同学们通过把七巧板还原，轻松地求出了图案的面积，这里还有两个不一样的平面图形，你能一眼看出这两个图形面积的大小吗？（不能）为什么？1.引导思考启发思考：这两个图形比较复杂，不能一眼看出它们面积的大小，想想过去我们是怎样研究图形面积计算问题的，你打算用什么样的办法来比较这两个图形的面积？生先独立思考，再在小组内交流自己的想法。
2.提出方法展开讨论生可能：数格子（比较麻烦）、转化成长方形①先用数方格的方法计算每个图形的面积后再比较生提出后，师引导：想到先算出每个图形的面积，再比较面积的大小，这是一个不错的思路。
但是为什么不直接计算面积，却要用数方格的方法？（图形比较复杂）怎样用数方格的方法得出它们的面积呢？数方格时要注意什么？你觉得用数方格的方法解决这个问题方便吗？②在不改变面积大小的前提下，将这两个图形转化成更为简单的图形，再进行比较如果学生没有想到这一方法，引导他们观察思考：每个图形中凸出的部分与凹进去的部分之间有什么关系？这会给我们解决问题带来什么帮助？如果学生提出了这一方法，师追问：你是怎样想到这个方法的？如果用这样的方法能够解决这一问题，这与数方格的方法相比，哪个会更简便？小结：面对这两个比较复杂的图形，同学开动脑筋，既想出了我们过去曾经用过的数方格的方法，也设想把这两个图形转化为简单一点的图形再来比较。