三因素方差分析.
方差分析(包括三因素)讲解
2、CLASS 变量表；
CLASS必须的MODEL之前。
3、MODEL 因变量表=效应；
输出因变量均数，对主效应均数间的检
4、MEANS 效应[/选择项]；
验。
5、ALPHA=p 显著性水平（缺省值为0.05）
是指因变量与自变量效应，模型如下：
1、主效应模型 MODEL y=a b c; (a b c是主效应，y是因变量）
计判断，得出结论。
5
方差分析的基本思想：把全部数据关于总均值的离差平方和 分解成几部分，每一部分表示某因素诸水平交互作用所产生 的效应，将各部分均方与误差均方相比较，从而确认或否认 某些因素或交互作用的重要性。
用公式概括为：
各因素引起
由个体差异 引起（误差）
总变异=组间变异+组内变异
种类：常用方差分析法有以下4种 1、完全随机设计资料的方差分析（单因素方差分析） 2、随机区组设计资料的方差分析（二因素方差分析） 3、拉丁方设计资料的方差分析（三因素方差分析） 4、R*C析因设计资料的方差分析（有交互因素方差分析）
3
第一节 概述
因素（因子）—— 可以控制的试验条件 因素的水平 —— 因素所处的状态或等级 单（双）因素方差分析——讨论一个（两个） 因素对试验结果有没有显著影响。
4
例如：某厂对某种晴棉漂白工艺中酸液浓度（g/k）进 行试验，以观察酸液浓度对汗布冲击强力有无显著影 响。
冲击强力 序号
1
浓度
2 3 4 56
计算出F值：
QA
4217.3
(3 1) 2 28.38
QE
1114.7
(3(6 1))
5
15
列表：
方差来源 因素A 试验误差 总误差
三因素方差分析的原理及应用
应， 为 因 素 Ｂ 的第 Ｊ个水 平 的效 应 ， 为 因 素 Ｃ 的第 ｋ个水 平 的效应 ．显然 ， ａ ， ， 满 足如 下
作者简介 ：郭
萍（ １ ９ ８ １ 一 ） ， 女， 山西 阳泉人 ， 青 岛理工大学琴 岛学 院讲 师．
第１ 期
郭 萍 ：三 因素方 差分 析 的原理及 应 用
４ １
一
ｘ
・一
ｘ
ＳＣ ｚ
∑（
ｋ
＝
一
一
：
，
ｌ
一
・
ｉ １
一 ＾ 一 ｘ 一 去 ｄ ｉ 一 １ ｉ 一 １ ｘ
１ 一１ 一 １
Ｓ 一∑ ∑ ∑ （ ｘ 驰一叉 一 一
一 １ Ｊ一 １ ｋ一 １
引 入ｓ Ｔ 一 ∑ ∑ ∑（ ｘ 驰 一 ） 一 ｓ ＋ ｓ Ａ ＋ ｓ ＋
ｉ 一１
Ｘ． 咄＋ ２ Ｘ） 。一 Ｓ 了 ＇ 一Ｓ ａ— Ｓ Ｂ— Ｓ ｃ ，
关 系式 ：
∑ａ 一 ０ ， ∑ 一 ０ ， ∑ 一 ０ ．
若 毋一 ＋ａ ＋ ＋ ， 则数学 模 型为
了一个 具 体 的 数 学 建 模 案 例 ， 并 通 过 ＭＡＴ Ｌ ＡＢ
实现 了该 案例 的求 解 ．求 解结 果 的一 致 性说 明 了
原理 推导 的 正确性 ．
ｆ ｘ 一 ＋∞＋ ＋ ＋ｅ （ ＝ ＝ ＝ １ ， ２ ， …， ｒ ；
Ｉ Ｊ一 １ ， ２ ， …， ｓ ； 是 ＝ ＝ ＝ １ ， ２ ， …， ） ；
方差分析的三个前提
方差分析的三个前提
方差分析是一种常见的统计分析方法，通常被用来比较两组及两组以上的实验数据，以及评估不同因素对结果和产出的影响。
这项统计分析要求有三个基本前提，包括可变性、等变性和正态分布。
首先，方差分析需要可变性，即变量(或因素)之间可以相互区分，而不存在重复或重叠的情况。
如果变量(或因素)没有充分的可变性，那么方差分析的结果将更加难以识别出每个变量(或因素)的独特作用。
其次，如果要进行方差分析，则需要满足等变性。
即所有变量(或因素)应具有相同的变异范围，以便精确地比较这些变量(或因素)之间的关系。
如果变量(或因素)没有达到等变性，那么可能会导致被检索出错误的结论，从而影响到统计分析的准确性和可靠性。
最后，方差分析还需要正态分布，这就要求试验单位在每个参与者测量的变量(或因素)上具有独立的性质。
正态分布的特征是，数据的分布在高维度实空间中服从对称性质，这就意味着数据在实质上是可比较的，从而可以进行评估和比较。
此外，数据在正态分布形状中也尽可能接近也就是说，峰、谷和颠峰部分之间的差异应该最小化，而不是有明显的趋势和噪音。
综上所述，方差分析的三个基本前提是可变性、等变性和正态分布。
这些前提的基础要求是必须满足的，以保证统计分析的正确性、可靠性和准确性。
因此，在实施方差分析前，必须充分考虑这三个规则，以确定因素的可变性、等变性和正态分布的程度，以确保分析结
果的准确性和可靠性。
Excel数据处理之三 方差分析
第三节方差分析
在数据分析工具库中提供了3种基本类型的方差分析：单因素方差分析、双因素无重复试验和可重复试验的方差分析，本节将分别介绍这三种方差分析的应用：
单因素方差分析
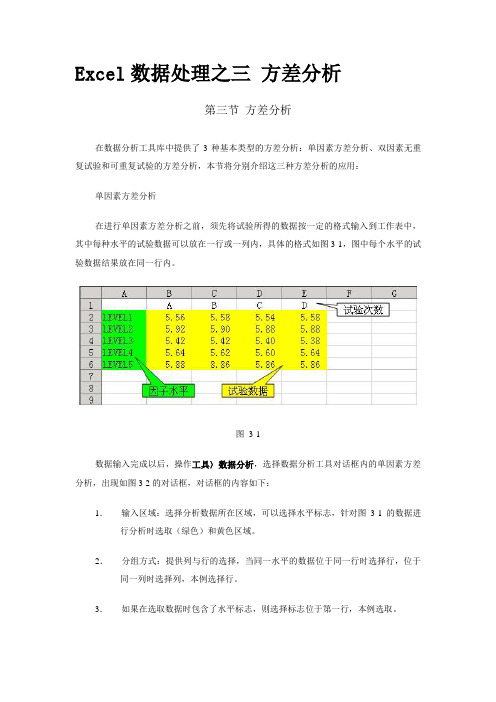
在进行单因素方差分析之前，须先将试验所得的数据按一定的格式输入到工作表中，其中每种水平的试验数据可以放在一行或一列内，具体的格式如图3-1，图中每个水平的试验数据结果放在同一行内。
图3-4
数据输入完成以后，操作工具〉数据分析，选择数据分析工具库中的双因素无重复方差分析，出现如图3-5的对话框，对话框的内容如下：
1．输入区域：选择数据所在区域，可以包含因素水平标志。
2．果数据输入时选择了因素水平标志，请选择标志按钮。
3．显著性水平α：根据实际情况输入，一般选择0.05。
4．输出选项：按需要选择分析结果存储的位置。
1．输入区域：选取图4-1数据表中的绿色和黄色区域，表示标志与数据。
2．分组方式：根据数据输入的方式选择逐行或逐列，此例选择逐列。
3．由于数据选择时包含了标志，所以要勾选标志位于第一行。
4．根据需要选择输出的位置。
图4-2
将信息按图4-2输入对话框后，选择确定，输出结果如图4-3所示。
图4-3
协方差分析
图3-5
分析图3-4中的数据，对话框如图3-5输入，分析结果输出如图3-6：
图3-6
双因素可重复方差分析
双因素可重复方差分析与双因素无重复方差分析数据输入的区别在于对重复试验数据的处理，如图3-7所示，就是将重复试验的数据叠加起来。
图3-7
数据输入完成以后，操作工具〉数据分析，选择数据分析工具库中的双因素可重复方差分析，出现如图3-8的对话框，对话框的内容基本与双因素无重复方差分析相同，区别在于每一样本的行数选项，在此输入重复试验的次数即可。
spssau三因素方差分析操作
三因素方差当X为定类数据，Y为定量数据时，通常使用的是方差分析进行差异研究。
X的个数为一个时，我们称之为单因素方差；X为2个时则为双因素方差；X为3个时则称作三因素方差，依次下去。
当X超过1个时，统称为多因素方差。
在实验研究中，比如研究者测试某新药对于胆固醇水平是否有疗效；研究者共招募72名被试，男女分别为36名，以及男女分别再细分使用新药和普通药物；同时高血压患者对于新药可能有干扰，因而研究者将被试是否患高血压也纳入考虑范畴中。
因而最终，X共分为三个，分别是药物(旧药和新药)、性别，是否患高血压；Y为胆固醇水平。
因而需要进行三因素方差分析即多因素方差分析。
特别提示：对于双因素方差，三因素方差分析；SPSSAU单独提供研究方法，并且提供更多指标输出比如交互效应或图形等；如果是实验研究，建议使用双因素，或者三因素方差分析等；针对X超过3个时，只能直接使用多因素方差分析；X均为定类数据，Y为定量数据。
SPSSAU分析结果表格示例如下：多因素方差分析结果平方和df F P 截距511.325 1 4397.621 0.000**性别0.340 1 2.925 0.092 是否高血压7.825 1 67.300 0.000** 药物0.824 1 7.091 0.010**残差7.907 68 null nullR²=0.547三因素方差案例Contents1背景 (2)2理论 (2)3操作 (2)4 SPSSAU输出结果 (4)5文字分析 (6)6剖析 (6)1背景某研究者测试新药对于胆固醇水平是否有疗效；研究者共招募72名被试，男女分别为36名，并且男性或女性中是否高血压患者各为18名，并且当前被试的胆固醇水平基本均保持在6.5左右。
最终X共分为三个，分别是药物(旧药和新药)、性别，是否患高血压；Y为胆固醇水平。
同时，明显的可以想到，实验前的胆固醇水平基数，很可能会影响到最终的胆固醇水平，因此“实验前胆固醇水平”是一个干扰因素，因此将其作为协变量纳入模型中。
三因素混合方差分析事后简单效应多重比较语法
概念笔记Main effect 一个因素的独立效应，即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较，不考虑其他因素。
Interaction 多个因素的联合效应，A因素的作用受到B因素的影响，即有交互——two-way interaction. 当一因素作用受到另外两个因素影响，即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用，A*B, A*R, B*R三重交互作用，A*B*C结果发现，A, B为被试间因素，交互作用SIG当二重交互作用SIG，需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG，需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上，R1 与R2 差异在A1B2水平结合上，R1 与R2 差异在A2B1水平结合上，R1 与R2 差异在A2B2水平结合上，R1 与R2 差异在A3B1水平结合上，R1 与R2 差异在A3B2水平结合上，R1 与R2 差异重复测量方差分析之后，如果三重交互作用显著，需要编辑语法，得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时，也会报告多重比较结果，会有更直观的对比结果。
如果三重交互作用SIG，需要进行简单简单效应检验。
固定某两个因素水平组合，考察研究者最感兴趣的那个变量的效应。
MANOV A R1 R2 BY A(1,3) B(1,2)/WSFACTORS=R(2)/PRINT=CELLINFO(MEANS)/WSDESIGN/DESIGN/WSDESIGN=R/DESIGN=MWITHIN B(1) WITHIN A(1)MWITHIN B(2) WITHIN A(1)MWITHIN B(1) WITHIN A(2)MWITHIN B(2) WITHIN A(2)MWITHIN B(1) WITHIN A(3)MWITHIN B(2) WITHIN A(3)上述语法内容是检验被试内变量R在被试间变量A, B 上的简单简单效应。
方差分析-统计学原理
H0 ：a1 =a2 =…=ar =0
第三节 两因素方差分析 随机区组设计资料的方差分析
一、 随机区组设计 随机区组设计（ randomized block design ），又称 配伍组设计，是配对设计的扩展。 具体做法是：先按影响试验结果的非处理因素 将受试对象配成区组（block），再将各区组内的受 试对象随机分配到不同的处理组，各处理组分别接 受不同的处理，试验结束后比较各组均数之间差别 有无统计学意义，以推断处理因素的效应。
各种变异之间的关系是：
SS总 SS处理 SS区组 SS误差
其中：
v总 v处理 v区组 v误差
v区组 n 1
v误差 (n 1)(g 1)
v总 N 1 v处理 g 1
（1）总变异：反映全部试验数据间大小不等的状况，
SS总 X 2 C
方差分析的基本概念
将衡量试验结果的标志称为试验指标。 将影响试验结果的条件称为因素。 因素在试验中所处的不同状态称为该因 素的水平。
只考察一个影响条件即因素的试验称为单因素 试验，相应的方差分析称为单因素方差分析。
二、变异分解 完全随机设计资料的方差分析表 变异来源 自由度 SS MS F 总变异
单因子方差分析的统计模型：
yij i ij , j 1, 2,..., mi , i 1, 2,..., r , 2 诸 ij 相互独立，且都服从N (0, )
模型可以改写为
yij ai ij , j 1, 2,..., mi , i 1, 2,..., r , r mi ai 0 i 1 相互独立，且都服从N(0, 2 ) ij
均数间的差异没有统计学意义；反 之，如果处理有作用，则组间变异 不仅包含随机误差，还有处理因素
方差分析(包括三因素)
2
15.1 17.5 20.1
3
15.8 17.1 18.9
4
14.8 15.9 18.2
5
17.1 18.4 20.5
6
15.0 17.7 19.7
A1 A2 A3
方差分析就是把总的 试验数据的波动分成
1、反映因素水平改变引起的波动。 2、反映随机因素所引起的波动。
然后加以比较进行统 计判断，得出结论。
2 ij 2 2 ij
m
n
m
n
T2 X mn i 1 j 1
m n 2 ij
12
同样可推出：
1 m 2 QE X Ti n i 1 i 1 j 1
2 ij
m
n
1 m 2 T2 QA Ti n i 1 mn
2、数据的简化： 试验数据经过变换
' X ij b( X ij a)
3
离差平方和 1.56 11.56 3.1 16.22
3
自由度 2 2 4 8
F值 FA=1.01 FB=7.46
F0.05(2,4) F0.01(2,4) 6.94 6.94 18.0 18.0
显著性
*
Q X
i 1 j 1
2 ij
T2 16.22 3 3
1 3 T2 2 QA Ti. 1.56 3 i 1 3 3
试验结果
假设：美中不足组合水平下服从正态分布、互相独立、方差相等。 所需要解决的问题是：所有Xij的均值是否相等。
18
假设检验：
1）在假设H0成立的条件下。 2）统计量
T2 Q X ml i 1 j 1
m l 2 ij
三水平试验方差分析
三水平试验方差分析适用于多种 数据类型，如连续型、分类型和 有序分类型数据，具有广泛的适 用性。
缺点
01
复杂性
三水平试验方差分析涉及多个处 理水平，导致模型复杂度高，对 数据的要求也较高。
02
对数据的要求
03
对软件的要求
该方法要求数据具有正态分布、 同方差性和独立性等假设，否则 可能导致分析结果的不准确。
5. 检验假设
检验组间方差与组内方差的差异是 否显著，以确定处理因素是否对响 应变量有显著影响。
6. 解释结果
解释方差分析的结果，并得出结论 。
方差分析的假设检验
01
假设检验是方差分析的核心部分，用于确定处理因素对响应变量的影响是否显 著。
02
它基于以下假设：组间方差与组内方差不相等，表示处理因素对响应变量有显 著影响；组间方差与组内方差相等，表示处理因素对响应变量没有显著影响。
实验结果的解释与讨论
结果解释
根据方差分析的结果，结合专业知识，对实 验结果进行解释，并探讨其实际意义和影响 。
结果讨论
对实验结果进行深入讨论，包括结果的可靠性、稳 定性、推广性等方面，并提出可能的改进和完善建 议。
文献综述
查阅相关文献，了解同类研究的现状和进展 ，对比和评价本研究的优缺点和创新点。
选择实验对象和样本量
根据研究问题和实验目的选择适当的 实验对象和样本量。
确定实验处理和变量
根据研究问题和实验目的确定适当的 实验处理和变量，并设计合理的实验 程序。
实施实验
按照实验设计进行实验，并记录实验 数据。
分析实验数据
对实验数据进行分析，包括数据的整 理、描述性统计、方差分析等。
解释和撰写实验结果
方差分析简介
方差分析简介1. 引言方差分析（analysis of variance，简称ANOV A）是一种假设检验方法，即基本思想可概述为：把全部数据的总方差分解成几部分，每一部分表示某一影响因素或各影响因素之间的交互作用所产生的效应，将各部分方差与随机误差的方差相比较,依据F分布作出统计推断，从而确定各因素或交互作用的效应是否显著。
因为分析是通过计算方差的估计值进行的，所以称为方差分析。
方差分析的主要目标是检验均值间的差别是否在统计意义上显著。
如果只比较两个均值，事实上方差分析的结果和t检验完全相同。
只所以很多情况下采用方差分析，是因为它具有如下两个优点：（1）方差分析可以在一次分析中同时考察多个因素的显著性，比t检验所需的观测值少；（2）方差分析可以考察多个因素的交互作用。
方差分析的缺点是条件有些苛刻，需要满足如下条件：（1）各样本是相互独立的；（2）各样本数据来自正态总体（正态性：normality）；（3）各处理组总体方差相等（方差齐性：homogeneity of variance）。
因此在作方差分析之前，要作正态性检验和方差齐性检验，如不满足上述要求，可考虑作变量变换。
常用的变量变换方法有平方根变换，平方根反正弦变换、对数变换及倒数变换等。
方差分析在医药、制造业、农业等领域有重要应用，多用于试验优化和效果分析中。
2. 单因素方差分析2.1 基本概念（1）试验指标：在一项试验中，用来衡量试验效果的特征量称为试验指标，有时简称指标，也称试验结果，通常用y表示。
它类似于数学中的因变量或目标函数。
试验指标用数量表示称为定量指标，如速度、温度、压力、重量、尺寸、寿命、硬度、强度、产量和成本等。
不能直接用数量表示的指标称为定性指标。
如颜色，人的性别等。
定性指标也可以转化为定量指标，方法是用不同的数表示不同的指标值。
（2）试验因素：试验中，凡对试验指标可能产生影响的原因都称为因素(factor)，也称因子或元，类似于数学中的自变量。
方差分析
类型2
20 21
类型4
18 22
20
18 15
33
27 40
16
26 17
19
这里，试验指标是电路的响应时间。电路类型为因素，这 一因素有四个不同的水平。试验的目的是为了考察各种类 型的电路的响应时间有无显著差异。
二
单因素试验
在例 1 中，我们在因素的每一个水平下进行了独立试
验，其结果是一个随机变量。表中的数据可看成来自三个 不同总体的样本值。将各个总体的均值依次记作1 , 2 , 3,按题意需检验假设 H0 ： 1 = 2 = 3
Anj j 来自具有相同方差s2，均值分别为j(j=1,2,…,s)的正态 总体N (j,s2) , j与s2未知。且设不同水平Aj 下的样本之间 相互独立。
由于 xij ~ N ( j , s 2 ), 即有 x ij j ~ N (0, s 2 ), 故xij பைடு நூலகம் j 可以看成随机误差. 记xij j ij , 则xij 可写成
而当H 1为真时， j 1 n j 0, 此时
s 2 j
SA 1 s 2 2 2 E( ) s n j j s s 1 s - 1 j1
又由（ ）式知， 13 SE E( ) s 2, ns
(18)
(19)
即不管H 0是否为真，S E /(n s)都是s 的偏估计。 S A /(s 1) 综上所述，根据分式F 的特性， S E /(n s ) 知检验问题（2） 的拒绝域具有形式
3 5 2 ij 2 ..
T 2 S T x 0.963912 (3.8) / 15 0.00124533 . 15 j 1 i 1 2 3 T2 T.. 1 .j SA (1.212 1.28 2 1.312 ) n 5 j ` n j
三因素方差分析
-----------+----------------------------------------------------
Total | 6.90318355 23 .300138415
10
三因素方差分析举例
Reduced Model 2:所有二级交互项P<0.05
Source | Partial SS df
-------------+-------------------------------------------------------
e|
0.915
0.743
0.12
0.9422
方差齐性检验的主要结果:P=0.2202>0.10
Source | Partial SS df
MS
F Prob > F
方差
7
三因素方差分析举例
残差的正态性检验结果：P=0.9422>0.05
Skewness/Kurtosis tests for Normality
------- joint ------
Variable | Pr(Skewness) Pr(Kurtosis) adj chi2(2) Prob>chi2
Residual | 2.78586636 18 .154770354
-----------+----------------------------------------------------
Total | 6.90318355 23 .300138415
11
三因素方差分析举例： 用角模型进行简单效应比较
变量定义
不用正氟醚 A=1
用正氟醚 A=2
三因素二水平2种方法分析结果
例：以辽宁生草冲积土大豆氮、磷、钾三要素肥料盆栽试验结果为例说明，重复五次，产量如下：A. 处理间方差分析：总平方和：（51.22+53.32+…+62.22）－4023572＝786.58处理间平方和：51（265.52+274.02+…+316.52）－4023572＝493.3 重复间平方和：81（466.22+474.72+…+488.62）－4023572＝56.31误差平方和：786.56－493.3－56.31＝237.10大豆氮、磷、钾肥效方差分析B ．因素间的方差分析：各因子及交互作用的效应如下： Ｎ的效应： （NPK-PK ）+(NP-P)+(NK-K)+(N-O)=16.0 P 的效应： (NPK-NK)+(NP-N)+(PK-K)+(P-O)=124.0 K 的效应： (NPK-NP)+((PK-P)+(NK-N)+(K-O)=58.0 NP 的交互作用：（NPK-PK-NK+K ）+(NK-N-P+O)=－19.0 NK 的交互作用：（NPK-PK-NP+N ）+(PK-P-K+O)=7.0 PK 的交互作用：(NPK-NK-NP+N)+(PK-P-K+O)=－17.5 NPK 的交互作用：NPK-PK-NK-NP+N+P+K-O=6.0 效应的平方和＝观察总次数的乘方该处理效应或交互作用N 的平方和＝8*5162＝6.4 P 的平方和＝8*51242＝384.44K 的平方和＝8*5582＝84.0 NP 的平方和＝8*5)19(2-＝9NK 的平方和＝8*572＝61.2 PK 的平方和＝8*5)5.17(2-＝7.6NPK 的平方和＝8*562＝0.9大豆氮、磷、钾肥效产量方差分析Ｃ。
用邓肯法对各处理进行多重比较：Ｓx ＝nSe＝546.8＝1.3克／盆查n=28时不同Ｐ下的SSR值并计算LSR值：大豆氮磷钾肥效的比较。
三因素方差分析.
三因素方差分析举例
Reduced Model 1：b*c项的P=0.5761，故剔除
Source | Partial SS df MS F Prob > F -----------+---------------------------------------------------Model | 4.16958384 6 .694930641 4.32 0.0079 a | .002016672 1 .002016672 0.01 0.9121 b | .077066736 1 .077066736 0.48 0.4981 c | .79935039 1 .79935039 4.97 0.0395 a*b | 1.9040668 1 1.9040668 11.84 0.0031 a*c | 1.33481659 1 1.33481659 8.30 0.0104 b*c | .052266656 1 .052266656 0.33 0.5761 Residual | 2.73359971 17 .160799983 -----------+---------------------------------------------------Total | 6.90318355 23 .300138415
三因素方差分析的基本概念三因素方差分析要求资料服从正态分布方差齐性三个因素的不同水平组合样本资料独立要求三个因素的不同水平组合情况的样本量相为二级交互作用称为一级交互作用称为主效应如果三因素方差分析模型中没有二级交互作用则称该模型为reducedmodel反之称为fullmodelabacbcabcabacbc某研究者以大白鼠作试验观察指标是肝重与体重之比研究正氟醚与观察指标的作用同时要考察用生理盐水和用戊巴比妥作为诱导药对正氟醚毒性作用的影响并且考略不同性别大白鼠对诱导物的作用和正氟醚毒性作用
三因素混合方差分析事后简单效应多重比较语法
概念笔记Main effect 一个因素的独立效应，即其不同水平引起的方差变异。
三因素的实验有三个主效应。
把某一因素的一个水平同该因素的其他水平比较，不考虑其他因素。
Interaction 多个因素的联合效应，A因素的作用受到B因素的影响，即有交互——two-way interaction. 当一因素作用受到另外两个因素影响，即三因素交互three-way interaction.重复测量一个因素的三因素混合设计3*2*2的混合设计A3*B2*R2 【A, B为被试间因素】需要分析的有——A, B, R 各自主效应二重交互作用，A*B, A*R, B*R三重交互作用，A*B*C结果发现，A, B为被试间因素，交互作用SIG当二重交互作用SIG，需要进行simple effect检验。
A因素水平在B因素某一水平上的变异。
A在B1水平上的简单效应A在B2水平上的简单效应B在A1水平上的简单效应B在A2水平上的简单效应B在A3水平上的简单效应如果三重交互作用SIG，需要进行三因素的简单简单效应分析simple simple effect. 某一因素的水平在另外两个因素的水平结合上的效应在A1B1水平结合上，R1 与R2 差异在A1B2水平结合上，R1 与R2 差异在A2B1水平结合上，R1 与R2 差异在A2B2水平结合上，R1 与R2 差异在A3B1水平结合上，R1 与R2 差异在A3B2水平结合上，R1 与R2 差异重复测量方差分析之后，如果三重交互作用显著，需要编辑语法，得出三个因素各自的简单效应某一因素在其他两个因素的某一实验条件内的简单效应检验三因素重复测量方差分析对应的会有3种简单效应检验结果SPSS在输出简单效应检验结果的同时，也会报告多重比较结果，会有更直观的对比结果。
如果三重交互作用SIG，需要进行简单简单效应检验。
固定某两个因素水平组合，考察研究者最感兴趣的那个变量的效应。
MANOV A R1 R2 BY A(1,3) B(1,2)/WSFACTORS=R(2)/PRINT=CELLINFO(MEANS)/WSDESIGN/DESIGN/WSDESIGN=R/DESIGN=MWITHIN B(1) WITHIN A(1)MWITHIN B(2) WITHIN A(1)MWITHIN B(1) WITHIN A(2)MWITHIN B(2) WITHIN A(2)MWITHIN B(1) WITHIN A(3)MWITHIN B(2) WITHIN A(3)上述语法内容是检验被试内变量R在被试间变量A, B 上的简单简单效应。
有交互影响的三因素方差分析的应用及MATLAB实现
有交互影响的三因素方差分析的应用及MATLAB实现郭萍【摘要】简化了有交互影响的三因素方差分析的计算方法,同时利用简化方法编程计算了具体的数学建模案例,并利用MATLAB实现了该案例的求解.【期刊名称】《沈阳大学学报》【年(卷),期】2019(031)003【总页数】5页(P252-256)【关键词】交互影响;三因素;方差分析;数学建模;计算程序;MATLAB【作者】郭萍【作者单位】青岛理工大学琴岛学院基础部,山东青岛 266106【正文语种】中文【中图分类】O29方差分析是科学试验及数据统计分析中的重要方法之一,它主要用于对试验结果数据变动的分析,了解哪些因素对指标产生显著影响[1].文献[1-5]中给出了单因素、双因素及三因素方差分析的原理,本文简化了文献[5]中有交互影响的三因素方差分析的计算方法, 同时利用简化方法编程计算了具体的数学建模案例,并通过MATLAB实现了该案例的求解.1 有交互影响的三因素方差分析原理[5]设有3个因素A、B、C,因素A取r个水平,分别记为A1,A2,…,Ar,因素B取s个水平,分别记为B1,B2,…,Bs,因素C取t个水平,分别记为C1,C2,…,Ct,在水平组合(Ai,Bj,Ck)下样本相互独立[4]且Xijk～N(μijk,σ2), i=1,2,…,r, j=1,2,…,s, k=1,2,…,t.数学模型为:故检验假设为:则有交互影响的三因素方差分析表见表1.表1 有交互影响的三因素方差分析表[5]Table 1 Three-factor variance analysis with interaction来源平方和自由度均方和F值ASAr-1MSA=SA/(r-1)FA=MSA/MSEBSBs-1MSB=SB/(s-1)FB=MSB/MSECSCt-1MSC=SC/(t-1)FC=MSC/MSEABSAB(r-1)(s-1)MSAB=SAB/(r-1)(s-1)FAB=MSAB/MSEACSAC(r-1)(t-1)MSAC=SAC/(r-1)(t-1)FAC=MSAC/MSEBCSBC(s-1)(t-1)NSBC=SBC/(t-1)(s-1)FBC=MSBC/MSEABCSABC(r-1)(s-1)(t-1)MSABC=SABC/(r-1)(s-1)(t-1)FABC=MSABC/MSEESErst(m-1)MSE=SE/rst(m-1)TSTn-1检验规则为:(1) 若FA>Fα(r-1,rst(m-1)),则拒绝H01,认为因素A对指标值的影响显著;(2)若FB>Fα(s-1,rst(m-1)),则拒绝H02,认为因素B对指标值的影响显著;(3)若FC>Fα(t-1,rst(m-1)),则拒绝H03,认为因素C对指标值的影响显著;(4)若FAB>Fα((r-1)(s-1),rst(m-1)),则拒绝H04,认为因素A与B交互作用显著;(5)若FAC>Fα((r-1)(t-1),rst(m-1)),则拒绝H05,认为因素A与C交互作用显著;(6)若FBC>Fα((s-1)(t-1),rst(m-1)),则拒绝H06,认为因素B与C交互作用显著;(7)若FABC>Fα((r-1)(s-1)(t-1),rst(m-1)),则拒绝H07,认为因素A、因素B与因素C交互作用显著.2 简化算法为了简化数据输入的工作量,同时也为了计算的简便,可以将初始数据进行“归整变换”,变换后再参与运算,即将初始数据减去一个常数,该常数为平均数附近的数值,然后乘上10的幂次,将小数点移去,即Y=10k(X-a).此变换后,数据是一些具有较少位数的整数,而且F值不变,这使得计算过程得到了很大的简化.3 数学建模案例求解及MATLAB实现3.1 数学建模案例某集团为了研究商品销售点所在的地理位置、销售点处的广告和销售点的装潢这3个因素对商品的影响程度,选了3个位置(如市中心黄金地段、非中心的地段、城乡结合部),两种广告形式,两种装潢档次在某个城市进行了搭配试验.表2是销售量的数据,在显著水平0.05下,检验不同地理位置、不同广告、不同装潢下的销售量是否有显著差异[6].表2 销售量数据Table 2 Sales data水平组合销售数据1销售数据2A1B1C1957960A1B1C2939923A1B2C1920920A1B2C2860870A2B1C18508 34A2B1C2832840水平组合销售数据1销售数据2A2B2C1865870A2B2C2850832A3B1C1880894A3B1C2820840A3B2C18638 53A3B2C28128103.2 数学建模案例的MATLAB实现MATLAB[7]统计工具箱中用ANOVAN作多因素方差分析.有交互影响的三因素方差分析命令为[p,t]=anovan(x,group,model,sstype,gnames),返回值p,当p>α时接受H0,说明因素对指标值无显著影响,当p<α时拒绝H0,说明因素对指标值有显著影响,t为方差分析表.编写程序如下:clc,clearx1=[957 939 920 860 850 832 865 850 880 820 863 812];group={[′A1′;′A1′;′A1′;′A1′;′A2′;′A2′;′A2′;′A2′;′A3′;′A3′;′A3′;′A3′;];[′B1′;′B1′;′B2′;′B2′;′B1′;′B1′;′B2′;′B2′;′B1′;′B1′;′B2′;′B2′;];[′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;′C1′;′C2′;]};[p1,t1]=anovan(x1,group,2,3,{′A′;′B′;′C′})求得p1=0.026 9,0.154 8,0.044 2,0.121 1,0.336 4,0.597 7,方差分析表,如表3. 表3 MATLAB实现的方差分析表Table 3 Analysis of variance of MATLAB implementation来源平方和自由度均方和F值P值A14077.227038.5836.230.0269B972.01972.005.000.1548C4107.014107.002 1.140.0442AB2820.521410.257.260.1211AC766.52383.251.970.3364BC75.01 75.000.390.5977E388.52194.25T23206.711由于ANOVAN只能解决在3个因素影响下一组数据中两两因素的交互作用,无法实现3个因素的交互作用,故由表3知,第一组数据下地理位置,装潢影响下得到的两个p值均小于0.05,故拒绝原假设,说明地理位置,装潢对该商品的销售量有显著影响.而广告及3个因素两两的交互作用对销售量没有显著的影响.综上所述,为了制定该商品更好的销售计划,地理位置、装潢都需要进行合理的选择.3.3 简化算法求解3个因素的交互作用由于MATLAB中已有的函数只能解决在3个因素影响下一组数据中两两因素的交互作用,无法实现3个因素的交互作用,故采用简化算法求解两组数据下3个因素的交互作用.按照销售数据1、销售数据2及简化的算法X-870,原始数据依次变为:87,69,50,-10,-20,-38,-5,-20,10,-50,-7-58,90,53,50,0,-36,-30,0,-38,24,-30,-17,-60.按照有交互影响的三因素方差分析原理及偏差平方和分解式, 编写程序如下:clc,clearx1=[87 69 50 -10 -20 -38 -5 -20 10 -50 -7 -58 90 53 50 0 -36 -30 0 -38 24 -30 -17 -60];t2=[sum(x1)]^2/24;st=(87^2+69^2+50^2+(-10)^2+(-20)^2+(-38)^2+(-5)^2+(-20)^2+10^2+(-50)^2+(-7)^2+(-58)^2+ 90^2+53^2+50^2+0^2+(-36)^2+(-30)^2+ 0^2+(-38)^2+ 24^2+(-30)^2+(-17)^2+(-60)^2)-t2a1=[87 69 50 -10 90 53 50 0];sum(a1);a2=[-20 -38 -5 -20 -36 -30 0 -38]; sum(a2);a3=[ 10 -50 -7 -58 24 -30 -17 -60]; sum(a3);sa=(sum(a1)^2+ sum(a2)^2+ sum(a3)^2)/8- t2b1=[87 69 -20 -38 10 -50 90 53 -36 -30 24 -30];sum(b1);b2=[50 -10 -5 -20 -7 -58 50 0 0 -38 -17 -60]; sum(b2);sb=(sum(b1)^2+ sum(b2)^2)/12-t2c1=[87 50 -20 -5 10 -7 90 50 -36 0 24 -17];sum(c1);c2=[69 -10 -38 -20 -50 -58 53 0 -30 -38 -30 -60]; sum(c2);sc=(sum(c1)^2+ sum(c2)^2)/12-t2ab1=[87 69 90 53]; sum(ab1);ab2=[50 -10 50 0]; sum(ab2);ab3=[-20 -38 -36 -30]; sum(ab3);ab4=[-5 -20 0 -38]; sum(ab4);ab5=[10 -50 24 -30]; sum(ab5);ab6=[-7 -58 -17 -60]; sum(ab6);sab=(sum(ab1)^2+ sum(ab2)^2+ sum(ab3)^2+ sum(ab4)^2+sum(ab5)^2+ sum(ab6)^2)/4-t2-sa-sbac1=[87 50 90 50]; sum(ac1);ac2=[69 -10 53 0]; sum(ac2);ac3=[-20 -5 -36 0]; sum(ac3);ac4=[-38 -20 -30 -38]; sum(ac4);ac5=[10 -7 24 -17]; sum(ac5);ac6=[-50 -58 -30 -60]; sum(ac6);sac=(sum(ac1)^2+ sum(ac2)^2+ sum(ac3)^2+ sum(ac4)^2+ sum(ac5)^2+ sum(ac6)^2)/4-t2-sa-scbc1=[87 -20 10 90 -36 24]; sum(bc1);bc2=[69 -38 -50 53 -30 -30]; sum(bc2);bc3=[50 -5 -7 50 0 -17]; sum(bc3);bc4=[-10 -20 -58 0 -38 -60]; sum(bc4);sbc=(sum(bc1)^2+ sum(bc2)^2+ sum(bc3)^2+ sum(bc4)^2)/6-t2-sb-sc abc=(87+90)^2+(69+53)^2+(50+50)^2+(-10)^2+[(-20)+(-36)]^2+[(-38)+(-30)]^2+(-5)^2+[(-20)+(-38)]^2+(10+24)^2+[(-50)+(-30)]^2+[(-7)+(-17)]^2+[(-58)+(-60)]^2;sabc=abc/2-sab-sac-sbc-sa-sb-sc-t2se=st-sa-sb-sc-sab-sac-sbc-sabcmsa=sa/2;msb=sb/1;msc=sc/1;msab=sab/2;msac=sac/2;msbc=sbc/1;msab c=sabc/2;mse=se/12;fa=msa/msefb=msb/msefc=msc/msefab=msab/msefac=msac/msefbc=msbc/msefabc=msabc/mse计算求得方差分析表,见表4.表4 方差分析表Table 4 The variance analysis results来源平方和自由度均方和F值ASA=27696.002MSA=13848.00FA=191.67BSB=2480.701MSB=2480.70FB= 34.33CSC=7993.501MSC=7993.50FC=110.64ABSAB=4596.602MSAB=2298. 30FAB=31.81ACSAC=1345.802MSAC=672.90FAC=9.31BCSBC=240.671MS BC=240.67FBC=3.33ABCSABC=397.582MSABC=198.79FABC=2.75ESE=867 .0012MSE=72.25TST=45618.0023由于FA=191.67>F0.05(2,12)=3.89,FB=34.33>F0.05(1,12)=4.75,FC=110.64>F0.05 (1,12)=4.75,FAB=31.81>F0.05(2,12)=3.89,FAC=9.31>F0.05(2,12)=3.89,所以在α=0.05显著性水平下,因素A、因素B和因素C的不同水平都对该商品的销售量有非常显著的影响, 因素A,B和因素A,C两两的交互作用对该商品的销售量有显著影响.又由于FB C=3.33<F0.05(1,12)=4.75,FA B C=2.75<F0.05(2,12)=3.89,所以因素B,C和因素A,B,C的交互作用对该商品的销售量没有有显著影响. 综上所述,为了制定该商品在该城市更好的销售计划,地理位置、广告、装潢都需要进行合理的选择.同时,还要兼顾不同位置与广告的搭配,以及不同位置与装潢的合理选择.4 结语本文基于有交互影响的三因素方差分析原理,针对地理位置、销售点处的广告和销售点的装潢这3个因素对商品的影响程度,采用MATLAB进行求解,但MATLAB中的函数具有一定的局限性.故对算法进行了简化,并利用简化算法对该案例进行求解.结果表明该算法具有实用性和可行性.参考文献:【相关文献】[1] 吴坚. 应用概率统计[M]. 2版. 北京:高等教育出版社, 2007:262.WU J. Applied probability and statistics[M]. 2nd ed. Beijing: Higher education press, 2007:262.[2] 张忠群. 概率论与数理统计[M]. 贵阳:贵州大学出版社, 2008:203.ZHANG Z Q. Probability theory and mathematical statistics[M]. Guiyang: Guizhou University Press, 2008:203.[3] 魏宗舒. 概率论与数理统计教程[M]. 北京:高等教育出版社, 2001:372-391.WEI Z S. Courseson probability theory and mathematical statistics[M]. Beijing: Higher Education Press, 2001:372-391.[4] 郭萍. 三因素方差分析的原理及应用[J]. 沈阳大学学报(自然科学版), 2015,27(1):40-43.GUO P. Principle and application of three factors analysis of variance[J].Journal of Shenyang University(natural science), 2015,27(1):40-43.[5] 郭萍. 有交互影响的三因素方差分析原理及应用[J]. 曲阜师范大学学报(自然科学版),2015,41(4):15-18.GUO P. The principle and application of three factor analysis of variance with the interaction[J]. Journal of Qufu Normal University(natural science), 2015,41(4):15-18. [6] 司守奎. 数学建模算法与程序[M]. 北京:国防工业出版社, 2007:225.SI S K. Mathematical modeling algorithm and program[M]. Beijing: National Defense Industry Press, 2007:225.[7] 孙建英. MATLAB平台下运筹学模型的仿真实验[J]. 沈阳大学学报(自然科学版),2016,28(4):337-339.SUN J Y. Simulation experiment of operational research modelon MATLAB platform[J]. Journal of Shenyang University(natural science), 2016,28(4):337-339.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7
三因素方差分析举例
残差的正态性检验结果：P=0.9422>0.05
Skewness/Kurtosis tests for Normality ------- joint -----Variable | Pr(Skewness) Pr(Kurtosis) adj chi2(2) Prob>chi2 -------------+------------------------------------------------------e | 0.915 0.743 0.12 0.9422
8
三因素方差分析举例
Full model结果：二级交互作用项P=0.0214<0.05
Source | Partial SS df MS F Prob > F -----------+---------------------------------------------------Model | .347361264 7 .049623038 1.55 0.2202 a | .00201666 1 .00201666 0.06 0.8049 b | .044490835 1 .044490835 1.39 0.2554 c | .048001913 1 .048001913 1.50 0.2382 a*b | .0244907 1 .0244907 0.77 0.3944 a*c | .003112983 1 .003112983 0.10 0.7591 b*c | .017424103 1 .017424103 0.54 0.4711 a*b*c | .207824069 1 .207824069 6.50 0.0214 Residual | .511622125 16 .031976383 -----------+---------------------------------------------------Total | .858983389 23 .037347104
6
三因素方差分析举例
1.
Stata命令： anova y a b c a*b a*c b*c a*b*c predict e,residual 计算残差 sktest e 残差的正态性检验 gen ee=abs(e) 计算残差的绝对值 anova ee a b c a*b a*c b*c a*b*c 方差 齐性检验
三因素方差分析
赵耐青 复旦大学卫生统计教研室
1 * Yes not geese…
三因素方差分析的基本概念
三因素方差分析要求资料服从正态分布，方差齐 性，三个因素的不同水平组合样本资料独立， 要求三个因素的不同水平组合情况的样本量相 同。 三因素方差分析的模型：
abc ... a c c ( )ab ( )ac ( )bc ( )abc
9
三因素方差分析举例
Reduced Model 1：b*c项的P=0.5761，故剔除
Source | Partial SS df MS F Prob > F -----------+---------------------------------------------------Model | 4.16958384 6 .694930641 4.32 0.0079 a | .002016672 1 .002016672 0.01 0.9121 b | .077066736 1 .077066736 0.48 0.4981 c | .79935039 1 .79935039 4.97 0.0395 a*b | 1.9040668 1 1.9040668 11.84 0.0031 a*c | 1.33481659 1 1.33481659 8.30 0.0104 b*c | .052266656 1 .052266656 0.33 0.5761 Residual | 2.73359971 17 .160799983 -----------+---------------------------------------------------Total | 6.90318355 23 .300138415
称 ( )abc 为二级交互作用，称 ( )ab ,( )ac ,( )bc 为一级交互作用， 称 a , c , c 为主效应，如果三因 素方差分析模型中没有二级交互作用，则称该 模型为reduced model，反之称为Full model
2
三因素方差分析举例
某研究者以大白鼠作试验，观察指标是肝 重与体重之比(%)，研究正氟醚与观察指 标的作用，同时要考察用生理盐水和用戊 巴比妥作为诱导药对正氟醚毒性作用的影 响，并且考略不同性别大白鼠对诱导物的 作用和正氟醚毒性作用。因此共有3个因 素：(1)是否用正氟醚，(2)诱导物 （3） 性别
5
三因素方差分析举例
1. 2.
3.
分析策略： 由于样本量较小，所以先考察残差正态性和用 levene检验方差齐性 如果资料满足方差齐性和正态性，则首先考察 是否存在二级交互作用，如果二级交互作用项 的P0.05，则用角模型进行简单效应比较 如果二级交互作用项的P>0.05，则剔除二级 交互作用项，考察一级交互作用项，剔除 P>0.05的一级交互作用项，如果还存在一级 交互作用项，则用用角模型进行简单效应比较. 如果不存在一级交互作用的P0.05，则根据 主效应进行统计推断。
3
三因素方差分析举例
资料和变量定义如下
B 因素 生理盐水 生理盐水 戊巴比妥 戊巴比妥 生理盐水 生理盐水 戊巴比妥 戊巴比妥 C 因素 肝重与体重比 yijkt 雌 雄 雌 雄 雌 雄 雌 雄 5.26 5.68 5 5.52 5.87 5.5 6.13 6.46 5.42 5.6 6.3 7.02 4.64 4.6 6.02 5.7 5.83 5.38 6.2 5.21 5.7 5.9 5.44 5.48
A 因素 不用正氟醚 不用正氟醚 不用正氟醚 不用正氟醚 用正氟醚 用正氟醚 用正氟醚 用正氟醚
变量定义 不用正氟醚 用正氟醚 用生理盐水 用戊巴比妥 雌 雄 A=1 A=2 B=1 B=tata数据格式
y 5.26 5.68 5.83 5 5.52 5.38 5.87 5.5 a 1 1 1 1 1 1 1 1 b 1 1 1 1 1 1 2 2 c 1 1 1 2 2 2 1 1
方差齐性检验的主要结果:P=0.2202>0.10
Source | Partial SS df MS F Prob > F -----------+---------------------------------------------------Model | .347361264 7 .049623038 1.55 0.2202