结构力学习题集9-结构动力计算
《结构力学习题集》(含答案)
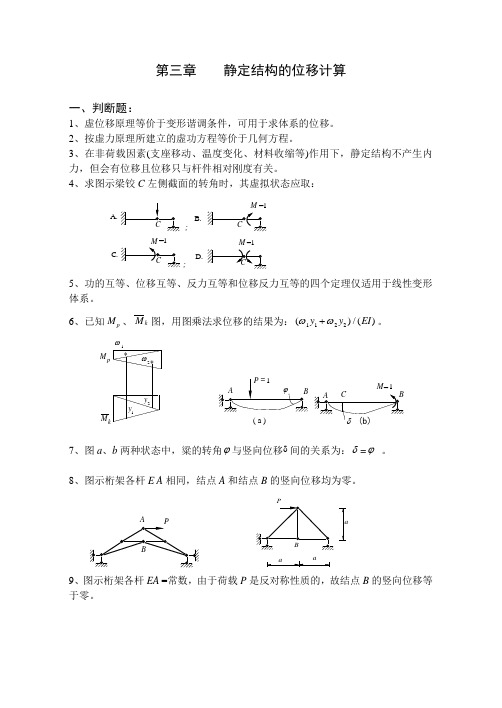
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M 17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l ll/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/2219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。
l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。
ll21、求图示结构B点的竖向位移，EI = 常数。
结构动力学计算题
无阻尼自由振动计算题(单位：kg、N = kg・m/s2、Pa = N/m2、)无阻尼自由振动运动方程：u(t) = u(0) cos w n t +丝^sinw湛；w n刚度k = F/* (kN/m)；自振圆频率3〃= £ = (rad/s)；无阻尼体系简谐荷载反应：其中频率比P = 0/w n；17(0) P o /? 1 P o 1u0)=状0)cos w n t + - sin啪 + 9t稳态反应等效静位移四=Po/k = P0/mw n2；稳态反应振幅I/。
= u st R d = y—K I1-P I阻尼c = 2mw n^ (kN * s/m)；阻尼比(=—=—— = 有阻尼圆频率c cr 2mw n 2nn ut+nW D = w n y/l-^2；有阻尼自振周期T D=L/房寻有阻尼体系动力方法系数R d= — = u st1/J[1一供]2 + [2〈仞2；拉格朗日方程计算题lagrange方程：，(茶J 一 *" += Q)；其中Q)为非有势力对应于广义坐标0/的广义力平面运动刚体的动能T = |mv c2+|/c w2,随质心平移的动能和绕质心转动的动能之和。
细直杆绕质心的转动惯量：J c—,对喘部：J z=■ ^mZ2；圆盘对其质心的转JL£O动惯量：]0— ^mr2o振型叠加法计算题(第一类型)频率方程:\[K] - a)2[M]| = 0得自振频率s由特征方程:([K] - 口2[的)｛勿=0；设｛飕)=1,得到｛破)和｛泌。
已知条件 1:切}i = [o.644，、{必2 = {-0.601，、切}3={-2.57＞、[M]= (0.311.52.可得振型质量:M n =同理可知M 2 = 2.456, M3 = 23.109。
1.5 ) 加已知条件 2： m (0)} = {2.5 }m,位(0)} = {2.25 m/s4.50)-0.6762.47可知 Mi = {0}7[M]{0h = (1 0.644 0.3)1 ・1.5 .2.。
(整理)《结构力学2》习题集同济版.
南华大学《结构力学II》习题集（适合于大土木工程各专业方向）组编：刘华良班级：姓名：学号：建筑工程与资源环境学院道路桥梁工程教研室衡阳2005年前言本习题集取材于第九章位移法9-l 确定下列各结构的位移法未知数目，并绘出基本结构。
9-2~9-3 用位移法计算下列结构内力．并绘出其弯矩图、剪力图和轴力图。
题9-2图题9-3图9-4~9-11 用位移法绘制下列结构弯矩图。
题9-4图题9-5图题9-6图题9-7图题9-8图题9-9图题9-10图题9-11图9-12~9-15 用位移法绘制下列具有斜杆的刚架的弯矩图。
题9-12图题9-13图题9-14图题9-15图9-16~9-17 列出下列结构的位移法典型方程式，并求出所有系数和自由项。
题9-16图题9-17图9-18~9-23 用位移法绘制下列具有无限刚性杆结构的M图。
题9-18图题9-19图题9-20图题9-21图题9-22图题9-23图9-24~9-26 用位移法绘制下列刚架M图。
题9-24图题9-25图题9-26图9-27 用位移法绘制图9-27所示结构弯矩图，并求桁架杆的轴向力。
题9-27图9-28 用位移法求图9-28所示桁架各杆轴向力。
题9-28图9-29 图9-29所示为一个三角形刚架，考虑杆件的轴向变形，试写出位移法的典型方程，并求出所有系数和自由项。
题9-29图9-30~9-31 用位移法计算图示有剪力静定杆组成的刚架的M图。
题9-30图题9-31图9-32~9-41 利用对称性，用位移法求作下列结构的M图。
题9-32图题9-33图题9-34图题9-35图题9-36图题9-37图题9-38图题9-39图题9-40图题9-41图9-42~9-48 试直接按平衡条件建立位移法方程计算题9-2、9-5、9-8、9-11、9-12、9-24、9-35，并绘出M图。
题9-42图题9-43图题9-44图题9-46图题9-47图题9-48图9-49~9-52 试用位移法求作下列结构由于支座位移产生的M图。
结构动力计算课后习题答案
结构动力计算课后习题答案结构动力计算是土木工程和机械工程领域中的一个重要分支，它涉及到结构在动力作用下的响应分析。
这门课程的课后习题通常要求学生运用所学的理论，解决实际工程问题。
以下是一些可能的习题答案示例，请注意，这些答案是基于假设的习题内容，实际的习题答案应根据具体的题目来确定。
习题1：单自由度系统的动力响应假设有一个单自由度系统，其质量为m，阻尼系数为c，刚度系数为k。
系统受到一个简谐激励F(t) = F0 * sin(ωt)，其中F0是激励力的幅值，ω是激励频率。
求系统的稳态响应。
答案：对于单自由度系统，其运动方程可以表示为：\[ m\ddot{x}(t) + c\dot{x}(t) + kx(t) = F_0 \sin(\omega t) \]稳态响应可以通过求解上述方程的特解来获得。
特解的形式为：\[ x(t) = X \sin(\omega t + \phi) \]其中，振幅X和相位角φ可以通过以下公式计算：\[ X = \frac{F_0}{\sqrt{(\omega^2 m - \omega^2)^2 +(c\omega)^2}} \]\[ \phi = \arctan\left(\frac{c\omega}{\omega^2 m -\omega^2}\right) \]习题2：多自由度系统的模态分析考虑一个两自由度系统，其质量矩阵、刚度矩阵和阻尼矩阵分别为：\[ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix},\quad K = \begin{bmatrix} k_1 & k_c \\ k_c & k_2\end{bmatrix}, \quad C = \begin{bmatrix} c_1 & 0 \\ 0 & c_2\end{bmatrix} \]求系统的自然频率和模态形状。
结构力学 结构的动力计算
小结
4. 两个自由度体系的自由振动有两个自振频率，数值较小的称为基本频率； 相应地有两个主振型。关键是如何计算结构的柔度系数或刚度系数，并验 证主振型的正交性。 5. 两个自由度体系的受迫振动，各质点的振幅、动力幅值没有一个统一的 动力系数，这是和单自由度体系受迫振动不同的。 6. 振型分析法将无限自由度体系的自由振动问题转化为单自由度体系的计 算问题。它将复杂的问题分解为简单的问题，使我们看出复杂运动与主振 型之间关系的规律。
子项目 结构的动力计算 知识链接
（2）冲击荷载 这类荷载在很短时间内，荷载值急剧增大（图 5 – 2a）或急剧减小（图 5 – 2b）。各种爆炸荷载都属于这一类。当升载时间趋于零时，就是突加荷载 （图 5 – 2c）。
子项目 结构的动力计算 知识链接
（3）随机荷载 这类荷载的特点是荷载随时间变化的规律很不规则，荷载在任一时刻 t 的数值无法事先确定，要通过记录和统计得到其规律和计算数值。如地 震作用的地面运动加速度（图 5 – 3）。
子项目 结构的动力计算 知识链接
3．动力计算的自由度 在进行动力计算时，也需选取一个合理的计算简图，但考虑惯性力的作用，需要 确定质量在运动中的状态。因此，体系的自由度是指为了确定运动过程中任一时 刻全部质量的位置所需要的独立几何参数的数目。 实际结构的质量都是连续分布的，在计算中常把连续分布的无限自由度问题简化 为有限自由度问题。
子项目 结构的动力计算
知识链接
概括起来，动力计算的基本特点： ① 动力响应与时间有关，即荷载、位移、内力等随时间急剧变化。 ② 建立平衡方程时要包括质量的惯性力。 2．动力荷载的分类 工程中常见的动力荷载有以下几种分类： （1）周期荷载 这类荷载随时间作周期性的变化。简谐荷载是周期荷载中最简单也是最 重要的一种，它随时间 t 的变化规律可用正弦或余弦函数表示，如图 5 – 1b 所示。具有偏心质量的机器（图 5 – 1a）运转时，传到结构上的 偏心力 P(t) 随时间 t 的变化规律可用Psinθt和Pcosθt表示。
结构动力学习题+讲解
&&(t ) + （ω2 – n2 ）S (t) = 0 --------------------------------------------（5） S
1．当 n >ω时（强阻尼） 方程（5）的解为： S (t) = A1sh n − ω t +A2ch n − ω t
2 2 2 2
从而，方程（4）的解为：
若时间 t 不是从 0 开始，而是从τ开始的，则（9）式写为：
y (t ) =
p∆t sinω（t-τ） mω
---------------------------------------（10）
写作： ，记ω2 =
K m
，2n =
C ，又可写作： m
& &(t ) + 2n y & (t ) +ω2 y (t ) = 0 y
利用常数变易法，令 y (t ) = e
− nt
---------------------------------------------（4）
S (t ) 代入方程（4）中 得：
K/2 VBA
48i/7L
2
A
取横梁为研究对象，Σ X=0，得：K= 4）振动方程
24 EI L3
即，
&(t ) - K y(t ) + Psinθt = 0 y - 2 m& &(t ) + y 2 m&
24 EI y(t ) = Psinθt L3
一、 无阻尼的自由振动
振动方程
&(t ) +K y (t ) = 0 ， m& y & &(t ) + y K y (t ) = 0 m
建筑结构力学讲义第九章 结构的动力计算
建筑力学
三、惯性力
当物体受外界因素的作用发生运动状态的 改变，即获得加速度时，物体由于惯性产生 对外界抵抗的作用力称为惯性力。正是由于 惯性力的作用使结构的动力计算具有不同于 静力计算的特点。
谢 谢
FP (t )
FP
-FP
简谐荷载
t
பைடு நூலகம்
建筑力学
2. 冲击荷载
这类荷载在很短的时间内，荷载值急剧 增大或急剧减小。
FP (t )
FP (t )
FP
FP
tr
a)
t
td
b)
t
核爆炸冲击波荷载曲线
化爆冲击波荷载曲线
建筑力学
3. 随机荷载 荷载在将来某一时刻的大小和方向无法事先 确定，称为非确定性荷载，或称为随机荷载， 例如地震荷载及风荷载就是随机荷载。
一般而言， TH / TJ ≥5，该荷载就可作为静荷 载处理。
建筑力学
3. 动力反应 在动荷载作用下，结构产生振动，结构的分 布质量和集中质量的位移、速度、加速度以及 作用在质量上的惯性力等都是时间 t 的函数， 结构任一截面的内力也是时间 t 的函数。上述 内力、位移、速度、加速度以及惯性力等统称 为结构的动力反应。 学习动力学就是要掌握动力反应的计算原理 和方法，并确定其随时间的变化规律。 另外，结构的自振频率、自振周期和阻尼特 性，以及多自由度体系的主振型等则是结构固 有的动力特性，这些参数对结构的动力分析有 着重要的影响。
建筑力学
2. 荷载周期与结构自振周期
一种荷载是否作为动荷载来处理，我们通 常用荷载周期TH与结构自振周期TJ的比值来 衡量。 如一种荷载的周期TH =1秒，而TJ =0.1秒， 有TH / TJ =10，则荷载对结构而言可当作静荷 载处理。若结构自振周期TJ =10秒，有TH / TJ =0.1，则该荷载就应作为动荷载来处理。
结构动力学习题+讲解
结构动力学*本章讨论结构在动力荷载作用下的反应。
**学习本章注重动力学的特征------惯性力。
*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律，从而找出其最大值作为设计的依据。
*动力学研究的问题：动态作用下结构或构件的强度、刚度及稳定性分析。
一、本章重点1．振动方程的建立2．振动频率和振型的计算3．振型分解法求解多自由度体系4．最大动位移及最大动应力二、基础知识1．高等数学2．线性代数3．结构力学三、动力荷载的特征1．大小和方向是时间t的函数例如：地震作用，波浪对船体的作用，风荷载，机械振动等2．具有加速度，因而产生惯性力四、动力荷载的分类1．周期性动力荷载例如：①机械运转产生的动力荷载，②打桩时的锤击荷载。
P（t） Pt t（机械运转荷载）（打桩荷载）2．冲击荷载例如：①爆炸力产生的动力荷载，②车轮对轨道连接处的冲击。
P（t）P（t）P（t）t t t（爆炸力动力荷载）（吊车起吊钢索的受力）（随机动力荷载）3．突加常量荷载例如：吊车起吊重物时钢索的受力。
4．随机动力荷载前3类荷在是时间t的确定函数，称为确定性动力荷载；而地震作用，波浪对船体的作用，风荷载等其作用大小只能用统计的方法获得。
五、动力荷载的计算方法1．原理：达朗贝尔原理，动静法建立方程2．计算工具：微分方程，线性代数，结构力学六、体系振动的自由度---------动力自由度结构具有质量，有质量在运动时就有惯性力。
在进行动力计算时，一般把结构的质量简化为若干质点的质量，整个结构的惯性力就成为各质点的惯性力问题。
1．质点简化的一般要求①简单，②能反映主要的振动特性例如：楼房；质量集中在各层楼板平面内水塔：质量集中在水箱部分梁：无限自由度集中质量（楼房质量集中）（水塔质量集中）（梁的质量集中）2．位移y（t）即指质点的位移y（t），其加速度为y&&)(t3．动力自由度的确定即质点位移数量的确定。
结构动力学习题
结构动力学一、填空题1、右图所示振动体系不计杆件的轴向变形，则 动力自由度数目是 。
2、单自由度体系只有当阻尼比ξ 1时才会产生振动现象。
3、已知结构的自振周期s T 3.0=，阻尼比04.0=ξ，质量m 在0,300==v mm y 的初始条件下开始振动，则至少经过 个周期后振幅可以衰减到mm 1.0以下。
4、多自由度框架结构顶部刚度和质量突然变 时，自由振动中顶部位移很大的现象称 。
二、判断以下说法是否正确.1、凡是大小、方向、作用点位置随时间变化的荷载，在结构动力计算中都必须看作动力荷载。
（ ）2、超静定结构体系的动力自由度数目一定等于其超静定次数。
（ ）3、为了避免共振，要错开激励频率和结构固有频率，一般通过改变激励频率来实现。
（ ）4、求冲击荷载作用下结构的反应谱曲线时一般不计阻尼的影响。
（ ）5、求静定的多自由度体系的频率和振型，一般采用刚度法比采用柔度法方便。
（ ）三、选择题1、对单自由度体系的自由振动，下列说法正确的是（ B ）A C 、振幅和初相角仅与初始条件有关 2、图示（a ）、（b A 、b a ωω<B 、∞→EA 时b a ωω≈C 、0→EA 时b a ωω≈D 、b a ωω=3、（1）无阻尼的自由振动（2）不计阻尼，零初始条件下t P θsin 产生的过渡阶段的振动 （3）有阻尼的自由振动（4）突加荷载引起的无阻尼强迫振动 A 、（1）（2）（3） B 、（1）（2）（4）4、右图的单自由度体系，结构的固有频率为ω A 、很小 B 、很大C 、接近静位移st y一、填空题。
（11分）1、2 （3分）2、< （3分）3、14 （3分）4、小鞭梢效应（3分）二、判断以下说法是否正确，对错误的说法加以改正。
（6×3分=18分）1、（×）改正：可简单地在“都是”前加上“不”；或改为“大小、方向、作用点位置随时间变化的荷载，只有使结构的质量产生显著加速度的在结构动力计算中才看作动力荷载。
结构动力学习题
结构动力计算习题习题9－1图示各系统的动力自由度为多少？都是什么？m m m m m m mm（1） （2） （3） （1）①△1x =△2x （2）①△1x =△2x =△3x （3）①△1y =△3y ②△1y ②△1y ②△2y ③△2y ③△3ymmmmmmmmm（4） （5） （6） （4）①△1x （5）①△1y （6）①△1y ②△1y =△2y ②△2x ②△2x ③△3y ③△2y =△3y ③△2y =△3ym m mm mm mm（7） （8） （9） （10） （7）①△1x =△2x （8）①△1x （9）①△1x （10）①△1x ②△2y ②△1y ②△2x ②△2x ③△2x ③△2y ④△2ym m mm m m mm m（11） （12） （13）（11）①△1x =△2x =△3x （12）①△1x =△2x =△3x =△4x （13）①△1x =△2x②△2y ②△1y ②△1y③△4y ③△2ym mm mm mmm（14） （15） （16） （17） （14）①△1x （15）①△1x （16）①△1x （17）①△1x =△2x ②△2x ②△1y ②△1y ②△2y ③△2x ③△2x ④△2y习题9－2图示各系统作强迫振动，已知激振力的频率与系统的自振频率之比，试求系统的动力系数β和最大动弯矩m ax d M 。
2l ltF θsin m2llmFFlM 图（1）32=ωθ， 2211ωθβ-=599411=-=， Fl M d 59m ax =tF θsin mlmlM 图FFl（2）32=ωθ， 2211ωθβ-=33211=-=， Fl M d 3m ax =ltF θsin lmM 图FFl /2（3）53=ωθ， 2211ωθβ-=255311=-=， 45m ax Fl M d = tF θsin mlmlM 图FFl（4）21=ωθ， 2211ωθβ-=22111=-=， Fl M d 2m ax =l /2tF θsin l /2mM 图FFl /4（5）32=ωθ， 2211ωθβ-=33211=-=， 43m ax FlM d =l l /2tF θsin mll /2mFFl /2M 图（6）21=ωθ， 2211ωθβ-=344111=-=， 32max Fl M d =llmtF θsin llmM 图FFl（7）43=ωθ， 2211ωθβ-=44311=-=， Fl M d 4m ax =mtF θsin ll /2M 图FFl /2Fl /2（8）31=ωθ， 2211ωθβ-=233111=-=， 43m ax Fl M d = mtF θsin ll /2mM 图F Fl /2Fl /2（9）31=ωθ， 2211ωθβ-=899111=-=， 169m ax Fl M d = 习题9－3求图示各系统的自振频率。
结构动力学结构动力学试卷(练习题库)(2023版)
结构动力学结构动力学试卷（练习题库）1、结构动力计算与静力计算的主要区别是什么？2、什么是动力自由度，确定体系动力自由度的目的是什么？3、结构动力自由度与体系几何分析中的自由度有何区别？4、结构的动力特性一般指什么？5、什么是阻尼、阻尼力，产生阻尼的原因一般有哪些？什么是等效粘滞阻尼？6、采用集中质量法、广义位移法（坐标法）和有限元法都可使无限自由度体系简化为有限自由度体系，它们采用的手7、建立运动微分方程有哪几种基本方法？各种方法的适用条件是什么？8、直接动力平衡法中常用的有哪些具体方法？它们所建立的方程各代表什么条件？9、刚度法与柔度法所建立的体系运动方程间有何联系？各在什么情况下使用方便？10、计重力与不计重力所得到的运动方程是一样的吗？11、自由振动的振幅与哪些量有关？12、什么叫动力系数，动力系数大小与哪些因素有关？单自由度体系位移动力系数与内力动力系数是否一样？13、若要避开共振应采取何种措施？14、增加体系的刚度一定能减小受迫振动的振幅吗？15、突加荷载与矩形脉冲荷载有何差别。
16、平断面假定17、弯曲要素18、梁的边界条件19、叠加原理20、三弯矩方程21、平断面假定22、梁的边界条件23、叠加原理24、三弯矩方程25、虚位移原理26、虚力原理27、位能驻值原理28、板条梁29、开口和闭口薄壁杆件。
30、应力的重新分布。
31、几何不变体32、自由度33、多余约束34、超静定结构35、形常数和载常数36、试简述影响线与内力图的区别？37、力法和位移法的解题思路？38、几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。
39、有多余约束的体系一定是几何不变体系。
40、计算自由度W小于等于零是体系几何不变的充要条件。
41、两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必须满足的条件。
42、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。
结构动力学计算题
=
−6.612375 = −2.6923 2.456 1 −2.570 2.470 1 1.5 2 1.5 2.25 4.50 = 15.05625 23.109
������ ������ 0 ������ ������
������3 0 =
������
������ 3
������ ������ 0 = ������3
=
������������ ������ ������������������
平面运动刚体的动能T = ������������������ 2 + ������������ ������ 2 ， 随质心平移的动能和绕质心转动的动能 之和。 细直杆绕质心的转动惯量：������������ = 动惯量：������������ = ������������ 2 。
=
0 0 0 ������ ������ ������������ ������ = ������ 1 ������1 ������ + ������ 2 ������2 ������ +
������3������30������
弯曲梁计算题 弯矩与曲率关系：M = −������������
������ 2 ������ ������ ,������ ������ 2 ������ ������������ ������������
= −������������������′′ ；剪力Q =
������ 2 ������ (������ ,������ ) ������ 2 ������
；
等截面梁自由振动偏微分方程：������
+ ������������
������ 4 ������ (������ ,������ ) ������ 4 ������
《结构力学习题集》9-结构动力计算
第九章 结构的动力计算一、是非题1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形，图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ，W =98.kN ，欲 使 顶 端 产 生 水 平位 移 ∆=001.m ，需 加 水 平 力 P =16kN ，则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ，杆 重 不 计 ，EA 为 常 数 ，在 C 点 的 竖 向 初 位 移 干 扰 下 ，W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ，图 示 体 系 的 运 动 方 程 为 ：m m X X h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭()二、选择题1、图 示 体 系 ，质 点 的 运 动 方 程 为 ： A ．()()()y l Ps in my EI =-77683θ t /； B ．()()my EI y l Ps in /+=19273θ t ； C ．()()my EI y l Ps in /+=38473θ t ； D ．()()()y l Ps in my EI =-7963θ t / 。
2、在 图 示 结 构 中 ，若 要 使 其 自 振 频 率 ω增 大 ，可 以A ．增 大 P ；B ．增 大 m ；C ．增 大 E I ； D ．增 大 l 。
结构的动力计算习题
《结构的动力计算》习题一、判断题1、图示等效体系的关系是：3211111k k k k ++=。
（ ）2、结构的动力反应只与初始条件及动荷载有关。
（ ）3、任何动力荷载作用下均可以采用公式：1221-⎪⎪⎭⎫⎝⎛-=ωθβ计算动力系数。
（ ） 4、外界感干扰力只影响振幅、不影响体系的自振频率。
（ ）5、体系的动力自由度数与质点的个数无关、也与结构静定或超静定无关。
（ ）6、图示体系各杆自重不计、EA =∞，则该体系在初始时刻的干扰力作用下将做竖向振动。
（ ）二、选择题1、增加单自由度体系的阻尼、但仍保持为低阻尼体系，其结果是（ ）。
A 、周期变长 B 、周期不变 C 、周期变短 D 、 周期视具体体系而定2、图示两个等效结构，正确的刚度关系是（ ）。
A 、k=k 1+k 2 B 、21111k k k += C 、21211k k k k k += D 、2112k kk k k +=3、图示体系不计阻尼，平稳阶段最大动位移y max =4Pl 3/7EI ，其最大动力弯矩为（ ）。
A 、3Pl /7 B 、4Pl /7 C 、12Pl /7 D 、4Pl /21 4、下列哪句话有错误或不够准确（）。
第3题图A、在多自由度体系自由振动问题中，主要问题是确定体系的全部自振频率和相应的主振型； B 、多自由度体系的自振频率不止一个，其个数与自由度个数相等；C 、每个自振频率都有自己相应的主振型，主振型就是多自由度体系振动时各质点的位移变化形式；D 、与单自由度体系相同，多自由度体系的自振频率和相应的主振型也是体系本身的固有性质。
5、图示单自由度体系自振周期的关系为（ ）。
A 、(a)=(c)B 、(a)=(b)C 、(b)=(c)D 、都不相等6、单自由度振动体系中，若质点在杆的中点，各杆EI 、l 相同，其自振周期的大小排列顺序为（A 、(c)＞(a)＞(b)B 、(c)＞(b)＞(a) C 、(a)＞(b)＞(c) D 、(b)＞(c)＞(a)三、分析计算题1、梁的抗弯刚度为EI2m3、柱的自重不计，求图示刚架的自振频率。
结构动力计算习题
160结构动力计算习题一．选择题8-1 体系的动力自由度是指（ ）。
A ．体系中独立的质点位移个数B ．体系中结点的个数C ．体系中质点的个数D ．体系中独立的结点位移的个数 8-2 下列说法中错误的是（ ）。
A ．质点是一个具有质量的几何点；B ．大小、方向作用点随时间变化的荷载均为动荷载；C ．阻尼是耗散能量的作用；D ．加在质点上的惯性力，对质点来说并不存在 8-3 图示体系EI =常数，不计杆件分布质量，动力自由度相同的为（ ）。
题8-3图A ．（a ）、（b ）、（c ）B ．（a ）、（b ）C ．（b ）、（c ）D ．（a ）、（c ） 8-4图示体系不计杆件分布质量，动力自由度相同的为（ ）。
(b )(c )题8-4图A ．（a ）、（b ）、（c ）B ．（a ）、（b ）C ．（b ）、（c ）D ．（a ）、（c ）8-5 若要提高单自由度体系的自振频率，需要（ ）。
A ．增大体系的刚度B ．增大体系的质量C ．增大体系的初速度D ．增大体系的初位移 8-6不计阻尼影响时，下面说法中错误的是（ ）。
A ．自振周期与初位移、初速度无关；B ．自由振动中，当质点位移最大时，质点速度为零；C ．自由振动中，质点位移与惯性力同时达到最大值；D ．自由振动的振幅与质量、刚度无关 8-7 若结构的自振周期为T ，当受动荷载)(P t F =t F θsin 0作用时，其自振周期T （ ）。
A ．将延长B ．将缩短C ．不变D ．与荷载频率θ的大小有关8-8 若图（a ）、（b ）和（c ）所示体系的自振周期分别为a T 、b T 和c T ，则它们的关系为（ ）。
(a)(b)(c)题8-8图A ．a T >b T >c TB ．a T >c T >b TC ．a T <c T <b TD ．a T =c T <b T 8-9 振幅计算公式βst y A =中的st y 为（ ）。
习题课12.结构动力计算(一)
EI → ∞
A
k a
a
(不计分布质量)
m EI → ∞ m 3aθ (t ) θ (t ) aθ (t ) 2aθ (t )
FR = 2aθ (t )k
∑M
A
=0
&& && 2aθ (t ) k ⋅ 2a = − maθ (t ) ⋅ a − 3maθ (t ) ⋅ 3a && 10ma 2θ (t ) + 4ka 2θ (t ) = 0
−u0θ 2 u0θ 2 y (t ) = 2 sin θ t = 2 2 θ −ω ω −θ 2
u0θ 2 θ2 y (t ) = 2 sin θ t = u0 ⋅ 2 ⋅ 2 ω −θ ω
1
= β yst sin θ t = A sin θ t
θ 1− 2 ω
2
sin θ t
β=
1
θ2 1− 2 ω
2）求 ω
g 980 ω= = = 3266.667 = 57.15(1 s ) −2 Wδ 40 × 0.75 ×10
3）求
ymax
∆ st = W δ = 40 × 0.75 × 10−2 = 30 × 10−2 m = 0.3cm
A= v0 198 2 y + = 0.3 + ω 57.15
&&(t ) + 0.75 k θ (t ) = 0 θ ml
k ω = 0.866 ml
三．重物自高处下落到梁中点即与梁一起振动，求 自振频率ω 、振幅A及最大挠度ymax 。（W=40kN ， h=20cm， l=6m， E=3×103kN/cm2 ， I=2×105cm4）
结构动力学列方程例题
5 m1 k11 y1 P1 (t ) P2 (t ) y 8
列运动方程练习题11：超静定刚架列运动方程
P(t )
m2
EI
EI1 EI1
m1 EI
EI
l l
P(t ) m2 2 y
y2 y1
自由度确定 加惯性力
P(t ) m2 2 y
y2 y1
附加约束
6i l
基本体系
1
m1 y
k11
ql 2 12
F1P
6i l
M 1图
q(t )
ql 12
2
M P图
k11 y1 F1P 0
k11
12i l2
F1P (m1 ) y
q(t )l q(t )l m1 y 2 2
m1 k11 y1 0 m1 y y
12 EI q(t )l y1 3 l 2
列运动方程练习题9：超静定刚架 y1
m
m
m1 y
y1
11
1
求单位力 引起位移
EI
l
EI
自由度-位移确定
施加惯性力 变成静力问题
l
y1 (m1 ) 11 y
1
X1 l
基本体系
l
M 1图
X1 1
1
l
M P图
1
3 l 8 5 l 8
3 l 8
m1 1 y
q(t )
6i l 6i l
m1 1 y
q(t )
q(t )
6i l
EI
l
6i l 6i l
1
6i l
6i l 6i l
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第九章 结构的动力计算一、是非题1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。
2、忽略直杆的轴向变形，图示结构的动力自由度为4个。
3、仅在恢复力作用下的振动称为自由振动。
4、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。
5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。
l /2l /2l /2l /2(a)(b)6、单 自 由 度 体 系 如 图 ，W =98.kN ，欲 使 顶 端 产 生 水 平位 移 ∆=001.m ，需 加 水 平 力 P =16kN ，则 体 系 的 自振 频 率 ω=-40s 1。
∆7、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。
8、由于阻尼的存在，任何振动都不会长期继续下去。
9、桁 架 ABC 在 C 结 点 处 有 重 物 W ，杆 重 不 计，EA 为 常 数 ，在 C 点 的 竖 向 初 位 移 干 扰 下 ，W 将 作 竖 向 自 由 振 动 。
AC10、不 计 阻 尼 时 ，图 示 体 系 的 运 动 方 程 为 ：m m XX h EI EI EI EI X X P t 00148242424012312⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭+--⎡⎣⎢⎤⎦⎥⎧⎨⎩⎫⎬⎭=⎧⎨⎩⎫⎬⎭&&&&()二、选择题1、图 示 体 系 ，质 点 的 运 动 方 程 为 ： A ．()()()y l Ps in my EI =-77683θ t &&/； B ．()()my EI y l Ps in &&/+=19273θ t ；C ．()()my EI y l Ps in &&/+=38473θ t ；D ．()()()y l Ps in my EI =-7963θ t &&/ 。
ll0.50.52、在 图 示 结 构 中 ，若 要 使 其 自 振 频 率 ω增 大 ，可 以A ．增 大 P ；B ．增 大 m ；C ．增 大 E I ；D ．增 大 l 。
lt )3、单 自 由 度 体 系 自 由 振 动 的 振 幅 取 决 于 ： A ．初 位 移 ；B ．初 速 度 ；C ．初 位 移 、初 速 度 与 质 量 ；D ．初 位 移 、初 速 度 与 结 构 自 振 频 率 。
4、考 虑 阻 尼 比 不 考 虑 阻 尼 时 结 构 的 自 振 频 率 ：A ．大 ；B ．小 ；C ．相 同 ；D ．不 定 ，取 决 于 阻 尼 性 质 。
5、已 知 一 单 自 由 度 体 系 的 阻 尼 比 ξ=12.，则 该 体 系自 由 振 动 时 的位 移 时 程 曲 线 的 形 状 可能为 ：D.C.B.A.6、图 a 所 示 梁 ，梁 重 不 计 ，其 自 振频 率 ()ω=76873EI ml /；今 在 集 中质 量 处 添 加 弹 性 支 承 ，如 图 b 所 示 ，则 该 体 系 的 自 振 频 率 ω为 ：A ．()76873EI ml k m //+；B ．()76873EI ml k m //-；C ．()76873EI ml k m //-； D ．()76873EI ml k m //+ 。
l l/2/2l l/2/2(a)(b)7、图 示 结 构 ，不 计 阻 尼 与 杆 件 质 量 ，若 要 其 发 生 共 振 ，θ 应 等 于 A ．23k m ； B ．k m 3；C ．25k m ；D ．k m5 。
tsin θl /2l /2l /28、图 示 两 自 由 度 体 系 中 ，弹 簧 刚 度为 C ，梁 的 EI = 常 数 ，其 刚 度 系 数 为 ：A ．k EI l k C k k 113221221480====/,, ； B ．k EI l C k C k k C 11322122148=+===-/,, ； C ．k EI l C k C k k C 11322122148=+===/,, ； D ．k EI l k C k k C 11322122148====/,, 。
l /2l /29、图 为 两 个 自 由 度 振 动 体 系 ，其 自 振 频 率 是 指 质 点 按 下 列 方 式 振 动 时 的 频 率 ：A ．任 意 振 动 ；B ．沿x 轴 方 向 振 动 ；C ．沿 y 轴 方 向 振 动 ；D ．按 主 振 型 形 式 振 动 。
10、图 示 三 个 主 振 型 形 状 及 其 相 应 的 圆 频 率 ω，三 个 频 率 的 关 系 应 为 ：A ．ωωωa b c <<； B ．ωωωb c a <<； C ．ωωωc a b <<； D ．ωωωa b c >> 。
(a)(b)(c)ωaωb ωc三、填充题1、不 计 杆 件 分 布 质 量 和 轴 向 变 形 ，刚 架 的 动 力 自 由 度 为 ：(a) ，(b) ，(c) ，(d) ，(e) ，(f) 。
(d)2、图示组合结构，不计杆件的质量，其动力自由度为 个。
3、图 示 简 支 梁 的 EI = 常 数 ，其 无 阻 尼 受 迫 振 动 的位 移 方 程 为 。
/3l /3l /3l4、图 示 体系 的 自 振 频 率 ω= 。
ll5、图 示 体 系 中 ，已 知 横 梁 B端 侧 移 刚 度 为 k 1 ，弹 簧 刚 度 为 k 2 ，则 竖 向 振 动 频 率 为 。
26、在 图 示 体 系 中 ，横 梁 的 质 量 为 m ，其 EI 1=∞；柱 高 为l ，两 柱 EI = 常 数 ，柱 重 不 计 。
不 考 虑 阻 尼 时 ，动 力 荷 载 的 频 率 θ=时 将发 生 共 振 。
P sin tθ 7、单 自 由 度 无 阻 尼 体 系 受 简 谐 荷 载 作 用 ，若 稳 态 受 迫 振 动 可 表 为 y y t =⋅⋅μθst sin ，则 式 中 μ 计 算 公 式 为 ， y s t 是 。
8、图 示 体 系 不 计 阻 尼 ，θωω=2(为 自 振 频 率 )，其 动 力 系 数 =μ 。
其中δ22等于。
10、多自由度体系自由振动时的任何位移曲线，均可看成的线性组合。
四、计算题1、图示梁自重不计，杆件无弯曲变形，弹性支座刚度为k，求自振频率ω。
l/2l/22、求图示体系的自振频率ω。
l l0.5l0.53、求图示体系的自振频率ω。
EI = 常数。
ll0.54、求图示结构的自振频率ω。
l l5、求图示体系的自振频率ω。
EI=常数，杆长均为l。
6、求图示体系的自振频率ω。
杆长均为l。
7、图示梁自重不计，W EI ==⨯⋅2002104kN kN m 2,，求自振圆频率ω。
B2m2m8、求图示单自由度体系的自振频率。
已知其阻尼比ξ=0.05。
m9、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 210、求图示体系的自振频率ω。
各杆EI = 常数。
a aal /2l /2(a)l /2l /2(b)12、图示桁架在结点C 中有集中重量W ，各杆EA 相同，杆重不计。
求水平自振周期T 。
3W m 3m13、忽略质点m 的水平位移，求图示桁架竖向振动时的自振频率ω。
各杆EA = 常数。
m 4m4m14、求图示体系的运动方程。
llm0.50.515、图示体系kN,5 s 20 kN/cm 102-124==⨯=P ,,EI θ 2cm kN, 480020==I W 。
求质点处最大动位移和最大动弯矩。
W4mm2sin P t16、图示体系，已知质量m = 300kg ，EI l =⨯⋅=910462N m m , ；支座B 的弹簧刚度系数k EI l 0348=/，干扰力幅值P =20kN ，频率θ=80s -1。
试计算该体系无阻尼时的动力放大系数μD1和当系统阻尼比ξ=005.时的有阻尼动力放大系数μD2 。
l /2l /217、求图示体系在初位移等于l/1000，初速度等于零时的解答。
θωω=020.( 为自振频率)，不计阻尼。
m18、图示体系受动力荷载作用，不考虑阻尼，杆重不计，求发生共振时干扰力的频率θ。
/3P tsin( )19、已知：m P ==38t, kN ，干扰力转速为150r/min ，不计杆件的质量，EI =⨯⋅6103kN m 2。
求质点的最大动力位移。
2m2m20、图示体系中，电机重kN 10=W 置于刚性横梁上，电机转速n r =500/min ，水平方向干扰力为) sin(kN 2)(t t P θ⋅=，已知柱顶侧移刚度kN/m 1002.14⨯=k，自振频率ω=-100s 1。
求稳态振动的振幅及最大动力弯矩图。
( )t m21、图示体系中，kN 10=W ，质点所在点竖向柔度m kN /10917.14-⨯=δ，马达动荷载P t t ()sin()=4kN θ，马达转速n r =600/min 。
求质点振幅与最大位移。
22、图示单自由度体系，欲使支座A 负弯矩与跨中点D 的正弯矩绝对值相等，求干扰力频率θ。
EI =常数。
ll /2l23、求图示体系支座弯矩M A 的最大值。
荷载P t P t (),.==004sin θθω 。
l l /2/224、求图示体系稳态阶段动力弯矩幅值图。
θωω=05.( 为自振频率)，EI = 常数，不计阻尼。
lll25、试 列 出 图 示 体 系 的 振 幅 方 程 。
12层间侧移刚度均为k 。
求自振频率及主振型。
m 1m 22127、求图示体系的自振频率并画出主振型图。
m28、求图示体系的自振频率和主振型。
EI = 常数。
l l29、求 图 示 体 系 的 自 振 频 率 及 绘 主 振 型 图 。
已 知 EI 24960010=⨯⋅kN cm 2， m l ==24kg m ， 。
.ll30、图示体系，设质量分别集中于各层横梁上，数值均为m 。
求第一与第二自振频率之比ωω12:。
231、求图示体系的自振频率和主振型。
m m m m 122==，。
32、求图示体系的频率方程。
l33、图示体系分布质量不计，EI = 常数。
求自振频率及 绘 主 振 型 图。
aa34、图示简支梁EI = 常数，梁重不计，m m m m 122==,，已求出柔度系数()δ123718=a EI /。
求自振频率及主振型。
aaa35、求图示梁的自振频率及主振型，并画主振型图。
杆件分布质量不计。
aaa36、图示刚架杆自重不计，各杆EI = 常数。
求自振频率和主振型。
2m2m2m37、求图示体系的自振频率及主振型图。