三角形角平分线练习题
三角形中线高角平分线的30题(有答案)ok
三角形高中线角平分线专项练习30题(有答案)1 如图，△ ABC 中，/ A=30 ° / B=70 ° CE 平分/ ACB , CD丄AB 于D, DF丄CE 于F.(1)试说明/ BCD= / ECD ;(2)请找出图中所有与/ B相等的角(直接写出结果).2. 如图，AD ABC的中线，BE为三角形ABD中线，(1)Z ABE=15 ° / BAD=35 ° 求/ BED 的度数；(2)在厶BED中作BD边上的高；(3)若厶ABC的面积为60, BD=5，则点E到BC边的距离为多少?3. 在△ ABC中，AD是BC边上的中线，若△ ABD和厶ADC的周长之差为4 (AB >AC ), AB与AC的和为14, 求AB和AC的长.4. 如图△ ABC中，/ A=20 ° CD是/ BCA的平分线，△ CDA中，DE是CA边上的高，又有/ EDA= / CDB，求 / B的大小.5. △ ABC 中，AD 丄BC , AE 平分/ BAC 交BC 于点E.(1)Z B=30 ° / C=70 ° 求/ EAD 的大小.(2)若/ B v/ C,贝U 2/EAD与/ C-Z B是否相等？若相等，请说明理由.6 .在△ ABC中，AD是高，AE是角平分线，/ B=20 ° / C=60 °求/ CAD和/ DAE的度数.E D7 .在△ ABC 中.(1)若/ A=60 ° AB、AC边上的高CE、BD交于点0.求/ BOC的度数.(如图)(2)若/ A为钝角，AB、AC边上的高CE、BD所在直线交于点0,画出图形，并用量角器量一量/ BAC+ / B0C=___________ °再用你已学过的数学知识加以说明.(3)由(1) (2)可以得到，无论/ A为锐角还是钝角，总有/ BAC+ / B0C= _ _ °R--------------------- C&在厶ABC中，已知/ ABC=60 ° / ACB=50 ° BE是AC上的高，CF是AB上的高，H是BE和CF的交点. 求/ ABE、/ ACF 和/ BHC的度数.9. 如图，△ ACB 中，/ ACB=90 ° / 1 = / B .(1)试说明CD是厶ABC的高；(2)如果AC=8 , BC=6 , AB=10，求CD 的长.10. 如图，已知△ ABC的高AD，角平分线AE，/ B=26 ° / ACD=56 °求/ AED的度数.11. 如图，△ ABC 中，/ ABC=40 °, / C=60 °, AD 丄BC 于D , AE 是/ BAC 的平分线.(1)求/ DAE的度数；(2)指出AD是哪几个三角形的高.6 .在△ ABC中，AD是高，AE是角平分线，/ B=20 ° / C=60 °求/ CAD和/ DAE的度数.12. 如图，在△ ABC中，/ ABC=66 ° / ACB=54 ° BE是AC上的高，CF是AB上的高，H是BE和CF的交点, 求/ ABE、/ ACF和/ BHC的度数.13. 如图，在△ ABC中，/ B=60 ° / C=20 ° AD ABC的高，AE为角平分线(1)求/ EAD的度数；(2)寻找/ DAE与/ B、/ C的关系并说明理由.14. 如图，已知：AD是厶ABC的角平分线，CE是厶ABC的高，/ BAC=60 ° / BCE=40 °求/ ADB的度数.15. 如图，AD是厶ABC的BC边上的高，AE是/ BAC的角平分线，(1)若/ B=47 ° / C=73 ° 求/ DAE 的度数.(2)若/ B= a；/ C= 3° ( aV 3),求/ DAE的度数(用含a B的代数式表示)16. 如图，在△ ABC中，AD是角平分线，/ B=60 ° / C=45°求/ ADB 和/ADC的度数.17. 已知△ ABC中，/ ACB=90 °CD为AB边上的高，BE平分/ ABC，分别交CD、AC于点F、E,求证：/ CFE= / CEF .18. 如图(1), △ ABC中，AD是角平分线，AE丄BC于点E.(1).若/ C=80 ° / B=50 ° 求/ DAE 的度数.(2).若/ C>/ B,试说明/ DAE=丄(/ C-Z B).2(3).如图(2)若将点A在AD上移动到A '处，A'E丄BC于点E.此时Z DAE变成Z DA 'E, (2)中的结论还正确吗？为什么？19. 如图，已知△ ABC的周长为21cm , AB=6cm , BC边上中线AD=5cm , △ ABD周长为15cm，求AC长.20. 我们知道，任何一个三角形的三条内角平分线相交于一点，如图，若△ ABC的三条内角平分线相交于点I，过I作DE丄AI分别交AB、AC于点D、E.(1)请你通过画图、度量，填写右上表(图画在草稿纸上，并尽量画准确)(2)从上表中你发现了Z BIC与Z BDI之间有何数量关系，请写出来，并说明其中的道理.Z BAC的度数40°60°90°120°21. 如图，△ ABC中，AD是高，AE、BF是角平分线，它们相交于点0, / CAB=50 ° / C=60 °求/ DAE和/ B0A 的度数.22. 如图，在△ ABC中，AE是中线，AD是角平分线，AF是高，填空:(1BE= =^L2(2 ) / BAD= 1(3) / AFB= "2=90°(4)S A ABC = S AABEAB=5cm , BC=3cm，那么△ ABM 与厶BCM的周长是差是多少?24 .在△ ABC中，AB=AC , AD是中线，△ ABC的周长为34cm , △ ABD的周长为30cm,求AD的长.25.如图，在三角形ABC中，AD是BC边上的中线，三角形ABD的周长比三角形ACD的周长小5，你能求出AC与AB的边长的差吗？27. 如图，/ BAD= / CAD，贝U AD是厶ABC的角平分线，对吗？说明理由.28. 如图，在△ ABC中，AD是BC边上的中线，△ ADC的周长比△ ABD的周长多5cm, AB与AC的和为11cm , 求AC 的长.29. 如图所示，AD是厶ABC的中线，AE是厶ACD的中线，已知DE=2cm，求BD , BE , BC的长.30. 如图所示，AD是厶ABC的中线，AB=6cm , AC=5cm，求△ ABD和厶ADC的周长的差.参考答案:1. (1)vZ B=70 °CD 丄AB 于D,•••/ BCD=90 °- 70 °20 °在厶ABC 中，•••/ A=30 ° / B=70 °•••/ ACB=180。
初三数学中考复习 三角形的角平分线 专题练习及答案
三角形的角平分线1. 在Rt△ABC中，∠C＝90°，若BC＝10，AD平分∠BAC交BC于点D，且BD∶CD＝3∶2，则点D到线段AB的距离为( )A. 3B. 4C. 5D. 62. 如图，已知DB⊥AN于点B，交AE于点O，OC⊥AM于点C，且OB＝OC，若∠EAN＝25°，则∠ADB等于( )A. 40°B. 50°C. 60°D. 75°3. 如图，AB∥CD，AD⊥DC，AE⊥BC，垂足分别为D，E，∠DAC＝35°，AD＝AE，则∠B等于( )A．50° B．60° C．70° D．80°4. 如图，在△ABC中，∠B＝30°，AD平分∠BAC，DE垂直平分AB，垂足为E，若BD＝6cm，则CD等于( )A. 1cmB. 2cmC. 3cmD. 5cm5. 如图，BO，CO分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3.若△ABC 的周长是22，则△ABC的面积是( )A. 28B. 30C. 32D. 336. 如图，在△ABC中，∠C＝90°，∠B＝30°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N为圆心，大于12MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法中正确的个数是( )①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC∶S△ABC＝1∶3.A．1个 B．2个 C．3个 D．4个7. 如图，AB∥CD，AD⊥DC，AE⊥BC，垂足分别为D，E，∠DAC＝35°，AD＝AE，则∠B等于( )A．50° B．60° C．70° D．80°8. 如图，O为△ABC内任意一点，OD⊥AB于点D，OE⊥AC于点E，OF⊥BC于点F，若OD＝OE＝OF，连接OA，OB，OC，下列结论不一定正确的是( )A．△BOD≌△BOF B．∠OAD＝∠OBF C．∠COE＝∠CO F D．AD＝AE 9. 如图，在△ABC中，∠ABC＝120°，∠C＝26°，且DE⊥AB，DF⊥AC，DE ＝DF，则∠ADC的度数为____．10. 如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA＝2，则PQ的最小值为11. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是△ABC的角平分线，DE⊥AB，垂足为E，DE＝1，则BC=12. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD是△ABC的角平分线．若CD＝3cm，则BD的长为____cm.13. 如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于点D，DE⊥AB 于点E，且AB＝6cm，则△BED的周长是____ cm.14. 如图，在△ABC中，∠BAC＝60°，点D在BC上，DE⊥AB于点E，DF⊥AC 于点F，且DE＝DF，若DE＝4，则AD＝____．15. 在△ABC中，∠C＝90°，O为△ABC三条角平分线的交点，OD⊥BC于点D，OE⊥AC于点E，OF⊥AB于点F，且AB＝10 cm，BC＝8 cm，AC＝6 cm，则点O到三边AB，AC，BC的距离分别为 cm， cm， cm 16. 如图，∠AOE＝∠BOE＝15°，EF∥OB，EC⊥OB，若EC＝1，则EF＝____．17. 如图，△ABC是等边三角形，P是∠ABC的平分线上一点，PE⊥AB于点E，线段BP的垂直平分线交BC于点F，垂足为点Q.若BF＝2，则PE的长为18. 如图，已知BE⊥AC，CF⊥AB，垂足分别为E，F，BE，CF相交于点D，若BD＝CD，求证：AD平分∠BAC.19. 如图，已知BD是∠ABC的平分线，AB＝BC，点P在射线BD上，PM⊥AD 于点M，PN⊥CD于点N.求证：PM＝PN.20. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，求AC的长．参考答案：11 1---8 BACCD DCB9. 137°10. 211. 312. 613. 614. 815. 2 2 216. 2 17. 318. 解：在△BDF 和△CDE 中，∠BFD ＝∠CED ＝90°，∠FDB ＝∠EDC ，BD ＝CD ，∴△BDF ≌△CDE(AAS)，∴DF ＝DE ，又∵DF ⊥AB ，DE ⊥AC ，∴AD 平分∠BAC19. 解：在△ABD 和△CBD 中，AB ＝CB ，∠ABD ＝∠CBD ，BD ＝BD ，∴△ABD ≌△CBD(SAS)，∴∠ADB ＝∠CDB ，又∵∠ADB ＋∠ADP ＝∠CDB ＋∠CDP ＝180°，∴∠ADP ＝∠CDP ，∴DP 平分∠ADC ，又∵PM ⊥AD ，PN ⊥CD ，∴PM ＝PN20. 解：过点D 作DF⊥AC，∵AD 是∠BAC 平分线，DE ⊥AB ，∴DF ＝DE ＝2，∵S △ABD ＝4×22＝4，∴S △ACD ＝7－4＝3， ∴2AC 2＝3，即AC ＝3。
三角形内、外角平分线专题练习
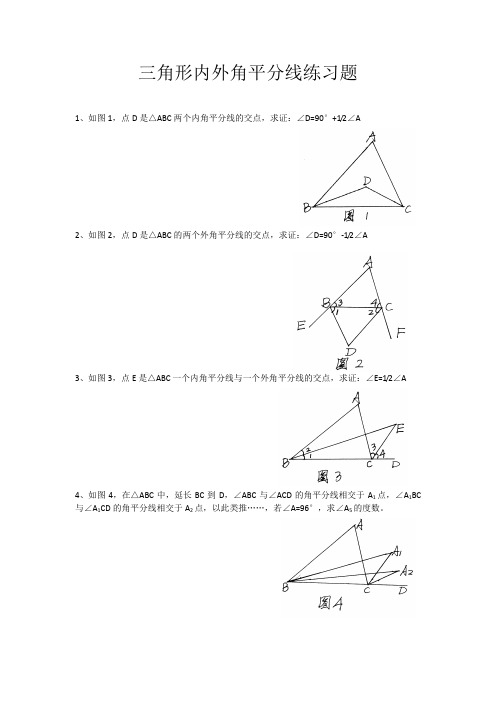
三角形内外角平分线练习题
1、如图1，点D是△ABC两个内角平分线的交点，求证：∠D=90°+1/2∠A
2、如图2，点D是△ABC的两个外角平分线的交点，求证：∠D=90°-1/2∠A
3、如图3，点E是△ABC一个内角平分线与一个外角平分线的交点，求证：∠E=1/2∠A
4、如图4，在△ABC中，延长BC到D，∠ABC与∠ACD的角平分线相交于A1点，∠A1BC 与∠A1CD的角平分线相交于A2点，以此类推……，若∠A=96°，求∠A5的度数。
5、如图5所示，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，求∠CAP的度数。
6、如图6，在△ABC中，∠B＜∠C，AQ平分∠BAC，AQ交BC于点Q，点T是AQ延长线上的一点，TH⊥BC于点H，证明：∠HTA=1/2（∠C—∠B）。
7、如图7，D是△ABC的BC边上的一点，且∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数。
8、如图8，在直角坐标系中，点A、B分别在x轴、y轴正半轴上移动，
BE是∠ABO的外角平分线，BE的反向延长线与∠OAB的平分线相交于点C，试问∠ACB的大小是否发生变化？如果保持不变，请给出证明。
9、已知三角形的三个外角的度数之比2：3：4，则它的最大内角的度数为（）A．90°B．110°C．100°D．120°。
三角形中线高角平分线的30题(有答案)ok
三角形中线高角平分线的30题(有答案)ok1.在三角形ABC中，角A为30°，角B为70°，CE为角ACB的平分线，CD垂直于AB于点D，DF垂直于CE于点F。
1) 证明角BCD等于角ECD。
2) 找出所有与角B相等的角。
2.在三角形ABC中，AD为中线，BE为三角形ABD的中线。
1) 已知角ABE为15°，角BAD为35°，求角BED的度数。
2) 在三角形BED中，作BD边上的高。
3) 若三角形ABC的面积为60，BD为5，求点E到BC边的距离。
3.在三角形ABC中，AD是BC边上的中线，已知三角形ABD和三角形ADC的周长之差为4（其中AB＞AC），AB与AC的和为14，求AB和AC的长度。
4.在三角形ABC中，角A为20°，CD为角BCA的平分线，DE为CA边上的高，已知角EDA等于角CDB，求角B的度数。
5.在三角形ABC中，AD⊥BC，AE为角BAC的平分线，已知角B为30°，角C为70°。
1) 求角EAD的度数。
2) 若角B小于角C，是否有2倍角EAD等于角C减去角B？请说明理由。
6.在三角形ABC中，AD为高，AE为角平分线，已知角B为20°，角C为60°，求角CAD和角DAE的度数。
7.在三角形ABC中。
1) 若角A为60°，AB和AC边上的高CE和BD交于点O，求角BOC的度数。
2) 若角A为钝角，AB和AC边上的高CE和BD所在直线交于点O，画出图形，并用量角器量一量角BAC加上角BOC的度数，再用已学过的数学知识加以说明。
3) 由(1)和(2)可以得到，无论角A为锐角还是钝角，总有角BAC加上角BOC等于180°。
8.在三角形ABC中，已知角ABC为60°，角ACB为50°，BE为AC上的高，CF为AB上的高，H为BE和CF的交点，求角ABE、角ACF和角BHC的度数。
三角形角平分线经典习题
例1．如图，已知：AD 是ABC ∆的角平分线，DE 、DF 分别是ABD ∆和ACD ∆的高.求证：AF AE =.例2．已知：如图，BD 是ABC ∠的平分线，BC AB =，P 在BD 上，AD PM ⊥，CD PN ⊥.求证：PN PM =.例3．如图，已知：在ABC ∆中AD 是BAC ∠的平分线，AB DE ⊥于E ，AC DF ⊥于F .求证：EF AD ⊥.例4．已知：如图，在ABC ∆中，︒=∠90C ，BC AC =，AD 是A ∠的平分线.求证：AB CD AC =+.例5、如图，已知DC AB //，︒=∠=∠90D A ，点E 在AD 上，BE 平分，CE 平分。
求证：DC AB BC +=。
例6．已知：如图，在ABC ∆中，BE 、CF 分别平分ABC ∠求证：点O 在A ∠的平分线上.针对性练习1、下列说法正确的有几个（ ）（1） 角的平分线上的点到角的两边的距离相等； （2） 三角形两个内角的平分线交点到三边距离相等；（3） 三角形两个内角的平分线的交点到三个顶点的距离相等；（4） 点E 、F 分别在∠AOB 的两边上，P 点到E 、F 两点距离相等，所以P 点在∠AOB 的平分线上； （5） 若OC 是∠AOB 的平分线，过OC 上的点P 作OC 的垂线，交OB 于D ，交OA 于E ，则线段PD 、PE 的长分别是P 点到角两边的距离A ．2B 3C 4D 5 2、在△ABC 中，∠C ＝090，BC ＝16cm ，∠A 的平分线AD 交BC 于D ， 且CD ：DB ＝3：5，则D 到AB 的距离等于＿＿＿＿3、已知：如图1，BD 是∠ABC 的平分线，DE ⊥AB 于E ，236cm S ABC =∆AB ＝18cm,BC ＝12cm,求DE 的长4．如图，已知：CD BD =，AC BF ⊥于F ，AB CE ⊥于E . 求证：D 在BAC ∠的平分线上.B 图1A D E5、已知：如图2， ∠B ＝∠C ＝090，M 是BC 中点，DM 平分∠ADC求证：AM 平分∠DAB6．如图，ABC ∆是等腰直角三角形，︒=∠90A ，BD 是ABC ∠的平分线，BC DE ⊥于E ，cm BC 10=，求DEC ∆的周长.7．如图，已知：在ABC ∆中，外角CBD ∠和BCE ∠的平分线BF ，CF 相交于点F .求证：点F 在DAE ∠的平分线上.8、如图，BC AD //，点E 在线段AB 上，ADE ∠， 求证：BC AD CD +=。
初一三角形角平分线经典例题
《角平分线》经典例题在直角三角形ABC中,∠A=90°,∠ABC的平分线BE交AC于E点,过E点作ED⊥BC于D点,已知AC=10cm,ΔCDE的周长为16cm,求CD的长.〔解析〕根据角平分线上的点到角的两边的距离相等可得AE=DE,从而求出DE+CE=AC,所以ΔCDE的周长=AC+CD,根据ΔCDE的周长及AC的长即可求得CD的长.解:∵BE为∠ABC的平分线,∠A=90°,DE⊥BC,∴AE=DE,∴DE+CE=AE+CE=AC=10cm,∵ΔCDE的周长为16cm,∴DE+CE+CD=16cm,∴CD=16-10=6(cm).如图(1)所示,已知∠ADC+∠ABC=180°,DC=BC.求证点C在∠DAB的平分线上.〔解析〕作CE⊥AB,CF⊥AD,垂足分别为E,F,利用∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,得出∠ABC=∠CDF,进而证得ΔCBE≌ΔCDF,得出FC=EC,即可求得结论.证明:如图(2)所示,作CE⊥AB,CF⊥AD,垂足分别为E,F,∴∠BEC=∠DFC=90°,∵∠ADC+∠ABC=180°,∠ADC+∠CDF=180°,∴∠ABC=∠CDF,在ΔCBE和ΔCDF中,∴ΔCBE≌ΔCDF(AAS),∴FC=EC,∴点C在∠DAB的平分线上.如图(1)所示,已知点P 是ΔABC 三条角平分线的交点,PD ⊥AB ,若PD =5,ΔABC 的周长为20,求ΔABC 的面积.〔解析〕作PE ⊥BC 于E ,PF ⊥AC 于F ,根据角平分线的性质定理得PE =PF =PD =5,然后根据三角形面积公式和S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC 得到S ΔABC =(AB +BC +AC ),再把ΔABC 的周长为20代入计算即可.解:作PE ⊥BC 于E ,PF ⊥AC 于F ,如图(2)所示,∵点P 是ΔABC 三条角平分线的交点,∴PE =PF =PD =5,∴S ΔABC =S ΔPAB +S ΔPBC +S ΔPAC=PD ·AB +PE ·BC +PF ·AC=(AB +BC +AC )=20=50.如图(1)所示,在RtΔABC 中,∠ACB =90°,且AC =b ,BC =a ,AB =c ,∠A 与∠B 的平分线交于点O ,O 到AB 的距离为OD.试探究OD 与a ,b ,c 的数量关系.〔解析〕过点O作OE⊥AC于E,OF⊥BC于F,然后根据角平分线上的点到角的两边的距离相等可得OD=OE=OF,然后证得四边形EOFC是正方形,从而证得OE=OF=FC=EC=OD,AE=AD,BD=BF,通过AB=AC-OD+BC-OD即可求解.解:如图(2)所示,过点O作OE⊥AC于E,OF⊥BC于F,∵∠BAC,∠ABC的平分线交于点O,OD⊥AB,∴OD=OE,OD=OF,∴OD=OE=OF,∵∠ACB=90°,∴四边形EOFC是正方形,∴OE=OF=FC=EC=OD,在RtΔOAE和RtΔOAD中,∴RtΔOAE≌RtΔOAD,∴AE=AD,同理BD=BF,∴AE+EC=AD+OD=AC=b,BF+CF=BD+OD=BC=a,∴AD=b-OD,BD=a-OD,∴AD+BD=a+b-2OD,即c=a+b-2OD,∴OD=(a+b-c).。
全等三角形角平分线专题
练习1、如图，AB∥DC， ∠BAC和∠ADC的平分线交于BC 上一点E. （1）求证：AD=AB+CD. （2）求证：BE=CE.
这两个结论是否还成立？
练习2、如图，在Rt△ABC中， AB=AC,∠BAC=90°，BD为△ABC 的角平分线，CE垂直于BD的延长 线于E.求证：BD=2CE.
（2）当∠C≠90°时 AB=10，FD=3. 求△ABF的面积.
练习3、如图，在△ABC中， ∠B=60°△ABC的角平分线AD和 CE相交于点O.求证：AE+CD=AC.
例2、如图，△ABC的角平分线BM 和CN相交于点P. 求证：AP平分∠BAC.
练习1、如图，OD平分∠AOB，DC 垂直于OA于C，∠A+∠B=180°. 求证：AO+BO=2CO.
2011-2012AC交BC于点F，BD垂直于 AF，交AF的延长线于点D.
（1）当∠C=90°时 求证：BD=AC.
2011-2012香坊区七年级下期末 已知在△ABC中，∠C=3∠B，AF 平分∠BAC交BC于点F，BD垂直于 AF，交AF的延长线于点D.
2010-2011香坊区七年级下期末 已知点C是∠MAN平分线上一点，∠BCD的两 边CB、CD分别与射线AM、AN相交于B、D两 点，且∠BCD+∠MAN=180°，过点C作 CE⊥AB，垂足为E. （3）在（2）的条件下， 若∠MAN=60°，连接BD， 作∠ABD的平分线BF交AD 于点F，交AC于点O， 连接 DO并延长交AB于 点G.BG=2,DF=5, 求线段BD的长.
例1、在△ABC中，AB＞AC.
（1）当AP是∠BAC角平分线时， AP交BC于点P，如图1所示。 求证：AB-AC＞BP-CP
角平分线的性质练习题
角平分线的性质练习题一、选择题1. 在三角形ABC中，BD是角B的平分线，若AB=5，BC=7，AC=6，那么BD的长度为：A. 4B. 6C. 8D. 无法确定2. 如果角平分线将三角形分成两个面积相等的部分，那么这两个部分的底边分别是：A. 相等B. 不相等C. 一个底边是另一个的两倍D. 底边长度无法确定3. 在三角形ABC中，角A的平分线与BC相交于点D，若AD=4，AC=8，那么AB的长度可能是：A. 6B. 8C. 10D. 12二、填空题4. 在三角形ABC中，如果角A的平分线将BC分为BD和DC两段，BD=DC，那么三角形ABD与三角形ACD的面积之比为________。
5. 若角平分线定理告诉我们，在三角形ABC中，如果BD是角B的平分线，则AB：AC=______：______。
6. 在三角形ABC中，如果角A的平分线与BC相交于点D，且AD垂直于BC，那么角B和角C的度数之和为________。
三、简答题7. 描述角平分线定理的内容，并给出一个应用此定理的几何问题。
8. 解释为什么在三角形中，角平分线可以将对边分成的两段长度与相邻两边成比例。
四、计算题9. 在三角形ABC中，已知角A的平分线AD与BC相交于点D，且BD=3，DC=4，AB=6，求AC的长度。
10. 在三角形ABC中，角B的平分线BE与AC相交于点E，已知AE=4，EC=6，AB=5，求BC的长度。
五、证明题11. 证明：在三角形ABC中，如果BD是角B的平分线，那么AB/AC = BD/DC。
12. 证明：如果点D在三角形ABC的边BC上，且AD是角A的平分线，那么三角形ABD与三角形ACD的面积相等。
六、综合题13. 在三角形ABC中，已知角A的平分线AD与BC相交于点D，且AD=2，BD=3，DC=4，AB=5，求BC的长度，并证明你的结论。
14. 给定三角形ABC，其中角A的平分线AD与BC相交于点D，角B的平分线BE与AC相交于点E。
七年级数学下册《第十二章全等三角形-角的平分线的性质》练习题
七年级数学下册《第十二章全等三角形-角的平分线的性质》练习题（含答案解析）学校:___________姓名：___________班级：___________一、填空题1．如图，点C 在AOB ∠的平分线上，CD OA ⊥于点D ，且1CD =，如果E 是射线OB 上一点，那么CE 长度的最小值是______．2．如图，点P 在AOB ∠内，因为PM OA ⊥，PN OB ⊥，垂足分别是M 、N ，PM PN =，所以OP 平分AOB ∠，理由是______．3．如图，ABC 的三边AB ，BC ，CA 的长分别是10，15，20，其三条角平分线相交于点O ，连接OA ，OB ，OC ，将ABC 分成三个三角形，则::ABO BCO CAO S S S 等于__________．4．如图所示，点O 在一块直角三角板ABC 上（其中30ABC ∠=︒），OM AB ⊥于点M ，ON BC ⊥于点N ，若OM ON =，则ABO ∠=_________度．5．如图，BE、CF都是ABC的角平分线，且110∠=︒，则ABDC∠=___________．二、单选题6．如图，OB平分∠AOC，D、E、F分别是射线OA、射线OB、射线OC上的点，D、E、F与O点都不重合，连接ED、EF若添加下列条件中的某一个．就能使DOE≅FOE，你认为要添加的那个条件是（）A．OD=OE B．OE=OF C．∠ODE =∠OED D．∠ODE=∠OFE<，将ABC以点A为中心逆时针旋转得到ADE，点D在BC边上，DE交7．如图，在ABC∆中，AB AC∠=∠，其中所有正确结论的AC于点F．下列结论：∠AFE DFC△△；∠DA平分BDE∠；∠CDF BAD序号是（）A．∠∠B．∠∠C．∠∠D．∠∠∠8．如图，三条公路两两相交，现计划在∠ABC中内部修建一个探照灯，要求探照灯的位置到这三条公路的距离都相等，则探照灯位置是∠ABC（）的交点．A．三条角平分线B．三条中线C ．三条高的交点D ．三条垂直平分线9．如图，Rt∠ABC 中，∠C ＝90°，AD 平分∠BAC ，交BC 于点D ，AB ＝10，S △ABD ＝15，则CD 的长为（ ）A ．2B ．3C ．4D ．5三、解答题10．已知40AOB ∠=︒．(1)用直尺和圆规作出AOB ∠的平分线OD （不写作法，但保留作图痕迹，写出结论）；(2)已知AOB ∠与BOC ∠互为补角，画出符合条件的所有可能的图形，并求出COD ∠的度数．11．如图，在由边长为1的小正方形组成的正方形网格中，一段圆弧经过网格的格点A 、B 、C ．(1)请完成如下操作：∠以点O 为原点，竖直和水平方向所在的直线为坐标轴，小正方形的边长为单位长，建立平面直角坐标系； ∠用直尺和圆规画出该圆弧所在圆的圆心D 的位置，不写作法，保留作图痕迹，并连接AD 、CD ．(2)请在（1）的基础上，解答下列问题：∠写出点的坐标：C ______、D ______；∠D 的半径为______（结果保留根号）；∠若扇形DAC 是一个圆锥的侧面展开图，则该圆锥的底面积为______（结果保留π）；∠若点E 的坐标为()7,0，试判断直线EC 与D 的位置关系，并说明理由．12．如图，已知AOC BOC ∠=∠，点P 在OC 上，PD OA ⊥，PE OB ⊥，垂足分别为D ，E ．求证：OPD OPE ≌．13．如图，∠ABC 中，∠ACB ＝90°，AB ＝10，BC ＝6，若点P 从点A 出发，以每秒1个单位长度的速度沿折线A －C －B －A 运动，设运动时间为t 秒（t ＞0）．(1)若点P 在AC 上，且满足P A ＝PB 时，求此时t 的值；(2)若点P 恰好在∠BAC 的平分线上，求t 的值．14．如图，在∠ABC 中，AD 是它的角平分线，且BD ＝CD ，DE ∠AB ，DF ∠AC ，垂足分别为E 、F ，求证：AB ＝AC参考答案：1．1【分析】过点C 作CE ∠OB 于点E ，根据角平分线的性质解答即可．【详解】解：过点C 作CE ∠OB 于点E ，∠点C 在∠AOB 的平分线上，CD ∠OA 于点D ，且CD ＝1，∠CE ＝CD ＝1，即CE 长度的最小值是1，故答案为：1．【点睛】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．2．角的内部到角两边距离相等的点在角的角平分线上【分析】根据角平分线判定定理即可得到结果．【详解】解：∠PM∠OA ，PN∠OB ，PM=PN∠OP 平分∠AOB （在角的内部，到角的两边距离相等的点在这个角的平分线上）故答案为：角的内部到角两边距离相等的点在角的角平分线上．【点睛】本题考查角平分线判定定理，掌握角平分线判定定理的内容是解题的关键．3．2：3：4【分析】过点O 分别向三边作垂线段，通过角平分线的性质得到三条垂线段长度相等，再通过面积比等于底边长度之比得到答案．【详解】解：过点O 分别向BC 、BA 、AC 作垂线段交于D 、E 、F 三点．∠CO 、BO 、AO 分别平分、、ACB CBA BAC ∠∠∠∠OD OE OF == ∠12ABO SAB OE =，12△BCO S BC OD =，12△CAO S AC OF = ∠::::10:15:202:3:4ABO BCO CAO S S S AB BC AC ===故答案为：2：3：4【点睛】本题考查了角平分线的性质，往三角形的三边作垂线段并得到面积之比等于底之比是解题关键．4．15【分析】根据ON BC ⊥，OM AB ⊥，OM ON =判断OB 是ABC ∠的角平分线，即可求解．【详解】解：由题意，ON BC ⊥，OM AB ⊥，OM ON =，即点O 到BC 、AB 的距离相等，∠ OB 是ABC ∠的角平分线，∠ 30ABC ∠=︒， ∠1152ABO ABC ∠=∠=︒． 故答案为：15．【点睛】本题考查角平分线的定义及判定，熟练掌握“到一个角的两边距离相等的点在这个角的平分线上”是解题的关键．5．40°##40度【分析】根据三角形的内角和定理以及角平分线的定义，列出算式计算即可．【详解】解：∠BE 、CF 都是∠ABC 的角平分线，∠∠A ＝180°−（∠ABC ＋∠ACB ），＝180°−2（∠DBC ＋∠BCD ）∠∠BDC ＝180°−（∠DBC ＋∠BCD ），∠∠A ＝180°−2（180°−∠BDC ）∠∠BDC ＝90°＋12∠A ，∠∠A ＝2（110°−90°）＝40°．【点睛】本题考查的是三角形内角和定理和角平分线的定义，用已知角表示出所求的角是解题的关键．6．D【分析】根据OB 平分∠AOC 得∠AOB =∠BOC ，又因为OE 是公共边，根据全等三角形的判断即可得出结果．【详解】解：∠OB 平分∠AOC∠∠AOB =∠BOC当∠DOE ∠∠FOE 时，可得以下结论：OD =OF ，DE =EF ，∠ODE =∠OFE ，∠OED =∠OEF ．A 答案中OD 与OE 不是∠DOE ∠∠FOE 的对应边，A 不正确；B 答案中OE 与OF 不是∠DOE ∠∠FOE 的对应边，B 不正确；C 答案中，∠ODE 与∠OED 不是∠DOE ∠∠FOE 的对应角，C 不正确；D 答案中，若∠ODE =∠OFE ，在∠DOE 和∠FOE 中，DOE FOE OE OEODE OFE =⎧⎪=⎨⎪=⎩∠∠∠∠ ∠∠DOE ∠∠FOE （AAS ）∠D 答案正确．故选：D ．【点睛】本题考查三角形全等的判断，理解全等图形中边和角的对应关系是解题的关键．7．D【分析】根据旋转的性质可得对应角相等，对应边相等，进而逐项分析判断即可求解．【详解】解：∠将ABC 以点A 为中心逆时针旋转得到ADE ，∠ADE ABC ≌，E C ∴∠=∠，AFE DFC ∠=∠，∴AFE DFC △△，故∠正确；ADE ABC ≌，AB AD ∴=，ABD ADB ∴∠=∠，ADE ABC ∠=∠，ADB ADE ∴∠=∠，∴DA 平分BDE ∠，故∠正确；ADE ABC ≌，BAC DAE ∴∠=∠，BAD CAE ∴∠=∠，AFE DFC△△，CAE CDF∴∠=∠，CDF BAD∠=∠∴，故∠正确故选D【点睛】本题考查了性质的性质，等边对等角，相似三角形的性质判定与性质，全等三角形的性质，掌握以上知识是解题的关键．8．A【分析】根据角平分线的性质即可得到探照灯的位置在角平分线的交点处，即可得到结论．【详解】解：∠探照灯的位置到这三条公路的距离都相等，∠探照灯位置是∠ABC的三条角平分线上，故选：A．【点睛】此题考查了角平分线的性质，数据角平分线的性质定理是解题的关键．9．B【分析】过点D作DE∠AB于E，根据角平分线上的点到角的两边距离相等可得DE＝CD，然后利用∠ABD 的面积列式计算即可得解．【详解】解：如图，过点D作DE∠AB于E，∠∠C＝90°，AD平分∠BAC，∠DE＝CD，∠S△ABD＝12AB•DE＝12×10•DE＝15，解得：DE＝3，∠CD＝3.故选：B.【点睛】本题考查了三角形的面积和角平分线的性质，能熟记角平分线上的点到角两边的距离相等是解此题的关键．10．(1)见解析(2)图见解析，60°或120°【分析】（1 ）根据角平分线的定义作出图形即可；（2）分两种情形，分别画出图形求解即可．（1）解：如图，射线OD即为所求．（2）解：如图，∠BOC与∠AOB、∠BOC'与∠AOB都互为补角，∠∠AOB=40°，且OD平分∠AOB，∠∠BOC=140°，∠BOC'=140°，∠AOD=∠BOD=12∠AOB=20°，当射线OA在∠BOC的外侧时，∠COD=∠BOC+∠BOD=140°+20°=160°；当射线OA在∠BOC'内部时，∠C'OD=∠BOC'-∠BOD=140°-20°=120°．综上，∠COD的度数为60°或120°．【点睛】本题考查作图 复杂作图，角平分线的定义，补角的定义等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．11．(1)答案见详解(2)∠62（，）；20（，）；∠∠54π；∠相切，理由见详解 【分析】（1）∠根据叙述，利用正方形的网格即可作出坐标轴；∠利用过三点的圆可得圆心为圆上任意两条弦的垂直平分线的交点，即可得到D ．（2）∠利用（1）中所作的坐标系，即可表示出点的坐标；∠在Rt OAD 中，利用勾股定理即可求得半径长；∠理由直角三角形全等可证得∠ADC =90°，则可求得AC 的长度，AC 的长就是圆锥的底面圆的周长，在利用圆的周长公式即可求得答案；∠利用勾股定理逆定理证明DCE 为直角三角形即可证得DC CE ⊥，从而即可得出结论．（1）∠如图，建立平面直角坐标系；∠利用过三点的圆可得圆心为圆上任意两条弦的垂直平分线的交点，即可得到D ，如图所示：（2）∠根据平面直角坐标系可得C （6，2）；D （2，0）；故答案为：C （6，2）；D （2，0）；∠在Rt AOD △中，90AOD ∠=︒,4AO =，2OD =，AD =故答案为：∠由∠得AD =在Rt DCF △中，90DFC ∠=︒，4DF =，2CF =，DC ∴在Rt AOD △和Rt DFC 中，AD DC OA DF=⎧⎨=⎩， ()Rt AOD Rt DFC HL ≅，DAO CDF ∴∠=∠，90DAO ADO ∠+∠=︒，90CDF ADO ∴∠+∠=︒，18090ADC ADO CDF ∴∠=︒-∠-∠=︒，AC ∴==，由2r π=，解得r =2254S r πππ∴===⎝⎭， ∴该圆锥的底面积为54π， 故答案为：54π． ∠直线EC 与D 相切，由图可知，在Rt CEF 中，90CFE ∠=︒，1EF =，2CF =，22222125CE EF CF ∴=+=+=，又由∠得DC =2220DC ==，2220525DC CE +=+=，22525DE ==，222DC CE DE ∴+=，∴DCE 为直角三角形，90DCE ∠=︒，DC CE ∴⊥，∴直线EC 与D 相切．【点睛】本题考查了不共线的三点确定圆心的方法、直线与圆相切的判定、根据平面直角坐标系写出点的坐标、勾股定理和圆锥的侧面展开图的弧长即为圆锥的底面圆的周长，垂径定理，圆锥的计算，正确求出弧长是难点．12．见解析【分析】根据角平分线的性质得PD PE =，再用HL 证明OPD OPE ≌．【详解】证明：∠AOC BOC ∠=∠，∠OC 为AOB ∠的角平分线，又∠点P 在OC 上，PD OA ⊥，PE OB ⊥，∠PD PE =，90PDO PEO ∠=∠=︒，又∠PO PO =（公共边），∠()HL OPD OPE ≌．【点睛】本题考查角平分线的性质，全等三角形的判定，利用合适的条件证明三角形全等是本题的关键． 13．(1)254 (2)323【分析】（1）连接PB ，在Rt ∠ABC 中，根据勾股定理得AC =6，由于AP ＝PB ＝t ，则PC ＝8-t ，在Rt ∠PCB 中，根据勾股定理得222PC BC PB +=，进行计算即可得；（2）由题意得，PC ＝t -8 ， PB ＝14-t ，过点P 作PE ∠AB ，由于AP 平分∠BAC ，且∠ACB ＝90°得PC ＝PE ，根据HL 得Rt ∠ACP ∠Rt ∠AEP ，即可得AC ＝AE ＝8， BE ＝2，在 Rt ∠PEB 中，根据勾股定理得222PE BE PB +=，进行计算即可得．（1）解：如图所示，连接PB ，∠在Rt ∠ABC 中，AB ＝10，BC ＝6，∠8AC =由于AP ＝PB ＝t ，则PC ＝8-t ，在Rt ∠PCB 中，根据勾股定理得：222PC BC PB +=222(8)6t t -+= 解得254t =， 即此时t 的值为254． （2）解：由题意得，PC ＝t -8 ， PB ＝14-t ，如图所示，过点P 作PE ∠AB ，由于AP 平分∠BAC ，且∠ACB ＝90°，∠ PC ＝PE ，在Rt ∠ACP 与Rt ∠AEP 中，PC PE AP AP =⎧⎨=⎩∠Rt ∠ACP ∠Rt ∠AEP （HL ），∠AC ＝AE ＝8， BE ＝2，在 Rt ∠PEB 中，根据勾股定理得，222PE BE PB +=，222(8)2(14)t t -+=- 解得：323t =， ∠当点P 在∠BAC 的平分线上时，t 的值为323． 【点睛】本题考查了勾股定理，角平分线的性质，全等三角形的判定和性质，解题的关键是掌握这些知识点．14．证明见解析【分析】根据角平分线的性质得到DE=DF，证明Rt∠BDE≅Rt∠CDF(HL)，根据全等三角形的性质得到结论．【详解】证明：∠AD是∠ABC的角平分线又∠DE∠AB于E，DF∠AC于F∠DE=DF，∠BED=∠CFD=90°又∠BD=CD∠Rt∠BED∠Rt∠CFD（HL）∠∠B=∠C∠AB=AC．【点睛】本题考查全等三角形的性质和判定，角平分线的性质，解题的关键是掌握这些性质定理进行证明．。
角平分线的性质练习题
角平分线的性质练习题角平分线是几何学中一个重要的概念，它在解决各种几何问题中起着重要的作用。
本文将通过一些练习题来探讨角平分线的性质。
练习题一：已知在△ABC中，角A的平分线交边BC于点D，证明AD是角A 的平分线。
解析：首先，我们可以利用角平分线的定义来解决这个问题。
角A的平分线是将角A分成两个相等的角的线段。
假设角BAD和角CAD是角A的平分线所分出的两个角，我们需要证明这两个角是相等的。
根据角平分线的定义，我们可以得出以下两个等式：∠BAD = ∠CAD （角平分线的定义）∠BAD + ∠CAD = ∠BAC （角的和等于整个角）将第一个等式代入第二个等式中，得到：∠CAD + ∠CAD = ∠BAC化简得：2∠CAD = ∠BAC由于∠CAD和∠BAD是同一个角的两个平分角，所以它们是相等的。
因此，AD是角A的平分线。
练习题二：已知在△ABC中，角A的平分线交边BC于点D，且AD=DC，证明△ABC是等腰三角形。
解析：要证明△ABC是等腰三角形，我们需要证明边AB和边AC的长度相等。
由于AD是角A的平分线，所以∠BAD = ∠CAD。
又已知AD=DC，所以△ADC 是一个等腰三角形。
根据等腰三角形的性质，我们可以得出以下结论：∠ADC = ∠ACD （等腰三角形的底角相等）由于∠BAD = ∠CAD，所以∠ADC = ∠ACD。
结合以上两个等式，我们可以得出：∠ADC = ∠ACD = ∠BAD = ∠CAD根据角的和等于整个角的性质，我们可以得到：∠ADC + ∠ACD + ∠BAD + ∠CAD = 180°将上述等式代入，得到：2∠ADC + 2∠ACD = 180°化简得：∠ADC + ∠ACD = 90°由于∠ADC和∠ACD是等腰三角形△ADC的两个底角，它们的和等于90°。
根据等腰三角形的性质，我们可以得出∠DAC = 90°。
解三角形(角平分线问题问题)(典型例题+题型归类练)(原卷版)
专题05 解三角形（角平分线问题问题）(典型例题+题型归类练) 一、必备秘籍角平分线如图，在ABC ∆中，AD 平分BAC ∠，角A ,B ,C 所对的边分别为a ，b ，c 核心技巧1：内角平分线定理：AB AC BD DC =或AB BDAC DC= 核心技巧2：等面积法(使用频率最高）ABC ABD ADC S S S ∆∆∆=+⇒111sin sin sin 22222A A AB AC A AB AD AC AD ⨯⨯=⨯⨯+⨯⨯ 核心技巧3：边与面积的比值：ABD ADCSAB AC S=核心技巧4：角互补：ADB ADC π∠+∠=⇒cos cos 0ADB ADC ∠+∠=在ADB ∆中有：222cos 2DA DB AB ADB DA DB +-∠=⨯;在ADC ∆中有：222cos 2DA DC AC ADC DA DC+-∠=⨯二、典型例题例题1．如图，已知AD 是ABC ∆中BAC ∠的角平分线，交BC 边于点D .（1）用正弦定理证明：AB BDAC DC=； （2）若120BAC ∠=︒，2AB =，1AC =，求AD 的长.第（2）问思路点拨：本小题已知，，，求的长.可利用第（1）问结论解答过程：根据余弦定理，，即，解得利用第(1)问结论由（1）知∴，得，；在与中，根据余弦定理得，且解得，即的长为．例题2．在ABC 中，内角,,A B C 所对的边分别为,,a b c 且πsin sin 3a B b A ⎛⎫=+ ⎪⎝⎭.(1)求角A 的大小；(2)若3AB =，1AC =，BAC ∠的内角平分线交BC 于点D ，求AD .第（2）问思路点拨：由（1）知，求角平分线长，，可优先考虑面积公式解答过程：由（1）知，由角平分线面积公式∴，∴．代入数据计算例题3．在ABC 中，3,AB =4,BC =线段BD 是B ∠的角平分线，且 6.ABDS =求BCD S △.思路点拨：已知在中，线段是的角平分线，且涉及角平分线问题，但是不知的大小，不适合直接用面积公式，但知，可考虑面积和边长的关系解答过程：平分由，代入代入例题4．在ABC中，D是BC的中点，1AB=，2AC=，32 AD=．（1）ABC的面积为________．（2）若AE为BAC∠的角平分线，E在线段BC上，则AE的长度为________．第（2）问思路点拨：由（1）知，可优先考虑面积公式解答过程：由可得即，从而.代入，计算例题5．在△ABC 中， AM 是BAC ∠的角平分线， 且交BC 于M . 已知23,2,3AM BM MC ===， 则AC = __________；思路点拨：在中，是的角平分线， 且交于. 已知，涉及到角平分线，又，可利用,得到的关系解答过程：由是的角平分线，又，得，设，则因为，则，利用余弦定理代入得：，整理得，解得或（舍）.所以.利用角互补关系（不适合面积公式）三、题型归类练1．三角形内角平分线定理：三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.请你认真思考，用三角形内角平分线定理解决问题：已知ABC 中，AD 为角平分线，3AB =，4AC =，5BC =，则AD =（ ）A ．127B ．157C ．7D ．72．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知，()(sin sin )(sin sin )a b A B c C B +-=+，若角A 的内角平分线AD 的长为2，则4b c +的最小值为（ ） A ．10B ．12C ．16D ．183．在△ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，若()sin sin sin a A c C b c B =+-，角A 的角平分线交BC 于点D ，且3AD c b ==，则a 的值为（ ）A ．72BC ．3D4．在ABC 中，CD 是ACB ∠的角平分线且4,||AB AD AD ==若||3CD =，则CDA ∠=__________，ABC的面积为__________．5．在ABC 中，60A ∠=，∠A 的角平分线与BC 边相交于D ．AD =BC =AB 边的长度为___．6．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，tan tan tan 0B C B C +=． (1)求角A 的大小；(2)若2BD DC =，AD ＝2，且AD 平分∠BAC ，求△ABC 的面积．注：三角形的内角平分线定理：在△PQR 中，点M 在边QR 上，且PM 为∠QPR 的内角平分线，有PQ QMPR MR=．7．记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知22cos cos (sin sin )sin 0C A A B B +-+=． (1)求C ；(2)若a ，b 为方程210200x x -+=的两个实数根，且C 的角平分线交AB 于点D ，求CD ．8．已知△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，BD 为∠ABC 的角平分线．(1)求证：::AD AB CD CB =；(2)若2BD =且26c a ==，求△ABC 的面积．9．已知△ABC 中，,,a b c 分别为内角,,A B C 的对边，且()()2sin 2sin 2sin a A b c B c b C =+++. (1)求角A 的大小；(2)设点D 为BC 上一点，AD 是ABC 的角平分线，且2AD =，3b =，求ABC 的面积.10．已知ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，点D 在BC 边上，AD 是角平分线，222sin sin sin sin sin C B C B A ++⋅=，且ABC 的面积为(1)求A 的大小及AB AC ⋅的值； (2)若4c =，求BD 的长．11．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，AD 为∠BAC 的角平分线，已知2c =且222223a c b cosA bc AD ⎛⎫+-=-= ⎪⎝⎭，(1)求△ABC 的面积；12．在ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，a =1b =，c =M 是BC 上的点． （1）若AM 是BAC ∠的角平分线，求BMCM的值； （2）若AM 是BC 边上的中线，求AM 的长．13．已知ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，点D 在AC 边上，BD 为ABC ∠的角平分线．32ABC ABD S S =△△．(1)求sin sin CA∠∠； (2)若BD b =，求cos ABC ∠的大小．。
三角形的角平分线、中线和高的专题训练50题
三角形的角平分线、中线和高1．已知，△ABC中，AD是BC边上的高，∠CAD=33°，则∠ACB= °．2．△ABC中，AD，CE是BC，AB边上的高，AD，CE相交于P，∠B=50°，则∠APC 的度数是．3．△ABC中，∠B的外角平分线的与∠C外角平分线相交于点P，且∠BPC=80°，则∠BAP的度数为．4．在Rt△ABC中，∠ACB=90°，∠CAB=30°，∠ACB平分线与∠ABC的外角平分线交于点E，连接AE，则∠AEB= ．5．如图，AD是△ABC的中线，AB=5，AC=3，△ABD的周长和△ACD的周长相差．&6．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（填“锐角三角形”，“直角三角形”，“钝角三角形”）7．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠B=46°，∠C=72°，则∠EAD= °．8．如图，AD、BE、CF是△ABC的三条中线，若△ABC的周长是a cm．则AE+CD+BF= cm．@9．如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D．则∠ECD= ．10．角平分线一定垂直于底边．11．在△ABC中，已知AD是角平分线，∠B=50°，∠C=70°，∠BAD= °．12．如图，在△ABC中，BD平分∠ABC，BE是AC边上的中线，如果AC=10cm，则AE=cm，如果∠ABD=30°，则∠ABC= ．13．如图六，在△ABC中，∠BAC是钝角，完成下列画图，并用适当的符号在图中表示；（1）AC边上的高；（2）BC边上的高．（在上图中直接画）[14．在△ABC中，AC=3cm，AD是△ABC中线，若△ABD周长比△ADC的周长大2cm，则BA= cm．15．△ABC中，∠A等于80度，则内角∠B、∠C的平分线相交所成的锐角为°．16．如图，在△ABC中，∠ACB=90°，∠A=20°，CD与CE分别是斜边AB上的高和中线，那么∠DCE= 度．·17．直角三角形中，两锐角的角平分线所夹的锐角是度．18．如图，在△ABC中，BE、CF分别是∠ABC和∠ACB的角平分线，并相交于点D，EG，FG分别是∠AEB和∠AFC的角平分线，并相交于点G，如果∠A=40°，那么∠CDB= ；∠G= ．19．如图，△ABC中，AD是BC边上的中线，已知AB=6cm，AC=4cm，则△ABD 和△ACD周长之差为．20．如图，Rt△ABC中，∠ACB=90°，∠A=40°，D为AB中点，CE⊥AB，则∠DCE= 度．》21．三角形中的角平分线、中线、高都是三条特殊的 （填直线、射线、线段）22．如图所示，BD 是△ABC 的中线，AD=2，AB+BC=5，则△ABC 的周长是 ．23．三角形一边上的中线把原三角形分成两个 相等的三角形．24．如图，AD 是△ABC 的中线，AE 是△ABD 的中线，若CE=9cm ，则BC= cm ．25．点D 是△ABC 中BC 边上的中点，若AB=3，AC=4，则△ABD 与△ACD 的周长之差为 ．、26．如图，AC 、BD 相交于O ，BE 、CE 分别平分∠ABD 、∠ACD ，且交于E ，若∠A=60°，∠D=40°，则∠E= ．27．如图，根据图形填空：（1）AD 是△ABC 中∠BAC 的角平分线，则∠ =∠ =21∠ ． （2）（2）AE 是△ABC 中线，则 = =21 . （3）AF 是△ABC 的高，则∠ =∠ =90°．28．如图，AD ⊥BC 于D ，那么图中以AD 为高的三角形有 个．29．如图所示：30．（1）在△ABC中，BC边上的高是；31．（2）在△AEC中，AE边上的高是．)32．我们都晓得，三角形的高是比较活泼的，它会出现在三角形的内部，也会出现在三角形的外部，然而，当它与三角形一边相会时，你可能找不到它了，今天就请你猜一猜，如果三角形的高与一边重合了，那么这是什么三角形呢答：三角形．31．在直角三角形、钝角三角形和锐角三角形这三种三角形中，有两条高在三角形外部的是三角形．32．如图，在△ABC中，AD、CE是边BC、AB上的高，若∠B=70°，∠CAD=30°，则∠BCE= ，∠ECA= ．.33．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：（1）∠BAC=2 ；（2）BC=2 ；（3）=90°．34．如图，∠ABD、∠ACD的平分线交于E，∠E=β1；∠EBD、∠ECD的平分线交于F，∠F=β2；如此下去，∠FBD、∠FCD的平分线的交角为β3；…若∠A=40°，∠D=32°，则β4为度．35．如图所示，在△ABC中，BC边上的高是，AB边上的高是；在△BCE中，BE 边上的高是；EC边上的高是；在△ACD中，AC边上的高是；CD边上的高是．36．在△ABC中，BO平分∠ABC，CO平分∠ACB，当∠A=50°时，∠BOC= ．）37．如图，在△ABC中，AC⊥BC，CD⊥AB于点D．则图中共有个直角三角形．38．已知：如图，在△ABC中，∠ACD是△ABC的外角，∠ABC与∠ACD的平分线相交于点A1，∠A1BC与∠A1CD的平分线相交于点A2，如果∠A2=m°，那么∠A= °（用含m的代数式表示）．39．如图，△ABC的∠B的外角的平分线与∠C的外角的平分线交于点P，连接AP．若∠BPC=50°，则∠PAC= 度．40．已知△ABC 中，∠A=α．在图（1）中∠B 、∠C 的角平分线交于点O 1，则可计算得∠BO 1C=90°+ 21α；在图（2）中，设∠B 、∠C 的两条三等分角线分别对应交于O 1、O 2，则∠BO 2C= ；请你猜想，当∠B 、∠C 同时n 等分时，（n-1）条等分角线分别对应交于O 1、O 2，…，O n-1，如图（3），则∠BO n-1C= （用含n 和α的代数式表示）．41．.42．如图，△ABC 中，∠ABC 和∠ACB 的平分线交于点O ，若∠BOC=115°， 则∠A= °．42．如图，已知△ABC 中，∠BAC=80°，∠C=60°，AD 、AE 分别是三角形的高和角平分线，则∠CAD=°，∠DAE= °．43．如图，在△ABC 中，∠A=α．∠ABC 与∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； …；∠A 2011BC 与∠A 2011CD 的平分线相交于点A 2012，得∠A 2012，则∠A 2012= ．44．如图，已知△ABC中，∠B=65°，∠C=45°，AD是∠ABC的高线，AE是∠BAC 的平分线，则∠DAE= ．45．如图，点O是△ABC的两条角平分线的交点，且∠A=40°，则∠BOC= ．·46．在△ABC中，∠A=80°，I是∠B，∠C的角平分线的交点，则∠BIC= °．47．如果三角形的三条高的交点落在一个顶点上，那么它的形状是．48．如图所示，CD是△ABC的中线，AC=9cm，BC=3cm，那么△ACD和△BCD的周长差是cm．49．如图，∠ACB是直角，CD是中线，CD=，BC=3，则AC= ．50．BM是△ABC中AC边上的中线，AB=5cm，BC=3cm，那么△ABM与△BCM 的周长之差为cm．。
角平分线的性质专项练习(含解析)
角平分线的性质专项练习一、单选题知识点一：角平分线的有关证明1．在Rt ABC 中，90B ︒∠=，AD 平分BAC ∠，交BC 于点D ，DE AC ⊥，垂足为点E ，若3BD =，则DE 的长为（ ）A ．3B ．32C ．2D ．62．如图，在△ABC 中，AB ＝6，BC ＝5，AC ＝4，AD 平分∠BAC 交BC 于点D ，在AB 上截取AE ＝AC ，则△BDE 的周长为( )A ．8B ．7C ．6D ．53．如图，在ABC 中，90,C AD ∠=平分,BAC DE AB ∠⊥于点,E 给出下列结论．CD ED =①;,AC BE AB +=② ③BDE BAC ∠=∠， DA ④平分CDE ∠，::BDE ACD S S AB AC =⑤其中正确的有（ ）个A ．5B ．4C ．3D ．2知识点二：角平分线的性质定理4．如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是（ ）A ．1B ．32C ．2D ．525．如图，在△ABC 中，AB ＝AC ，AD 是中线，DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F ，则下列四个结论中：①AB 上任一点与AC 上任一点到D 的距离相等；②AD 上任一点到AB ，AC 的距离相等；③∠BDE ＝∠CDF ；④∠1＝∠2；其中正确的有( )A ．1个B ．2个C ．3个D ．4个6．如图，AB ∥CD ，BP 和CP 分别平分∠ABC 和∠DCB ，AD 过点P ，且与AB 垂直．若AD ＝8，则点P 到BC 的距离是（ ）A ．8B ．6C ．4D ．27．如图，已知在四边形ABCD 中，90BCD ∠=︒，BD 平分ABC ∠，6AB =，9BC =，4CD =，则四边形ABCD 的面积是（ ）A．24 B．30 C．36 D．42知识点三：角平分线判定定理=，则（）8．如图，AC AD=，BC BDA．CD垂直平分AD B．AB垂直平分CDC．CD平分ACB∠D．以上结论均不对9．如图,已知AB∥CD，PE⊥AB，PF⊥BD，PG⊥CD，垂足分别E、F、G，且PF=PG=PE，则∠BPD=（）．A．60°B．70°C．80°D．90°10．如图所示，若DE⊥AB，DF⊥AC，则对于∠1和∠2的大小关系下列说法正确的是（）A．一定相等B．一定不相等C．当BD=CD时相等D．当DE=DF时相等11．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A ．线段CD 的中点B ．OA 与OB 的中垂线的交点C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点知识点四：角平分线性质的实际应用12．如图，在ABC ∆中，90︒∠=C ，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于( )A ．4B ．3C ．2D ．113．如图，Rt △ABC 中，∠C=90°，AD 平分∠BAC ，交BC 于点D ，若AB=14，S △ABD=14，则CD=（ ）A ．4B ．3C ．2D ．114．如图，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为E ，S △ABC ＝7，DE ＝2，AB ＝4，则AC 长是（ ）A ．6B ．5C ．4D ．3知识点五：尺规作图-角平分线15．尺规作图作AOB ∠的平分线方法如下：以O 为圆心，任意长为半径画弧交OA 、OB 于C 、D ，再分别以点C 、D 为圆心，以大于12CD 长为半径画弧，两弧交于点P ，作射线OP ，由作法得OCP ODP ≌的根据是（ ）A ．SASB ．ASAC ．AASD ．SSS16．如图，在ABC ∆中，,40AC BC A =∠=︒，观察图中尺规作图的痕迹，可知BCG ∠的度数为（）A ．40︒B ．45︒C ．50︒D ．60︒17．如图1，已知ABC ∠，用尺规作它的角平分线．如图2，步骤如下，第一步：以B 为圆心，以a 为半径画弧，分别交射线BA ，BC 于点D ，E ；第二步：分别以D ，E 为圆心，以b 为半径画弧，两弧在ABC ∠内部交于点P ；第三步：画射线BP ．射线BP 即为所求．下列正确的是（ ）A ．a ，b 均无限制B ．0a >，12b DE >的长C ．a 有最小限制，b 无限制D ．0a ≥，12b DE <的长18．如图,观察图中尺规作图痕迹,下列说法错误的是( )A ．OE 是AOB ∠的平分线B ．OC OD =C ．点C,D 到OE 的距离不相等D ．AOE BOE ∠=∠二、填空题 知识点一：角平分线的有关证明19．如图，已知△ABC 的周长是21，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于D ，且OD ＝4，△ABC 的面积是_____．20．如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。
三角形的角平分线、中线和高的专题训练50题
三角形的角平分线、中线和高的专题训练50题1. 在△ABC中，角A的角平分线交对边BC于点D，若BD=DC，求证：∠B=∠C。
【解答】设∠BAD=∠CAD=x，由于角A的角平分线BD、CD分别相交对边BC于点D，所以AD是△ABC的角平分线。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
根据等边三角形的性质可知∠B=∠C。
2. 在△ABC中，角A的角平分线交对边BC于点D，若∠BAD=30°，求∠B和∠C的度数。
【解答】设∠BAD=∠CAD=x，根据题意可知角A的角平分线BD、CD分别相交对边BC于点D。
由于∠BAD=30°，所以x=30°。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
又由等边三角形的性质可知∠B=∠C，即∠B=∠C=75°。
3. 在△ABC中，角B的角平分线交对边AC于点D，若∠BAD=80°，求∠ABC的度数。
【解答】设∠BAD=∠DAC=x，根据题意可知角B的角平分线AD相交对边AC于点D。
由于∠BAD=80°，所以x=80°。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$又由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
由等边三角形的性质可知∠ABC=∠ACB，设∠ABC=∠ACB=y，则∠ADB=∠ADC=180°-2x=20°。
再由三角形内角和为180°可知∠B+∠ADC=180°，即y+20°=180°，解得y=160°。
所以∠ABC=∠ACB=160°。
4. 在△ABC中，角A的角平分线交对边BC于点D，若∠B=70°,∠C=50°，求∠BAD的度数。
角平分线练习
TQ PN MOED CBA1.4 角平分线 第1课时 角平分线一、选择题1．在Rt △ABC 中，∠A=90°，∠ABC 的平分线BD 交AC 于点D ，AD=3，AB=4，则D到BC 的距离是（ ） A ．3 B ．4 C ．5 D ．6（第1题） （第2题）2．如图，MP ⊥NP ，MQ 为△NMP 的角平分线，MT ＝MP ，连结TQ ，则下列结论不正确的是（ ）（A ）TQ ＝PQ ． （B ）∠MQT ＝∠MQP ．（C ）∠QTN ＝90o． （D ）∠NQT ＝∠MQT ． 3．如图，AB ＝AC ，AE ＝AD ，则①△ABD ≌△ACE ；②△BOE ≌△COD ；③O 在∠BAC 的平分线上，以上结论（ ）（A ）都正确． （B ）都不正确． （C ）只有一个正确． （D ）只有一个不正确．（第3题） （第4题）4．已知：如图，△ABC 中，AB ＝AC ，BD 为∠ABC 的平分线，∠BDC ＝60o，则∠A 的度数是（ ） （A ）10o． （B ）20o． （C ）30o． （D ）40o． 5．如果一个三角形的一条角平分线恰好是对边上的高，那么这个三角形是（ ） （A ）直角三角形． （B ）等腰三角形． （C ）等边三角形． （D ）等腰直角三角形． 6．如图，在△ABC 中，AD 平分∠BAC ，DE ⊥AB 于E ，DF ⊥AC 于F ，M 为AD 上任意一点，则下列结论错误的是（ ）（A ）DE ＝DF ． （B ）ME ＝MF ． （C ）AE ＝AF ． （D ）BD ＝DC ．7．已知：如图，BE 、CF 是△ABC 的角平分线，BE 、CF 相交于DCBAMF ED CB AFEDCBAAFE DCBAD ，∠A ＝50o ，则∠BDC 的度数是（ ） （第6题）（A ）70o． （B ）120o． （C ）115o． （D ）130o．二、填空题 8．到一个角的两边距离相等的点在 ．9．直角三角形中，两锐角的角平分线所成的锐角等于 ．10．如下图，已知AB ∥CD ，O 为∠A 、∠C 的角平分线的交点，OE ⊥AC 于E ，且OE=2，则两平行线间AB 、CD 的距离等于 .11.已知△ABC 中，AD 是角平分线，AB=5，AC=3，且S △ADC =6，则S △ABD = .三、解答题12．如图，BD ＝CD ，BF ⊥AC ，CE ⊥AB ．求证：D 在∠BAC 的角平分线上．13．如图，在△ABC 中，∠B ＝∠C ，点D 是BC 的中点，DE ⊥AB ，DF ⊥AC ，E ，F 为垂足，求证：D 在∠BAC 的角平分线上．ONM PC BA ABCDENMDC A14．已知：如图，Rt △ABC 中，∠C ＝90o，AC ＝BC ,AD 为∠BAC 的平分线，AE ＝BC ，DE ⊥AB垂足为E ，求证△DBE 的周长等于AB ．15．如图，已知PA ⊥ON 于A ，PB ⊥OM 于B ，且PA ＝PB ．∠MON ＝50o，∠OPC ＝30o，求∠PCA的大小．16．如图，AE 平分∠BAC ，BD ＝DC ，DE ⊥BC ，EM ⊥AB ，EN ⊥AC ．求证：BM ＝CN ．AB C DF NPM17．已知：如图，PA 、PC 分别是△ABC 外角∠MAC 与∠NCA 的平分线，它们交于P ，PD ⊥BM于M ，PF ⊥BN 于F ．求证：BP 为∠MBN 的平分线．1.4 角平分线第2课时 三角形的三条内角平分线1．三角形中，到三边距离相等的点是（ ）（A ）三条高线交点． （B ）三条中线交点．（C ）三条角平分线交点． （D ）三边垂直平分线交点．2.如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ） A ．△ABC 的三条中线的交点 B ．△ABC 三条角平分线的交点 C ．△ABC 三条高所在直线的交点 D ．△ABC 三边的中垂线的交点FE O DCAB3.在△ABC 中，∠B ，∠C 平分线的交点P 恰好在BC 边的高AD 上，则△ABC 一定是（ ） A ．直角三角形 B ．等边三角形 C ．等腰三角形D ．等腰直角三角形4．如图，△ABC 中，∠C ＝90o，点O 为△ABC 的三条角平分线的交点，OD ⊥BC ，OE ⊥AC ，OF ⊥AB ，点D 、E 、F 分别是垂足，且AB ＝10cm ，BC ＝8cm ，CA ＝6cm ，则点O 到三边AB 、AC 和BC 的距离分别等于（ ）（A ）2cm 、2cm 、2cm ． （B ）3cm 、3cm 、3cm ． （C ）4cm 、4cm 、4cm ． （D ）2cm 、3cm 、5cm ．5.如图，O 是△ABC 内一点，且O 到三边AB 、BC 、CA 的距离OF=OD=OE ，若∠BAC=70°，∠BOC=_______.6.如图，直线l 、l ′、l ″表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有________处.7.如图，已知△ABC 的周长是21，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于D ，且OD=4，求△ABC 的面积．。
三角形的高中线角平分线练习题
三角形的高中线角平分线练习题文件管理序列号：[K8UY-K9IO69-O6M243-OL889-三角形的高、中线、角平分线练习题1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。
2、三角形的三条中线、三条角平分线、三条高都是（）A．直线 B．射线 C．线段 D．射线或线段3、如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形 B．直角三角形C．钝角三角形 D．不能确定4、能把三角形的面积分成两个相等的三角形的线段是（）A．中线B．高C．角平分线 D．以上三种情况都正确5、如图若∠BAF=∠CAF，则____是△ABD的角平分线，____是△ABC的角平分线6、如图AB⊥AC，则AB是△ABC的边____上的高，也是△BDC的边______上的高，也是△ABD的边____上的高.FB CDAB CD7、如图BD 、AE 分别是△ABC 的中线、角平分线，AC=10cm ，∠BAC=700，则AD=_____，∠BAE=____.8、在△ABC 中，AE 是中线，AD 是角平分线，AF 是高，填空： ⑴BE ＝___＝21_____；⑵∠BAD=_____=21_____；⑶∠AFB=_____=909、在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.10、在△ABC 中AB=AC ，AC 上的中线BD 把三角形的周长分为24cm 和30cm 的两个部分，求三角形的三边长。
11、要使四边形木架(用四根木条钉成)不变形，至少要再钉上几根木条？五边形木架和六边形木架呢？n 边形木架呢？BD。
角平分线的性质练习题
角平分线的性质练习题练习1：已知三角形ABC，角A的角平分线AD与边BC相交于点D。
证明：AD是角A的角平分线。
证明：首先，连接AD。
在△BDA和△CDA中，我们有：∠BDA = ∠CDA (角平分线的性质)∠ABD = ∠ACD (已知角平分线)BD = CD (角平分线与两边相交，且到两条边距离相等)根据三角形的SAS（边角边）相等定理，△BDA ≌△CDA。
由于△BDA ≌△CDA，我们可以得出以下结论：∠BAD = ∠CAD (对应角相等定理)∠BAC = ∠BAD + ∠CAD (角的加法）∠BAC = ∠CAD + ∠CAD (代入∠BAD = ∠CAD)∠BAC = 2∠CAD (合并项)AD是角A的角平分线。
练习2：已知三角形ABC，角B的角平分线BE与边AC相交于点E，角C 的角平分线CF与边AB相交于点F。
证明：EF平行于BC。
证明：首先，连接EF。
在△BEC和△CBF中，我们有：∠BEC = ∠CBF (角平分线的性质)∠BCE = ∠BCF (已知角平分线)根据三角形的AA（角角）相似定理，△BEC ∼△CBF。
由于△BEC ∼△CBF，我们可以得出以下结论：∠EBC = ∠FCB (对应角相等定理)考虑△BEF，我们有：∠BEF = ∠BEC + ∠CBF (角的加法）∠BEF = ∠FCB + ∠CBF (代入∠BEC = ∠CBF)∠BEF = ∠FCB + ∠EBC (代入∠FCB = ∠EBC)∠BEF = ∠EBC + ∠EBC (合并项)∠BEF = 2∠EBC同样地，考虑△BFC：∠BFC = ∠BCF + ∠BCE (角的加法）∠BFC = ∠BCF + ∠EBC (代入∠BCE = ∠EBC)∠BFC = ∠EBC + ∠EBC (代入∠BCF = ∠EBC)∠BFC = 2∠EBC由于∠BEF = 2∠EBC，且∠BFC = 2∠EBC，我们可以得出以下结论：∠BEF = ∠BFC (两个角相等）考虑△BEF和△BFC，在两个三角形中，我们有：∠BEF = ∠BFC (已证明的结论)EF平行于BC (对应角相等定理)因此，EF平行于BC。
三角形外角平分线定理例题
1.三角形的一个外角等于与它不相邻的两个内角之和，那么这个外角的平分线与三角形的一边相交，将这边分为两部分，这两部分与三角形的另外两个顶点连线，所构成的角中，哪一个角是直角？A. 靠近三角形顶点的角B. 靠近三角形外角顶点的角C. 两个角都不是直角D. 无法确定（正确答案）2.三角形ABC中，角A的外角平分线与边BC的延长线相交于点D，那么角A与角D的关系是？A. 角A等于角DB. 角A大于角DC. 角A小于角D（正确答案）D. 角A与角D的大小关系无法确定3.三角形的一个外角平分线与三角形的一边的延长线相交，则这个外角平分线与三角形的一边所夹的角等于？A. 相邻的一个内角B. 不相邻的一个内角的一半C. 不相邻的一个内角（正确答案）D. 相邻的一个外角的一半4.在三角形ABC中，若角A的外角平分线与边BC相交于点D，则角D与角A、角B的关系为？A. 角D = 角A + 角BB. 角D = 角A - 角BC. 角D = (角A - 角B) / 2（正确答案）D. 角D = 角B - 角A5.三角形的一个外角的平分线与三角形的一边相交，将这个角分为两个相等的角，这两个角与三角形的内角有何关系？A. 这两个角都等于相邻的内角B. 这两个角都等于不相邻的内角的一半C. 其中一个角等于不相邻的内角，另一个角等于相邻的内角的一半D. 其中一个角等于不相邻的内角，另一个角与相邻的内角无关（正确答案）6.在三角形ABC中，角A的外角平分线与边BC的延长线相交于点D，若角A =60度，则角D的度数为？A. 30度B. 60度C. 90度D. 无法确定，因为需要知道角B的度数（正确答案）7.三角形的一个外角的平分线与三角形的一边相交，则这个角的两个邻角（与三角形内部相邻的角）之和等于？A. 90度B. 180度（正确答案）C. 270度D. 360度8.在三角形ABC中，若角A的外角平分线与边BC相交于点D，且角B = 角C，则角D与角A的关系为？A. 角D = 角A / 2B. 角D = 角AC. 角D = 180度 - 角A（正确答案）D. 角D = 90度 - 角A / 2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角形角平分线练习题求证：AE?AF.例2．已知：如图，BD是?ABC的平分线，AB?BC，P在BD上，PM?AD，PN?CD.求证：PM?PN.例3．如图，已知：在?ABC中AD是?BAC的平分线，DE?AB于E，DF?AC于F.求证：AD?EF.例4．已知：如图，在?ABC中，?C?90?，AC?BC，AD 是?A的平分线.求证：AC?CD?AB.例5、如图，已知AB//DC，?A??D?90?，点E在。
求证：BC?AB?DC。
例6．已知：如图，在?ABC中，BE、CF分别平分?ABC 求证：点O在?A的平分线上.11、下列说法正确的有几个角的平分线上的点到角的两边的距离相等；三角形两个内角的平分线交点到三边距离相等；三角形两个内角的平分线的交点到三个顶点的距离相等；点E、F分别在∠AOB的两边上，P点到E、F两点距离相等，所以P点在∠AOB的平分线上；若OC是∠AOB的平分线，过OC上的点P作OC的垂线，交OB于D，交OA于E，则线段PD、PE的长分别是P点到角两边的距离A．B C D52、在△ABC中，∠C＝900，BC＝16cm，∠A的平分线AD交BC于D，且CD：DB＝3：5，则D到AB的距离等于＿＿＿＿3、已知：如图1，BD是∠ABC的平分线，DE⊥AB于E，S?ABC?36cmAB＝18cm,BC＝12cm,求DE的长4．如图，已知：BD?CD，BF?AC于F，CE?AB于E.求证：D在?BAC的平分线上.图15、已知：如图2，∠B＝∠C＝90，M是BC中点，DM 平分∠ADC 求证：AM平分∠DAB图2BDCM6．如图，?ABC是等腰直角三角形，?A?90?，BD是?ABC 的平分线，DE?BC于E，BC?10cm，求?DEC的周长.27．如图，已知：在?ABC中，外角?CBD和?BCE的平分线BF，CF相交于点F.求证：点F在?DAE的平分线上.8、如图，AD//BC，点E在线段AB 上，?ADE??CDE，?DCE??ECB，求证：CD?AD?BC。
C9、已知：如图3，在△ABC中，∠B＝600，△ABC的角平分线AD、CE线相交于点O求证：AE+CD＝ACE图DC10.如图在△ABC中,∠BAC＝100°,∠ACB＝,若∠DAC＝20°,求∠CED的度数.11.在四边形ABCD中,BC﹥BA,AD＝CD,BD平分∠ABC,∠C＝7234姓名： 11.1.1知识点：三角形的边11、现有两根木棒，它们的长分别为40cm和50cm，若要钉成一个三角形木架，则在下列四根木棒中应选取A．10cm长的木棒B．40cm长的木棒 C．90cm长的木棒D．100cm长的木棒拓展训练：1.已知一个三角形的两边长分别是3cm和4cm，则第三边长x的取值范围是．?若x是奇数，则x的值是______；则它的周长为______；?若x?是偶数，?则x?的值是______ 。
.等腰三角形的两边长是4和9，则第三边长是，若其两边是6和10，则其周长是。
.△ABC的三边是a、b、c，则a-b-c-b-a4.已知三角形的三边长分别为2、x、10，则三角形的周长为奇数，求x的值。
测试题一、选择题:1.已知三条线段的比是:①1:3:4;②1:2:3;③1:4:6;④3:3:6;⑤6:6:10;⑥3:4:5.其中可构成三角形的有1、三角形：不在同一条直线上的线段首位顺次相接组成的封闭图形、三角形分类3、三角形的三边关系：两边之和大于第三边，两边之差小于第三边、三角形：不在同一条直线上的线段首位顺次相接组成的封闭图形、三角形分类6、三角形的三边关系：两边之和大于第三边，两边之差小于第三边测试题1.由______________的三条线段______相接所组成得图形叫做三角形。
2.如图，三角形的三边分别是________或______，三角形的内角分别是__________，三角形的顶点分别是_______ ，这个三角形记作______，读作____________. .三角形按边的关系可分为和，而等腰三角形又分A.1个B.2个C.3个C.4个为和。
三角形按内角大小可分为、2.如果三角形的两边长分别为3和5,则周长L的取值范围是和。
A.6 4.三角形两边的和第三边，三角形两边的差第三边。
.现有两根木棒,它们的长度分别为20cm和30cm,若不改变木棒的长度, 要钉成一个三角形木架,5.三角形的三边分别为2、x、5，则整数x = 。
6.等腰三角形的周长为16，其一边长为6，则另两边长为。
7.已知三角形的两边长是3cm和8cm ，则此三角形的第三边长可能是 A.cm B.cm C.cm D.13cm8.一个三角形的三边长是 m 、、5，那么m的取值范围是 A.3 9.下列选项中，给出的三条线段不能组成三角形的是A.a+1,a+2,a+B.三边之比为2:3:4C.30cm，8cm ，10cmD.3k ，4k ，5k 10.下列说法中正确的是A.等腰三角形一腰的长至少要大于底边长的一半B.三角形按边的关系分为不等边三角形、等边三角形C.长度为5、6、10的三条线段不能组成三角形D.等腰三角形的两边长是1和2，则其周长为4或5应在下列四根木棒中选取A.10cm的木棒B.20cm的木棒;C.50cm的木棒D.60cm 的木棒.已知等腰三角形的两边长分别为3和6,则它的周长为A. B.1 C.1 D.12或155.已知三角形的三边长为连续整数,且周长为12cm,则它的最短边长为A.2cm B.3cm C.4cm D.5cm6.已知三角形的周长为9,且三边长都是整数,则满足条件的三角形共有A.2个 B.3个 C.4个 D.5个二、填空题:1.若三角形的两边长分别是2和7,则第三边长c的取值范围是_______;当周长为奇数时,第三边长为________;当周长是5的倍数时,第三边长为________.2.若等腰三角形的两边长分别为3和7,则它的周长为_______; 若等腰三角形的两边长分别是3和4,则它的周长为_____.3.若等腰三角形的腰长为6,则它的底边长a的取值范围是________;若等腰三角形的底边长为4,则它的腰长b的取值范围是_______.4.若五条线段的长分别是1cm,2cm,3cm,4cm,5cm,则以其中三条线段为边可构成______个三角形..已知等腰三角形ABC中,AB=AC=10cm,D为AC边上一点,且BD=AD,△BCD的周长为15cm,则底边BC11、三角形中线：连接顶点和对边中点，所得线段叫做三角形的中线的长为__________.6.已知等腰三角形的两边长分别为4cm和7cm,且它的周长大于16cm,则第三边长为_____. 三、基础训练:1. 如图所示,已知P是△ABC内一点,试说明PA+PB+PC>12. A2.已知等腰三角形的两边长分别为4,9,求它的周长. C四、提高训练:设△ABC的三边a,b,c的长度都是自然数,且a≤b≤c,a+b+c=13,则以a,b,c 为边的三角形共有几个?五、探索发现:若三角形的各边长均为正整数,且最长边为9,则这样的三角形的个数是多少?11.1.2三角形的高、中线、角平分线知识点：7、三角形的高：过三角形的一个顶点向对边做垂线，所得垂线段的长度叫做三角形的高、三角形中线：连接顶点和对边中点，所得线段叫做三角形的中线9、三角形的角平分线：做一个角的平分线交对边于一点，所得线段叫做角平分线 10、三角形的高：过三角形的一个顶点向对边做垂线，所得垂线段的长度叫做三角形的高 12、三角形的角平分线：做一个角的平分线交对边于一点，所得线段叫做角平分线 13、三角形的高：过三角形的一个顶点向对边做垂线，所得垂线段的长度叫做三角形的高 14、三角形中线：连接顶点和对边中点，所得线段叫做三角形的中线15、三角形的角平分线：做一个角的平分线交对边于一点，所得线段叫做角平分线测试题三角形的高： 1、从△ABC的顶点A向作垂线，垂足为D,所得线段AD叫做△ABC的边BC上的高。
作出下列三角形三边上的高：B C B C2、上面第1图中，AD是△ABC的边BC上的高，则∠ADC=∠= 。
、由作图可得出如下结论：三角形的三条高线所在的直线相交于点；锐角三角形的三条高相交三角形的；钝角三角形的三条高所在直线相交三角形的；直角三角形的三条高相交三角形的；交点我们叫做三角形的垂心。
4、对应练习：如图所示，画△ABC的一边上的高，下列画法正确的是．5．三角形的高线是．A．直线B．射线C．线段 D．以上都不对.画出①、②、③三个△ABC各边的高,并说明是哪条边的高.AAABCBC B① ②③AB边上的高是线段____AB边上的高是线段____ AB边上的高是线段____ BC边上的高是_________ BC边上的高是_________BC边上的高是_________AC边上的高是_________ AC边上的高是_________AC边上的高是_________.下列说法正确的是A.三角形的三条高相交于三角形内部一点的三角形是钝角三角形B.三角形的三条高相交于三角形内部一点的三角形是锐角三角形C.三角形的三条高都在三角形内部的是直角三角形D.三角形的三条高中只有一条高在三角形内部的，是钝角三角形8.三角形的三条高相交于一点吗？锐角三角形、直角三角形、钝角三角形他们的三条高各交于什么位置？三角形的中线1.连接△ABC顶点A和，所得线段AD叫做△ABC的边BC上的中线。
.画出①、②、③三个△ABC各边的中线,并说明是哪条边的中线.AAABBCCCB① ② ③AB边上的中线是线段____ AB边上的中线是线段____ AB边上的中线是线段____ BC边上的中线是_______ BC边上的中线是________ BC边上的中线是_________ AC边上的中线是_______ AC边上的中线是_________AC边上的中线是_________ 写出图中所有相等关系的线段：___________________________________、由作图可得出如下结论：三角形的三条中线相交于点；锐角三角形的三条中线相交三角形的；钝角三角形的三条中线相交三角形的；直角三角形的三条中线相交三角形的；交点我们叫做三角形的重心。
14、AD是△ABC的边BC上的中线，则有BD = = ，25、对应练习：如图，D、E是边AC的三等分点，图中有个三角形，BD是三角形中边上的中线，BE是三角形中边上的中线三角形的角平分线1.画∠A的平分线AD，交于D，所得线段AD叫做△ABC 的角平分线。
.认识并会画三角形的角平分线A画出△ABC各角的角平分线, 并说明是哪角的角平分线.ABBC∠ABC的角平分线是线段____ ∠ABC的角平分线是线段____ ∠BAC的角平分线是__________ ∠BAC的角平分线是__________ ∠ACB的角平分线是___________∠ACB的角平分线是___________ 写出图中所有相等关系的角: ___________________、作出下列三角形三角的角平分线：BCBC4、AD是△ABC的∠BAC的角平分线，则∠BAD=∠ =、由作图可得出如下结论：三角形的三条角平分线相交于点；锐角三角形的三条角平分线相交三角形的；钝角三角形的三条角平分线相交三角形的；直角三角形的三条角平分线相交三角形的；交点我们叫做三角形的内心。