七年级数学平行练习
人教版七年级数学下册平行线同步测试(含答案)

5.2.1 平行线一、选择题1.在同一平面内,下列说法中,错误的是( )A.过两点有且只有一条直线B.过一点有无数条直线与已知直线平行C.过直线外一点有且只有一条直线与已知直线平行D.过一点有且只有一条直线与已知直线垂直2.若直线a∥b,b∥c,则a∥c的依据是( ))A.平行公理B.等量代换C.等式的性质D.平行于同一条直线的两条直线互相平行3.下列说法错误的是( )A.过一点有且只有一条直线与已知直线平行B.平行于同一条直线的两条直线平行C.若a∥b,b∥c,c∥d,则a∥dD.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交4.如图,AB∥CD,EF∥AB,AE∥MN,BF∥MN,由图中字母标出的互相平行的直线共有( )A.4组B.5组C.6组D.7组5.点P,Q都是直线l外的点,下列说法正确的是( )A.连接PQ,则PQ一定与直线l垂直B.连接PQ,则PQ一定与直线l平行C.连接PQ,则PQ一定与直线l相交D.过点P能画一条直线与直线l平行6.在同一平面内的两条不重合的直线的位置关系( )A.有两种:垂直或相交B.有三种:平行,垂直或相交C.有两种:平行或相交D.有两种:平行或垂直二、填空题7.在同一平面内,直线a与b满足下列条件,把它们的位置关系填在后面的横线上.(1)a与b没有公共点,则a与b ;(2)a与b有且只有一个公共点,则a与b ;(3)a与b有两个公共点,则a与b .8.如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:.9.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上.理由是。
10.如图所示,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外一点,现想过点E作河岸CD的平行线,只需过点E作,其理由是。
11.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必。
12.观察下图所示的长方体,回答下列问题.(1)用符号表示两棱的位置关系:A1B1AB,AA1AB,A1D1C1D1,AD BC;(2)AB与B1C1所在的直线不相交,它们平行线(填“是”或“不是”).由此可知,在内,两条不相交的直线才是平行线.三、解答题13.在同一平面内,有三条直线a,b,c,它们之间有哪几种可能的位置关系?画图说明.14.如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD 与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?参考答案5.2.1 平行线一、选择题1.在同一平面内,下列说法中,错误的是(B)A.过两点有且只有一条直线B.过一点有无数条直线与已知直线平行C.过直线外一点有且只有一条直线与已知直线平行D.过一点有且只有一条直线与已知直线垂直2.若直线a∥b,b∥c,则a∥c的依据是(D)A.平行公理B.等量代换C.等式的性质D.平行于同一条直线的两条直线互相平行3.下列说法错误的是(A)A.过一点有且只有一条直线与已知直线平行B.平行于同一条直线的两条直线平行C.若a∥b,b∥c,c∥d,则a∥dD.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交4.如图,AB∥CD,EF∥AB,AE∥MN,BF∥MN,由图中字母标出的互相平行的直线共有(C)A.4组B.5组C.6组D.7组5.点P,Q都是直线l外的点,下列说法正确的是(D)A.连接PQ,则PQ一定与直线l垂直B.连接PQ,则PQ一定与直线l平行C.连接PQ,则PQ一定与直线l相交D.过点P能画一条直线与直线l平行6.在同一平面内的两条不重合的直线的位置关系(C)A.有两种:垂直或相交B.有三种:平行,垂直或相交C.有两种:平行或相交D.有两种:平行或垂直二、填空题7.在同一平面内,直线a与b满足下列条件,把它们的位置关系填在后面的横线上.(1)a与b没有公共点,则a与b平行;(2)a与b有且只有一个公共点,则a与b相交;(3)a与b有两个公共点,则a与b重合.8.如图,在下面的方格纸中,找出互相平行的线段,并用符号表示出来:CD∥MN,GH∥PN.9.如图,PC∥AB,QC∥AB,则点P,C,Q在一条直线上.理由是经过直线外一点,有且只有一条直线与这条直线平行.10.如图所示,直线AB,CD是一条河的两岸,并且AB∥CD,点E为直线AB,CD外一点,现想过点E作河岸CD的平行线,只需过点E作AB的平行线即可,其理由是平行于同一条直线的两条直线平行.11.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必相交.12.观察下图所示的长方体,回答下列问题.(1)用符号表示两棱的位置关系:A1B1∥AB,AA1⊥AB,A1D1⊥C1D1,AD ∥BC;(2)AB与B1C1所在的直线不相交,它们不是平行线(填“是”或“不是”).由此可知,在同一平面内,两条不相交的直线才是平行线.三、解答题13.在同一平面内,有三条直线a,b,c,它们之间有哪几种可能的位置关系?画图说明.解:有四种可能的位置关系,如下图:14.如图所示,取一张长方形的硬纸板ABCD,将硬纸板ABCD对折使CD 与AB重合,EF为折痕.把长方形ABFE平放在桌面上,另一个面CDEF无论怎么改变位置总有CD∥AB存在,你知道为什么吗?解:因为AB∥EF,CD∥EF,所以CD∥AB.。
人教版七年级下册数学平行线证明题训练

人教版七年级下册数学平行线证明题训练1.已知:如图,180BAP APD ∠+∠=︒,12∠=∠.求证:E F ∠=∠. 证明:∵180BAP APD ∠+∠=︒,(______)∵AB CD ∥.(______)∵BAP APC ∠=∠.(______)∵12∠=∠,(______)∵12BAP APC ∠-∠=∠-∠.(______)即EAP FPA ∠=∠.∵______.(______)∵E F ∠=∠.(______)2.如图,点E 在DF 上,点B 在AC 上,∵1=∵2,∵C =∵D ,试说明:AC ∵DF ,将过程补充完整.解:∵∵1=∵2(已知)∵1=∵3( )∵∵2=∵3(等量代换)∵EC ∵DB (同位角相等,两直线平行)∵∵C =∵ABD ( )又∵∵C =∵D (已知)∵∵D =∵ABD ( )∵AC ∵DF ( )3.填空:(将下面的推理过程及依据补充完整)如图,己知:CD 平分∵ACB ,AC DE ∥、CD EF ∥,求证:EF 平分∵DEB . 证明:∵CD 平分∵ACB (已知),∵∵DCA =__________________(_________________).∵AC DE ∥(已知),∵∵DCA =__________________.∵DCE CDE ∠=∠(等量代换),DCE BEF ∠=∠(_________________),∵_____________=_____________(等量代换).∵EF 平分∵DEB (_________________)4.完成下面推理过程.在括号内的横线上填上推理依据.如图,已知:AB EF ∥,EP EQ ⊥,90EQC APE ∠+∠=︒,求证:AB CD ∥. 证明:∵AB EF ∥,∵APE PEF ∠=∠(_________).∵EP EQ ⊥,∵90PEQ ∠=︒(__________).即90QEF PEF ∠+∠=︒.∵90APE QEF ∠+∠=︒∵90EQC APE ∠+∠=︒,∵EQC ∠=_________(_______).∵EF CD ∥(___________).∵AB CD ∥(_________).5.在横线上填上适当的内容,完成下面的证明.如图,∵E =∵1,∵3+∵ABC =180°,BE 是∵ABC 的角平分线,求证:DF∥AB .证明:∵BE 是∵ABC 的角平分线∵∵1=∵2(________________)又∵∵E =∵1∵∵E =∵2(___________)∵____∥____(____________________)∵∵A +∵ABC =180°(____________________)又∵∵3+∵ABC =180°∵____=____(________________)∵DF∥AB (____________________).6.在下面解答中填空.如图,,,12AB BF CD BF ⊥⊥∠=∠,试说明3E ∠=∠.解:∵,AB BF CD BF ⊥⊥(已知),∵∵ABF=∵________________=90°(垂直的定义).∵12∠=∠(已知),∵AB//EF(__________________________________).∵CD//EF(平行于同一条直线的两条直线互相平行).∠=∠(___________________________________).∵3E7.如图,已知直线AB∵CD,∵B=50°,∵BEC=25°,EC平分∵BEF.(1)请说明AB∵EF的理由;(2)求∵DCE的度数.8.如图,EF∵BC,∵1=∵C,∵2+∵3=180°,试说明∵ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.解:∵∵1=∵C,(已知)∵GD∵ .()∵∵2=∵DAC.()∵∵2+∵3=180°,(已知)∵∵DAC+∵3=180°.(等量代换)∵AD∵EF.()∵∵ADC=∵.()∵EF∵BC,(已知)∵∵EFC=90°.()∵∵ADC=90°.(等量代换)60°.请问:(1)GD 与CB 有怎样的位置关系?为什么?(2)求∵ACB 的度数.10.如图,已知,12,34AB CD ∠=∠∠=∠∥,求证:D DCE ∠=∠.11.如图,在∵ABC 中,CD ∵AB ,垂足为D ,点E 在BC 上,EF ∵AB ,垂足为F .(1)CD 与EF 平行吗?请说明理由;(2)如果∵1=∵2,且∵3=110°,求∵ACB 的度数.12.如图,在∵ABC中,E、G分别是AB、AC上的点,F、D是BC上的点,连接EF、AD、DG,AD∥EF,∵1+∵2=180°.(1)说明:AB∥DG;(2)若∵2=145°,∵B=35°,说明:DG是∵ADC的平分线.13.如图,已知AB∵CD,∵2+∵3=180°,DA平分∵BDC,CE∵FE于点E,∵1=70°.(1)求证:AD∵CE;(2)求∵F AB的度数.14.如图,已知F是四边形BCDE的边BE上一点,CB与DF的延长线相交于点A,其中∵A=∵ADE.(1)若∵EDC=3∵C,求∵C的度数;(2)若∵C=∵E,求证:BE∥CD.15.如图,已知点D、E、F分别在ABC的边AB、AC、BC上,∵1+∵2=180°,∵3=∵B,请说明∵DEC+∵C= 180°的理由16.如图,在∵ABC中,点D、E分别在AB、BC上,且DE∵AC,∵1=∵2.(1)求证:AF∵BC;(2)若AC平分∵BAF,∵B=50°,求∵1的度数.17.如图,已知∵1=52°,∵2=128°,∵C=∵D.求证:∵A=∵F.18.如图,B ,E 分别是AC ,DF 上的点,180A ABF ∠+∠=︒,A F ∠=∠,求证:AC DF ∥.19.请根据条件进行推理,得出结论,并在括号内注明理由.已知,如图,AB DC ∥,直线EF 分别交AB 、CD 于点G 、H ,GM 、HN 分别平分∵BGH 与∵DHF .求证:GM HN ∥;证明:∵AB DC ∥(已知),∵∵BGH=∵DHF (__________________),∵GM 、HN 分别平分∵BGH 与∵DHF , ∵∵_____=12∵BGH ,∵_____=12∵DHF (__________________),∵∵_____=∵_____(__________________),∵GM //HN (__________________________).20.(1)(问题)如图1,若AB CD ∥,40AEP ∠=︒,50PFC ∠=︒,求EPF ∠的度数.(3)(联想拓展)如图3所示,在(2)的条件下,已知60EPF ∠=︒,120PFC ∠=︒,PEA ∠的平分线和PFC ∠的平分线交于点G ,直接写出G ∠的度数.。
七年级数学下册平行线的判定练习题

七年级数学下册平行线的判定练习题(含答案解析)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,下列四个结论:①①1=①3;①①B =①5;①①B +①BAD =180º;①①2=①4;①①D +①BCD =180º.能判断AB ①CD 的个数有 ( )A .2个B .3个C .4个D .5个2.如图,//AB CD ,120BAE ∠=︒,40DCE ∠=︒,则AEC ∠=( )A .70︒B .80︒C .90︒D .100︒3.如图,已知直线a ,b 被直线c 所截,下列条件不能判断a ①b 的是( )A .①2=①6B .①2+①3=180°C .①1=①4D .①5+①6=180°4.如图点E 在BC 的延长线上,则下列条件中,不能判定AB ∥CD 的是( )A .①1=①2B .①B =①DCEC .①3=①4D .①D +①DAB =180°5.如图所示,在下列四组条件中,能判断//AB CD 的是( )A .12∠=∠B .180BAD ABC ∠+∠=︒ C .34∠=∠D .ABD BDC ∠=∠6.下列给出的条件能够推理出a b ∥的是( )A .12∠=∠B .24∠∠=C .34∠=∠D .14180∠+∠=︒二、填空题7.如图,木工师傅用角尺画平行线的依据是_________________________.8.已知:如图,在三角形ABC 中,CD AB ⊥于点D ,连接DE ,当1290∠+∠=︒时,求证:DE ∥BC . 证明:①CD AB ⊥(已知),①90ADC ∠=︒(垂直的定义).①1∠+________90=︒,①1290∠+∠=︒(已知),①________2=∠(依据1:________),①∥DE BC (依据2:________).9.如图,写出能判定AB①CD的一对角的数量关系:___________________.BC ,DO①AB,则①O的半径10.如图,AB是①O的直径,CB切①O于B,连结AC交①O于D,若8cmOA=___________cm.11.如图,用符号语言表达定理“内错角相等,两直线平行”的推理形式:①_____,①a①b.三、解答题12.请完成下面的推理过程:如图,已知①D=108°,①BAD=72°,AC①BC于C,EF①BC于F.求证:①1=①2.证明:①①D=108°,①BAD=72°(已知)①①D+①BAD=180°AB CD()①//①①1= ( )又①AC ①BC 于C ,EF ①BC 于F (已知)①EF // ( )①①2= ( )①①1=①2( )13.如图,四边形ABCD 中,①A =①C =90°,BE 平分①ABC ,DF 平分①ADC ,则BE 与DF 有何位置关系?试说明理由.14.如图,已知AC ①BC 于点C ,①B =70º,①ACD =20º.(1)求证:AB //CD ;(2)在不添加任何辅助线的情况下,请补充一个条件________,使BC //AD .15.如图所示,在四边形ABCD 中,ABC ∠的角平分线及外角DCE ∠的平分线所在的直线相交于点F ,若A α∠=,D β∠=.(1)如图(a )所示,180αβ+>,试用α,β表示F ∠,直接写出结论.(2)如图(b )所示,180αβ+<,请在图中画出F ∠,并试用α,β表示F ∠.(3)一定存在F ∠吗?若有,写出F ∠的值;若不一定,直接写出α,β满足什么条件时,不存在F ∠.16.下面是王倩同学的作业及自主探究笔记,请认真阅读并补充完整.【作业】如图①,直线12l l ∥,ABC 与DBC △的面积相等吗?为什么?解:相等.理由如下:设1l 与2l 之间的距离为h ,则12ABC SBC h =⋅,12DBC S BC h =⋅△. ①ABC DBC S S =.【探究】(1)如图①,当点D 在1l ,2l 之间时,设点A ,D 到直线2l 的距离分别为h ,h ',则ABC DBC S h S h ='△△.证明:①ABC S(2)如图①,当点D 在1l ,2l 之间时,连接AD 并延长交2l 于点M ,则ABC DBC S AM S DM=△△.证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒, ①AE ∥ .①AEM △∽ . ①AE AM DF DM=. 由【探究】(1)可知ABC DBCS S =△△ , ①ABC DBC S AM S DM=△△. (3)如图①,当点D 在2l 下方时,连接AD 交2l 于点E .若点A ,E ,D 所对应的刻度值分别为5,1.5,0,ABC DBCS S △△的值为 .17.如图,在下列括号中填写推理理由①①1=135°(已知),①①3=①135°( )又①①2=45°(已知),①①2+①3=45°+135°=180°,①a ①b ( )18.已知:如图,点E在线段CD上,EA、EB分别平分①DAB和①ABC,①AEB=90°,设AD=x,BC=y,且(x﹣2)2+|y﹣5|=0.(1)求AD和BC的长.(2)试说线段AD与BC有怎样的位置关系?并证明你的结论.(3)你能求出AB的长吗?若能,请写出推理过程,若不能,说明理由.19.如图,AB=CD,BC=DA,求证:AB①CD,BC①DA.参考答案:1.A【分析】根据同位角相等、内错角相等、同旁内角互补的两直线平行分别判断即可.【详解】解:①①13∠=∠,①//AD BC ,无法推出//AB CD ;①①5B ∠=∠,①//AB CD ;①①180B BAD ∠+∠=°,①//AD BC ,无法推出//AB CD ;①①24∠∠=,①//AB CD ;①①180D BCD ∠+∠=︒①//AD BC ,无法推出//AB CD ,综上所述,能判断//AB CD 的是:①①,有2个,故选:A .【点睛】题考查了平行线的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.2.D【分析】过点E 作//EF AB ,先根据平行线的判定可得//EF CD ,再根据平行线的性质分别可得AEF ∠和CEF ∠的度数,然后根据角的和差即可得.【详解】如图,过点E 作//EF AB ,120BAE ∠=︒,18060AEF BAE ∴∠=︒-∠=︒,又//AB CD ,//EF CD ∴,40DCE CEF ∴=∠=∠︒,6040100AEC AEF CEF ∴∠=∠+∠=︒+︒=︒,故选:D .【点睛】本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题关键.3.D【分析】根据同位角相等,内错角相等,同旁内角互补来判定两直线平行.【详解】解:A ,①2和①6是内错角,内错角相等两直线平行,能判定a ①b ,不符合题意;B ,①2+①3=180°,①2和①3是同旁内角,同旁内角互补两直线平行,能判定a ①b ,不符合题意;C ,①1=①4,由图可知①1与①2是对顶角,①①1=①2=①4,①2和①4互为同位角,能判定a ①b ,不符合D ,①5+①6=180°,①5和①6是邻补角,和为180°,不能判定a ①b ,符合题意;故选:D .【点睛】此题主要考查了平行线的判定,结合平行线判定的条件是解决这道题的关键.4.C【分析】根据平行线的判定定理进行逐一分析解答即可.【详解】解:A 、正确,符合“内错角相等,两条直线平行”的判定定理;B 、正确,符合“同位角相等,两条直线平行”的判定定理;C 、错误,若①3=①4,则AD ①BE ;D 、正确,符合“同旁内角互补,两条直线平行”的判定定理;故选:C .【点睛】本题考查的是平行线的判定定理,比较简单.5.D【分析】根据平行线的判定定理求解判断即可.【详解】解:A 、①①1=①2,①AD //BC (内错角相等,两直线平行),故此选项不符合题意;B 、①①BAD +①ABC =180°,①AD //BC (同旁内角互补,两直线平行),故此选项不符合题意;C 、①①3=①4,①AD //BC (内错角相等,两直线平行),故此选项不符合题意;D 、①①ABD =①BDC ,①AB //CD (内错角相等,两直线平行),故此选项符合题意;故选:D .【点睛】此题主要考查了平行线的判定,熟记平行线的判定定理是解题关键.6.D【分析】根据平行线的判定逐一判定即可.【详解】解:A.由12∠=∠不能推理出a b ∥,故不符合题意;B.由24∠∠=不能推理出a b ∥,故不符合题意;C.由34∠=∠不能推理出a b ∥,故不符合题意;D. ①①4+①5=180°时能推出a b ∥,又①①1=①5,①由14180∠+∠=︒能推理出a b ∥,故符合题意;【点睛】本题考查了平行线的判定定理,解决此题的关键是清楚平行线的判定定理同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.7.在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.【分析】在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行.【详解】解:在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行. 故答案为在同一平面内,垂直于同一条直线的两条直线平行或根据同位角相等两直线平行【点睛】本题考查的是平行线的判定,熟知平行线的判定方法是解答此题的关键8. EDC ∠ EDC ∠ 同角的余角相等 内错角相等,两直线平行【分析】根据垂直的定义及平行线的判定定理即可填空.【详解】①CD AB ⊥(已知),①90ADC ∠=︒(垂直的定义).①1∠+EDC ∠90=︒,①1290∠+∠=︒(已知),①EDC ∠2=∠(同角的余角相等),①//DE BC (内错角相等,两直线平行).故答案为:EDC ∠;EDC ∠;同角的余角相等;内错角相等,两直线平行.【点睛】此题考查了平行线的判定与性质,熟记 “内错角相等,两直线平行”是解题的关键.9.①BAC =①ACD (或①B +①BCD =180°或①D +①BAD =180°)【分析】根据平行线的判定定理进行填空.【详解】解:由“内错角相等,两直线平行”可以添加条件①BAC =①ACD .由“同旁内角互补,两直线平行”可以添加条件①B +①BCD =180°,或①D +①BAD =180°.故答案为:①BAC =①ACD (或①B +①BCD =180°或①D +①BAD =180°).【点睛】本题考查了平行线的判定.解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力. 10.4【分析】先根据切线的性质得出BC①AB,再根据平行线的判定得出BC OD∥,再根据平行线分线段成比例,得出OD AOBC AB=,根据点O是AB的中点,8BC=cm,求出OD,即可得出结果.【详解】解:①CB切①O于B,①BC①AB,①DO①AB,①BC OD∥,①OD AOBC AB=,①点O是AB的中点,①2AB AO=,①12 OD AOBC AB==,①8BC=cm,①OD=4cm,①OA=OD,①OA=4cm.故答案是:4.【点睛】本题主要考查了切线的性质,平行线的判定,平行线分线段成比例,根据切线的性质,结合已知条件,求出BC OD∥,是解题的关键.11.①4=①1【分析】两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.【详解】解:①①4=①1,①a①b.故答案为:①4=①1.【点睛】本题主要考查平行线的判定,熟记判定方法是解题的关键.12.见解析【分析】由直线相交及平行的相关定理性质即可得到答案.【详解】解:①①D=108°,①BAD=72°(已知)①①D+①BAD=180°①//AB CD(同旁内角互补,两直线平行)①①1=3∠(两直线平行,内错角相等)又①AC ①BC 于C ,EF ①BC 于F (已知)①EF //AC (垂直于同一直线的两条直线平行)①①2=3∠(两直线平行,同位角相等)①①1=①2(等量代换)【点睛】本题考查直线相交及平行的相关定理性质,熟练掌握相关知识是解题的关键.13.BE ①DF ,理由见解析【分析】根据四边形的内角和定理和①A =①C =90°,得①ABC +①ADC =180°;根据角平分线定义、等角的余角相等易证明和BE 与DF 两条直线有关的一对同位角相等,从而证明两条直线平行.【详解】解:BE ①DF .理由如下:①①A =①C =90°,①①ABC +①ADC =180°①BE 平分①ABC ,DF 平分①ADC ,①①1=①2=12①ABC ,①3=①4=12①ADC ,①①1+①3=12(①ABC +①ADC )=12×180°=90°, 又①①1+①AEB =90°,①①3=①AEB①BE ①DF【点睛】本题考查了四边形的内角和是360°、角平分线定义、等角的余角相等和平行线的判定,考察的知识点较多,只有熟练掌握,才能运用自如.14.(1)证明见解析(2)AC ①AD (答案不唯一)【分析】(1)由题意易求出110BCD BCA ACD ∠=∠+∠=︒,即可利用同旁内角互补,两直线平行证明; (2)由在同一平面内,垂直于同一条直线的两条直线互相平行,即可补充条件为:AC ①AD .(答案不唯一)(1)证明:①AC ①BC ,①90ACB ∠=︒,①110BCD BCA ACD ∠=∠+∠=︒,①180BCD B ∠+∠=︒,①AB CD ;(2)补充条件:AC ①AD ,①AC ①AD ,AC ①BC①BC //AD .故答案为:AC ①AD .【点睛】本题考查垂直的定义,平行线的判定.掌握平行线的判定条件是解题关键.15.(1)()1902F αβ∠=+-︒;(2)图见解析,()1902F αβ∠=︒-+,证明见解析;(3)180αβ+=︒时,不存在F ∠,证明见解析.【分析】(1)先根据四边形的内角和求出360D ABC CB βα∠=︒-∠-+,再根据角平分线的定义、邻补角的定义得出1,19022ABC F FBC DC E B C ∠=︒-∠∠∠=,然后根据三角形的外角性质即可得; (2)先根据角平分线的定义画出图形,再参照题(1):由四边形的内角和求出360D ABC CB βα∠=︒-∠-+,再根据角平分线的定义、对顶角的性质得出11,9022GBC ABC BCF DCB ∠=∠∠=︒-∠,然后根据三角形的外角性质即可得;(3)由题(1)和(2)可知,当180αβ+>︒和180αβ+<︒时,存在F ∠的值,因此,考虑当180αβ+=︒时,F ∠是否存在.证明如下:先根据四边形的内角和得出180ABC DCB ∠+∠=︒,再根据邻补角的定义得出180DCE DCB ∠+∠=︒,从而得出ABC DCE ∠=∠,然后根据角平分线的定义可得出GBC ECF ∠=∠,最后根据平行线的判定得出//BG CF ,即可得证.【详解】(1)()1902F αβ∠=+-︒,求解过程如下: 在四边形ABCD 中,,A D αβ∠=∠=360360DCB ABC D A αβ∠=︒-∠-=︒∴∠-+-∠ BF 平分ABC ∠,CF 平分DCE ∠1,2111(180)90222FBC DCE DCB DCB ABC FCE ∴∠=∠=︒-∠=︒-∠∠∠= F FC FB E C ∠=∠-∴∠119022DC AB B C =︒∠-∠- 902)1(DCB ABC =︒-∠+∠ 190(362)0αβ=︒-︒--)1(902βα=-+︒; (2)由题意,画ABC ∠的角平分线及外角DCE ∠的平分线所在的直线相交于点F ,则所要画的F ∠如下图所示.求解过程如下:①()360ABC DCB A D ∠+∠=︒-∠+∠,且A α∠=,D β∠=①360D ABC CB βα∠=︒-∠-+①BG 平分ABC ∠,CH 平分DCE ∠ ①1111,(180)902222GBC ABC ECH DCE DCB DCB ∠=∠∠=∠=︒-∠=︒-∠ 1902BCF ECH DCB ∴∠=∠=︒-∠ ①GBC ∠是BCF ∆的一个外角①GBC F BCF ∠=∠+∠①F GBC BCF ∠=∠-∠11(90)22ABC DCB =∠-︒-∠ 1()902ABC DCB =∠+∠-︒ 1(360)902αβ=︒---︒ 190()2αβ=︒-+;(3)当180αβ+=︒时,不存在F ∠.证明过程如下:①()360ABC DCB A D ∠+∠=︒-∠+∠,且A α∠=,D β∠=①360180ABC DCB αβ∠+∠=︒--=︒180DCE DCB ∠+∠=︒ABC DCE ∴∠=∠①BG 平分ABC ∠,CF 平分DCE ∠ ①11,22GBC ABC ECF DCE ∠=∠∠=∠GBC ECF ∴∠=∠①//BG CF故当180αβ+=︒时,不存在F ∠.【点睛】本题考查了四边形的内角和、三角形的外角性质、角平分线的定义、平行线的判定等知识点,较难的是题(3),综合题(1)和(2)的题设与结论,正确提出假设是解题关键.16.(1)证明见解析(2)证明见解析 (3)73【分析】(1)根据三角形的面积公式可得11,22ABC DBC S S BC h BC h '=⋅=⋅,由此即可得证; (2)过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,先根据平行线的判定可得AE DF ,再根据相似三角形的判定可证AEM DFM ~,根据相似三角形的性质可得AE AM DF DM =,然后结合【探究】(1)的结论即可得证;(3)过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,先根据相似三角形的判定证出AME DNE ~,再根据相似三角形的性质可得73AM AE DN DE ==,然后根据三角形的面积公式可得12ABC S BC AM =⋅,12DBC S BC DN =⋅,由此即可得出答案. (1) 证明:12ABC SBC h =⋅,12DBC BC h S '=⋅, ABC DBC Sh S h ∴='. (2)证明:过点A 作AE BM ⊥,垂足为E ,过点D 作DF BM ⊥,垂足为F ,则90AEM DFM ∠=∠=︒,AE DF ∴∥.AEM DFM ~∴.AE AM DF DM∴=. 由【探究】(1)可知ABC DBC SAE S DF =, ABC DBC SAM S DM∴=. (3)解:过点A 作AM BC ⊥于点M ,过点D 作DN BC ⊥于点N ,则90AME DNE ∠=∠=︒,AM DN ∴, AME DNE ∴~, AM AE DN DE∴=, 点,,A E D 所对应的刻度值分别为5,1.5,0,5 1.5 3.5AE ∴=-=, 1.5DE =,3.571.53AM DN ∴==, 又12ABC S BC AM =⋅,12DBC S BC DN =⋅, 73ABC DBC S AM S DN =∴=, 故答案为:73.【点睛】本题考查了相似三角形的判定与性质、平行线的判定、三角形的面积等知识点,熟练掌握相似三角形的判定与性质是解题关键.17.对顶角相等,同旁内角互补,两直线平行【分析】根据图形由对顶角相等,及平行线的判定中同旁内角互补,两直线平行可直接得出理由;【详解】①①1=135°(已知),①①3=①135°(对顶角相等)又①①2=45°(已知),①①2+①3=45°+135°=180°,①a ①b (同旁内角互补,两直线平行)故答案为:对顶角相等;同旁内角互补,两直线平行【点睛】本题考查了对顶角相等;平行线的判定中同旁内角互补,两直线平行;重点掌握平行线判定定理. 18.(1)2AD =,5BC =;(2)//AD BC ,见解析;(3)能,见解析【分析】(1)根据算术平方根和绝对值的非负性即可得出AD 、BC 的长度;(2)根据题意证明180BAD ABC ∠+∠=︒即可得出结果;(3)延长AE 交直线BC 于F ,先证明①AEB ①①FEB ,然后证明()ADE FCE ASA ∆≅∆,即可得出结果.【详解】解:(1)2(2)|5|0x y -+-=,20x ∴-=,50y -=,解得2x =,5y =,即2AD =,5BC =;(2)//AD BC .理由如下:EA 、EB 分别平分DAB ∠和ABC ∠,12BAE BAD ∴∠=∠,12ABE ABC ∠=∠, 1()2BAE ABE BAD ABC ∴∠+∠=∠+∠, 90AEB ∠=︒,90BAE ABE ∴∠+∠=︒,180BAD ABC ∴∠+∠=︒,//AD BC ∴;(3)能.理由如下:延长AE 交直线BC 于F ,如图,//AD BC ,DAF F ∴∠=∠,而DAF BAF ∠=∠,BAF F ∴∠=∠,在①AEB 和①FEB 中90BAE F BEA BEF BE BE ⎧∠=∠⎪∠=∠=⎨⎪=⎩,①①AEB ①①FEB (AAS )AB FB ∴=,AE =EF .在①ADE 和①FCE 中DAE F AE FEAED FEC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ADE FCE ASA ∴∆≅∆,2AD CF ∴==,527AB BF ∴==+=.【点睛】本题考查了算术平方根和绝对值的非负性,角平分线的定义,平行线的判定,全等三角形的判定与性质,熟知相关性质定理是解本题的关键.19.见解析【分析】连接AC ,利用SSS 得到ABC CDA △△≌,利用全等三角形的对应角相等得到两对内错角相等,利用内错角相等两直线平行即可得证.【详解】证明:连接AC ,在ABC 和CDA 中,AB CD BC AD AC CA =⎧⎪=⎨⎪=⎩,①()ABC CDA SSS ≌,①BAC DCA ACB CAD ∠=∠∠=∠, ,①//AB DC ,//AD BC .【点睛】此题考查了全等三角形的判定与性质,以及平行线的判定,熟练掌握全等三角形的判定与性质是解本题的关键.。
(简化)七年级数学平行线与垂直线练习题

(简化)七年级数学平行线与垂直线练习题七年级数学平行线与垂直线练题
本文档旨在提供一些关于平行线和垂直线的练题,以帮助七年级数学学生巩固这方面的知识。
练题一:平行线问题
1. 请画出以下每组直线中的平行线对:
- 直线1: y = 2x + 3
- 直线2: y = 2x + 5
- 直线3: y = -3x + 2
- 直线4: y = -3x - 1
2. 若直线l与直线m平行,直线m与直线n平行,是否可以得出直线l与直线n平行的结论?请解释并给出一组例子。
练题二:垂直线问题
1. 请画出以下每组直线中的垂直线对:
- 直线1: y = 2x + 3
- 直线2: y = -1/2x + 5
- 直线3: y = -3x + 2
- 直线4: y = 1/3x - 1
2. 若直线a与直线b垂直,直线b与直线c垂直,是否可以得
出直线a与直线c垂直的结论?请解释并给出一组例子。
练题三:平行线和垂直线问题
1. 请画出以下直线组合中的平行线和垂直线对,并判断其关系:
- 直线1: y = 2x + 3
- 直线2: y = -1/2x + 5
- 直线3: y = 2x + 3
- 直线4: y = -2x - 1
2. 若直线d与直线e平行,直线e与直线f垂直,是否可以得
出直线d与直线f的关系?请解释并给出一组例子。
以上是关于平行线和垂直线的练习题,希望能帮助你巩固相关知识。
如果有任何问题,请随时向老师或同学寻求帮助。
人教版七年级下册数学平行线及其判定第2课时平行线的判定——利用同位角、第三直线 同步练习

5.2 平行线及其判定第2课时平行线的判定——利用“同位角、第三直线”基础训练知识点1 由“同位角相等”判定两直线平行1.如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为_______________,理由是______________.2.如图,直线a,b被直线c所截,下列条件能使a∥b的是( )A.∠1=∠6B.∠2=∠6C.∠1=∠3D.∠5=∠73.如图,能判定EB∥AC的条件是( )A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠C=∠EBD4.如图,已知∠1=∠2,则下列结论正确的是( )A.AD∥BCB.AB∥CDC.AD∥EFD.EF∥BC5.如图,CD平分∠ACE,且∠B=∠ACD,可以得出的结论是( )A.AD∥BCB.AB∥CDC.CA平分∠BCDD.AC平分∠BAD知识点2 由“第三直线”判定两直线平行6.如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB______CD.7.在每一步推理后面的括号内填上理由.(1)如图①,因为AB∥CD,EF∥CD,所以AB∥EF(____________).(2)如图②,因为AB∥CD,过点F作EF∥AB(____________),所以EF∥CD(____________).8.在同一个平面内,不重合的两个直角,如果它们有一条边共线,那么另一条边( )A.互相平行B.互相垂直C.共线D.互相平行或共线9.三条直线a,b,c,若a∥c,b∥c,则a与b的位置关系是( )A.a⊥bB.a∥bC.a⊥b或a∥bD.无法确定易错点填错理由而致错10.如图,已知AB⊥BD于点B,CD⊥BD于点D,∠1=∠2,试问CD与EF平行吗?为什么?解:CD∥EF.理由:因为∠1=∠2( ),所以AB∥EF( ).因为AB⊥BD,CD⊥BD,所以AB∥CD( ).所以CD∥EF( ).提升训练考查角度1 利用“同位角相等”说明两直线平行11.如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC. 解:因为BE平分∠ABD,所以∠ABE=∠DBE( ).因为∠ABE=∠C,所以∠DBE=∠C,所以BE∥AC( ).12.如图,已知∠1=68°,∠2=68°,∠3=112°.(1)因为∠1=68°,∠2=68°(已知),所以∠1=∠2.所以∥(同位角相等,两直线平行).(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°,所以∠4=68°.又因为∠2=68°,所以∠2=∠4,所以∥(同位角相等,两直线平行).考查角度2 利用“同位角”“第三直线”(平行或垂直)判定平行13.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?解:a与c平行.理由:因为∠1=∠2( ),所以a∥b( ).因为∠3=∠4( ),所以b∥c( ).所以a∥c( ).14.如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.(1)方法一:用“同位角相等”说明.(2)方法二:用“第三直线”说明.探究培优拔尖角度1 利用平行线、垂线的基本事实说明三点共线15.在同一平面内,已知A,B,C是直线l同旁的三个点.(1)若AB∥l,BC∥l,则A,B,C三点在同一条直线上吗?为什么?(2)若AB⊥l,BC⊥l,则A,B,C三点在同一条直线上吗?为什么?拔尖角度2 利用同位角探究两线段的位置关系16.如图所示,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F, 问:CE与DF的位置关系怎样?试说明理由.参考答案1.【答案】AB∥CD;同位角相等,两直线平行2.【答案】B3.【答案】D4.【答案】C解:找出∠1和∠2是直线AD,EF被直线CD所截而形成的同位角,因此由∠1=∠2可得出AD∥EF.5.【答案】B6.【答案】∥7.【答案】(1)平行于同一条直线的两条直线平行(2)过直线外一点,有且只有一条直线与这条直线平行;平行于同一条直线的两条直线平行8.【答案】D9.【答案】B解:由平行于同一条直线的两条直线互相平行知选B.10.已知;同位角相等,两直线平行;在同一平面内,垂直于同一条直线的两条直线互相平行;平行于同一条直线的两条直线互相平行分析:本题学生容易混淆判定两直线平行的几种方法,从而导致错误.11.【答案】角平分线的定义;同位角相等,两直线平行12.【答案】(1)a;b (2)b;c13.【答案】已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行14.解:(1)方法一:因为∠1=90°,∠2=90°,所以∠1=∠2.所以CD∥EF.(2)方法二:因为∠1=90°,∠2=90°,所以CD⊥AB,EF⊥AB.所以CD∥EF.15.解:(1)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.(2)在同一条直线上.理由:因为直线AB,BC都经过点B,且都与直线l垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC为同一条直线,所以A,B,C三点在同一条直线上.16.解:CE∥DF.理由如下:因为BD平分∠ABC,CE平分∠ACB,所以∠DBC=错误!未找到引用源。
人教版七年级下册数学平行线的判定及性质证明题训练(含答案)

人教版七年级下册数学平行线的判定及性质证明题训练(含答案)1.如图,三角形ABC 中,点D 在AB 上,点E 在BC 上,点F ,G 在AG 上,连接,,DG BG EF .己知12∠=∠,3180ABC ∠+∠=︒,求证:∥BG EF .将证明过程补充完整,并在括号内填写推理依据.证明:∵_____________(已知)∴∥DG BC (_______________________)∴.CBG ∠=________(____________________)∵12∠=∠(已知)∴2∠=________(等量代换)∴∥BG EF (___________________)2.如图,已知12∠=∠,A F ∠=∠,试说明C D ∠=∠的理由.解:把1∠的对顶角记作3∠,所以13∠=∠(对顶角相等).因为12∠=∠(已知),所以23∠∠=( ),所以 ∥ ( ).(请继续完成接下去的说理过程)3.如图,CD ∥AB ,点O 在直线AB 上,OE 平分∠BOD ,OF ⊥OE ,∠D =110°,求∠DOF 的度数.4.如图,DH 交BF 于点E ,CH 交BF 于点G ,12∠=∠,34∠=∠,5B ∠=∠.试判断CH 和DF 的位置关系并说明理由.5.已知:如图,直线DE//AB.求证:∠B+∠D=∠BCD.6.如图,已知AB CD∥,BE平分ABC∠,CE平分BCD∠,求证1290∠+∠=︒.证明:∵BE平分ABC∠(已知),∴2∠=(),同理1∠=,∴1122∠+∠=,又∵AB CD∥(已知)∴ABC BCD∠+∠=(),∴1290∠+∠=︒.7.请把下列证明过程及理由补充完整(填在横线上):已知:如图,BC,AF是直线,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.证明:∵AD∥BC(已知),∴∠3=().∵∠3=∠4(已知),∴∠4=().∵∠1=∠2(已知),∴∠1+∠CAF=∠2+∠CAF().即∠BAF=.∴∠4=∠BAF.().∴AB∥CD().8.如图,已知∠A=120°,∠FEC=120°,∠1=∠2,试说明∠FDG=∠EFD.请补全证明过程,即在下列括号内填上结论或理由.解:∵∠A=120°,∠FEC=120°(已知),∴∠A=().∴AB∥().又∵∠1=∠2(已知),∴EF ∥ ( ).∴∠FDG =∠EFD ( ).9.在三角形ABC 中,CD AB ⊥于D ,F 是BC 上一点,FH AB ⊥于H ,E 在AC 上,EDC BFH ∠=∠.(1)如图1,求证:∥DE BC ;(2)如图2,若90ACB ∠=︒,请直接写出图中与ECD ∠互余的角,不需要证明.10.已知:如图,直线MN HQ ∥,直线MN 交EF ,PO 于点A ,B ,直线HQ 交EF ,PO 于点D ,C ,DG 与OP 交于点G ,若1103∠=︒,277∠=︒,396∠=︒.(1)求证:EF OP ∥;(2)请直接写出CDG ∠的度数.11.如图直线a b ∥,直线EF 与,a b 分别和交于点,,A B AC AB AC ⊥、交直线b 于点C .(1)若160∠=︒,直接写出2∠= ;(2)若3,4,5AC AB BC ===,则点B 到直线AC 的距离是 ;(3)在图中直接画出并求出点A 到直线BC 的距离.12.如图,已知AB CD ,BE 平分∠ABC ,∠CDE = 150°,求∠C 的度数.13.如图,在ABC 中,CD 平分ACB ∠交AB 于D ,EF 平分AED ∠交AB 于F ,已知ADE B ∠=∠,求证:EF CD ∥.14.已知:如图,AB ∥CD ∥EF ,点G 、H 、M 分别在AB 、CD 、EF 上.求证:GHM AGH EMH ∠∠∠=+.15.如图所示,点B 、E 分别在AC 、DF 上,BD 、CE 均与AF 相交,A F ∠=∠,C D ∠=∠,求证:12∠=∠.16.如图,在ABC 中,DE ∥AC ,DF ∥AB .(1)判断∠A 与∠EDF 之间的大小关系,并说明理由.(2)求∠A +∠B +∠C 的度数.17.已知:如图,ABC 中,点D 、E 分别在AB 、AC 上,EF 交DC 于点F ,32180∠+∠=︒ ,1B ∠=∠.(1)求证:∥DE BC ;(2)若DE 平分ADC ∠,33B ∠=∠,求2∠的度数.18.如图,AB ∥DG ,∠1+∠2=180°.(1)试说明:AD ∥EF ;(2)若DG 是∠ADC 的平分线,∠2=142°,求∠B 的度数.19.问题情境:如图1,AB CD ∥,130PAB ∠=︒,120PCD ∠=︒,求APC ∠的度数.小明的思路是:如图2,过P 作PE AB ∥,通过平行线性质,可得APC ∠=______.问题迁移:如图3,AD BC ∥,点P 在射线OM 上运动,ADP α∠=∠,BCP β∠=∠.(1)当点P 在A 、B 两点之间运动时,CPD ∠、α∠、β∠之间有何数量关系?请说明理由.(2)如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合),请你直接写出CPD ∠、α∠、β∠之间有何数量关系.20.直线AB CD∠.∥,直线EF分别交AB、CD于点M、N,NP平分MND(1)如图1,若MR平分EMB∠,则MR与NP的位置关系是.∠,则MR与NP有怎样的位置关系?请说明理由.(2)如图2,若MR平分AMN(3)如图3,若MR平分BMN∠,则MR与NP有怎样的位置关系?请说明理由.参考答案:1.解:证明:∵3180ABC ∠+∠=︒(已知)∴∥DG BC (同旁内角互补,两直线平行)∴.1CBG ∠=∠(两直线平行,内错角相等)∵12∠=∠(已知)∴2CBG ∠=∠(等量代换)∴∥BG EF (同位角相等,两直线平行)2.解:把1∠的对顶角记作3∠,所以13∠=∠(对顶角相等).因为12∠=∠(已知),所以23∠∠=(等量代换),所以//BD CE (同位角相等,两直线平行),所以4C ∠=∠(两直线平行,同位角相等),又因为A F ∠=∠,所以//DF AC (同位角相等,两直线平行),所以4D ∠=∠(两直线平行,内错角相等),所以C D ∠=∠(等量代换).故答案为:等量代换;BD ;CE ;同位角相等,两直线平行.3.解:∵CD AB ∥∴110DOB D ∠=∠=︒∵OE 平分∠BOD ∴1552DOE DOB ∠=∠=︒ 又∵OF ⊥OE∴90EOF ∠=︒∴905535DOF EOF DOE ∠=∠-∠=︒-︒=︒故答案为:35︒4.解:CH DF,理由如下:∵34∠=∠,∴CD BF,∴5180BED∠+∠=︒,∵5B∠=∠,∴180B BED∠+∠=︒,∴BC DH,∴2H∠=∠,∵12∠=∠,∴1H∠=∠,∴CH DF.5.证明:过点C作CF∥AB,∴∠B=∠BCF,∵DE//AB.CF∥AB,∴CF∥DE,∴∠D=∠DCF,∴∠BCD=∠BCF+∠DCF=∠B+∠D.6.证明:∵BE平分∠ABC(已知),∴∠2=12∠ABC(角平分线的定义),同理∠1=12∠BCD,∴∠1+∠2=12(∠ABC+∠BCD),又∵AB∥CD(已知)∴∠ABC +∠BCD =180°(两直线平行,同旁内角互补 ),∴∠1+∠2=90°. 故答案为:12∠ABC ;角平分线的定义;12∠BCD ;(∠ABC +∠BCD );180°;两直线平行,同旁内角互补.7.证明:∵AD ∥BC (已知),∴∠3=∠CAD (两直线平行,内错角相等).∵∠3=∠4(已知),∴∠4=∠CAD (等量代换).∵∠1=∠2(已知),∴∠1+∠CAF =∠2+∠CAF (等式的性质).即∠BAF =∠CAD .∴∠4=∠BAF .(等量代换).∴AB ∥CD (同位角相等,两直线平行).8.解:∵∠A =120°,∠FEC =120°(已知),∴∠A =∠FEC (等量代换),∴AB ∥EF (同位角相等,两直线平行),又∵∠1=∠2(已知),∴AB ∥CD (内错角相等,两直线平行),∴EF ∥CD (平行于同一条直线的两直线互相平行),∴∠FDG =∠EFD (两直线平行,内错角相等),故答案为:∠FEC ;等量代换;EF ;同位角相等,两直线平行;内错角相等,两直线平行;CD ;平行于同一条直线的两直线互相平行;两直线平行,内错角相等.9.证明:∵CD AB ⊥,FH AB ⊥,∴//CD FH ,∴BCD BFH ∠=∠.∵EDC BFH ∠=∠,∴BCD EDC ∠=∠,∴//ED BC .(2)与ECD ∠互余的角有:EDC BCD BFH A ∠∠∠∠,,,.证明:∵//ED BC ,∴90DEC ACB ∠=∠=︒,EDC BCD ∠=∠,∴90ECD EDC ∠+∠=︒,90ECD BCD ∠+∠=︒.∵//CD FH ,∴BCD BFH ∠=∠,∴90ECD BFH ∠+∠=︒.∵CD AB ⊥,∴90ACD A ∠+∠=︒,即90ECD A ∠+∠=︒.综上,可知与ECD ∠互余的角有:EDC BCD BFH A ∠∠∠∠,,,.10.解:(1)∵1103∠=︒,∴77∠=︒ABC ,∵277∠=︒,∴2ABC ∠=∠,∴EF OP ∥;(2)∵MN HQ ∥,EF OP ∥,∴1103∠=∠=∠=︒FDC FAB ,3180∠+∠=︒FDG ,∵396∠=︒,∴180********∠=︒-∠=︒-︒=︒FDG ,∴1038419∠=∠-∠=︒-︒=︒CDG FDC FDG .11.解:(1)∵a b ∥,∴12180BAC ∠+∠+∠=︒,∵AC AB ⊥,160∠=︒,∴230∠=︒,故答案为:30︒;(2)∵AC AB⊥,∴点B到直线AC的距离为线段4AB=,故答案为:4;(3)如图所示:过点A作AD BC⊥,点A到直线BC的距离为线段AD的长度,∵AC AB⊥,∴ABC∆为直角三角形,∴1122ABCS AC AB BC AD∆=⨯⨯=⨯⨯,即1134522AD ⨯⨯=⨯⨯,解得:125 AD=,∴点A到直线BC的距离为125.12.解:∵∠CDE=150°,∴∠CDB=180°-∠CDE=30°,又∵AB CD,∴∠ABD=∠CDB=30°,∵BE平分∠ABC,∴∠ABC=2∠ABD=60°,∵AB CD,∴∠C=180°-∠ABC=120°.13.证明:ADE B∠=∠(已知),DE//BC∴(同位角相等,两直线平行),ACB AED∴∠=∠(两直线平行,同位角相等),CD 平分ACB ∠,EF 平分AED ∠(已知),12ACD ACB ∴∠=∠,12AEF AED ∠=∠(角平分线的定义), ACD AEF ∴∠=∠(等量代换).EF //CD ∴(同位角相等,两直线平行).14.证明:∵AB ∥CD (已知)∴1AGH ∠=∠(两直线平行,内错角相等) 又 ∵CD ∥EF (已知)∴2EMH ∠=∠,(两直线平行,内错角相等) ∵12GHM ∠∠∠=+(已知)∴GHM AGH EMH ∠∠∠=+(等式性质)15.证明:∵A F ∠=∠,∴AC DF ∥,∴ABD D ∠=∠,又∵C D ∠=∠,∴ABD C ∠=∠,∴DB CE ∥,∴13∠=∠,∵23∠∠=,∴12∠=∠.16.(1)两角相等,理由如下:∵DE ∥AC ,∴∠A =∠BED (两直线平行,同位角相等).∵DF ∥AB ,∴∠EDF =∠BED (两直线平行,内错角相等), ∴∠A =∠EDF (等量代换).(2)∵DE ∥AC ,∴∠C =∠EDB (两直线平行,同位角相等).∵DF ∥AB ,∴∠B =∠FDC (两直线平行,同位角相等).∵∠EDB +∠EDF +∠FDC =180°,∴∠A +∠B +∠C =180°(等量代换).17.解:(1)∵32180∠+∠=︒,∠2+∠DFE =180°, ∴∠3=∠DFE ,∴EF //AB ,∴∠ADE =∠1,又∵1B ∠=∠,∴∠ADE =∠B ,∴DE //BC ,(2)∵DE 平分ADC ∠,∴∠ADE =∠EDC ,∵DE //BC ,∴∠ADE =∠B ,∵33B ∠=∠∴∠5+∠ADE +∠EDC =3B B B ∠+∠+∠=180°, 解得:36B ∠=︒,∴∠ADC =2∠B =72°,∵EF //AB ,∴∠2=∠ADC =180°-108°=72°,18.(1)∵AB ∥DG ,∴∠BAD =∠1,∵∠1+∠2=180°,∴∠BAD +∠2=180°.∵AD ∥EF .(2)∵∠1+∠2=180°且∠2=142°,∴∠1=38°,∵DG 是∠ADC 的平分线,∴∠CDG =∠1=38°,∵AB ∥DG ,∴∠B =∠CDG =38°.19.解:问题情境:∵AB ∥CD ,PE ∥AB ,∴PE ∥AB ∥CD ,∴∠A +∠APE =180°,∠C +∠CPE =180°,∵∠P AB =130°,∠PCD =120°,∴∠APE =50°,∠CPE =60°,∴∠APC =∠APE +∠CPE =50°+60°=110°;(1)CPD αβ∠=∠+∠;过点P 作PQ AD ∥,又因为AD BC ∥,所以PQ AD BC ∥∥,则ADP DPE ∠=∠,BCP CPE ∠=∠,所以CPD DPE CPE ADP BCP ∠=∠+∠=∠+∠;(2)情况1:如图所示,当点P 在B 、O 两点之间时,过P 作PE ∥AD ,交ON 于E ,∵AD ∥BC ,∴AD ∥BC ∥PE ,∴∠DPE =∠ADP =∠α,∠CPE =∠BCP =∠β, ∴∠CPD =∠DPE -∠CPE =∠α-∠β,情况2:如图所示,点P 在射线AM 上时,过P 作PE ∥AD ,交ON 于E ,∵AD ∥BC ,∴AD ∥BC ∥PE ,∴∠DPE =∠ADP =∠α,∠CPE =∠BCP =∠β, ∴∠CPD =∠CPE -∠DPE =∠β-∠α20.(1)如题图1,AB CD ∥EMB END ∴∠=∠MR 平分EMB ∠,NP 平分MND ∠.11,22EMR EMB ENP END ∴∠=∠∠=∠ EMR ENP ∴∠=∠∴MR ∥NP ;(2)如题图2,AB CD ∥AMN END ∴∠=∠MR 平分AMN ∠,NP 平分MND ∠.11,22RMN AMN ENP END ∴∠=∠∠=∠ RMN ENP ∴∠=∠∴MR ∥NP ;(3)如图,设,MR PN 交于点Q ,过点Q 作QG AB ∥AB CD ∥180BMN END ∴∠+∠=︒,QG CD ∥ ,MQG BMR GQN PND ∴∠=∠∠=∠ MR 平分BMN ∠,NP 平分MND ∠.11,22BMR BMN PND END ∴∠=∠∠=∠ 90BMR PND ∴∠+∠=︒90MQN MQG NQG ∴∠=∠+∠=︒ ∴MR ⊥NP ;。
浙教版2022年七年级数学下册第1章平行线平行线练习(含答案)

浙教版2022年七年级数学下册第1章平行线平行线练习(含答案)第1章平行线1.1平行线知识点1平行线的概念在同一个平面内,不相交的两条直线叫做平行线.“平行”用符号“∥”表示,直线a和b是平行线,记做a∥b,读做“a平行b”.平行线的定义包含三层意思:(1)“在同一平面内”是前提条件;(2)“不相交”就是说两条直线没有交点;(3)平行线指的是“两条直线”,而不是“两条射线”或“两条线段”.1.下列说法正确的是()A.在同一平面内,不相交的两条线段是平行线段B.不相交的两条直线是平行线C.在同一平面内,不重合的两条直线的位置关系只有相交和平行两种D.在同一平面内,不相交的两条射线是平行线知识点2平行线的画法用三角尺和直尺画平行线.如图1-1-1所示,把三角尺的一边紧靠直线CD,用直尺紧靠三角板尺的另一边,沿直尺推动三角尺,然后过三角尺的一边画直线AB,这时就可画出CD的平行线AB.图1-1-12.如图1-1-2所示,过三角形ABC的三个顶点分别作它对边的平行线,标出交点,并将平行线用“∥”符号表示出来.图1-1-2知识点3平行线的性质过直线外一点只能画一条已知直线的平行线,过直线上一点不能画已知直线的平行线.3.先在纸上画三角形ABC,再任取一点P,过点P画一条直线与BC 平行,则这样的直线()A.有且只有一条B.有两条C.不存在D.有一条或不存在一利用平行线的性质进行简单的推理教材例题变式题在同一平面内,已知直线AB∥EF,直线CD与AB相交于点P,试问直线CD与EF相交吗?为什么?[归纳总结]由本题可以得出一个常用的结论:在同一平面内,如果一条直线与一组平行线中的一条相交,那么它必定与其余的直线都相交.二平面内直线交点个数的探究教材补充题已知平面内有三条互不重合的直线,请画图探究它们的位置关系并说出它们的交点个数.[反思]判断下列说法是否正确,并说明理由.(1)不相交的两条直线叫做平行线;(2)过一点有且只有一条直线与已知直线平行.一、选择题1.在同一平面内两条不重合直线的位置关系有()A.两种:平行或相交23B.两种:平行或垂直C.三种:平行、垂直或相交D.两种:垂直或相交2.如图1-1-3,在同一平面内,过点C作线段AB的平行线,下列说法正确的是()图1-1-3A.不能作B.只能作一条C.能作两条D.能作无数条3.下列关于平行的表示方法正确的是()A.a∥AB.AB∥cdC.A∥BD.a∥b4.下列四边形中,AB与CD不平行的是()图1-1-5.在同一平面内,有三条互不重合的直线,其中只有两条是平行的,那么交点有()A.0个B.1个C.2个D.3个6.下列结论正确的是()A.不相交的直线互相平行B.不相交的线段互相平行C.不相交的射线互相平行D.有公共点的直线一定不平行7.已知直线a,b在同一平面内且不相交,直线c也在这一平面内,且c与a相交,则()A.b与c相交B.b与c平行C.b与c平行或相交D.b与c的位置关系不确定二、填空题8.如图1-1-5所示,AE∥BC,AF∥BC,则A,E,F三点________,理由是____________________.图1-1-59.把图1-1-6中互相平行的线段一一写出来:______________________________________.4图1-1-610.列举现实生活中体现平行的一个例子:________.11.在同一平面内,有两条直线l1与l2.(1)若l1与l2没有公共点,则l1与l2________;(2)若l1与l2有且只有一个公共点,则l1与l2________;(3)若l1与l2有两个公共点,则l1与l2________.三、解答题12.如图1-1-7,在长方体中,A1B1∥AB,AD∥BC,你能找出图中的平行线吗?图1-1-713.如图1-1-8所示,点P在∠AOB的一边OA上,点Q在∠AOB的另一边OB上,按下列要求画图:(1)过点P,Q的直线;(2)过点P画平行于OB的直线;(3)过点Q画平行于OA的直线.图1-1-814.如图1-1-9,点P是∠ABC内一点.(1)过点P画一条直线平行于直线AB,且与BC交于点D;(2)过点P画一条直线垂直于直线BC,垂足为E;(3)过点P作直线AB的垂线段PF.图1-1-91.[实践操作题]如图1-1-10所示,D,E是线段AC的三等分点.(1)过点D作DF∥BC交AB于点F,过点E作EG∥BC交AB于点G;(2)量出AF,FG,GB的长度(精确到0.1cm),你有什么发现?(3)量出FD,GE,BC的长度(精确到0.1cm),你有什么发现?(4)根据(3)中发现的规律,若FD=1.5cm,则EG=________cm,BC=________cm.图1-1-102.[操作探究]我们知道在同一平面内,两条平行直线的交点有0个,两条相交直线的交点有1个,平面内三条平行直线的交点有0个,经过同一点的三条直线的交点有1个……(1)平面上有三条互不重合的直线,请画图探究它们的交点个数;(2)若平面内的五条直线恰有4个交点,请画出符合条件的所有图形;(3)在平面内画出10条直线,使它们的交点个数恰好是32.详解详析5【预习效果检测】1.[解析]C根据平行线的概念“在同一平面内,不相交的两条直线叫做平行线”即可得出答案.[点评]正确理解平行线的概念是解决本题的关键.学习此概念时,我们要特别注意“在同一平面内”“不相交”“直线”等关键词.2.解:如图所示.过点A作BC边的平行线,过点B作AC边的平行线,过点C作AB边的平行线,两两相交于点D,E,F,所以DE∥BC,EF∥AC,DF∥AB.3.[解析]D当点P在直线BC外时,根据“经过直线外一点,有且只有一条直线与这条直线平行”这个基本事实,可知有且仅有一条;但当点P在直线BC上时,就不存在这样的直线,故本题应选择D.【重难互动探究】例1[解析]由于直线AB,EF的位置关系已确定,AB与CD的位置关系也确定了,根据平行线的性质即可确定CD与EF的位置关系.解:直线CD与EF相交.因为AB∥EF,CD与AB相交于点P,而过点P只能作一条直线AB与EF平行,所以直线CD与EF相交.例2[解析]在同一平面内,两条不重合直线的位置关系只有两种:相交和平行.若在同一平面内有三条或三条以上直线,其位置关系就变得比较复杂,交点个数也不确定,因此需分类讨论进行探究.解:①如图①,三条直线互相平行,此时交点个数为0;②如图②,三条直线相交于一点,此时交点个数为1;③如图③,三条直线两两相交且不交于同一点,此时交点个数为3;④如图④,其中两条直线互相平行且都与第三条直线相交,此时交点个数为2.【课堂总结反思】[反思](1)不正确,理由:在同一平面内,不相交的两条直线叫做平行线.(2)不正确,理由:过直线外一点,有且只有一条直线与这条直线平行;过直线上一点,不能画已知直线的平行线.【作业高效训练】[课堂达标]1.A2.B3.D4.D5.C6.D7.A68.[答案]共线经过直线外一点,有且只有一条直线与这条直线平行9.[答案]GH∥MN,EF∥AB,CD∥PQ10.[答案]如双杠.两条笔直的铁轨等(答案不唯一,写出一个即可) 11.[答案](1)平行(2)相交(3)重合12.解:图中的平行线有AB∥DC∥D1C1∥A1B1,AD∥BC∥B1C1∥A1D1,AA1∥BB1∥CC1∥D D1.13.[解析]借助三角尺和直尺画平行线.用三角尺和直尺画图,其基本步骤如下:一落:三角尺的一边落在已知直线上;二靠:紧靠三角尺其余两边中的任意一边放上直尺;三移:三角尺沿直尺移动,使三角板尺的边经过已知点;四画:沿三角尺过已知点的一边画直线.解:如图所示.14.解:如图所示.[数学活动]1.解:(1)如图所示.(2)测量略,AF=FG=GB.(3)测量略,FD∶GE∶BC=1∶2∶3或FD+BC=2GE.(4)34.52.解:(1)如图所示.(2)如图所示.(3)如图所示.78。
人教版七年级数学下册第五章相交线与平行线复习训练题
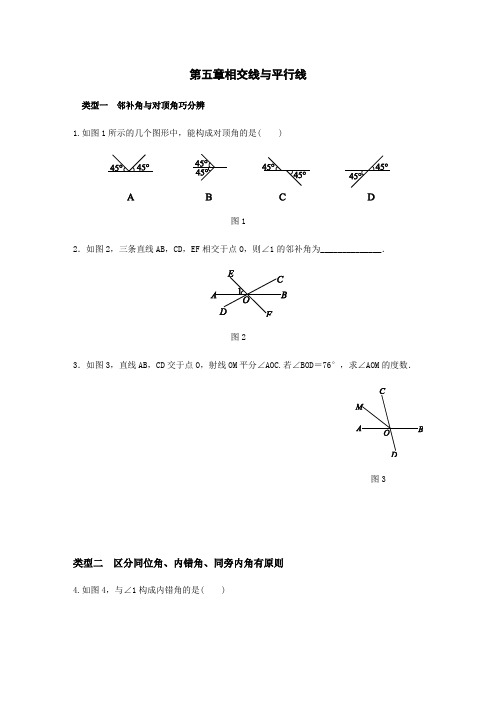
第五章相交线与平行线类型一邻补角与对顶角巧分辨1.如图1所示的几个图形中,能构成对顶角的是( )图12.如图2,三条直线AB,CD,EF相交于点O,则∠1的邻补角为______________.图23.如图3,直线AB,CD交于点O,射线OM平分∠AOC.若∠BOD=76°,求∠AOM的度数.图3类型二区分同位角、内错角、同旁内角有原则4.如图4,与∠1构成内错角的是( )图4A.∠2 B.∠3 C.∠4 D.∠55.如图5,直线DE经过点C,则∠A的内错角是________,∠A的同旁内角是________________.图56.如图6,E是AB延长线上一点,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?(1)∠A和∠D;(2)∠A和∠CBA;(3)∠C和∠CBE.图6类型三掌握相交的特殊情形——垂直7.如图7,已知AB,CD相交于点O,OE⊥CD,垂足为O,∠AOC=30°,则∠BOE等于( )图7A .30°B .60°C .120°D .130°8.如图8所示,在直角三角形ABC 中,∠ACB=90°,CD⊥AB 于点D ,则点A 到BC 的距离为线段______的长度;点A到CD 的距离为线段______的长度;点C 到AB 的距离为线段______的长度.图8类型四 平行线的判定和性质9.如图9,直线a ,b 被直线c 所截,下列说法正确的是( )A .当∠1=∠2时,一定有a∥bB .当a∥b 时,一定有∠1=∠2C .当a∥b 时,一定有∠1+∠2=90°D .当∠1+∠2=180°时,一定有a∥b10.如图10,已知AB∥CD,∠1=60°,则∠2=________°.图9图1011.如图11,不添加辅助线,请你写出一个能判定EB∥AC的条件:________________________.图1112.如图12,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,求∠2的度数.图1213.如图13,已知∠1+∠2=180°,∠DEF=∠A,试判断∠ACB与∠DEB的大小关系,并说明理由.图1314.如图14所示,已知OP∥QR∥ST,连接PR,SR,猜想∠1,∠2,∠3三个角之间的关系,并说明理由.图14类型五命题与定理须细辨15.下列语句不是命题的是( )A.若a<0,b<0,则ab>0B.用三角板画一个60°的角C.对顶角相等D.互为相反数的两个数的和为016.下列命题中,是真命题的是( )A.对顶角相等B.同位角相等C.若a2=b2,则a=bD.若a>b,则-2a>-2b17.将下列命题改写成“如果……那么……”的形式.(1)直角都相等;(2)末位数字是5的整数能被5整除;(3)三角形的内角和是180°.类型六平移平移的特征:图形的平移变换中,图形的形状、大小、方向都不发生改变,只是改变了图形的位置;平移前后图形的对应点的连线平行(或在同一条直线上)且相等.18.下列现象中,不属于平移的是( )A.钟表的指针转动B.电梯的升降C.火车在笔直的铁轨上行驶D.传送带上物品的运动19.如图15,将周长为8的三角形ABC沿BC方向向右平移1个单位长度得到三角形DEF,则四边形ABFD的周长为( )图15A.6 B.8 C.10 D.12类型七方程思想在几何中的应用20.如图16,已知a∥b,∠1=(3x+70)°,∠2=(5x+22)°,求∠1的补角的度数.图16类型八开放型问题21.给出下列三个论断:①∠B+∠D=180°;②AB∥CD;③BC∥DE.请你以其中两个论断作为已知条件,填入“已知”栏中,以一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并说明理由.已知:如图17,________________________.结论:________________________.图17类型九探究型问题22.【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:如图18①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.理由如下:过点P作PQ∥AB.∴∠BAP+∠APQ=180°.∵AB∥CD,PQ∥AB,∴PQ∥CD,∴∠PCD+∠CPQ=180°.∴∠BAP+∠APC+∠PCD=∠BAP+∠APQ+∠CPQ+∠PCD=180°+180°=360°.【问题解决】(1)如图②,AB∥CD,点P在AB与CD之间,可得∠BAP,∠APC,∠PCD间的等量关系是________________________________________________________________________;(2)如图③,AB∥CD,点P ,E 在AB 与CD 之间,AE 平分∠BAP,CE 平分∠DCP,写出∠AEC 与∠APC 间的等量关系,并写出理由;(3)如图④,AB∥CD,点P ,E 在AB 与CD 之间,∠BAE=13∠BAP,∠DCE=13∠DCP ,可得∠AEC与∠APC 间的等量关系是________________________.图18答案1.D2.∠BOE 和∠AOF 3.解:∵∠BOD=76°, ∴∠AOC=∠BOD=76°. ∵射线OM 平分∠AOC,∴∠AOM=12∠AOC=12×76°=38°.4.B5.∠ACD ∠ACB,∠ACE 和∠B6.解:(1)∠A 和∠D 是直线AE ,DC 被直线AD 所截而成的同旁内角. (2)∠A 和∠CBA 是直线AD ,BC 被直线AE 所截而成的同旁内角. (3)∠C 和∠CBE 是直线DC ,AE 被直线BC 所截而成的内错角. 7.C 8.AC AD CD 9.D 10.12011.答案不唯一,如∠C=∠EBD 12.解:∵AB∥CD,∴∠2=∠BEG,∠BEF+∠1=180°. ∵∠1=50°,∴∠BEF=130°. ∵EG 平分∠BEF,∴∠BEG=12∠BEF=65°, ∴∠2=65°.13.解:∠ACB=∠DEB.理由:∵∠1+∠2=180°,∠1+∠DFE=180°,∴∠2=∠DFE,∴AB∥EF,∴∠DEF=∠BDE.∵∠DEF=∠A,∴∠A=∠BDE,∴AC∥DE,∴∠ACB=∠DEB.14.解:∠2+∠3=180°+∠1.理由:∵OP∥QR,∴∠2+∠QRP=180°,∴∠QRP=180°-∠2.∵QR∥ST,∴∠3=∠QRS=∠1+∠QRP=∠1+180°-∠2.∴∠2+∠3=180°+∠1.15.B16. A17.解:(1)如果几个角是直角,那么它们都相等.(2)如果一个整数的末位数字是5,那么它能被5整除.(3)如果一个图形是三角形,那么它的内角和是180°.18.A19. C20.解:如图,因为a∥b,所以∠1=∠3.又因为∠1=(3x+70)°,∠2=(5x+22)°,∠2+∠3=180˚,所以(3x +70)°+(5x+22)°=180°,解得x=11,所以∠1=(3x+70)°=103°.又因为180°-103°=77°,所以∠1的补角的度数为77°.21.解:答案不唯一,符合题意的情况有3种,即①②→③;①③→②;②③→①,任选其中一种即可.已知:如图17,∠B+∠D=180°,AB∥CD.结论:BC∥DE.理由:因为AB∥CD,所以∠B=∠C(两直线平行,内错角相等).又因为∠B+∠D=180°,所以∠C+∠D=180°,所以BC∥DE(同旁内角互补,两直线平行).22.解:(1)如图②,作PE∥AB,得∠APE=∠BAP.∵AB∥CD,AB∥PE,∴CD∥PE,∴∠CPE=∠PCD,∴∠APC=∠APE+∠CPE=∠BAP+∠PCD.故答案为∠APC=∠BAP+∠PCD.(2)∠APC=2∠AE C.理由:设∠EAB=∠EAP=x,∠ECD=∠ECP=y.由(1)可知:∠AEC=x+y,∠APC=2x+2y,∴∠APC=2∠AE C.(3)设∠EAB=a,∠DCE=b,则∠BAP=3a,∠DCP=3b. 由题意得∠AEC=a+b,∠APC+3a+3b=360°,∴∠APC+3∠AEC=360°.故答案为∠APC+3∠AEC=360°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学平行练习
班级姓名学号
1.判断:
①两条不相交的直线是平行线. ()
②过一点有且只有一条直线与已知直线平行. ()
③在同一平面内不相交的两条射线必平行. ()
④在同一平面内,和第三条直线都不相交的两条直线平行. ()
⑤过两条相交直线外一点A,能画一条直线与这两条直线都平行. ()
⑥同一平面内的三条直线,它们的交点个数可能是0或3. ()
2.如果两条直线都和第三条直线相交,则()
A.这两条直线相交
B.这两条直线平行
C.这两条直线平行或相交
D.不能确定
3.下列说法中,正确的个数有()
①在同一平面内,两条不相交的线段是平行线;
②一条直线有无数条平行线;
③同一平面内有两条直线不相交,这两条直线一定是平行线;
④过直线外一点可以作无数条直线与已知直线平行.
A.0个
B.1个
C.2个
D.3个
4.平行用符号“____”来表示,例如直线a和直线b互相平行,记作:__________.
5.在同一平面内,两条直线的位置关系有_______________.
6.如图,在正方体中:
⑴找出与棱A1D1平行的棱:________________________;
⑵棱A1A所在直线与棱________________所在直线不相交,
但也不平行.
7.如图所示:EF//AB,FC//AB,则点E、C、F在一条直线上.
理由是: .
8.用三角尺和直尺按下列要求画图:
⑴在图①中,过点A画直线l∥BC;
⑵在图②中,过点C画CE∥DA,与AB相交于点E,过点C画CF∥DB,与AB的
延长线相交于点F.
①②
9.如右图所示,在方格纸上:
(1)已有的四条线段中,哪些是互相平行的?
(2)过点M画AB的平行线;
过点N画GH的平行线. (仅用直尺)
10.如图,已知线段AB、BC、CA,AB=AC,按要求画图:
⑴画出∠BAC的平分线AD交BC于D;
⑵画出∠ABC的平分线BE交AC于E;
⑶过点E画BC的平行线EF交AB于F,并连接FC;
⑷通过观察、度量,你发现了哪些结论?请把它们写出来.(至少写3条,不需要写理由)
11.如图,在同一平面内,一组互相平行的直线共n条(n为大于1的正整数),它们和两
条平行线a、b相交,构成若干个“#”字形,设构成的“#”字形个数为x,请填写下表:
……。
