一阶电路的零输入响应
零输入响应和零状态响应

uc 24e 20V t t 0 i1 uC 4 6 e 20 A
5F + i1
uC 4
分流得:
i2
2 3
i1
4e
t
20 A
i3
1 3
i1
2e
t 20
A
-
广东海洋大学
信息学院
徐国保
Lecture_11 零输入响应和零状态响应
2. RL电路的零输入响应
R1 US
Ri
作业 3.8,3.12,3.13
信息学院
徐国保
Lecture_11 零输入响应和零状态响应
一、知识回顾
Q1:什么叫换路定理?
iL
L (0+)= L (0-) 抢答开始!
+ u (t)
-
iL(0+)= iL(0-)
A1:换则路电瞬感间电,流若(电磁感链电)压换保路持前为后有保限持值不,变。
换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。
令 =RC , 称为一阶电路的时间常数
RC
欧法
欧
库 伏
欧安伏秒
秒
广东海洋大学
信息学院
徐国保
Lecture_11 零输入响应和零状态响应
=RC
p 1 1
RC
时间常数 的大小反映了电路过渡过程时间的长短
大 → 过渡过程时间长 小 → 过渡过程时间短
信息学院
徐国保
Lecture_11 零输入响应和零状态响应
1t
一阶电路的零输入响应

dt
50 1 e1500t 0.05 1500 e1500t
50 25e1500tV
第17页/共26页
§10.4 一阶电路的全响应 一、全响应的分解
全响应:电路中输入激励和储能元件的储能共同产生的响应。
R
+
+ uR – i
–US
C
uC 0 U0
电路方程
ui US
+u US-U0 C
一、RC电路的零输入响应
12 i
uC i
特征根
p
1
+ U0
—
R0
+ C uC
—
+ R uR
—
U0
U0
R
uC
i
0
RC
t
uC Ae RC t 0
确定积分常数
t
uC 0 U0
uC 0 U0
电路方程
uR uC 0
电压与电流的关系
u R iR
电路方程
RC
duC dt
uC
0
t>0
通解
uC Aept
二、全响应的分解
1.全响应可分解为稳态分量和瞬态分量。
t
uC = uC′+ uC″ = US + (U0 - US)e
τ
稳态分量 瞬态分量
强制分量 自由分量
2.全响应可分解为零输入响应和零状态响应。
t
t
uc = uc1 + uc2 = U0e τ + US(1-e τ )
零输入响应 零状态响应
uC US
+ uR –
uR uC i
+
R+i
(电路分析)一阶电路的零输入响应
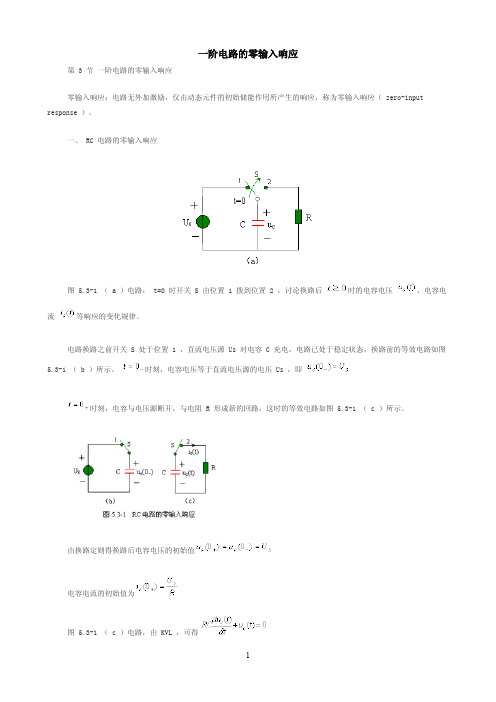
一阶电路的零输入响应第 3 节一阶电路的零输入响应零输入响应:电路无外加激励,仅由动态元件的初始储能作用所产生的响应,称为零输入响应( zero-input response )。
一、 RC 电路的零输入响应图 5.3-1 ( a )电路, t=0 时开关 S 由位置 1 拨到位置 2 ,讨论换路后时的电容电压、电容电流等响应的变化规律。
电路换路之前开关 S 处于位置 1 ,直流电压源 Us 对电容 C 充电,电路已处于稳定状态,换路前的等效电路如图5.3-1 ( b )所示。
时刻,电容电压等于直流电压源的电压 Us ,即时刻,电容与电压源断开,与电阻 R 形成新的回路,这时的等效电路如图 5.3-1 ( c )所示。
由换路定则得换路后电容电压的初始值电容电流的初始值为图 5.3-1 ( c )电路,由 KVL ,可得用积分变量分离法进行求解,得式中,为 RC 电路的时间常数( time constant ),当 R 的单位为Ω, C 的单位为 F 时,τ的单位是秒( s )。
时间常数:时间常数是反映一阶电路过渡过程进展快慢的一个重要的参数,其大小仅取决于电路的结构和参数。
τ越大,响应衰减的速度就越慢;τ越小,响应衰减的速度就越快。
用表示电路换路后的响应,用表示该响应的初始值,则 RC 一阶电路的零输入响应可表示为RC 电路零输入响应的规律RC 电路换路后,各处的零输入响应都是从初始值开始,按指数规律衰减。
衰减得快慢由时间常数τ决定。
二、 RL 电路的零输入响应图 5.3-3 ( a )是 RL 动态电路。
电路换路之前开关 S 处于位置 1 , t=0 时开关 S 由位置 1 拨到位置 2 。
下面讨论换路后时的电感电流、电感电压等响应的变化规律。
时刻,电路换路之前开关 S 处于位置 1 ,直流电流源 Is 对电感 L 充电,电路已处于稳定状态,换路前的等效电路如图 5.3-3 ( b )所示。
t=0 时,开关 S 拨到位置 2 ,时,电感与电流源断开,而与电阻 R 形成新的回路,这时的等效电路如图5.3-3 ( c )所示。
一阶RC电路的零状态与零输入响应

2022/9/10
2022/9/10
一 四、一过阶渡R过C程电路零输入响应的实例
解: 在开关由位置1拨向位置2的瞬间,电容电压不能越变,因此可得
uC (0 ) uC (0 ) 6V
将连接于电容两端的电阻等效为一个电阻,其阻值为
R 8 6 3 10k 63
的电流为 I0 US R1,
电感中储存一定的 能量。在 t 0,开 关S由位置1拨向位 置2处。
一 三、一过阶渡R过L程电路的零输入响应的分析
一阶RL电路的零输入响应的定性分析
在换路的瞬间,由于电感的电流不能突变,即 iL (0 ) iL (0 ) I0 , 此时电阻 端电压 uR (0 ) I 0 R 。根据KVL可知,电感上的电压立即从换路前的零值突变
得到如图(b)所示电路,其时间常数为
RC 10103 5106 5102 s 0.05s
uC
t
U0e
6e V 20t
iC
U0
t
e
R
- 6 e20t 10 10 3
0.6e20t mA
一 四、一过阶渡R过C程电路零输入响应的实例
例:电路如下图所示,t 0 时开关由位置1拨向位置2,求 t 0 时
而电阻消耗的能量为
Q
0 uC dq
U 0
S
CuC
duC
1 2
CU
2 S
WR
i 2 Rdt
0
U
2 S
0R
2t
e RC dt
1 2
CU
2 S
由此可见,在充电过程中电源所提供的能量,一半储存在电容的电场中, 一半消耗在电阻上。且电阻上消耗的能量与R无关,充电效率总是50%。
§5-5 一阶电路的零输入响应

uC (0 ) 0
零状态响应
X
1.基本概念
零输入响应(zero input response--z.i.r):在没有外加 激励作用下,仅由动态元件的初始储能产生的响应。 零状态响应 (zero state response--z.s.r) :动态元件 的初始储能为零,仅由外加激励产生的响应。 全响应 (complete response--c.r) :零输入响应与零 状态响应之和。
X
例题1 已知 t 0时电路处于稳态, t 0时开关打开。
解: t 0:
求 t 0时的 i ( t ) 。
1 1 3 RC 1 3 2 s 1 u ( t ) C F t 2 t 2 2 uC ( t ) uC (0 ) e 60e V, t 0 t t duC 1 1 i ( t ) C 60e 2 15e 2 A, t 0 dt 2 2
返回
X
2.一阶RC电路的零输入响应
u (0 S(t 0) 已知 C ) U 0, t 0 时发生换路,开关S闭合。 + 求 t 0 时的 uC ( t )、i ( t )、uR ( t )。R uR (t ) KVL方程:
i(t )
+ C
uC (t )
-
uR uC 0 duC uR Ri , i C dt duC RC uC 0, t 0 dt
R 1 s ——RL电路的固有频率 L
y t y(0 ) e , t 0
线性非时变电路的零输入响应满足叠加性,即如果 初始值增加K倍,则响应也增加K倍。
一阶电路的零输入响应零状态响应

2 0
WR
i2Rdt
0
0(I0eL/tR)2Rdt
I02R
0
e
2t
L/Rdt
I02R(L2/ReR2tC)| 0
1 2
LI 0 2
上页 下页
例1 t=0时 , 打开开关K,求uv。 电压表量程:50V
K(t=0) R=10
10V
+
uV
–
V RV 10k
有一过渡期
0
t1新的稳定状态 t
过渡状态
上页
下页
(t →)
i
K 未动作前,电路处于稳定状态
K
R+
US
uL L
–
iU S R, uL0
K US
i
R+
uL L
–
K 断开瞬间
i0, uL
注意工程实际中的过电压过电流现象
上页 下页
换路
支路接入或断开 电路结构、状态发生变化
电路参数变化
过渡过程产生的原因
(1) 由0-电路求 uC(0-)或iL(0-)
例1 求 iC(0+)
10k
+
10V -
10k 40k
+ uC(0-) -电
+
i
40k iC
+ uC
- 10V k
-
uC(0)8V
(2) 由换路定律
容 开 路
+ 10V
-
i 10k iC (0+)
0+等效电路
uC(0)uC(0)8V
+
8V
(3) 由0+等效电路求 iC(0+)
一阶电路的全响应和零响应区别

一阶电路的全响应和零响应区别
引起电路响应的因素有两个方面,一是电路的激励,而是动态元件储存的初始能量.当激励为零,仅由动态元件储存的初始能量引起的响应叫零输入响应;当动态元件储存的初始能量为零,仅由激励引起的响应叫零状态响应;两个同时引起的响应叫全响应. 零状态响应是指在t=0-时,电容器的电压为0,电感器的电流为0;
零输入响应是指在t=0-时,电源的输入为0;下面早点介绍一阶电路的全响应。
全响应:非零初始状态的电路受到外加激励时电路中产生的响应,称为全响应。
1.RC电路的全响应的分析
(非齐次微分方程)
解答为:uC = uC' + uC''
得RC电路的全响应的通式:
2.RC电路的全响应通式的两种分解方式
(1)全响应(complete response)
= 强制响应(forced response)+自由响应(natural response)
= 稳态响应(steady-state response) +暂态响应(transient response)(2)全响应= 零状态响应+ 零输入响应
全响应小结:
(1)全响应的不同分解方法只是便于更好地理解过渡过程的本质;
(2)零输入响应与零状态响应的分解方法其本质是叠加,因此只适用于线性电路;
(3)零输入响应与零状态响应均满意齐性原理,但全响应不满意。
一阶电路的零输入响应

3、原始能量增大A倍,则零输入响应将相应增大A倍,这种原始能量与零输 入响应的线性关系称为零线性。
零输入响应就是无电源一阶线性电路,在初始储能作用下产生的响应,
其形式表示为:
f (t) f (0) et
t 0
式中 f (0) 为变量的初始值 uC (0 ) 或 iL (0 )
为时间常数 RC (电容)
L R
(电感)
一、RC电路的零输入响应
如右图,已知uc(0-)=U0,K于t=0 时刻闭合,分析t≧0时uc(t) 、 i(t)的变化规律。
0
一阶常系数齐次微分方程
其特征根方程:
S 1 0
特征根
RC
1
S
RC
uc (t )
Ae st
1t
Ae RC (t
0)
又有初始条件: uc(0+) = uc(0-) =U0 (换路定理)
1t
uc (t ) U0e RC (t 0)
i(t ) C duc
U0
1t
e RC (t
0)
dt
R
i(t)
E
uL(t)的变化规律。
R0 K R
iL
+ L uL
-
(a) 分析:t<0时已达稳态,L中电流为I0=E/R0
t≧0时,电感以初始储能来维持电流iL (t)(放电)
①
换路后( t≧0),由KVL有:
L diL dt
RiL (t ) 0
即:
diL dt
R L
iL (t )
0
特征根:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
