3-8 曲率
大物课后习题 答案

1-3 一质点在xOy 平面上运动,运动方程为x =3t +5, y =21t 2+3t -4.式中t 以 s 计,x ,y 以m 计.(1)以时间t 为变量,写出质点位置矢量的表示式;(2)求出t =1 s 时刻和t =2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算t =0 s 时刻到t =4s 时刻内的平均速度;(4)求出质点速度矢量表示式,计算t =4 s 时质点的速度;(5)计算t =0s 到t =4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算t =4s 时质点的加速度(请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式).解:(1) j t t i t r)4321()53(2-+++=m (4) 1s m )3(3d d -⋅++==j t i tr v则 j i v734+= 1s m -⋅(6) 2s m 1d d -⋅==j tv a这说明该点只有y 方向的加速度,且为恒量。
1-4 在离水面高h 米的岸上,有人用绳子拉船靠岸,船在离岸S 处,如题1-4图所示.当人以0v (m ·1-s)的速率收绳时,试求船运动的速度和加速度的大小.图1-4解: 设人到船之间绳的长度为l ,此时绳与水面成θ角,由图可知 222s h l +=将上式对时间t 求导,得ts stl ld d 2d d 2= 题1-4图根据速度的定义,并注意到l ,s 是随t 减少的, ∴ ts v v tl v d d ,d d 0-==-=船绳即 θcos d d d d 00v v sl tl s l ts v ==-=-=船或 sv s h slv v 02/1220)(+==船将船v 再对t 求导,即得船的加速度32022222002)(d d d d d d sv h sv sls v slv s v v st s l tl s tv a =+-=+-=-==船船1-6 已知一质点作直线运动,其加速度为 a =4+3t 2s m -⋅,开始运动时,x =5 m , v =0,求该质点在t =10s 时的速度和位置. 解:∵ t tv a 34d d +==分离变量,得 t t v d )34(d += 积分,得12234c t t v ++=由题知,0=t ,00=v ,∴01=c 故 2234t t v += 又因为 2234d d t t tx v +==分离变量, t t t x d )234(d 2+=积分得 232212c t t x ++=由题知 0=t ,50=x ,∴52=c 故 521232++=t t x所以s 10=t 时m70551021102sm 190102310432101210=+⨯+⨯=⋅=⨯+⨯=-x v1-8 质点沿半径为R 的圆周按s =2021bt t v -的规律运动,式中s 为质点离圆周上某点的弧长,0v ,b 都是常量,求:(1)t 时刻质点的加速度;(2) t 为何值时,加速度在数值上等于b . 解:(1) bt v ts v -==0d dRbt v Rva b t v a n 202)(d d -==-==τ则 240222)(Rbt v b aa a n-+=+=τ加速度与半径的夹角为20)(arctanbt v Rb a a n--==τϕ(2)由题意应有2402)(Rbt v b b a -+==即 0)(,)(4024022=-⇒-+=bt v Rbt v b b∴当bv t 0=时,b a =1-10 以初速度0v =201s m -⋅抛出一小球,抛出方向与水平面成幔 60°的夹角,求:(1)球轨道最高点的曲率半径1R ;(2)落地处的曲率半径2R . (提示:利用曲率半径与法向加速度之间的关系)解:设小球所作抛物线轨道如题1-10图所示.题1-10图(1)在最高点,o0160cos v v v x == 21sm 10-⋅==g a n又∵ 1211ρv a n =∴m1010)60cos 20(22111=︒⨯==n a v ρ(2)在落地点,2002==v v 1sm -⋅,而 o60cos 2⨯=g a n ∴ m 8060cos 10)20(22222=︒⨯==n a v ρ2-3 283166-⋅===sm m f a x x2167-⋅-==s m mf a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=2101200872167452832sm dt a v v s m dt a v v y y y x x x于是质点在2s 时的速度18745-⋅--=sm ji v(2) mji j i jt a i t a t v r y x 874134)167(21)4832122(21)21(220--=⨯-+⨯⨯+⨯-=++= 2-4 (1)∵dtdv mkv a =-=分离变量,得m kdt v dv -=即⎰⎰-=vv tmkdt v dv 0mkt ev v -=ln ln∴ tmk e v v -=0(2)⎰⎰---===tttmk mk ekmv dt ev vdtx 000)1((3)质点停止运动时速度为零,即t →∞, 故有⎰∞-=='000kmv dt ev x tmk(4)当t=km 时,其速度为ev ev ev v km m k 0100===-⋅-即速度减至v 0的e1.2-7由题知,小球落地时间为0.5s .因小球为平抛运动,故小球落地的瞬时向下的速度大小为v 1=gt=0.5g ,小球上跳速度的大小亦为v 2=0.5g .设向上为y 轴正向,则动量的增量 Δp=mv 2-mv 1 方向竖直向上,大小 |Δp |=mv 2-(-mv 1)=mg碰撞过程中动量不守恒.这是因为在碰撞过程中,小球受到地面给予的冲力作用.另外,碰撞前初动量方向斜向下,碰后末动量方向斜向上,这也说明动量不守恒. 2-12 (1)由题知,F 合为恒力,∴ A 合=F ·r=(7i-6j)·(-3i+4j+16k)=-21-24=-45 J (2)w tA N 756.045==∆=(3)由动能定理,ΔE k =A=-45 J2-15 弹簧A 、B 及重物C 受力如题2-15图所示平衡时,有题2-15图 F A =F B =Mg 又 F A =k 1Δx 1 F B =k 2Δx 2所以静止时两弹簧伸长量之比为 1221k k x x =∆∆弹性势能之比为12222211121212k k x k x k E E p p=∆∆=2-20 两小球碰撞过程中,机械能守恒,有222120212121mv mv mv +=即 222120v v v += ①3-7 观测者甲乙分别静止于两个惯性参考系S 和S '中,甲测得在同一地点发生的两事件的时间间隔为 4s ,而乙测得这两个事件的时间间隔为 5s .求: (1) S '相对于S 的运动速度.(2)乙测得这两个事件发生的地点间的距离.解: 甲测得0,s 4==x t ∆∆,乙测得s 5=t ∆,坐标差为12x x x '-'='∆′ (1)∴ t cv tx cv t t ∆-∆=∆+∆='∆22)(11)(λγ54122='∆∆=-t t cv解出 c c t t c v 53)54(1)(122=-='∆∆-=8108.1⨯= 1s m -⋅(2) ()0,45,=∆=∆'∆=∆-∆='∆x tt t v x x γγ∴ m 1093453458⨯-=-=⨯⨯-=-='c c t v x ∆γ∆负号表示012<'-'x x . 3-8 一宇航员要到离地球为5光年的星球去旅行.如果宇航员希望把这路程缩短为3光年,则他所乘的火箭相对于地球的速度是多少? 解: 2220153,1513βββ-=-=-=='则l l∴ c c v 542591=-=3-11 根据天文观测和推算,宇宙正在膨胀,太空中的天体都远离我们而去.假定地球上观察到一颗脉冲星(发出周期无线电波的星)的脉冲周期为 0.50s ,且这颗星正沿观察方向以速度0.8c 离我们而去.问这颗星的固有周期为多少?解: 以脉冲星为S '系,0='∆x ,固有周期0τ='∆t .地球为S 系,则有运动时t t '∆=∆γ1,这里1t ∆不是地球上某点观测到的周期,而是以地球为参考系的两异地钟读数之差.还要考虑因飞行远离信号的传递时间,ct v 1∆∴ t cv t c t v t t ∆+'∆=∆+∆=∆γγ11′)1(cv t +'=∆γ6.01)8.0(112=-=c c γ则 γλτ)8.01(5.0)1(0c c cv t t +++∆='∆=s 1666.08.13.06.01)8.01(5.0==+=3-16 静止在S 系中的观测者测得一光子沿与x 轴成︒60角的方向飞行.另一观测者静止于S ′系,S ′系的x '轴与x 轴一致,并以0.6c 的速度沿x 方向运动.试问S ′系中的观测者观测到的光子运动方向如何? 解: S 系中光子运动速度的分量为c c v x 500.060cos ο==c c v y 866.060sin ο==由速度变换公式,光子在S '系中的速度分量为c ccc c c v cu u v v xx x143.05.06.016.05.0122-=⨯--=--='c ccc c v cu v cu v xyy 990.05.06.01866.06.011122222=⨯-⨯-=--='光子运动方向与x '轴的夹角θ'满足692.0tan -=''='xy v v θθ'在第二象限为ο2.98='θ在S '系中,光子的运动速度为c v v v y x='+'='22 正是光速不变. 3-17 (1)如果将电子由静止加速到速率为0.1c ,须对它作多少功?(2)如果将电子由速率为0.8c 加速到0.9c ,又须对它作多少功?解: (1)对电子作的功,等于电子动能的增量,得)111()1(222020202--=-=-==cv c m c m cm mcE E k k γ∆)11.011()103(101.922831--⨯⨯⨯=-161012.4-⨯=J=eV 1057.23⨯(2) )()(2021202212c m c m c m c m E E E k k k---=-='∆)1111(221222202122cv cv c m cm c m ---=-=))8.0119.011(103101.92216231---⨯⨯⨯=-J 1014.514-⨯=eV 1021.35⨯=4-2 劲度系数为1k 和2k 的两根弹簧,与质量为m 的小球按题4-2图所示的两种方式连 接,试证明它们的振动均为谐振动,并分别求出它们的振动周期.题4-2图解:(1)图(a)中为串联弹簧,对于轻弹簧在任一时刻应有21F F F ==,设串联弹簧的等效倔强系数为串K 等效位移为x ,则有111x k F x k F -=-=串222x k F -=又有 21x x x +=2211k F k F k F x +==串所以串联弹簧的等效倔强系数为2121k k k k k +=串即小球与串联弹簧构成了一个等效倔强系数为)/(2121k k k k k +=的弹簧振子系统,故小球作谐振动.其振动周期为2121)(222k k k k m k m T +===ππωπ串(2)图(b)中可等效为并联弹簧,同上理,应有21F F F ==,即21x x x ==,设并联弹簧的倔强系数为并k ,则有2211x k x k x k +=并故 21k k k +=并 同上理,其振动周期为212k k m T +='π4-5 一个沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表示.如果0=t 时质点的状态分别是:(1)A x -=0;(2)过平衡位置向正向运动; (3)过2A x =处向负向运动; (4)过2A x -=处向正向运动.试求出相应的初位相,并写出振动方程. 解:因为 ⎩⎨⎧-==000sin cos φωφA v A x将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有)2cos(1πππφ+==t TA x)232cos(232πππφ+==t T A x)32cos(33πππφ+==t TA x)452cos(454πππφ+==t TA x4-7 有一轻弹簧,下面悬挂质量为g 0.1的物体时,伸长为cm 9.4.用这个弹簧和一个质量为g 0.8的小球构成弹簧振子,将小球由平衡位置向下拉开cm 0.1后 ,给予向上的初速度10scm 0.5-⋅=v ,求振动周期和振动表达式.解:由题知 12311mN 2.0109.48.9100.1---⋅=⨯⨯⨯==x g m k而0=t 时,-12020s m 100.5m,100.1⋅⨯=⨯-=--v x ( 设向上为正)又 s 26.12,51082.03===⨯==-ωπωT mk 即m102)5100.5()100.1()(22222220---⨯=⨯+⨯=+=∴ωv x A45,15100.1100.5tan 022000πφωφ==⨯⨯⨯=-=--即x v∴ m )455cos(1022π+⨯=-t x4-8 图为两个谐振动的t x -曲线,试分别写出其谐振动方程.题4-8图解:由题4-8图(a),∵0=t 时,s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ即 1s rad 2-⋅==ππωT故 m )23cos(1.0ππ+=t x a由题4-8图(b)∵0=t 时,35,0,2000πφ=∴>=v A x01=t 时,22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯=∴ πω65=故 m t x b )3565cos(1.0ππ+=4-12 试用最简单的方法求出下列两组谐振动合成后所得合振动的振幅:(1) ⎪⎩⎪⎨⎧+=+=cm )373cos(5cm )33cos(521ππt x t x (2)⎪⎩⎪⎨⎧+=+=cm)343cos(5cm )33cos(521ππt x t x 解: (1)∵ ,233712πππφφφ=-=-=∆∴合振幅 cm 1021=+=A A A (2)∵ ,334πππφ=-=∆∴合振幅 0=A4-13 一质点同时参与两个在同一直线上的简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动的振动幅和初相,并写出谐振方程。
高等数学第三章 第7节 曲率

3 2 2
6 (4 sin2 t 9 cos2 t )
3 2
(4 5 cos2 t )
3 2
3 2
要使 k 最大, 必有 (4 5 cos 2 t ) 最小,
3 t , 2 2
此时 k 最大,
18
练习题
一、填空题: 1 、曲率处处为零的曲线为________ ;曲率处处相等 的曲线为__________. 2 、抛 物 线 y x 2 4 x 3 在 (2,-1) 处 的 曲 率 为 ________;曲率半径为_________. 3 、曲 线 y ln( x 1 x 2 ) 在 (0,0) 处 的 曲 率 为 ___________. 二、求曲线 y ln(sec x ) 在点 ( x , y ) 处的曲率及曲率半 径. x a cos3 t t t 0 处的曲率 . 三、求曲线 在 3 y a sin t y2 x 四、证明曲线 y a cosh 在任何一点处曲率半径为 . a a
s
ds
存在的条件下, K
ds
.
6
注意(1)直线的曲率处处为零。
(2) 圆上各点处的曲率等于半径的 倒数,且半径越小曲率越大.
如图所示 , 有
s R 1 K lim s 0 s R
M s R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
抛物线在顶点处的曲率 最大.
11
三、曲率圆与曲率半径
定义 设曲线 y f ( x ) 在点
y
D 1 k
M
y f ( x)
M ( x , y ) 处的曲率为k ( k 0). 在点 M 处的曲线的法线上 , 在凹的一侧取一点D, 使 DM
地理信息系统算法第三章

a
a、b称为长度元素
扁率反映了椭球体的 扁平程度
椭圆的第一偏心率:
a2 −b2 e′ = b 椭圆的第二偏心率:
e= a2 −b2 a
e和e’反映椭球体的扁平程 和 反映椭球体的扁平程 偏心率越大, 度,偏心率越大,椭球愈 扁
3.4.2 地球椭球体的相关公式
W
W 顾及 a = c 1−e2 和 =V 1−e2,则上式又可写为
c N= V (3-13) (3-
卯酉圈曲率半径
由图看出, 由图看出, (3(3-14) 也就是说,卯酉圈曲率半径恰好等于椭球面和短轴之间的一段法线 的长度,亦即卯酉圈的曲率中心位于椭球的旋转轴上。 N与B有关,是纬度B的函数,且随B的增大而增大,变化规律如下表 有关,是纬度B的函数,且随B
3.4.2 地球椭球体的相关公式
2.地球椭球参数间的相互关系 2.地球椭球参数间的相互关系
由前面式子得:
a2 − b2 e2 = a2
a2 − b2 e'2 = b2
b2 2 1− e = 2 a
a2 1+ e = 2 b
2
并得: 推得:
(1− e2 )(1+ e'2 ) = 1
e2 e2 ' = 1+ e 2 '
e2 '
e2 = 1− e2
同理可得: a = b 1+ e'2 L L = a 1− e2 L b
c = a 1+ e'2 L L = c 1− e2 L a
e' = e 1+ e'2 L L = e' 1− e2 L e
proe教程(曲面曲率)
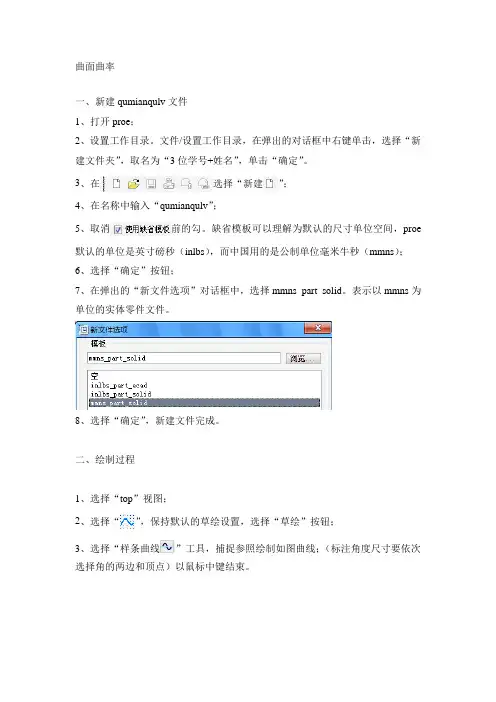
曲面曲率一、新建qumianqulv文件1、打开proe;2、设置工作目录。
文件/设置工作目录,在弹出的对话框中右键单击,选择“新建文件夹”,取名为“3位学号+姓名”,单击“确定”。
3、在选择“新建”;4、在名称中输入“qumianqulv”;5、取消前的勾。
缺省模板可以理解为默认的尺寸单位空间,proe 默认的单位是英寸磅秒(inlbs),而中国用的是公制单位毫米牛秒(mmns);6、选择“确定”按钮;7、在弹出的“新文件选项”对话框中,选择mmns_part_solid。
表示以mmns为单位的实体零件文件。
8、选择“确定”,新建文件完成。
二、绘制过程1、选择“top”视图;2、选择“”,保持默认的草绘设置,选择“草绘”按钮;3、选择“样条曲线”工具,捕捉参照绘制如图曲线;(标注角度尺寸要依次选择角的两边和顶点)以鼠标中键结束。
4、修改尺寸。
此时所有尺寸为灰色,表示是“弱尺寸”。
双击长度尺寸,修改为25。
双击高度尺寸,修改为70。
曲线的两端均为90度。
修改后,尺寸颜色变为亮色,表示是强尺寸。
5、在“菜单栏”选择“插入”,选择“扫描”-“曲面”,在下拉“菜单管理器”中选择“选取轨迹”按鼠标中建选择默认设置。
6、进入截面绘制阶段,选择工具栏命令绘制如图直线,并将角度修改为88度,高度修改为87、选择工具栏结束截面绘制,按鼠标中键确定。
8、选择工具栏“基准平面”工具,选择top平面,输入平移距离为12,选择确定9、选择工具栏工具,选择DTM1平面,进入草绘绘制,选择命令,绘制如图曲线,尺寸修改方法同上。
10、选择“草绘2”,在菜单栏选择“编辑”,选择“填充”命令。
11,选择工具栏工具,点击工具栏按钮,选择front面,继续选择工具选择平面按钮,按shift键捕捉两个已知面的端点,绘制如图所示平面曲线,点结束。
11、双击所绘曲线,进去编辑命令,左键点击曲线端点,然后长按右键点击黄色线段,在下拉菜单中选择“曲面曲率”,在曲线的另一端点进行同样操作,得到如图所示曲线12,用同样方法绘制如图所示曲线,选择命令,点击front面,在点出窗口中输入36,用同样方法在DTM2上建立曲线,如图所示。
超短半径水平井介绍

径向井眼及主井结构图
柔性造斜钻具钻出井是短半径井,也可能 是超短半径井,但不属于径向井
①柔性钻挺 ④旋转 ②不旋转的柔性壳体
⑥外径 3-3/4”
不旋转
②轴承密封
径向水平钻井的基本工艺过程
1. 通井和磨铣套管(1.5へ3米长); 2. 扩大井眼(直径约0.6米); 3. 下入斜向器,井下锚定器定位;
钻出的孔眼形状规则 破岩效率高。
旋转射流破岩过程示意图
凸锥井底流场UV矢量放大图
轴向速度
切向速度
径向速度
旋转射流扩展角随旋流强度的变化规律
(1)、(2)--不同旋流强度的钻头 (3)--旋流强度为零的钻头
破碎坑直径随泵压的关系 • 泵压相同,旋转射流比普通射流的钻孔直径高多倍。
(1)、(2)--不同旋流强度的钻头 (3)--旋流强度为零的钻头
5) 高压密封的工作寿命可以达到15.5小时以上; 未出现压力降低和或排量增加等现象,创造 了高压密封寿命记录。 6) 进行6次钻进,钻出了5个水平分支井眼,创 造了单井水平分支井眼数量最多记录。其中 长度超过10米的有3个分支,总长度达41.93m。 也是目前国内一口井中水平分支井眼总长度 的最好记录。
井口进液和光杆送进高压密封
光杆送钻接单根技术
原理:多级,替换
•水力破岩钻头
具体要求:
形成一个较大截面积的规则井眼;
以较小的射流压力和排量高速破岩;
具有足够长的使用寿命。
导向元件 钻杆
旋转射流
喷头 喷嘴
回流 井底圆锥
多喷嘴
锥形射流喷嘴
旋转射流喷嘴
旋转射流喷嘴特点:
大面积钻孔
破碎坑深度随泵压的关系
(1) 门限压力降低40%以上;(2)破岩深度大; (3) 破岩体积高几十到上百倍。
《物理光学》§3-8用牛顿环测量透镜的曲率半径

分振幅干涉的基本内容回顾
由于两相干光束会聚角为2 由于两相干光束会聚角为2α, α楔形板的楔角。 λ 则,等厚条纹的间距为 则,等厚条纹的间距为 e = 2nα 由 Δ=2nhcosθ2(+λ/2)=m λ可知 =2nhcosθ (+λ 随着θ 随着θ2的增大,条纹将会发生弯曲,其规 律是朝向楔棱方向凸出。 薄膜的干涉与此原理相同,也是等厚条纹。 薄膜的干涉与此原理相同,也是等厚条纹。
D2 N= ∆C 4λ
§3-9 平面干涉仪
§3-9 平面干涉仪
是利用两个表面(一个是标准平面,一个是被检 平面)之间的楔形空气层产生的等厚干涉条纹检 L G G 验平面零件的仪器。 M 一、 原理: S 如图:
1 2
O ①标准平板G1; ①标准平板G1; 通常有很小的楔角,目的是使上表面和下表面的 反射光束分开一定角度,使上表面反射光束移出 视场之外。 ②被检测平板和标准平板之间的楔角和方向可以 通过它所在的调节盘进行调节,因而条纹间距和 方向可以随之变化。
分振幅干涉的基本内容回顾
一、平行平板——等倾条纹 平行平板——等倾条纹 由于光程差Δ=2nhcosθ (+λ 由于光程差Δ=2nhcosθ2(+λ/2)=m λ 故:若nh是均匀的,则条纹 故:若nh是均匀的,则条纹是θ2的函数; 即, θ2相同,则Δ相同、 m相同; 相同,则Δ 此时在观察屏上将形成环形条纹; 条纹是入射光对平行平板倾角相同的点的 条纹是入射光对平行平板倾角相同的点的 轨迹,且其定域面在无穷远处,须用望远 系统或在透镜焦平面上来观察其干涉图。
分振幅干涉的基本内容回顾
两类分振幅干涉装置产生的定域干涉图 (条纹)分别对应于: 平行平板——等倾条纹 平行平板——等倾条纹 楔形平板——等厚条纹 楔形平板——等厚条纹 其共同特点在于: 其共同特点在于: 光程相差Δ=2nhcosθ (+λ/2)的两束相干 光程相差Δ=2nhcosθ2(+λ/2)的两束相干 光分别由同一入射光在平板的上下两表面 产生。 其不同点在于: 其不同点在于:
7 空间曲线的曲率和挠率——【多元函数微分学】
弧微分公式 曲率的概念与曲率的计算 曲率圆与曲率半径
2007年8月
南京航空航天大学 理学院 数学系
1
一、弧微分公式
(1) 曲线弧由直角坐标方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2 1 y2 dx
2007年8月 南京航空航天大学 理学院 数学系
2
(2) 曲线弧由参数方程给出:
M
s
R M
可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ;
R 愈大, 则K 愈小 , 圆弧弯曲得愈小 .
2007年8月
南京航空航天大学 理学院 数学系
6
2.曲率的计算公式 K d .
ds
设y f ( x)二阶可导,
有 arctan y,
tan y,
d
y 1 y2
dx,
ds 1 y2dx. k
y 3.
(1 y2 )2
2007年8月 南京航空航天大学 理学院 数学系
7
设曲线方程为
x (t),
y
(t
),
(t), (t)二阶可导,
dy (t) , dx (t)
d2y dx2
(t )
(t) (t) 3(t)
(t) .
k
(t )
(t )
(t) (t)
3
.
[ 2(t ) 2(t )]2
y
a1
cost
一拱的弧长。
0 t 2
解 由公式得
l 2 [a(1 cost)]2 (a sin t)2 dt 0
o
2a
2
2a
1 costdt 2a 2 sin t dt
无缝线路轨道稳定计算
轨道工程
• 由上述基本假定可知,轨道横向变形位移函数yf 可以通过位移参数f来表示。设轨道的总势能为Π , 并表示为位移参数f的函数Π (f)。根据势能驻值 原理,轨道结构体系的力学平衡方程为:
( f ) 0 f
第36页
轨道工程
• 轨道结构的总势能Π由三部分能量组成:
( f ) A1 A2 A3 0 f f f f
0
0
+
=
+
第 8页
轨道工程
安全温升法
其主要出发点是:当钢轨温升幅值小于 △TS 时,无论轨道的原始弯曲以及外力作 用所引起的横向变形积累扩展到何等程度, 其轴向温度压力不会超过B点,线路也不会 发生胀轨跑道。
第 9页
轨道工程
极限状态法
其主要出发点是:轨道横向位移超过2mm 时,将易于形成轨道横向变形积累,增大 钢轨弯曲矢度,逐渐降低无缝线路的稳定 性,最后导致无缝线路胀轨跑道。
第21页
轨道工程
STRONG MEDIUM 道 床 横 向 阻 力
WEAK
轨枕横向位移
第22页
轨道工程
轨道框架刚度
• 轨道框架刚度反映轨道框架抵抗横向弯曲 的能力。轨道框架刚度越大,抵抗横向弯 曲变形的能力就越强。轨道框架刚度是两 股钢轨的横向水平刚度及钢轨与轨枕节点 间的阻矩抵抗横向弯曲能力的总和。
A1 -钢轨温度压力所作的 功
A2 -轨道框架抵抗弯曲变 形所作的功
A3 道床横向阻力所作的功
第37页
轨道工程
( f f oe ) 4 2 EI 3 Ql 2 l P 4 2 f f oe 3 ' l R
2
(
工程力学第六章答案 梁的变形-工程力学梁的弯曲答案
第五章梁的变形测试练习1.判断改错题5-1-1梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零.()5-1-2两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关。
()5-1-3悬臂梁受力如图所示,若A点上作用的集中力P在A B段上作等效平移,则A截面的转角及挠度都不变。
()5-1-4图示均质等直杆(总重量为W),放置在水平刚性平面上,若A端有一集中力P作用,使A C部分被提起,C B部分仍与刚性平面贴和弯矩均为零。
()5-1-5挠曲线近似微分方程不能用于求截面直梁的位移。
()5-1-6等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
()5-1-7两简支梁的抗刚度E I及跨长2a均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的。
()5-1-8简支梁在图示任意荷载作用下,截面C产生挠度和转角,若在跨中截面C又加上一个集中力偶M0作用,则梁的截面C的挠度要改变,而转角不变。
()题5-1-3图B题5-1-4图C5-1-9 一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。
( ) 5-1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )2.填空题5-2-1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在 和 。
5-2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则21P P 。
5-2-3 应用叠加原理求梁的变形时应满足的条件是: 。
5-2-4 在梁的变形中挠度和转角之间的关系是 。
5-2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是 ,连续条件是 。
5-2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是,题5-1-9图题5-1-10图题5-2-2图连续条件是 。
眼科检查的正常值
眼科检查的正常值眼球前后径24mm,垂直径23mm,水平径23.5mm前内轴长(角膜内面~视网膜内面)22.12mm,容积6.5ml,重量7g突出度12~14mm,两眼相差不超过2mm睑裂平视时高8mm,上睑遮盖角膜1~2mm,长26~30mm 内睑间距30~35mm,平均34mm外睑间距88~92mm,平均90mm睑板中央部宽度上睑6~9mm,下睑5mm睫毛上睑100~150mm根,下睑50~75根。
平视时倾斜度分别110°~130°,100°~120°,寿命3~5个月。
拔除后1周生长1~ 2mm,10周可达正常长度结膜结膜囊深度(睑缘至穹隆部深处)上方20mm,下方10mm 穹隆结膜与角膜距离上下方均为8~10mm,颞侧14mm,鼻侧7mm泪器泪小点直径0.2~0.3mm,距内眦6~6.5mm泪小管直径0.5~0.8mm,垂直部1~2mm,水平部8mm直径可扩张3倍泪囊长10mm,宽3mm鼻泪管全长18mm,下口位于下鼻甲前端之后16mm泪囊窝长17.86mm,宽8.01mm泪腺眶部20mm311mm35mm,重0.75g睑部15mm37mm33mm,重0.2g泪液正常清醒状态下,每分钟分泌0.9~2.2ul每眼泪液量7~12ul比重1.008,PH 7.35,屈光指数1.336渗透压295~309mOms/L,平均305mOms/L眼眶深40~50mm,容积25~28ml视神经孔直径4~6mm,视神经管长4~9mm眼外肌肌腱肌宽度内直肌10.3mm,外直肌9.2mm,上直肌10.8mm,下直肌9.8mm,上斜肌9.4mm,下斜肌9.4mm直肌止点距角膜缘内直肌5.5mm,下直肌6.5mm,外直肌6.9mm,上直肌7.7mm锯齿缘距角膜缘7~8mm赤道部距角膜缘14.5mm黄斑部距下斜肌最短距离(下斜肌止端鼻侧缘内上)2.2mm,距赤道18~22mm角膜横径11.5~12mm,垂直径10.5~11mm厚度中央部0.5~0.55mm,周边部1mm曲率半径前面7.8mm,后面6.8mm屈光力前面+48.83D,后面-5.88D,总屈光力+43D屈光指数1.337内皮细胞数2899±410/mm2角膜缘宽1.5~2mm巩膜厚度眼外肌附着处0.3mm,赤部0.4~0.6mm,视神经周围1.0mm 瞳孔直径 2.5~4mm(双眼差<0.25mm)瞳距男60.9mm,女58.3mm前房中央深度2.5~3mm房水容积0.15~0.3ml,前房0.2ml,后房0.06ml比重1.006,PH 7.5~7.6屈光指数1.3336~1.336生成速率(2~3)ul/min氧分压55mmHg,二氧化碳分压40~60mmHg睫状体宽度约6~7mm晶状体直径9mm,厚度4mm,体积0.2ml曲率半径前面10mm,后面6mm屈光指数1.437屈光力前面+7D,后面+11.66D,总屈光力+19D玻璃体容积4.5ml,屈光指数1.336脉络膜平均厚度约0.25mm,脉络膜上腔间隙10~35um视网膜视盘直径1.531.75mm黄斑直径2mm,中心凹位于视乳头颞侧缘3mm,视盘中心水平线下0.8mm视网膜动脉直径比例动脉∶静脉=2∶3视网膜中央动脉收缩压60~75mmHg,舒张压mmHg视神经全长40mm(眼内段1,眶内段25~30,管内段6~10,颅内段10) 视功能检查视野用直径为3mm的白色视标,检查周边视野正常:颞侧90°,鼻侧60°,上方55°,下方70°用蓝、红、绿色视标检查,周边视野依次递减10°左右立体视觉立体视敏度<60弧秒对比敏感度函数曲线呈倒“U”型,也称为山型或钟型泪液检查泪膜厚度7um,总量7.4ul,更新速度12%~16%min,PH6.5~ 7.6,渗压296~308mOsm/L泪膜破裂时间10~45s;<10s为泪膜不稳定Schirmer试验正常值10~45mm/5min;<10mm/5min为低分泌, <5mm/5min为干眼眼压和青光眼的有关数据平均值10~21mmHg;病理值>21mmHg双眼差异不应大于5mmHg24h波动范围不应大于8mmHg房水流畅系数(C) 正常值0.19~0.65ul/(min2mmHg)病理值<0.12ul/(min2mmHg)房水流量(F) 正常值1.84±0.05ul/min,>4.5ul/min为分泌过高压畅比(P/C) 正常值≤100病理值≥120巩膜硬度(E) 正常值0.0215C/D比值正常<0.3,两眼相差<0.2,>0.6为异常饮水试验饮水前后相差正常值<5mmHg病理值>8mmHg暗室试验试验前后眼压相差正常值<5mmHg病理值>8mmHg暗室加俯卧试验试验前后眼压相差正常值≤5mmHg病理值>8mmHg眼底荧光血管造影臂-脉络膜循环时间平均8.4s臂-视网膜循环时间为7~12s附錄眼科檢查的正常值解剖生理部分眼球前後徑24mm,垂直徑23mm,水準徑23 5mm眼內軸長(角膜內面~視網膜內面)22 12mm,容積6 5ml,重量7g突出度12~14mm,兩眼相差不超過2mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设曲线方程 y f (x) 有二阶导数。
在 x 处切线倾角 ( x) arctan f ' ( x) .
M ( x0 , f ( x0 ))到 M' ( x0 x, f ( x0 x))
的转角为 ( x0 x ) ( x0 ) .
弧长 s | MM '|| MM ' | x 2 y 2
弯曲程度与转角有关
对于右图的两条 但是, 相切于P1 和 P2 的曲线, 它们的转角相同但弯曲 , 程度不同 .
P1
P2
弯曲程度与弧长有关
假定:弯度与转角成正比,与弧长成反比
1
M2
2
M3
弧长相同时,转角大者 弯度大;
M1
P1
P2
转角相同时,弧长小者 弯度大。
按照上述假定, 建立度量弯曲程度的数学模型—— 曲率
| y"|
2 3/ 2
O
x
曲 率
思考题
x a( t sin t ); t (0, 2 ) t为何值时, 曲线 y a(1 cos t ),
的曲率最小? 求出最小曲率, 写出该点的曲率半径. | y | 1 解 K (t ) ,要使K(t)最小, 3 t 2 2 4a | sin | [1 ( y ) ] 2 t t 等价于 | sin |最大, 故当 | sin | 1,即 t 2 2 1 1 曲率最小, 且 K min , R 4a . K 4a
可得 K
' ( t ) " ( t ) ' ( t ) " ( t )
' ( t ) ' ( t )
2 2
3/ 2
'| (f "( x )( t ) ' ( t|)y"" ( t ) t ) " | | K K 3/ 2 / 23 / 2 2x )2 2 y32 1 ''( ( t ) ' ( t ) ' f 1
K ( R sin t )( R sin t ) ( R cos t )( R cos t )
( R sin t )
2
( R sin t ) )
2
3/ 2
1 R
感觉3: 抛物线在顶点处的弯度最大
K
1 y'
| y"|
2 3ቤተ መጻሕፍቲ ባይዱ 2
检验3: 设抛物线的方程为 y ax2 bx c
©
x 2 y2 s
lim
x 0
f " ( x0 ) 1 f ' ( x0 )2 1 f ' ( x0 )
2
1 f ' ( x )
0
| f "( x0 ) |
2 3/ 2
, 于是可得, 曲线方程 y f ( x ) 有二阶导数时 在 x 处的曲率
K lim , ( x0 x ) ( x0 ) . x 0 s
x 2 y 2 可以证明:lim 1. x 0 | s | / x 于是 K lim x 0 s / x
lim
x 0
/ x x 2 y2 / x
模型检验 检验K 是否符合人们关于“弯 度”的感觉经验。 感觉1: 直线是不弯曲的,其“弯度”应该处处为零。 检验1: 设直线方程为 y ax b,
显然曲率处处为K 0 . 则 y" 0.
感觉2: 圆上各个点的“弯度”应处处相同。
检验2: 设圆的方程为x R cost , y R sint .
记K , 称为MM' 上的平均曲率 s 当x 0时, ' M . 若极限 K lim M 存在, x 0 s
称之为曲线在点M 处的曲率.
s | MM ' || MM ' | x 2 y 2 . ( x ) arctan f ' ( x ) .
解:砂轮的半径应不超过抛物线上曲率半径的最小值。
| 1.6 | 由曲率公式, 在点 x 处的曲率为 K [1 (1.6 x ) 2 ]3 / 2 其最大值为 K 1.6 ,
则曲率半径的最小值 1 为R 0.625. 1.6
砂轮的直径不超过 .25 1
y
y 0.8 x 2
K
1 y'
§3.8
曲 率
建立度量曲线弯曲程度的数学模型
—— 曲率
如何描述弯曲
1
M2
设弧 M1 M2 与弧 M2 M3 长度相同 .
弧 M2 M3 比弧 M1 M“弯得多” . 2
2
M3
M1
点 M1 与 M2处各自切线间的夹角 1 称为点M1 到 M2的转角.
点 M2 到 M3的转角 2 1 .
| 2a | 则 y' 2ax b , y" 2a. K [1 ( 2ax b ) 2 ]3 / 2
b 当 x 时K 取得最大值 . (抛物线的顶点处) 2a
例. 计算双曲线 xy 1 在点(, 11 )处的曲率 .
1 1 2 此时有 y , y' 2 , y" 3 . x x x 则 y' (1) 1 , y"(1) 2 .
y' (1 y'2 ) x0 y"
y
x x0
1 y'2 , y0 y"
y f ( x)
x x0
( , )
M ( x0 , y0 )
O
x
抛物线 y 0.8 x 2 , 现在要用 例4. 设工件内表面的截线是 砂轮磨其内表面,问砂 轮的直径多大时才比较 合适?
|2| 1 于是 K . 2 3/ 2 [1 ( 1) ] 2
设 M ( x0 , y0 ) 是曲线 y f ( x ) 上的点,在曲线凹向的 一侧 与该曲线相切于M ,且与曲线曲率相同的 圆称为曲率圆 1 设点 M 处的曲率为K , 则R 称为该点的曲率半径 . K 可以证明曲率圆的圆心 坐标 ( , ) 为:
K
1 f ' ( x)
| f "( x ) |
2 3/ 2
1 y'
| y"|
2 3/ 2
x (t ) 当曲线方程是由参数方 程 , t ( , ) 给出时, y (t )
'(t ) " ( t ) ' ( t ) ' ( t ) " ( t ) 由参数方程的导数 y' , y" ' (t ) '2 ( t )
