等腰等边三角形测试题
等腰等边三角形典型题

等腰等边三角形典型题一、等腰三角形典型题1. 题目:在等腰△ABC中,AB = AC,∠A = 50°,求∠B和∠C的度数。
- 解析:因为AB = AC,所以△ABC是等腰三角形,等腰三角形两底角相等。
三角形内角和为180°,已知∠A=50°,设∠B = ∠C = x,则可列方程x + x+50° = 180°,2x=180° - 50°,2x = 130°,解得x = 65°,所以∠B = ∠C = 65°。
2. 题目:等腰三角形的一个角是70°,求这个等腰三角形的顶角的度数。
- 解析:分两种情况讨论。
- 当这个70°的角是底角时,因为等腰三角形两底角相等,所以另一个底角也是70°,根据三角形内角和为180°,则顶角为180°-70°×2 = 180° - 140°=40°。
- 当这个70°的角是顶角时,顶角就是70°。
3. 题目:已知等腰三角形的腰长为5cm,底边长为6cm,求这个等腰三角形的面积。
- 解析:先作等腰三角形底边上的高。
因为等腰三角形三线合一(底边上的高、中线、顶角平分线三线合一),所以底边上的高将底边平分。
底边长为6cm,则底边的一半是3cm。
根据勾股定理,高h=√(5^2)-3^{2}=√(25 - 9)=√(16) = 4cm。
三角形面积S=(1)/(2)×底×高=(1)/(2)×6×4 = 12cm^2。
二、等边三角形典型题1. 题目:等边三角形ABC的边长为6,求它的高和面积。
- 解析:- 求高:因为等边三角形三线合一,设等边三角形的高为h,边长为a = 6,根据勾股定理h=√(a^2)-<=ft((a)/(2))^{2}=√(6^2)-3^{2}=√(36 - 9)=√(27)=3√(3)。
2022年中考数学总复习:等腰三角形,等边三角形

2022年中考数学总复习训练:等腰三角形,等边三角形一、选择题1. 已知等边△ABC的边长为a,则它的面积是()A.a2 B.a2 C.a2D.a22. 以下列各组数据为边长,可以构成等腰三角形的是( )A.1,1,2 B.1,1,3C.2,2,1 D.2,2,53. 具备下列条件的三角形为等腰三角形的是链接听P27例1归纳总结( )A.有两个角分别为20°,120°B.有两个角分别为40°,80°C.有两个角分别为30°,60°D.有两个角分别为50°,80°4. 如图,△ABC与△关于直线MN对称,P为MN上任一点,下列结论中错误的是( )(A)△是等腰三角形. (B)MN垂直平分.(C)△ABC与△面积相等.(D)直线AB、的交点不一定在MN上.5. 以下叙述中不正确的是( ).A.等边三角形的每条高线都是角平分线和中线;B.有一个内角为60°的等腰三角形是等边三角形;C.等腰三角形一定是锐角三角形;D.在一个三角形中,如果有两条边相等,那么它们所对的角也相等;反之,在一个三角形中,如果有两个角相等,那么它们所对的边也相等.6. 如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )A.12B.13C.14D.157. 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )A. AE =ECB. AE =BEC. ∠EBC =∠BACD. ∠EBC =∠ABE8. 如图,把一长方形纸片ABCD 沿EG 折叠后,点A 、B 分别落在A ′、B ′的位置上,EA ′与BC 相交于点F ,已知∠1=130°,则∠2的度数是( )A.40°B.50°C.65°D.80°9. 下列条件不能得到等边三角形的是( )A .有两个内角是60°的三角形B .有一个角是60°的等腰三角形C .腰和底相等的等腰三角形D .有两个角相等的等腰三角形10. 如图,等边三角形ABC 中,D 为BC 的中点,BE 平分∠ABC 交AD 于E ,若△CDE 的面积等于1,则△ABC 的面积等于( )A .2B .4C .6D .1211. 如图,在△ABC 中,AB =AC ,BC =12,E 为AC 边的中点,线段BE 的垂直平分线交边BC 于点D.设BD =x ,tan ∠ACB =y ,则( )A. x -y 2=3 B. 2x -y 2=9C. 3x -y 2=15D. 4x -y 2=2112. 如图, △ABC 和△CDE 均为等腰直角三角形,点B,C,D 在一条直线上,点M 是AE 的中点,下列结论:①tan ∠AEC=; ②S ⊿ABC +S ⊿CDE ≥S ⊿ACE ; ③BM ⊥DM;④BM=DM.正确结论的个数是( )A.1个 B.2个 C.3个 D.4个二、填空题13. 如图,△ABC 中,AB =AC ,∠C =30°,DA ⊥BA 于A ,BC =4.2 cm ,则AD =__________. CD BC M E C A14. 若等腰三角形的一个底角为72°,则这个等腰三角形的顶角为 .15. 已知等腰三角形的一个外角为130°,则它的顶角的度数为 .16. 等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝,则这个三角形的底边长为 ㎝.17. △ABC 为等边三角形,D 、E 、F 分别在边BC 、CA 、AB 上,且AE=CD=BF ,则△DEF 为___三角形.18. 如图所示的正方形网格中,网格线的交点称为格点.已知A 、B 是两格点,如果C 也是图中的格点,且使得△ABC 为等腰三角形,则点C 的个数是( ).A .6B .7C .8D .919. 在边长为4的等边三角形ABC 中,D 为BC 边上的任意一点,过点D 分别作DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F ,则DE+DF= .20. 如图,是等边三角形,点是边上任意一点,于点, 于点.若,则_____________.三、解答题21. 如图,点E ,F 在BC 上,BE =CF ,∠A =∠D ,∠B =∠C ,AF 与DE 交于点O.(1)求证:AB =DC ;(2)试判断△OEF 的形状,并说明理由.ABC △D BC DE AB ⊥E DF AC ⊥F 4BC =BE CF +=22. 如图,等腰直角△ABC 中,CA=CB ,点E 为△ABC 外一点,CE=CA ,且CD 平分∠ACB 交AE 于D ,且∠CDE=60°.求证:△CBE 为等边三角形.23. 如图,已知Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D ,∠BAC 的平分线分别交BC ,CD 于点E ,F.求证:△CEF 是等腰三角形.24. 已知:如图,△ABD 为等边三角形,△ACB 为等腰三角形且∠ACB =90°,DE ⊥AC 交AC 延长线于E ,求证:DE =CE.25. 如图1,在ABC 中,90,1A AB AC ∠=︒==,点D ,E 分别在边,AB AC 上,且1AD AE ==,连接DE .现将ADE 绕点A 顺时针方向旋转,旋转角为()0360αα︒︒<<,如图2,连接,,CE BD CD .(1)当0180α︒<<︒时,求证:CE BD =;(2)如图3,当90α=︒时,延长CE 交BD 于点F ,求证:CF 垂直平分BD ;(3)在旋转过程中,求BCD 的面积的最大值,并写出此时旋转角α的度数.26. (1)如图14-63,下列每个图形都是由若干个边长为1的等边三角形组成的等边三角形,它们的边长分别为1,2,3,…,设边长为n 的等边三角形由s 个小等边三角形组成,按此规律推断s 与n 有怎样的关系;(2)现有一个等角六边形ABCDEF (六个内角都相等的六边形,如图14-64),它的四条边长分别是2、5、3、1,求这个等角六边形的周长;(3)(2)中的等角六边形能否用(1)中最小的等边三角形无空隙拼合而成?如果能,请求出需要这种小等边三角形的个数.27. (1) 如图1,在正方形ABCD 中,点E,F 分别在边BC,CD 上,AE,BF 交于点O,∠AOF =90°,求证:BE =CF.(2) 如图2,在正方形ABCD 中,点E,H,F,G 分别在边AB,BC,CD,DA 上,EF,GH 交于点O,∠FOH =90°, EF =4.求GH 的长.图1 图2(3) 已知点E,H,F,G 分别在矩形ABCD 的边AB,BC,CD,DA 上,EF,GH 交于点O,∠FOH =90°,EF =4. 直接写出下列两题的答案:①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).图3 图428. 在△ABC中,AC=BC,,点D为AC的中点.(1)如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连结CF,过点F作,交直线AB于点H.判断FH与FC的数量关系并加以证明.(2)如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.。
初二数学等腰与等边复习题及解析

初二数学等腰与等边复习题一.选择题(共10小题)1.(2015•内江)如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为()A.40°B.45°C.60°D.70°2.(2015•南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为()A.35°B.40°C.45°D.50°3.(2012•齐齐哈尔模拟)如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE 相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种4.(2015•宿迁)若等腰三角形中有两边长分别为2和5,则这个三角形的周长为()A.9 B.12 C.7或9 D.9或125.(2015秋•南开区期末)下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有()A.①②③ B.①②④ C.①③D.①②③④6.(2015秋•沙河市期末)如图,已知△ABC中,AB=AC,AD=AE,∠BAE=30°,则∠DEC 等于()A.7.5°B.10°C.15°D.18°7.(2009•呼和浩特)在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7 B.11 C.7或11 D.7或108.(2010•青岛模拟)如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管()根.A.2 B.4 C.5 D.无数9.(2003•青海)若等腰三角形一腰上的高等于腰长的一半,则此三角形的底角等于()A.75°B.15°C.75°或15°D.30°10.(2014秋•昆山市校级期末)已知等腰三角形的一个外角等于100°,则它的顶角是()A.80°B.20°C.80°或20°D.不能确定二.填空题(共5小题)11.(2016春•沈丘县期末)等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为60°或120°.12.(2013秋•西城区期末)如图,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是2a+12.13.(2009秋•通州区期末)如图,在△ABC中,AB=AC,D,E分别是AC,AB上的点,且BC=BD,AD=DE=EB,则∠A=45度.14.(2014秋•吴中区校级期中)已知等腰三角形一腰上的中线将它周长分成18cm和9cm 两部分,则这个等腰三角形的底边长是3cm.15.已知a、b、c为△ABC的三条边,且满足a2+ab﹣ac﹣bc=0,b2+bc﹣ba﹣ca=0,则△ABC 是等边三角形.三.解答题(共2小题)16.(2015秋•蓬江区期末)如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.17.(2013秋•孝感校级期末)图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.初二数学等腰与等边复习题参考答案与试题解析一.选择题(共10小题)1.(2015•内江)如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为()A.40°B.45°C.60°D.70°【分析】根据平行线的性质可得∠CBD的度数,根据角平分线的性质可得∠CBA的度数,根据等腰三角形的性质可得∠C的度数,根据三角形内角和定理可得∠BAC的度数.【解答】解:∵AE∥BD,∴∠CBD=∠E=35°,∵BD平分∠ABC,∴∠CBA=70°,∵AB=AC,∴∠C=∠CBA=70°,∴∠BAC=180°﹣70°×2=40°.故选:A.【点评】考查了平行线的性质,角平分线的性质,等腰三角形的性质和三角形内角和定理.关键是得到∠C=∠CBA=70°.2.(2015•南宁)如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为()A.35°B.40°C.45°D.50°【分析】先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.【解答】解:∵△ABD中,AB=AD,∠B=70°,∴∠B=∠ADB=70°,∴∠ADC=180°﹣∠ADB=110°,∵AD=CD,∴∠C=(180°﹣∠ADC)÷2=(180°﹣110°)÷2=35°,故选:A.【点评】本题考查的是等腰三角形的性质,熟知等腰三角形的两底角相等是解答此题的关键.3.(2012•齐齐哈尔模拟)如图,在△ABC中,D、E分别是AC、AB上的点,BD与CE 相交于点O,给出四个条件:①OB=OC;②∠EBO=∠DCO;③∠BEO=∠CDO;④BE=CD.上述四个条件中,选择两个可以判定△ABC是等腰三角形的方法有()A.2种B.3种C.4种D.6种【分析】①②:求出OBC=∠OCB,推出∠ACB=∠ABC即可的等腰三角形;①③:证△EBO≌△DCO,得出∠EBO=∠DCO,求出∠ACB=∠ABC即可;②④:证△EBO≌△DCO,推出OB=OC,求出∠ABC=∠ACB即可;③④:证△EBO≌△DCO,推出∠EBO=∠DCO,OB=OC,求出∠OBC=∠OCB,推出∠ACB=∠ABC即可.【解答】解:有①②,①③,②④,③④,共4种,①②,理由是:∵OB=OC,∴∠OBC=∠OCB,∵∠EBO=∠DCO,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形;①③,理由是:∵在△EBO和△DCO中,∴△EBO≌△DCO,∴∠EBO=∠DCO,∵∠OBC=∠OCB(已证),∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;②④,理由是:∵在△EBO和△DCO中,∴△EBO≌△DCO,∴OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;③④,理由是:∵在△EBO和△DCO中,∴△EBO≌△DCO,∴∠EBO=∠DCO,OB=OC,∴∠OBC=∠OCB,∴∠EBO+∠OBC=∠DCO+∠OCB,即∠ABC=∠ACB,即AB=AC,∴△ABC是等腰三角形;故选C.【点评】本题考查了等腰三角形的性质和判定,全等三角形的性质和判定的应用,通过做此题培养了学生的推理能力和辨析能力,题目比较好,但是一道比较容易出错的题目.4.(2015•宿迁)若等腰三角形中有两边长分别为2和5,则这个三角形的周长为()A.9 B.12 C.7或9 D.9或12【分析】题目给出等腰三角形有两条边长为5和2,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.【解答】解:当腰为5时,根据三角形三边关系可知此情况成立,周长=5+5+2=12;当腰长为2时,根据三角形三边关系可知此情况不成立;所以这个三角形的周长是12.故选:B.【点评】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.5.(2015秋•南开区期末)下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有()A.①②③ B.①②④ C.①③D.①②③④【分析】根据等边三角形的判定判断.【解答】解:①两个角为60度,则第三个角也是60度,则其是等边三角形,故正确;②这是等边三角形的判定2,故正确;③三个外角相等则三个内角相等,则其是等边三角形,故正确;④根据等边三角形三线合一性质,故正确.所以都正确.故选D.【点评】此题主要考查学生对等边三角形的判定的掌握情况.6.(2015秋•沙河市期末)如图,已知△ABC中,AB=AC,AD=AE,∠BAE=30°,则∠DEC 等于()A.7.5°B.10°C.15°D.18°【分析】根据等腰三角形性质求出∠C=∠B,根据三角形的外角性质求出∠B=∠C=∠AED+α﹣30°,根据∠AED=∠ADE=∠C+α,得出等式∠AED=∠AED+α﹣30°+α,求出即可.【解答】解:∵AC=AB,∴∠B=∠C,∵∠AEC=∠B+∠BAE=∠B+30°=∠AED+α,∴∠B=∠C=∠AED+α﹣30°,∵AE=AD,∴∠AED=∠ADE=∠C+α,即∠AED=∠AED+α﹣30°+α,∴2α=30°,∴α=15°,∠DEC=α=15°,故选C.【点评】本题考查了等腰三角形的性质,三角形的内角和定理,三角形的外角性质等知识点的应用,主要考查学生运用定理进行推理的能力,本题有一点难度,但题型不错.7.(2009•呼和浩特)在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为()A.7 B.11 C.7或11 D.7或10【分析】题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.【解答】解:设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②解方程组①得:,根据三角形三边关系定理,此时能组成三角形;解方程组②得:,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7;故选C.【点评】本题考查等腰三角形的性质及相关计算.学生在解决本题时,有的同学会审题错误,以为15,12中包含着中线BD的长,从而无法解决问题,有的同学会忽略掉等腰三角形的分情况讨论而漏掉其中一种情况;注意:求出的结果要看看是否符合三角形的三边关系定理.故解决本题最好先画出图形再作答.8.(2010•青岛模拟)如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管()根.A.2 B.4 C.5 D.无数【分析】因为每根钢管的长度相等,可推出图中的5个三角形都为等腰三角形,再根据外角性质,推出最大的∠0BQ的度数(必须≤90°),就可得出钢管的根数.【解答】解:如图所示,∠AOB=15°,∵OE=FE,∴∠GEF=∠EGF=15°×2=30°,∵EF=GF,所以∠EGF=30°∴∠GFH=15°+30°=45°∵GH=GF∴∠GHF=45°,∠HGQ=45°+15°=60°∵GH=HQ,∠GQH=60°,∠QHB=60°+15°=75°,∵QH=QB∴∠QBH=75°,∠HQB=180﹣75°﹣75°=30°,故∠OQB=60°+30°=90°,不能再添加了.故选C.【点评】根据等腰三角形的性质求出各相等的角,然后根据三角形内角和外角的关系解答.9.(2003•青海)若等腰三角形一腰上的高等于腰长的一半,则此三角形的底角等于()A.75°B.15°C.75°或15°D.30°【分析】等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成立,因而应分两种情况进行讨论.【解答】解:当高在三角形内部时,由已知可求得三角形的顶角为30°,则底角是75°;当高在三角形外部时,三角形顶角的外角是30°,则底角是15°;所以此三角形的底角等于75°或15°,故选C.【点评】考查了等腰三角形的性质,以及含特殊角的直角三角形;熟记三角形的高相对于三角形的三种位置关系是解题的关键,本题易出现的错误是只是求出75°一种情况,应当注意需要分类讨论.10.(2014秋•昆山市校级期末)已知等腰三角形的一个外角等于100°,则它的顶角是()A.80°B.20°C.80°或20°D.不能确定【分析】此外角可能是顶角的外角,也可能是底角的外角,需要分情况考虑,再结合三角形的内角和为180°,可求出顶角的度数.【解答】解:①若100°是顶角的外角,则顶角=180°﹣100°=80°;②若100°是底角的外角,则底角=180°﹣100°=80°,那么顶角=180°﹣2×80°=20°.故选C.【点评】当外角不确定是底角的外角还是顶角的外角时,需分两种情况考虑,再根据三角形内角和180°、三角形外角的性质求解.二.填空题(共5小题)11.(2016春•沈丘县期末)等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为60°或120°.【分析】等腰三角形的高相对于三角形有三种位置关系,三角形内部,三角形的外部,三角形的边上.根据条件可知第三种高在三角形的边上这种情况不成了,因而应分两种情况进行讨论.【解答】解:当高在三角形内部时,顶角是120°;当高在三角形外部时,顶角是60°.故答案为:60°或120°.【点评】此题主要考查等腰三角形的性质,熟记三角形的高相对于三角形的三种位置关系是解题的关键,本题易出现的错误是只是求出120°一种情况,把三角形简单的认为是锐角三角形.因此此题属于易错题.12.(2013秋•西城区期末)如图,在△ABC中,AB=AC,∠A=60°,BE⊥AC于E,延长BC到D,使CD=CE,连接DE,若△ABC的周长是24,BE=a,则△BDE的周长是2a+12.【分析】根据在△ABC中,AB=AC,∠A=60°,可得△ABC的形状,再根据△ABC的周长是24,可得AB=BC=AC=8,根据BE⊥AC于E,可得CE的长,∠EBC=30°,根据CD=CE,可得∠D=∠CED,根据∠ACB=60°,可得∠D,根据∠D与∠EBC,可得BE与DE的关系,可得答案.【解答】解:∵在△ABC中,AB=AC,∠A=60°,∴△ABC是等边三角形,∵△ABC的周长是24,∴AB=AC=BC=8,∵BE⊥AC于E,∴CE=AC=4,∠EBC=∠ABC=30°,∵CD=CE,∴∠D=∠CED,∵∠ACB是△CDE的一个外角,∴∠D+∠CED=∠ACB=60°∴∠D=30°,∴∠D=∠EBC,∴BE=DE=a,∴△BED周长是DE+BE+BD=a+a+(8+4)=2a+12,故答案为:2a+12.【点评】本题考查了等腰三角形的判定与性质,有一个角是60°的等腰三角形是等边三角形,等腰三角形的性质:等边对等角,等腰三角形的判定:等角对等边..13.(2009秋•通州区期末)如图,在△ABC中,AB=AC,D,E分别是AC,AB上的点,且BC=BD,AD=DE=EB,则∠A=45度.【分析】根据已知条件结合图形,列出相关角的关系,然后利用三角形的内角和求解.【解答】解:∵AB=AC,BC=BD,∴∠C=∠ABC=∠BDC,∵AD=DE=EB,∴∠EBD=∠EDB,∠A=∠AED,又∠EBD+∠EDB=∠AED,即2∠EDB=∠A,又∠A+∠AED=∠EDB+∠BDC,即2∠A=∠EDB+∠BDC,由⇒∠A=⇒∠A=∠C,又由三角形内角和定理得:∠A+∠ABC+∠C=180°,即4∠A=180°,∴∠A=45°.故答案为:45.【点评】本题考查了等腰三角形的性质,及三角形内角和定理;此题需灵活运用等腰三角形的性质,通过寻找相关角之间的关系求解是正确解答本题的关键.14.(2014秋•吴中区校级期中)已知等腰三角形一腰上的中线将它周长分成18cm和9cm 两部分,则这个等腰三角形的底边长是3cm.【分析】设腰长为xcm,底为ycm,则可知2x+y=18+9,x+x=18或9,可求得y.【解答】解:设腰长为xcm,底为ycm,则由题意可知x+x=18或9,解得x=12或6,而三角形的周长为2x+y=18+9,当x=12时可解得y=3,此时三角形的三边为12cm,12cm,3cm,满足三角形的三边关系,此时底边长为3cm,当x=6时可解得y=15,此时三角形的三边为6cm,6cm,15cm,此时6+6<15,不满足三角形的三边关系,不合题意;综上可知底边长为3cm.故答案为:3.【点评】本题主要考查等腰三角形的性质,由条件分两种情况求得三角形的各边长再利用三角形的三边关系进行验证是解题的关键,注意方程思想的应用.15.已知a、b、c为△ABC的三条边,且满足a2+ab﹣ac﹣bc=0,b2+bc﹣ba﹣ca=0,则△ABC 是等边三角形.【分析】分析题目中的a2+ab﹣ac﹣bc=0,b2+bc﹣ba﹣ca=0,可知a=b=c,所以该三角形为正三角形.【解答】解:∵a2+ab﹣ac﹣bc=0∴a(a+b)﹣c(a+b)=0∴(a﹣c)(a+b)=0∵a+b>0∴a﹣c=0∴a=c∵b2+bc﹣ba﹣ca=0∴b(b+c)﹣a(b+c)=0∴(b﹣a)(b+c)=0∵b+c>0∴b﹣a=0∴b=a∴a=b=c∴△ABC是等边三角形【点评】该题主要考查等边三角形的判定和有理数的运算(即方程式的化简).三.解答题(共2小题)16.(2015秋•蓬江区期末)如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;(2)当∠A=40°时,求∠DEF的度数.【分析】(1)由AB=AC,∠ABC=∠ACB,BE=CF,BD=CE.利用边角边定理证明△DBE ≌△CEF,然后即可求证△DEF是等腰三角形.(2)根据∠A=40°可求出∠ABC=∠ACB=70°根据△DBE≌△CEF,利用三角形内角和定理即可求出∠DEF的度数.【解答】证明:∵AB=AC,∴∠ABC=∠ACB,在△DBE和△CEF中,∴△DBE≌△CEF,∴DE=EF,∴△DEF是等腰三角形;(2)∵△DBE≌△CEF,∴∠1=∠3,∠2=∠4,∵∠A+∠B+∠C=180°,∴∠B=(180°﹣40°)=70°∴∠1+∠2=110°∴∠3+∠2=110°∴∠DEF=70°【点评】此题主要考查学生对等腰三角形的判定与性质的理解和掌握,此题主要应用了三角形内角和定理和平角是180°,因此有一定的难度,属于中档题.17.(2013秋•孝感校级期末)图1、图2中,点C为线段AB上一点,△ACM与△CBN都是等边三角形.(1)如图1,线段AN与线段BM是否相等?证明你的结论;(2)如图2,AN与MC交于点E,BM与CN交于点F,探究△CEF的形状,并证明你的结论.【分析】(1)等边三角形的性质可以得出△ACN,△MCB两边及其夹角分别对应相等,两个三角形全等,得出线段AN与线段BM相等.(2)平角的定义得出∠MCN=60°,通过证明△ACE≌△MCF得出CE=CF,根据等边三角形的判定得出△CEF的形状.【解答】解:(1)∵△ACM与△CBN都是等边三角形,∴AC=MC,CN=CB,∠ACM=∠BCN=60°.∴∠MCN=60°,∠ACN=∠MCB,在△ACN和△MCB中,∴△ACN≌△MCB(SAS).∴AN=BM.(2)∵△ACN≌△MCB,∴∠CAE=∠CMB.在△ACE和△MCF中∴△ACE≌△MCF(ASA).∴CE=CF.∴△CEF的形状是等边三角形.【点评】本题考查了SAS﹣﹣两边及其夹角分别对应相等的两个三角形全等,ASA﹣﹣两角及其夹边分别对应相等的两个三角形全等,同时考查了等边三角形的性质和判定.。
等腰三角形与等边三角形的综合练习题

等腰三角形与等边三角形的综合练习题在几何学中,等腰三角形和等边三角形是两个基本的三角形类型。
虽然它们具有一些共同点,但也有一些不同之处。
本文将为您提供一些相关的综合练习题,以帮助您更好地理解和应用这两种三角形。
练习题1:等边三角形的性质和相关计算题目:已知一个等边三角形ABC,边长为a。
请计算以下内容:1. 三角形ABC的内角和是多少?2. 计算三角形ABC的高和面积。
3. 求三角形ABC的外接圆半径。
4. 若等边三角形ABC的周长为15cm,求边长a的值。
解答:1. 由于等边三角形的三个内角相等,所以三角形ABC的内角和为180°。
2. 等边三角形ABC的高等于边长,因此三角形ABC的高为a。
根据三角形面积公式,三角形ABC的面积S = 1/2 * a * a * sin60°= a² * √3 / 4。
3. 由于等边三角形的外接圆半径等于边长的一半,所以三角形ABC 的外接圆半径为a / 2。
4. 根据等边三角形的性质,边长a乘以3即为等边三角形的周长。
所以3a = 15,解得a = 5。
练习题2:等腰三角形的性质和相关计算题目:已知一个等腰三角形DEF,底边DE = 8cm,等腰边DF = EF = 6cm。
请计算以下内容:1. 三角形DEF的内角和是多少?2. 求三角形DEF的高和面积。
3. 已知等腰三角形DEF的底边DE = 8cm,求EF的值,使得三角形DEF的面积为12平方厘米。
解答:1. 由于等腰三角形的两个底角相等,所以三角形DEF的内角和为180°。
2. 等腰三角形DEF的高可以通过勾股定理计算,即高h = √(DF² - (DE/2)²) = √(6² - (8/2)²) = √16 = 4。
根据三角形面积公式,三角形DEF的面积S = 1/2 * DE * h = 1/2 * 8 * 4 = 16 平方厘米。
等腰三角形和等边三角形练习题
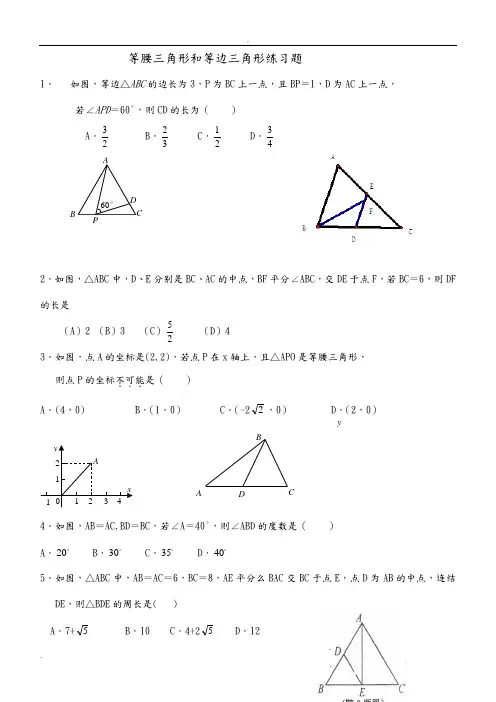
等腰三角形和等边三角形练习题
1. 如图,等边△ABC 的边长为 3,P 为 BC 上一点,且 BP=1,D 为 AC 上一点,
若∠APD=60°,则 CD 的长为( )
A. 3 2
A
B. 2 3
C. 1 2
D. 3 4
60° D
BP
C
2.如图,△ABC 中,D、E 分别是 BC、AC 的中点,BF 平分∠ABC,交 DE 于点 F,若 BC=6,则 DF
A
第 8 题图
A.6
B.7
C.8
D.9
17.已知等腰三角形的一个角为 70°,则另外两个角的度数是( )
A.55°,55° B.70°,40° C.55°,55°或 70°,40° D.以上都不对
18.已知:一等腰三角形的两边长
x、y
满足方程组
2x 3x
-y 2y
3, 8,
则此等腰三角形的周长为(
连接 BD.若 BD 平分∠ABC,则下列结论错误的是
A
E
D
B
A.BC=2BE B.∠A=∠EDA
C.BC=2AD
D.BD⊥AC
C
16.如图所示的正方形网格中,网格线的交点称为格点.已知 A 、B 是两格点,如果 C 也是图中
的格点,且使得 ABC 为等.腰.三.角.形.,则点 C 的个数是
.
.
B
A. 0 x 3
B. x 3 C. 3 x 6
D. x 6
22.如图,吴伯伯家有一块等边三角形的空地 ABC,已知点 E、F 分别是边 AB、AC 的中点,量得
.
.
EF=5 米,他想把四边形 BCFE 用篱笆围成一圈放养小鸡,则需用篱笆的长是
初二等边等腰三角形练习题

初二等边等腰三角形练习题1. 一张纸的两边折成直角,假设与底边相交的边长为x,则三角形的底边长是多少?解答:根据题意,我们可以得知该三角形是一个等边等腰三角形。
由于等边三角形的三条边相等,所以底边的长度也等于x。
2. 若等边等腰三角形的底边长为12cm,请求出其高度和面积。
解答:由于等边三角形的三个边长相等,所以底边长为12cm,其他两边也为12cm。
根据等腰三角形的性质,高度是底边的中垂线,也就是连接底边中点和顶点的线段。
由于等边三角形的中垂线也是高度,所以高度也等于底边的一半,即6cm。
由于等边三角形的面积公式为S = (边长^2 * √3) / 4,所以面积为:S = (12^2 * √3) / 4≈ 36√3 cm²3. 一个等边等腰三角形的面积为48√3 cm²,求其底边长和高度。
解答:设等边等腰三角形的底边长为x,根据面积公式可得:48√3 = (x^2 * √3) / 4解方程可得:x = 8所以三角形的底边长为8cm。
由于等边三角形的高度也是中垂线,所以高度等于底边的一半,即4cm。
4. 若一个等边等腰三角形的底边与高度的比值为5:4,求其底边长和高度。
解答:设等边等腰三角形的底边长为5x,高度为4x。
由于等边三角形的边长相等,所以5x = 4x。
解方程可得:x = 0。
由于代入比值后出现问题,说明题目存在错误或矛盾。
5. 某个等边等腰三角形的顶角是80度,求其底边长和高度。
解答:由于等边等腰三角形的三个角相等,所以底角和顶角也等于80度。
根据三角形内角和定理可得:底角的度数 + 底角的度数 + 顶角的度数 = 180度。
代入已知条件,可得:底角的度数 + 底角的度数 +80度 = 180度,解方程可得:底角的度数 = 50度。
由于等边三角形的底角和顶角是相等的,所以底角也等于50度。
根据三角函数的定义可知:底边长 / 顶角的正弦值 = 高度 / 底角的正弦值。
初中数学综合复习等腰三角形(含等边三角形)部分4
初中数学综合复习等腰三角形(含等边三角形)部分4一、选择题1. 如图,梯形ABCD中,AD∥BC,DE∥AB,DE=DC,∠C=80°.则∠A等于()A.80°B.90°C.100°D.110°【答案】C2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是A、85°B、80°C、75°D、70°【答案】A3.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以A n为顶点的内角度数是( )A.(12)n·75°B.(12)n-1·65°C.(12)n-1·75°D.(12)n·85°【答案】C4.如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=5.若A点的坐标为(﹣3,1),B、C两点在方程式y=﹣3的图形上,D、E两点在y轴上,则F点到y轴的距离为何?()A1A2A3A4CBDEF…第11题图第10题图AB CDEA .2B .3C .4D .5分析:如图,作AH 、CK 、FP 分别垂直BC 、AB 、DE 于H 、K 、P .由AB =BC ,△ABC ≌△DEF ,就可以得出△AKC ≌△CHA ≌△DPF ,就可以得出结论.解:如图,作AH 、CK 、FP 分别垂直BC 、AB 、DE 于H 、K 、P . ∴∠DPF =∠AKC =∠CHA =90°. ∵AB =BC , ∴∠BAC =∠BCA . 在△AKC 和△CHA 中。
等腰三角形和等边三角形习题例题
等腰三角形的性质应用及判定【例1】 如图,△ABC 中,D 、E 分别是AC 、AB 上的点,BD 与CE 交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.(1) 上述三个条件中,哪两个条件可判定△ABC 是等腰三角形(用序号写出所有情形)(2) 选择第(1)小题中的一种情形,证明△ABC 是等腰三角形【例2】如图,△ABC 为等边三角形,延长BC 到D,又延长BA 到E ,使AE=BD,连接CE,DE 。
求证:△CDE 为等腰三角形【例3】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的个数有( ) ①DC '平分∠BDE②BC 长为(22 )a ③△BC 'D 是等腰三角形 ④△CED 的周长等于BC 的长个 个 个 个【例4】如图,△ABC 是边长为1的正三角形,△BDC 是顶角为120°的等腰三角形,以D 为顶点作一个60°的∠MDN ,点M,N 分别在AB,AC 上,则△AMN 的周长是A E BC ODE A B C DD BE C DBC 'EA CB A MNDB C【例5】已知一个等腰三角形两内角的度数比为1:4,则这个等腰三角形顶角的度数为()°°°或120°°【例6】等腰三角形两边长分别为4和9,则第三边长为【例7】如图,点O事等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,则△COD是等边三角形;(1)当α为多少度时,△AOD是等腰三角形?(2)求证:△COD是等边三角形(3)当α=150°时,试判断△AOD的形状,并说明理由等边三角形的性质应用及判定【例8】如图,在等边△ABC中,点D,E分别在边BC,AB上,BD=AE,AD与CE交于点F.求证:(1)AD=CE;(2)求∠DFC的度数。
初中数学特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析
特殊三角形(等腰三角形、等边三角形、30°直角三角形)常考题及答案解析1.(2020秋•喀什地区期末)下列说法错误的是()A.等腰三角形的两个底角相等B.等腰三角形的高、中线、角平分线互相重合C.三角形两边的垂直平分线的交点到三个顶点距离相等D.等腰三角形顶角的外角是其底角的2倍2.(2020秋•顺城区期末)已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为()A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm 3.(2017•海南)已知△ABC的三边长分别为4、4、6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画()条.A.3B.4C.5D.6 4.(2019•白银)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰△ABC中,∠A=80°,则它的特征值k=.5.(2013•凉山州)已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是.6.(2020秋•五常市期末)如图,点D、E在△ABC的边BC上,AD=AE,BD=CE.(1)求证:AB=AC;(2)若∠BAC=108°,∠DAE=36°,直接写出图中除△ABC与△ADE外所有的等腰三角形.7.(2019秋•龙岩期末)如图,AB=AC,AE=EC=CD,∠A=60°,若EF=2,则DF=()A.3B.4C.5D.6 8.(2006•烟台)如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于()A.25°B.30°C.45°D.60°9.(2020秋•慈溪市期中)已知:如图,AB=BC,∠A=∠C.求证:AD=CD.10.(2014秋•青山区期中)已知:如图,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF.求证:△DEF是等边三角形.11.(2018秋•六合区期中)如图,△ABC为等边三角形,BD平分∠ABC交AC于点D,DE ∥BC交AB于点E.(1)求证:△ADE是等边三角形.(2)求证:AE=AB.12.(2017•裕华区校级模拟)已知,如图,△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.13.(2012秋•姜堰市校级期中)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC =α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)△COD是什么三角形?说明理由;(2)若AO=n2+1,AD=n2﹣1,OD=2n(n为大于1的整数),求α的度数;(3)当α为多少度时,△AOD是等腰三角形?14.(2000•内蒙古)如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连接CE,DE.求证:EC=ED.15.(2020秋•连山区期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=()A.2B.4C.6D.816.(2020秋•肇州县期末)如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AE=6cm,则AC=()A.6cm B.5cm C.4cm D.3cm 17.(2020秋•朝阳县期末)如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为()A.4.5B.5C.5.5D.618.(2020秋•抚顺县期末)右图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,则DE长为.19.(2020秋•宽城区期中)如图,△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AC于D,交AB于E,CD=2,则AD等于()A.10B.8C.6D.420.(2020秋•无棣县期中)如图,在△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是()A.4B.4.5C.5D.721.(2020秋•云县期中)如图,点D是AB的中点,DE⊥AC,AB=7.2,∠A=30°,则DE=()A.1.8B.2.4C.3.6D.4.822.(2020秋•北碚区校级期中)如图,已知∠AOB=60°,P在边OA上,OP=8,点M,N在边OB上,PM=PN,若MN=5,则ON的长度是()A.9B.6.5C.6D.5.523.(2020秋•天宁区校级期中)如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P 在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有()A.6个B.5个C.4个D.3个24.(2020秋•连江县期中)如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE ⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是()A.2﹣x B.3﹣x C.1D.2+x 25.(2020秋•赣榆区期中)如图,在△ABC中,AB=AC=6,∠BAC=120°,AD是△ABC 的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长是()A.5B.2C.4D.326.(2019秋•勃利县期末)如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D 作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有()①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.A.①②③B.①②④C.②③④D.①②③④27.(2019春•秦淮区期末)如图,△ABC是等边三角形,P是三角形内任意一点,D、E、F分别是AC、AB、BC边上的三点,且PF∥AB,PD∥BC,PE∥AC.若PF+PD+PE=a,则△ABC的边长为()A.a B.a C.a D.a28.下列说法中,正确的个数是()①三条边都相等的三角形是等边三角形;②有一个角为60°的等腰三角形是等边三角形;③有两个角为60°的三角形是等边三角形;④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形A.1个B.2个C.3个D.4个29.(2020•和平区三模)如图,在边长为2的等边三角形ABC中,D为边BC上一点,且BD=CD.点E,F分别在边AB,AC上,且∠EDF=90°,M为边EF的中点,连接CM交DF于点N.若DF∥AB,则CM的长为()A.B.C.D.30.(2020秋•天心区期中)下列说法错误的是()A.有一个角是60°的等腰三角形是等边三角形B.如果一个三角形有两个角相等,那么这两个角所对的边相等C.等腰三角形的角平分线,中线,高相互重合D.三个角都相等的三角形是等边三角形.31.(2019春•杏花岭区校级期中)关于等边三角形,下列说法中错误的是()A.等边三角形中,各边都相等B.等腰三角形是特殊的等边三角形C.两个角都等于60°的三角形是等边三角形D.有一个角为60°的等腰三角形是等边三角形32.(2019•城步县模拟)一个六边形的六个内角都是120°(如图),连续四条边的长依次为1,3,3,2,则这个六边形的周长是()A.13B.14C.15D.16 33.(2018•柳州一模)如图,在四边形ABCD中,∠A=∠B=60°,∠D=90°,AB=2,则CD长的取值范围是()A.<CD<B.CD>2C.1<CD<2D.0<CD<34.(2018秋•罗庄区期中)如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=()A.30°B.45°C.60°D.90°参考答案与试题解析1.【考点】线段垂直平分线的性质;等腰三角形的性质.【专题】线段、角、相交线与平行线;三角形;推理能力.【分析】根据等腰三角形的性质即可判断A;根据三角形的高、角平分线、中线的定义和等腰三角形的性质即可判断B;根据角平分线的性质即可判断C;根据三角形的外角性质和等腰三角形的性质即可判断D.【解答】解:A.等腰三角形的两底角相等,故本选项不符合题意;B.等腰三角形的两个底角的高、角平分线和中线不一定互相重合,故本选项符合题意;C.过O作OM⊥AB于M,OQ⊥AC于Q,ON⊥BC于N,∵O是∠ABC和∠ACB的角平分线的交点,∴OM=ON,ON=OQ,∴OM=ON=OQ,即三角形的两边的垂直平分线的交点到三个顶点的距离相等,故本选项不符合题意;D.∵AB=AC,∴∠B=∠C,∵∠EAC=∠B+∠C,∴∠EAC=2∠B,即等腰三角形顶角的外角是其底角的2倍,故本选项不符合题意;故选:B.【点评】本题考查了角平分线的性质,等腰三角形的性质,三角形的外角性质等知识点,能灵活运用知识点进行推理是解此题的关键.2.【考点】三角形三边关系;等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】分两种情况讨论:当4cm为腰长时,当4cm为底边时,分别判断是否符合三角形三边关系即可.【解答】解:①若4cm是腰长,则底边长为:20﹣4﹣4=12(cm),∵4+4<12,不能组成三角形,舍去;②若4cm是底边长,则腰长为:=6.5(cm).则腰长为6.5cm.故选:B.【点评】此题考查等腰三角形的性质与三角形的三边关系.此题难度不大,注意掌握分类讨论思想的应用是解此题的关键.3.【考点】等腰三角形的判定.【专题】三角形.【分析】根据等腰三角形的性质,利用4作为腰或底边长,得出符合题意的图形即可.【解答】解:如图所示:当AC=CD,AB=BG,AF=CF,AE=BE时,都能得到符合题意的等腰三角形(AD,AE,AF,AG分别为分割线).故选:B.【点评】此题主要考查了等腰三角形的判定以及应用设计与作图等知识,正确利用图形分类讨论得出是解题关键.4.【考点】等腰三角形的性质.【专题】等腰三角形与直角三角形.【分析】可知等腰三角形的两底角相等,则可求得底角的度数.从而可求解.【解答】解:①当∠A为顶角时,等腰三角形两底角的度数为:=50°∴特征值k==②当∠A为底角时,顶角的度数为:180°﹣80°﹣80°=20°∴特征值k==综上所述,特征值k为或故答案为或【点评】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意到本题中,已知∠A的度数,要分∠A是顶角和底角两种情况,以免造成答案的遗漏.5.【考点】非负数的性质:绝对值;非负数的性质:算术平方根;三角形三边关系;等腰三角形的性质.【专题】压轴题;分类讨论.【分析】先根据非负数的性质列式求出x、y的值,再分4是腰长与底边两种情况讨论求解.【解答】解:根据题意得,x﹣4=0,y﹣8=0,解得x=4,y=8,①4是腰长时,三角形的三边分别为4、4、8,∵4+4=8,∴不能组成三角形,②4是底边时,三角形的三边分别为4、8、8,能组成三角形,周长=4+8+8=20,所以,三角形的周长为20.故答案为:20.【点评】本题考查了等腰三角形的性质,绝对值非负数,算术平方根非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出x、y的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.6.【考点】等腰三角形的判定.【专题】几何图形.【分析】(1)首先过点A作AF⊥BC于点F,由AD=AE,根据三线合一的性质,可得DF=EF,又由BD=CE,可得BF=CF,然后由线段垂直平分线的性质,可证得AB=AC.(2)根据等腰三角形的判定解答即可.【解答】证明:(1)过点A作AF⊥BC于点F,∵AD=AE,∴DF=EF,∵BD=CE,∴BF=CF,∴AB=AC.(2)∵∠B=∠BAD,∠C=∠EAC,∠BAE=∠BEA,∠ADC=∠DAC,∴除△ABC与△ADE外所有的等腰三角形为:△ABD、△AEC、△ABE、△ADC,【点评】此题考查了等腰三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.7.【考点】等边三角形的判定与性质.【专题】数形结合;三角形;等腰三角形与直角三角形;运算能力;推理能力.【分析】过点E作EG⊥BC,交BC于点G,先证明△ABC是等边三角形,再证明∠AFE =90°,然后利用等腰三角形的“三线合一”性质及角平分线的性质定理求得EG的长,随后利用含30度角的直角三角形的性质求得DE的长,最后将EF与DE相加即可.【解答】解:如图,过点E作EG⊥BC,交BC于点G∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∴∠AEF=30°,∴∠AFE=90°,即EF⊥AB,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴EG=EF=2,在Rt△DEG中,DE=2EG=4,∴DF=EF+DE=2+4=6;方法二、∵AB=AC,∠A=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵EC=CD,∴∠CED=∠CDE=∠ACB=30°,∵△ABC是等边三角形,AE=CE,∴BE平分∠ABC,∴∠ABE=∠CBE=30°=∠CDE,∴BE=DE,∠BFD=90°,∴BE=2EF=4=DE,∴DF=DE+EF=6;故选:D.【点评】本题考查了等边三角形的判定与性质、等腰三角形的“三线合一”性质及含30度角的直角三角形的性质,熟练掌握相关性质及定理是解题的关键.8.【考点】等边三角形的判定与性质.【分析】先根据图形折叠的性质得出BC=CE,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE=BE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.【解答】解:△ABC沿CD折叠B与E重合,则BC=CE,∵E为AB中点,△ABC是直角三角形,∴CE=BE=AE,∴△BEC是等边三角形.∴∠B=60°,∴∠A=30°,故选:B.【点评】考查直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力.9.【考点】等腰三角形的判定与性质.【专题】几何图形.【分析】连接AC,根据等边对等角得到∠BAC=∠BCA,因为∠A=∠C,则可以得到∠CAD=∠ACD,根据等角对等边可得到AD=DC.【解答】证明:连接AC,∵AB=BC,∴∠BAC=∠BCA.∵∠BAD=∠BCD,∴∠CAD=∠ACD.∴AD=CD.【点评】重点考查了等腰三角形的判定方法,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.10.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.【解答】证明:∵△ABC是等边三角形,∴AB=BC=AC,∵AD=BE=CF,∴AF=BD,在△ADF和△BED中,,∴△ADF≌△BED(SAS),∴DF=DE,同理DE=EF,∴DE=DF=EF.∴△DEF是等边三角形.【点评】此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.11.【考点】平行线的性质;等腰三角形的判定与性质;等边三角形的判定与性质.【专题】几何图形.【分析】(1)根据等边三角形的性质和平行线的性质证明即可.(2)根据等边三角形的性质解答即可.【解答】证明:(1)∵△ABC为等边三角形,∴∠A=∠ABC=∠C=60°.∵DE∥BC,∴∠AED=∠ABC=60°,∠ADE=∠C=60°.∴△ADE是等边三角形.(2)∵△ABC为等边三角形,∴AB=BC=AC.∵BD平分∠ABC,∴AD=AC.∵△ADE是等边三角形,∴AE=AD.∴AE=AB.【点评】此题考查等边三角形的判定和性质,关键是根据等边三角形的性质和平行线的性质解答.12.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题.【分析】根据等边△ABC中AD=BE=CF,证得△ADE≌△BEF≌△CFD即可得出△DEF 是等边三角形.【解答】解:∵△ABC为等边三角形,且AD=BE=CF,∴AE=BF=CD,又∵∠A=∠B=∠C=60°,∴△ADE≌△BEF≌△CFD(SAS),∴DE=EF=FD,∴△DEF是等边三角形.【点评】本题主要考查了等边三角形的判定与性质和全等三角形判定,根据已知得出△ADE≌△BEF≌△CFD是解答此题的关键.13.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】分类讨论.【分析】(1)根据旋转的性质可得CO=CD,∠OCD=60°,根据有一个角是60°的等腰三角形是等边三角形解答;(2)利用勾股定理逆定理判定△AOD是直角三角形,并且∠ADO=90°,从而求出∠ADC=150°,再根据旋转变换只改变图形的位置不改变图形的形状与大小可得α=∠ADC;(3)根据周角为360°用α表示出∠AOD,再根据旋转的性质表示出∠ADO,然后利用三角形的内角和定理表示出∠DAO,再分∠AOD=∠ADO,∠AOD=∠DAO,∠ADO=∠DAO三种情况讨论求解.【解答】解:(1)△COD是等边三角形.理由如下:∵△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,∴△COD是等边三角形;(2)∵AD2+OD2=(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2=AO2,∴△AOD是直角三角形,且∠ADO=90°,∵△COD是等边三角形,∴∠CDO=60°,∴∠ADC=∠ADO+∠CDO=90°+60°=150°,根据旋转的性质,α=∠ADC=150;(3)∵α=∠ADC,∠CDO=60°,∴∠ADO=α﹣60°,又∵∠AOD=360°﹣110°﹣α﹣60°=190°﹣α,∴∠DAO=180°﹣(190°﹣α)﹣(α﹣60°)=180°﹣190°+α﹣α+60°=50°,∵△AOD是等腰三角形,∴①∠AOD=∠ADO时,190°﹣α=α﹣60°,解得α=125°,②∠AOD=∠DAO时,190°﹣α=50°,解得α=140°,③∠ADO=∠DAO时,α﹣60°=50°,解得α=110°,综上所述,α为125°或140°或110°时,△AOD是等腰三角形.【点评】本题考查了等边三角形的判定与性质,旋转变换只改变图形的位置不改变图形的形状与大小的性质,勾股定理逆定理,等腰三角形的性质,(3)用α表示出△AOD的各个内角是解题的关键,注意要分情况讨论.14.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【专题】证明题;压轴题.【分析】首先延长BD至F,使DF=BC,连接EF,得出△BEF为等边三角形,进而求出△ECB≌△EDF,从而得出EC=DE.【解答】证明:延长BD至F,使DF=BC,连接EF,∵AE=BD,△ABC为等边三角形,∴BE=BF,∠B=60°,∴△BEF为等边三角形,∴∠F=60°,在△ECB和△EDF中∴△ECB≌△EDF(SAS),∴EC=ED.【点评】此题主要考查了等边三角形的性质与判定以及全等三角形的判定等知识,作出辅助线是解决问题的关键.15.【考点】含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】根据同角的余角相等求出∠BCD=∠A=60°,再根据30°角所对的直角边等于斜边的一半求出AC、AB的长,然后根据BD=AB﹣AD计算即可得解.【解答】解:∵∠ACB=90°,CD⊥AB,∴∠BCD+∠ACD=90°,∠A+∠ACD=90°,∴∠BCD=∠A=60°,∴∠ACD=∠B=30°,∵AD=2,∴AC=2AD=4,∴AB=2AC=8,∴BD=AB﹣AD=8﹣2=6.故选:C.【点评】本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.16.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形.【分析】根据线段垂直平分线的性质得到EB=EA,根据等腰三角形的性质得到∠EAB=∠B=15°,根据三角形的外角的性质求出∠AEC=30°,根据直角三角形的性质计算.【解答】解:∵DE垂直平分AB,∴EB=EA,∴∠EAB=∠B=15°,∴∠AEC=30°,∴AC=AE=3(cm),故选:D.【点评】本题考查的是线段垂直平分线的性质,直角三角形的性质,在直角三角形中,30°角所对的直角边等于斜边的一半.17.【考点】等腰三角形的性质;含30度角的直角三角形.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°.∵DF∥AB,∴∠F=∠BAE=30°.∴∠DAF=∠F=30°,∴AD=DF.∵AB=11,∠B=30°,∴AD=5.5,∴DF=5.5故选:C.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.18.【考点】含30度角的直角三角形.【专题】推理填空题.【分析】根据直角三角形的性质求出BC,根据三角形中位线定理计算即可.【解答】解:∵∠A=30°,BC⊥AC,∴BC=AB=3.7,∵DE⊥AC,BC⊥AC,∴DE∥BC,∵点D是斜梁AB的中点,∴DE=BC=1.85m,故答案为:1.85m.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.19.【考点】线段垂直平分线的性质;含30度角的直角三角形.【专题】计算题;等腰三角形与直角三角形;运算能力;推理能力.【分析】先由直角三角形的性质求出∠ABC的度数,由AB的垂直平分线交AC于D,交AB于E,垂足为E,可得BD=AD,由∠A=30°可知∠ABD=30°,故可得出∠DBC =30°,根据CD=2可得出BD的长,进而得出AD的长.【解答】解:连接BD,∵在△ABC中,∠C=90°,∠A=30°,∴∠ABC=60°.∵AB的垂直平分线交AC于D,交AB于E,∴AD=BD,DE⊥AB,∴∠ABD=∠A=30°,∴∠DBC=30°,∵CD=2,∴BD=2CD=4,∴AD=4.故选:D.【点评】此题考查了线段垂直平分线的性质以及含30°角的直角三角形的性质.熟练掌握直角三角形的性质是解题的关键.20.【考点】垂线段最短;含30度角的直角三角形.【专题】解直角三角形及其应用;推理能力.【分析】在Rt△ABC中,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”可求出AB的长,由点P是BC边上一动点结合AC,AB的长,即可得出AP长的取值范围,再对照四个选项即可得出结论.【解答】解:在Rt△ABC中,∠C=90°,∠B=30°,AC=3,∴AB=2AC=6.∵点P是BC边上一动点,∴AC≤AP≤AB,即3≤AP≤6.故选:D.【点评】本题考查了含30度角的直角三角形以及垂线段最短,通过解含30度角的直角三角形,求出AB的长是解题的关键.21.【考点】含30度角的直角三角形.【专题】等腰三角形与直角三角形;运算能力.【分析】求出AD的长,再根据含30°角的直角三角形的性质得出DE=AD,即可求出答案.【解答】解:∵点D是AB的中点,AB=7.2,∴AD=AB=3.6,∵DE⊥AC,∴∠DEA=90°,∵∠A=30°,∴DE=AD=1.8,故选:A.【点评】本题考查了含30°角的直角三角形的性质,能根据含30°角的直角三角形的性质得出DE=AD是解此题的关键.22.【考点】等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】过P作PC⊥MN于C,先由等腰三角形的性质得CM=CN=2.5,再由含30°角的直角三角形的性质求出OC的长,然后由OC+CM求出ON的长即可.【解答】解:过P作PC⊥MN于C,如图所示:∵PM=PN,MN=5,∴CM=NC=MN=2.5,在Rt△OPC中,∠AOB=60°,∴∠OPC=30°,∴OC=OP=4,则ON=OC+CM=4+2.5=6.5,故选:B.【点评】本题考查的是含30°角的直角三角形的性质、等腰三角形的性质等知识;熟练掌握含30°角的直角三角形的性质和等腰三角形的性质是解题的关键.23.【考点】三角形内角和定理;等腰三角形的判定;含30度角的直角三角形.【专题】等腰三角形与直角三角形;几何直观.【分析】根据等腰三角形的判定和含30°的直角三角形的性质解答即可.【解答】解:如图所示:以B为圆心,BC长为半径画弧,交直线m于点P4,P2,以A为圆心,AC长为半径画弧,交直线m于点P1,P3,边AC和BC的垂直平分线都交于点P3位置,因此出现等腰三角形的点P的位置有4个,故选:C.【点评】此题考查等腰三角形的判定,关键是根据等腰三角形的判定和含30°的直角三角形的性质解答.24.【考点】列代数式;等边三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】利用等边三角形的性质可得AB=BC=AC=4,∠B=∠C=60°,再利用含30度角的直角三角形的性质进行计算即可.【解答】解:∵△ABC是等边三角形,∴AB=BC=AC=4,∠B=∠C=60°,∵PD⊥BC,DE⊥AC,∴BD=PB,CE=CD,∵P A=x,∴BP=4﹣x,∴BD=PB=2﹣x,∴CD=4﹣(2﹣x)=2+x,∴CE=1+x,∴AE=4﹣(1+x)=3﹣x,故选:B.【点评】此题主要考查了等边三角形的性质和含30度角的直角三角形的性质,关键是掌握在直角三角形中,30°角所对的直角边等于斜边的一半.25.【考点】平行线的性质;等腰三角形的性质;含30度角的直角三角形.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形三线合一的性质可得到AD⊥BC,∠BAD=∠CAD,从而可得到∠BAD=60°,∠ADB=90°,再根据角平分线的性质即可得到∠DAE=∠EAB=30°,从而可推出AD=DF,根据直角三角形30度角的性质即可求得AD的长,即得到了DF 的长.【解答】解:∵△ABC是等腰三角形,D为底边的中点,∴AD⊥BC,∠BAD=∠CAD,∵∠BAC=120°,∴∠BAD=60°,∠ADB=90°,∵AE是∠BAD的角平分线,∴∠DAE=∠EAB=30°,∵DF∥AB,∴∠F=∠BAE=30°,∴∠DAF=∠F=30°,∴AD=DF,∵AB=6,∠B=30°,∴AD=AB=3,∴DF=3,故选:D.【点评】本题考查了含30°角的直角三角形,等腰三角形的判定与性质,平行线的性质等知识点,能求出AD=DF是解此题的关键.26.【考点】等边三角形的判定与性质.【专题】等腰三角形与直角三角形.【分析】由在△ABC中,∠ACB=90°,DE⊥AB,易证得∠DCA=∠DAC,继而可得①∠DCB=∠B正确;由①可证得AD=BD=CD,即可得②CD=AB正确;易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠DCB=90°,∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B;故①正确;∴CD=BD,∵AD=CD,∴CD=AB;故②正确;∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形;故③错误;∵若∠E=30°,∴∠A=60°,∴△ACD是等边三角形,∴∠ADC=60°,∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°,∴CF=DF,∴DE=EF+DF=EF+CF.故④正确.故选:B.【点评】此题考查了等腰三角形的性质与判定以及直角三角形的性质.注意证得D是AB 的中点是解此题的关键.27.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;多边形与平行四边形.【分析】延长EP交BC于点G,延长FP交AC于点H,证出四边形AEPH、四边形PDCG 均为平行四边形,得出PE=AH,PG=CD.证出△FGP和△HPD也是等边三角形,得出PF=PG=CD,PD=DH,得出PE+PD+PF=AH+DH+CD=AC即可.【解答】解:延长EP交BC于点G,延长FP交AC于点H,如图所示:∵PF∥AB,PD∥BC,PE∥AC,∴四边形AEPH、四边形PDCG均为平行四边形,∴PE=AH,PG=CD.又∵△ABC为等边三角形,∴△FGP和△HPD也是等边三角形,∴PF=PG=CD,PD=DH,∴PE+PD+PF=AH+DH+CD=AC,∴AC=a;故选:D.【点评】本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.28.【考点】等腰三角形的判定与性质;等边三角形的判定与性质.【专题】三角形.【分析】根据等边三角形的判定、轴对称的性质即可判断;【解答】解:①三条边都相等的三角形是等边三角形;正确.②有一个角为60°的等腰三角形是等边三角形;正确.③有两个角为60°的三角形是等边三角形;正确.④底角的角平分线所在的直线是这等腰三角形的对称轴,则这个三角形是等边三角形;正确.故选:D.【点评】本题考查等边三角形的判定和性质、等腰三角形的判定和性质、轴对称等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.29.【考点】平行线的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等边三角形边长为2,在Rt△BDE中求得DE的长,再根据CM垂直平分DF,在Rt△CDN中求得CN,最后根据线段和可得CM的长.【解答】解:∵等边三角形边长为2,BD=CD,∴BD=,CD=,∵等边三角形ABC中,DF∥AB,∴∠FDC=∠B=60°,∵∠EDF=90°,∴∠BDE=30°,∴DE⊥BE,∴BE=BD=,DE=,如图,连接DM,则Rt△DEF中,DM=EF=FM,∵∠FDC=∠FCD=60°,∴△CDF是等边三角形,∴CD=CF=,∴CM垂直平分DF,∴∠DCN=30°,DN=FN,∴Rt△CDN中,DN=,CN=,∵M为EF的中点,∴MN=DE=,∴CM=CN+MN=+=,故选:C.【点评】本题主要考查了三角形的综合应用,解决问题的关键是掌握等边三角形的性质、平行线的性质、线段垂直平分线的判定等.熟练掌握这些性质是解题的关键.30.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.【分析】根据等腰三角形的性质和等边三角形的性质和判定逐个进行分析判断,即可得到答案.【解答】解:A.有一个角为60°的等腰三角形是等边三角形,故本选项不合题意;B.如果一个三角形有两个角相等,那么这两个角所对的边相等,故本选项不合题意;C.等腰三角形顶角的角平分线,底边的中线,高相互重合,说法错误,故本选项符合题意;D.三个角都相等的三角形是等边三角形,故本选项不合题意;故选:C.【点评】本题考查了等边三角形的判定和性质,等腰三角形的性质,熟练掌握等边三角形的判定和性质定理是解题的关键.31.【考点】等腰三角形的性质;等边三角形的判定与性质.【专题】等腰三角形与直角三角形;推理能力.。
等腰三角形与等边三角形专项练习(精品测试卷)(2022年最新)
6.若式子 有意义,则一次函数 的图象可能是()
A. B. C. D.
7.要使直线y=(2m-3)x+(3n+1)的图象经过一、二、四象限,则m与n的取值为( )
A.m> ,n> B.m>3,n>-3
C.m< ,n< D.m< ,n>
8.为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,那么11只饭碗摞起来的高度更接近()
13.如果直线y=2x+m不经过第二象限,那么实数m的取值范围是___.
14.表格描述的是y与x之间的函数关系:
x
…
-2
0
2
4
…
y=kx+b
…
3
-1
m
n
…
则m与n的大小关系是____________.
15.如图,直线y=kx+b经过A(-2,-1)和B(-3,0)两点,则不等式-3≤-2x-5<kx+b的解集是_______________.
18.(2020秋•杨浦区校级期中)如图,AD是△ABC的高,∠B=2∠C,BD=5,BC=25,求AB的长.
19.(2020秋•朝阳区校级期中)如图,在△ABC中,∠B=2∠C,AD⊥BC,垂足为D,判断AB、CD和BD这三条线段的数量关系(用等式表示),并证明.
20.(2020春•延庆区期中)已知:在△ABC中,AB=AC,DE∥AB,DF∥AC.
25.(2020秋•慈溪市期中)已知:如图,AB=BC,∠A=∠C.求证:AD=CD.
26.(2020秋•泰兴市期中)已知:如图,AB=AD,∠ABC=∠ADC.求证:BC=DC.
27.(2020春•渭南期中)已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
