湖北省荆州中学高二上学期期末考试数学(文)Word版含答案
荆州中学高二数学(文)上学期期末试卷及答案

荆州中学高二上学期数学(文科)期末试卷姓名:_________班级:________ 得分:________一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知椭圆2214y x +=,则其焦点的坐标为( ) A.()3,0± B. ()0,3± C. ()3,0± D. ()0,3± 2.已知变量x 与变量y 负相关,且由观测数据计算得到样本的平均数4, 6.5x y ==,则由该观测数据算得的线性回归方程可能是 ( )A .2 1.5y x =-B .0.8 3.3y x =+C .214.5y x =-+D .0.69.1y x =-+ 3.下列说法不正确...的是( ) A .若“p q ∨”为假命题,则,p q 均为假命题 B .“1x =”是“1x ≥”的充分不必要条件 C .“1sin 2x =”的必要不充分条件是“6x π=” D .若命题p :200,0x R x ∃∈≥,则命题p ⌝:2,0x R x ∀∈<4 .如右图所示,程序框图(算法流程图)的输出结果是( )A .16B .2524C .34D .11125. 从3台甲型彩电和2台乙型彩电中任选两台,其中两种品牌的彩电都齐全的概率是( )A.310B.15C.35D.45共有学生2000名,各年级男、女生人数如下表:6. 某校如果从全校学生中随机抽取一名学生,抽到二年级女生的概率为0.19.现用分层抽样的方法在全校学生中分年级抽取64名学生参加某项活动,则应在三年级中抽取的学生人数为( )A . 24B . 18C . 12D . 16 7.已知()()1ln f x f x x '=+,则()f e =( ) A. 1e +B. eC. 2e +D. 38.某三棱锥的三视图如右图所示,则该三棱锥的表面积是( ) A.2+ 5B.4+ 5C.2+2 5D.59. 过抛物线24y x =的焦点作直线交抛物线于,A B 两点,线段AB 的中点的横坐标为3,则 线段AB 的长为( )A .5B . 8C . 7D . 9 10. 曲线y =x 3-2x +1在点(1,0)处的切线方程为( )A .y =x -1B .y =-x +1C .y =2x -2D .y =-2x +2 11.如图,四棱锥S-ABCD 的底面为正方形,SD ⊥底面ABCD , 则下列结论中不正确...的是( ) A .AC ⊥SBB .AB ∥平面SCDC .AB 与SC 所成的角等于DC 与SA 所成的角D .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角12.F 是双曲线2222:1(0,0)x y C a b a b-=>>的右焦点,过点F 向C 的一条渐近线引垂线,垂足为A ,交另一条渐近线于B ,若2AF FB =,则双曲线C 的离心率为( )A. 2B. 2C.233D.143二、填空题:本大题共4小题,每小题5分,共20分. 请将答案填在答题卡对应题号.......的位置上.答错位置,书写不清,模棱两可均不得分.13.已知椭圆x 210-m +y 2m -2=1,长轴在y 轴上,若焦距为4,则m =________.14.下列各数)9(85 、)4(1000 、)2(111111中最小的数是___________.15.已知函数()331f x x x =-+,则2()2f '= . 16.已知函数()1f x kx =+,其中实数k 随机选自区间[2,1]-,对[0,1],()0x f x ∀∈≥的概率是 .三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分) 设a 是实数,对函数22()233f x x x a a =-++-和抛物线C :24y x =,有如下两个命题::p 函数()f x 的最小值小于0;:q 抛物线24y x =上的动点2(,)4a M a 到焦点F 的距离大于2. 已知“p ⌝”和“p q ∧”都为假命题,求实数a 的取值范围.18.(本小题满分12分)已知圆C 过点()1,4A ,()3,2B ,且圆心C 在直线30x y +-=上. (1)求圆C 的方程;(2)若点(),P x y 是圆C 上的动点,z x y =+,求z 的最大值.19. 本小题满分12分)某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:(1)求第四个小组的频率以及频率分布直方图中第四个小矩形的高; (2)估计这次考试的及格率(60分及60分以上为及格)和平均分;20. (本题满分12分)已知四棱柱1111ABCD A B C D -的底面ABCD 是边长为2的菱形, ACBD O =,123AA =,1BD AA ⊥,160BAD A AC ∠=∠=, 点M 是棱AA 1的中点.(1) 求证:A 1O ⊥平面ABCD ;(2) 求三棱锥AMD B -的体积.21.(本小题满分12分)设椭圆2222:1y x M a b+=(0a b >>)经过点(1, 2)P ,其离心率与双曲线122=-y x 的离心率互为倒数. (Ⅰ)求椭圆M 的方程;(Ⅱ) 动直线:2l y x m =+交椭圆M 于A B 、两点,求PAB ∆面积 的最大值.22.(本小题满分12分)已知平面直角坐标系xoy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线1C 方程为2sin ρθ=;2C 的参数方程为11232x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).(Ⅰ)写出曲线1C 的直角坐标方程和2C 的普通方程;(Ⅱ)设点P 为曲线1C 上的任意一点,求点P 到曲线2C 距离的取值范围.荆州中学2016~2017学年度上学期期 末 考 试 卷年级:高二 科目:数学(文科) 命题人:陈静 审题人:鄢先进参考答案一、选择题(本大题共12小题,每小题5分,共60分)题号 1234 5 67 8 9 10 11 12 答案D C C DCD A C B ACC二、填空题(本大题共4小题,每小题5分,共20分.) 13. 8 14. )2(111111 15. 32- 16. 23三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17. p ⌝和p q ∧都是假命题,p ∴为真命题,q 为假命题. ………………2分2222()233(1)34f x x x a a x a a =-++-=-++-,2min ()340f x a a ∴=+-<,所以,41a -<<; ………………6分又抛物线24y x =的准线为1x =-,q 为假命题,2124a MF ∴=+≤,22a ∴-≤≤. ………………10分 故所求a 的取值范围为[2,1)-. ………………12分18.解答:(1)设圆心坐标为(a,b),则222222(1)(3)(3)(2)30a b r a b r a b ⎧-+-=⎪-+-=⎨⎪+-=⎩解得:1,2,2a b r ===,故圆的方程为:4)2()1(22=-+-y x ………………6分(2)令z x y =+,即y x z =-+,当这条直线与圆相切时,它在y 轴上的截距最大或最小,可求得最大值为:223+ ………………12分19.解答:(1)第四小组分数在[70,80)内的频率为:1-(0.005+0.01+0.015+0.015+0.025)⨯10=0.30 则第四个小矩形的高为=0.03………6分(2)由题意60分以上的各组频率和为:(0.015+0.03+0.025+0.005)×10=0.75, 故这次考试的及格率约为75%, 由45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,得本次考试中的平均分约为71: ………12分 20.(1) 11BD AA BD AC BD A AC ⊥⊥⊥,得面于是1BD A O ⊥, AC BD O ⋂= 菱形 ……6分 (2)体积转换法:因为⊥O A 1平面ABCD , M 为O A 1的中点, 所以M 到平面ABCD 的距离为23211=O A , 三角形ABD 的面积为3, 23==--ABD M AMD B V V ………12分 21. (Ⅰ2,则椭圆的离心率为22c e a ==,由已知,得22222221122a b a b c c a+=⎪⎪=+⎨⎪⎪=⎪⎩,∴⎪⎩⎪⎨⎧===222b c a ,所求椭圆M 的方程为 22142y x +=. …………………4分(Ⅱ)由⎪⎩⎪⎨⎧=++=142222y x mx y ,得2242240x mx m ++-=,由0)4(16)22(22>--=∆m m 得,2222m -<<,设1122(,),(,)A x y B x y ,1222x x m ∴+=-,21244m x x -= . ∴2121212||12||3()4AB x x x x x x =+-=⋅+-2221343422m m m =⋅-+=-. 又P 到AB 的距离为3||m d =. 则2222211||11||34(4)(8)22222322ABCm m m S AB d m m m ∆==-=-=- …………………10分221(8)2222ABCm m S ∆+-∴≤⋅= 当且仅当2(22,22)m =±∈-取等号.∴max ()2ABC S ∆=. …………………12分 22.解:(I )曲线1C 方程为2sin ρθ=,可得22sin ρρθ=,可得222x y y += ∴1C 的直角坐标方程:()2211x y +-=,2C 的参数方程为11232x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩,消去参数t 可得:2C 330x y -+=.…(5分)(II )由(I )知,1C 为以(0,1)为圆心,r=1为半径的圆,1C 的圆心(0,1)到C2的距离为3311231d-==<+,则1C 与2C 相交,P 到曲线2C 距离最小值为0,最大值为312dr ++=, 则点P 到曲线2C 距离的取值范围为31[0,]2+.……(10分)(完)。
湖北省荆州中学-度高二数学上学期期末考试卷(文科)

湖北省荆州中学2008-2009学年度高二数学上学期期末考试卷(文科)一、选择题(本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合要求的.)1. 在平面直角坐标系中,直线10x +=的倾斜角为( )A .56π B . 3π C . 6π D .23π2. 过点(2,4)M -作圆C :25)1()2(22=-+-y x 的切线l ,直线023:1=++a y ax l 与l 平行,则1l 与l 之间的距离是是( )A .512 B . 528 C .58 D .52 3. 若不等式组220x y x y y x y a-0⎧⎪+⎪⎨⎪⎪+⎩≥,≤,≥,≤表示的平面区域是一个三角形,则a 的取值范围是( )A .43a ≥B .01a <≤C .413a ≤≤D .01a <≤或43a ≥ 4. 已知椭圆171622=+y x 上一点P 到左准线距离为8,则点P 到右焦点的距离是( ) A .27 B .2 C .213 D .6 5. 已知12,F F 为平面内两个定点,126FF =,动点M 满足126MF MF -=,则动点M 的轨迹是( )A .椭圆B .双曲线C . 抛物D .线两条射线6. 若抛物线22(0)y px p =>上横坐标为6的点到焦点的距离等于8,则焦点到准线的距离是( )A .8B .4C .6D .27. 设坐标原点为O ,抛物线24y x =与过焦点的直线交于,A B 两点,则,OA OB 的夹角为A .锐角B .直角C . 钝角D .无法确定8. 已知AB 为过双曲线22221x y a b-=的右焦点F 的弦,则以AB 为直径的圆与双曲线右准线的位置关系是( )A .相离B .相切C .相交D .不确定9. 如图,,,,,,A B C D E F 分别为正方体相应棱的中点,对于直线,,AB CD EF ,下列结论正确的是( )A .AB CD B .CD 与EF 异面C .AB 与CD 相交 D .AB 与EF 异面10. 下列命题中,正确的是( ) A .经过不同的三点有且只有一个平面 B .平行于同一平面的两条直线互相平行C .分别和两条异面直线都相交的两条直线是异面直线D .若一个角的两边和另一个角的两边分别平行,则这两个角相等或互补二、填空题(本大题共5小题,每小题5分,满分25分) 11.离心率e =5x =的椭圆的标准方程是 . 12.过点(1,4)P 作直线与两坐标轴的正半轴相交,当直线与坐标轴的两截距之和最小时,该直线的方程为 .13.点(3,1)和(4,6)-在直线320x y a -+=的两侧,则a 的取值范围是 .14.已知O 的方程是2220x y +-=,'O 的方程是228100x y x +-+=,由动点P 向O和'O 所引的切线长相等,则运点P 的轨迹方程是__________________.15.给出下列四个命题①若动点(,)M x yx y =+,则动点M 的轨迹是双曲线;AD CB②经过两直线280x y +-=和210x y -+=的交点且与向量(3,4)垂直的直线方程为4360x y --=;③若直线1y ax =-与焦点在x 轴上的椭圆2215x y m+=总有公共点,则15m ≤<; ④若不等式|2|||x x a a -+-≥在R 上恒成立,则a 的最大值为1. 其中正确命题的序号是 .三、解答题(本大题共6小题,满分75分.解答须写出文字说明、证明过程和演算步骤.) 16.(本小题满分12分)已知两直线12:40,:(1)0l ax by l a x y b -+=-++=,求分别满足下列条件的,a b 的值.(Ⅰ)直线1l 过点(3,1)--,并且直线1l 与直线2l 垂直; (Ⅱ)直线1l 与直线2l 平行,并且坐标原点到1l 、2l 的距离相等.17.(本小题满分12分)在ABC ∆中,点(1,5),(5,5),(6,2)A B C --. (Ⅰ)分别求AC 边上的中线、BC 边上的高线所在的直线的方程; (Ⅱ)求ABC ∆的外接圆的方程.18.(本小题满分12分)已知直线l 的方程为4521+=x y ,抛物线C :px y 22=(p >0)的顶点关于直线l 的对称点在该抛物线的准线上.(Ⅰ)求抛物线C 的方程;(Ⅱ)是否存在实数k ,使得直线l :2-=kx y 与抛物线C 交于A ,B 两点,且以AB 为直径的圆经过坐标原点,若存在求出直线l 的方程,若不存在,说明理由.19.(本小题满分12分)已知双曲线22221(0,0)x y a b a b -=>>的右焦点为F ,过点F 作直线PF 垂直于该双曲线的一条渐近线1l 于P . (Ⅰ)求该双曲线方程;(Ⅱ)设,A B 为双曲线上两点,若点(1,2)N 是线段AB 的中点,求直线AB 的方程.20. (本小题满分13分)如图,梯形ABCD 的底边AB 在y 轴上,原点O 为AB 的中点,|||2,33AB CD AC BD ==-⊥M 为CD 的中点.(Ⅰ)求点M 的轨迹方程;(Ⅱ)过M 作AB 的垂线,垂足为N ,若存在正常数0λ,使0M P P N λ=,且P 点到,A B的距离和为定值,求点P 的轨迹E 的方程;(Ⅲ)过1(0,)2的直线与轨迹E 交于,P Q 两点,且0OP OQ =,求此直线方程.21.(本小题满分14分)已知曲线C 是到点1328P ⎛⎫- ⎪⎝⎭,和到直线58y =-距离相等的点的轨迹.l 是过点(10)Q -,的直线,M 是C 上(不在l 上)的动点;A B ,在l 上,MA l ⊥,MB x ⊥轴(如图).(Ⅰ)求曲线C 的方程; (Ⅱ)求出直线l 的方程,使得2QBQA为常数.参 考 答 案2.填空题11.22154x y += 12.26y x =-+ 13.(7,24)- 14.32x = 15.③④ 3.解答题 16. 解:(Ⅰ)12,(1)()10,l l a a b ⊥∴++-⋅= 即20a a b --= ①又点(3,1)--在1l 上, 所以340a b -++= ② 由①②解得: 2, 2.a b == …………5分(II )因为1l ∥2l 且2l 的斜率为1a -,所以1l 的斜率也存在,即1a a b =-,1a b a=-. 故1l 和2l 的方程可分别表示为14(1):(1)0,a l a x y a--++= 2:(1)01al a x y a-++=- (9分) 因为原点到1l 和2l 的距离相等. 所以141a aa a-=-⇒2a =或23a =.因此22a b =⎧⎨=-⎩或232a b ⎧=⎪⎨⎪=⎩. …………12分17.解(Ⅰ)AC 边上的中线所在的直线的方程75100x y --= …………4分BC 边上的高所在的直线的方程7360x y -+=…………8分(Ⅱ)ABC ∆的外接圆的方程2242200x y x y +---=…………12分 18. 解(Ⅰ)由题意可得直线l :4521+=x y ① 过原点垂直于l 的直线方程为 x y 2-= ②解①②得21-=x . …………………………………………3分 ∵抛物线的顶点关于直线l 的对称点在该抛物线的准线上. ∴2212⨯-=-p ,2=p ∴抛物线C 的方程为x y 42=. ………………………6分(II )⎩⎨⎧-==242kx y x y ,∴04)1(42=++-x k kx ∴⎩⎨⎧≠>∆002k ∴021≠->k k 且1224(1)k x x k ++=2214kx x =∙………………………9分 设A (11,y x )B (22,y x )∵O 在以AB 为直径的圆上,∴OA ⊥OB ,∴1212x x y y +=0………10分将已知代入得21=k . 综上知当21=k 时221:-=x y l 满足题意.…………………………12分 19. 解:(Ⅰ)设半焦距为C ,则F (C ,0),直线l 1的方程为by x a=,直线PF 的方程为()ay x c b=--解方程组,().b y x a a y x c b ⎧⎪⎪⎨⎪⎪⎩==-- 可得2(,)a ab P c c,又已知P点坐标为∴1,a b c = ∴双曲线方程为221.2y x -=…………………6分 (II )设A (x 1, y 1), B (x 2, y 2),则有221122221,21.2y x y x ⎧⎪⎪⎪⎨⎪⎪⎪⎩-=-=②-①, 得21212121()()()()2x x x x y y y y -+=-+.∴k AB =2121212121.22y y x x y y x x -+===+- 即直线AB 的方程为21(1)y x -=⨯-, 即10.x y -+=…………………12分20. 解:(Ⅰ)设点M 的坐标为(,)(0)M x y x ≠,则(,1(,1C x y D x y -+又(0,(0,3A B 由AC BD ⊥有0AC BD =,即(,1)(,1)0x y x y -+=, ∴221(0)x y x +=≠.……………………………………3分(II )设(,)P x y ,则()0(1),M x y λ+,代入M 的轨迹方程有2220(1)1(0).x y x λ++=≠① ②即0221(0)12()1x y x λ+=≠+, ∴P 的轨迹方程为椭圆(除去长轴的两个端点).要P 到A 、B 的距离之和为定值,则以A 、B为焦点,故22011(1)λ-=+. ∴0 2.λ= 从而所求P 的轨迹方程为2291(0)x y x +=≠………………8分 (3)易知l 的斜率存在,设方程为1.2y kx =+ 联立2291x y +=,有223(9)0.4k x kx ++-= 设P (x 1, y 1), Q (x 2, y 2),则1212223,94(9)k x x x x k k -+=-=++. ∵0OP OQ =,而12120.x x y y +=121211022x x kx kx ⎛⎫⎛⎫∴+++= ⎪⎪⎝⎭⎝⎭ 整理,得22223(1)10.44(9)2(9)k k k k -+-+=++∴k = 即所求l的方程为1.2y x =+………………………………13分 21. (Ⅰ)解:设(,)N x y 为C上的点,则N 到直线58y =-的距离为58y +.58y =+. 化简,得曲线C 的方程为21()2y x x =+.……………………6分(II)解法一:设2(,)2x xM x+,直线l:y kx k=+,则(,)B x kx k+,从而1QB=+.在Rt△QMA中,因为22(1)(1)4xQM x=++,222(1)()21xx kMA+k+-=.所以222222(1)(2)4(1)xQ A Q M A M k xk+=-=++QA=,222(112QB k xQA k x+k++=⋅当k=2时,2QBQA=l方程为220x y-+=……………14分解法二:设2(,)2xπM x+,直线直线l:y kx k=+,则(,)B x kx k+,从而1QB=+过(1,0)-垂直于l的直线l1:(1)1y=xk-+,因为QA MH=,所以QA=,212QB xQA x+k+=,当k =2时,2QB QA= 从而所求直线l 方程为220x y -+=……………………14分。
湖北荆州中学21-22学度高二上年末考试-数学(文)

湖北荆州中学21-22学度高二上年末考试-数学(文)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1. 下列有关命题的说法正确的是( ).A 命题“若21x =,则1x =”的否命题为:“若21x =,则1x ≠”; .B 命题“x R ∃∈,220x x ++<”的否定是“x R ∀∈,220x x ++≥”; .C 命题“若x y =,则22x y =”的逆否命题是假命题 ;.D 已知m n N ∈、,命题“若m n +是奇数,则m n 、这两个数中一个为奇数,另一个为偶数”的逆命题为假命题.2. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) .A 2- .B 2 .C 4- .D 43. 给出下列程序语句:0 THEN 2*1 IF 0 THEN 0 ^21 END IF END IF PRINT INPUT x xIF x y x ELSEx y ELSE y x y>=+===-“”;运行时,从键盘输入2-,则输出结果为( ).A 2- .B 1 .C 3 .D 04. 如图表示甲、乙两名运动员每场竞赛得分的茎叶图.则甲得分的中位数与乙得分的中位数之和为( ).A 56分 .B 57分 .C 58分 .D 59分5. 45a =是直线4(1)90x a y -++=与直线2(1)60a x ay --+=垂直的( ) .A 充分不必要条件 .B 必要不充分条件.C 充分必要条件 .D 既不充分也不必要条件6. 执行如图所示的程序框图,输出的T 等于( ).A 10 .B 15 .C 20 .D 307. 某校共有学生2000名,各年级男、女生人数如下表:假如从全校学生中随机抽取一名学生,抽到二年级女生的概率为0.19.现用分层抽样的方法在全校学生中分年级抽取64名学生参加某项活动,则应在三年级中抽取的学生人数为( ).A 24 .B 18 .C 12 .D 168. 若点A 的坐标为(3, 2),F 为抛物线22y x =的焦点,点P 是抛物线上的一动点,则||||PA PF +取最小值时点P 的坐标为( ).A (0, 0) .B (1, 1).C (2, 2) .D 1(, 1)29. 若右边框图所给程序运行的结果20102011S =,那么判定框中能够填入的关于k 的判定条件是( ).A 2010k < .B 2009k <.C 2010k > .D 2009k >10. 过双曲线222:1y M x b-=的左顶点A 作斜率为1的直线l .若l 与双曲线M 的两条渐近线分别相交于点B C 、,且B 是AC 的中点,则双曲线M的离心率为( ) .A52.B 103 .C 5 .D 10二、填空题(本大题共5小题,每小题5分,共25分)11. 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),……,第五组[17,18].右图是按上述分组方法得到的频率分布直方图. 若成绩大于或等于14秒且小于16秒认为良好,则该班在这次百米测试中成绩良好的人数为 .12. 椭圆2214x y +=的两个焦点分别为12F F 、,过1F 作垂直于x 轴的直线与椭圆相交,其中一个交点为P ,则2||PF = .13.过点(3, 1)M -且被点M 平分的双曲线2214x y -=的弦所在直线方程为 . 14. 设2()4f x x a =+(那个地点0a >),若对[1,1]x ∀∈-,()f x 的值差不多上集合{|014}y y a ≤≤+的元素,则实数a 的取值范畴为 . 15. 如图,把椭圆2212516x y +=的长轴AB 分成8等分,过每个分点作x 轴的垂线交椭圆的上半部分于1234567P P P P P P P 、、、、、、七个点,F 是椭圆的左焦点,则1234567||||||||||||||PF P F P F P F P F P F P F ++++++= .三、解答题(本大题共6小题,共75分,解承诺写出文字说明、证明过程或演算步骤.) 16.(本小题满分12分) 设a 是实数,对函数22()233f x x x a a =-++-和抛物线C :24y x =,有如下两个命题::p 函数()f x 的最小值小于0;:q 抛物线24y x =上的点2(, )4a M a 到其准线的距离2d >.已知“p ⌝”和“p q ∧”都为假命题,求a 的取值范畴.17. (本小题满分12分)某流感中心对温差与甲型51H N 病毒感染数之间的相关关系进行研究,他们每天在实验室放入数量相同的甲型51H N 病毒和100头家禽,然后分别记录了12月11号至12月15号每天昼夜温差与实验室里100头家禽的感染数,得到如下资料:日 期 12月11号 12月12号 12月13号 12月14号 12月15号 温 差 10 13 1112 7感染数 2332242917(Ⅰ)求这5天的平均感染数和方差;(Ⅱ)从12月11号至12月15号中任取两天,这两天的感染数分别记为x ,y .用{, }x y 的形式列出所有的差不多事件({, }x y 和{, }y x 视为同一事件),并求事件“||9x y -≥”的概率.(参考公式:方差2222121[()()()]n sx x x x x x n=-+-++-)18. (本小题满分12分)士兵甲和士兵乙进行射击竞赛.甲一次射击命中9环的概率为45,命中10环的概率为110;乙一次射击命中9环的概率为34,命中10环的概率为15. (Ⅰ)现在甲和乙各自独立地同时向目标靶打一发子弹,求(1)事件“甲命中环数不低于9环”的概率;(2)事件“乙命中环数低于9环”的概率;(Ⅱ)若士兵甲连打三发子弹,在目标靶上的着弹点A B C 、、刚好是边长为3 cm 的等边三角形的三个顶点.士兵乙瞄准ABC ∆区域打(可不能打到ABC ∆外)第四发子弹, 则乙此次射击的着弹点距A B C 、、的距离都超过1 cm 的概率为多少?(弹孔大小忽略不计)19. (本小题满分12分)如图,直线1:2l y x =与抛物线2148y x =-交于A B 、两点,线段AB 的垂直平分线与直线1l :10y x =-交于点D .(Ⅰ)求点D 的坐标;(Ⅱ)当动点P 在抛物线上运动时,求点P 到直线1l 的距离的最小值.20.(本小题满分13分)已知双曲线12222=-by a x (0a >,0b >)的渐近线方程为33=±y x ,左焦点为(2,0)F -.(Ⅰ)求双曲线的方程; (Ⅱ)已知直线12y x n =+交双曲线于不同的两点A B 、,若FA FB ⊥,求实数n 的值.21.(本小题满分14分)设椭圆2222:1y x M a b +=(0a b >>)通过点(1, 2)P ,其离心率22e =.(Ⅰ)求椭圆M 的方程;(注意椭圆的焦点在y 轴上哦!) (Ⅱ) 直线:2l y x m =+交椭圆于A B 、两点,且PAB ∆的面积为2,求m 的值.参考答案一、选择题1. 1 2 3 4 5 6 7 8 9 102. B DCBACDCA D二、填空题 11. 27 12. 7213. 3450x y +-= 14. [2,3] 15. 35 三、解答题 16. p ⌝和p q ∧差不多上假命题,p ∴为真命题,q 为假命题. ………………2分2222()233(1)34f x x x a a x a a =-++-=-++-,2min ()340f x a a ∴=+-<,因此,41a -<<; ………………6分又抛物线24y x =的准线为1x =-,q 为假命题,2124a d ∴=+≤,22a ∴-≤≤. ………………10分 故所求a 的取值范畴为[2,1)-. ………………12分17. (Ⅰ)这5天的平均感染数为23322429171252555++++==,方差222222(2325)(3225)(2425)(2925)(1725)13426.855s -+-+-+-+-=== .………………6分(Ⅱ)所有差不多事件为:{23,32},{23,24},{23,29},{23,17},{32,24},{32,29},{32,17},{24,29},{24,17},{29,17},差不多事件总数为10,记满足||9x y -≥的事件为A ,则事件A 包含的差不多事件为{23,32},{32,17},{29,17},因此,3()10P A =. 故事件||9x y -≥的概率为310. ………………12分18. (Ⅰ)(1)记“一次射击甲命中环数不低于9环”为事件E ,“甲一次射击命中9环”为事件1E ,“甲一次射击命中10环”为事件2E ,则12E E E =+,12,E E 互斥,所求概率为1212419()()()()51010P E P E E P E P E =+=+=+=. ………………4分(2) 记“一次射击乙命中环数不低于9环”为事件F ,同(1),3119()4520P F =+=, 又“乙一次射击命中环数低于9环”与F 为对立事件,故所求概率为19112020-=. ………………8分 (Ⅱ)因为着弹点若与A B C 、、的距离都超过1cm ,则着弹点就不能落在分别以A B C 、、为中心,半径为1cm 的三个扇形区域内,只能落在图中阴影部分内. 因为193=33sin 6024ABC S ∆⨯⨯=图中阴影部分的面积为213312342ABC S S ππ∆'=-⨯⨯⨯=-,故所求概率为23127ABCS p S π∆'==-. ………………12分(Ⅱ)设P 点坐标为00(,)x y ,P 到直线1l 的距离为d ,则200148y x =-, 22200000001|410|8228282x x d -+-====2082=,当04x =时,min 282d ==P ∴到直线1l 的距离的最小值为22.………………12分20. (Ⅰ)双曲线渐近线方程为3y x =±,3b a ∴=,223a b ∴=,又F 为(2,0)-,2c ∴=,2224a b c ∴+==,因此223,1a b ==,双曲线方程为 2213x y -=.………………5分(Ⅱ)设A B 、坐标分别为11(,)x y 、22(,)x y ,由方程组221213y x n x y ⎧=+⎪⎪⎨⎪-=⎪⎩,得22133(1)04x nx n --+=,其2221943(1)31204n n n ∆=+⨯⨯+=+>, 1212x x n +=,21212(1)x x n =-+,FA FB ⊥,0FA FB ∴=,1122(2,),(2,)FA x y FB x y =+=+,1212(2)(2)0x x y y ∴+++=,而112211,22y x n y x n =+=+, 121211(2)(2)()()022x x x n x n ∴+++++=,即2121254()4042n x x x x n +++++=,2254(12)(1)124042n n n n +∴⨯-++⨯++=,2824110n n -+=,……………11分 因此64n ±=. ………………13分21.(Ⅰ)由已知,得222222112ab a bc c a+=⎪⎪=+⎨⎪⎪=⎪⎩,∴⎪⎩⎪⎨⎧===222b c a ,所求椭圆M 的方程为 22142y x +=. ………………5分(Ⅱ)由⎪⎩⎪⎨⎧=++=142222y x m x y ,得22440x m ++-=,由0)4(16)22(22>--=∆m m得,m -<<1122(,),(,)A x y B x y,122x x m ∴+=-,21244m x x -= .∴12|||AB x x =-===………………10分。
湖北省荆州中学2022-2023学年高二年级上册学期期末考试数学答案

荆州中学2021级高二上学期期末考试数学试题命题人: 杨俊祎审题人:张 静 朱代文一、单项选择题:本题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若方程表示焦点在轴上的椭圆,则实数的取值范围是( )22216x y a a +=+y a A. B. 3a >2a <-C. 或 D. 或3a >2a <-20a -<<0<<3a 【答案】D 【解析】【分析】根据椭圆焦点在轴上,可得,解出范围即可.y 226,0a a a +<≠【详解】解:由题知表示焦点在轴上的椭圆,22216x y a a +=+y 则有: ,226a a a ⎧<+⎨≠⎩解得:或.20a -<<0<<3a 故选:D2. 设、,向量,,且,,则()x y ∈R (),1,1a x =()1,,1b y =()3,6,3c =-a c ⊥ //bc a b += A. B. C. D. 43【答案】D 【解析】【分析】利用空间向量垂直与共线的坐标表示求出、的值,求出向量的坐标,利用空间向量的模x y a b +长公式可求得结果.【详解】因为,则,解得,则,a c ⊥ 3630a c x ⋅=-+=1x =()1,1,1a = 因为,则,解得,即,//b c 136y =-=2y -()1,2,1b =-所以,,因此,.()2,1,2a b +=-3a b +==故选:D.3. 设、是两条不同的直线,、、是三个不同的平面,则下列命题正确的是( )m n αβγA. 若,则 B. 若,则,m n n α⊥⊂m α⊥,//m n m α⊥n α⊥C. 若,则 D. 若,则//,//m n αα//m n ,αββγ⊥⊥//αγ【答案】B 【解析】【分析】根据线线、线面、面面的位置关系,对选项进行逐一判断即可.【详解】选项A. 一条直线垂直于一平面内的,两条相交直线,则改直线与平面垂直则由,不能得出,故选项A 不正确.,m n n α⊥⊂m α⊥选项B. ,则正确,故选项B 正确.,//m n m α⊥n α⊥选项C. 若,则与可能相交,可能异面,也可能平行,故选项C 不正确.//,//m n ααm n 选项D. 若,则与可能相交,可能平行,故选项D 不正确.,αββγ⊥⊥αγ故选:B4. 金刚石的成分为纯碳,是自然界中存在的最坚硬物质,它的结构是由8个等边三角形组成的正八面体.若某金刚石的棱长为2,则它外接球的体积为()B. C.163π83π【答案】A 【解析】【分析】求得外接球的半径,进而计算出外接球体积.【详解】设,正八面体的棱长为,AC BD O = 2根据正八面体的性质可知:,OA OB OC OD OE =====所以是外接球的球心,且半径,O R =所以外接球的体积为.34π4ππ33R ⨯=⨯=故选:A5. 已知是等差数列的前项和,,则的最小值为( )n S {}n a n 13140,0S S <>n S A.B.C.D.6S 7S 8S 13S 【答案】B 【解析】【分析】根据等差数列的前项和公式和性质可得:,且,进而求解.n 780,0a a <>87a a >【详解】因为是等差数列的前项和,n S {}n a n 由可得:,所以,130S <11313713()1302a a S a +==<70a <由可得:,所以,140S >114147814()(07)2a a a a S ==+>+780a a +>则有,所以等差数列的前项为负值,从第项开始为正值,87a a >{}n a 78所以的最小值为,n S 7S 故选:.B6. 直线分别与x 轴,y 轴交于两点,点在圆,则面积的取20x y +-=,A B P 22420x y x +++=PAB 值范围是( )A.B.C. D. [2,6][4,12]【答案】C 【解析】【分析】由题意首先求得的长度,然后确定圆上的点到直线的距离,最后确定三角形面积的ABAB 'd 取值范围.【详解】解:因为,所以.()()2,0,0,2A B AB =圆的标准方程,圆心,22(2)2x y ++=()2,0C -圆心到直线的距离为C AB d =所以,点到直线的距离的取值范围为:,P AB d '所以.[]12,62PAB S AB d '=∈ 故选:C.7. 等比数列的前项和为,,,则为( ){}n a n n S 27S =691S =4S A. B. 2832C. D. 28或-2121【答案】A 【解析】【分析】根据等比数列前项和公式,列出的表达式,两式相除可推出,解出n 26,S S 42120q q +-=,再根据,即可求出结果.23q =()2421S S q =+【详解】设公比为.{}n a q ()0q ≠当时,,,则应有,该方程组无解,所以.1q =1n a a =1n S na =216127691S a S a ==⎧⎨==⎩1q ≠由已知可得,,()212171a q S q-==-()6161911a q S q-==-两式相除可得,,整理可得,24113q q ++=42120q q +-=解得或(舍去),所以.23q =24q =-23q =所以.()41411a q S q-=-()()221111a q q q-+=-()2217428S q =+=⨯=故选:A.8. 已知是椭圆与双曲线的公共焦点,是它们的一个公共点,且,线段的垂直平12F F ,P 12PF PF >1PF 分线过,若椭圆的离心率为,双曲线的离心率为,则的最小值为( )2F 1e 2e 2122e e +A. 8B. 6C. 4D. 2【答案】B 【解析】【分析】由于线段的垂直平分线过,所以有,再根据双曲线和椭圆的定义,求出1PF 2F 122F F PF =的表达式,然后利用基本不等式来求得最小值.2c 【详解】设椭圆对应的参数为,双曲线对应的参数为,11,,a b c 22,,a b c 由于线段的垂直平分线过,所以有.1PF 2F 1222FF P F c ==根据双曲线和椭圆的定义有,11122222PF c a PF c a ⎧+=⎪⎨-=⎪⎩两式相减得到,即,()1242c a a =-122a a c -=,2,00>>a c 所以,2121222224222e a a c ce c a c a+=+=++46≥+=当且仅当即等号成立,即最小值为.2222a cc a =22c a =6故选:B.【点睛】思路点睛:本小题考查双曲线的定义和几何性质,考查椭圆的定义和几何性质,是一个综合性较强的题目,由于椭圆和双曲线有公共的焦点,所以焦距相同,也就是有相同,对于两个曲线的公共交点来c 说,即满足椭圆的定义,又满足双曲线的定义,根据定义可列出方程.再利用基本不等式可求得最小值.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,有选错的得0分,部分选对得2分.9. 数列2,0,2,0,…的通项公式可以是()A. ,1(1)n n a =--*Nn ∈B.,n a =*Nn ∈C.,a n ={2,n 为奇数0.n 为偶数*N n ∈D.,1(1cos π)2n a n =-*Nn ∈【答案】AC 【解析】【分析】对选项逐一分析,从而确定正确答案.【详解】A 选项,,符合题意.12342,0,2,0,a a a a ==== B 选项,,不合题意.10a =C 选项,符合题意.n a D 选项,,不合题意.11a =故选:AC10. (多选)朱世杰是元代著名数学家,他所著的《算学启蒙》是一部在中国乃至世界最早的科学普及著作,《算学启蒙》中涉及一些“堆垛”问题,主要利用“堆垛”研究数列以及数列的求和问题.现有100根相同的圆形铅笔,小明模仿“堆垛”问题,将它们全部堆放成纵断面为等腰梯形的“垛”,要求层数不小于2,且从最下面一层开始5每一层比上一层多1根,则该“等腰梯形垛”堆放的层数可以是( )A. 4B. 5C. 7D. 8【答案】BD 【解析】【分析】设最上面一层放根,一共放层,则最下面一层放根,利用等差数列的前项1a (2)n n 1(1)a n +-n 和公式可得,结合,可得为200的因数,且为偶数,逐一验证120021a n n =+-*1N a ∈n 200(1)2n n +-各个选项即可得解.【详解】解:设最上面一层放根,一共放层,1a (2)n n 则最下面一层放根,1(1)a n +-于是,1(21)1002n a n +-=整理得,120021a n n =+-因为,*1N a ∈所以为200的因数,且为偶数,n 200(1)2n n +- 当时,,为奇数,不符合题意,4n =200(14)474+-=当时,,符合题意,5n =200(15)365+-=当时,,不符合题意,7n =200158(17)77+-=当时,,符合题意,8n =200(18)188+-=所以,8满足题意.5n =故选:BD .11. 在平面直角坐标系xOy 中,点,动点M 到点F 的距离与到直线的距离相等,记M 的轨()1,0F =1x -迹为曲线C .若过点F 的直线与曲线C 交于,两点,则( )()11,A x y ()22,B x y A.121y y =-B. 的面积的最小值是2OAB C. 当时,2AF BF=92A B =D. 以线段OF 为直径的圆与圆相离()22:31N x y -+=【答案】BCD 【解析】【分析】由题意可知点M 的轨迹是以 F 为焦点 , 直线为准线的抛物线,结合抛物线的相关知识可=1x -以判断ABC ,结合圆与圆的位置关系的相关知识,可判断D【详解】依据题意动点M 到点 F ( 1 , 0 ) 的距离与它到直线的距离相等,=1x -由抛物线定义知点M 的轨迹是以 F 为焦点 , 直线为准线的抛物线,=1x -所以点 P 的轨迹 C 的方程为24,y x =对于A , 取 AB ⊥ x 轴,则故A 错误;12 4,y y =-对于B ,显然直线AB 的斜率不为 0 , 设直线AB 的方程为,1x my =+联立整理可得214x my y x =+⎧⎨=⎩2440, y my --=所以124,y y m +=12 4,y y =-所以,Δ1211222OAB S OF y y =⋅-==当时取等号,所以的面积的最小值是 2, 所以B 正确;0m =OAB C 中,时 , 则 2AF BF=2,AF FB =所以()1122(1,)21,,x y x y --=-③ ,122y y =-而①,②,124,y y m +=12 4,y y =-①②③联立可得 22121215()24282m x x m y y m =+=++=+=由抛物线的性质可得所以C 正确;12592,22AB x x p =++=+=D 中 , 以OF 为直径的圆的方程为, 圆心半径2211(24x y -+=1(,0),2C 112r =圆的圆心半径22:(3)1N x y -+=()3,0,N 21,r =所以圆心距121513312222CN r r =-=>+=+=可得两个圆相离,所以 D 正确;故选: BCD .12. 矩形ABCD 中,,AC 将矩形折成一个大小为的二面角,若=2AB AD =θB AC D --,则下列结论正确的有( )1cos 3θ=A. 四面体ABCDB. 点B 与D 之间的距离为C. 异面直线AC 与BD 所成角为45°D. 直线AD 与平面ABC 【答案】ACD 【解析】【分析】分别作,垂足为E ,F ,利用向量法求出,可判断B ,由题可得,BE AC DF AC ⊥⊥BD =平面,然后利用棱锥的体积公式可得A ,利用向量法求出判断C ,CD ⊥ABD V =,AC BD 根据等积法结合条件可得直线AD 与平面ABC 所成角的正弦值判断D.【详解】分别作,垂足为E ,F ,则,,BE AC DF AC ⊥⊥,EB FDθ= 由已知可得,,1,2EB FD AE CF EF =====因为,BD BE EF FD =++ 所以222||()BD BD BE EF FD ==++ 2222BE EF FD BE FD=+++⋅,343π)8θ=+++-=所以,故B 错误;BD =因为,2AB CD ==AD BC ==所以,即,22212CD BD BC +==CD BD ⊥同理,AB BD ⊥又,平面,CD AD ⊥,,AD BD D AD BD =⊂ ABD 则平面,CD ⊥ABD 所以四面体ABCD 的体积为,故A正确;11122332ABD V S CD =⨯=⨯⨯⨯=由题可得,,,30CAD ∠=︒60CAB ∠=︒则()AC BD AC AC AD AB AD A AC B⋅=⋅-=⋅-⋅,442cos 608=⨯-⨯︒=︒则,得,cos ,AC BD AC BD AC BD ⋅===⋅,45AC BD =︒所以异面直线与所成的角为,故C 正确;AC BD 45︒设点到平面为,则,D ABCd D ABC C ABD V V --=所以,1112332ABC S d d ⋅=⨯⨯⨯=所以d =设直线AD 与平面ABC 所成角为,则D 正确.αsin d AD α===故选:ACD .三、填空题:本题共4小题,每小题5分,共20分.13. 设是等差数列的前项和,已知,,则_______.n S {}n a n 23a =611a =7S =【答案】49【解析】【详解】.()26777144922a a S +⨯===14. 设双曲线:的右焦点为,过于、两点,若C 22221(0,0)x y a b a b -=>>F F C A B,则的离心率为__________.5AB FB = C 【答案】65【解析】【分析】设直线的方程,与双曲线方程消去并化简.设,,,,利用根与系数的关AB x 1(A x 1)y 2(B x 2)y 系得到,.通过,得到代入上式消去得关于、、的等式,结合12y y +12y y 5AB FB = 124y y =-2y a b c 解之得双曲线的离心率..222b c a =-【详解】直线过点直线的方程为 AB (c,0)F ∴AB )y x c =-与双曲线联立,2222:1(0,0)x y C a b a b -=>>消去,得 ,x (222241)03b a y cy b -++=设,,,,1(A x 1)y 2(B x 2)y ,12y y ∴+=4122233b y y a b -=-,可得 5AB FB = 124yy =-代入上式得,,∴23y -=42222343b y a b --=-消去并化简整理,得,2y 22243(3)34c a b =-将代入化简,得,解之得,222b c a =-223625c a =65c a =因此,该双曲线的离心率.65e =故答案为:.6515. 已知数列的通项公式为,则数列的前项和_______.{}n c (21)3n n c n =-⋅{}n c n n S =【答案】()1313n n ++-⋅【解析】【分析】利用错位相减法求数列的前项和即可.{}n c n n S 【详解】由数列的通项公式为,{}n c (21)3n n c n =-⋅所以数列的前项和为:{}n c n ,①123133353(21)3nn S n =⨯+⨯+⨯++-⋅ 则: ,②23413133353(21)3n n S n +=⨯+⨯+⨯++-⋅ ①②:,-123113232323(21)32n n n S n +=⨯+⨯+⨯++⨯--⋅- 即,1231232323233(21)32n n n n S +-=⨯+⨯+⨯++⨯---⋅ 即,()1231233333(2132)n n n n S +=⋅++++---⋅- 即,()131323(21)3132n n n n S +-⨯-=⨯---⋅-即,()13313(21)32n n n S n +-=⨯----⋅即,1133312(2)3n n n S n ++-=----⋅即,()162132n n S n +-=---⋅所以,()1313n n S n +=+-⋅故答案为:.()1313n n ++-⋅16. 阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德被称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点A 、B 的距离之比为λ(λ>0,λ≠1),那么点M 的轨迹就是阿波罗尼斯圆.下面,我们来研究与此相关的一个问题.已知圆:x 2+y 2=1和点,点B (1,1),1,02A ⎛⎫- ⎪⎝⎭M 为圆O 上动点,则2|MA |+|MB |的最小值为_____.【解析】【分析】由题意,取点K (﹣2,0),连接OM 、MK .由△MOK∽△AOM,可得,推出2MK OM MA OA ==MK =2MA ,在△MBK 中,MB+MK≥BK,推出2|MA|+|MB|=|MB|+|MK|的最小值为BK 的长.【详解】如图所示,取点K (﹣2,0),连接OM 、MK .∵OM=1,OA =,OK =2,∴,122MK OM MA OA ==∵∠MOK=∠AOM,∴△MOK∽△AOM,∴,∴MK=2MA ,2MK OM MA OA ==∴|MB|+2|MA|=|MB|+|MK|,在△MBK 中,|MB|+|MK|≥|BK|,∴|MB|+2|MA|=|MB|+|MK|的最小值为|BK|的长,∵B(1,1),K (﹣2,0).=.【点睛】本题考查直线与圆的方程的应用,坐标与图形的性质、相似三角形的判定和性质、三角形的三边关系、两点之间的距离公式等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中档题.四、解答题:本题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤.17. 已知圆和直线.22:2420C x y x y +--+=:10l ax y a +--=(1)判断直线与圆的位置关系;l C (2)求直线被圆截得的最短弦长及此时直线的方程.l C l【答案】(1)相交(2)1y =【解析】【分析】(1)根据直线过定点以及点与圆的位置关系即可得到结果;(2)当当直线时,直线被圆截得的弦长最短,结合弦长公式即可得到最短弦长及直线的方l CM ⊥l C l 程.【小问1详解】因为直线,即恒过定点:10l ax y a +--=()110a x y -+-=()1,1M 又因为圆,即22:2420C x y x y +--+=()()22123x y -+-=即圆心,半径为()1,2C r =因为1CM ==<所以点在圆内,即直线与圆相交.M l C 【小问2详解】当直线时,直线被圆截得的弦长最短,l CM ⊥l C=即最短弦长为又因为点横坐标相同,故直线轴,,M C MC x ⊥则直线的斜率为l 0所以直线的方程为l 1y =18. 在数列中,.{}n a *112,431,N n n a a a n n +==-+∈(1)设,求证:数列是等比数列;n n b a n =-{}n b (2)求数列的前项和.{}n a 【答案】(1)证明见解析;(2)数列的前项和为.{}n a 24132n n n -++【解析】【分析】(1)由条件证明对于任意的,为常数即可.*N n ∈1n n b b +(2)结合(1)的结论求得数列的通项公式,再由分组求和法求和.{}n a 【小问1详解】由已知又,,所以,111b a =-12a =11b =因为,*1431,N n n a a n n +=-+∈所以,又()()114n n a n a n +-+=-n n b a n =-所以,,因为,所以,14n n b b +=*N n ∈11b =0n b ≠*N n ∈所以,14n n b b +=*Nn ∈所以数列是首项为1,公比为4的等比数列.{}n b 【小问2详解】由(1),可知,14n n a n --=所以数列的通项公式为.{}n a 14n na n -=+设数列的前项和为,则{}n a n S ,123n n S a a a a =+++⋅⋅⋅+所以,()()()()01214142434n n S n -=++++++⋅⋅⋅++,01214142434n n S n -=++++++⋅⋅⋅++,()()01214444123n n S n -=+++⋅⋅⋅+++++⋅⋅⋅+,()114142n n n n S +-=+-所以,24132n n n n S -+=+所以数列的前项和为.{}n a 24132n n n -++19. 已知在中,角,,的对边分别为,,,且ABC ∆A B C a b c cos cos B C bc +=(1)求的值;b (2)若,求面积的最大值.cos2B B +=ABC ∆【答案】(1)b =【解析】【详解】分析:(1)在式子中运用正弦、余弦定理后可得.(2)由cos cos B C b c +=b =经三角变换可得,然后运用余弦定理可得,从cos 2B B +=3B π=2232a c ac ac ac ac =+-≥-=而得到,故得.3ac≤1sin 2S ac B =≤详解:(1)由题意及正、余弦定理得,22222222a c b a b c abc abc +-+-+=整理得,222a abc=∴b =(2)由题意得,cos 2sin 26B B B π⎛⎫+=+= ⎪⎝⎭∴,sin(+=16B π)∵,()0,B π∈∴,62B ππ+=∴.3B π=由余弦定理得,2222cos b a c ac B =+-∴,2232a c ac ac ac ac =+-≥-= ,当且仅当时等号成立.3ac ∴≤a c ==∴.11sin 322S ac B =≤⨯=∴.ABC ∆点睛:(1)正、余弦定理经常与三角形的面积综合在一起考查,解题时要注意整体代换的应用,如余弦定理中常用的变形,这样自然地与三角形的面积公式结合在一起.222()2a c a c ac +=+-(2)运用基本不等式求最值时,要注意等号成立的条件,在解题中必须要注明.20. 如图,平面,平面,,,,⊥AE ABCD //BF ADE //CF AE AD AB ⊥1AB AD ==.2AE BC ==(1)求证:;//AD BC (2)求直线与平面所成角的余弦值.CE BDE 【答案】(1)见解析 (2【解析】【分析】(1)由线面平行判定定理得平面,面面平行判定定理平面平面,再由//CF ADE //BCF ADE 面面平行性质定理解决即可.(2)建立空间直角坐标系,空间向量法解决即可.【小问1详解】证明:由题知,,平面,平面,//CF AE CF ⊄ADE AE ⊂ADE所以平面,//CF ADE 因为平面,平面,//BF ADE ,,BF CF F BF CF =⊂ BCF 所以平面平面,//BCF ADE 因为平面平面,平面平面BCF ⋂ABCD AD =ADE ABCD BC=所以.//AD BC 【小问2详解】根据题意,建立以为原点,A 分别以得方向为轴,轴,轴正方向得空间直角坐标系,,,AB AD AE x yz 因为平面,平面,,,,,⊥AE ABCD //BF ADE //CF AE AD AB ⊥1AB AD ==2AE BC ==所以,0,0,01,0,01,2(),(),(),(,00,1,0),(0,,)02A B C D E所以,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=-- 设为平面的法向量,(,,)n x y z = BDE 所以,即,令,可得,00n BD n BE ⎧⋅=⎪⎨⋅=⎪⎩ 020x y x z -+=⎧⎨-+=⎩0z =(2,2,1)n = 设直线与平面所成角为CE BDE θ所以,2424sin 339||||CE n CE n θ⋅--+===⋅所以cos θ=所以直线与平面所成角的CE BDE 21. 己知等比数列的前项和为,且.{}n a n n S ()129N n n a S n *+=+∈(1)求数列的通项公式;{}n a (2)记,证明:.3log n n b a =1223111112n n b b b b b b ++++< 【答案】(1)13n n a +=(2)证明见解析【解析】【分析】(1)令,可得出,令时,由可得,两式作1n =2129a a =+2n ≥129n n a S +=+129n n a S -=+差可得推导出数列为等比数列,确定该数列的公比,求出的值,进而可求得等比数列的通项{}n a 1a {}n a 公式;(2)求得,利用裂项求和法可证得原不等式成立.111112n n b b n n +=-++【小问1详解】因为,则当时,,129n n a S +=+1n =2112929a S a =+=+当时,由可得, 2n ≥129n n a S +=+129n n a S -=+所以,即,112()2n n n n n a a S S a +-=-=-13n n a a +=因为是等比数列,则该数列的公比为,则,{}n a 3213a a =所以,即,11293a a +=19a =所以数列的通项公式.{}n a 11933n n n a -+=⨯=【小问2详解】由(1)得,3log 1n n b a n ==+所以,()()111111212n n b b n n n n +==-++++故 .12231111111111111233412222n n b b b b b b n n n +⎛⎫⎛⎫⎛⎫+++=-+-++-=-< ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭ 22. 已知抛物线C :,F 为抛物线C 的焦点,是抛物线C 上点,且;()220x py p =>()0,1M x 2MF =(1)求抛物线C 的方程;(2)过平面上一动点作抛物线C 的两条切线PA ,PB (其中A ,B 为切点),求(),2P m m -的最大值.11AF BF +【答案】(1);24x y =(2【解析】【分析】(1)根据焦半径公式求出的值即可得抛物线方程;p (2)首先根据导数的几何意义,求出切线,进而求出直线的方程,根据焦半径公式,将,PA PB AB 转化成两点纵坐标的关系式,由韦达定理进行化简,从函数的角度运用换元法求其最大11AF BF+,A B 值.【小问1详解】依题意得:=122p MF +=∴,∴,2p =24p =所求抛物线的方程为;2C 24x y =【小问2详解】抛物线的方程为,即∴,2C 24x y =24x y ='2x y =设,,则切线PA ,PB 的斜率分别为,.()11,A x y ()22,B x y (),2P m m -12x 22x 所以切线PA :,()1112x y y x x -=-∴,又,,211122x x y x y =-+2114x y = 11220y x x y ∴-+=同理可得切线PB 的方程为,22220y x x y -+=因为切线PA ,PB 均过点,所以,,(),2P m m -112240y mx m -+-=222240y mx m -+-=所以,为方程的两组解.()11,x y ()22,x y 2240y mx m -+-=所以直线AB 的方程为.2240y mx m -+-=联立方程,消去x 整理得,222404y mx m x y -+-=⎧⎨=⎩()()2222420y m m y m --++-=∴,∴.()()()222222442480m m m m m m ∆=-+--=-+≥m R ∈∴,21224y y m m +=-+()2122y y m =-由抛物线定义可知,,11AF y =+21BF y =+所以11AF BF AF BF AF BF ++=∵()()()121212111AF BF y y y y y y =++=+++,2269m m =-+∴2223+112612+2692269m AF BF m m AF BF AF BF m m m m +-+===+-+-+令32m t R +=∈∴原式,21111454522221221222t t t t t =+=++=-++-≤【点睛】关键点睛:(1)抛物线标准方程的四种形式以及对应的焦半径公式需要掌握;(2)运用导数的几何意义可以求曲线的切线方程;(3)直线的求解办法需要认真理解;AB (4)对所求式子的合理转化要与韦达定理联系;11AF BF +(5)求最值时应考虑函数值域求法或者基本不等式.。
湖北省荆州中学2017-2018学年高二上学期期末数学试卷(文科) Word版含解析

2017-2018学年湖北省荆州中学高二(上)期末数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.曲线在x=1处切线的倾斜角为()A.1 B.C.D.2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件3.某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为()A.,s2+1002B. +100,s2+1002C.,s2D. +100,s24.若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx在x=1处有极值,则a+b等于()A.2 B.3 C.6 D.95.从抛物线y2=4x上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△PMF的面积为()A.5 B.10 C.15 D.206.某店一个月的收入和支出总共记录了N个数据a1,a2,…a N,其中收入记为正数,支出记为负数.该店用下边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的()A.A>0,V=S﹣T B.A<0,V=S﹣T C.A>0,V=S+T D.A<0,V=S+T7.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为()A.2,6 B.2,7 C.3,6 D.3,78.已知双曲线的一条渐近线的斜率为,且右焦点与抛物线的焦点重合,则该双曲线的离心率等于()A.B.C.2 D.29.若函数f(x)=x2+ax+在(,+∞)上是增函数,则a的取值范围是()A.[﹣1,0] B.[﹣1,+∞)C.[0,3]D.[3,+∞)10.椭圆=1的焦点为F1、F2,椭圆上的点P满足∠F1PF2=600,则△F1PF2的面积是()A.B.C.D.11.已知f(x)、g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)﹣f(x)g′(x)<0,,,则关于x的方程有两个不同实根的概率为()A.B.C.D.12.定义方程f(x)=f′(x)的实数根x0叫做函数的“新驻点”,若函数g(x)=sinx(0<x <π),h(x)=lnx(x>0),φ(x)=x3(x≠0)的“新驻点”分别为a,b,c,则a,b,c的大小关系为()A.a>b>c B.c>b>a C.a>c>b D.b>a>c二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=x2+mx+1,若“∃x0>0,f(x0)<0”为真,则m的取值范围是.14.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,则炮弹爆炸点的轨迹是.15.下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,已知图甲中从左向右第一组的频数为4000.在样本中记月收入在[1000,1500),[1500,2000),[2000,2500),[2500,3000),[3000,3500),[3500,4000]的人数依次为A1、A2、…、A6.图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,则样本的容量n=;图乙输出的S=.(用数字作答)16.给出下列:①已知a,b,m都是正数,且,则a<b;②已知f′(x)是f(x)的导函数,若∀x∈R,f′(x)≥0,则f(1)<f(2)一定成立;③“∃x∈R,使得x2﹣2x+1<0”的否定是真;④“x≤1,且y≤1”是“x+y≤2”的充要条件.其中正确的序号是.(把你认为正确的序号都填上)三、计算题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视(2)用分层抽样的方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.18.已知p:m∈R且m+1≤0,q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假且p∨q为真,求m的取值范围.19.设有关x的一元二次方程9x2+6ax﹣b2+4=0.(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.20.统计表明某型号汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数为y=x+8(0<x<120)(1)当x=64千米/小时时,行驶1000千米耗油量多少升?(2)若油箱有22.5升油,则该型号汽车最多行驶多少千米?21.已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)若曲线y=f(x)与y=2x+m有三个不同的交点,求实数m的取值范围.22.已知椭圆C: +=1(a>b>0)经过(1,1)与(,)两点.(Ⅰ)求椭圆C的方程;(Ⅱ)过原点的直线l与椭圆C交于A、B两点,椭圆C上一点M满足|MA|=|MB|.求证: ++为定值.2015-2016学年湖北省荆州中学高二(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.曲线在x=1处切线的倾斜角为()A.1 B.C.D.【考点】利用导数研究曲线上某点切线方程.【分析】欲求在x=1处的切线倾斜角,先根据导数的几何意义可知k=y′|x=1,再结合正切函数的值求出角α的值即可.【解答】解:∵,∴y′=x2,设曲线在x=1处切线的倾斜角为α,根据导数的几何意义可知,切线的斜率k=y′|x=1=12=1=tanα,∴α=,即倾斜角为.故选C.2.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】先根据mn>0看能否得出方程mx2+ny2=1的曲线是椭圆;这里可以利用举出特值的方法来验证,再看方程mx2+ny2=1的曲线是椭圆,根据椭圆的方程的定义,可以得出mn >0,即可得到结论.【解答】解:当mn>0时,方程mx2+ny2=1的曲线不一定是椭圆,例如:当m=n=1时,方程mx2+ny2=1的曲线不是椭圆而是圆;或者是m,n都是负数,曲线表示的也不是椭圆;故前者不是后者的充分条件;当方程mx2+ny2=1的曲线是椭圆时,应有m,n都大于0,且两个量不相等,得到mn>0;由上可得:“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的必要不充分条件.故选B.3.某公司10位员工的月工资(单位:元)为x1,x2,…,x10,其均值和方差分别为和s2,若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为()A.,s2+1002B. +100,s2+1002C.,s2D. +100,s2【考点】极差、方差与标准差;众数、中位数、平均数.【分析】根据变量之间均值和方差的关系和定义,直接代入即可得到结论.【解答】解:由题意知y i=x i+100,则=(x1+x2+…+x10+100×10)=(x1+x2+…+x10)=+100,方差s2= [(x1+100﹣(+100)2+(x2+100﹣(+100)2+…+(x10+100﹣(+100)2]=[(x1﹣)2+(x2﹣)2+…+(x10﹣)2]=s2.故选:D.4.若a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx在x=1处有极值,则a+b等于()A.2 B.3 C.6 D.9【考点】利用导数研究函数的极值.【分析】根据极值点导数为0,可构造关于a,b的方程,解方程求出a+b的值;【解答】解:a>0,b>0,且函数f(x)=4x3﹣ax2﹣2bx在x=1处有极值,可知f′(1)=0,而f′(x)=12x2﹣2ax﹣2b故12﹣2a﹣2b=0故a+b=6故选C5.从抛物线y2=4x上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△PMF的面积为()A.5 B.10 C.15 D.20【考点】抛物线的简单性质.【分析】先设处P点坐标,进而求得抛物线的准线方程,进而求得P点横坐标,代入抛物线方程求得P的纵坐标,进而利用三角形面积公式求得答案.【解答】解:设P(x0,y0),依题意可知抛物线准线x=﹣1,∴x0=5﹣1=4,∴|y0|==4,∴△MPF的面积为×5×4=10,故选:B.6.某店一个月的收入和支出总共记录了N个数据a1,a2,…a N,其中收入记为正数,支出记为负数.该店用下边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的()A.A>0,V=S﹣T B.A<0,V=S﹣T C.A>0,V=S+T D.A<0,V=S+T【考点】设计程序框图解决实际问题.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知S表示月收入,T表示月支出,V表示月盈利,根据收入记为正数,支出记为负数,故条件语句的判断框中的条件为判断累加量A的符号,由分支结构的“是”与“否”分支不难给出答案,累加完毕退出循环后,要输出月收入S,和月盈利V,故在输出前要计算月盈利V,根据收入、支出与盈利的关系,不难得到答案.【解答】解析:月总收入为S,支出T为负数,因此A>0时应累加到月收入S,故判断框内填:A>0又∵月盈利V=月收入S﹣月支出T,但月支出用负数表示因此月盈利V=S+T故处理框中应填:V=S+T故选A>0,V=S+T7.如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的平均数为17,乙组数据的中位数为17,则x,y的值分别为()A.2,6 B.2,7 C.3,6 D.3,7【考点】茎叶图.【分析】根据茎叶图,由甲组数据的平均数求出x的值,乙组数据的中位数求出y的值.【解答】解:根据茎叶图,知甲组数据的平均数为=17,∴x=3;乙组数据的中位数为17,∴y=7;∴x,y的值分别为3,7.故选:D.8.已知双曲线的一条渐近线的斜率为,且右焦点与抛物线的焦点重合,则该双曲线的离心率等于()A.B.C.2 D.2【考点】双曲线的简单性质.【分析】确定抛物线的焦点坐标,利用双曲线的性质,可得几何量的关系,从而可得双曲线的离心率.【解答】解:抛物线的焦点坐标为.双曲线的右焦点为(c,0),则.渐近线为,因为一条渐近线的斜率为,所以,即,所以b2=2a2=c2﹣a2,即c2=3a2,即,故选B.9.若函数f(x)=x2+ax+在(,+∞)上是增函数,则a的取值范围是()A.[﹣1,0] B.[﹣1,+∞)C.[0,3]D.[3,+∞)【考点】利用导数研究函数的单调性;二次函数的性质.【分析】求出函数f(x)的导函数,由导函数在(,+∞)大于等于0恒成立解答案【解答】解:由f(x)=x2+ax+,得f′(x)=2x+a﹣=,令g(x)=2x3+ax2﹣1,要使函数f(x)=x2+ax+在(,+∞)是增函数,则g(x)=2x3+ax2﹣1在x∈(,+∞)大于等于0恒成立,g′(x)=6x2+2ax=2x(3x+a),当a=0时,g′(x)≥0,g(x)在R上为增函数,则有g()≥0,解得+﹣1≥0,a≥3(舍);当a>0时,g(x)在(0,+∞)上为增函数,则g()≥0,解得+﹣1≥0,a≥3;当a<0时,同理分析可知,满足函数f(x)=x2+ax+在(,+∞)是增函数的a的取值范围是a≥3(舍).故选:D.10.椭圆=1的焦点为F1、F2,椭圆上的点P满足∠F1PF2=600,则△F1PF2的面积是()A.B.C.D.【考点】椭圆的简单性质.【分析】利用椭圆定义和余弦定理,列出方程组,求出|PF1|•|PF2|=,由此能求出△F1PF2的面积.【解答】解:∵椭圆=1的焦点为F1、F2,椭圆上的点P满足∠F1PF2=600,∴由椭圆定义得:|PF1|+|PF2|=20,∴|PF1|2+|PF2|2+2|PF1|•|PF2|=400,①由余弦定理得:•|PF2|cos∠F1PF2=4×36,②联立①②,得:|PF1|•|PF2|=,∴△F1PF2的面积是S=|PF1|•|PF2|•sin60°=×=.故选:A.11.已知f(x)、g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)﹣f(x)g′(x)<0,,,则关于x的方程有两个不同实根的概率为()A.B.C.D.【考点】几何概型.【分析】根据函数的单调性和导数之间的关系求出a的值,然后利用几何概型的概率公式即可得到结论.【解答】解:∵f(x)=a x g(x),∴,∵f′(x)g(x)﹣f(x)g′(x)<0∴[]′=<0,即函数,单调递减,即0<a<1.又,则a+,解得a=.∵关于x的方程abx2+x+=0(b∈(0,1))有两个不同实根,∴△=2﹣10ab>0,即0<b<,∴根据几何概型的概率公式可知所求的概率P=,故选:B12.定义方程f(x)=f′(x)的实数根x0叫做函数的“新驻点”,若函数g(x)=sinx(0<x <π),h(x)=lnx(x>0),φ(x)=x3(x≠0)的“新驻点”分别为a,b,c,则a,b,c的大小关系为()A.a>b>c B.c>b>a C.a>c>b D.b>a>c【考点】导数的运算.【分析】由题意求导可得sina=cosa(0<a<π),lnb=(b>0),c3=3c2(c≠0),从而判断大小.【解答】解:∵g(x)=sinx(0<x<π),h(x)=lnx(x>0),φ(x)=x3(x≠0),∴g′(x)=cosx(0<x<π),h′(x)=(x>0),φ(x)=3x2(x≠0),∴sina=cosa(0<a<π),lnb=(b>0),c3=3c2(c≠0),∴a=,1<b<e,c=3,故a<b<c,故选B.二、填空题(本大题共4小题,每小题5分,共20分)13.已知函数f(x)=x2+mx+1,若“∃x0>0,f(x0)<0”为真,则m的取值范围是(﹣∞,﹣2).【考点】特称.【分析】根据““∃x0>0,f(x0)<0”为真”,不等式对应的是二次函数,利用二次的图象与性质加以解决即可.【解答】解:因为函数f(x)=x2+mx+1的图象过点(0,1),若“∃x0>0,f(x0)<0”为真,则函数f(x)=x2+mx+1的图象的对称轴必在y轴的右侧,且与x轴有两个交点,∴△=m2﹣4>0,且﹣>0,即m<﹣2,则m的取值范围是:(﹣∞,﹣2).故答案为:(﹣∞,﹣2).14.已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,则炮弹爆炸点的轨迹是双曲线靠近B点的那一支.【考点】双曲线的标准方程.【分析】设A(﹣400,0)、B、M(x,y)为曲线上任一点,根据|MA|﹣|MB|为常数,推断M点轨迹为双曲线靠近B点的那一支.【解答】解:设A(﹣400,0)、B、M(x,y)为曲线上任一点,则||MA|﹣|MB||=340×2=680<800.∴M点轨迹为双曲线靠近B点的那一支.故答案为:双曲线靠近B点的那一支.15.下图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图,已知图甲中从左向右第一组的频数为4000.在样本中记月收入在[1000,1500),[1500,2000),[2000,2500),[2500,3000),[3000,3500),[3500,4000]的人数依次为A1、A2、…、A6.图乙是统计图甲中月工资收入在一定范围内的人数的算法流程图,则样本的容量n=10000;图乙输出的S=6000.(用数字作答)【考点】循环结构;频率分布直方图.【分析】先弄清算法功能,然后根据频率分布直方图的矩形面积表示频率求出频率,从而求出月收入在[1000,1500)的频数,再利用样本容量=求出样本容量,最后利用流程图的含义求出图乙输出的S.【解答】解:∵月收入在[1000,1500)的频率为0.0008×500=0.4,且有4000人∴样本的容量,由图乙知输出的S=A2+A3++A6=10000﹣4000=6000.故答案为:10000,600016.给出下列:①已知a,b,m都是正数,且,则a<b;②已知f′(x)是f(x)的导函数,若∀x∈R,f′(x)≥0,则f(1)<f(2)一定成立;③“∃x∈R,使得x2﹣2x+1<0”的否定是真;④“x≤1,且y≤1”是“x+y≤2”的充要条件.其中正确的序号是①③.(把你认为正确的序号都填上)【考点】的否定;不等关系与不等式.【分析】对于:①②③④中的②④可通过举反例进行否定:对于②若f(x)是常数函数,则f(1)<f(2)不成立;故错;对于④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;对于①③可根据不等式的性质进行证明其正确性.【解答】解:对于:①已知a,b,m都是正数,且⇒ab+b>ab+a⇒a<b;正确;②若f(x)是常数函数,则f(1)<f(2)不成立;故错;③“∃x∈R,使得x2﹣2x+1<0”的否定是“∀x∈R,使得x2﹣2x+1≥0”真;正确;④若“x=1.8,且y=0.1”则“x+y≤2”不能推得“x≤1,且y≤1”故④错;正确的序号是①③.故答案为:①③.三、计算题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)17.某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视(2)用分层抽样的方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率.【考点】分层抽样方法;古典概型及其概率计算公式.【分析】(1)分析表格可得,收看新闻节目的观众多为年龄大的.(2)用样本容量乘以收看新闻节目的观众中,年龄大于40岁的观众所占的比例,即得所求.(3)由(2)知,抽取的5名观众中,有2名观众的年龄处于20至40岁,故所求概率为,运算求得结果.【解答】解:(1)由表格可得,收看新闻节目的观众与年龄有关,收看新闻节目的观众多为年龄大的.…(2)应抽取的人数为:(人).…(3)由(2)知,抽取的5名观众中,有2名观众的年龄处于20至40岁,3名观众的年龄大于40岁.…所求概率为:.…18.已知p:m∈R且m+1≤0,q:∀x∈R,x2+mx+1>0恒成立,若p∧q为假且p∨q为真,求m的取值范围.【考点】复合的真假.【分析】分别解出p,q的m的取值范围,p∧q为假且p∨q为真,可得p,q必然一真一假.【解答】解:p:m∈R且m+1≤0,解得m≤﹣1.q:∀x∈R,x2+mx+1>0恒成立,∴△=m2﹣4<0,解得﹣2<m<2.∵p∧q为假且p∨q为真,∴p,q必然一真一假.当p真q假时,,解得m≤﹣2,当p假q真时,,解得﹣1<m<2.∴m的取值范围是m≤﹣2或﹣1<m<2.19.设有关x的一元二次方程9x2+6ax﹣b2+4=0.(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.【考点】几何概型;列举法计算基本事件数及事件发生的概率.【分析】(1)利用有序实数对表示基本事件,由古典概型公式解答;(2)表示a,b满足的区域,求出面积,利用几何概型解答.【解答】解:(1)由题意,知基本事件共有9个,可用有序实数对表示为(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),其中第一个表示a的取值,第二个表示b的取值…由方程9x2+6ax﹣b2+4=0的△=36a2﹣36(﹣b2+4)≥0⇒a2+b2≥4…∴方程9x2+6ax﹣b2+4=0有实根包含7个基本事件,即(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).∴此时方程9x2+6ax﹣b2+4=0有实根的概率为…(2)a,b的取值所构成的区域如图所示,其中0≤a≤3,0≤b≤2…∴构成“方程9x2+6ax﹣b2+4=0有实根”这一事件的区域为{(a,b)|a2+b2≥4,0≤a≤3,0≤b≤2}(图中阴影部分).∴此时所求概率为…20.统计表明某型号汽车在匀速行驶中每小时的耗油量y(升)关于行驶速度x(千米/小时)的函数为y=x+8(0<x<120)(1)当x=64千米/小时时,行驶1000千米耗油量多少升?(2)若油箱有22.5升油,则该型号汽车最多行驶多少千米?【考点】导数在最大值、最小值问题中的应用.【分析】(1)由题意可得当x=64千米/小时,要行驶1000千米需要小时,代入函数y的解析式,即可得到所求值;(2)设22.5升油能使该型号汽车行驶a千米,代入函数y的式子,可得.令,求出导数和单调区间,可得h(x)的最小值,进而得到a 的最大值.【解答】解:(1)当x=64千米/小时,要行驶1000千米需要小时,要耗油升;(2)设22.5升油能使该型号汽车行驶a千米,由题意得(x+8)•=22.5,可得.令,,令h'(x)=0⇒x=80,当x∈(0,80)时,h'(x)<0,h(x)为减函数;当x∈(80,20)时,h'(x)>0,h(x)为增函数.即有当x=80时,h(x)取最小值,此时a取最大值200.故若油箱有22.5升油,则最多可行驶200千米.21.已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)若曲线y=f(x)与y=2x+m有三个不同的交点,求实数m的取值范围.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(Ⅰ)求出导函数f′(x),令f′(x)=0,求出方程的根,求解f′(x)<0和f′(x)<0,即可求得f(x)的单调区间;(Ⅱ)根据题意可知f(x)=2x+m,将f(x)代入整理,令g(x)=,则有g(x)=m,将问题转化为函数y=g(x)与y=m有三个不同的交点,利用导数研究函数g(x)的单调性和极值,从而可以求得实数m的取值范围.【解答】解:(Ⅰ)∵函数,∴f'(x)=x2﹣3x+2,令f'(x)=0,解得x=1或x=2,∴当x<1或x>2时,f'(x)>0,当1<x<2时,f'(x)<0,∴f(x)的单调递增区间为(﹣∞,1),(2,+∞),单调递增区间为(1,2);(Ⅱ)令f(x)=2x+m,即,∴,设g(x)=,∵曲线y=f(x)与y=2x+m有三个不同的交点,∴函数y=g(x)与y=m有三个不同的交点,令g'(x)=0,解得x=0或x=3,当x<0或x>3时,g'(x)>0,当0<x<3时,g'(x)<0,∴g(x)在(﹣∞,0),(3,+∞)单调递增,在(0,3)单调递减,∵,画出函数g(x)的大值图象如右图,∴实数m的取值范围为.22.已知椭圆C: +=1(a>b>0)经过(1,1)与(,)两点.(Ⅰ)求椭圆C的方程;(Ⅱ)过原点的直线l与椭圆C交于A、B两点,椭圆C上一点M满足|MA|=|MB|.求证: ++为定值.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(I)把(1,1)与(,)两点代入椭圆方程解出即可.(II)由|MA|=|MB|,知M在线段AB的垂直平分线上,由椭圆的对称性知A、B关于原点对称.①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点;同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点;直接代入计算即可.②若点A、B、M不是椭圆的顶点,设直线l的方程为y=kx(k≠0),则直线OM的方程为,设A(x1,y1),B(x2,y2),与椭圆的方程联立解出坐标,即可得到=,同理,代入要求的式子即可.【解答】解析(Ⅰ)将(1,1)与(,)两点代入椭圆C的方程,得解得.∴椭圆PM2的方程为.(Ⅱ)由|MA|=|MB|,知M在线段AB的垂直平分线上,由椭圆的对称性知A、B关于原点对称.①若点A、B是椭圆的短轴顶点,则点M是椭圆的一个长轴顶点,此时=.同理,若点A、B是椭圆的长轴顶点,则点M在椭圆的一个短轴顶点,此时=.②若点A、B、M不是椭圆的顶点,设直线l的方程为y=kx(k≠0),则直线OM的方程为,设A(x1,y1),B(x2,y2),由解得,,∴=,同理,所以=2×+=2,故=2为定值.2016年9月6日。
湖北省荆州市直荀中学高二数学文上学期期末试题含解析

湖北省荆州市直荀中学高二数学文上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D—ABC的体积为()A. B. C. D.参考答案:略2. 已知函数f(x)=ax2+c,且=2,则a的值为()A.1B.C.-1D. 0参考答案:A略3. 已知F为椭圆的一个焦点且MF=2,N为MF中点,O为坐标原点,ON长为()A.2 B.4C.6 D.8参考答案:B略4. 在中,若,则的形状是()A.不能确定B.等腰三角形C.直角三角形D.等腰或直角三角形参考答案:D5. 记抛物线f(x)=x﹣x2与x轴所围成的平面区域为M,该抛物线与直线y=x所围成的平面区域为A,若向区域M内随机抛掷一点P,则点P落在区域A的概率为()A.B.C.D.参考答案:A【考点】几何概型.【分析】求出函数与x轴和y=x的交点坐标,根据积分的几何意义求出对应的区域面积,结合几何概型的概率公式进行计算即可.【解答】解:由f(x)=x﹣x2=0得x=0或x=1,即B(1,0),由得x﹣x2=x,得x=x2,得x=0或x=,即C(,0),由积分的定义得区域A的面积S=∫(x﹣x2)dx=(x2﹣x3)|=﹣=,区域M的面积S=∫(x﹣x2﹣x)dx=(x2﹣x3)|=[()2﹣()3]|=﹣=,则若向区域M内随机抛掷一点P,则点P落在区域A的概率P==,故选:A.6. 各项都是正数的等比数列的公比,且成等差数列,则的值为()A. B.C. D .或参考答案:B略7. 对任意实数,定义运算,其中是常数,等式右边的运算是通常的加法和乘法运算。
已知,并且有一个非零常数,使得对任意实数,都有,则的值是()A. B.C. D.参考答案:B略8. 在等比数列{}中,=8,=64,,则公比q为()(A)2 (B)3 (C)4 (D)8参考答案:D9. 下列命题中正确的是()A.“m=”是“直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互平行”的充分不必要条件B.“直线l垂直平面α内无数条直线”是“直线l垂直于平面α”的充分条件C.已知、、为非零向量,则“?=?”是“=”的充要条件D.p:存在x∈R,x2+2x+2 016≤0.则¬p:任意x∈R,x2+2x+2016>0.参考答案:D【考点】命题的真假判断与应用.【分析】由两直线平行与系数的关系列式求得m判断A;由线面垂直的判定判断B;由平面向量数量积的运算判断C;写出特称命题的否定判断D.【解答】解:直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互平行?,得m=.∴“m=”是“直线(m+2)x+3my+1=0与直线(m﹣2)x+(m+2)y﹣3=0相互平行”的既不充分也不必要条件,故A错误;直线l垂直平面α内无数条直线,不一定有直线垂直平面,∴“直线l垂直平面α内无数条直线”不是“直线l垂直于平面α”的充分条件,故B错误;、、为非零向量,由?=?不能得到=,反之,由=能够得到?=?,∴“?=?”是“=”的必要不充分条件,故C错误;p:存在x∈R,x2+2x+2 016≤0.则¬p:任意x∈R,x2+2x+2016>0,故D正确.故选:D.10. 已知点F是双曲线的右焦点,点E是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若∠AEB是钝角,则该双曲线的离心率e的取值范围是()A.B.C.(2,+∞)D.参考答案:C考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:利用双曲线的对称性及∠AEB是钝角,得到AF>EF,求出AF,CF得到关于a,b,c的不等式,求出离心率的范围.解答:解:∵双曲线关于x轴对称,且直线AB垂直x轴∴∠AEF=∠BEF∵∠AEB是钝角,∴AF>EF∵F 为右焦点,过F 且垂直于x 轴的直线与双曲线交于A 、B 两点,∴AF=,∵EF=a+c∴>a+c ,即c 2﹣ac ﹣2a 2>0解得>2或<﹣1双曲线的离心率的范围是(2,+∞) 故选:C .点评: 本题考查双曲线的对称性、考查双曲线的三参数关系:c 2=a 2+b 2、考查双曲线的离心率问题就是研究三参数a ,b ,c 的关系.二、 填空题:本大题共7小题,每小题4分,共28分11. 从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:根据上表可得回归直线方程:=0.56x+,据此模型预报身高为172cm 的高三男生的体重为 .参考答案:70.12kg【考点】线性回归方程. 【专题】概率与统计.【分析】根据所给的表格做出本组数据的样本中心点,根据样本中心点在线性回归直线上,利用待定系数法做出a 的值,得到线性回归方程,根据所给的x 的值,代入线性回归方程,预报身高为172cm 的高三男生的体重.【解答】解:由表中数据可得==170,==69,∵(,)一定在回归直线方程y=0.56x+a 上,∴69=0.56×170+a, 解得a=﹣26.2 ∴y=0.56x﹣26.2,当x=172时,y=0.56×172﹣26.2=70.12. 故答案为:70.12kg .【点评】本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.利用线性回归方程预测函数值,题目的条件告诉了线性回归方程的系数,省去了利用最小二乘法来计算的过程.属于基础题.12. 设x >0,y >0.且2x ﹣3=()y ,则+的最小值为 .参考答案:3【考点】基本不等式.【分析】2x ﹣3=()y ,可得x+y=3.再利用“乘1法”与基本不等式的性质即可得出. 【解答】解:∵2x ﹣3=()y ,∴x﹣3=﹣y ,即x+y=3.又x >0,y >0.则+===3,当且仅当y=2x=2时取等号.∴+的最小值为3. 故答案为:3.13. 设为等差数列的前项和,若,,则参考答案:914. 平面上有两点,点在圆周上,则使得取最小值时点的坐标参考答案:15. .已知函数,则从小到大的顺序为。
湖北省荆州市2017-2018学年高二上学期期末考试 数学文 Word版含答案
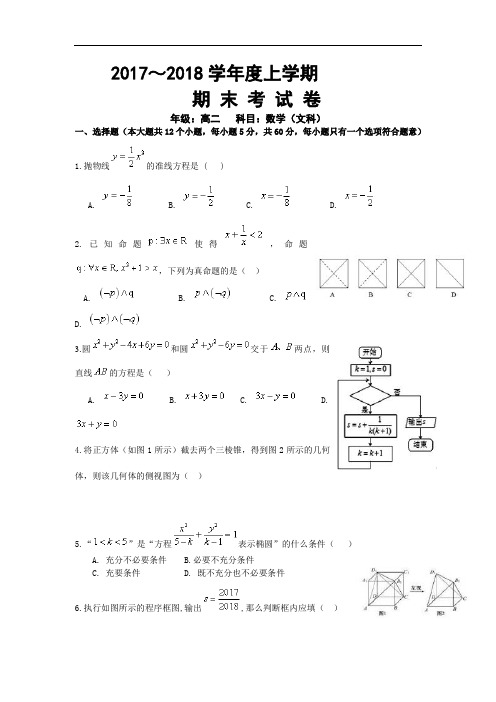
2017~2018学年度上学期期末考试卷年级:高二科目:数学(文科)一、选择题(本大题共12个小题,每小题5分,共60分,每小题只有一个选项符合题意)1.抛物线的准线方程是 ( )A. B. C. D.2.已知命题使得,命题,下列为真命题的是()A. B. C.D.3.圆和圆交于两点,则直线的方程是()A. B. C. D.4.将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的侧视图为()5.“”是“方程表示椭圆”的什么条件()A. 充分不必要条件B.必要不充分条件C. 充要条件D. 既不充分也不必要条件6.执行如图所示的程序框图,输出,那么判断框内应填()A. B.C. D.7.已知正三棱锥的侧棱长是底面边长的3倍,则侧棱与底面所成的角的余弦值为()A. B. C. D.8.若为圆的弦的中点,则直线的方程为().A. B. C. D.9.已知圆:,定点,是圆上的一动点,线段的垂直平分线交半径于点,则点的轨迹的方程是()A. B. C. D.10.甲、乙两名同学打算在下午自习16:00-17:00期间去向杨老师问问题,预计解答完一个学生的问题需要15分钟.若甲乙两人在16:00-17:00内的任意时刻去问问题是相互独立的,则两人独自去时不需要等待的概率是()A. B. C. D.11.已知,且,则的最小值为()A. 2B.C. 4D.12.将一颗六个面分别标有点数1,2,3,4,5,6的正方体形状的骰子投掷两次,第一次、第二次出现的点数分别记为,设直线与平行的概率为,相交的概率为,则圆上到直线的距离为的点的个数是()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共4个小题,每小题5分,共20分)13.学生,在高三8次月考的化学成绩用茎叶图表示如图,其中学生的平均成绩与学生的成绩的众数相等,则__________.14.在中,三顶点,,,点在内部及边界运动,则最大值为_________.15.在球面上有四个点,如果则该球的表面积为________.16.已知、、是双曲线上不同的三点,且、两点关于原点对称,若直线、的斜率乘积,则该双曲线的离心率_______.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本题满分10分)在中,角、、的对边分别为、、,已知.(Ⅰ)求角的值.(Ⅱ)若,求的面积的值.18.(本题满分12分)已知,,.(Ⅰ)若是的充分不必要条件,求实数的取值范围;(Ⅱ)若,“”为真命题,“”为假命题,求实数的取值范围.19.(本题满分12分)为对期中七校联考成绩进行分析,随机抽查了其中3000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.(Ⅰ)求成绩在的频率;(Ⅱ)根据频率分布直方图估算出样本数据的平均数和中位数;(Ⅲ)我校共有880人参加这次考试,请根据频率。
湖北省荆州中学2021-2022学年高二上学期期末考试数学Word版

荆州中学2020级高二年级上学期期末考试数 学 试 题一、单选题(共8个小题,每小题5分,共40分,在每小题列出的四个选项中,选出符合题目要求的一项)1.设n S 为等差数列{}n a 的前n 项和,已知23a =,611a =,则7S =( ) A.13 B.35 C.49 D.632.双曲线12422=-y x 的焦点到渐近线的距离为( )A .2B .2C .6D .363.设m 、n 是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是( ) A.若,m n n α⊥⊂,则m α⊥ B.若,//m n m α⊥,则n α⊥C.若//,//m n αα,则//m nD.若,αββγ⊥⊥,则//αγ4.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点分别为1F ,2F ,O 为坐标原点,P 为双曲线在第一象限上的点,直线PO ,2PF 分别交双曲线C 的左,右支于另一点M ,N ,若12||3||PF PF =,且260MF N ∠=︒,则双曲线的离心率为( )A B .3 C .2 D 5. 已知n S 是等差数列{}n a 的前n 项和,70a >,110S <,则n S 的最小值为( ) A. 4SB. 5SC. 6SD. 7S6. 抛物线C 的焦点为F ,准线为l ,焦点F 在准线l 上的射影为点K ,过F 任作一条直线交抛物线C 于B A ,两点,则AKB ∠为( ) A .锐角B .直角C .钝角D .锐角或直角7.设)(x f 为可导函数,且12)1()1(lim 0-=--→xx f f x ,则曲线)(x f y =在点))1(,1(f 处的切线的斜率是( )A.2B.-1C.12D.-28. 已知等比数列}{n a 中41,252==a a ,则1433221+⋅++⋅+⋅+⋅n n a a a a a a a a 等于( ) A.)41(16n -- B.)21(16n- C.)41(332n -- D.)21(332n --二、多项选择题(共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,有选错的得0分,部分选对得2分)9.直线:1(1)l x m y -=-和圆2220x y y +-=的位置关系是( )A .相离B .相切或相离C .相交D .相切10.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,…,则下列说法正确的是( ) A .此数列的第20项是200 B .此数列的第19项是180C .此数列偶数项的通项公式为222n a n=D .此数列的前n 项和为(1)n S n n =⋅-11.如图所示,一个底面半径为2的圆柱被与其底面所成的夹角为45θ=︒的平面所截,截面是一个椭圆,则( ) A. 椭圆的长轴长为4 B. 椭圆的离心率为24C. 椭圆的方程可以为22142x y +=D. 椭圆上的点到焦点的距离的最小值为22-12.在数学课堂上,教师引导学生构造新数列:在数列的每相邻两项之间插入此两项的和,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列.将数列1,2进行构造,第1次得到数列1,3,2;第2次得到数列1,4,3,5,2;…;第()*n n ∈N 次得到数列1,123,,,,k x x x x ,2;…记1212n k a x x x =+++++,数列{}n a 的前n 项为n S ,则 ( )A .12nk += B .133n n a a +=- C .()2332n a n n =+ D .()133234n n S n +=+-三、填空题:本题共4小题,每小题5分,共20分.13.若函数()42f x ax bx c =++满足()'12f =,则()1f '-= .14.已知数列{}n a 满足11a =,且11nn n a a a +=+.则数列{}n a 的通项公式为n a =_______. 15. 平行六面体1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,12AA =,11120A AD A AB ∠=∠=︒,则对角线1BD 的长度为________.16.若椭圆22221(0)x y a b a b+=>>和圆222()2b x y c +=+(c 为椭圆的半焦距)有四个不同的交点,则椭圆的离心率e 的取值范围是________.四、解答题(共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(本小题10分)已知以点A (-1,2)为圆心的圆与直线:270l x y ++=相切.过点B (-2,0)的动直线m 与圆A 相交于M ,N 两点. (1)求圆A 的方程;(2)当|MN |=219时,求直线m 的方程.18.(本题满分12分)在公差为d 的等差数列{}n a 中,已知110a =,且123,22,5a a a +成等比数列. (1)求n a ;(2)若0d <,求12n a a a +++.19.(本小题12分)如图,四棱锥P -ABCD 中,P A ⊥平面ABCD ,AD ∥BC ,∠BAD =120o ,AB =AD =2,点M 在线段PD 上,且DM =2MP ,PB ∥平面MAC . (1)求证:平面MAC ⊥平面P AD ;(2)若P A =6,求平面P AB 和平面MAC 所成锐二面角的余弦值.20.(本小题12分)已知数列}{n a 的前n 项和22nn S n +=.(1)求数列}{n a 的通项公式; (2)求数列}2{nna 的前n 项和n T .21.(本小题满分12分)已知抛物线C 的方程为28x y =,点)(0,4M ,过点M 的直线交抛物线于A B 、两点. (1)求△OAB 面积的最小值(O 为坐标原点); (2)2211AMBM+是否为定值?若是,求出该定值;若不是,说明理由.22.(本小题满分12分)已知椭圆C :()222210x y a b a b +=>>1F ,2F分别为椭圆C 的左,右焦点,M 为椭圆C 上一点,12MF F △的周长为4+. (1)求椭圆C 的方程;(2)P 为圆225x y +=上任意一点,过P 作椭圆C 的两条切线,切点分别为A ,B ,判断PA PB ⋅是否为定值?若是,求出定值;若不是,说明理由.荆州中学高二年级期末考试数学试题参考答案一、单项选择题二、多项选择题三、填空题13.-2 14. 15.216.四、解答题17.解:(1)设圆A 的半径为R .因为圆A 与直线l 1:x +2y +7=0相切, 所以R =|-1+4+7|5=2 5.所以圆A 的方程为(x +1)2+(y -2)2=20. (2)当直线l 与x 轴垂直时,易知x =-2符合题意;当直线l 与x 轴不垂直时,设直线l 的方程为y =k (x +2),即kx -y +2k =0.由于|MN |=219,于是⎝ ⎛⎭⎪⎫|-k -2+2k |k 2+12+(19)2=20,解得k =34, 此时,直线l 的方程为3x -4y +6=0.所以所求直线l 的方程为x =-2或3x -4y +6=0. 18.解:由题意知:22131(22)510a a a a ⎧+=⎨=⎩即2(222)50(102)d d +=⨯+解得:4d =或1d =- ①当4d =时,110,10(1)446n a a n n =∴=+-⨯=+ ②1d =-时,110,10(1)(1)11n a a n n =∴=+-⨯-=-综上知:当4d =时,46n a n =+;当1d =-时,11n a n =-.(2)01d d <∴=-,,即12(21)11,2n n n n n a n S a a a -=-=+++=①当111n ≤≤时,0,n a ≥此时|n a |=n a∴|1a |+|2a |+…+|n a |=12(21)2n n n n a a a S -+++==②当12n ≥时,此时|1a |+|2a |+…+|11a |+|12a |+…+|n a |=121112n a a a a a +++---=111111(21)(21)()211011022n n n n n n S S S S S ----=-=-=+ 综上知:|1a |+|2a |+…+|n a |=(21),1112(21)100,122n n n n n n -⎧≤≤⎪⎪⎨-⎪+≥⎪⎩19(1)连接BD 交AC 于点E ,连接ME ,如图所示:∵//PB 平面MAC ,PB ⊂平面PBD ,平面PBD 平面MAC ME =,∴//PB ME ,∴2DE DM ADBE PM BC===,∴1BC =,∵2AB =,60ABC ∠= ∴1412232AC =+-⨯⨯=,∴2224AC BC AB +==,090ACB ∠=,∴90CAD ∠=,CA AD ⊥,又∵PA ⊥平面ABCD ,CA ⊂平面ABCD ,∴PA CA ⊥,∵PA AD A ⋂=,∴CA ⊥平面PAD ,∵CA ⊂平面MAC ,∴平面MAC ⊥平面PAD ; (2)如图所示:以A 为原点,AC ,AD ,AP 分别为x ,y ,z 轴建系,则()()))20,0,6,0,0,0,3,1,0,3,0,0,0,,43P A BCM ⎛⎫- ⎪⎝⎭,∴()()()20,0,6,3,1,0,0,,4,3,0,03PA AB MA AC ⎛⎫=-=-=--= ⎪⎝⎭,设平面PAB 和平面MAC 的一个法向量分别为()()11112222,,,,,n x y z n x y z ==,平面PAB 与平面MAC 所成锐二面角为θ, ∴()11111160·01,3,0·030z n PA n n AB y -=⎧⎧=⎪⎪⇒⇒=⎨=-=⎪⎩,222222240·0130,3,2·030y z n MA n n AC x ⎧⎧--==⎪⎪⎛⎫⇒⇒=-⎨ ⎪=⎝⎭⎪⎪=⎩⎩,∴121233cos 37n n n n θ===20.解:(1)当1=n 时,111==S a , 当2≥n 时,n n n n n S S a n n n =-+--+=-=-2)1()1(2221所以n a n =(2)因为n n n T 223222132++++= ,1432221-23222121++++++=n n n nn T两式相减得:111322212211)211(2122121212121++++-=---=-++++=n n n n n n n n n T 所以n n n T 222+-=21、(1);(2)由题意知,直线AB 斜率k 存在,不妨设其方程为4y kx =+,联立抛物线C 的方程可得28320x kx --=,设)(11,A x y ,)(22,B x y ,则128x x k +=,1232x x =-, 所以AM =,BM = 所以)()(22222212111111k x k xAMBM+=+++)()()()()(22121222221264121161321k x x x x k k x x ++-===++. 22.由题可知,224c e a c a ==+=+2,a c ==222a b c =+,解得1b =,故椭圆的标准方程为:2214x y +=;如图所示,当PB 平行于y 轴时,PA 恰好平行于x 轴,()()()0,12,0,2,1A B P ,()()2,0,0,1PA PB =-=-,0PA PB ⋅=;当PB 不平行于y 轴时,设()00,P x y ,设过点P 的直线为()00y k x x y =-+,联立()220014x y y k x x y ⎧+=⎪⎨⎪=-+⎩得()()()2220000418410k x k y kx x y kx ⎡⎤++-+--=⎣⎦, 令0∆=得()()()2222000064164110ky kx k y kx ⎡⎤∆=--+--=⎣⎦,化简得()22200004210x k x y k y --+-=,设12,PA PB k k k k ==,则20122014y k k x -⋅=-,又2205x y +=, 故220012220014144y x k k x x --⋅===---,即0PA PB ⋅=. 综上所述,0PA PB ⋅=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
荆州中学2017~2018学年度上学期期 末 考 试 卷年级:高二 科目:数学(文科)一、选择题(本大题共12个小题,每小题5分,共60分,每小题只有一个选项符合题意)1.抛物线212y x =的准线方程是 ( ) A. 18y =- B. 12y =- C. 18x =- D. 12x =- 2.已知命题p :R x ∃∈使得12x x +<,命题2q :R,1x x x ∀∈+>,下列为真命题的是( ) A. ()q p ⌝∧ B. ()p q ∧⌝ C.q p ∧ D. ()()p q ⌝∧⌝ 3.圆22460x y x y +-+=和圆2260x y y +-=交于A B 、两点,则直线AB 的方程是( )A. 30x y -=B. 30x y +=C. 30x y -=D. 30x y +=4.将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的侧视图为( )5.“15k <<”是“方程22151x y k k +=--表示椭圆”的什么条件( ) A. 充分不必要条件 B.必要不充分条件C. 充要条件D. 既不充分也不必要条件6.执行如图所示的程序框图,输出20172018s =,那么判断框内应填( )A. 2017?k ≤B. 2018?k ≥C. 2017?k ≥D. 2018?k ≤7.已知正三棱锥的侧棱长是底面边长的3倍,则侧棱与底面所成的角的余弦值为( )A. 128.若()2,2P -为圆()221100x y -+=的弦AB 的中点,则直线AB 的方程为( ). A.260x y --= B.220x y ++= C.220x y +-= D.260x y --=9.已知圆1F : ()22236x y ++=,定点()22,0F , A 是圆1F 上的一动点,线段2F A 的垂直平分线交半径1F A 于P 点,则P 点的轨迹C 的方程是( ) A. 22143x y += B. 22134x y += C. 22195x y += D. 22159x y += 10.甲、乙两名同学打算在下午自习16:00-17:00期间去向杨老师问问题,预计解答完一个学生的问题需要15分钟.若甲乙两人在16:00-17:00内的任意时刻去问问题是相互独立的,则两人独自去时不需要等待的概率是( ) A.316 B. 516 C. 716 D. 91611.已知0,0a b >>,且3a b +=,则14a b+的最小值为( ) A. 2 B. 3 C. 4 D. 5 12.将一颗六个面分别标有点数1,2,3,4,5,6的正方体形状的骰子投掷两次,第一次、第二次出现的点数分别记为a b 、,设直线1:2l ax by +=与2:22l x y +=平行的概率为1P ,相交的概率为2P ,则圆22:16C x y +=上到直线126211()PxP y -+=的距离为2的点的个数是( )A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共4个小题,每小题5分,共20分)13.学生A , B 在高三8次月考的化学成绩用茎叶图表示如图,其中学生A 的平均成绩与学生B 的成绩的众数相等,则m =__________.14.在ABC ∆中,三顶点()2,4A , ()1,2B -, ()1,0C ,点(),P x y 在ABC ∆内部及边界运动,则z x y =-最大值为_________.15.在球面上有,,,A B C D 四个点,如果,,AD AB AB BC ⊥⊥,BC AD ⊥1,AD = 2,AB =3,BC =则该球的表面积为________.16.已知A 、B 、P 是双曲线22221x y a b-=上不同的三点,且A 、B 两点关于原点O 对称,若直线PA 、PB 的斜率乘积3PA PB k k ⋅=,则该双曲线的离心率e =_______.三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(本题满分10分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,已知cos cos cos a B b A C +=. (Ⅰ)求角C 的值. (Ⅱ)若43CA CB ⋅=,求ABC ∆的面积ABC S ∆的值.18.(本题满分12分)已知0m >, 2:280p x x --≤, :22q m x m -≤≤+.(Ⅰ)若p 是q 的充分不必要条件,求实数m 的取值范围;(Ⅱ)若3m =,“p q ∨”为真命题,“p q ∧”为假命题,求实数x 的取值范围.19.(本题满分12分)为对期中七校联考成绩进行分析,随机抽查了其中3000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.(Ⅰ)求成绩在[)600,700的频率;(Ⅱ)根据频率分布直方图估算出样本数据的平均数和中位数; (Ⅲ)我校共有880人参加这次考试,请根据频率分布直方图估计我校成绩在[)650,700这段的人数?20.(本题满分12分)已知直线10ax y -+=与圆22:6440C x y x y +-++=交于,A B 两点,过点()5,1P -的直线l 与圆C 交于,M N 两点,(Ⅰ)若直线l 垂直平分弦AB ,求实数a 的值; (Ⅱ)若4MN =,求直线l 的方程;21.(本题满分12分)已知三棱锥A BCD -中,BCD ∆是等腰直角三角形,且BC CD ⊥,4BC =,AD ⊥平面BCD ,2AD =.(Ⅰ)求证:平面ABC ⊥平面ADC(Ⅱ)若E 为AB 的中点,求点A 到平面CDE 的距离.22.(本题满分12分) 已知椭圆22154x y +=,过右焦点2F 的直线l 交椭圆于M , N 两点. (Ⅰ)若8OM ON ⋅=-l 的方程; (Ⅱ)若直线l 的斜率存在,线段MN 的中垂线与x 轴相交于点(),0P a ,求实数a 的取值范围.荆州中学2017—2018学年上学期高二年级期末考试文科数学试题参考答案及评分标准一、 选择题BCABB ADACD BB二、 填空题13:514:1 15:14π 16:2三、解答题17、解:(1)cos cos cos a B b A C +=由正弦定理得sin cos sin cos cos A B B A C C +=,∴sin()cos A B C C +=∴sin cos C C C =cos 2C ∴= 又0C π<<, ∴π4C =.…………………………………5分(2)∵cos CA CB ab C ⋅===∴11sin ()222ABC S ab C ab ∆===10分 18、解:(1)记命题p 的解集为A=[-2,4], 命题q 的解集为B=[2-m ,2+m],∵p 是q 的充分不必要条件 ∴∴22{ 24m m -≤-+≥,解得: 4m ≥. …………………………………5分(2)∵“p q ∨”为真命题,“p q ∧”为假命题,∴命题p 与q 一真一假,①若p 真q 假,则241,,5x x or x -≤≤⎧⎨<->⎩»,解得:[)2,1x ∈-- …………………8分②若p 假q 真,则2,,415x or x x <->⎧⎨-≤≤⎩,解得: (]4,5x ∈. ………………11分 综上得: [)(]2,14,5x ∈--. ………………………………………12分19、解:(1)根据频率分布直方图,得:成绩在[600,700)的频率为0.003500.001500.2⨯+⨯= ;…………………………………………2分(2)设样本数据的平均数为a ,中位数为b ,0.002504250.004504750.00550525a =⨯⨯+⨯⨯+⨯⨯0.005505750.003506250.00150675+⨯⨯+⨯⨯+⨯⨯540= …………………………………………………………5分根据直方图估计中位数b 在[500,550)段0.002500.004500.005(500)0.5b ⨯+⨯+⨯-=解得540b = ……………………………………………………8分所以数据的平均数和中位数都是540(3)成绩在[650,700)的频率为:0.001×50=0.05,所以我校880名学生生中成绩在[650,700)的人数为:0.05×880=44(人),……12分20、解:(Ⅰ)由于圆22:6440C x y x y +-++=即22:(3)(2)9C x y -++=圆心()3,2C -,半径为3,直线10ax y -+=即1y ax =+ 由于l 垂直平分弦AB ,故圆心()3,2C -必在直线l 上,所以l 的过点()5,1P -和()3,2C - 所以2AB k a ==-, …………………………………………………………6分 (Ⅱ)设直线l 的方程是(5)1y k x =--, C 到l 的距离解得2k =-, ……………………………………………………………10分 所以l 的方程是:2(5)1y x =--- 即l 方程为: 290x y +-= ………………………………………………12分 21、解:(1)证明:AD ⊥平面,BCD BC ⊂平面BCD ,AD BC ∴⊥, 又,BC CD CD AD D ⊥=,BC ∴⊥平面ACD ,又BC ⊂平面ABC ,∴平面ABC ⊥平面ACD . …………………………………5分(2)由已知可得CD =,取CD 中点为F ,连结EF ,132ED EC AB ===,ECD ∴∆为等腰三角形,EF ∴= ECD S ∆= …………………………………8分由(1)知BC ⊥平面,ACDE ∴到平面ACD 的距离为122BC =, 4ACD S ∆=,……………10分 设A 到平面CED 的距离为d ,有11233A ECD ECD E ACD ACD V S d V S -∆-∆=⋅⋅==⋅⋅,解得d =A ∴到平面CDE………………………………12分 22、解:(1)当直线l 的斜率不存在时,M ⎛ ⎝⎭,1,N ⎛ ⎝⎭, 161OM ON ⋅=-1分 当直线l 的斜率存在时,设()11,M x y , ()22,N x y ,直线l 的方程为()1y k x =-,① 又椭圆的方程为22154x y +=,② 由①②可得()222254105200k x k x k +-+-=, ∴21221054k x x k +=+, 212252054k x x k -+=+,…………………………………3分 ∴()22121212216154k y y k x x x x k -⎡⎤=-++=⎣⎦+,…………………………………4分 ∴OM ON x x ⋅=,解得24k =,………………………5分 ∴2k =±,即直线l 的方程为()21y x =-或()21y x =--.………………………6分(2)由(1)可知()121228254k y y k x x k k -+=+-=+, 设MN 的中点为Q ,即22254,5454k k Q k k ⎛⎫- ⎪++⎝⎭, …………………………8分 1PQ MN k k ⋅=-,直线PQ 的方程是令0y =解得10分 当0k =时, M , N 为椭圆长轴的两个端点,则点P 与原点重合,当0k ≠时, 10,5a ⎛⎫∈ ⎪⎝⎭,…………………………………………………11分综上所述,存在点P 且10,5a ⎡⎫∈⎪⎢⎣⎭.………………………………………12分。
