2010年南沙区初中毕业班综合测试一数学参考答案与评分标准
2010年中考模拟试卷 数学参考答案及评分标准
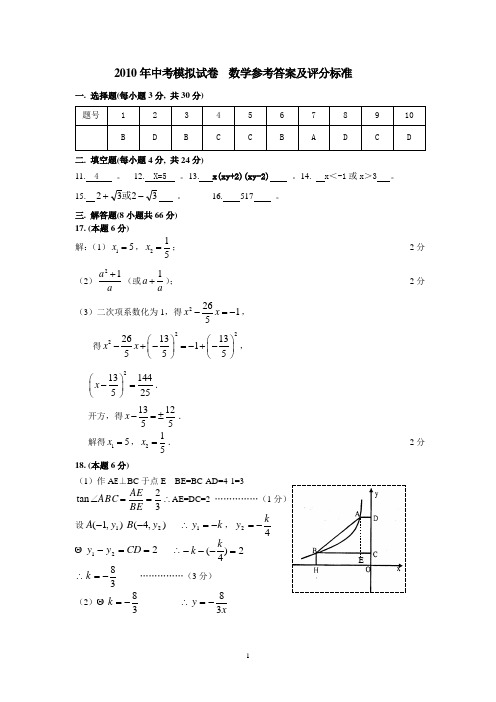
2010年中考模拟试卷 数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二. 填空题(每小题4分, 共24分)11. 4 。
12. X=5 。
13. x(xy+2)(xy-2) 。
14. x <-1或x >3 。
15. 232-+或。
16. 517 。
三. 解答题(8小题共66分) 17. (本题6分) 解:(1)15x =,215x =; ·························································································· 2分(2)21a a+(或1a a+); ··························································································· 2分(3)二次项系数化为1,得22615x x -=-,得2222613131555x x ⎛⎫⎛⎫-+-=-+- ⎪ ⎪⎝⎭⎝⎭,213144525x ⎛⎫-= ⎪⎝⎭. 开方,得131255x -=±.解得15x =,215x =. ···························································································· 2分18. (本题6分)(1)作A E ⊥BC 于点E BE=BC-AD=4-1=332tan ==∠BEAE ABC ∴AE=DC=2 ……………(1分)设),1(1y A -),4(2y B -∴k y -=1,42k y -= 221==-CD y y ∴2)4(=---k k∴38-=k ……………(3分)(2) 38-=k ∴xy 38-=E∴当4-=x 时32)4(38=-⨯-=y ∴32=BH ……………(5分)∴BHOC ABCD ABHODS S S 矩形梯形五边形=+32424121⨯+⨯+⨯)(=323385==+… (6分)19. (本题6分)(1)连接BC 由作图可知:AC=BC=DC 易证:︒=∠90ABD …………… (3分)(2)略 …………… (3分) 20. (本题8分) 解:解:(1)12············································································································ 1分(2)13························································································································ 3分(3)根据题意,画树状图: ························································································· 6分由树状图可知,共有16种等可能的结果:11,12,13,14,21,22,23,24,31,32,33,34,41,42,43,44.其中恰好是4的倍数的共有4种:12,24,32,44. 所以,P (4的倍数)41164==. ··············································································· 8分或根据题意,画表格:·································································································· 6分第一次第二次1 2 3 4 1 11 12 13 14 2 21 22 23 24 3 31 32 33 34 441424344由表格可知,共有16种等可能的结果,其中是4的倍数的有4种,所以,P (4的倍数)41164==.·························································································· 8分21. (本题8分)(1)200;……………………………………2分(2)a = 0.45, b = 70 ……………………4分(每空1分) (3)126;……………………………………6分 (4)900. ……………………………………8分 22. (本题10分)1 2 3 4 1第一次第二次 1 2 3 4 21 2 3 4 31 2 3 44开始解:(1)在R t AEB △中,A C B C = ,12C E A B ∴=,C B C E ∴=,C E B C B E ∴∠=∠. 90CEF CBF ∠=∠=,BEF EBF ∴∠=∠,EF BF ∴=.90BEF FED ∠+∠= ,90EBD EDB ∠+∠=,FED ED F ∴∠=∠.EF FD = .BF FD ∴=. ······································································································· (3分) (2)由(1)BF FD =,而B C C A =,C F A D ∴∥,即AE C F ∥.若A C E F ∥,则A C E F =,BC B F ∴=.BA BD ∴=,45A ∠= .∴当045A <∠< 或4590A <∠<时,四边形A C F E 为梯形. ························ (6分) (3)作G H B D ⊥,垂足为H ,则G H A B ∥.14D G D A =,14D H D B ∴=.又F 为B D 中点,H ∴为D F 的中点.G H ∴为D F 的中垂线.G D F G F D ∴∠=∠. 点G 在E D h 上,E F D G F D ∴∠∠≥.180EFD FDE DEF ∠+∠+∠=,180GFD FDE DEF ∴∠+∠+∠≤. 3180EDF ∴∠≤.60EDF ∴∠≤.又90A EDF ∠+∠=,3090A ∴∠<≤.∴当3090A ∠<≤时,D E 上存在点G ,满足条件14D G D A =. ···················(10分)23. (本题10分)解:(1)购进C 种玩具套数为:50-x -y (或47-54x -1011y )……2分(2)由题意得405550()2350x y x y ++-= 整理得230y x =-……5分 (3)①利润=销售收入-进价-其它费用(5040)(8055)(6550)(50)200p x y x y =-+-+----又∵230y x =- ∴整理得15250p x =+……7分②购进C 种电动玩具的套数为:5050(230)803x y x x x --=---=-据题意列不等式组102301080310x x x ≥⎧⎪-≥⎨⎪-≥⎩,解得70203x ≤≤ ∴x 的范围为70203x ≤≤,且x 为整数 x 的最大值是23 ……9分∵在15250p x =+中,15k =>0 ∴P 随x 的增大而增大∴当x 取最大值23时,P 有最大值,最大值为595元.此时购进A 、B 、C 种玩具分别为23套、16套、11套.……10分AB CD F EMGH24. (本题12分) 解:(1)21(8180)18y x x =--,令0y =得281800x x --=,()()18100x x -+= ∴18x =或10x =-∴(18,0)A ;………………………1分 在21410189y x x =--中,令0x =得10y =即(0,10)B -;………………2分由于B C ∥OA ,故点C 的纵坐标为-10,由2141010189x x -=--得8x =或0x =即(8,10)C -且易求出顶点坐标为98(4,)9-……………………………………3分于是,(18,0),(0,10),(8,10)A B C --,顶点坐标为98(4,)9-。
2010年中考模拟试卷 数学参考答案及评分标准

2010年中考模拟试卷 数学参考答案及评分标准一、选择题(每小题3分,共30分)二、填空题(每小题4分,共24分) 11. -- 2 ,例如 12.6,2.5 13.231a14. -2<a ≤ -1 15.3 16.),(24245--P ,),(2010201020P ,2512三、解答题(6+6+6+8+8+10+10+12=66分)17(本题6分)解:(1).原式233133--+=-1 ················································ (3分) (2)原式=()()21222---+a a a a ··················································································· (1分) =()()()2222-++-a a a a =()()222-+-a a a ························································································· (1分) =21+a ····················································································································· (1分) 18(本题6分)解:(1)S=πrl=50×20π=1000π ……..……………………….(2分)(2)θ=0001443605020360.=⨯=lr…………………………………………………(2分) 剪去的扇形纸片的圆心角=360°-2×144°=72°………………………………………(2分)19(本题6分)解:(1)当射线BA 绕点B 按顺时针方向旋转45度时与⊙O 相切……(1分) 理由如下:如图,设切点为F ,连OF.则OF ⊥BF ,在直角三角形OBF 中,︒=∠=∠∴==45,4,22BOF OBF OB OF ∴∠ABF=45°..(2分)(2)(2)过O 画OH ⊥MN 于H ,易知∠AOB=30°,∴OH=21OB=2 在直角三角形OMH 中,OM ︒=∠︒=∠∴=90,45,22MON MOH …………………(1分)()()422221224122-=⨯-⨯=-=∴∆ππMON MON S S S 扇形弓形∴线段MN 与⌒MN 所围成图形的面积为2π-4………………………………………………(2分) 20. (本题8分)(1)用直尺和圆规作△ABC ………………… (4分) (2)① 作ACB ∠的平分线交AB 于D ; ……………………(1分)② 过D 点作DE ⊥BC ,垂足为E .……………................(1分)(3)△ ADC ≌△ EDC ;△ ACD ∽△ ABC .(每写对一对得1分)21.(本题8分)(1)80 ,25%、40%、30%································· 4分(2)补全条形图(如右图)………2分(3)520…………………………….2分22.(本题10分)(1) 1 , 2 。
2010年天津市初中毕业生学业考试数学试卷答案

2010年天津市初中毕业生学业考试 数学试题参考答案及评分标准评分说明:1.各题均按参考答案及评分标准评分。
2.若考生的非选择题答案与参考答案不完全相同但言之有理,可酌情评分,但不得超过该题所分配的分数。
一、选择题:本大题共10小题,每小题3分,共30分. (1)A (2)B (3)C (4)A (5)B (6)D(7)C(8)C(9)B(10)D二、填空题:本大题共8小题,每小题3分,共24分. (11)23(12)(3,0)(13)C E ∠=∠(答案不惟一,也可以是AB FD =或AD FB =) (14)(15) 13 (16) 22y x x =+-(17(18)(Ⅰ)AD C D '=(答案不惟一,也可以是AE C F '=等);(Ⅱ)①②③三、解答题:本大题共8小题,共66分. (19)(本小题6分) 解: ∵ 211,84 1.x x x x ->+⎧⎨+<-⎩解不等式①,得2x >. 解不等式②,得3x >. ∴ 原不等式组的解集为3x >.①②(20)(本小题8分)解:(Ⅰ)∵ 点2A (1 ),在这个函数的图象上,∴ 21k =-.解得3k =. (Ⅱ)∵ 在函数1k y x-=图象的每一支上,y 随x 的增大而减小, ∴ 10k ->.解得1k >. (Ⅲ)∵ 13k =,有112k -=.∴ 反比例函数的解析式为12y x=. 将点B 的坐标代入12y x=,可知点B 的坐标满足函数关系式, ∴ 点B 在函数12y x=的图象上. 将点C 的坐标代入12y x=,由1252≠,可知点C 的坐标不满足函数关系式,∴ 点C 不在函数12y x=的图象上. (21)(本小题8分)解:(Ⅰ)观察条形图,可知这组样本数据的平均数是62 6.54717.52816.810x ⨯+⨯+⨯+⨯+⨯==.∴ 这组样本数据的平均数为6.8.∵ 在这组样本数据中,6.5出现了4次,出现的次数最多, ∴ 这组数据的众数是6.5.∵ 将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5, 有6.5 6.56.52+=, ∴ 这组数据的中位数是6.5. (Ⅱ)∵ 10户中月均用水量不超过7 t 的有7户,有 7503510⨯=. ∴ 根据样本数据,可以估计出小刚所在班50名同学家庭中月均用水量不超过7 t 的约有35户.(22)(本小题8分)解:(Ⅰ)∵ AB 是⊙O 的直径,AP 是切线,∴ 90BAP ∠=︒.在Rt △PAB 中,2AB =,30P ∠=︒, ∴ 2224BP AB ==⨯=.由勾股定理,得AP == (Ⅱ)如图,连接OC 、AC ,∵ AB 是⊙O 的直径, ∴ 90BCA ∠=︒,有90ACP ∠=︒. 在Rt △APC 中,D 为AP 的中点, ∴ 12CD AP AD ==. ∴ DAC DCA ∠=∠. 又 ∵OC OA =, ∴OAC OCA ∠=∠.∵ 90OAC DAC PAB ∠+∠=∠=︒, ∴ 90OCA DCA OCD ∠+∠=∠=︒. 即 OC CD ⊥.∴ 直线CD 是⊙O 的切线.(23)(本小题8分)解:根据题意,可知45ACB ∠=︒,60ADB ∠=︒,50DC =.在Rt △ABC 中,由45BAC BCA ∠=∠=︒,得BC AB =. 在Rt △ABD 中,由tan ABADB BD∠=,得tan tan 60AB AB BD AB ADB ===∠︒.又 ∵ BC BD DC -=,∴50AB =,即(3150AB =. ∴118AB =≈. 答:该兴趣小组测得的摩天轮的高度约为118 m .AD(24)(本小题8分)解:(Ⅰ)①8000(1)x +;②28000(1)x +;(Ⅱ)28000(1)9680x +=; (Ⅲ)10.1x =,2 2.1x =-;(Ⅳ)10.1x =,2 2.1x =-都是原方程的根,但2 2.1x =-不符合题意,所以只取0.1x =; (Ⅴ)10 . (25)(本小题10分)解:(Ⅰ)如图,作点D 关于x 轴的对称点D ',连接CD '与x 轴交于点E ,连接DE .若在边OA 上任取点E '(与点E 不重合),连接CE '、DE '、DE''. 由DE CE D E CE CD D E CE DE CE '''''''+=+>=+=+, 可知△CDE 的周长最小.∵ 在矩形OACB 中,3OA =,4OB =,D 为OB∴ 3BC =,2D O DO '==,6D B '=. ∵ OE ∥BC ,∴ Rt △D OE '∽Rt △D BC ',有OE D OBC D B'='. ∴ 2316D O BC OE D B '⋅⨯==='. ∴ 点E 的坐标为(1,0).(Ⅱ)如图,作点D 关于x 轴的对称点D ',在CB 边上截取2CG =,连接D G '与x 轴交于点E ,在EA 上截取2EF =. ∵ GC ∥EF ,GC EF =,∴ 四边形GEFC 为平行四边形,有GE CF =. 又 DC 、EF 的长为定值,∴ 此时得到的点E 、F 使四边形CDEF 的周长最小. ∵ OE ∥BC ,∴ Rt △D OE '∽Rt △D BG ', 有OE D OBG D B'='.∴ ()21163D O BG D O BC CG OE D B D B ''⋅⋅-⨯====''. ∴ 17233OF OE EF =+=+=.∴ 点E 的坐标为(13,0),点F 的坐标为(73,0).(26)(本小题10分)解:(Ⅰ)当2b =,3c =时,抛物线的解析式为223y x x =-++,即2(1)4y x =--+.∴ 抛物线顶点E 的坐标为(1,4).(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E 在对称轴1x =上,有2b =,∴ 抛物线的解析式为22y x x c =-++(0c >).∴ 此时,抛物线与y 轴的交点为0( )C c ,,顶点为1( 1)E c +,. ∵ 方程220x x c -++=的两个根为11x =21x = ∴ 此时,抛物线与x轴的交点为10()A,10()B . 如图,过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE = S △BCF . ∵ S △BCE = S △ABC , ∴ S △BCF = S △ABC . ∴BF AB == 设对称轴1x =与x 轴交于点D ,则12DF AB BF =+=由EF ∥CB ,得EFD CBO ∠=∠. ∴ Rt △EDF ∽Rt △COB .有ED CODF OB=. ∴=.结合题意,解得 54c =. ∴ 点54(0 )C ,,52( 0)B ,.x设直线BC 的解析式为y mx n =+,则 5,450.2n m n ⎧=⎪⎪⎨⎪=+⎪⎩ 解得 1,25.4m n ⎧=-⎪⎪⎨⎪=⎪⎩ ∴ 直线BC 的解析式为1524y x =-+.(Ⅲ)根据题意,设抛物线的顶点为( )E h k ,,(0h >,0k >) 则抛物线的解析式为2()y x h k =--+, 此时,抛物线与y 轴的交点为2(0 )C h k -+,,与x轴的交点为0()A h,0()B h .0h >) 过点E 作EF ∥CB 与x 轴交于点F ,连接CF , 则S △BCE = S △BCF . 由S △BCE = 2S △AOC ,∴ S △BCF = 2S △AOC .得2)BF AO h ==. 设该抛物线的对称轴与x 轴交于点D . 则122DF AB BF h =+=. 于是,由Rt △EDF ∽Rt △COB ,有ED CODF OB=. ∴2=2220h k -+=.结合题意,解得h =① ∵ 点( )E h k ,在直线43y x =-+上,有43k h =-+. ② ∴1=. 有1k =,12h =. ∴ 抛物线的解析式为234y x x =-++.。
2010年中考模拟试卷 数学参考答案及评分标准

2010年中考模拟试卷 数学参考答案及评分标准一. 仔细选一选 (本题有10个小题, 每小题3分, 共30分)二. 认真填一填 (本题有6个小题, 每小题4分, 共24分)11、36b a 12、 2.5 13、a=0或a=2 14、1:5 15、(3,2);(55,358) 16、①②④三. 全面答一答 (本题有8个小题, 共66分) 17.(本小题满分6分)212(2212010))(-+-----π=221211+--+…………………分=227-……………………………2分18.(本小题满分6分)解:原式=x-1 …………………………………4分(从33x -<<的范围内选取一个合适的整数x 代入求值。
其中x ≠±1,0)……2分 19.(本小题满分6分)解:(1)如图所示:……………………………………4分(注:每正确画出1个图且痕迹清晰得2分,)(2)规律:若三角形为锐角三角形,则其最小覆盖圆为该三角形的 外接圆;……………1分 若三角形为直角或钝角三角形, 则其最小覆盖圆是以三角形 最长边(直角或钝角所对的边) 为直径的圆.……………1分20.(本小题满分8分)(1)如图(1).连结AC ,由∠1=∠2,∠APC =∠DPE∴△ACP ∽△DEP .…………………………………2分DEAC DP =∴P A 又AP 25=,∴DE=25221÷⨯=52………………2分(2)如图(2).当Rt Rt ADP QCP △∽△时有得:1QC =.∴Q 与B 重合,0BQ ∴=……………2分 如图(3),当Rt Rt ADP PCQ △∽△时,有QCPD PCAD =,得=QC 41,即43=BQ ………………………2分∴当0BQ =或43=BQ 时,三角形AD P 与以点Q C P ,,为顶点的三角形相似.21.(本小题满分8分)解:(1)1(10%15%30%15%5%)25%a =-++++=. ······································ 1分初一学生总数:2010%200÷=(人). ······················································ 1分 (2)活动时间为5天的学生数:20025%50⨯=(人).活动时间为7天的学生数:2005%10⨯=(人). ········································· 2分频数分布直方图(如图)······················ 1分(3)活动时间为4天的扇形所对的圆心角是36030%108⨯=°°. ························· 1分(4)该市活动时间不少于4天的人数约是6000(30%25%15%5%)4500⨯+++=(人). ························································ 2分(第21题图)人数22.(本小题满分10分) (1)27……………..2分(2)△ABC 如图②所示 ……………2分S △ABC=2a ·4a-21a ·2a-21a ·4a-21×2a ·2a=23a……………….2分(3)构造△ABC 如图③所示(图没有但面积算对不扣分) S △ABC=3m ·4n-21m ·4n-213m ·2n-21×2m ·2n=5mn …………….2分23.(本小题满分10分)⑴ 图略。
中考冲刺--初中毕业班综合测试(一)答题卡(数学)

注意事项: 1. 选择题作答必须用 2B 铅笔,修改时用塑 料橡皮擦干净。笔答题作答必须用黑色签 字笔填写,答题不得超出答题框。 2. 保持卡面清洁,不要折叠,不要弄破。
姓名:__________ 试室号:__________
南沙区教育发展中心制
22. (12 分)
23. (12 分)
l D C B
A
O
学校:_________ 24.(14 分)
姓名:__________ 试室号:__________
座位号:________
D
G
C
F H
A 图1
D1
E
B
G1 H1
C1
F1 E1 图2
A1 j
B1
D H A 图3 E B
考
座位号:________
号
一、选择题(每小题 3 分,共 30 分)
1 2 3 6 7 8
9 分) 4 二、填空题 (每小题 3 分,共 18 11. 5 12. 10 13.
14.
15.
16.
三、解答题(共 102 分) 17.(9 分)
数学答题卡第ຫໍສະໝຸດ 1 面/共 6 面南沙区教育发展中心制
请不要在此区域答题或书写
G F
C
数学答题卡 第 5 面/共 6 面
南沙区教育发展中心制
y C B D 1 O 1 A x
18.(9 分)
19.(10 分) 解:(1)
平均数 甲 乙 7 众数 方差 1.2 2.2
(2)
学校:_________ 20. (10 分)
姓名:__________ 试室号:__________
2010年中考模拟试卷 数学参考答案及评分标准
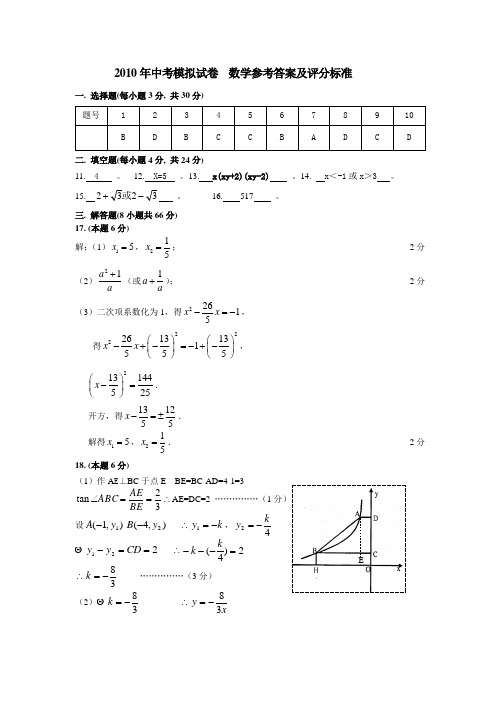
2010年中考模拟试卷 数学参考答案及评分标准一. 选择题(每小题3分, 共30分)二. 填空题(每小题4分, 共24分)11. 4 。
12. X=5 。
13. x(xy+2)(xy-2) 。
14. x <-1或x >3 。
15. 232-+或。
16. 517 。
三. 解答题(8小题共66分) 17. (本题6分) 解:(1)15x =,215x =; ··································································································· 2分 (2)21a a+(或1a a +); ···································································································· 2分(3)二次项系数化为1,得22615x x -=-, 得2222613131555x x ⎛⎫⎛⎫-+-=-+- ⎪ ⎪⎝⎭⎝⎭,213144525x ⎛⎫-=⎪⎝⎭. 开方,得131255x -=±. 解得15x =,215x =. ····································································································· 2分18. (本题6分)(1)作A E ⊥BC 于点E BE=BC-AD=4-1=332tan ==∠BE AE ABC ∴AE=DC=2 ……………(1分) 设),1(1y A -),4(2y B - ∴k y -=1,42ky -=221==-CD y y ∴2)4(=---kk∴38-=k ……………(3分)(2) 38-=k ∴x y 38-=E∴当4-=x 时 32)4(38=-⨯-=y ∴32=BH ……………(5分)∴BH O C ABCD ABH O D S S S 矩形梯形五边形=+32424121⨯+⨯+⨯)(=323385==+ … (6分) 19. (本题6分)(1)连接BC 由作图可知:AC=BC=DC 易证:︒=∠90ABD …………… (3分)(2)略 …………… (3分) 20. (本题8分) 解:解:(1)12······················································································································ 1分 (2)13··································································································································· 3分 (3)根据题意,画树状图: ································································································· 6分由树状图可知,共有16种等可能的结果:11,12,13,14,21,22,23,24,31,32,33,34,41,42,43,44.其中恰好是4的倍数的共有4种:12,24,32,44. 所以,P (4的倍数)41164==. ······················································································· 8分或根据题意,画表格: ··········································································································· 6分第一次第二次1 2 3 41 11 12 13 14 2 21 22 23 24 3 31 32 33 34441424344由表格可知,共有16种等可能的结果,其中是4的倍数的有4种,所以,P (4的倍数)41164==. ·································································································· 8分 21. (本题8分)(1)200;……………………………………2分(2)a = 0.45, b = 70 ……………………4分(每空1分) (3)126;……………………………………6分 (4)900. ……………………………………8分 22. (本题10分)1 2 3 4 1 第一次 第二次 1 2 3 4 2 1 2 3 4 3 1 2 3 4 4 开始解:(1)在Rt AEB △中,AC BC =,12CE AB ∴=,CB CE ∴=,CEB CBE ∴∠=∠.90CEF CBF ∠=∠=,BEF EBF ∴∠=∠,EF BF ∴=. 90BEF FED ∠+∠=,90EBD EDB ∠+∠=,FED EDF ∴∠=∠.EF FD =. BF FD ∴=. ················································································································ (3分) (2)由(1)BF FD =,而BC CA =,CF AD ∴∥,即AE CF ∥.若AC EF ∥,则AC EF =,BC BF ∴=.BA BD ∴=,45A ∠=.∴当045A <∠<或4590A <∠<时,四边形ACFE 为梯形. ··························· (6分) (3)作GH BD ⊥,垂足为H ,则GH AB ∥.14DG DA =,14DH DB ∴=. 又F 为BD 中点,H ∴为DF 的中点.GH ∴为DF 的中垂线.GDF GFD ∴∠=∠.点G 在ED h 上,EFD GFD ∴∠∠≥.180EFD FDE DEF ∠+∠+∠=,180GFD FDE DEF ∴∠+∠+∠≤. 3180EDF ∴∠≤.60EDF ∴∠≤.又90A EDF ∠+∠=,3090A ∴∠<≤.∴当3090A ∠<≤时,DE 上存在点G ,满足条件14DG DA =. ···················· (10分) 23. (本题10分)解:(1)购进C 种玩具套数为:50-x -y (或47-54x -1011y )……2分 (2)由题意得405550()2350x y x y ++-= 整理得230y x =-……5分 (3)①利润=销售收入-进价-其它费用(5040)(8055)(6550)(50)200p x y x y =-+-+----又∵230y x =-∴整理得15250p x =+……7分②购进C 种电动玩具的套数为:5050(230)803x y x x x --=---=-据题意列不等式组102301080310x x x ≥⎧⎪-≥⎨⎪-≥⎩,解得70203x ≤≤ ∴x 的范围为70203x ≤≤,且x 为整数 x 的最大值是23 ……9分∵在15250p x =+中,15k =>0 ∴P 随x 的增大而增大∴当x 取最大值23时,P 有最大值,最大值为595元.此时购进A 、B 、C 种玩具分别为23套、16套、11套.……10分AB CD F EM GH24. (本题12分) 解:(1)21(8180)18y x x =--,令0y =得281800x x --=,()()18100x x -+= ∴18x =或10x =-∴(18,0)A ;………………………1分在21410189y x x =--中,令0x =得10y =即(0,10)B -;………………2分 由于B C ∥OA ,故点C 的纵坐标为-10,由2141010189x x -=--得8x =或0x = 即(8,10)C -且易求出顶点坐标为98(4,)9-……………………………………3分于是,(18,0),(0,10),(8,10)A B C --,顶点坐标为98(4,)9-。
2010年中考模拟试卷 数学参考答案及评分标准

2)12(21-x2010考模拟试卷 数学参考答案及评分标准一、选择题(每小题3分,共30分)二、填空题(每小题4分,共24分)11. 12.___12 或16或20_ 13.14.___26或28或34 15 16.三、解答题(6+6+6+8+8+10+10+12=66分)17.解:(1)若axy b 与-5xy 为同类项,∴b=1∵和为单项式 ∴⎩⎨⎧==15b a ……………………………………3分(2) 若 4xy 2与axy b 为同类项∴b=2 ∵axy b +4xy 2=0 ∴a=-4 ∴⎩⎨⎧=-=24b a ……………………………………3分18.解:2221121x x x x x x --⋅+-+=2)1()1)(1(1)1(--+∙+-x x x x x x ……………………………………2分=x ……………………………………1分解2320x x -+=得x 1=1,x 2=2 ……………………………………1分∵当x=1时原方程分母为零,无意义,∴x=2 ……………………………………1分 ∴原式=x=2 ……………………………………1分 19.(1)14、15、4.3(从左至右)(2) 图略;A 稳定,B 型受季节影响大。
建议略21.(8分)正确,半菱形ABCD ,它的对角线互相平分,而AB=AD,CB=CD ,两个等边 △ABD, △BCD 所以AC 垂直平分BD 。
假设AC 交BD 与O ,半菱形的面积=S △ABD+S △BCD=1/2AO*BD+1/2CO*BD=1/2BD*(AO+CO)=1/2BD*AC. 所以 半菱形的面积等于两条对角线乘积的一半 22.(10分)1223-∙n解:(1)将194t m =⎧⎨=⎩,和390t m =⎧⎨=⎩,代入一次函数m kt b =+中,有94903k b k b =+⎧⎨=+⎩,.296k b =-⎧∴⎨=⎩,.296m t ∴=-+. 经检验,其它点的坐标均适合以上解析式, 故所求函数解析式为296m t =-+.(2)设前20天日销售利润为1p 元,后20天日销售利润为2p 元. 由221111(296)514480(14)578422p t t t t t ⎛⎫=-++=-++=--+ ⎪⎝⎭, 120t ≤≤,∴当14t =时,1p 有最大值578(元).由2221(296)20881920(44)162p t t t t t ⎛⎫=-+-+=-+=-- ⎪⎝⎭.2140t ≤≤且对称轴为44t =,∴函数2p 在2140t ≤≤上随t 的增大而减小.∴当21t =时,2p 有最大值为2(2144)1652916513--=-=(元).578513> ,故第14天时,销售利润最大,为578元.(3)2111(296)5(142)4809642p t t a t a t a ⎛⎫=-++-=-+++- ⎪⎝⎭对称轴为(142)142122a t a -+==+⎛⎫⨯- ⎪⎝⎭.120t ≤≤,∴当14220a +≥即3a ≥时,1p 随t 的增大而增大.又4a < ,34a ∴<≤. 23.(10分)解:阅读理解:m= 1 (填1m不扣分),最小值为 2 ; 思考验证:∵AB 是的直径,∴AC ⊥BC,又∵CD ⊥AB,∴∠CAD=∠BCD=90°-∠B, ∴Rt △CAD ∽Rt △BCD, CD 2=AD·DB, ∴若点D 与O 不重合,连OC ,在Rt △OCD 中,∵OC>CD,∴2a b +若点D 与O 重合时,OC=CD,∴2a b+=综上所述,2a ba b ++≥即,当CD 等于半径时,等号成立.探索应用:设12(,)P x x , 则12(,0),(0,)C x D x ,123,4CA x DB x∴=+=+, 1112(3)(4)22ABCD S CA DB x x∴=⨯=+⨯+四边形,化简得:92()12,S x x =++990,06x x x x >>∴+≥ ,只有当9,3x x x==即时,等号成立.∴S ≥2×6+12=24,∴S 四边形ABCD 有最小值24.此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD 是菱形.24.(12分)(1)①2AB = ……………………………………………………2分842OA ==,4OC =,S 梯形OABC =12 ……………………2分 ②当42<<t 时,直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积-直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………4分 (2) 存在 ………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …(每个点对各得1分)……5分萧山区南阳初中 刘东旭 金 凯。
2010大连市数学一模答案及评分标准

大连市2010年初中毕业升学考试试测(一)数学参考答案与评分标准一、选择题1.A ; 2.C ; 3.C ; 4.B ; 5.C ; 6.D ; 7.B ; 8.D 二、填空题9.3; 10.x ≥2; 11.15; 12.—1; 13.30; 14.21<x <3; 15.41; 16.10; 17.(3,3) 三、解答题18.原式=4)2)(12(1222-++-⨯--a a a a a a …………………………………………………3分 =)2)(2()2()1(122-++-⨯--a a a a a a …………………………………………………………6分 =1-a ………………………………………………………………9分 当12+=a 时,原式=21)12(=-+……………………………………12分19.证明:∵四边形ABCD 是等腰梯形 ∴∠B =∠C …………………………………………………3分 ∵DE =DC ∴∠DEC =∠C ……………………………………………6分 ∴∠B =∠DEC …………………………………………8分 ∴AB ∥DE ………………………………………………10分 ∵AD ∥BC ∴四边形ABED 是平行四边形……………………………12分20.1.680…………………………………………………………………………………3分2.306…………………………………………………………………………………6分 3.20…………………………………………………………………………………9分 4.15×(1-35%-20%)=6.75(万人)……………………………………………11分 答:估计其中期望每平方米房价在5000~7000元的有6.75万人.……………12分 四、解答题 21.(1)如图,作AD ⊥BC 于点D …………………… ……1分在R t △ABD 中,AD =AB sin45°=42222=⨯…………2分AB CE D在R t △ACD 中,∵∠ACD =30°∴AC =2AD =24≈6.5………………………3分即新传送带AC 的长度约为6.5米.…………4分(2)结论:货物MNPQ 应挪走.……………………………………………………5分 解:在R t △ABD 中,BD =AB cos45°=42222=⨯…………………………6分 在R t △ACD 中,CD =AC cos30°=622324=⨯……………………………7分 ∴CB =CD —BD =)26(22262-=-≈2.1…………………………………8分 ∵PC =PB —CB ≈4—2.1=1.9<2 ∴货物MNPQ 应挪走.………………………………………………………………9分 22.(1)结论:PC 是⊙O 的切线. ……………………………………………………1分证明:连接OC ∵CB ∥PO ∴∠POA =∠B, ∠POC =∠OCB ∵OC=OB ∴∠OCB=∠B ∴∠POA =∠POC ……………………………………………………………………2分 又∵OA=OC ,OP=OP ∴△APO ≌△CPO ∴∠OAP =∠OCP …………………………………3分 ∵P A 是⊙O 的切线 ∴∠OAP=90°………………………………………4分∴∠OCP=90° ∴PC 是⊙O 的切线. ……………………………5分 (2)连接AC ∵AB 是⊙O 的直径 ∴∠ACB =90°………………………………………6分 由(1)知 ∠PCO=90°, ∠B=∠OCB=∠POC ∴∠ACB =∠PCO ……………………………………………………………………7分 ∴△ACB ∽△PCO ……………………………………………………………………8分∴PCACOC BC =…………………………………………………………………………9分 MCBAP Q NDA B O PC∴2534463432222=-=-=⋅=BC AB BC AC OC PC ………………………10分 23.结论:AB =kCD ………………………………………………………………………1分 证明:(方法一)在OA 上取一点E ,使OE =k OC ,连接EB , …………………2分 ∵OB = k OD , ∴k OCOEOD OB ==……………………………………………………………………3分 ∵∠AOB =∠COD ∴△OEB ∽△OCD ……………………………………………………………………4分 ∴k ODOBCD EB ==,即EB =kCD ∠OEB =∠OCD …………………………………………………………………………6分 ∵∠OAB +∠OCD =1800 ∴∠OAB +∠OEB =1800 ∵∠AEB +∠OEB =1800 ∴∠OAB=∠AEB ………………………………………………………………………7分 ∴EB =AB ………………………………………………………………………………8分 ∴AB =kCD …………………………………………………………………………9分 (方法二)延长OC 到点E ,使OE =k1OA ,连接DE .证明△DOE ∽△BOA ,再证 明△DCE 是等腰三角形,进而证出结论. (方法三)作DE ⊥OC 交OC 的延长线于E ,作BF ⊥OA 于F ,证明△DOE ∽△BOF , 再证明△DCE ∽△BAF ,进而证出结论. (评分标准参照证法一)选择(1)结论:AB =CD …………………………………………………………………………1分 证明:(方法一)在OA 上取一点E ,使OE = OC ,连接EB ……………………2分 ∵OB =OD ,∠AOB =∠CODOAB (D )C图3OABCD图2E O ABC D图1E∴△OEB ≌△OCD ……………………………………………………………………3分 ∴EB =CD ,∠OEB =∠OCD ……………………………………………………………4分 ∵∠OAB +∠OCD =1800 ∴∠OAB +∠OEB =1800 ∵∠AEB +∠OEB =1800 ∴∠OAB=∠AEB ………………………………………………………………………5分 ∴EB =AB ………………………………………………………………………………6分 ∴AB =CD ………………………………………………………………………………7分 (方法二)延长OC 到点E ,使OE =OA ,连接DE .证明△DOE ≌△BOA ,再证明△DCE 是等腰三角形,进而证出结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年南沙区初中毕业班综合测试(一)数学参考答案与评分标准说明:(一)《答案》中各行右端所注分数表示正确作完该步应得的累加分数,全卷满分150分;(二)有些题后面附有评分细则,请各位老师评卷前认真阅读; (三)《答案》中的解法只是该题解法中的一种或几种,如果考生的解法和本《答案》不同,可参照本答案中的标准给分。
二、填空题(本题共有6小题,每小题3分,共18分) 11. 1≥x 12. 1x = 13.xy6-=14.(2)(2)x x -+ 15.216.31n + 说明:第13题用其他字母表示也可。
三、解答题(本大题共9小题,满分102 分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分9分)解:∵0<a ,0a b -< …………1分 ∴a a -= ,()ab a b -=-- …………4分∴a b a a b -=+- …………6分 ()a a b =--- …………8分 2a b =-+ …………9分18.(本小题满分9分)解:⎩⎨⎧>-<-xx x 21132① ②由①得 2<x …………………2分 由②得 1-<x …………………4分不等式组的解集为1-<x …………………6分 解集在数轴上的表示略。
…………………9分 19.(本小题满分10分) 解: (1)⑵只要学生用统计数据对所持观点说理是合理的即可.例如,选甲运动员参赛,理由:①从平均数看两人平均成绩一样;②从方差看,甲的方差小于乙的方差,甲的成绩比乙稳定,故选择甲运动员参赛.或者选乙运动员参赛,理由:①从众数看,乙比甲的成绩好;②从发展趁势看,乙比甲潜能更大,故选择乙运动员参赛. 20.(本小题满分10分) 解:(1)23…………………………3分 (2)答:该游戏不公平 …………………………4分CB AC B A A B C CB A 第二次 第一次树状图: ………… 7分∴摸出两张牌面图形都是轴对称图形的概率是49, ……………… 8分 摸出两张牌面图形不都是轴对称图形的概率是59. ……………… 9分P (小华赢) < P(小明赢) .∴此游戏不公平. ……………………………………… 10分21.(本小题满分12分)………………………………………6分………………………………………10分解:(1)由图象可知:点A 的坐标是(2),4……… 1分/A 的坐标是(,2)-4……………… 3分(2)设直线1l 的解析式是1y k x =,……… 4分得124k = 即12k = ……… 5分 ∴ 直线1l 的解析式是2y x =……… 6分设直线1l 绕点O 逆时针旋转090后的直线解析式是2y k x =,……… 7分把点/A (,2)-4代入2y k x =,得22k =-4,解得212k =-即12y x =-……… 8分 ∴ 直线2l 的解析式是122y x =-+ ……………… 9分 说明:可用其他方法求直线2l 的解析式。
(3)满足条件的点P 有三种情形,作出一种得1分. 22.(本小题满分12分)解:(1)设A B ,两种型号的设备每台的价格分别是,a b 万元则 ……1分2326a b b a -=⎧⎨-=⎩ ……4分 1210a b =⎧∴⎨=⎩所以A B ,两种型号的设备每台的价格分别是12万元和10万元 ……6分 (2)设购买污水处理设备A 型设备x 台,B 型设备(10)x -台,则:……7分l1210(10)105x x +-≤ …………………9分 2.5x ∴≤ ………………10分x 取非负整数012x ∴=,,则有三种购买方案:①A 型设备0台,B 型设备10台;②A 型设备1台,B 型设备9台;③A 型设备2台,B 型设备8台; ……12分23. (本小题满分12分)(1)证明:连结OC ,直线l与⊙O 相切于点COC l ⊥∴……………… 1分AD l ⊥ OC ∴∥AD ……………… 2分 12∠=∠∴……………… 3分又 OA OC =23∠=∠∴……………… 4分 13∠=∠∴……………… 5分即AC 平分∠DAB ……………… 6分 (2)解法一:连结BC ,AB 是直径,90ACB ADC ∠==∠∴……………… 7分由(1)知,13∠=∠ADC ∆∴∽ACB ∆……………… 9分 ADACAC AB=∴……………… 10分 24AC AB AD ===∴直径AB 的长是4. (12)分解法二:在Rt ADC ∆中,AD=3,AC=∴cos 1∠==……………… 8分即0130∠=……………… 9分 由(1)知,03130∠=∠= 连结BC ,AB 是直径, 90ACB ∠=∴……………… 10分在Rt ABC ∆中,cos 3ACAB∠=……………… 11分0cos30AB=4AB = ∴直径AB 的长是4.……………… 12分评分细则:第2问解法较多,其它解法参照本评分说明分步给分;24.(本小题满分14分)解:(1)① ∵ 点E F G H ,,,在四条边上的运动速度相同∴ AE =BF =CG =DH ……………………1分 ∵四边形ABCD 是正方形,∴∠A =∠B =90°,AB =DA ∴ EB =HA ∴△AEH ≌△BFE (S.A.S )……………………2分 解法一: ∴EH =FE (全等三角形的对应边相等)同理可得:EH =FE =GF =HG∴四边形EFGH 是菱形。
……………………3分 又 ∵∠BEF +∠BFE =90°,∠AEH =∠BFE ∴∠BEF +∠AEH =90° ∴∠FEH =90°∴四边形EFGH 为正方形。
(有一个角是直角的菱形是正方形)……………4分 解法二: ∴∠AEH =∠BFE (全等三角形的对应角相等)又 ∵∠BEF +∠BFE =90° ∴∠BEF +∠AEH =90° ∴∠FEH =90°同理可得∠FEH =∠GFE =∠HGF =90°∴ 四边形EFGH 是矩形。
……………………3分 由 △AEH ≌△BFE ,可得EH =FE∴四边形EFGH 为正方形。
(有一组邻边相等的矩形是正方形)……………4分 ② 解法一:由题意知:111210B C D S S cm ==1正方形A 正方形EFGH …………………5分又 216S cm =正方形ABCD ……………………6分∴ 四个直角三角形的面积之和是216106cm -= ……………………7分 ∴ 正方形E 1F 1G 1H 1的面积为21064cm -= ……………………8分 解法二:设直角三角形的两条直角边的长分别为a 、b (设a b >),则有22410a b a b +=⎧⎨+=⎩,……………………6分(列对一个给1分) 得6ab =,……………………7分∴ 正方形E 1F 1G 1H 1的面积为222()24a b a ab b -=-+=2cm …………………8分 解法三:设直角三角形的两条直角边的长分别为a 、b (设a b >), 则有22410a b a b +=⎧⎨+=⎩,……………………6分(列对一个给1分)得31a b =⎧⎨=⎩,……………………7分∴ 中间小正方形的面积为22()(31)4a b -=-=2cm ……………………8分(2)四边形EFGH 的面积存在最小值,理由如下:……………………9分由条件,易证AEH CGF △≌△,EBF GDH △≌△. 作H M AE ⊥于M ,作FN EB ⊥,交EB 的延长线于N , 设运动t 秒后,四边形EFGH 的面积S 取最小值,则 AE t =,4AH t =-,又30HAM ∠=,11(4)22HM AH t ∴==-.同理得1122FN BF t ==.∴11(4)24AEHSAE HM t t ==-△·,………………………10分 11(4)24EBF S EB FN t t ==-△·. ······························ 11分 又428ABCD S =⨯=正方形,………………………12分∴四边形EFGH 的面积2184(4)484S t t tt =--=-+·.………………………13分∴2(2)4S t =-+,当2t =秒时,四边形EFGH 的面积取最小值等于42cm ………………………14分25、(本小题满分14分)解:(1)设抛物线的解析式为:2(1)4y a x =-+ …………………… 1分把A (3,0)代入解析式求得1-=a …………………… 2分 所以22(1)423y x x x =--+=-++ …………………… 3分设直线AB 的解析式为:y kx b =+由223y x x =-++求得B 点的坐标为)3,0( …………………… 4分 把)0,3(A ,)3,0(B 代入y kx b =+中解得:3,1=-=b k ……………………… 5分所以, 直线AB 的解析式为3y x =-+ ……………………… 6分 (2)因为C 点坐标为(1,4),设D 的坐标为1(1,)y则12y = ……………………… 7分 所以CD =4-2=2 ……………………… 8分32321=⨯⨯=∆CAB S (平方单位) ……………………… 9分 (3)假设存在符合条件的点P ,设P 点的横坐标为x ,△P AB 的铅垂高为h , 则22(23)(3)3h x x x x x =-++--+=-+ ……… 11分 由S △P AB =89S △CAB 得:389)3(3212⨯=+-⨯⨯x x ……………………… 12分 化简得:091242=+-x x解得,23=x ……………………… 13分 将23=x 代入223y x x =-++中, 解得P 点坐标为)415,23( ……………………… 14分。
