矩法估计ppt课件
合集下载
结构可靠分析的一次二阶矩法课件

03 结构可靠性分析的数学模 型
结构可靠性分析的基本概念
01
02
03
结构可靠性
指结构在规定条件下和规 定时间内,完成预定功能 的概率。
结构可靠度
描述结构在规定条件下和 规定时间内完成预定功能 的概率值。
结构失效概率
结构在规定条件下和规定 时间内未能完成预定功能 的概率。
结构可靠性分析的数学模型建立
高。
一次二阶矩法的缺点
高阶矩信息丢失
该方法仅用到了一阶和二阶矩,对于高阶矩的信息未进行利用, 可能导致精度损失。
对异常值敏感
由于该方法基于概率分布的统计特性,对于异常值或离群点较为敏 感,可能导致分析结果的偏差。
假设条件限制
该方法的应用基于一系列假设条件,如随机变量的独立性、分布的 对称性等,这些假设在实际问题中可能不成立。
随着科技的进步,结构可靠性分析方法也 在不断发展和完善,为工程实践提供了更 可靠的依据。
02 一次二阶矩法的基本原理
一次二阶矩法的定义
一次二阶矩法是一种基于概率的可靠性分析方法,通过对结构或系统的极限状态 方程进行一阶和二阶矩的近似计算,得到结构的可靠指标和失效概率。
该方法基于概率论和数理统计的基本原理,通过数学手段将结构的可靠性和失效 概率联系起来。
建立结构功能函数
根据结构的特点和设计要 求,建立结构功能函数, 描述结构的性能状态。
确定随机变量
分析影响结构性能的各种 因素,确定随机变量,如 荷载、材料属性等。
确定极限状态
根据结构功能函数,确定 结构的极限状态方程,即 失效边界。
结构可靠性分析的数学模型求解
一次二阶矩法
采用一次二阶矩法求解结构的可靠度 ,即利用随机变量的均值和方差计算 结构的失效概率。
1矩估计和极大似然估计
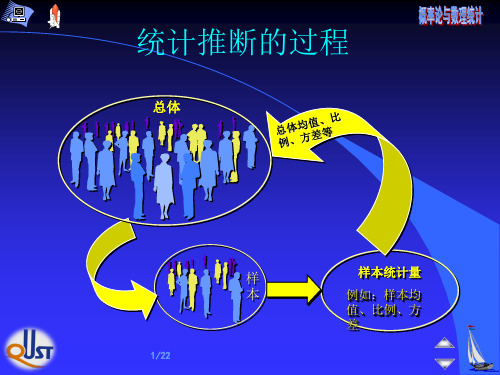
16/22
设总体 X 的分布函数中含 k 个未知参数
1 , 2 , k .
步骤一:记总体 X 的 m 阶原点矩 E(Xm)为 am , m =1,2,„,k. 一般地, am (m =1, 2, „, K) 是总体分布 故, 中参数或参数向量 (1, 2, „, k) 的函数。 am (m=1, 2, „, k) 应记成: am(1,2,…,k), m =1, 2, „, k.
13/22
例3:设总体X的均值为,方差为2,求 和 2 的矩估计。
解:由
E(X) , 2 2 2 E(X ) .
^ X, 即 ^ n 2 1 2 2 X i X . n i 1
14/22
即
ˆ X, ˆ2 1 n 2 (Xi X ) . n i 1
依样本对参数θ 做出估计,或估计参数 θ 的 某个已知函数 g(θ ) 。 这类问题称为参数估计。 参数估计包括:点估计和区间估计。
4/22
为估计参数 µ ,需要构造适当的统计量 T( X1, X2 , „ , Xn ), 一旦当有了样本,就将样本值代入到该统计 量中,算出一个值作为 µ的估计, 称该计算 值为 µ的一个点估计。
故,均值,方差2的矩估计为
ˆ X, 即 n 1 2 1 n 2 2 S . ˆ ( X X ) i n n i 1
15/22
如:正态总体N( , 2) 中 和2的矩估计为
ˆ X, ˆ2 1 n 2 ( X X ) . i n i 1
19/22
又如:若总体 X∼ U(a, b),求a, b的矩估计。
解:列出方程组
ˆ, E( X ) 2 ˆ Var ( X ) .
广义矩估计61页PPT

yi h(Xi,)i i 1,n
n
xji i 0
i1
j1,2, ,k
n
xji(yih (X i, ) )0 j1 ,2 , ,k
i 1
• 一组矩条件,普通最小二乘估计的正规方程组。
yi h(Xi,)i i 1,n
n
zji i 0
i1
of GMM Estimation, Econometrica 50, p1029-1054 • 关于GMM 的总结 A. Pagan and M. Wickens, 1989: A Survey of Some Recent Economertic Methods, Economic Journal 99, p962-1025
• 关于GMM发展的讨论
R. Davidson and J. MacKinnon, 1993: Estimation and Inference in Econometrics, New York Oxford Univ. Press
一、广义矩估计的概念
⒈几个重要的性质
• 从方法论角度
– 变量设定的相对性:直接与间接、内生与外生、随机 与确定。
• 如果满足所有基本假设,OLS的正规方程组为:
yi (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)0 yix1i (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)x1i 0 yix2i (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)x2i 0
• 如果x2为随机变量,z1为它的工具变量,IV的正 规方程组为:
yi (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)0 yix1i (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)x1i 0 yiz1i (ˆ0 ˆ1x1i ˆ2x2i ˆ3x3i)z1i 0
参数估计

(2)再用样本k阶矩代替相应的总体k阶矩
上一页
下一页
返回
设 总 体X ~ N ( , 2 ), , 2 未 知 , 设 例1: ( X 1 , X 2 ,..., X n )为 来 自 总 体 的 样 本 , 求 X 与 2的 矩 估 计 量 。
解:先建立待估参数与总体矩的关系
维随机变量,样本的联合概率密度为:
f ( x1 , x2 ,, xn ) f X 1 ( x1 ) f X 2 ( x2 ) f X n ( xn )
f ( x1 , ) f ( x2 , ) f ( xn , ) f ( xi , )
i 1
n
显然上式也为θ的函数,记作 L( ),即
L( ) f ( xi , )
i 1 n
我们称 L( ) 为似然函数。
小结:
似然函数
n p( x i ; ) i 1 L( ) n f ( x i ; ) i 1
由上可知,求极大似然估计值就是求使 L( ) 取最大的θ值。 下面我们用例子来说明求解极大似然估计值的步骤。
6
3
[ x dx x dx]
2 3 0 0
2
用样本k阶矩代替相应的总体k阶矩,得θ的矩估计量:
ˆ 2X
2)将数据代入,得θ的矩估计值为:
ˆ 2x 2 1 xi 8.9 8 i 1
8
计 算 器 的 使 用
例3:设总体X在区间[a,b]上服从均匀分布, a , b
实为 发生的概率。
根据极大似然原理,
概率大的事件在一次观测中更容易发生。
现在只做一次抽样, 事件 { X 1 x1 , X 2 x2 ,, X n xn } 故 认为其概率较大。 认为其概率较大。 也即我们应选择 使 L( ) 取最大值。 我们把使 L( ) 取最大值的 值称为 的极大 竟然发生了,
《广义矩估计》课件

《广义矩估计》课件
目录
CONTENTS
• 引言 • 广义矩估计的基本理论 • 广义矩估计的算法 • 广义矩估计的实例分析 • 广义矩估计的扩展和改进 • 结论与展望
01 引言
广义矩估计的定义
广义矩估计是一种统计估计方法,它 通过使用样本矩来估计未知参数。这 种方法基于样本矩和总体分布之间的 关系,通过最小化误差函数来求解参 数的估计值。
实例三:时间序列模型的广义矩估计
总结词
时间序列模型是用于描述时间序列数据之间 关系的模型,常见的有ARMA模型、 ARIMA模型等。广义矩估计也可以用于时 间序列模型的参数估计。
详细描述
在实例三中,我们将介绍如何使用广义矩估 计对时间序列模型的参数进行估计。我们将 首先介绍时间序列模型的基本概念和假设, 然后介绍如何利用广义矩估计方法对模型参 数进行估计,并给出具体的计算步骤和实例 分析。
03 广义矩估计的算法
算法的基本步骤
确定模型
根据数据特征和问题背景选择合适的概率模 型。
估计参数
利用样本数据和所选矩,通过优化算法求解 模型参数。
确定矩
根据所选模型,确定需要使用的矩(如一阶 矩、二阶矩等)。
验证估计
使用统计方法验证估计的参数是否符合所选 模型。
算法的实现细节
数据预处理
对原始数据进行清洗、去噪、标准化等处理 ,确保数据质量。
参数矩估计的步骤
首先计算样本数据的矩,然后利用这些矩和已知的总体分布关系来估计未知参 数。
广义矩估计的原理
广义矩估计的定义
广义矩估计是一种基于样本数据的矩来估计未知参数的统计方法,它不仅利用了 样本数据的矩信息,还利用了已知的总体分布信息。
广义矩估计的步骤
目录
CONTENTS
• 引言 • 广义矩估计的基本理论 • 广义矩估计的算法 • 广义矩估计的实例分析 • 广义矩估计的扩展和改进 • 结论与展望
01 引言
广义矩估计的定义
广义矩估计是一种统计估计方法,它 通过使用样本矩来估计未知参数。这 种方法基于样本矩和总体分布之间的 关系,通过最小化误差函数来求解参 数的估计值。
实例三:时间序列模型的广义矩估计
总结词
时间序列模型是用于描述时间序列数据之间 关系的模型,常见的有ARMA模型、 ARIMA模型等。广义矩估计也可以用于时 间序列模型的参数估计。
详细描述
在实例三中,我们将介绍如何使用广义矩估 计对时间序列模型的参数进行估计。我们将 首先介绍时间序列模型的基本概念和假设, 然后介绍如何利用广义矩估计方法对模型参 数进行估计,并给出具体的计算步骤和实例 分析。
03 广义矩估计的算法
算法的基本步骤
确定模型
根据数据特征和问题背景选择合适的概率模 型。
估计参数
利用样本数据和所选矩,通过优化算法求解 模型参数。
确定矩
根据所选模型,确定需要使用的矩(如一阶 矩、二阶矩等)。
验证估计
使用统计方法验证估计的参数是否符合所选 模型。
算法的实现细节
数据预处理
对原始数据进行清洗、去噪、标准化等处理 ,确保数据质量。
参数矩估计的步骤
首先计算样本数据的矩,然后利用这些矩和已知的总体分布关系来估计未知参 数。
广义矩估计的原理
广义矩估计的定义
广义矩估计是一种基于样本数据的矩来估计未知参数的统计方法,它不仅利用了 样本数据的矩信息,还利用了已知的总体分布信息。
广义矩估计的步骤
概率论与数理统计-点估计-矩法估计

x
dx
2
2
0
故令
1
n
n
i2
i 1
2ˆ2
n
于是解得 的矩估计量为
ˆ
1 2n
i2
i 1
估计量的评价 标准
点估计有多种方法,同一个未知参数用不同的方法可得 到不同的估计量,那一个估计量好呢?必须有个评价标准。 评价标准有多种,用不同方法评价,得到的结论也不一样。
因此,说一个估计量的好坏,必须说明是用那一个评价标准 评价的。否则,是没有意义的。
点估计的求法: (两种) 矩估计法和极大似然估计法.
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
理论依据: 大数定律
由辛钦大数定理知,
可以用
X
1 n
n i 1
Xi去估计EX,
如.求一个战士的射击命中率?
估计量,这个估计量称为矩估计量.
例2.设 : (, 2),求, 2的矩法估计量。
解:p( ,, 2 )
1
e
(
x )2 2 2
2
E x
1
(x )2
e 2 2 dx
2
xR
E 2 x2
1
(x )2
e 2 2 dx 2 2
2
列方程组:
2
1 n
n i1
2 1
n
i
n i 1
点估计问题就是要构造一个适当的统计量
ˆ(1,2 ,L ,n ),用它的观察值ˆ(x1, x2 ,L , xn ) 来估计未知参数 .
ˆ(1,2,L ,n )称为 的估计量. 通称估计,
矩阵分析课件精品PPT

典型例题解析
例1
求矩阵A的特征值和特征向量,其中A=[[3,1],[2,2]]。
例2
已知矩阵A的特征值为λ1=2, λ2=3,对应的特征向量为 α1=[1,1]T, α2=[1,-1]T,求矩阵A。
解析
首先求出矩阵A的特征多项式为f(λ)=(λ-1)(λ-4),解得特 征值为λ1=1, λ2=4。然后分别将特征值代入(A-λI)x=0求 解对应的特征向量。
应用举例
通过克拉默法则求解二元、三元线性方程组,并验证解的正确性 。
典型例题解析
01
例题1
求解三元线性方程组,通过高斯消元 法得到增广矩阵的上三角形式,然后 回代求解未知数列向量x。
02
03
例题2
例题3
判断四元线性方程组的解的情况,通 过计算系数矩阵的行列式|A|以及替换 列向量后的矩阵行列式|Ai|,根据克 拉默法则判断方程组的解是唯一解、 无解还是无穷多解。
特殊类型矩阵介绍
01
02
03
04
方阵
行数和列数相等的矩阵称为方 阵。
零矩阵
所有元素都是零的矩阵称为零 矩阵。
对角矩阵
除主对角线外的元素全为零的 方阵称为对角矩阵。
单位矩阵
主对角线上的元素全为1,其 余元素全为0的方阵称为单位 矩阵。
矩阵性质总结
Байду номын сангаас
01
结合律
02
交换律
03 分配律
04
数乘结合律
数乘分配律
• 对于每一个特征值m,求出齐次线性方程组(A-mI)x=0的一个基础解系,则A对应于特征值m的全部特征向量(其中I是与A 同阶的单位矩阵)。
特征值和特征向量求解方法
矩法估计[一类资料]
![矩法估计[一类资料]](https://img.taocdn.com/s3/m/93e58a3827d3240c8447efeb.png)
估计量,这个估计量称为矩估计量.
,k的
专业荟萃
10
例2.设 (, 2),求, 2的矩法估计量。
解:p( ,, 2 )
1
e
(
x )2 2 2
2
E x
1
(x )2
e 2 2 dx
2
xR
E 2 x2
1
(x )2
e 2 2 dx 2 2
2
列方程组:
2
1 n
n i1
2 1
1
x
2ex Fra bibliotekdx2
2
0
故令
1
n
n
i2
i 1
2ˆ2
n
于是解得 的矩估计量为
ˆ
1 2n
i2
i 1
专业荟萃
15
估计量的评价 标准
点估计有多种方法,同一个未知参数用不同的方法可得 到不同的估计量,那一个估计量好呢?必须有个评价标准。 评价标准有多种,用不同方法评价,得到的结论也不一样。
因此,说一个估计量的好坏,必须说明是用那一个评价标准 评价的。否则,是没有意义的。
bˆ 4.48 专业0荟.3萃962 3 5.1662
12
例4:设总体X的概率密度如下:求的矩法估计量ˆ ?
并求 D(ˆ) ?
6x 3(
P(x)
解: EX=
0
xP(x)dx x6x
-
0
x)
3 (
,
0
x)
x
其它
dx
2
列方程 2 X
解方程得 ˆ 2X 即为的矩法估计量。
又 EX2 = -
设总体的分布函数形式已知, 但它的一个或 多个参数为未知, 借助于总体的一个样本来估计 总体未知参数称为点估计问题.
,k的
专业荟萃
10
例2.设 (, 2),求, 2的矩法估计量。
解:p( ,, 2 )
1
e
(
x )2 2 2
2
E x
1
(x )2
e 2 2 dx
2
xR
E 2 x2
1
(x )2
e 2 2 dx 2 2
2
列方程组:
2
1 n
n i1
2 1
1
x
2ex Fra bibliotekdx2
2
0
故令
1
n
n
i2
i 1
2ˆ2
n
于是解得 的矩估计量为
ˆ
1 2n
i2
i 1
专业荟萃
15
估计量的评价 标准
点估计有多种方法,同一个未知参数用不同的方法可得 到不同的估计量,那一个估计量好呢?必须有个评价标准。 评价标准有多种,用不同方法评价,得到的结论也不一样。
因此,说一个估计量的好坏,必须说明是用那一个评价标准 评价的。否则,是没有意义的。
bˆ 4.48 专业0荟.3萃962 3 5.1662
12
例4:设总体X的概率密度如下:求的矩法估计量ˆ ?
并求 D(ˆ) ?
6x 3(
P(x)
解: EX=
0
xP(x)dx x6x
-
0
x)
3 (
,
0
x)
x
其它
dx
2
列方程 2 X
解方程得 ˆ 2X 即为的矩法估计量。
又 EX2 = -
设总体的分布函数形式已知, 但它的一个或 多个参数为未知, 借助于总体的一个样本来估计 总体未知参数称为点估计问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
由辛钦大数定律
设有一个统计总体的分布函数F(x, ),
其中 为未知参数.的范围是已知(称为参数空间)
现从该总体中抽取样本
1 , 2 , ...n
要依据该样本对参数 作出估计,或估计 的某个已知函数 g( ).
这类问题称为参数估计.(一般分点估计, 区间估计)
4
一、点估计问题的提法
设总体的分布函数形式已知, 但它的一个或 多个参数为未知, 借助于总体的一个样本来估计 总体未知参数称为点估计问题.
6
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 . 理论依据: 大数定律
7
由辛钦大数定理知,
可以用
X
1 n
n i 1
Xi去估计EX,
如.求一个战士的射击命中率?
事实上是我们已经知道X服从两点分布,
i2
ˆ =
解方程组:得
ˆ 2
1 n
n i1
(i
)2
即为和 2的矩法估计量。
11
例3 总体在[a,b]上均匀分布,a, b为未知参数,
(1,2 K ,n)为样本,求a, b的矩法估计量?
解:由前面的知识得 E = a+b , E 2 a2 ab b2
2
3
列方程组得
a+b 2
第六 章
点估计
1
6.1矩法估计
一、点估计问题的提法 二、矩法估计的求法 三、估计量的评价 标准
2
现在我们来介绍一类重要的统计推断问题
参数估计问题是利用从总体抽样得到的信息 来估计总体的某些参数或者参数的某些函数.
估计新生儿的平均体重
估计废品率 估计湖中鱼数
估计平均降雨量
… …
3
参数估计问题的一般提法
我们会计算出
1n
x
n
xi 28.695
i1
S2n
1 n
n
(xi x)2
i1
0.9185
来作为总体的期望、方差的点估计:
ˆ =28.695 ˆ 2 0.9815
这种方法就是替换原则:用样本矩去替换总体相应的矩 说的更本质一些,依据的原理是大数定律:
样本矩 np相应的总体矩
9
矩估计法的具体步骤:
a2
1 n
ab 3
n
i1
b2
i
1 n
n
i2
i1
aˆ
3( 2 2 )
解方程组得:
aˆ bˆ
3S 3S
即为a, b的矩法估计量。
若(4.5 5.0 4.7 4.0 4.2)为一组样本观测值,
算得 x 4.48 s 0.3962,则可得 a, b的矩法估计值
分别为 aˆ 4.48 0.3962 3 3.7938
bˆ 4.48 0.3962 3 5.1662
12
例4:设总体X的概率密度如下:求的矩法估计量ˆ ?
并求 D(ˆ) ?
6x 3(
P(x)
解: EX=
0
xP(x)dx x6x
-
0
x)
3 (
,
0
x)
x
其它
dx
2
列方程 2 X
解方程得 ˆ 2X 即为的矩法估计量。
又 EX2 = -
x2P(x)dx
0
x2 6x 3( x) dx 6 2 20
DX=EX2 (EX)2 6 2 20 ( 2)2 2 20
所以
D(ˆ)=D(2X)=4D(X)=4
2
20n
2
5n
13
例5 设总体 的分布密度为
p(x; )
1
x
e
( x , 0)
2
(1,2,L n) 为总体 的样本,求参数 的矩估
点估计问题就是要构造一个适当的统计量
ˆ(1,2 ,L ,n ),用它的观察值ˆ(x1, x2 ,L , xn ) 来估计未知参数 .
ˆ(1,2, ,n )称为 的估计量. 通称估计,
ˆ(x1, x2,
, xn )称为 的估计值.
简记为ˆ.
5
二、估计量的求法
由于估计量是样本的函数, 是随机变量, 故 对不同的样本值, 得到的参数值往往不同, 求估 计量的问题是关键问题. 点估计的求法: (两种) 矩估计法和极大似然估计法.
任务是估计参数p,
我们根据伯努里大数定理
显然可以用
n
n
1 n
n i 1
Xi去估计参数p.
用样本方差S2估计总体的方差DX,
8
例1:对某型20辆汽车纪录5L汽油所行驶的里程数, 29.8 27.6 28.3 27.9 30.1 28.7 29.9 28.0 27.9 28.7 28.4 27.2 29.5 28.5 28.0 30.0 29.1 29.8 29.6 26.9
2
e
x
dx
2
2
0
故令
1
n
n
i2
i 1
2ˆ2
n
于是解得 的矩估计量为
ˆ
1 2n
i2
i 1
15
估计量的评价 标准
点估计有多种方法,同一个未知参数用不同的方法可得 到不同的估计量,那一个估计量好呢?必须有个评价标准。 评价标准有多种,用不同方法评价,得到的结论也不一样。
因此,说一个估计量的好坏,必须说明是用那一个评价标准 评价的。否则,是没有意义的。
估计量,这个估计量称为矩估计量.
10
例2.设 : (, 2),求, 2的矩法估计量。
解:p( ,, 2 )
1
e
(
x )2 2 2
2
E x
1
(x )2
e 2 2 dx
2
xR
E 2 x2
1
(x )2
n
n i1
2 1
n
i
n i 1
(1).求出E j (1,2, ,k ) j 1, 2, k
(2).令 j
j
1 n
n
ij ;
i 1
j
1, 2,L
,k
这是一个包含 k 个未知参数1,2,L ,k 的方程组.
(3).解出其中1,2,L ,k , 用ˆ1,ˆ2,L ,ˆk表示.
(4).用方程组的解ˆ1,ˆ2,L ,ˆk分别作为1,2,L ,k的
1.相合性:设总体X的概率函数为f(x, ), 为未知参数,
ˆn n (X1, X2,....Xn )为的一个估计量,n为样本容量,
若对任意 0,
lim
n
P(
ˆn
) 1
成立,
则称ˆn为的相合估计量。(一致估计量)
由定义可知, 估计量 ˆn P (未知参数) 16
依据伯努利大数定律: 频率 i 是概率P的相合估计量,
计量.
解:由于 p(x; )只含有一个未知参数 ,一般
只需求出E 便能得到 的矩估计量,但是
E
xp(x; )dx
x
1
x
e dx 0
2
14
即 E 不含有 ,故不能由此得到 的矩估 计量.为此, 求
E( 2)
x2 p(x; )dx
x e dx 2 1
|x|
2
1
x
由辛钦大数定律
设有一个统计总体的分布函数F(x, ),
其中 为未知参数.的范围是已知(称为参数空间)
现从该总体中抽取样本
1 , 2 , ...n
要依据该样本对参数 作出估计,或估计 的某个已知函数 g( ).
这类问题称为参数估计.(一般分点估计, 区间估计)
4
一、点估计问题的提法
设总体的分布函数形式已知, 但它的一个或 多个参数为未知, 借助于总体的一个样本来估计 总体未知参数称为点估计问题.
6
一、 矩估计法 它是基于一种简单的“替换” 思想建立起来的一种估计方法 . 是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 . 理论依据: 大数定律
7
由辛钦大数定理知,
可以用
X
1 n
n i 1
Xi去估计EX,
如.求一个战士的射击命中率?
事实上是我们已经知道X服从两点分布,
i2
ˆ =
解方程组:得
ˆ 2
1 n
n i1
(i
)2
即为和 2的矩法估计量。
11
例3 总体在[a,b]上均匀分布,a, b为未知参数,
(1,2 K ,n)为样本,求a, b的矩法估计量?
解:由前面的知识得 E = a+b , E 2 a2 ab b2
2
3
列方程组得
a+b 2
第六 章
点估计
1
6.1矩法估计
一、点估计问题的提法 二、矩法估计的求法 三、估计量的评价 标准
2
现在我们来介绍一类重要的统计推断问题
参数估计问题是利用从总体抽样得到的信息 来估计总体的某些参数或者参数的某些函数.
估计新生儿的平均体重
估计废品率 估计湖中鱼数
估计平均降雨量
… …
3
参数估计问题的一般提法
我们会计算出
1n
x
n
xi 28.695
i1
S2n
1 n
n
(xi x)2
i1
0.9185
来作为总体的期望、方差的点估计:
ˆ =28.695 ˆ 2 0.9815
这种方法就是替换原则:用样本矩去替换总体相应的矩 说的更本质一些,依据的原理是大数定律:
样本矩 np相应的总体矩
9
矩估计法的具体步骤:
a2
1 n
ab 3
n
i1
b2
i
1 n
n
i2
i1
aˆ
3( 2 2 )
解方程组得:
aˆ bˆ
3S 3S
即为a, b的矩法估计量。
若(4.5 5.0 4.7 4.0 4.2)为一组样本观测值,
算得 x 4.48 s 0.3962,则可得 a, b的矩法估计值
分别为 aˆ 4.48 0.3962 3 3.7938
bˆ 4.48 0.3962 3 5.1662
12
例4:设总体X的概率密度如下:求的矩法估计量ˆ ?
并求 D(ˆ) ?
6x 3(
P(x)
解: EX=
0
xP(x)dx x6x
-
0
x)
3 (
,
0
x)
x
其它
dx
2
列方程 2 X
解方程得 ˆ 2X 即为的矩法估计量。
又 EX2 = -
x2P(x)dx
0
x2 6x 3( x) dx 6 2 20
DX=EX2 (EX)2 6 2 20 ( 2)2 2 20
所以
D(ˆ)=D(2X)=4D(X)=4
2
20n
2
5n
13
例5 设总体 的分布密度为
p(x; )
1
x
e
( x , 0)
2
(1,2,L n) 为总体 的样本,求参数 的矩估
点估计问题就是要构造一个适当的统计量
ˆ(1,2 ,L ,n ),用它的观察值ˆ(x1, x2 ,L , xn ) 来估计未知参数 .
ˆ(1,2, ,n )称为 的估计量. 通称估计,
ˆ(x1, x2,
, xn )称为 的估计值.
简记为ˆ.
5
二、估计量的求法
由于估计量是样本的函数, 是随机变量, 故 对不同的样本值, 得到的参数值往往不同, 求估 计量的问题是关键问题. 点估计的求法: (两种) 矩估计法和极大似然估计法.
任务是估计参数p,
我们根据伯努里大数定理
显然可以用
n
n
1 n
n i 1
Xi去估计参数p.
用样本方差S2估计总体的方差DX,
8
例1:对某型20辆汽车纪录5L汽油所行驶的里程数, 29.8 27.6 28.3 27.9 30.1 28.7 29.9 28.0 27.9 28.7 28.4 27.2 29.5 28.5 28.0 30.0 29.1 29.8 29.6 26.9
2
e
x
dx
2
2
0
故令
1
n
n
i2
i 1
2ˆ2
n
于是解得 的矩估计量为
ˆ
1 2n
i2
i 1
15
估计量的评价 标准
点估计有多种方法,同一个未知参数用不同的方法可得 到不同的估计量,那一个估计量好呢?必须有个评价标准。 评价标准有多种,用不同方法评价,得到的结论也不一样。
因此,说一个估计量的好坏,必须说明是用那一个评价标准 评价的。否则,是没有意义的。
估计量,这个估计量称为矩估计量.
10
例2.设 : (, 2),求, 2的矩法估计量。
解:p( ,, 2 )
1
e
(
x )2 2 2
2
E x
1
(x )2
e 2 2 dx
2
xR
E 2 x2
1
(x )2
n
n i1
2 1
n
i
n i 1
(1).求出E j (1,2, ,k ) j 1, 2, k
(2).令 j
j
1 n
n
ij ;
i 1
j
1, 2,L
,k
这是一个包含 k 个未知参数1,2,L ,k 的方程组.
(3).解出其中1,2,L ,k , 用ˆ1,ˆ2,L ,ˆk表示.
(4).用方程组的解ˆ1,ˆ2,L ,ˆk分别作为1,2,L ,k的
1.相合性:设总体X的概率函数为f(x, ), 为未知参数,
ˆn n (X1, X2,....Xn )为的一个估计量,n为样本容量,
若对任意 0,
lim
n
P(
ˆn
) 1
成立,
则称ˆn为的相合估计量。(一致估计量)
由定义可知, 估计量 ˆn P (未知参数) 16
依据伯努利大数定律: 频率 i 是概率P的相合估计量,
计量.
解:由于 p(x; )只含有一个未知参数 ,一般
只需求出E 便能得到 的矩估计量,但是
E
xp(x; )dx
x
1
x
e dx 0
2
14
即 E 不含有 ,故不能由此得到 的矩估 计量.为此, 求
E( 2)
x2 p(x; )dx
x e dx 2 1
|x|
2
1
x
