计算流体力学(中科院力学所)_第3讲-差分方法1
计算流体力学CFD的基本方法与应用

CFD的作用像在计算机上做实验,故也称数值实验, 它 不但能取代很多实验工作,而且能做实验室无法进 行的研究。
作, Patankar也在美国工程师协会的协助下,举行了大范围的培训, 皆在推广应用 CFD。 1985年的第四界国际计算流体力学会议上,Spalding 作了 CFD 在工程 设计中的应用前景的专题报告。他将工程中常见的流动、传热、化学 反应等分为十大类问题,并指出CFD都有能力加以解决。
2、CFD的发展历程
性、可靠性及工业化推广应用。
1977年,Spalding等开发的用于预测二维边界层内的迁移现象的GENMIX 程序公开,其后,他们首先意识到公开计算源程序很难保护自己的知 识产权。
在1981年,组建的CHAM公司将包装后的计算软件(PHONNICS-凤凰)正 式投放市场,开创了CFD商业软件的先河。
LES——穷人的DNS
CFD的未来,近期的展望
CFD的未来,远期的展望
• 非线性计算方法的突破 • LES模型的逐步成熟 • 大规模计算、并行计算的发展可以解决DNS、LES、非定
常计算的海量计算等问题 • 先进的湍流模型,反应动力学模型,多相流模型等的逐
步ቤተ መጻሕፍቲ ባይዱ善
CFD的路还很长很长
• CFD是一个新兴的学科 • CFD具有重要的应用 • CFD还有很多问题
计算流体力学CFD的基本 方法与应用
CFD (Computational Fluid Dynamics) 计算流体力学——为您打开通向高科技之门
计算流体力学CFD课件

V
dV
0
空间位置固定的无穷小微团模型 V 0 t
随流体运动的无穷小微团模型
方程不同形式之间的转换
空间位置固定的有限控制体模型 tV dVSVdS0
空间位置固定的无穷小微团模型 V 0 t
方程不同形式之间的转换
空间位置固定的无穷小微团模型 V 0 t
随流体运动的无穷小微团模型
流动控制方程经常用物质导数来表达。
物质导数(运动流体微团的时间变化率)
采用流体微团模型来理解物质导数的概念:
沿流线运动的无穷小 流体微团,其速度等 于流线上每一点的当
物质导数(运动流体微团的时间变化率)
流体微团在流场中的运动-物质导数的示意图
物质导数(运动流体微团的时间变化率)
考虑非定常流动:
随流体运动的无穷小微团模型
动量方程
作用在流体微团上的体 积力的X方向分量=
fxdxdydz
随流体运动的无穷小微团模型
动量方程
作用在流体微 团上的X方向的 压力=
动量方程
作用在流体微 团上的X方向的 正应力=
动量方程
作用在流体微 团上的X方向的 切应力=
动量方程
作用在流体微 团上的X方向总 的表面力=
t
或
txuyv zw0
空间位置固定的无穷 小微团模型
空间位置固定的无穷小微团模型
连续性方程:
txuyv zw0
或
V0
t
空间位置固定的无穷 小微团模型
随流体运动的无穷小微团模型
随流体运动的无穷小微团模型
连续性方程 流体微团的质量:
质量守恒定律
随流体运动的无穷小 微团模型
随流体运动的无穷小微团模型
流体微团在流场中的 运动-物质导数的示 意图
中科院计算流体力学最新讲义CFD115讲差分方法3共42页PPT资料
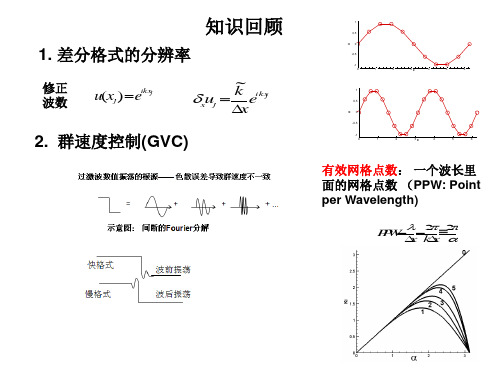
1. 差分格式的分辨率
修正 波数
u(xj ) eikxj
~
xuj
k eikxj x
2. 群速度控制(GVC)
u
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
u
有效网格点数: 一个波长里 面的网格点数 (PPW: Point per Wavelength)
PPW xk2 x2
差分方程单调性(无振荡)条件: 差分方程 (1)中的系数非负
u n j 1 tu n j u n j 1 2 x u n j 1 R 1 x 2 e (u n j 1 2 u n j u n j 1 )
t/x
u n j 1 ( R e 1 x 1 2 ) u n j 1 ( 1 R 2 e x ) u n j ( R e 1 x 2 1 ) u n j 1
双曲型守恒方程
u f (u) 0 t x
特点: 沿特征线 d/xd t a, u不变
a f u
特征线未相交—— 总变差不变
特征线相交—— 总变差减小
结论: 单个双曲型方程,总变差不增 (Total Variation Diminishing: TVD)
Copyright by Li Xinliang
分离流—— 对粘性敏感
Von Neumann
(b1x)2I
x
U x
U x
MacCormack
a2x3ቤተ መጻሕፍቲ ባይዱ
|u|c2pU
x
计算流体力学有限差分法

计算流体力学有限差分法流体力学有限差分法(Finite Difference Method,FDM)是一种常用的计算流体力学的方法。
它是基于流体力学基本方程对系统求解压力、速度和位置变化的一种近似数值方法,这些方程可以使用有限差分法求解得到准确结果。
一、流体力学有限差分法的概念1、端点条件:端点条件是差分方程组确定变量的边界条件,主要有边界条件和内部条件。
2、场变量定义:流动的物质可以用速度、压力和密度来描述,这种变量称为场变量。
3、有限差分法:有限差分法试图使描述精度在最小情况下得到一个可以接受的结果。
它将待求解区域划分为若干个小块,并且计算每一个小块上的变量。
4、边界条件:边界条件是用来描述物理事件发生的时候的物理量,如压力、流动量等。
二、流体力学有限差分法的基本步骤1、数学模型:开发有限差分方程,用来描述流体力学问题,这种模型可以由流体力学的基本方程得到。
2、网格划分:将区域网格划分成更小的网格,为了更准确的解决流体力学问题。
3、空间离散:将每一个网格按照有限差分公式空间离散,获得离散的压力方程式。
4、时间离散:在解决大规模动态流体力学问题时,通过一个更小的时间步骤进行求解。
5、求解:用适当的方法和算法求解有限差分方程式,获得求解结果。
三、流体力学有限差分法的优势1、高精度:使用此法,可以获得较高数值精度,从而准确描述流体力学过程。
2、计算效率:该方法可以快速找出有效的解决方案,并且计算效率更高。
3、计算能力:此方法可以处理复杂的物理问题,而且没有太多的硬件限制。
4、收敛性:当求解复杂的物理问题时,有限差分法不太容易出现"收敛"的情况。
5、可靠性:此方法可以快速、准确的求解出可靠的结果,相对于其他求解方法,其精度更高。
四、总结流体力学有限差分法是一种常用的计算流体力学的方法。
它易于实施,并且可以获得较高数值精度,从而准确描述流体力学过程。
处理复杂的物理问题时,它可以提供较快、较准确的结果,更能可靠性和可靠性更好。
第13章 计算流体力学CFD(3)PPT课件

误差与稳定性分析
根据von Neumann(冯诺伊曼)稳定性分析方法,设 误差随空间和时间符合如下Fourier级数分布: 则
97
误差与稳定性分析
稳定性要求
故放大因子
G eat 1
98
误差与稳定性分析
下面采用von Neumann(冯诺伊曼)稳定性分析方法 分析如下差分方程的稳定性:
由于误差也满足差分方程,故有
90
误差与稳定性分析
A=偏微分方程的精确解(解析解)
D=差分方程的精确解 离散误差=A-D
91
误差与稳定性分析
D=差分方程的精确解 N=在某个有限精度的计算机上实际计算出来的解
(数值解) 舍入误差==N-D
N=D+
92
误差与稳定性分析
数值解N=精确解D+误差 数值解N满足差分方程,于是有
93
误差与稳定性分析
在网格点3: 在网格点4: 在网格点5:
A,B,Ki 均为已知量
78
隐式方法
在网格点6:
A,B,Ki 均为已知量
T7 为边界条件,已知量
79
隐式方法
于是有关于T2,T3,T4,T5, T6这五个未知数的五个方程
A,B,Ki 均为已知量
80
隐式方法
写成矩阵形式:
81
隐式方法
系数矩阵是一个三对角矩阵,仅在三条对角线上有非 零元素。 求解线性代数方程组的标准方法是高斯消去法。应用 于三对角方程组,通常采用托马斯算法(国内称为追 赶法)求解。
113
22
有限差分基础
对Y方向的二阶导数有:
二阶中心差分(关于Y方向二阶导数)
23
有限差分基础
西交大《计算流体动力学》课件CFD第三章

n
n
n
u i u i 1 u o x x x i
n n
n
计算流体动力学课程
西安 2005年3月
XJTU
2.构造差分格式的方法
一阶导数的差商表达式 名称 一阶前向差商 表达式
f i 1 f i x
f i f i 1 x
f x i
t 0
边界条件
t 0
计算流体动力学课程
西安 2005年3月
XJTU
1. 有限差分方法
网格划分及方程离散化
t (j,n) n x
x j j x
j 0 ,1, 2 , J
t n nt
n 0 ,1, 2 ,
u
n j
u j u j x , n t
n n n n
ui
n 1
ui
n 1
t
x
u
n i 1
u i 1
n
西安 2005年3月
XJTU
3.模型方程的差分格式
u t u x 0
格式名称
二阶精度的两步 MacCormack显示格式
ui u
n 1
格式表达式
u
n i
t
x
u
n i 1
二阶精度的时间-中 心隐式格式
ui
n 1
ui
n
计算流体动力学课程
西安 2005年3月
XJTU
3.模型方程的差分格式
u t b u
2
x
2
格式名称 时间一阶精度、空间二 阶精度的显示格式 二阶精度的三层 Richardson显示格式 二阶精度的Crank- u u t Nicolson隐式格式
计算流体力学(中科院力学所_李新亮)——_经典转载 (1)

0 31 32 G3 (U ) 33 C p T u 31 v 32 w 33 Copyright by Li Xinliang Pr Re z
ui u j i j ), ( x j xi ij (2 ui 2 divV ), i j xi 3
波音787 波音777
Copyright by Li Xinliang 8
CFD 面临的挑战及主要任务:
多尺度复杂流动的数学模型化; 湍流的计算模型; 转捩的预测模型; 燃烧及化学反应模型; 噪声模型…… 可处理间断及多尺度流场的高分辨率、强鲁棒性、高效数值方法; 高精度激波捕捉法; 间断有限元法; …… 可处理复杂外形、易用性强的算法; 复杂外形—— 网格生成工作量大 多块分区算法; 无网格法; 粒子算法;
Mach10 正激波
60°
平板
Copyright by Li Xinliang
5
连续解 微分方程
U ( F Fv ) (G G v ) ( H H v ) 0 t x y z
Mach10 正激波
↓
网格划分 数值方法
60°
平板
↓
解的离散表示 代数方程
↓
Copyright by Li Xinliang
2
第1讲 流体力学基本方程
• 计算流体力学(CFD) 的概念及意义 • 流体力学的基本方程 • 偏微分方程组的类型 重点: 了解N‐S方程的由来及物理含义,熟练掌握N‐S方程 了解偏微方程的基本类型
Copyright by Li Xinliang 3
u v u 2 p u uv U v F1 (U ) uv F2 (U ) v 2 p uw vw w u ( E p ) E v ( E p )
应用计算流体力学基础AppliedComputationalFluidMechanics.ppt

Talor级数展开法:
q(x)
q(xi
)
(x
பைடு நூலகம்
xi
)
q x
i
(x
xi 2!
)2
2q x2
i
(x
xi n!
)n
nq xn
i
H
向前差分: x xi1 向后差分: x xi1
中心差分? x xi1 and x xi1
qi1 2qi qi1
x
(x)2
有限差分法
4 其他导数的差分逼近式
交叉导数项
边界导数项
有限差分法
补充:三次样条插值函数与紧致差分格式
三次样条插值函数满足: (1) 分区间光滑,每一小区间上为不高于三次的多项式; (2) 整个区间一阶和二阶导数连续。
在区间(xi-1,xi)内,令hi=xi-xi-1
有限差分法
2 一阶导数的差分逼近式
差分逼近的精度:
如果截断误差 r (x)m fm (x)m1 fm1 O(xm )
则称该格式为导数的m阶差分逼近式
向前差分? 向后差分? 中心差分?
有限差分法
2 一阶导数的差分逼近式
待定系数法:
利用 xi , xi1, xi2 三点如何构造一个二阶的差分逼近?
相容性
数 学 模 型
离 散 方 程 稳定性
精 确 解
数 值 解
收敛性
Lax定理:给定的适定线性的初值问题的微分方程,若与它逼近 的差分方程和它是相容的,则差分方程的稳定性是其收敛性的充
分必要条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(等距网格) 等距网格)
u 2u = 2 t x
0 ≤ x ≤ 1,0 ≤ t ≤ T
u j +1 u j u + O (x) = x x j u j +1 u j 1 u + O( x 2 ) = 2x x j
u 1 2u 1 3u 2 u j +1 = u j + ( ) j x + ( 2 ) j x + ( 3 ) j x 3 ...... x 2! x 3! x
分析误差对网格步长的依赖关系 lg err 斜率为精度的阶数 (通常用最小二乘法计算)
常用的模: 常用的模: φ 1 模: 2 模: φ 无穷模: 无穷模
j 1
= =
∑φ
j
j
j 2
1 N
j
∑φ
j
2 j
φj
∞
= max φ j
lg x
典型的文章: 提出方法+理论分析 + 算例验证
Copyright by Li Xinliang
Shu-Osher问题的计算结果 (Li et 问题的计算结果 al. Init. J. Num. Fluid. 2005)
航空领域权威的考核算例—— DPW标准计算模型 航空领域权威的考核算例 标准计算模型
Copyright by Li Xinliang 常用一、 常用一、二维算例整理后已发到流体中文网 6
基本概念: 基本概念:
a. 差分表达式及截断误差 差分表达式及截断误差:
精度 (1阶) 截断误差 (2阶)
2 u u j +1 u j 1 u 2 x + L = x 2! x j x j
u j +1 u j 1 1 3u u + ( 3 ) j x 2 = 2x 3! x x j
n +1 n u n u n1 x u u u j u j x 2 t t 2 j j +a = +a u xx + u xxx + utt + uttt + ...... t x t x 2 6 2 6
微分方程=差分方程 截断误差 微分方程 差分方程+截断误差 差分方程
u n +1 u n j j t
讲义、 流体中文网) 流体论坛” “ 讲义、课件上传至 (流体中文网) -> “流体论坛” ->“ CFD基础理论 ” 流体中文网 基础理论
1 Copyright by Li Xinliang
有限差分法( ) 第三讲 有限差分法(1) 教材第3.1、 节及第 节及第4章 (教材第 、3.2节及第 章)
2 u u j +1 u j u x 2 = x 2! + L x x j j
u j +1 u j 1 1 3u u = + ( 3 ) j x 2 2x 3! x x j
u n +1 u n j j t
=
1 +1 +1 u n+1 2u n +1 + u n1 j j j 2 x
∑ ( j 3)
j =1
4
k
a j = bk
k = 0 ,1, 2 ,3
格式优化; 格式优化; 分析; 通过数值计算手段进行 Fourier分析 分析 ……
Copyright by Li Xinliang
7
§ 3.1 有限差分法基本原理 1. 差分方法的基本原理 离散点上利用Taylor展开,把微分转化成差分 展开, 微分转化成差分 离散点上利用 展开 转化成
研究CFD的计算手段 的计算手段 研究
例: 差分格式构造
理论方法: 手工推导系数(工作量大) 理论方法: 手工推导系数(工作量大) 数值方法: 数值方法: 通过数值手段推导系数
u = a1u j 2 + a2 u j 1 + a3u j + a4 u j +1 + O(3 ) x j
数值求解, 数值求解,获得系数
2
理论研究
“计算流体力学”作为一个学 计算流体力学” 其研究手段依然包括理论、 科, 其研究手段依然包括理论、 实验及数值模拟。 实验及数值模拟。
流体 力学
实验研究
理论研究: 理论研究: 格式推导、 稳定性分析, 格式推导、 稳定性分析, 精度/误差分析 误差分析, 精度 误差分析,……
数值研究
计算流体力学 数值计算技术、 (数值计算技术、 计算方法研究) 计算方法研究) 实验研究: 实验研究: 数值实验, 数值实验, 采用 实际问题考核方法 的正确性
4
理论分析的局限性: 对于复杂系统(非线性方程、非线性格式) 理论分析的局限性: 对于复杂系统(非线性方程、非线性格式)非常困难
研究CFD的实验手段 的实验手段 研究
思想: 通过具体算例来研究(考核,分析…) 思想: 通过具体算例来研究(考核,分析 )差分方法 例: 精度分析 du 差分离散 dx
处理复杂网格不够灵 相对简单外形的 高精度计算 活 不易提高精度( 不易提高精度(二阶 复杂外形的工程 以上方法复杂) 以上方法复杂) 计算 对于复杂方程处理困 多用于固体力学 等 难 外形、 外形、边界条件简单 简单外形的高精 度计算 精度不易提高 复杂外形的工Xinliang
波数空间单一的依赖关系: 波数空间单一的依赖关系: vk = f (u k )
线性差分系统: 针对一个单波 研究经过差 一个单波, 一个单波 分系统后的变化就可以了解该系统。 Fourier误差分析; Fourier稳定性分析
Copyright by Li Xinliang
原理: 原理: 线性系统,输入一个波, 线性系统,输入一个波,只能 输出一个波(且波数不变)。 输出一个波(且波数不变)。 非线性系统会产生多个谐波
计算流体力学讲义
有限差分法( ) 第三讲 有限差分法(1)
李新亮 lixl@ ;力学所主楼 力学所主楼219; 82543801 ;
知识点: 知识点:
差分方法的理论基础 (相容、收敛、稳定性;Lax等价定理;精度、修正方程; 守恒性) 相容、收敛、稳定性; 等价定理;精度、修正方程 守恒性) 等价定理 差分格式的构造 差分格式的Fourier分析 差分格式的 分析
t
+a
u n u n1 j j x
x
x ax 2 t t 2 = ut + a u x + u xx u xxx + utt + uttt + ...... 2 6 2 6
=0
差分方程=微分方程 截断误差 差分方程 微分方程-截断误差 微分方程 新的微分方程(修正方程) ≡ 新的微分方程(修正方程)
后
j-1 j
前
j+1 …
其他: 向前( 偏心差分; 其他: 向前(后)偏心差分
c.
差分方程 经差分离散后的方程, 经差分离散后的方程,称为差分方程
u u +a =0 t x
u n +1 u n j j t +a u n u n1 j j x =0
如何确定精度? 如何确定精度? 1) 理论方法, 给出误差表达式 ) 理论方法, 2)数值方法, 给出误差对 x )数值方法, 的数值依赖关系
2维算例: 维算例: 维算例 后台阶、 问题、 激波干扰、 前/后台阶、双马赫反射、二维 后台阶 双马赫反射、二维Riemann问题、漩涡 激波干扰、翼 问题 漩涡-激波干扰 型扰流、 型扰流、圆柱绕流 3维复杂算例: 维复杂算例: 维复杂算例 各向同性湍流的DNS, 槽道湍流的 槽道湍流的DNS, 激波 边界层干扰的 激波-边界层干扰的 边界层干扰的DNS 各向同性湍流的
1 2u a 2u TE = 2 t + 2 x + L 2! t j 2! x j
n n
微分方程
差分方程
截断误差: 截断误差:
Copyright by Li Xinliang
9
d. 差分方程的修正方程
修正方程—— 差分方程准确逼近(无误差逼近)的方程 差分方程准确逼近(无误差逼近) 修正方程
例:Fourier分析 分析 线性系统: 线性系统: 线性方程+ 线性方程 线性格式 初始值 差分系统 (解差分 解差分 方程) 方程 数值解( 数值解(特 定时刻离散 的函数值) 的函数值)
记为: v j = Φu j Φ 是差分算子,把离散函数 是差分算子, 有限点列) (有限点列){u j }映射为另 一个离散函数 {v j }
传统计算方法: 有限差分法, 有限元法, 谱方法(谱元法) 传统计算方法: 有限差分法, 有限体积法 , 有限元法, 谱方法(谱元法)等; 最近发展的方法: 基于粒子的算法(格子 ),无网格 最近发展的方法 基于粒子的算法(格子-Boltzmann, BGK),无网格 ), 优点 有限差分法 有限体积法 有限元法 谱方法 粒子类方法 简单成熟, 简单成熟,可构造高精 度格式 守恒性好, 守恒性好,可处理复杂 网格 基于变分原理, 基于变分原理,守恒性 好 精度高 算法简单, 算法简单,可处理复杂 外形 缺点 适用范围
差分表达式
b. 前差、后差、中心差 前差、后差、
u j +1 u j u + O (x) = x x j u j u j 1 u + O (x) = x j x u j +1 u j 1 u + O( x 2 ) = 2x x j
前差 后差 中心差
… j-2
修正方程
u n +1 u n j j
+a
u n u n1 j j
等价于
x x 2 t t 2 ut + a u x + u xx u xxx utt uttt + ...... = 0 2 6 2 6
