中科院计算流体力学最新讲义CFD1112讲湍流及转捩2
合集下载
【计算流体力学】第13讲-湍流与转捩2
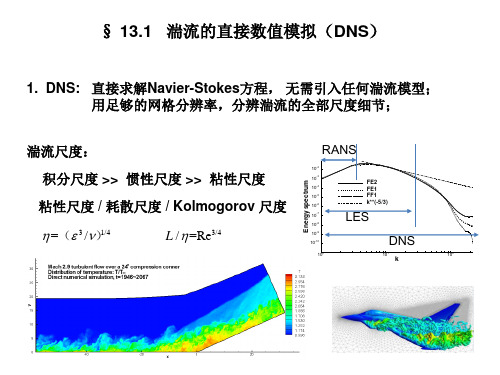
DNS: 研究该问题的有力手段 尚无他人DNS报道
a
头激波
边
界
横流
层 转
捩
线
示例2：有攻角小头钝锥边界层转捩的DNS 2） 计算参数及方法
Ren(头半径度量)
10000
Ma (攻角) Tw(壁温) T 半锥角
6
1度
294K
79K 5
数值计算： 自主开发的程序(OpenCFD-SC)
直接数值模拟； 高精度差分法
湍流的产生、 拟序涡演化、 摩阻/热流/雷诺应力
抑制湍流、 利用湍流
湍流模型
评估模型、 改进模型
湍射流的涡量分布：DNS
RANS
3. DNS对计算资源需求强烈
年代
2080
2045
2010 2000 1990
1980
DNS LES
Splart 的 预期
非定常
RANS/DES
粘性NS方程 (RANS)、定常
t C f k2 /
U
* ij
Sij Sij *ij*ij
根据实验结果 C 不是常数
C
A0
1 AsU *k
/
A0 4.0, As
6 cos, 1 cos1( 3
6w),
w
Sij S jk Ski (Sij Sij )3/2
3） 低Reynolds数k-模型
t
C
f
k(k
)
近壁区进行了修正，增大 了湍流粘性系数
u j xi
2 3
uk xk
2 3
ij
k
t C f k2 /
C 0.09
f exp(3.4 / (1 0.02Ret )2)
湍流力学课件二
哈尔滨工业大学燃烧工程研究所
纵向和横向相关函数的形状讨论
对涡的形式，很难给出准确的分布曲线， 从均匀性出发，
u2 ( 2 )u2 ( 2 r ) u2 ( 2 r )u2 ( 2 )
u2 ( 2 r ) u2 ( 2 r ) u2 ( 2 ) u2 ( 2 ) ( 2 r ) ( 2 r )
哈尔滨工业大学燃烧工程研究所
同样可得到积分时间尺度
可以理解为保持湍流行为中最大时间尺度一种 度量
TE E ( )d
0
在均匀湍流场内有一常数平均速度<U1>，假
定 U1 u1 ，则在流场内一固定空间点上所观 测到u1(t) 随时间变化情况，可以近似的看成是 由在沿着过此点的x1方向的直线上分布的速度 空间变化，设想被冻结起来，以平均速度 <U1>移过此点形成——Taylor冻结流假设。
2 4 2
哈尔滨工业大学燃烧工程研究所
2
2
曲线原点可得密切抛物线方程为
2 E ( ) 1 2 E
其中
1 u1 1 2E 2 2 2 E 2u1 t 2 t t 0 1
2
，τ E为一个时间尺度。
表示了脉动速度脉动u1(t)最快变化的时间尺度 的代表，从耗散角度讲，它是指小涡生存时间， 因为与Taylor微尺度之间密切联系，称为欧拉 耗散涡时间尺度。它不仅与流场内湍流结构有 关，且与主流速度对该点输运特性有关。
当r→0时，K-H方程变为
2 d u 2 2 u (t ) 10 2 dt g 3
或
2 d 3 u 2 u ( t ) 15 2 dt 2 g
计算流体力学CFD课件
V
dV
0
空间位置固定的无穷小微团模型 V 0 t
随流体运动的无穷小微团模型
方程不同形式之间的转换
空间位置固定的有限控制体模型 tV dVSVdS0
空间位置固定的无穷小微团模型 V 0 t
方程不同形式之间的转换
空间位置固定的无穷小微团模型 V 0 t
随流体运动的无穷小微团模型
流动控制方程经常用物质导数来表达。
物质导数（运动流体微团的时间变化率）
采用流体微团模型来理解物质导数的概念：
沿流线运动的无穷小 流体微团，其速度等 于流线上每一点的当
物质导数（运动流体微团的时间变化率）
流体微团在流场中的运动－物质导数的示意图
物质导数（运动流体微团的时间变化率）
考虑非定常流动：
随流体运动的无穷小微团模型
动量方程
作用在流体微团上的体 积力的X方向分量＝
fxdxdydz
随流体运动的无穷小微团模型
动量方程
作用在流体微 团上的X方向的 压力＝
动量方程
作用在流体微 团上的X方向的 正应力＝
动量方程
作用在流体微 团上的X方向的 切应力＝
动量方程
作用在流体微 团上的X方向总 的表面力＝
t
或
txuyv zw0
空间位置固定的无穷 小微团模型
空间位置固定的无穷小微团模型
连续性方程：
txuyv zw0
或
V0
t
空间位置固定的无穷 小微团模型
随流体运动的无穷小微团模型
随流体运动的无穷小微团模型
连续性方程 流体微团的质量：
质量守恒定律
随流体运动的无穷小 微团模型
随流体运动的无穷小微团模型
流体微团在流场中的 运动－物质导数的示 意图
第15讲-湍流及转戾
更复杂的非线性项： 出现了压力关连项： 粘性项也是非线性的：
(3.1)
ui u j
pui
u i ij
ij (T )Sij (u)
(Sij ui , j u j ,i 2 / 3uk ,k ij )
热传导项也是非线性的：
qi T,i
当马赫数不是很高时，粘性项及热传导项的非线性是很弱的
3 3
3/ 2 6 ( x ) e
2
/ 2 1
d
如采用Gaussian型滤波有如下性质 设 f 的滤波尺度为
f
e
6 ( x ) 2 / 2
d f ( )e 6 ( ) e
2
/ 2
d
相当于
2
尺度的滤波
f ( )e
3/ 2
6 ( x ) 2 / 2 6 ( ) 2 / 2
x
2. 滤波的性质
f g f g
A.若采用Box 滤波及谱截断滤波则：
f f
令： f f f
则:
f 0,
f g f g,
B. 若采用一般的滤波器则：
f f
6 f ( x) 1
6 f ( x) 2 6 2
3 常用的衰减函数： D 1 exp(( y / A ) )
ห้องสมุดไป่ตู้
, A 25
算出 ij 后，乘以该 函数即可
（2）相似模型
ij ui u j ui u j
u
大尺度 小尺度
u
u
假设不同尺度对雷诺应力的贡献是相似的
将上式中的 u i 换成 u i 得
(3.1)
ui u j
pui
u i ij
ij (T )Sij (u)
(Sij ui , j u j ,i 2 / 3uk ,k ij )
热传导项也是非线性的：
qi T,i
当马赫数不是很高时，粘性项及热传导项的非线性是很弱的
3 3
3/ 2 6 ( x ) e
2
/ 2 1
d
如采用Gaussian型滤波有如下性质 设 f 的滤波尺度为
f
e
6 ( x ) 2 / 2
d f ( )e 6 ( ) e
2
/ 2
d
相当于
2
尺度的滤波
f ( )e
3/ 2
6 ( x ) 2 / 2 6 ( ) 2 / 2
x
2. 滤波的性质
f g f g
A.若采用Box 滤波及谱截断滤波则：
f f
令： f f f
则:
f 0,
f g f g,
B. 若采用一般的滤波器则：
f f
6 f ( x) 1
6 f ( x) 2 6 2
3 常用的衰减函数： D 1 exp(( y / A ) )
ห้องสมุดไป่ตู้
, A 25
算出 ij 后，乘以该 函数即可
（2）相似模型
ij ui u j ui u j
u
大尺度 小尺度
u
u
假设不同尺度对雷诺应力的贡献是相似的
将上式中的 u i 换成 u i 得
中科院计算流体力学最新讲义CFD115讲差分方法3共42页PPT资料
知识回顾
1. 差分格式的分辨率
修正 波数
u(xj ) eikxj
~
xuj
k eikxj x
2. 群速度控制(GVC)
u
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
u
有效网格点数： 一个波长里 面的网格点数 （PPW: Point per Wavelength)
PPW xk2 x2
差分方程单调性（无振荡）条件： 差分方程 （1）中的系数非负
u n j 1 tu n j u n j 1 2 x u n j 1 R 1 x 2 e (u n j 1 2 u n j u n j 1 )
t/x
u n j 1 ( R e 1 x 1 2 ) u n j 1 ( 1 R 2 e x ) u n j ( R e 1 x 2 1 ) u n j 1
双曲型守恒方程
u f (u) 0 t x
特点： 沿特征线 d/xd t a， u不变
a f u
特征线未相交—— 总变差不变
特征线相交—— 总变差减小
结论： 单个双曲型方程，总变差不增 （Total Variation Diminishing： TVD）
Copyright by Li Xinliang
分离流—— 对粘性敏感
Von Neumann
(b1x)2I
x
U x
U x
MacCormack
a2x3ቤተ መጻሕፍቲ ባይዱ
|u|c2pU
x
1. 差分格式的分辨率
修正 波数
u(xj ) eikxj
~
xuj
k eikxj x
2. 群速度控制(GVC)
u
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
1
0.5
0
-0.5
-1
0
1
2
3x
4
5
6
u
有效网格点数： 一个波长里 面的网格点数 （PPW: Point per Wavelength)
PPW xk2 x2
差分方程单调性（无振荡）条件： 差分方程 （1）中的系数非负
u n j 1 tu n j u n j 1 2 x u n j 1 R 1 x 2 e (u n j 1 2 u n j u n j 1 )
t/x
u n j 1 ( R e 1 x 1 2 ) u n j 1 ( 1 R 2 e x ) u n j ( R e 1 x 2 1 ) u n j 1
双曲型守恒方程
u f (u) 0 t x
特点： 沿特征线 d/xd t a， u不变
a f u
特征线未相交—— 总变差不变
特征线相交—— 总变差减小
结论： 单个双曲型方程，总变差不增 （Total Variation Diminishing： TVD）
Copyright by Li Xinliang
分离流—— 对粘性敏感
Von Neumann
(b1x)2I
x
U x
U x
MacCormack
a2x3ቤተ መጻሕፍቲ ባይዱ
|u|c2pU
x
计算流体力学(中科院力学所_李新亮)——_经典转载 (1)
0 31 32 G3 (U ) 33 C p T u 31 v 32 w 33 Copyright by Li Xinliang Pr Re z
ui u j i j ), ( x j xi ij (2 ui 2 divV ), i j xi 3
波音787 波音777
Copyright by Li Xinliang 8
CFD 面临的挑战及主要任务：
多尺度复杂流动的数学模型化; 湍流的计算模型； 转捩的预测模型； 燃烧及化学反应模型； 噪声模型…… 可处理间断及多尺度流场的高分辨率、强鲁棒性、高效数值方法； 高精度激波捕捉法； 间断有限元法; …… 可处理复杂外形、易用性强的算法； 复杂外形—— 网格生成工作量大 多块分区算法； 无网格法； 粒子算法；
Mach10 正激波
60°
平板
Copyright by Li Xinliang
5
连续解 微分方程
U ( F Fv ) (G G v ) ( H H v ) 0 t x y z
Mach10 正激波
↓
网格划分 数值方法
60°
平板
↓
解的离散表示 代数方程
↓
Copyright by Li Xinliang
2
第1讲 流体力学基本方程
• 计算流体力学(CFD) 的概念及意义 • 流体力学的基本方程 • 偏微分方程组的类型 重点: 了解N‐S方程的由来及物理含义，熟练掌握N‐S方程 了解偏微方程的基本类型
Copyright by Li Xinliang 3
u v u 2 p u uv U v F1 (U ) uv F2 (U ) v 2 p uw vw w u ( E p ) E v ( E p )
计算流体力学(中科院力学所)_第12讲-不可压流动
V = 0 V 1 2 + V V = p + V t Re p + β V = 0 t V 1 2 + V V = p + V t Re
Vn
Step 1 : 得到 时间步的值 得到n
Step 2: 进行如下内迭代直至收敛
p k +1 p k + β V k = 0 t V k +1 V k 1 2 n + V n V n = p k + V t Re
在v的网格点上离散 交错网格示意图 压力p 压力 速度 u 速度v 速度
p pi , j p = i , j +1 y x i , j +1/ 2
pi , j
ui +1 / 2, j
vi , j +1 / 2
注： 对流项通常采用迎风格式离散
u
Copyright by Li Xinliang
拟压缩性方法 求解压力Poisson方程法 求解压力 方程法 涡流函数法 Simple方法 方法
讲义、 流体中文网） 流体论坛” “ 讲义、课件上传至 (流体中文网） -> “流体论坛” ->“ CFD基础理论 ” 流体中文网 基础理论 讲课录像及讲义上传至网盘 /browse.aspx/.Public
u13 L u1n u 23 L u 2 n u 33 L u3n L L u nn
a j x j 1 + b j x j + c j x j +1 = d j
x j = A j x j +1 + B j
2
Copyright by Li Xinliang
知识回顾
迭代法
2u 2u + = f ( x, y ) x 2 y 2 u = g ( x, y )
Vn
Step 1 : 得到 时间步的值 得到n
Step 2: 进行如下内迭代直至收敛
p k +1 p k + β V k = 0 t V k +1 V k 1 2 n + V n V n = p k + V t Re
在v的网格点上离散 交错网格示意图 压力p 压力 速度 u 速度v 速度
p pi , j p = i , j +1 y x i , j +1/ 2
pi , j
ui +1 / 2, j
vi , j +1 / 2
注： 对流项通常采用迎风格式离散
u
Copyright by Li Xinliang
拟压缩性方法 求解压力Poisson方程法 求解压力 方程法 涡流函数法 Simple方法 方法
讲义、 流体中文网） 流体论坛” “ 讲义、课件上传至 (流体中文网） -> “流体论坛” ->“ CFD基础理论 ” 流体中文网 基础理论 讲课录像及讲义上传至网盘 /browse.aspx/.Public
u13 L u1n u 23 L u 2 n u 33 L u3n L L u nn
a j x j 1 + b j x j + c j x j +1 = d j
x j = A j x j +1 + B j
2
Copyright by Li Xinliang
知识回顾
迭代法
2u 2u + = f ( x, y ) x 2 y 2 u = g ( x, y )
计算流体力学课件-part1
➢模型方程：具有原控制方程的基本特征，但是往往可以 得到精确解，依次来揭示原控制方程的一些数学特征
2024/2/28
19
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的概念
➢完整方程
连续方程
动量方程
能量方程
2024/2/28
20
❖Computational Fluid Dynamics
沿特征线，扰动波的幅值不变，传播速度为c
则在t>0时，传播过程如下图：
2024/2/28
27
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的特征
➢单波方程
➢c>0时，传播沿x正向 ➢C<0时，传播沿x负向 ❖扰动波以有限速度传播是双曲型方程的重要 特征（波形和波幅可能会变化，此处为什么不 变？）
如何表达初始形状三角形
如何存储数据 如何积分
数值积分，HOW？
如何显示结果
TECPLOT
尝试改变几个常数，看看结果有何变化，常数反映了什么？
2024/2/28
22Biblioteka ❖Computational Fluid Dynamics
回顾
控制方程
模型方程
➢NS ➢EULER ➢Impressible NS ➢RANS
➢单波方程可以模拟EULER方程的一些特征
2024/2/28
28
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的特征
2024/2/28
19
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的概念
➢完整方程
连续方程
动量方程
能量方程
2024/2/28
20
❖Computational Fluid Dynamics
沿特征线，扰动波的幅值不变，传播速度为c
则在t>0时，传播过程如下图：
2024/2/28
27
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的特征
➢单波方程
➢c>0时，传播沿x正向 ➢C<0时，传播沿x负向 ❖扰动波以有限速度传播是双曲型方程的重要 特征（波形和波幅可能会变化，此处为什么不 变？）
如何表达初始形状三角形
如何存储数据 如何积分
数值积分，HOW？
如何显示结果
TECPLOT
尝试改变几个常数，看看结果有何变化，常数反映了什么？
2024/2/28
22Biblioteka ❖Computational Fluid Dynamics
回顾
控制方程
模型方程
➢NS ➢EULER ➢Impressible NS ➢RANS
➢单波方程可以模拟EULER方程的一些特征
2024/2/28
28
❖Computational Fluid Dynamics
计算流体流体力学
第二讲 典型模型方程的数学性质
模型方程的特征
计算流体力学课件概述
2018/12/24
13
能源工业：图a是CFD模拟的500 [Mwe]电站煤粉锅炉炉内
燃烧。结果显示了在燃烧器喷流交叉形成的高温、高氧区， NOX生成速率大。
图b显示的是管壳换热器的流线及温度分布。同时考虑管外 流体、管内流体、以及管壁部分的耦合传热。
图c是模拟燃料电池中氧浓度的分布。用户开发了专门的电 化学反应模型，通过催化层的电化学反应速率模拟当地的电 流密度。
2018/12/24 8
CFD拥有包括流体流动、传热、辐射、多相流 、化学反应、燃烧等问题丰富的通用物理模 型；还拥有诸如气蚀、凝固、沸腾、多孔介 质、相间传质、非牛顿流、喷雾干燥、动静 干涉、真实气体等大批复杂
现象的实用模型。
2018/12/24
9
航空航天：图a为模拟美国F22战斗机的结果，图中 显示的是对称面上的马赫数分布。计算共采用了 260万个网格单元。模拟的升力、阻力及力矩系数 都与实验值吻合的很好。 图b是某飞机多段翼周围的压力分布 图c是美国J-31型涡轮喷气发动机的整机模拟。包 括进气道、压缩机、燃烧室、尾喷管四个部分。
图c 模拟出添加剂的浓度分布。改变添加剂的投放位置，用 CFD模拟来优化添加剂浓度分布，以达到最好的防腐效果
2018/12/24
15
冶金工业：图a 模拟的钢水铸造过程，图中显示的是铸造
模具内的流线及表面温度分布 图b是模拟连续加热炉，该炉采用直接加热方式，从图中温度 分布可以看出，钢带有一角的温度过高，这会影响钢产品的 质量。 图c是模拟优化铸造炉内烧嘴的类型和位置。很好地模拟出了 融池内因浮力驱动产生的二次流现象，及诸如回流区、涡、 表面波的发展、温度分布的不均匀性等设计缺陷。
2018/12/24
10
计算流体力学-中国科学院力学所研究生教育网
计算流体力学Computational Fluid Dynamics类型：属性：专业基础课课时/学分：60/3一、预修课程流体力学；空气动力学；偏微分方程数值解法二、内容简介和教学要求本课程包含基础及应用两个部分。
基础部分讲述流体力学方程组及其物理含义，双曲型方程组的数理性质，有限差分法及有限体积法的理论基础及计算方法等；应用部分介绍国内外当前流行的高速流动和不可压缩流动的主要解法，网格生成技术，计算流体力学当前的主要问题、最新计算方法、及发展动向等。
此外还介绍了并行计算的基础知识及湍流计算方法等。
本课程的特点是强调基础、突出应用，希望学生通过学习这一课程，对计算流体力学有一个系统深入的理解，具有一定的理论基础和较强的解决实际问题的能力。
同时，在这一课程中也注意把课程学习和研究所的工作结合起来，使学生到研究所后能立即开展和计算流体力学有关的研究工作。
本课程还将讲授并行程序设计的基本内容，使得学生们能够了解并行程序设计的基本思想及编程方法，并能编制基本的并行计算程序。
为培养学生独立思考和独立工作的能力，本课程采用启发的课程讲习方法，鼓励学生在掌握基础知识的基础上自己动手编制程序，以便加深对计算流体力学本质的理解和增强对实际问题的感性认识。
力求学生们学完该课程后，能够独立编写计算流体力学程序。
三、简要目录第一章引论1.1 计算流体力学及其特征1.2 计算流体力学的发展第二章流体力学方程组及模型方程2.1 流体力学基本方程2.2 模型方程及其数学性质2.3 双曲型方程组的初边值问题2.4 Riemann 间断解第三章有限差分方法3.1 差分方法基本概念3.2 差分方程的有效性及稳定性分析3.3 数值解的精度及分辨率分析3.4 数值解中的耗散效应、色散效应及群速度控制第四章有限体积法4.1有限体积法的基本思4.2 表面积近似及体积积分近似4.3 插值算法4. 4 边界条件处理第五章代数方程的数值求解5.1 直接法5.2 迭代法5.3 分裂算法5.4 近似因式分解算法5.5 多重网格法第六章激波处理与高速流动的数值方法6.1 捕获激波的主要方法6.2 激波捕获精度分析及提高捕获激波精度的方法6.3 Godunov类算法6.4 TVD方法6.5 NND算法6.6 紧致格式及其应用6.7 WENO方法简介6.8 群速度控制格式简介第七章不可压缩粘性流动数值解法7.1 不可压缩流动基本方程组特点和困难7.2 涡量流函数算法7.3 原始变量算法第八章网格生成技术8.1 网格生成技术的基本思想8.2 代数网格法8.3 微分方程法8.4 自适应网格8.5 无结构网格简介第九章 MPI并行程序设计初步9.1 MPI并行程序设计的基本概念9.2 MPI并行程序设计的主要方法9.3 CFD程序的并行优化第十章湍流的数值模拟10.1 工程湍流模式方法10.2 大涡模拟方法10.3 直接数值模拟方法10.4 分离涡模拟方法10.5 转捩的计算四、教材1.计算流体力学（傅德薰、马延文）高等教育出版社， 20022. 计算空气动力学（傅德薰、马延文）国防工业出版社，1996五、参考书1.计算流体力学方法及应用（阎超）北京航空航天大学出版社 20062.计算流体力学（祈孝康、刘儒动、蒋伯诚）国防科大出版社 19893.一维流体力学差分方法（水鸿寿）国防工业出版社 1998教学方式课堂讲授为主,配合课程内结合实例进行编程练习六、考核方式闭卷考试与开卷考试结合。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
生成项最为关键，对湍流粘性系数的 影响最大。 更简单的模型（零方程）， 仅保留了生成项
这是湍流模型的 “主要矛盾”
混合长模型也是这么 假设的
感想： 生成项很多情况下都是最重要的
工资是“生成项”， 消费是“耗散项”，把钱给其他人（家人、亲朋等）是“扩散项”
显然“生成项”是最重要的。
Copyright by Li Xinliang
涡量
Copyright by Li Xinliang
8
外层模型
外 层 特点 1） 间歇性
层流-湍流交替出现
Klebnoff间歇公式（根据实验
得到的经验公式）：
F K( ly ,e) b 1 5 .5 (y /)6 1 1为纯湍流，0为纯层流
特点2） 类似尾迹流动的亏损律
F (y)y [1ex y p /A ()] y
xi Rexjxj
xj
(uiuj)
R u'i u'j
称为Reynolds 应力
Copyright by Li Xinliang
4
3. Reynolds平均N-S方程的求解
Rij u'i u'j
未知量，必须用已知量表 示才能求解
ui 0 xi
ui t
uiuj xj
1 p 2ui xi xjxj
t xj
xi xjxj
时间平均； 空间平均； 系综平均
脉动
ui ui u
0
uiu j
u iu j ( u i u 'i)u j( u 'j) u iu j u 'iu 'j u iu 'j u ju 'i
ui 0 xi
RANS
比N-S方程多了该项
ui t
uiuj xj
1p 1 2ui
程序实现方便
2 方程模型
： k
k
SST
方法2） Reynolds应力模型
给出 R u'i u'j 的控制方程
Copyright by Li Xinliang
5
§ 12.3 常用的涡粘性模型
14.3.1 零方程模型—— Baldwin-Lomax (BL)模型
术语“N方程模型”指计算湍流粘性系数 t 时，使用了N个偏微分方程
y 2 2 2 2v ˆiR e u y 2 2 2 y 2u 2 v ˆ
3. O-S方程的求解 差分法 （Malik的紧致差分法）
(AB)x0
全局法： 解出全部特征值
局部法 F()AB0
Copyright by Li Xinliang
2
§ 12.1 湍流的工程模式理论——RANS
1. 为什么用湍流模型
N-S方程适用于湍流，但其解过于复杂 如果网格分辨率不够，数值解误差较大
例1： 压缩折角流动： 如果网格分辨率 不足，且不用湍流模型，则分离区过大
压缩折角流动
例2： 有攻角机翼流动，如果分辨率不 足，且不用湍流模型，则造成“非物理 分离”
常用方法—— 进行平均，求解平均 量满足的方程
Copyright by Li Xinliang
13
近壁修正—— 保证近壁处湍流粘性系数快速衰减到0
vt v~fv1 最终的湍流粘性系数
3
fv1
, 3cv 31
v ~/v,
cv17.1
衰减函数
1
0.8
0.6
fv1
0.4
0.2
00
10
20
30
40
^v/v
衰减函数 f v1 的图像
Copyright by Li Xinliang
扩散型
xj
jdV
Φnds
内部不会产生， 也不会消失
对于一方程模型（k-模型）
k 3/2 l
由量纲分析得出
Copyright by Li Xinliang
11
12.3.3 一方程模型—— Spalart-Allmaras (S-A)模型
构造原则： 经验 + 量纲分析
湍流场中标量方 程的一般形式：
内层及外层的设定
FF t out k lew bak e
t
(t )in l25 .5 (y /)6 1
边界层厚度 不易计算
用 ymax 估算边 界层厚度
FKle(by)15.5Cykmleabyx61
ym /C ax kleb
Ckleb0.3
F (y)y [1ex y p /A ()] y
零方程模型直接写出 t 的表达式，简便 BL模型是 Plantdl混合长模型的推广
亏
对数律
损
律
外
尾迹亏损律
层 内 湍流核心区 层 过渡区
t
l2
u y
,
l ky
过 渡
混合长模型
区 壁面律
粘性子层区
t 0
内层统一 表达式
A 26
lk[y 1exp y(/A)] 近壁区趋近于0， 远壁区趋近于 k y
(t )in l2
主项： 小涡拉伸 粘性耗散
D D tc 1ku iu l u x li c 2k 2 x l (t/
) x l
1 .3 ,c 1 1 .4 ~ 1 1 .4 ,c 2 5 1 .9 ~ 1 .92
近壁区仍需衰减处理—— “低Reynolds数k-模型”
固壁边界条件： k0,0 与物理情况不符，近壁需要特殊处理
*k
* 0.09
的模化方程：
t u j x j ku 'iu 'j x u ij
2 x j t/
*
k
w x j
生成
耗散 扩散
5/9,3/40
* k
w*
2
y1
固壁边界条件： k 0
10 6 y12
k-模型近壁准确性优于k-模型；
但外层预测准确性不如后者
y1 第1个点到壁面的距离
y较小时趋近于k-模式 y较大时趋近于k-模式
兼具k-及k-模式的优点，是目前应用最广泛的湍流模型之一
Copyright by Li Xinliang
17
§ 12.4 非涡粘模型
涡粘模型的基本假设：
t u'iu'j t xuij u xij 3 2ijk
实际使用时，经 常不考虑该项
不符合物理规律： （涡）粘性是各向同性； 雷诺应力为湍流脉动影响——各向异性
12
2） 耗散项与到壁面的距离有关，越远耗散越小
cw1
fw
v~ d
2
cw 1cb1/k2(1cb2)/
c b 2 0 .6,k 2 0 2 .4,1 2 /3
fw
1
c6 w3
g6
c6 w3
g
grcw 2(r6r)r,S ~kv ~ 2d2
湍流粘性系数越大，耗散越大 离壁面越近，耗散越大
舍弃涡粘假设， 直接针对 t u'i u'j 构造模型，更为合理
写出脉动量
u i
的方程，乘以
u
j
并平均，得到雷诺
应力 u 'i u ' j 的控制方程：
出现三阶统计矩
合理的不 一定好用
D D u i u j t u i u l u x l j u j u l u x l i 2 u x l i u x l j x l u i u j u l 1 p 'ju l i iu l j u x i u l 1 p ' x u i j u x i j
t u j x j P 2 2 ( 1 F 1 ) 2 x k j x j x j t/w x k j
Pw 2
F 1ta n m h m in a 20x .9k 9 y,5y2 0 0 ,C 4k D 2y k2 2
2） k方程模型
ij S ij
湍流扩散—— 以湍流粘性系
数进行的扩散
k t uj x k j u 'iu 'j x u ij xj t/ k x k j
u'i
u'j
txuij
uj xi
32ijk
t
c
k2
k 1
c 0.09~0.11
u'i u'i x j x j
x j j
Copyright by Li Xinliang
15
12.3.5 k-两方程模型
用 方程代替湍流耗散率 方程
t k/
由量纲分析得到
k t u j x k j u 'iu 'j x u ij*k xj t/ k * x k j
/k “比耗散率”
k t uj x k j u 'iu 'j x u ij xj ckk2 x k j
内层 0.3
Fmax
y
ymax
Copyright by Li Xinliang
10
12.3.2 一方程模型 —— k-方程模型
1） 湍动能方程 （不可压缩）
1 k 2 u'i u'i
生成
耗散 粘性扩散
湍流扩散
推导方法
获得扰动量
u
i
的方程，
两端乘以
u
i
并平均即可
k t u j x k j u 'iu 'j x u i j x j x k j x j 1 2 u 'iu 'iu 'j 1 p 'u 'j
固壁
Copyright by Li Xinliang
16
12.3.6 k- SST (Shear-Stress-transport)两方程模式